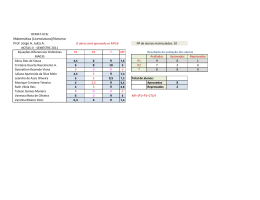
D E M A T - DEPARTAMENTO DE MATEMÁTICA E ESTATÍSTICA
ENGENHARIA DE PRODUÇÃO: Noturno
GEOMETRIA ANALÍTICA E ÁLGEBRA LINEAR
Semestre II – 2010
PROVA NO 2
Nome do aluno:.......................................................................................................................................
1. (3,0 p) Dada a Matriz
 2 1 3
A   0 2 1 
 5 1 3 
Calcule
a. adj  A
b. det  A
c.
A1
2. (4,0 p) Mostre que
 x2
d 
1
dx 
0

1
0  2 x x  1 3   x2


2 x  1 x3    1 2 x  1 x3    0
x
2  0
x
2  0
x  1 3   x2
 
2 3x 2    1
x
2   0
x 1 3 

2 x  1 x3 
1
0 
Observe atentamente a igualdade acima e enuncie a propriedade que ela ilustra.
3. (3,0 p) Mostre que a área do triângulo na Figura 1 é dada pelo determinante
x1
1
x2
2
x3
y1 1
y2 1
y3 1
Figura 1. Triângulo arbitrário.
Prof. Jorge A. Julca A. | www.ufsj.edu.br/demat/jorge.php 10-11-2010