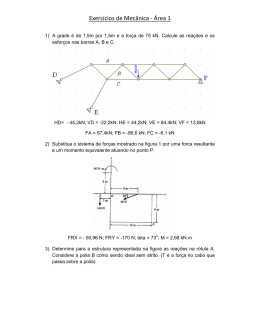
Unisanta - Mecânica Geral - Prof. Damin - Aula n.º _____ - Data ___/____/______
ESTÁTICA DO SISTEMA DE SÓLIDOS.
(Nóbrega, 1980)
Definições.
Ao sistema de sólidos denomina-se estrutura cuja finalidade é suportar
ou transferir forças.
Forças Internas.
São aquelas em que a ação e reação, pertencem ao sistema.
Forças Externas.
• Quando a ação (ou reação) não pertencem ao sistema.
• Para o cálculo das forças externas, o sistema pode ser considerado como um só corpo rígido,
aplicando-lhe, então, as equações da Estática, a esta altura ele pode se apresentar
hiperestático (n.º de incógnitas > n.º de equações).
• Para o cálculo das forças internas, a estrutura é desmembrada e as equações da Estática são
aplicadas a cada membro. Na passagem de um membro para outro deve ser observado
cuidadosamente o Princípio da ação e reação, aqui o sistema todo pode se tornar isostático
(n.º de incógnitas = n.º de equações). É conveniente começar o cálculo pela parte da
qual se conheça o maior número de forças.
Exemplo 9: (Nóbrega, 1980)
Determinar as forças em cada barra. As
barras, o fio e a polia são de pesos
desprezíveis.
A
Apoios C e B do tipo articulação.
Solução:
a
a
E
C
a
D
a
B
P
Página nº 34
Unisanta - Mecânica Geral - Prof. Damin - Aula n.º _____ - Data ___/____/______
Exemplo 10:
(Merian e Kraig, 1999 - e - TP3 2º semestre de 1999)
A estrutura desenhada abaixo é plana e suporta as cargas de 30 lb e 50 lb,
observe que todas as dimensões lineares estão em polegadas, despreze o
peso do pórtico e calcule as forças que atuam em todos os elementos da
estrutura:
Solução:
Página nº 35
Unisanta - Mecânica Geral - Prof. Damin - Aula n.º _____ - Data ___/____/______
Exercício 10:
20 cm
D
A
B
30 cm
Determine a força na
barra BD e a reação
vincular em C, sendo os
apoios D e C articulações.
C
15 cm
60 kg
D
20 cm
Desenhe o Diagrama de Corpo Livre
A
B
30 cm
C
15 cm
Página nº 36
Unisanta - Mecânica Geral - Prof. Damin - Aula n.º _____ - Data ___/____/______
Exercício 11
Determine as reações externas e as forças que atuam em cada barra.
As barras têm pesos desprezíveis.
20 N
4m
2m
C
E
10 N
2m
2m
B
2m
A
D
Página nº 37
Unisanta - Mecânica Geral - Prof. Damin - Aula n.º _____ - Data ___/____/______
TRELIÇAS
(Nóbrega, 1980)
Treliça é a estrutura rígida formada por barras articuladas nas extremidades (nós).
Treliças Simples.
• No plano, são formadas a partir de um triângulo, adicionando-se duas barras para
cada nó.
• No espaço são formadas a partir de um tetraedro, adicionando-se três barras para
cada nó.
• Resolver uma treliça é determinar os esforços em cada barra.
• Após a determinação dos esforços externos (reações vinculares ou de apoios)
considerando a treliça como um sólido, calculam-se os esforços internos, em cada
barra.
Estaticidade:
(Moliterno, 1995)
Pelo exposto anteriormente. uma treliça plana pode sempre ser formada partindo
de 3 barras articuladas nas suas extremidades, e, adicionando-se a estas. duas novas barras para
cada nova articulação.
Seja a Figura acima, admitindo o triângulo A com os nós ou vértices I, II e III,
formado pelas barras 1. 2 e 3. Adicionando as barras 4 e 5. temos o triângulo B e a articulação
ou nó IV, Do mesmo modo, adicionando as barras 6 e 7. temos o triângulo C e a articulação ou
nó V. Procedendo nessa sucessão. formamos a treliça da Figura. Durante essa formação,
observamos que são necessários 3 barras para os 3 primeiros nós, e cada nó seguinte mais duas
barras.
"Uma vez que este processo pode ser estendido indefinidamente, concluímos
também que uma treliça plana pode sempre ser formada. partindo de 3 barras articuladas uma as
outras nas suas extremidades. e, adicionadas a estas, duas novas barras, para cada nova
articulação.''
Nessas Condições:
Sendo b o número de barras (lados dos triângulos) e n número de nós (vértices
dos triângulos)
Página nº 38
Unisanta - Mecânica Geral - Prof. Damin - Aula n.º _____ - Data ___/____/______
Na formação da treliça temos:
3 barras = 3 nós
triângulo A
5 barras = 4 nós
triângulo A+B
7 barras = 5 nós
triângulo A+B+C
11 barras = 7 nós
treliça
Exprimindo-se matematicamente, temos:
b = 3 + 2 × (n − 3)
b = 3+ 2× n − 6
b = 2× n − 3
Treliças Hipostáticas
(Moliterno, 1995)
Há também um caso que a treliça satisfaz a relação b = 2n - 3, mas é estaticamente
indeterminada, pela falta de um painel triangular, portanto falha no esquema (desenho abaixo)
torna-se hipostática.
19 =2 x 11 - 3 = 19
17 =2 x 10 - 3 = 17
Métodos de Cálculo:
Método dos Nós.
Impõe-se o equilíbrio de cada nó, como é feito na Estática do Ponto, partindo-se do nó
com menos incógnitas e passa-se ao nó seguinte através da barra pelo princípio da
Ação e Reação. Para n nós, aplica-se o método (n-1) vezes.
Este método é útil quando as barras não têm peso e não estão sujeitas à forças não
entre as extremidades, pois nestes casos as forças suportadas pelas barras estão ao
longo das mesmas.
Página nº 39
Unisanta - Mecânica Geral - Prof. Damin - Aula n.º _____ - Data ___/____/______
Método das Barras.
Impõe-se o equilíbrio de cada barra e através das equações da Estática, determinam-se
as forças nos nós. É o que deve ser aplicado quando a barra estiver sujeita à forças não
axiais entre as extremidades ou a momentos.
Para uma treliça no plano de n nós, sujeita à forças externas aplicadas somente nos
nós, temos:
2n = b + 3
No espaço a relação se modifica para:
3n = b + 3
Método das Seções.
(Moliterno, 1992 e Merian and Kraige, 1999)
É outro método, derivado do método das barras, que consiste em:
• Determinar as reações vinculares (apoios) da treliça e efetuar um corte que passe
por 3 barras desconhecidas.
• Admite-se que todas as barras sejam solicitadas à tração; assim, as barras
submetidas à tração são positivas e as submetidas à compressão são negativas.
• Calcular a soma das forças verticais e horizontais e a soma dos momentos das
forças exteriores e nas barras em relação ao ponto de interseção de 2 (duas) forças
desconhecidas. Impor condição de equilíbrio nas equações, ou seja, somatória nula.
Exemplo 11: (Gieck, 1979) - Método das Seções: Processo de “Ritter”.
Calcular a força na barra U2, da treliça desenhada abaixo:
Efetuar corte X-X pelas barras O2 - D2 - U2.
Escolher o Ponto C (ponto de interseção) das barras O2 e D2, como ponto de referência para
cálculo dos momentos; assim, os momentos das forças das barras O2 e D2 são nulos.
F3
F2
F1
C
O2
X
F4
O1
D1
F5
U1
FA
Solução:
a
D2
U2
b
X
FB
c
Σ Mc = 0
+ a.Fu2 + b.F2 - c.(FA - F1) = 0
Fu2 = {-b.F2 + c.(FA - F1)}/ a
Logo:
Página nº 40
Unisanta - Mecânica Geral - Prof. Damin - Aula n.º _____ - Data ___/____/______
Análise das Forças nas Barras:
As barras que constituem a estrutura, assim como, os nós, são submetidos a
forças de tração e compressão. Dessa forma, quando se diz, que a força “traciona” a barra o
mesmo acontece com o nó (Princípio da Ação e Reação).
Observe os esquemas abaixo:
Ilustrações do Livro La Estructura de H. Werner Rosenthal - Editora Blume. Espanha. 1975.
Na primeira figura (esquerda) os nós estão sendo tracionados, logo a barra é tracionada.
Na figura à direita os nós são comprimidos, portanto, a barra á comprimida.
Na figura isolada (central) os nós são tracionados = barra tracionada.
Exemplo 12:
Calcular a Força em cada barra da treliça. Todas as barras têm comprimento igual a 1,5 m.
4 kN
6 kN
Página nº 41
Unisanta - Mecânica Geral - Prof. Damin - Aula n.º _____ - Data ___/____/______
Exercício 12:
Determine a força aplicada em cada
elemento da treliça mostrada abaixo, e as
reações
vinculares
em
A
e
B,
respectivamente apoio simples móvel
(bilateral) e apoio fixo (articulação).
2 kN
30º
2m
A
2m
2m
B
Página nº 42