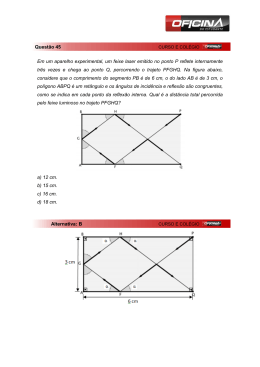
TÓPICOS DE
ANÁLISE E TOPOLOGIA
EM VARIEDADES
Armando Machado
UNIVERSIDADE DE LISBOA
Faculdade de Ciências
Departamento de Matemática
1997
ii
Classificação A.M.S. (1991): 58-01
ISBN: 972-8394-07-1
ÍNDICE
Introdução
v
Capítulo I. Medida e Integração em Variedades
§1. Medida de Lebesgue sobre os espaços euclidianos
§2. Medida de Lebesgue sobre as variedades
§3. Teoremas de Fubini e da mudança de variáveis
§4. Coordenadas polares generalizadas e medidas das esferas
§5. Teorema de Sard
Exercícios
1
1
6
13
18
21
27
Capítulo II. Tópicos de Álgebra Multilinear
§1. Relações entre espaços vectoriais reais e complexos
§2. Espaços de aplicações multilineares
§3. Grupo simétrico e sinal de uma permutação
§4. Aplicações multilineares alternadas. O determinante
§5. Produto exterior
§6. Produto interior
§7. Orientação de espaços vectoriais reais
§8. Elemento de volume e operadores ‡
Exercícios
37
37
39
45
48
57
64
67
79
88
Capítulo III. Formas Diferenciais e Teorema de Stokes
§1. Campos tensoriais e formas diferenciais
§2. Derivada exterior duma forma diferencial
§3. Derivada de Lie duma forma diferencial
§4. Integral duma forma diferencial
§5. Teorema de Stokes
§6. Versões clássicas do teorema de Stokes
§7. Operador prismático e lema de Poincaré
§8. Aplicação à demonstração de resultados topológicos
§9. Teorema de Stokes singular. Ângulo sólido orientado
Exercícios
99
99
107
120
130
133
140
143
149
156
170
Capítulo IV. Introdução à cohomologia de de Rham
§1. Cohomologia de de Rham
§2. Produtos e somas de complexos de cocadeias
§3. Sucessão exacta de Mayer-Vietoris
§4. Cohomologia com suporte compacto
§5. Dualidade de Poincaré
§6. Aplicação à demonstração de resultados topológicos
§7. Invariância topológica da cohomologia
Exercícios
195
195
202
213
225
234
251
261
268
iv
Índice
Índice de Símbolos
293
Índice Remissivo
297
Bibliografia
301
INTRODUÇÃO
Este texto teve a sua origem num curso semestral de Análise em Variedades
destinado aos estudantes do último ano da licenciatura em Matemática da Faculdade de Ciências da Universidade de Lisboa. Uma versão anterior foi publicada
nos Textos e Notas do CMAF em dois volumes há cerca de vinte anos ([13])
mas sucessivas mudanças na organização do curso e na sensibilidade do autor
conduziram à necessidade de uma reformulação de quase todos os assuntos.
De certo modo, o texto constitui uma sequência do livro [10], do qual retoma
as notações e a filosofia: As variedades estudadas são sempre “variedades
concretas”, ou seja, subvariedades de um certo espaço vectorial de dimensão
finita. Como então, a razão por que nos limitamos ao estudo destas está no
desejo de chegarmos tão depressa quanto possível aos resultados interessantes,
sem perder tempo com definições e resultados que, apesar de triviais, demoram a
explicar e são, por vezes, frustrantes. Temos ainda em conta que este texto se
destina também a estudantes cuja área principal de interesse não é a Geometria e
que poderiam ser desencorajados por um tratamento desde o início demasiado
abstracto; o ponto de vista que, para estes, queremos sublinhar é o de que a
Geometria pode ser olhada, em parte, como o estudo da Análise no quadro dos
conjuntos não abertos.
É claro que um estudante não deve terminar a licenciatura em Matemática,
especialmente se os seus interesses se centrarem na área da Geometria, sem
saber o que é uma variedade abstracta, quais os exemplos fundamentais desta
importante estrutura e como, no quadro destas, se generaliza a Geometria
Clássica; trata-se de uma noção fundamental em muitos ramos da Matemática
contemporânea, que é impossível ignorar. Se é verdade que, na estrutura actual
da licenciatura em Matemática é sem dúvida na disciplina em que este curso se
baseia que essa noção deve ser abordada, pensamos que isso pode ser feito de
forma paralela ao desenvolvimento fundamental do curso, dando em cada caso
indicações sumárias sobre o modo como as noções apresentadas no quadro
concreto podem ser adaptadas ao quadro abstracto. De qualquer modo, somos de
opinião que a abordagem, mesmo que resumida, do conceito de variedade
abstracta iria prejudicar a coerência interna deste texto, pelo que preferimos
apresentá-la noutro lugar.
No primeiro capítulo abordamos o estudo da medida de Lebesgue sobre as
variedades contidas num espaço euclidiano. Colocamo-nos, para isso, no quadro
da integração em espaços de medida abstracta, tal como pode ser encontrada, por
exemplo, nos livros de Rudin [16] ou Lang [9] ou no texto [11] do autor.
Supomos, em particular, conhecida a medida de Lebesgue nos borelianos de ‘8 ,
incluindo a fórmula de integração por mudança de variáveis, e passamos daí,
primeiro, de forma trivial, para os borelianos de um espaço euclidiano
vi
Introdução
(independência da escolha da base ortonormada) e depois para os borelianos de
uma subvariedade de um espaço euclidiano. Para estes últimos começamos por
examinar o que se passa com os borelianos pequenos, essencialmente os que
estão contidos no domínio de uma carta, e partimos daí para os borelianos gerais,
tendo em conta o facto de cada um destes ser união de uma família numerável de
borelianos pequenos disjuntos dois a dois. Ao contrário do que se faz
usualmente no quadro da medida como funcional, ou quando se define
directamente o integral duma forma diferencial, as partições da unidade não
jogam aqui nenhum papel. Examinamos em seguida o modo como o teorema de
Fubini e a mudança de variáveis se comportam no quadro da medida de
Lebesgue sobre as variedades e sublinhamos, a propósito, que o quadro natural
para as coordenadas esféricas em dimensão maior ou igual a $ parece ser o de
duas coordenadas, uma real e outra, generalizada, com valores na hipersuperfície
esférica unitária. Terminamos o capítulo com uma demonstração do teorema de
Sard baseada na apresentada por Milnor em [15]. Esse teorema tem muitas
aplicações importantes em Geometria e vai ser utilizado, em particular, no
terceiro e quarto capítulos.
No segundo capítulo examinamos os resultados de Álgebra Multilinear que
são essenciais para o estudo posterior das formas diferenciais. Supomos,
naturalmente, que o leitor tem os conhecimentos básicos de Álgebra Linear que
se aprendem normalmente ao nível do primeiro ano da licenciatura, incluindo o
estudo das matrizes e respectivos determinantes e as propriedades básicas dos
espaços vectoriais com produto interno. Se num ou noutro caso, como a
propósito do sinal de uma permutação ou na discussão da orientação de um
espaço vectorial real, retomamos questões que se poderiam considerar
conhecidas, isso deve-se ao desejo de conservar alguma coerência num assunto
que temos necessidade de examinar um pouco mais profundamente. Todas as
secções deste capítulo são essenciais para o que se segue, com a possível
excepção da que se debruça sobre o produto interior, cujos casos de utilização
podem normalmente ser substituídos por argumentos ad hoc simples.
O terceiro capítulo constitui a parte central deste texto. As formas
diferenciais aparecem essencialmente como funções com valores em espaços de
aplicações multilineares alternadas e na definição do conceito de suavidade e do
operador de diferenciação exterior tira-se partido de modo essencial do espaço
vectorial ambiente, através da utilização de prolongamentos das formas
diferenciais, que são aplicações com valores em espaços vectoriais fixados. Por
exemplo, o diferencial exterior é definido a partir do antissimetrizado da
derivada usual de um prolongamento e não por colagem de definições locais nos
domínios das cartas, a resolução do problema da independência do
prolongamento sendo resolvida através da fórmula alternativa que utiliza campos
vectoriais e os respectivos parênteses de Lie. A derivada de Lie de uma forma
diferencial na direcção de um campo vectorial é definida no mesmo espírito,
apesar de não ser posteriormente utilizada neste trabalho. O integral de um forma
diferencial de grau 8 sobre uma variedade orientada com a mesma dimensão é
definida, utilizando um produto interno auxiliar no espaço ambiente, como o
integral, para a medida de Lebesgue sobre a variedade, da componente da forma
Introdução
vii
diferencial no elemento de volume, o facto de este integral não depender do
produto interno considerado aparecendo então como uma consequência
particular da invariância do integral pelas imagens recíprocas. Provamos, em
seguida, o teorema de Stokes para as formas diferenciais, por redução, como é
usual, ao teorema fundamental do Cálculo Integral, via mudança de variáveis e
um argumento de partição da unidade, e mostra-se como resultados clássicos do
Cálculo Vectorial podem ser obtidos a partir de casos particulares do teorema de
Stokes. O operado prismático é definido, mais uma vez, de modo global, tirando
partido do espaço vectorial ambiente, e é utilizado em seguida na demonstração
do lema de Poincaré. Referem-se ainda as aplicações clássicas do teorema de
Stokes à demonstração de resultados topológicos, como o teorema do ponto fixo
de Brouwer, o teorema da inexistência de retracção da bola sobre a esfera e o
teorema da esfera despenteada, estabelecendo-se, em particular, os teoremas de
aproximação de aplicações contínuas por aplicações suaves, que permitem
passar das versões suaves para as versões contínuas dos resultados referidos.
Enuncia-se, enfim, o teorema de Stokes singular, consequência trivial do
teorema de Stokes original, e aplica-se este resultado ao exame da noção de
ângulo sólido orientado, com aplicações à teoria do grau.
O quarto capítulo retoma o estudo das formas diferenciais, sob o ponto de
vista da Álgebra Homológica, e constitui uma introdução ao estudo da
cohomologia de de Rham das variedades. O lema de Poincaré, estudado no
terceiro capítulo, exprime que, numa variedade contráctil, as formas diferenciais
exactas são exactamente aquelas que são fechadas. Os espaços de cohomologia
de de Rham, que medem o “grau de falsidade” deste resultado no caso de uma
variedade arbitrária, são introduzidos na primeira secção, bem como as
respectivas propriedades de functorialidade, enquadrados numa primeira
aproximação aos conceitos básicos da Álgebra Homológica, e são demonstradas
algumas propriedades elementares, em particular as que relacionam a
cohomologia de grau ! com as componentes conexas da variedade. Na secção 2
é estudada a compatibilidade da cohomologia dos complexos de cocadeias com
os produtos e as somas, depois de apresentar uma definição geral destes, no
espírito da Teoria das Categorias mas sem recorrer explicitamente a esta,
destinada a evitar referências repetitivas às múltiplas identificações necessárias.
Como aplicação, mostra-se que a cohomologia de uma variedade, união disjunta
de uma família de abertos, vai ser um produto das cohomologias desses abertos,
o que, quando se toma como abertos as componentes conexas da variedade,
permite reduzir o cálculo dos espaços de cohomologia ao caso particular das
variedades conexas. Na secção 3, depois de introduzir mais um resultado geral
de Álgebra Homológica, o lema da serpente, é estudada a sucessão exacta de
Mayer-Vietoris, que permite efectuar os primeiros cálculos explícitos de espaços
de cohomologia não triviais, nomeadamente os das esferas W 8 § ‘8" . Na
secção 4 são estudadas as formas diferenciais com suporte compacto bem como
a versão da cohomologia de de Rham a elas associada, versão que se revela
extremamente importante para o estudo das variedades não compactas, mas que
também é útil, como instrumento auxiliar, mesmo quando o objectivo do estudo
se centra nas variedades compactas. Tendo em vista aplicações posteriores é
viii
Introdução
calculada explicitamente a cohomologia de de Rham com suporte compacto dos
espaços ‘8 e, mais geralmente, dos produtos de intervalos abertos. Na secção 5
é estudado o teorema de dualidade de Poincaré, que mostra que cada espaço de
cohomologia de de Rham de uma variedade de dimensão 7, orientada e sem
bordo, é isomorfo ao dual do espaço de cohomologia com suporte compacto, de
grau complementar. A técnica de demonstração que seguimos é a que
encontrámos em [7] e baseia-se num lema “algo misterioso”, mas que se revela
útil em muitas aplicações. Como instrumentos auxiliares, é estudado um
resultado importante de Álgebra Homológica, o lema dos cinco, a cohomologia
com suporte compacto de uma variedade, união disjunta de subconjuntos
abertos, é identificada como uma soma das cohomologias com suporte compacto
desses abertos e é estudada uma versão da sucessão exacta de Mayer-Vietoris
para os espaços de cohomologia com suporte compacto. Entre as outras
aplicações do lema atrás referido, que temos pena de não ter tido possibilidade
de apresentar, citamos o teorema de de Rham, que relaciona a cohomologia de
de Rham de uma variedade com o dual da sua homologia singular, uma noção do
âmbito da Topologia Algébrica, assim como o teorema de Küneth, que permite
estudar a cohomologia de um produto de variedades; a primeira ter-nos-ia
exigido um estudo prévio dos conceitos básicos da Homologia Singular e a
segunda imporia um estudo da noção geral de produto tensorial, em ambos os
casos aumentando a dimensão deste trabalho para além do que estava nos nossos
planos. Na secção 6 aplicam-se os resultados anteriormente obtidos, em
particular os que respeitam à cohomologia com suporte compacto, à
demonstração de resultados importantes de natureza topológica como o teorema
de Jordan-Brouwer e o teorema de Brouwer da invariância do domínio. Por fim,
na secção 7, utilizando as vizinhanças tubulares das variedades compactas sem
bordo e, mais geralmente dos subconjuntos compactos de uma variedade sem
bordo, assim como técnicas de aproximação de aplicações contínuas por
aplicações suaves, é estabelecida a invariância topológica da cohomologia de de
Rham das variedades compactas sem bordo. A invariância topológica no quadro
mais geral, que não estudamos aqui, poderia ser obtida com técnicas de
aproximação mais elaboradas (cf., por exemplo, [8]) ou, alternativamente,
através do estudo do teorema de de Rham.
No fim de cada capítulo é proposta uma lista mais ou menos longa de
exercícios, destinados a testar a compreensão dos assuntos estudados e a
apresentar outros que complementam aqueles.
CAPÍTULO I
Medida e Integração em Variedades
§1. Medida de Lebesgue sobre os espaços euclidianos.
Neste capítulo vamos supor conhecida a noção de medida positiva sobre
uma 5 -álgebra de partes dum certo conjunto, assim como as propriedades
gerais de tais medidas e dos integrais correspondentes. De um modo geral,
as 5 -álgebras que utilizaremos serão as 5 -álgebras dos borelianos de
espaços topológicos. Vamos relembrar especialmente os dois resultados
seguintes, que serão utilizados inúmeras vezes ao longo do capítulo:
I.1.1 Sejam \ um espaço topológico, . uma medida definida nos borelianos de
\ e 0 À \ Ä Ò!ß _Ó uma função mensurável, que permitimos possa tomar o
valor _. Fica então definida uma nova medida .0 nos borelianos de \ ,
pela fórmula
.0 ÐEÑ œ ( 0 ÐBÑ . .ÐBÑ.
E
Além disso, para cada função mensurável 1À \ Ä Ò!ß _Ó,
( 1ÐBÑ . .0 ÐBÑ œ ( 1ÐBÑ0 ÐBÑ . .ÐBÑ,
\
\
uma fórmula idêntica sendo válida, no caso em que a função 0 toma valores
em Ò!ß _Ò e a função 1 é integrável e toma valores em ‘ ou, mais
geralmente, num espaço vectorial I de dimensão finita.
s espaços topolóI.1.2 (Teorema trivial de mudança de variáveis) Sejam \ e \
s , respectivagicos e . e .
s medidas definidas nos borelianos de \ e de \
s um homeomorfismo compatível com as medidas, no
mente. Seja :À \ Ä \
sentido que, para cada boreliano E § \ , se tenha .
sÐ:ÐEÑÑ œ .ÐEÑ. Para
s Ä Ò!ß _Ó, tem-se então
cada função mensurável 1À \
sÐCÑ œ ( 1Ð:ÐBÑÑ . .ÐBÑ,
( 1ÐCÑ . .
s
\
\
uma fórmula idêntica sendo válida no caso em que a função 1 é integrável e
toma valores em ‘ ou, mais geralmente, num espaço vectorial I de
dimensão finita.
2
Cap. I. Medida e Integração em Variedades
Vamos também supor conhecidas as propriedades gerais da medida de
Lebesgue .8 , definida nos borelianos de ‘8 , em particular, os resultados
que enunciamos em seguida, sobre a mudança de variáveis:
I.1.3 Suponhamos que 0À ‘8 Ä ‘8 é um isomorfismo. Notamos então -0 o valor
absoluto do determinante da matriz de 0 na base canónica de ‘8 , e dizemos
que -0 é o coeficiente de dilatação do isomorfismo 0. Esta designação é
justificada pelo facto de, para cada boreliano E § ‘8 , ter-se
.8 Ð0ÐEÑÑ œ -0 .8 ÐEÑ.
Repare-se que, como se reconhece imediatamente, é suave a aplicação de
P3=9 Б8 à ‘8 Ñ em Ó!ß _Ò, que a cada 0 associa -0 .
I.1.4 Sejam Y § ‘8 e Z § ‘8 dois abertos e :À Y Ä Z um difeomorfismo de
classe G " . Para cada B − Y , tem-se então que H:B é um isomorfismo de ‘8
sobre ‘8 , que vai ter um coeficiente de dilatação -H:ÐBÑ , e ficamos portanto
com uma aplicação contínua de Y em Ó!ß _Ò, que a cada B associa -H:ÐBÑ .
Tem-se então, para cada boreliano E § Y ,
.8 Ð:ÐEÑÑ œ ( -H:ÐBÑ . .8 ÐBÑ.
E
I.1.5 Sejam Y § ‘8 e Z § ‘8 dois abertos e :À Y Ä Z um difeomorfismo de
classe G " . Para cada aplicação mensurável 1À Z Ä Ò!ß _Ó, tem-se então
( 1ÐCÑ . .8 ÐCÑ œ ( 1Ð:ÐBÑÑ-H:ÐBÑ . .8 ÐBÑ,
Z
Y
a mesma fórmula sendo válida no caso em que 1 é uma função integrável
com valores em ‘ ou, mais geralmente, num espaço vectorial I de dimensão
finita.
Repare-se que I.1.5 se pode deduzir muito facilmente a partir de I.1.4, por
utilização dos resultados I.1.1 e I.1.2 enunciados atrás. Com efeito,
podemos definir uma medida .w nos borelianos de Y , pondo
.w ÐEÑ œ .8 Ð:ÐEÑÑ, tendo-se então que :À Y Ä Z é automaticamente um
homeomorfismo compatível, quando se considera em Y a medida .w e em
Z a medida .8 . Resulta então de I.1.4 que .w é também a medida definida
pela função mensurável positiva B È -H:ÐBÑ . A igualdade de I.1.5 resulta
então de que ambos os membros são iguais a 'Y 1Ð:ÐBÑÑ ..w ÐBÑ. Um
raciocínio deste tipo vai ser repetido em várias situações ao longo deste
capítulo.
Seja I um espaço vectorial de dimensão 8. Sabemos que I tem uma
topologia canónica, a saber, a associada a qualquer das suas normas, pelo
que faz sentido falar dos borelianos de I . Além disso, se 0À I Ä ‘8 é um
isomorfismo, então 0 é também um homeomorfismo, pelo que um
conjunto E § I é boreliano se, e só se, 0ÐEÑ é um boreliano de ‘8 . Uma
§1. Medida de Lebesgue sobre os espaços euclidianos
3
tentativa natural para definir uma medida de Lebesgue .I , nos borelianos
de I , seria a de pôr .I ÐEÑ œ .8 Ð0ÐEÑÑ, mas uma tal tentativa não
resulta, uma vez que o segundo membro da igualdade anterior dependerá,
em geral, do isomorfismo 0 escolhido. Para definir uma medida de
Lebesgue nos borelianos de I , vamos ser obrigados a fixar em I uma
estrutura suplementar, a saber, um produto interno (para medir é
necessário uma réguaá ), por outras palavras, vamos supor que I é um
espaço euclidiano. Note-se que, quando considerarmos ‘8 como espaço
euclidiano, estará implícito, salvo aviso em contrário, que o produto
interno considerado é o canónico, isto é, aquele para o qual a base
canónica é ortonormada.
I.1.6 (Lema) Se 0À ‘8 Ä ‘8 é um isomorfismo ortogonal, então -0 œ ".
Dem: Seja F § ‘8 a bola fechada de centro ! e raio ". O facto de F ser um
conjunto compacto, de interior não vazio, implica que .8 ÐFÑ é finito e não
nulo. Uma vez que 0ÐFÑ œ F , donde .8 ÐFÑ œ -0 .8 ÐFÑ, concluímos que
-0 œ ". Alternativamente, pode-se também notar que a matriz de 0 na base
canónica de ‘8 é uma matriz ortogonal, portanto com determinante igual a "
ou ".
I.1.7 Sejam I um espaço euclidiano e 0ß (À I Ä ‘8 dois isomorfismos
ortogonais. Para cada boreliano E § I tem-se então .8 Ð0ÐEÑÑ œ .8 Ð(ÐEÑÑ,
pelo que fica bem definida uma medida .I , nos borelianos de I , a que
chamaremos medida de Lebesgue sobre I , pela igualdade
.I ÐEÑ œ .8 Ð0ÐEÑÑ, onde 0À I Ä ‘8 é um isomorfismo ortogonal arbitrário.
Em particular, escolhendo para 0 o isomorfismo idêntico de ‘8 , vemos que a
medida de Lebesgue do espaço euclidiano ‘8 é precisamente .8 .
Dem: É uma consequência imediata do facto de se ter (ÐEÑ œ ( ‰ 0" Ð0ÐEÑÑ,
onde ( ‰ 0" À ‘8 Ä ‘8 é um isomorfismo ortogonal.
I.1.8 No caso em que I é um espaço vectorial de dimensão ! (com o único
produto interno possível!), definimos a medida de Lebesgue sobre I , como
sendo a medida de contagem, isto é, a definida por .I ÐgÑ œ ! e
.I ÐÖ!×Ñ œ ". Esta definição pode ser olhada como um caso particular da
definição geral precedente, por quem não sinta vertigens ao tentar descobrir o
que é a medida de Lebesgue em ‘! .
I.1.9 Sejam I e J espaços euclidianos e 0À I Ä J um isomorfismo. Existe
então um, e um só, número real -0 ! (a que chamaremos coeficiente de
dilatação de 0), tal que, para cada boreliano E § I , .J Ð0ÐEÑÑ œ -0 .I ÐEÑ.
Esse número real pode ser obtido do seguinte modo: Escolhem-se
isomorfismos ortogonais !À I Ä ‘8 e " À J Ä ‘8 , e então -0 é então o
coeficiente de dilatação do isomorfismo " ‰ 0 ‰ !" À ‘8 Ä ‘8 .
Dem: A unicidade de um real -0 , verificando a condição do enunciado, é
uma consequência trivial de existirem em I borelianos de medida finita e
não nula (uma vez que existem em ‘8 ). Quanto à existência de -0 naquelas
condições, basta fixarmos isomorfismos ortogonais !À I Ä ‘8 e
4
Cap. I. Medida e Integração em Variedades
" À J Ä ‘8 , e verificar, o que é trivial, que o coeficiente de dilatação do
isomorfismo " ‰ 0 ‰ !" , de ‘8 sobre ‘8 , verifica as referidas condições.
I.1.10 Sejam I , J e K espaços euclidianos. Tem-se então:
a) Se 0À I Ä J é um isomorfismo ortogonal, então -0 œ ", em particular, o
coeficiente de dilatação de M.I À I Ä I é igual a ";
b) Se 0À I Ä J e (À J Ä K são isomorfismos, então -(‰0 œ -( -0 ;
c) Se 0À I Ä J é um isomorfismo, então -0" œ "Î-0 .
Dem: A alínea a) resulta de que, se 0À I Ä J é um isomorfismo ortogonal,
então, escolhendo isomorfismos ortogonais !À I Ä ‘8 e " À J Ä ‘8 , o
isomorfismo " ‰ 0 ‰ !" , de ‘8 sobre ‘8 , é também ortogonal. Quanto à
alínea b), escolhemos em I um boreliano de medida finita e não nula (tais
conjuntos existem em ‘8 , e portanto também em I ), e notamos que
-(‰0 .I ÐEÑ œ .K Ð(Ð0ÐEÑÑÑ œ -( .J Ð0ÐEÑÑ œ -( -0 .I ÐEÑ.
donde -(‰0 œ -( -0 . A alínea c) resulta imediatamente das alíneas a) e b).
I.1.11 Se I e J são espaços euclidianos, podemos considerar no espaço
vectorial I ‚ J um produto interno, definido por
ØÐBß CÑß ÐBw ß Cw ÑÙ œ ØBß Bw Ù ØCß Cw Ù.
Salvo aviso em contrário, será este o produto interno que se considera em
I ‚ J , quando se olha para este espaço como espaço euclidiano. Observe-se
que, quando se identifica o produto cartesiano ‘7 ‚ ‘8 a ‘78 , da maneira
usual, o produto interno canónico de ‘78 é precisamente o associado aos
produtos internos de ‘7 e de ‘8 .
I.1.12 Se I e J são espaços euclidianos, então a medida de Lebesgue .I‚J , nos
borelianos de I ‚ J , é a medida produto das medidas .I e .J .
Dem: Uma vez que I e J , com as medidas de Lebesgue, .I e .J , nos
respectivos borelianos, são espaços de medida 5 -finitos (por isso acontecer
aos espaços ‘8 ), tudo o que temos que verificar é que, quaisquer que sejam
os borelianos E § I e F § J , tem-se .I‚J ÐE ‚ FÑ œ .I ÐEÑ ‚ .J ÐFÑ.
Consideremos, para isso, isomorfismos ortogonais !À I Ä ‘8 e " À J Ä ‘8 ,
e reparemos que vem também ortogonal o isomorfismo -À I ‚ J Ä ‘78 ,
definido por ß
-ÐBß CÑ œ Ð!" ÐBÑß á ß !7 ÐBÑß "" ÐCÑß á ß "8 ÐCÑÑ,
isomorfismo que não é mais do que a composição do isomorfismo ! ‚ " , de
I ‚ J sobre ‘7 ‚ ‘8 , com o isomorfismo canónico ‘7 ‚ ‘8 Ä ‘78 .
Tem-se então que -ÐE ‚ FÑ é a imagem de !ÐEÑ ‚ " ÐFÑ pelo isomorfismo
canónico, pelo que
.I‚J ÐE ‚ FÑ œ .78 Ð-ÐE ‚ FÑÑ œ .7 Ð!ÐEÑÑ.8 Ð" ÐFÑÑ œ .I ÐEÑ.J ÐFÑ,
como queríamos.
§1. Medida de Lebesgue sobre os espaços euclidianos
5
seJ
s , e os isomorfismos !À I Ä I
s
I.1.13 Sejam os espaços euclidianos I , J , I
s
s
s
e " À J Ä J . Considerando então o isomorfismo ! ‚ " À I ‚ J Ä I ‚ J ,
tem-se -!‚" œ -! ‚ -" .
Dem: Sejam E § I e F § J borelianos de medida finita e não nula. Tem-se
então
-!‚" .I ÐEÑ.J ÐFÑ œ -!‚" .I‚J ÐE ‚ FÑ œ .I‚J
s s Ð! ‚ " ÐE ‚ FÑÑ œ
œ .I‚J
s s Ð!ÐEÑ ‚ " ÐFÑÑ œ .I
s Ð!ÐEÑÑ.J
s Ð" ÐFÑÑ œ -! -" .I ÐEÑ.J ÐFÑ.
Na prática, interessará ter processos que permitam determinar o
coeficiente de dilatação de um isomorfismo entre espaços euclidianos,
sem fazer explicitamente a composição do isomorfismo com
isomorfismos para os espaços ‘8 . É nesse sentido que demonstramos os
dois resultados seguintes, o primeiro de enunciado mais simples e
justificação mais directa, mas o segundo de utilização bastante mais
frequente.
I.1.14 Sejam I e J espaços euclidianos e 0À I Ä J um isomorfismo. Dadas
duas bases ortonormadas, B" ß á ß B8 de I e C" ß á ß C8 de J , tem-se então
que o coeficiente de dilatação -0 é igual ao valor absoluto do determinante da
matriz de 0 naquelas bases.
Dem: Sejam !À I Ä ‘8 e " À J Ä ‘8 os isomorfismos ortogonais, que
aplicam as bases ortonormadas consideradas na base canónica de ‘8 . É então
imediato constatar que a matriz de 0 nas bases consideradas é igual à matriz
do isomorfismo " ‰ 0 ‰ !" À ‘8 Ä ‘8 nas bases canónicas, pelo que a
asserção resulta de I.1.9 e de I.1.3.
I.1.15 Sejam I e J espaços euclidianos e 0À I Ä J um isomorfismo. Seja
B" ß á ß B8 uma base ortonormada de I , e seja, para cada " Ÿ 3ß 4 Ÿ 8,
13ß4 œ Ø0ÐB3 Ñß 0ÐB4 ÑÙ.
Tem-se então que o coeficiente de dilatação -0 é a raiz quadrada do determinante da matriz dos 13ß4 (em particular, este determinante é estritamente positivo).
Dem: Seja C" ß á ß C8 uma base ortonormada de J , e sejam +34 os elementos
da matriz de 0 nas bases consideradas, isto é, os definidos por
0ÐB4 Ñ œ " +3ß4 C3 .
3
Pelo resultado anterior, sabemos que -0 é o valor absoluto do determinante da
matriz E de elementos +3ß4 . Vem
6
Cap. I. Medida e Integração em Variedades
14ß5 œ Ø0ÐB4 Ñß 0ÐB5 ÑÙ œ " +3ß4 +3ß5 ,
3
pelo que o elemento 14ß5 é o elemento da linha 4 e da coluna 5 da matriz
produto E‡ ‚ E, onde E‡ nota a transposta da matriz E. Se atendermos ao
facto que
detÐE‡ ‚ EÑ œ detÐE‡ Ñ ‚ detÐEÑ œ detÐEÑ# ,
concluímos finalmente que o determinante da matriz dos 14ß5 é igual a -0# .
§2. Medida de Lebesgue sobre as variedades.
O nosso objectivo nesta secção é o de definir a medida de Lebesgue dos
borelianos de uma subvariedade Q , de dimensão 7, de um espaço
euclidiano I , noção que vai generalizar a medição de comprimentos
sobre curvas ou de áreas sobre superfícies. Antes de examinarmos o modo
como esta se define, e por uma questão técnica relacionada com a
possibilidade de tratar o caso das variedades com bordo, teremos
necessidade de uma versão ligeiramente mais geral dos resultados I.1.4 e
I.1.5, em que os abertos Y e Z são substituidos por borelianos totais.
Comecemos por enunciar um lema de Teoria da Medida, que será
utilizado mais de uma vez.
I.2.1 (Lema) Sejam I um espaço vectorial de dimensão finita, \ § I um
boreliano e . e .w duas medidas definidas nos borelianos de \ , tais que, para
cada + − \ , exista um aberto Y de \ , com + − Y , tal que, para cada
boreliano E § Y , .ÐEÑ œ .w ÐEÑ (as medidas coincidem localmente).
Tem-se então . œ .w .
Dem: Para cada + − \ , seja Y+ um aberto de \ , com + − Y+ , tal que, para
cada boreliano E § Y+ , .ÐEÑ œ .w ÐEÑ. Chamemos pequenos aos borelianos
E de \ , que estão contidos nalgum dos conjuntos Y+ . Vamos ver que \ é
uma união numerável de abertos pequenos \8 , com 8 − . Para isso,
consideremos uma base numerável de abertos para \ (uma vez que ‘8 tem
uma base numerável de abertos, o mesmo vai acontecer a I , e portanto
também a todo o subconjunto de I ) e tomemos para sucessão \8 uma sucessão dos elementos dessa base de abertos que estão contidos nalgum dos Y+ .
O facto de a união dos \8 ser efectivamente \ vem de que, para cada
+ − \ , vai existir um aberto da base, contendo + e contido em Y+ . Dado um
boreliano E § \ arbitrário, podemos agora considerar os borelianos
E8 § E, onde E8 vai ser o conjunto dos pontos de E, que estão em \8 , mas
§2. Medida de Lebesgue sobre as variedades
7
não estão em nenhum dos \5 , com 5 8; é imediato constatar que E vai ser
a união dos borelianos E8 , que são pequenos e disjuntos dois a dois, donde,
finalmente,
.ÐEÑ œ " .ÐE8 Ñ œ " .w ÐE8 Ñ œ .w ÐEÑ.
8
8
I.2.2 Dado um espaço vectorial I , de dimensão finita, vamos dizer que um
conjunto \ § I é total se, para cada B − \ , o espaço vectorial tangente
XB Ð\Ñ é igual a I . Como exemplos de conjuntos totais, temos:
a) Se Y § I é aberto, então Y é total;
b) Mais geralmente, se Y é aberto num sector W de I , então Y é total;
c) Mais geralmente ainda, se I tem dimensão 7 e se Q § I é uma
variedade com a mesma dimensão 7, eventualmente com bordo, então Q é
total.
I.2.3 (Generalização de I.1.4) Sejam \ß ] § ‘8 dois borelianos totais e
:À \ Ä ] um difeomorfismo de classe G " . Para cada boreliano E § \ ,
tem-se então
.8 Ð:ÐEÑÑ œ ( -H:ÐBÑ . .8 ÐBÑ,
E
em que a função integranda do segundo membro é uma função contínua de X
em Ó!ß _Ò.
s um aberto de ‘8 , contendo \ , e :
s Ä ‘8 um prolongaDem: Sejam Y
sÀ Y
"
mento de classe G de :. É claro que, para cada B, H:B é uma restrição de
H:
sB , pelo que, uma vez que \ é total, H:B œ H:
sB , em particular, a
8
8
s
continuidade da aplicação H:
À
Y
Ä
PÐ
‘
à
‘
Ñ
implica
a continuidade da
s
aplicação de \ em Ó!ß _Ò, que a B associa -H:ÐBÑ . Para cada + − \ ,
H:
s+ œ H:+ é um isomorfismo de ‘8 sobre ‘8 , pelo que o teorema da
função inversa garante a existência de um aberto Y de ‘8 , com + − Y , tal
que a restrição de :
s a Y seja um difeomorfismo de Y sobre um aberto Z de
‘8 . Aplicando I.1.4 a esta restrição, concluímos que, para cada boreliano
E § \ Y , a igualdade do enunciado é verificada. Uma vez que ambos os
membros da igualdade do enunciado definem medidas sobre os borelianos de
\, o resultado é agora uma consequência do lema I.2.1.
I.2.4 (Generalização de I.1.5) Sejam \ß ] § ‘8 dois borelianos totais e
:À \ Ä ] um difeomorfismo de classe G " . Para cada aplicação mensurável
1À ] Ä Ò!ß _Ó, tem-se então
( 1ÐCÑ . .8 ÐCÑ œ ( 1Ð:ÐBÑÑ-H:ÐBÑ . .8 ÐBÑ,
]
\
a mesma fórmula sendo válida no caso em que 1 é uma função integrável
com valores em ‘ ou, mais geralmente, num espaço vectorial de dimensão
8
Cap. I. Medida e Integração em Variedades
finita.
Dem: Tal como nas observações que foram feitas a seguir a I.1.5,
consideramos a medida .w , sobre os borelianos de \ , definida por
.w ÐEÑ œ .8 Ð:ÐEÑÑ, tendo-se então que o difeomorfismo : é, por definição,
compatível, quando se considera em \ a medida .w e em ] a medida .8 .
Resulta de I.2.3 que .w é também a medida definida pela função mensurável
positiva B È -H:ÐBÑ , pelo que a igualdade do enunciado resulta de que, por
I.1.1 e I.1.2, ambos os membros são iguais a '\ 1Ð:ÐBÑÑ . .w ÐBÑ.
I.2.5 Sejam I um espaço vectorial de dimensão finita e Q § I uma variedade
de dimensão 7. Tem-se então que Q é reunião de uma família numerável de
compactos, em particular, Q é um boreliano de I .
Dem: Vamos começar por mostrar que, se Z é um aberto num sector W dum
espaço vectorial J , de dimensão 7, então Z é reunião de uma família
numerável de compactos. Para isso definimos, para cada natural 8,
O8 œ ÖB − W ± .ÐBß W Ï Z Ñ "
e mBm Ÿ 8×,
8
omitindo a primeira condição no caso em que Z œ W , e reparamos que Z
vem união dos O8 e que estes são compactos, por serem limitados e fechados
em W , logo também em I .
Para cada + − Q , seja agora :+ À Y+ Ä Z+ um difeomorfismo, com + − Y+ ,
Y+ aberto de Q e Z+ aberto num sector dum espaço vectorial de dimensão
7. Consideremos uma base numerável de abertos de Q e notemos [8 uma
numeração dos abertos da base que estão contidos nalgum dos Y+ . É então
fácil constatar que Q é a união dos [8 e que cada [8 é homeomorfo a um
aberto dum sector dum espaço vectorial de dimensão 7, sendo portanto uma
reunião numerável de compactos, de onde se deduz que Q é também um
reunião numerável de compactos. O facto de Q ser um boreliano de I
resulta agora de que os compactos de Q vão ser fechados em I , logo
borelianos.
I.2.6 Sejam I um espaço vectorial de dimensão finita e Q § I uma variedade
de dimensão 7. Vamos dizer que um boreliano E § Q é pequeno, se existir
um aberto Y de Q , com E § Y , um boreliano Z de ‘7 , e um difeomorfismo de classe G " :À Z Ä Y . Repare-se que Z é então,
automaticamente, um boreliano total de ‘7 , visto que, para cada B − Z ,
XB ÐZ Ñ vai ser um subespaço vectorial de ‘7 , isomorfo a X:ÐBÑ ÐQ Ñ, que tem
dimensão 7, pelo que XB ÐZ Ñ tem dimensão 7, e portanto XB ÐZ Ñ œ ‘7 .
I.2.7 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão 7.
s de Q ,
Seja E § Q um boreliano pequeno. Sejam os abertos Y e Y
7
s de ‘ , e os difeomorfismos de classe G "
contendo E, os borelianos Z e Z
s ÄY
s . Sendo então F œ :" ÐEÑ e F
sœ:
:À Z Ä Y e :
sÀ Z
s" ÐEÑ, tem-se
§2. Medida de Lebesgue sobre as variedades
9
( -H:ÐBÑ . .7 ÐBÑ œ ( -H:sÐBÑ . .7 ÐBÑ,
s
F
F
s,
onde as funções integrandas são aplicações contínuas, definidas em Z e Z
respectivamente, e com valores em Ó!ß _Ò.
Dem: Considerando eventualmente um prolongamento de classe G " de : a
um aberto de ‘7 , contendo Z , vemos que é contínua a aplicação de Z em
PБ7 à IÑ, que a B associa H:B , pelo que a caracterização do coeficiente de
dilatação, dada em I.1.15, mostra-nos que é contínua a aplicação de Z em
Ó!ß _Ò, que a B associa -H:ÐBÑ .
s de Q
Reparemos agora que, substituindo eventualmente os abertos Y e Y
s
por Y Y , e as aplicações : e :
s por restrições convenientes, ficamos redus.
zidos a provar a igualdade do enunciado no caso particular em que Y œ Y
"
"
s
Tem-se então que : ‰ :
sÀ Z Ä Z é um difeomorfismo de classe G entre
borelianos totais de ‘7 , ao qual podemos aplicar I.2.%. Notando então ;^s a
função característica de um conjunto ^ , obtemos
( -H:ÐCÑ . .7 ÐCÑ œ ( ;Fs ÐCÑ-H:ÐCÑ . .7 ÐCÑ œ
F
œ ( ;Fs Ð:
s
Z
Z
"
‰:
sÐBÑÑ-H:Ð:" ‰:sÐBÑÑ -HÐ:" ‰:sÑÐBÑ . .7 ÐBÑ œ
œ ( ;Fs ÐBÑ -H:Ð:" ‰:sÐBÑщÐHÐ:" ‰:sÑÐBÑÑ . .7 ÐBÑ œ
s
Z
œ ( -H:sÐBÑ . .7 ÐBÑ.
s
F
Repare-se que, no resultado anterior, quando falamos no coeficiente de
dilatação de H:ÐBÑ, estamos a referir-nos ao coeficiente de dilatação de
um isomorfismo de ‘7 , com a sua estrutura euclideana canónica, sobre o
subespaço vectorial X:ÐBÑ ÐQ Ñ de I , com o produto interno induzido pelo
produto interno deste espaço euclidiano.
I.2.8 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão 7.
Para cada boreliano pequeno E § Q , define-se então a sua medida de
Lebesgue (relativa a Q ), .Q ÐEÑ, pela fórmula
.Q ÐEÑ œ ( -H:ÐBÑ . .7 ÐBÑ,
F
onde :À Z Ä Y é um difeomorfismo de classe G " , com Z boreliano de ‘7 e
Y aberto de Q , contendo E, e F œ :" ÐEÑ.
Repare-se que é o resultado I.2.7 que garante que a definição anterior é
legítima, isto é, que o resultado obtido não depende do difeomorfismo :
10
Cap. I. Medida e Integração em Variedades
escolhido. Pelo contrário, é evidente que a medida de Lebesgue nos
borelianos pequenos de Q vai depender do produto interno fixado no
espaço ambiente I .
I.2.9 Sejam I um espaço euclidiano de dimensão 7, e olhemos para I como
variedade de dimensão 7. Tem-se então que todo o boreliano E § I é
pequeno, e a sua medida de Lebesgue .I ÐEÑ é a mesma, quer se considere I
como espaço euclidiano ou como variedade.
Dem: Considerar um isomorfismo ortogonal :À ‘7 Ä I .
I.2.10 (Lema) Sejam I um espaço euclidiano e Q § I uma variedade de
dimensão 7. Dado um boreliano pequeno \ § Q , tem-se então que a
restrição da aplicação .Q ao conjunto dos borelianos contidos em \ é uma
medida sobre os borelianos de \ .
Dem: Trata-se de uma demonstração imediata, a partir da definição da
medida de Lebesgue dos borelianos pequenos.
I.2.11 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão 7.
Tem-se então:
a) Todo o boreliano E de Q é união de uma família numerável de borelianos
pequenos disjuntos dois a dois;
b) Existe uma, e uma só, medida .Q , sobre os borelianos de Q , que nos
borelianos pequenos tome o valor definido em I.2.) (dizemos que .Q é a
medida de Lebesgue da variedade Q , associada ao produto interno de I ).
Dem: Para cada + − Q , seja Y+ um aberto de Q , com + − Y+ , que seja
difeomorfo a um aberto num sector de ‘7 , o qual vai ser, em particular, um
boreliano de ‘7 . Fixemos uma base numerável de abertos de Q e notemos
[8 uma numeração dos abertos desta base que estão contidos nalgum dos
Y+ . É então fácil constatar que Q é a união dos abertos pequenos [8 . Dado
o boreliano E § Q , podemos, para cada natural 8, considerar o conjunto E8
dos B − E, que estão em [8 , mas não estão em nenhum dos [3 com 3 8,
tendo-se então que os E8 são borelianos pequenos disjuntos dois a dois e que
E é a união dos E8 . Ficou portanto provada a alínea a) do enunciado. A
asserção de unicidade da alínea b) é uma consequência de a), visto que, se o
boreliano E é a união de uma família numerável de borelianos pequenos, E8 ,
disjuntos dois a dois, então não pode deixar de ser .Q ÐEÑ œ ! .Q ÐE8 Ñ.
8
Suponhamos que o boreliano E de Q se decompõe de duas maneiras
distintas como união numerável de borelianos pequenos disjuntos dois a dois:
E œ E8 œ F5 . Tem-se então que cada E8 é a união em 5 dos E8 F5 ,
8
5
que são disjuntos dois a dois, e cada F5 é a união em 8 dos E8 F5 , que são
disjuntos dois a dois, pelo que, tendo em conta o lema anterior,
§2. Medida de Lebesgue sobre as variedades
11
" .Q ÐE8 Ñ œ " " .Q ÐE8 F5 Ñ œ " .Q ÐE8 F5 Ñ œ
8
8
5
8ß5
5
8
5
œ " " .Q ÐE8 F5 Ñ œ " .Q ÐF5 Ñ.
Faz portanto sentido definir, para cada boreliano E § Q , pequeno ou não,
.Q ÐEÑ œ ! .Q ÐE8 Ñ, onde os E8 constituem uma família arbitrária de bore8
lianos pequenos disjuntos dois a dois e de união E. É claro que, se o
boreliano E fosse pequeno, a definição de .Q ÐEÑ coincide com a já
conhecida, visto que se pode considerar a decomposição em que um dos E8 é
E e os restantes são vazios. É também fácil constatar que a aplicação .Q ,
assim definida no conjunto de todos os borelianos de E, é uma medida.
I.2.12 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão !,
isto é, um subconjunto de I cuja topologia induzida é a topologia discreta.
Tem-se então que todos os subconjuntos E § Q são abertos em Q , em
particular borelianos, e um tal boreliano é pequeno se, e só se, ele é vazio ou
constituído por um único elemento. É claro que, uma vez que o coeficiente
de dilatação de um isomorfismos entre espaços vectoriais de dimensão ! é
sempre igual a ", vem .Q ÐgÑ œ ! e .Q ÐÖ+×Ñ œ ", pelo que podemos
concluir que a medida de Lebesgue .Q nos borelianos de Q é a medida de
contagem, isto é, que .Q ÐEÑ é o número de elementos de E, se este é finito,
e que .Q ÐEÑ œ _, se E é infinito. Concluímos, ao mesmo tempo, tendo
em conta a alínea a) do resultado anterior, que toda a variedade de dimensão
!, Q § I , é finita ou numerável, o que podia evidentemente ser também
demonstrado de modo directo.
I.2.13 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão 7.
s § Q outra variedade com a mesma dimensão. Para cada boreliano
Seja Q
s , tem-se então . s ÐEÑ œ .Q ÐEÑ.
E§Q
Q
s , podemos considerar um aberto Y de Q , com
Dem: Para cada + − Q
+ − Y , um boreliano Z de ‘7 e um difeomorfismo :À Z Ä Y . Tem-se
s é um aberto de Q
s , contendo +, e a restrição de : vai ser
então que Y Q
"
s Ñ, de ‘7 , sobre Y Q
s . Resulta
um difeomorfismo do boreliano : ÐY Q
s , que é
daqui, e da fórmula de I.2.8, que, para cada boreliano E § Y Q
s , tem-se
automaticamente pequeno, tanto para Q como para Q
.Q ÐEÑ œ .Qs ÐEÑ. A asserção do enunciado é agora uma consequência do
lema I.2.1.
I.2.14 Dados o espaço euclidiano I e a variedade de dimensão 7, Q § I ,
nota-se simplesmente .ÐQ Ñ a medida de Lebesgue .Q ÐQ Ñ, da variedade
Q , considerada como boreliano nela mesma. Repare-se que, tendo em conta
o resultado anterior, tem-se também .ÐQ Ñ œ .Qs ÐQ Ñ, qualquer que seja a
s § I com a mesma dimensão e contendo Q .
variedade Q
12
Cap. I. Medida e Integração em Variedades
I.2.15 (Lema) Sejam I um espaço euclidiano de dimensão 8 e Q § I uma
variedade de dimensão 7 8. Tem-se então .I ÐQ Ñ œ !.
Dem: Seja + − Q arbitrário. Sendo : o índice da variedade Q no ponto +,
7:
podemos considerar um aberto Z de ‘7
‚ ‘: , com ! − Z , um
: œ‘
aberto Y de Q , com + − Y , e um difeomorfismo :À Z Ä Y , com :Ð!Ñ œ +.
s de ‘7 , contendo Z , e um
Podemos então considerar um aberto Z
s
prolongamento suave :
sÀ Z Ä I de :. Vem que H:
sÐ!Ñ œ H:Ð!Ñ é um
isomorfismo de ‘7 sobre X+ ÐQ Ñ, pelo que, sendo /" ß á ß /7 a base canónica
de ‘7 , ficamos com um sistema linearmente independente de vectores de I ,
H:
s! Ð/" Ñß á ß H:
s! Ð/7 Ñ, que podemos completar com 8 7 vectores
D7" ß á ß D8 , de modo a obter uma base de I . Consideremos então a
s ‚ ‘87 , de ‘8 , em I , definida por
aplicação < do aberto Z
<Ð>" ß á ß >8 Ñ œ :
sÐ>" ß á ß >7 Ñ >7" D7" â >8 D8 ,
aplicação que é suave e cuja derivada em ! aplica a base canónica de ‘8 na
base referida de I . Aplicando o teorema da função inversa, concluímos a
s , e de um aberto [˜ de
existência de um aberto Z˜ de ‘7 , com ! − Z˜ § Z
87
˜
‘
, com ! − [ , tais que a restrição de < a Z˜ ‚ [˜ seja um
difeomorfismo sobre um aberto de I . Tem-se então que :ÐZ Z˜ Ñ é um
aberto de Q , contendo +, e, para cada boreliano E contido neste aberto, sai
.I ÐEÑ œ !, visto que, sendo F § Z Z˜ o boreliano tal que
E œ :ÐFÑ œ :
sÐFÑ œ <ÐF ‚ Ö!×Ñ,
.I ÐEÑ é dado por um integral sobre o subconjunto F ‚ Ö!× de ‘8 , o qual
tem medida nula, visto que Ö!× tem medida nula em ‘87 , por ser 8 7.
Tendo em conta o lema I.2.1, concluímos agora que a restrição de .I aos
borelianos de Q é a medida identicamente nula, em particular
.I ÐQ Ñ œ !.
I.2.16 Sejam I um espaço euclidiano, Q § I uma variedade de dimensão 7 e
\ § Q uma variedade de dimensão 5 7. Tem-se então .Q Ð\Ñ œ !.
Dem: Seja + − \ arbitrário. Sejam Y um aberto de Q , com + − Y , Z um
aberto num sector de ‘7 e :À Z Ä Y um difeomorfismo. Sendo então
] œ :" ÐY \Ñ, vem que ] é uma variedade de dimensão 5 , donde, pelo
lema anterior, .7 Ð] Ñ œ !. Deduzimos daqui que
.Q Ð\ Y Ñ œ ( -H:ÐBÑ . .7 ÐBÑ œ !.
]
Provámos portanto que, para cada boreliano E, contido no aberto Y \ de
\ , que contém +, tem-se .Q ÐEÑ œ !, donde, mais uma vez pelo lema I.2.1, a
restrição aos borelianos de \ da medida .Q é identicamente nula, em
particular .Q Ð\Ñ œ !.
I.2.17 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão 7.
Tem-se então:
§2. Medida de Lebesgue sobre as variedades
13
a) Se Y § Q é um aberto não vazio, então .Q ÐY Ñ !;
b) Para cada + − Q , existe um aberto Y de Q , com + − Y , tal que
.Q ÐY Ñ _;
c) Para cada compacto O § Q , tem-se .Q ÐOÑ _.
Dem: a) Seja + − Y . Uma vez que Y é também uma variedade de dimensão
7, podemos considerar um aberto Y w de Y , com + − Y w , um aberto Z w de
7:
‘7
‚ ‘: , com ! − Z w , e um difeomorfismo :À Z w Ä Y w , com
: œ‘
:Ð!Ñ œ +. Existe então < ! tal que Ò!ß <Ó7 § Z w , donde .Q ÐZ w Ñ <7 !,
o que implica, uma vez que os coeficientes de dilatação são estritamente
positivos,
.Q ÐY Ñ .Q ÐY w Ñ œ ( -H:ÐBÑ . .7 ÐBÑ !.
Zw
b) Como anteriormente, consideremos um aberto Y w de Q , com + − Y w , um
aberto Z w de ‘:7 œ ‘7: ‚ ‘: , com ! − Z w , e um difeomorfismo
:À Z w Ä Y w , com :Ð!Ñ œ +. A continuidade da aplicação de Z w em Ó!ß _Ò,
que a cada B associa -H:ÐBÑ , permite-nos escolher < ! tal que o conjunto
Z œ Ó<ß <Ò7: ‚ Ò!ß <Ò: œ Ó<ß <Ò7 ‘7
:
esteja contido em Z w e que, para um certo V !, -H:ÐBÑ Ÿ V , para todo o B
naquele conjunto. Sendo então Y œ :ÐZ Ñ, que é um aberto de Q , contendo
+, vem
.Q ÐY Ñ œ ( -H:ÐBÑ . .7 ÐBÑ Ÿ V .7 ÐZ Ñ _.
Z
c) Suponhamos que O § Q é um compacto. Para cada + − O , podemos,
pelo que vimos em b), considerar um aberto Y+ de Q , com + − Y+ , tal que se
tenha .Q ÐY+ Ñ _. Uma vez que a família dos Y+ é uma cobertura aberta
do compacto O , podemos considerar uma parte finita N de O , tal que O
esteja contido na união dos Y+ , com + − N , de onde concluímos que
.Q ÐOÑ Ÿ " .Q ÐY+ Ñ _.
+−N
§3. Teoremas de Fubini e da mudança de variáveis.
Recordemos que um espaço de medida se diz 5 -finito se for união de uma
família numerável de conjuntos mensuráveis de medida finita.
Recordemos ainda que, dados dois espaços topológicos, com bases
numeráveis de abertos, munidos de medidas 5 -finitas sobre os respectivos
borelianos, fica definida, sobre a classe dos borelianos do seu produto
14
Cap. I. Medida e Integração em Variedades
cartesiano, uma medida, chamada medida produto, definida pela condição
de ser a única que, num produto cartesiano de dois borelianos, toma como
valor o produto das medidas destes. Para determinar a medida de
borelianos do produto cartesiano, assim como para determinar o integral
de funções definidas neste, pode-se então aplicar o teorema de Fubini, que
reduz a determinação de um integral duplo a um cálculo iterado de
integrais simples. Será assim especialmente bem recebido um resultado
que nos assegure que a medida de Lebesgue, sobre o produto de duas
variedades, vai ser a medida produto das medidas de Lebesgue sobre cada
uma dessas variedades.
I.3.1 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão 7.
Tem-se então que a medida de Lebesgue .Q , sobre os borelianos de Q , é
5-finita.
Dem: É uma consequência do facto de toda a variedade ser união de uma
família numerável de compactos e de cada um destes ter medida finita.
s espaços euclidianos e consideremos sobre I ‚ I
s o
I.3.2 Sejam I e I
correspondente produto interno, definido por
ØÐ?ß ?Ñß
s Ð@ß s@ÑÙ œ Ø?ß @Ù Ø?ß
s s@Ù.
s §I
s duas variedades, de dimensões 7 e 8, respectivaSejam Q § I e Q
s §I‚I
s , com
mente e consideremos a correspondente variedade Q ‚ Q
dimensão 7 8. A medida de Lebesgue .Q ‚Qs é então a medida produto
das medidas .Q e .Qs .
s§Q
s são borelianos
Dem: Vamos começar por provar que, se E § Q e E
s
s
s abertos
pequenos, então .Q ‚Qs ÐE ‚ EÑ œ .Q ÐEÑ ‚ .Qs ÐEÑ. Sejam Y e Y
s§Y
s , respectivamente, com E § Y e E
s, Z e Z
s borelianos de ‘7
de Q e Q
s ÄY
s dois difeomorfismos.
e de ‘8 , respectivamente, e :À Z Ä Y e :
sÀ Z
s, Z ‚ Z
s
s
s
Tem-se então que Y ‚ Y é um aberto de Q ‚ Q , contendo E ‚ E
78
s
s
é um boreliano de ‘
e :‚:
sÀ Z ‚ Z Ä Y ‚ Y é um difeomorfismo.
Tendo em conta I.1.13 e o teorema de Fubini, para funções em
s ,
sœ:
‘78 œ ‘7 ‚ ‘8 , obtemos, notando F œ :" ÐEÑ e F
s" ÐEÑ
s œ(
.Q ‚Qs ÐE ‚ EÑ
œ(
s
F‚F
s
F‚F
-HÐ:‚:sÑÐBßCÑ . .78 ÐBß CÑ œ
-H:ÐBÑ -H:sÐCÑ . .78 ÐBß CÑ œ
œ ( -H:ÐBÑ Š( -H:sÐCÑ . .8 ÐCÑ‹ . .7 ÐBÑ œ
F
s
F
s .
s . .7 ÐBÑ œ .Q ÐEÑ ‚ . s ÐEÑ
œ ( -H:ÐBÑ .Qs ÐEÑ
Q
F
Para terminar a demonstração, tudo o que temos que ver é que a igualdade
s, e não apenas para
anterior é válida para borelianos arbitrários E e E
§3. Teoremas de Fubini e da mudança de variáveis
15
s são uniões de famílias
borelianos pequenos. Ora, sabemos que E e E
s5 Ñ5− ,
numeráveis de borelianos pequenos disjuntos dois a dois, ÐE4 Ñ4− e ÐE
s é a união, para Ð4ß 5Ñ em ‚ ,
respectivamente, tendo-se então que E ‚ E
s
dos borelianos pequenos E4 ‚ E5 , que são disjuntos dois a dois, donde
s œ ".
s
s
.Q ‚Qs ÐE ‚ EÑ
s ÐE4 ‚ E5 Ñ œ " .Q ÐE4 Ñ .Q
s ÐE4 Ñ œ
Q ‚Q
4ß5
4ß5
s5 щ œ .Q ÐEÑ ‚ . s ÐEÑ
s .
œ ˆ" .Q ÐE4 щ ‚ ˆ" .Qs ÐE
Q
4
5
Para terminar esta secção, vamos estabelecer uma fórmula de mudança de
variáveis para difeomorfismos entre subvariedades de espaços
euclidianos, começando com um lema, que será um caso particular do
resultado final.
I.3.3 (Lema) Sejam I um espaço euclidiano, Q § I uma variedade de
dimensão 7, Y um aberto de Q , Z um boreliano de ‘7 e :À Z Ä Y um
difeomorfismo de classe G " . Para cada aplicação mensurável
1À Y Ä Ò!ß _Ó, tem-se então
( 1ÐCÑ . .Q ÐCÑ œ ( 1Ð:ÐBÑÑ-H:ÐBÑ . .7 ÐBÑ.
Y
Z
w
Dem: Consideremos a medida . , definida nos borelianos de Z , por
.w ÐFÑ œ .Q Ð:ÐFÑÑ. Por definição, vem que o difeomorfismo :À Z Ä Y é
compatível com as medidas, quando se considera em Z a medida .w e em Y
a medida .Q . Tendo em conta I.2.8, vem que a medida .w está também
definida por .w ÐFÑ œ 'F -H:ÐBÑ . .7 ÐBÑ, pelo que a igualdade do enunciado é
uma consequência de que, por I.1.1 e I.1.2, ambos os membros são iguais a
' 1Ð:ÐBÑÑ . .w ÐBÑ.
Z
s espaços euclidianos, Q § I e Q
s §I
s duas variedades de
I.3.4 Sejam I e I
s um difeomorfismo de classe G " . Para cada
dimensão 7 e :À Q Ä Q
boreliano E § Q , tem-se então
.Qs Ð:ÐEÑÑ œ ( -H:ÐBÑ . .Q ÐBÑ,
E
em que a função integranda do segundo membro é uma aplicação contínua de
Q em Ó!ß _Ò.1
1O
símbolo -H:ÐBÑ designa, naturalmente, o coeficiente de dilatação do isomorfismo
s Ñ, quando se considera nestes dois espaços vectoriais os
H:ÐBÑÀ XB ÐQ Ñ Ä X:ÐBÑ ÐQ
s.
produtos internos induzidos pelos dos espaços ambientes I e I
16
Cap. I. Medida e Integração em Variedades
Dem: Comecemos por mostrar a continuidade da aplicação de Q em
Ó!ß _Ò, que a cada B associa o coeficiente de dilatação -H:ÐBÑ . Para isso,
dado + − Q arbitrário, consideremos um aberto Y de Q , com + − Y , um
boreliano Z de ‘7 e um difeomorfismo !À Z Ä Y . Vem então que
: ‰ !À Z Ä :ÐY Ñ é um difeomorfismo de classe G " , com :ÐY Ñ aberto em
s , e sabemos, por I.2.7, que são contínuas as aplicações de Z em Ó!ß _Ò,
Q
que a cada C em Z
associam respectivamente -H!ÐCÑ e
-HÐ:‰!ÑÐCÑ œ -H:Ð!ÐCÑÑ ‚ -H!ÐCÑ , o que nos permite concluir que é também
contínua a aplicação de Z em Ó!ß _Ò, que a C associa -H:Ð!ÐCÑÑ , donde, por
composição com !" , a continuidade da aplicação de Y em Ó!ß _Ò, que a B
associa -H:ÐBÑ . Da arbitrariedade de + resulta agora a continuidade em Q da
função considerada.
Uma vez que ambos os membros da igualdade do enunciado, quando
considerados como funções do boreliano E de Q , são medidas sobre os
borelianos de Q , resulta, do lema I.2.1, que será suficiente demonstrar a
igualdade no caso particular em que E é um boreliano pequeno de Q . Sejam
portanto Y um aberto de Q , com E § Y , Z um boreliano de ‘7 e
!À Z Ä Y um difeomorfismo. Tem-se então que : ‰ !À Z Ä :ÐY Ñ é um
s , pelo que, tendo em
difeomorfismo de classe G " , com :ÐY Ñ aberto de Q
conta o lema anterior e a definição em I.2.8, vem, com F œ !" ÐEÑ,
( -H:ÐCÑ . .Q ÐCÑ œ ( ;Es ÐCÑ-H:ÐCÑ . .Q ÐCÑ œ
E
Y
œ ( ;Es Ð!ÐBÑÑ-H:Ð!ÐBÑÑ -H!ÐBÑ . .7 ÐBÑ œ
Z
œ ( -H:Ð!ÐBÑщH!ÐBÑ . .7 ÐBÑ œ ( -HÐ:‰!ÑÐBÑ . .7 ÐBÑ œ
F
F
œ .Qs Ð: ‰ !ÐFÑÑ œ .Qs Ð:ÐEÑÑ.
s espaços euclidianos, Q § I e Q
s §I
s variedades de
I.3.5 Sejam I e I
s um difeomorfismo. Se 1À Q
s Ä Ò!ß _Ó é uma
dimensão 7 e :À Q Ä Q
aplicação mensurável, tem-se então
( 1ÐCÑ . .Qs ÐCÑ œ ( 1Ð:ÐBÑÑ-H:ÐBÑ . .Q ÐBÑ,
s
Q
Q
a mesma fórmula sendo válida no caso em que 1 é uma função integrável
com valores em ‘ ou, mais geralmente, num espaço vectorial de dimensão
finita.
Dem: Trata-se, mais uma vez, de uma consequência dos resultados básicos
de Teoria da Medida, I.1.1 e I.1.2, visto que podemos definir uma medida .w
nos borelianos de Q , por .w ÐEÑ œ .Qs Ð:ÐEÑÑ œ 'E -H:ÐBÑ . .Q ÐBÑ, tendo-se
então que ambos os membros da igualdade do enunciado vão ser iguais a
' 1Ð:ÐBÑÑ . .w ÐBÑ.
Q
§3. Teoremas de Fubini e da mudança de variáveis
17
s espaços euclidianos, Q § I e Q
s §I
s duas
I.3.6 (Corolário) Sejam I e I
s
variedades de dimensão 7 e :À Q Ä Q um difeomorfismo de classe G " ,
que seja uma isometria, isto é, tal que, para cada B − Q , o isomorfismo
s Ñ seja um isomorfismo ortogonal. Tem-se então:
H:B À XB ÐQ Ñ Ä X:ÐBÑ ÐQ
a) Para cada boreliano E § Q , .Qs Ð:ÐEÑÑ œ .Q ÐEÑ;
s Ä Ò!ß _Ó, tem-se
b) Para cada função mensurável 1À Q
( 1ÐCÑ . .Qs ÐCÑ œ ( 1Ð:ÐBÑÑ . .Q ÐBÑ,
s
Q
Q
a mesma fórmula sendo válida no caso em que 1 é uma função integrável
com valores em ‘ ou, mais geralmente, num espaço vectorial de dimensão
finita.
Dem: É uma consequência dos dois resultados anteriores, visto que, uma vez
que H:B é um isomorfismo ortogonal, tem-se -H:ÐBÑ œ ".
I.3.7 (Corolário) Sejam I um espaço euclidiano, Q § I uma variedade de dimensão 7 e + − I um vector fixado. Tem-se então que a translação
+ Q § I é também uma variedade de dimensão 7 e tem lugar uma
isometria 7+ À Q Ä + Q , definida por 7+ ÐBÑ œ + B, em particular, para
cada boreliano E § Q , .+Q Ð+ EÑ œ .Q ÐEÑ.
s espaços euclidianos e 0À I Ä I
s um isomorfismo
I.3.8 (Corolário) Sejam I e I
ortogonal. Para cada variedade Q § I , de dimensão 7, tem-se então que
s é também uma variedade de dimensão 7 e a restrição de 0 é uma
0ÐQ Ñ § I
isometria de Q sobre 0ÐQ Ñ, em particular, para cada boreliano E § Q ,
.0ÐQ Ñ Ð0ÐEÑÑ œ .Q ÐEÑ.
I.3.9 (Corolário) Sejam I um espaço euclidiano, Q § I uma variedade de
dimensão 7 e - − ‘ Ï Ö!× um real não nulo. Tem-se então que o conjunto
homotético -Q § I é também uma variedade de dimensão 7 e,
considerando as estruturas riemanianas induzidas pelo produto interno de I ,
vem, para cada boreliano E § Q , .-Q Ð-EÑ œ l-l7 .Q ÐEÑ.
Dem: Tem lugar o difeomorfismo :À Q Ä -Q , definido por :ÐBÑ œ -B,
pelo que o resultado ficará provado, se virmos que, para todo o B − Q , se
tem -H:ÐBÑ œ l-l7 . Ora, considerando uma base ortonormada A" ß á ß A7 de
XB ÐQ Ñ, tem-se H:B ÐA4 Ñ œ -A4 pelo que, na notação de I.1.15, a matriz dos
13ß4 œ ØH:B ÐA3 Ñß H:B ÐA4 ÑÙ é a matriz diagonal de tipo 7 ‚ 7, com os
elementos da diagonal iguais a - # , tendo portanto determinante igual a - #7 . O
coeficiente de dilatação, igual à raiz quadrada deste determinante, é portanto
igual a l-l7 .
s é um isomorfismo entre
Não se deve ficar com a ideia que, se 0À I Ä I
espaços euclidianos, então, para cada variedade de dimensão 7, Q § I
e cada boreliano E de Q , seja válida a fórmula .0ÐQ Ñ Ð0ÐEÑÑ œ -0 .Q ÐEÑ.
Na verdade, esta fórmula seria válida no caso em que a função integranda
18
Cap. I. Medida e Integração em Variedades
do segundo membro de I.3.4 fosse constante e com valor -0 , mas o que se
passa é que, sendo :À Q Ä 0ÐQ Ñ o difeomorfismo restrição de 0, H:B
vai ser o isomorfismo restrição de 0, mas o seu coeficiente de dilatação
não será, em geral, igual ao de 0, nem sequer constante, visto depender do
espaço vectorial tangente XB ÐQ Ñ § I . O que se passou, nos corolários
anteriores, é que, para certos isomorfismos particulares, chegámos à
conclusão que a função integranda referida era efectivamente constante.
§4. Coordenadas polares generalizadas e medidas das esferas.
As coordenadas polares, que estamos habituados a utilizar em ‘# ,
associam a cada par ÐBß CÑ − ‘# Ï Ö!×, um par Ð<ß :Ñ, em que < é a norma
de ÐBß CÑ (<# œ B# C# ) e : um dos seus argumentos (B œ < cosÐ:Ñ,
C œ < sinÐBÑ). É claro que o argumento está definido a menos de um
múltiplo de #1, de modo que, para se obter um verdadeiro difeomorfismo
entre abertos de ‘# , que permita, por exemplo, integrar por mudança de
variáveis, é costume escolher a determinação do argumento que está no
intervalo Ó!ß #1Ò, o que obriga a tirar do domínio do sistema de
coordenadas a parte positiva do eixo dos B; isso não oferece
inconveniente, do ponto de vista da integração, uma vez que este conjunto
é de medida nula. As coordenadas polares definem então um difeomorfismo de ‘# Ï ÐÒ!ß _Ò ‚ Ö!×Ñ sobre Ó!ß _Ò ‚ Ó!ß #1Ò, e elas são utilizadas com frequência para calcular a medida de conjuntos com simetria
radial e o integral sobre tais conjuntos de funções com o mesmo tipo de
simetria (isto é, funções cujo valor depende apenas de <). Para
resolvermos o mesmo tipo de problema em dimensões superiores, vamos
introduzir umas coordenadas polares generalizadas, que, mesmo no caso
de ‘# , são um pouco mais simples que as coordenadas polares usuais.
Observe-se que o que se costuma usar em ‘$ , para substituir as
coordenadas polares, as coordenadas esféricas, têm um comportamento
muito menos agradável que aquelas (em particular, o coeficiente de
dilatação não é função só de <) e as coisas ainda piorariam se
prosseguíssemos na mesma via para dimensões superiores.
I.4.1 Sejam I um espaço euclidiano de dimensão 7 ", e notemos W § I a
hipersuperfície esférica de centro ! e raio ", definida por
W œ ÖB − I ± mBm œ "×,
conjunto que sabemos ser uma variedade, sem bordo, de dimensão 7 ".
Recordemos ainda que, para cada B − W , o espaço vectorial tangente XB ÐWÑ é
o conjunto dos vectores A − I tais que ØAß BÙ œ !. Tem então lugar um
difeomorfismo
§4. Coordenadas polares generalizadas e medidas das esferas
19
:À Ó!ß _Ò ‚ W Ä I Ï Ö!×, :Ð<ß BÑ œ <B,
cujo inverso está definido por
:" ÐCÑ œ ÐmCmß
C
Ñ.
mCm
Além disso, para cada Ð<ß BÑ − Ó!ß _Ò ‚ W , tem-se, para o coeficiente de
dilatação,
-H:Ð<ßBÑ œ <7" .
Dem: É imediato que : é uma aplicação suave com valores em I Ï Ö!×, e o
facto de ser um difeomorfismo, com o inverso referido no enunciado, vem de
que tem lugar uma aplicação suave I Ï Ö!× Ä Ó!ß _Ò ‚ W , que a cada C
C
associa ÐmCmß mCm
Ñ, aplicação que se verifica facilmente ser um inverso
bilateral de :. Para calcularmos o coeficiente de dilatação, dado
Ð<ß BÑ − Ó!ß _Ò ‚ W , consideramos uma base ortonormada A" ß á ß A7" de
XB ÐWÑ, e reparamos que podemos considerar a base ortonormada
Ð"ß !Ñß Ð!ß A" Ñß á ß Ð!ß A7" Ñ de XÐ<ßBÑ ÐÓ!ß _Ò ‚ WÑ œ ‘ ‚ XB ÐWÑ, a qual
vai ser aplicada, por H:Ð<ßBÑ na base de I formada pelos vectores
Bß <A" ß á ß <A7" . Uma vez que estes vectores são ortogonais dois a dois,
vemos que a matriz associada dos 13ß4 (cf. I.1.15) é uma matriz diagonal, com
um dos elementos da diagonal igual a " e os restantes 7 " elementos
iguais a <# . O determinante desta matriz é portanto igual a <#Ð7"Ñ , pelo que o
coeficiente de dilatação, igual à raiz quadrada deste determinante, é igual a
<7" .
Nas condições do resultado anterior, dado C œ :Ð<ß BÑ − I Ï Ö!×,
olharemos para < e B como sendo as coordenadas polares generalizadas
de C, a primeira a sua norma e a segunda caracterizando a sua direcção,
Repare-se que a segunda coordenada não é um número real, mas um
elemento da hipersuperfície esférica W .
I.4.2 Para cada inteiro 8 !, vamos notar 58 a medida .ÐWÑ da hipersuperfície
esférica, de centro ! e raio ", num espaço euclidiano I de dimensão 8 "
(reparar que W é então uma variedade de dimensão 8). O facto de esta
medida não depender do espaço euclidiano I , de dimensão 8 ", que se
considera, é uma consequência imediata da invariância da medida pelos
isomorfismos ortogonais, que estudámos em I.3.), visto que é imediato que
um tal isomorfismo aplica a hipersuperfície esférica sobre a hipersuperfície
esférica. O facto de W ser uma variedade compacta e não vazia, implica que
58 é finito e não nulo.
I.4.3 Sejam I um espaço euclidiano de dimensão 8 " e F § I a bola fechada
de centro ! e raio ". Tem-se então
20
Cap. I. Medida e Integração em Variedades
.I ÐFÑ œ
58
.
8"
Dem: Considerando o difeomorfismo :À ]0,_[ ‚ S Ä E Ï {0}, que define
as coordenadas polares generalizadas, tem-se B Ï {0} œ :(]0,1] ‚ S), pelo
que, tendo em conta o facto de se ter .I ÐÖ!×Ñ œ !, por Ö!× ser uma
variedade de dimensão inferior à de I , e aplicando o teorema de Fubini e a
fórmula de integração por mudança de variáveis, obtemos
.I ÐFÑ œ .I Ð:ÐÓ!ß "Ó ‚ WÑÑ œ (
œ(
"
!
>8 . .Ó!ß"Ó‚W Ð>ß BÑ œ
Ó!ß"Ó‚W
"
Š( >8 . .W ÐBÑ‹ .> œ (
W
58 >8 .> œ
!
58
.
8"
I.4.4 (Corolário) Seja I um espaço euclidiano de dimensão 8 ". Para cada
< !, sejam W< e F< a hipersuperfície esférica de centro ! e raio < e a bola
fechada de centro ! e raio <. Tem-se então
.ÐW< Ñ œ 58 <8 ,
.I ÐF< Ñ œ
58 <8"
.
8"
Dem: Basta atender a que W< e F< são as imagens de W e de F , pela
homotetia de razão <, tendo então em conta I.3.9.
Vamos agora estabelecer uma fórmula que nos permite calcular recursivamente as constantes 58 . Uma vez que essa fórmula vai dar 58# a partir
de 58 , começamos por determinar 5! e 5" , obtendo resultados que não
espantarão ninguém…
I.4.5 Tem-se 5! œ # e 5" œ #1.
Dem: Considerando ‘ como espaço euclidiano de dimensão ", do modo
usual, vem que W § ‘ é a variedade de dimensão !, constituída pelos dois
elementos " e ", pelo que, uma vez que nas variedades de dimensão ! a
medida de Lebesgue é a medida de contagem, vemos que 5! œ #.
Consideremos agora ‘# como espaço euclidiano de dimensão #, do modo
usual. Vem que a hipersuperfície esférica de centro Ð!ß !Ñ e raio " é a
circunferência
W œ ÖÐBß CÑ − ‘# ± B# C# œ "×.
Sabemos que tem lugar uma bijecção suave
:À Ó!ß #1Ò Ä W Ï ÖÐ"ß !Ñ×, :Ð>Ñ œ ÐcosÐ>Ñß sinÐ>ÑÑ,
e o teorema da função inversa garante-nos que esta bijecção é um difeomorfismo, visto que W Ï ÖÐ"ß !Ñ× é uma variedade, sem bordo, com dimensão 1, e
§4. Coordenadas polares generalizadas e medidas das esferas
21
o facto de se ter :w Ð>Ñ œ ÐsinÐ>Ñß cosÐ>ÑÑ Á !, implica que H:> é uma
aplicação linear injectiva, logo um isomorfismo de ‘ sobre X:Ð>Ñ ÐWÑ. Uma
vez que .W ÐÖÐ"ß !Ñ×Ñ œ ! e que -H:Ð>Ñ œ m:w Ð>Ñm œ ", obtemos
5# œ .W Ð:ÐÓ!ß #1ÒÑÑ œ (
#1
" .> œ #1.
!
158
I.4.6 Para cada 8 !, tem-se 58# œ #8"
.
Dem: Sejam I um espaço euclidiano de dimensão 8 " e J um espaço
euclidiano de dimensão #, e consideremos sobre o espaço vectorial I ‚ J ,
de dimensão 8 $, a estrutura associada de espaço euclidiano. Notemos F< ,
F<w e F<ww as bolas fechadas de centro ! e raio < em I , J e I ‚ J , respectivamente. Uma vez que, para cada B − I , o conjunto ÖC − J ± ÐBß CÑ − F"ww ×
é vazio, se B  F" , e é igual a F<w , com < œ È" mBm# , se B − F" , caso em
que este conjunto tem medida
.J ÐF<w Ñ œ
5" < #
œ 1<# œ 1Ð" mBm# Ñ,
#
obtemos, pelo teorema de Fubini,
58#
œ .I‚J ÐF"ww Ñ œ ( 1Ð" mBm# Ñ . .I ÐBÑ,
8$
F"
donde, usando coordenadas polares generalizadas para calcular este integral,
e notando W a hipersuperfície esférica de centro ! e raio " de I ,
"
58#
œ ( Š( 1>8 Ð" ># Ñ . .W ÐCÑ‹ .> œ
8$
!
W
"
"
"
#158
œ ( 158 Ð>8 >8# Ñ .> œ 158 Ð
ќ
,
8" 8$
Ð8 "ÑÐ8 $Ñ
!
pelo que a conclusão do enunciado resulta de multiplicar ambos os membros
desta igualdade por 8 $.
I.4.7 A título de exemplo de aplicação dos resultados anteriores, podemos apresentar a seguinte tabela com os primeiros valores de 58 :
8
58
!
#
"
#1
#
%1
$
#1 #
%
)1 #
$
&
1$
'
"'1$
"&
22
Cap. I. Medida e Integração em Variedades
§5. Teorema de Sard.
s §I
s duas variedades sem bordo, com dimensões 7 e
I.5.1 Sejam Q § I e Q
s uma aplicação suave. Diz-se que um
8, respectivamente, e seja 0 À Q Ä Q
ponto B − Q é um ponto regular de 0 se a aplicação linear
s Ñ é sobrejectiva; caso contrário, diz-se que B é um
H0B À XB ÐQ Ñ Ä X0 ÐBÑ ÐQ
s é um valor regular de 0 se,
ponto crítico de 0 . Diz-se que um ponto C − Q
"
todos o B − 0 ÐÖC×Ñ são pontos regulares; caso contrário, isto é, se existe
um ponto crítico B − 0 " ÐÖC×Ñ, diz-se que C é um valor crítico de 0 .
s para
A importância dos valores regulares é que eles são os pontos C − Q
os quais se pode garantir que a imagem recíproca 0 " ÐÖC×Ñ é uma
subvariedade, eventualmente vazia, de Q . O teorema de Sard, de que nos
ocupamos nesta secção, vai garantir a existência de muitos valores
regulares, provando mesmo que o conjunto dos valores críticos é de
medida nula. Repare-se que, no caso em que 7 8, todos os pontos de
Q são críticos, pelo que os valores regulares de 0 são simplesmente
aqueles que não pertencem a 0 ÐQ Ñ.
s §I
s duas variedades e 0 À Q Ä Q
s uma
I.5.2 (Lema) Sejam Q § I e Q
aplicação contínua. Seja E § Q um subconjunto localmente fechado, isto é,
um conjunto que seja intersecção de um fechado de Q com um aberto de Q .
s.
Tem-se então que 0 ÐEÑ é um boreliano de Q
Dem: Seja E œ Y F , com Y aberto em Q e F fechado em Q . O
conjunto E é portanto fechado em Y e, uma vez que Y é uma variedade,
podemos considerar, por I.2.5, uma família numerável de compactos O: de
união Y . Tem-se então que E é a união numerável dos compactos F O: ,
pelo que 0 ÐEÑ é a união numerável dos compactos 0 ÐF O: Ñ, sendo assim
um boreliano.
s §I
s duas variedades sem bordo, com dimensões 7 e
I.5.3 Sejam Q § I e Q
s uma aplicação suave. Tem-se então que o
8, respectivamente, e 0 À Q Ä Q
conjunto G dos pontos críticos de 0 é fechado em Q e o conjunto 0 ÐGÑ dos
s.
seus valores críticos é um boreliano de Q
Dem: Suponhamos que B! − Q é um ponto regular de 0 . Pelo teorema da
derivada sobrejectiva, podemos considerar um aberto Y de Q , com B! − Y ,
s de Q
s , com 0 ÐY Ñ œ Y
s , espaços vectoriais J
s e K , com dimenum aberto Y
s
s
s e
sões 8 e 7 8, respectivamente, abertos Z de J e [ de K , com ! − Z
s
s
s
! − Z , e difeomorfismos :À Z ‚ [ Ä Y e :
sÀ Z Ä Y , com :Ð!ß !Ñ œ B! e
s ‚[ ÄZ
s seja a primeira
:
sÐ!Ñ œ 0 ÐB! Ñ, de modo que :
s" ‰ 0ÎY ‰ :À Z
s
projecção. Para cada Ð+ß ,Ñ − Z ‚ [ , podemos então concluir que a com-
§5. Teorema de Sard
23
posta
s ‚K ÄJ
s
H:
s0 Ð:Ð+ß,ÑÑ ‰ H0:Ð+ß,Ñ ‰ H:Ð+ß,Ñ œ HÐ:
s" ‰ 0ÎY ‰ :ÑÐ+ß,Ñ À J
vai ser a primeira projecção, em particular sobrejectiva, e portanto, uma vez
que H:
s0 Ð:Ð+ß,ÑÑ e H:Ð+ß,Ñ são isomorfismos,
sÑ
H0:Ð+ß,Ñ À X:Ð+ß,Ñ ÐQ Ñ Ä X0 Ð:Ð+ß,ÑÑ ÐQ
vai ser uma aplicação linear sobrejectiva. Concluímos assim que Y está
contido no conjunto dos pontos regulares de 0 , o que mostra que este
conjunto é aberto em Q e portanto que G é fechado em Q . Em particular, G
é localmente fechado pelo que, pelo lema anterior, 0 ÐGÑ é um boreliano de
s .
Q
s §I
s é uma variedade, podemos sempre considerar sobre I
s um
I.5.4 Se Q
produto interno, e dados dois produtos internos nessas condições, resulta de
s de Q
s que os borelianos E
s , para os quais
aplicar I.3.4 à identidade de Q
s œ !, com a medida relativa a um dos produtos internos são os
.Qs ÐEÑ
mesmos que têm medida nula relativamente ao outro. É assim legítimo falar
s , sem referir o produto interno de I
s que
de borelianos de medida nula de Q
se está a considerar.
s §I
s duas variedades e 0 À Q Ä Q
s uma
I.5.5 (Lema) Sejam Q § I e Q
aplicação contínua. Seja E § Q um subconjunto localmente fechado tal que,
para cada B − E, exista um aberto Y de Q , com B − Y e 0 ÐY EÑ de
medida nula (repare-se que Y E é também localmente fechado, pelo que
0 ÐY EÑ é boreliano). Tem-se então que 0 ÐEÑ tem medida nula.
Dem: Consideremos uma base numerável de abertos de Q e sejam Y8 , com
8 − , os abertos Y dessa base que verificam a propriedade de 0 ÐY EÑ ter
medida nula. A condição do enunciado implica que E § - Y8 , pelo que
0 ÐEÑ œ - 0 ÐE Y8 Ñ, pelo que o facto de cada 0 ÐE Y8 Ñ ter medida nula
implica que 0 ÐEÑ tem medida nula.
s §I
s duas variedades sem bordo,
I.5.6 (Teorema de Sard) Sejam Q § I e Q
s uma aplicação
com dimensões 7 e 8, respectivamente, e seja 0 À Q Ä Q
suave. Sendo G § Q o conjunto dos pontos críticos de 0 , tem-se então que
o conjunto 0 ÐGÑ, dos valores críticos de 0 , é um boreliano de medida nula de
s.
Q
Dem: A demonstração que apresentamos é baseada na que se encontra no
livro de Milnor, citado na bibliografia. Para maior clareza, vamos dividi-la
em várias alíneas:
a) Comecemos por reparar que o resultado é trivialmente verdadeiro no caso
em que 8 œ !. Com efeito, tem-se então que todos os pontos de Q são
trivialmente regulares, pelo que G œ g e 0 ÐGÑ œ g. Nas alíneas seguintes
vamos supor sempre que 8 !.
b) Vamos demonstrar o resultado por indução em 7. Comecemos por supor
24
Cap. I. Medida e Integração em Variedades
que 7 œ !. Neste caso Q é um conjunto finito ou numerável (cf. I.2.12).
Resulta daqui que 0 ÐQ Ñ é um conjunto finito ou numerável pelo que 0 ÐGÑ é
uma união finita ou numerável de conjunto unitários, que têm medida nula
(cf. I.2.15), o que mostra que 0 ÐGÑ tem medida nula.
c) Seja 7 " tal que o resultado seja válido sempre que a variedade Q
tenha dimensão 7 ". Para terminar a demonstração, temos que ver que o
resultado é ainda válido quando Q tem dimensão 7.
d) Vamos examinar agora o caso particular em que Q é um aberto Y de ‘7
s é ‘8 . Consideramos portanto um aberto Y de ‘7 e uma
e em que Q
aplicação suave 0 À Y Ä ‘8 , com as componentes 04 À Y Ä ‘, " Ÿ 4 Ÿ 8, e
notamos G § Y o conjunto dos pontos singulares de 0 , que sabemos ser
fechado em Y . Para cada inteiro : ", notamos G: o subconjunto de G
formado pelos pontos B − Y tais que H5 0B œ !, para cada " Ÿ 5 Ÿ :. Os
conjuntos G: são evidentemente fechados em Y , que verificam G: ¨ G:" , e
notamos G_ a intersecção dos G: , que é ainda fechada em Y . Tem-se que G
é a união de G Ï G" com os conjuntos G: Ï G:" e com G_ , conjuntos esses
que são todos localmente fechados em Y , pelo que 0 ÐGÑ vai ser a união de
0 ÐG Ï G" Ñ com os 0 ÐG: Ï G:" Ñ e com 0 ÐG_ Ñ, pelo que, para ver que o
boreliano 0 ÐGÑ tem medida nula, basta verificarmos que têm medida nula os
borelianos 0 ÐG Ï G" Ñ, 0 ÐG: Ï G:" Ñ e 0 ÐG_ Ñ. É isso que vamos fazer nas
três próximas alíneas.
e) Seja B! − G Ï G" arbitrário. Existe então A − ‘7 tal que H0B! ÐAÑ Á !, e
portanto, para alguma componente 4, H04 B! ÐAÑ Á !. Por continuidade, podemos escolher um aberto Z de Y , com B! − Z , tal que, para cada B − Z ,
H04 B ÐAÑ Á !. Para cada , − ‘, seja Q, § Z ,
Q, œ ÖB − Z ± 04 ÐBÑ œ ,×,
que vai ser assim uma variedade de dimensão 7 ". Suponhamos que
C œ ÐC" ß á ß C4" ß ,ß C4" ß á ß C8 Ñ é um valor crítico de 0ÎZ À Z Ä ‘8 ; vemos
então que, existe B − Q, tal que 0 ÐBÑ œ C e H0B Б7 Ñ Á ‘8 e portanto, uma
vez que H0B Б7 Ñ contém o vector H0B ÐAÑ, que não pertence ao hiperplano
‘4" ‚ Ö!× ‚ ‘84 de ‘8 , H0B Б7 Ñ não vai conter esse hiperplano, que não
é mais do que XC Б4" ‚ Ö,× ‚ ‘84 Ñ; C é portanto também um valor crítico
da aplicação suave
0ÎQ, À Q, Ä ‘4" ‚ Ö,× ‚ ‘84 ;
compondo com o difeomorfismo canónico ‘4" ‚ Ö,× ‚ ‘84 Ä ‘8" ,
concluímos então que ÐC" ß á ß C4" ß C4" ß á ß C8 Ñ é um valor crítico da
aplicação suave de Q, em ‘8" , definida por
B È Ð0" ÐBÑß á ß 04" ÐBÑß 04" ÐBÑß á ß 08 ÐBÑÑ.
Pela hipótese de indução, concluímos que, para cada , − ‘, o conjunto H,
dos ÐC" ß á ß C4" ß C4" ß á ß C8 Ñ − ‘8" tais que
§5. Teorema de Sard
25
ÐC" ß á ß C4" ß ,ß C4" ß á ß C8 Ñ − 0 ÐG Z Ñ
tem medida nula em ‘8" e podemos aplicar o teorema de Fubini para
garantir que
.8 Ð0 ÐG Z ÑÑ œ ( .8" ÐH, Ñ ., œ !,
‘
e portanto que também .8 Ð0 ÐÐG Ï G" Ñ Z ÑÑ œ !. Podemos agora aplicar o
lema anterior para concluir que .8 Ð0 ÐG Ï G" ÑÑ œ !.
f) Seja B! − G: Ï G:" arbitrário. Tem-se portanto H: 0B! œ ! e
H:" 0B! Á !, pelo que existem A" ß á ß A:" em ‘7 tais que
D:" 0B! ÐA" ß á ß A:" Ñ Á ! e podemos escolher uma componente 4 tal que
H:" 04 B! ÐA" ß á ß A:" Ñ Á !. Por continuidade, podemos escolher um aberto
Z de Y , com B! − Z , tal que, para cada B − Z , H:" 04 B ÐA" ß á ß A:" Ñ Á !.
Notemos 1À Z Ä ‘ a aplicação suave definida por
1ÐBÑ œ H: 04 B ÐA# ß á ß A:" Ñ.
Uma vez que, para cada B − Z , H1B ÐA" Ñ Á !, vemos que o conjunto
Q œ ÖB − Z ± 1ÐBÑ œ !× é uma variedade de dimensão 7 ". Mais uma
vez pela hipótese de indução, o conjunto dos valores críticos de
0ÎQ À Q Ä ‘8 tem medida nula. Mas, para cada B − Z ÐG: Ï G:" Ñ, vem
H: 0B œ !, em particular 1ÐBÑ œ !, donde B − Q , e o facto de se ter
H0B œ ! implica que B é um ponto crítico de 0ÎQ e portanto 0 ÐBÑ um valor
crítico desta aplicação. Vemos portanto que .8 Ð0 ÐZ ÐG: Ï G:" ÑÑÑ œ !
pelo que, mais uma vez pelo lema anterior, 0 ÐG: Ï G:" Ñ tem medida nula.
g) Vamos utilizar nesta alínea as normas do máximo de ‘7 e ‘8 como
normas de trabalho, reparando que, se B œ ÐB" ß á ß B7 Ñ − ‘7 e < !, a
bola fechada F < ÐBÑ não é mais do que o produto de intervalos #
7
4œ"
ÒB4 <ß B4 <Ó.
Seja B! œ ÐB! " ß á ß B ! 7 Ñ − G_ arbitrário e fixemos < ! tal que
F < ÐB! Ñ § Y . Mostremos, por indução em :, a existência, para cada : !,
de um número real V: ! tal que, sempre que B − F < ÐB! Ñ G_ e
C − F < ÐB! Ñ, se tenha
m0 ÐCÑ 0 ÐBÑm Ÿ V: mC Bm: .2
Para : œ !, basta-nos tomar para V! o máximo da função contínua
m0 ÐCÑ 0 ÐBÑm sobre o compacto F < ÐB! Ñ ‚ F < ÐB! Ñ. Suponhamos o resultado
verdadeiro para um certo : e para qualquer aplicação suave definida em Y e
com valores num espaço vectorial normado de dimensão finita (a constante
2Esta
demonstração por indução podia ser substituída por uma aplicação da fórmula de
Taylor numa versão conveniente.
26
Cap. I. Medida e Integração em Variedades
V: dependendo evidentemente da função). Podemos então, para a função
s : ! tal que, sempre
suave H0 , que se anula nos pontos de G_ , escolher V
que B − F < ÐB! Ñ G_ e C − F < ÐB! Ñ, se tenha
s : mC Bm: ,
mH0C m œ mH0C H0B m Ÿ V
e deduzimos daqui, pelo teorema da média,
s : mC Bm:" ,
m0 ÐCÑ 0 ÐBÑm Ÿ V
s : , para terminar a demonstração por
bastando-nos portanto tomar V:" œ V
indução da nossa asserção. Fixemos agora um natural R " e reparemos
que F < ÐB! Ñ vai ser união dos R 7 subconjuntos do tipo F <ÎR ÐB! Ñ, com B! da
forma
ÐB! " <
Ð#5" "Ñ<
Ð#57 "Ñ<
ß á ß B! 7 <
Ñ,
R
R
com " Ÿ 5" Ÿ R ß á ß " Ÿ 57 Ÿ R (olhar para cada uma destas bolas na
forma de um produto de intervalos). Se ! fôr um índice tal que em F <ÎR ÐB! Ñ
exista um ponto D − G_ , vem, para cada B − F <ÎR ÐB! Ñ,
m0 ÐBÑ 0 ÐDÑm Ÿ V : mB Dm: Ÿ V: Ð
#< :
Ñ ,
R
:
o que mostra que 0 ÐF <ÎR ÐB! ÑÑ § F V Ð0 ÐDÑÑ, com V œ V: Ð #<
R Ñ , e portanto
.8 Ð0 ÐF <ÎR ÐB! ÑÑÑ Ÿ Ð#V: Ð
#< : 8
Ñ Ñ
R
(atender, mais uma vez, à caracterização das bolas de ‘8 como produtos de
intervalos). Somando as desigualdades anteriores, para os índices ! tais que
F <ÎR ÐB! Ñ G_ não é vazio, concluímos que
.8 Ð0 ÐF < ÐB! Ñ G_ ÑÑ Ÿ R 7 Ð#V: Ð
#< : 8
Ñ Ñ œ Ð#V: Ð#<Ñ: Ñ8 R 7:8 .
R
Fixando : tal que 7 :8 !, o segundo membro da desigualdade anterior
converge para ! quando R converge para _, pelo que, passando ao limite
essa desigualdade, concluímos que .8 Ð0 ÐF < ÐB! Ñ G_ ÑÑ œ !, donde
também, para a bola aberta, .8 Ð0 ÐF< ÐB! Ñ G_ ÑÑ œ !. Aplicando o lema
anterior, concluímos agora que 0 ÐG_Ñ tem medida nula.
h) Tal como observámos em d), o que vimos nas três últimas alíneas mostra
que o teorema de Sard, com Q de dimensão 7, está demonstrado no caso
s é ‘8 . Passemos, por fim, à
particular em que Q é um aberto de ‘7 e Q
s um aberto de
demonstração no caso geral. Seja B! − G arbitrário. Sejam Z
s , com 0 ÐB! Ñ − Z
s, Y
s um aberto de ‘8 e <À Z
s ÄY
s um difeomorfismo.
Q
Sejam Z um aberto de Q , com B! − Z , Y um aberto de ‘7 e :À Y Ä Z um
§5. Teorema de Sard
27
difeomorfismo; se necessário reduzindo estes abertos, podemos já supor que
s . O facto de a derivada de um difeomorfismo ser um isomorfismo
0 ÐZ Ñ § Z
implica, tendo em conta o teorema de derivação da função composta, que
s § ‘8 se, e só se, :ÐBw Ñ é
Bw − Y é um ponto crítico de < ‰ 0ÎZ ‰ :À Y Ä Y
um ponto crítico de 0 , pelo que 0 ÐG Z Ñ é a imagem por <" do conjunto
dos valores críticos de < ‰ 0ÎZ ‰ :, conjunto esse que tem medida nula, pelo
caso particular já estudado. Concluímos assim, tendo em conta I.3.4, que
0 ÐG Z Ñ tem medida nula, pelo que, mais uma vez pelo lema anterior,
0 ÐGÑ tem medida nula.
I.5.7 (Nota) Uma vez que a definição de ponto crítico ou de valor crítico apenas
faz intervir a derivada de primeira ordem da função 0 , poderíamos ser
levados a pensar na possibilidade de o teorema de Sard ser verdadeiro apenas
com a exigência de 0 ser de classe G " . Se examinarmos a demonstração
precedente, verificamos que tivémos necessidade de trabalhar com derivadas
de ordem superior e, de facto, um exemplo clássico de Whitney (cf. [20])
mostra que a classe G " não é em geral suficiente. Com uma demonstração
mais cuidadosa, pode-se verificar que o teorema é válido para as aplicações
de classe G : , onde o inteiro : depende apenas de 7 e 8 (cf. [4], problema 2
de XVI.23). Por exemplo, quando 7 Ÿ 8, pode-se mostrar que a classe G " é
suficiente.
s §I
s duas variedades sem bordo, com
I.5.8 (Corolário) Sejam Q § I e Q
s uma aplicação suave.
dimensões 7 e 8, respectivamente, e seja 0 À Q Ä Q
s
Para cada aberto não vazio Z de Q , existe então um elemento C − Z que
seja valor regular de 0 .
Dem: Se isso não acontecesse, Z estaria contido no conjunto dos valores
críticos de 0 , que ia ter então medida estritamente positiva (cf. I.2.17).
s §I
s duas variedades sem bordo, com
I.5.9 (Corolário) Sejam Q § I e Q
s uma aplicação suave.
dimensões 7 e 8, respectivamente, e seja 0 À Q Ä Q
s , tendo portanto,
Se 7 8, tem-se então que 0 ÐQ Ñ tem medida nula em Q
s
em particular, interior vazio em Q .
Dem: Basta atender a que todos os elementos de 0 ÐQ Ñ são trivialmente
valores críticos de 0 .
EXERCÍCIOS
Ex I.1 Sejam I e J espaços euclidianos e 0À I Ä J um isomorfismo. Seja
B" ß á ß B8 uma base de I , não obrigatoriamente ortonormada, e sejam, para
" Ÿ 3ß 4 Ÿ 8, 1w3ß4 œ ØB3 ß B4 Ù e 13ß4 œ Ø0ÐB3 Ñß 0ÐB4 ÑÙ. Mostrar que o coeficiente
de dilatação -0 é então igual à raiz quadrada do quociente do determinante da
matriz dos 13ß4 pelo determinante da matriz dos 1w3ß4 . Sugestão: Utilizar I.1.15,
28
Cap. I. Medida e Integração em Variedades
compondo 0 com um isomorfismo (À ‘8 Ä I , que aplique o elemento /3 da
base canónica em B3 .
Ex I.2 Sejam I um espaço euclidiano, Q § I um conjunto, N § ‘ um intervalo com mais que um elemento, e 0 À N Ä Q um difeomorfismo. Mostrar
que Q é então uma variedade de dimensão " e que .ÐQ Ñ œ 'N m0 w Ð>Ñm .>.
Ex I.3 Calcular .ÐQ Ñ, onde Q § ‘$ é o hemisfério
Q œ ÖÐBß Cß DÑ ± B# C# D # œ ", D !×,
que é uma variedade de dimensão #. Sugestão: Mostrar que se tem
.ÐQ Ñ œ .ÐQ w Ñ, onde Q w é a variedade de dimensão #,
Q w œ ÖÐBß Cß DÑ ± B# C# D # œ ", D !×.
Ex I.4 (Lema de Álgebra Linear) Sejam dados 8 números, reais ou complexos,
+" ß á ß +8 , e consideremos a matriz do tipo 8 ‚ 8, cujo elemento da linha 3 e
coluna 4 é $3ß4 +3 +4 . Mostrar que o determinante desta matriz é igual a
" +"# â +8# . O que se poderá dizer, sem repetir a demonstração, sobre
o determinante da matriz de elementos $3ß4 +3 +4 ?
Ex I.5 Seja Q § ‘7 uma variedade de dimensão 7, seja 0 À Q Ä ‘ uma
aplicação suave e seja K § ‘7" o respectivo gráfico,
K œ ÖÐBß >Ñ − ‘7 ‚ ‘ ± B − Q , > œ 0 ÐBÑ×.
Mostrar que K é uma variedade de dimensão 7 e que
`0
`0
.ÐKÑ œ ( Ë"
ÐBÑ# â
ÐBÑ# . .7 ÐB" ß á ß B7 Ñ.
`B
`B
"
7
Q
Ex I.6 Calcular a área do elipsóide de revolução de ‘$ ,
Q œ ÖÐBß Cß DÑ ± #B# #C# D # œ #×.
Ex I.7 Sejam I um espaço euclidiano, de dimensão 7 ", e \ § I um
boreliano. Mostrar que se tem
.I Ð\Ñ œ (
_
!
.W> ÐW> \Ñ .>,
onde, para cada < !, W< é a hipersuperfície esférica de centro ! e raio <
(variedade de dimensão 7 ").
Ex I.8 Sejam I um espaço euclidiano e G § I um cone boreliano. Define-se
então o ângulo sólido de G (ou simplesmente ângulo, se I tem dimensão #)
como sendo o número real maior ou igual a !
Exercícios
29
+81ÐGÑ œ .W ÐW GÑ,
onde W é a hipersuperfície esférica de centro ! e raio " de I . Suponhamos
agora que I tem dimensão #, e sejam B e C dois vectores linearmente independentes de I . Seja G o conjunto dos vectores =B >C , com
=ß > − Ò!ß _Ò. Mostrar que G é um cone boreliano, que ! +81ÐGÑ 1 e
que
cosÐ+81ÐGÑÑ œ
ØBß CÙ
.
mBmmCm
Sugestão: Pode-se já supor que B e C têm norma ". Considerar o real
! − Ó!ß 1Ò tal que cosÐ!Ñ œ ØBß CÙ e o vector
Aœ
"
cosÐ!Ñ
C
B.
sinÐ!Ñ
sinÐ!Ñ
Mostrar que Bß A é uma base ortonormada de I e que tem lugar uma bijecção suave 0 À Ò!ß #1Ò Ä W , definida por
0 Ð>Ñ œ cosÐ>ÑB sinÐ>ÑA.
Mostrar que se tem
0 Ð>Ñ œ
sinÐ! >Ñ
sinÐ>Ñ
B
C,
sinÐ!Ñ
sinÐ!Ñ
e deduzir que a restrição de 0 é um difeomorfismo de Ò!ß !Ó sobre G W .
Nota: Este exercício permite fazer a ponte entre a definição intuitiva de
ângulo de dois vectores e a respectiva definição formal, feita a partir da
ØBßCÙ
equação cosÐ!Ñ œ mBmmCm
.
Ex I.9 Seja I um espaço euclidiano de dimensão 7. Para cada número real
! !, seja 0! À I Ä ‘ a aplicação contínua, definida por
0! ÐBÑ œ
"
.
" mBm!
Determinar para que valores de ! a função 0! tem integral finito, relativamente à medida .I .
Ex I.10 Demonstrar a fórmula
B
( / .B œ È1,
#
‘
#
#
#
#
tendo em conta a identidade /B C œ /B ‚ /C e calculando o integral
desta função em ‘# de dois modos distintos, utilizando, por um lado, o
teorema de Fubini e, por outro lado, coordenadas polares (eventualmente
30
Cap. I. Medida e Integração em Variedades
generalizadas). Utilizar um truque análogo para calcular, para cada inteiro
#
_
8 !, o integral '! B8 /B .B, em função das constantes 58 .
Ex I.11 Sejam I um espaço euclidiano de dimensão 8 e Q § I uma variedade
de dimensão 7, compacta e não vazia. Chama-se então centro de figura ou
baricentro de Q o vector de I
,+<ÐQ Ñ œ
"
( B . .Q ÐBÑ
.ÐQ Ñ Q
(reparar que se trata de um integral de uma função vectorial).
a) Mostrar que a definição anterior não apresenta problemas, isto é, que
.ÐQ Ñ é finito e não nulo e que a função integranda é efectivamente
integrável;
b) Mostrar que, se + − I , então ,+<Ð+ Q Ñ œ + ,+<ÐQ Ñ
(comportamento do baricentro com as translações);
c) Mostrar que, se 0À I Ä I é um isomorfismo ortogonal ou uma homotetia,
então ,+<Ð0ÐQ ÑÑ œ 0Ð,+<ÐQ ÑÑ;
d) Mostrar que, se 0À I Ä I é um isomorfismo arbitrário, e se 7 œ 8, então
,+<Ð0ÐQ ÑÑ œ 0Ð,+<ÐQ ÑÑ;
e) No caso em que a variedade Q tem um certo grau de simetria, pode-se,
em geral, garantir a priori que o baricentro de Q se localiza num certo
subconjunto de I . Assim, por exemplo, ninguém terá a mínima dúvida em
prever que o baricentro de um triângulo isósceles se encontra sobre a
mediatriz da base e que o baricentro de um círculo ou de um quadrado se
encontra no respectivo centro. Dar uma definição conveniente de elemento
de simetria de uma variedade Q § I , de modo a poder garantir que, se uma
variedade Q possui um tal elemento de simetria, então o seu baricentro
pertence a esse elemento de simetria. No sentido de simplificar, limitar a
definição ao caso em que o elemento de simetria é um subespaço vectorial de
I, o caso geral, em que ele pode ser um subespaço afim, reduzindo-se a este,
tendo em conta o comportamento do baricentro com as translações.
Ex I.12 Seja E § Ó!ß _Ò ‚ ‘ uma variedade de dimensão 8 (onde 8 pode ser
!, " ou #). Seja F § ‘$ o conjunto de revolução definido por E:
F œ ÖÐBß Cß DÑ ± ÐÈB# C# ß DÑ − E×
(uma superfície de revolução, se 8 œ ", um sólido de revolução se 8 œ #).
Exercícios
31
Figura 1
Mostrar que, sendo W a circunferência de centro ! e raio " de ‘# , F é uma
variedade de dimensão 8 ", difeomorfa a W ‚ E, e que
.ÐFÑ œ #1( B . .E ÐBß CÑ
E
(cf. a figura 1).
Ex I.13 Verificar que o exercício anterior implica os dois teoremas seguintes
(teoremas de Pappus):
1) A área descrita por uma curva plana, que roda em torno dum eixo desse
plano, de um dos lados do qual ela está, é igual ao produto do comprimento
da curva pelo perímetro da circunferência descrita pelo seu baricentro.
2) O volume do sólido de revolução, descrito por uma área plana, que roda
em torno de um eixo, de um dos lados do qual ela está, é igual ao produto da
área da figura pelo perímetro da circunferência descrita pelo seu baricentro.
Mostrar como estes resultados podem ser úteis, para determinar, sem contas,
a área exterior e o volume de um anel de espessura #< e diâmetro máximo
#< #V, ou a localização do baricentro de um semi-círculo ou de uma
semi-circunferência.
Ex I.14 Seja 8 " e notemos W a hipersuperfície esférica de ‘8" de centro ! e
raio ". Consideremos a aplicação
32
Cap. I. Medida e Integração em Variedades
0 À ‘8 Ä W Б8 ‚ Ó!ß _ÒÑ,
definida por
0 ÐDÑ œ Ð
D
"
ß
Ñ
È" mDm# È" mDm#
Figura 2
(aplicação inversa da projecção central). Mostrar que 0 é um difeomorfismo
e calcule o coeficiente de dilatação -H0 ÐBÑ (Sugestão: Exercício I.4). Utilizar
este resultado para mostrar que se tem, para cada 8 ",
58 œ 58" ‚ (
_
!
#>8"
ÐÈ" ># Ñ8"
.>.
Ex I.15 Seja 8 " e notemos W a hipersuperfície esférica de ‘8" , de centro ! e
´
raio ". Consideremos a projecção estereografica
0 À W Ï ÖÐ!ß "Ñ× Ä ‘8 ,
definida por
0 ÐBß >Ñ œ
(onde se identifica ‘8" a ‘8 ‚ ‘).
B
">
Exercícios
33
Figura 3
Mostrar que 0 é um difeomorfismo, e utilizar o difeomorfismo inverso para
provar que
58 œ (
‘8
#8
.C.
Ð" mCm# Ñ8
Utilizando coordenadas esféricas generalizadas para calcular o integral anterior, obter a seguinte fórmula de recorrência:
58 œ 58" ‚ (
_
!
#8 >8"
.>.
Ð" ># Ñ8
Ex I.16 Seja 8 " e notemos W e W w as hipersuperfícies esféricas de centro ! e
raio ", de ‘8" e de ‘8 , respectivamente. Consideremos a aplicação
1 1
0 À Ó ß Ò ‚ W w Ä W Ï ÖÐ!ß "Ñß Ð!ß "Ñ×,
# #
definida por
0 Ð>ß BÑ œ ÐcosÐ>ÑBß sinÐ>ÑÑ
(podemos dizer que > é a latitude e B a longitude generalizada de 0 Ð>ß BÑ).
a) Mostrar que 0 é um difeomorfismo e que
-H0 Ð>ßBÑ œ cosÐ>Ñ8" .
b) Utilizar a alínea anterior para mostrar que, para cada 8 ", tem lugar a
34
Cap. I. Medida e Integração em Variedades
seguinte fórmula de recorrência
58 œ 58" ‚ (
1
#
1#
cosÐ>Ñ8" .>.
s um espaço
Ex I.17 (O integral paramétrico) Sejam I um espaço euclidiano, I
s
s
vectorial de dimensão finita e Q § I e Q § I duas variedades, a primeira
das quais compacta e de dimensão 7. Sejam J um espaço vectorial de
s Ä J uma aplicação de classe G " .
dimensão finita e 0 À Q ‚ Q
s Ä J , definida
a) Mostrar que tem lugar uma aplicação de classe G " , 1À Q
por
1ÐCÑ œ ( 0 ÐBß CÑ . .Q ÐBÑ,
Q
s e A − XC ÐQ
s Ñ, tem-se
e que, para cada C − Q
H1C ÐAÑ œ ( H# 0ÐBßCÑ ÐAÑ . .Q ÐBÑ.
Q
b) Mostrar que, no caso em que a aplicação 0 é de classe G 5 (onde
" Ÿ 5 Ÿ _), a aplicação 1 é também de classe G 5 .
s de I
s , contendo Q
s e tal que Q
s seja
Sugestão: Considerando um aberto Y
s , 0 pode ser prolongada a Q ‚ Y
s , como aplicação de classe
fechado em Y
s é um
G 5 , o que permite demonstrar apenas o caso particular em que Q
s
aberto de I . Do mesmo modo, sendo Y um aberto de I , contendo Q , tal
s , como aplicação
que Q seja fechado em Y , 0 pode ser prolongada a Y ‚ Q
5
de classe G . Fazendo uma indução em 5 , basta demonstrar o caso em que
5 œ ". Utilizando a continuidade uniforme, no sentido forte, de 0 sobre um
compacto Q ‚ ÖC! × e o facto de se ter .ÐQ Ñ _, demonstrar a
continuidade de 1 em C! . Utilizando a continuidade uniforme, no sentido
forte, de H0 sobre um compacto Q ‚ ÖC! ×, mostrar que, dado $ !, vem,
para C suficientemente próximo de C! e B − Q , mH0ÐBßCÑ H0ÐB! ßC! Ñ m Ÿ $ ,
aplicando, em seguida, o teorema da média para majorar
m1ÐCÑ 1ÐC! Ñ ( H# 0ÐBßC! Ñ ÐC C! Ñ . .Q ÐBÑm.
Q
Ex I.18 (Teorema de Sard para variedades com bordo) Sejam Q § I e
s §I
s variedades, a segunda das quais sem bordo, e 0 À Q Ä Q
s uma
Q
aplicação suave. Generalizando o que foi feito no caso em que Q também
não tem bordo, dizemos que um ponto B − Q é um ponto regular de 0 se,
sendo 4 ! tal que B − `4 ÐQ Ñ, B é um ponto regular da restrição
s e, caso contrário, dizemos que B é um ponto crítico de
0Î`4 ÐQ Ñ À `4 ÐQ Ñ Ä Q
s que são
0 . Como antes, chamam-se valores críticos de 0 aos elementos de Q
Exercícios
35
imagem de algum ponto crítico e valores regulares de 0 aos restantes
s . Mostrar que o conjunto dos valores críticos de 0 tem
elementos de Q
s . Sugestão: Aplicar o teorema de Sard já estudado à
medida nula em Q
restrição de 0 a cada um dos `4 ÐQ Ñ.
Ex I.19 Sejam I um espaço vectorial de dimensão 8, Y um aberto de I e
O § Y um conjunto compacto. Mostrar que existe uma variedade compacta,
sem cantos, de dimensão 8, Q § Y , tal que O § `! ÐQ Ñ. Sugestão: Pelo
teorema da partição da unidade, e depois de substituir eventualmente Y por
um aberto mais pequeno que seja limitado, considerar uma função suave
0 À I Ä Ò!ß "Ó, nula fora duma certa parte compacta de Y e tal que 0 ÐBÑ œ ",
para cada B − O . Construir a variedade Q a partir dum valor regular de 0 no
intervalo Ó!ß "Ò.
Ex I.20 Sejam I um espaço vectorial de dimensão 7, E § I uma variedade de
dimensão 8, eventualmente com bordo, J um espaço vectorial de dimensão
R e 0 À E Ä J uma imersão injectiva, isto é, uma aplicação injectiva de
classe G _ tal que, para cada B − E, H0B À XB ÐEÑ Ä J seja uma aplicação
linear injectiva.
a) Supondo que R #8 " e considerando em J um produto interno, mostrar que existe um subespaço vectorial K § J , com dimensão R ", tal que,
sendo 1K À J Ä K a projecção ortogonal, a aplicação 1K ‰ 0 À E Ä K seja
ainda uma imersão injectiva. Sugestão (cf. Guillemin e Pollack): Considerar
as aplicações suaves 1À E ‚ E ‚ ‘ Ä J e 2À X ÐEÑ Ä J , definidas por
1ÐBß Cß >Ñ œ >Ð0 ÐBÑ 0 ÐCÑÑ e 2ÐBß ?Ñ œ H0B Ð?Ñ, e utilizar o teorema de Sard
para determinar A Á ! em J que não pertença à imagem de nenhuma
daquelas aplicações. Tomar para K o espaço dos vectores ortogonais a A.
b) Raciocinando por indução, mostrar que existe uma imersão injectiva
2À E Ä ‘#8" .
Ex I.21 Chama-se grupo de Lie a uma variedade K § I , munida de uma
estrutura de grupo cuja multiplicação seja suave, enquanto aplicação
K ‚ K Ä K.
a) Se K § I é um grupo de Lie, mostrar que, para cada B − K , têm lugar
difeomorfismos PB À K Ä K e VB À K Ä K , definidos por PB ÐCÑ œ B † C e
VB ÐCÑ œ C † B. Deduzir daqui que um grupo de Lie é sempre uma variedade
sem bordo e com a mesma dimensão em todos os pontos.
s§I
s um morfismo de
s grupos de Lie e 0 À K Ä K
b) Sejam K § I e K
s os elementos neutros e B − K, mostrar
grupos suave. Sendo / − K e s/ − K
s é injectiva (resp.
que a aplicação linear H0B À XB ÐKÑ Ä X0 ÐBÑ ÐKÑ
s for injectiva
sobrejectiva) se, e só se, a aplicação linear H0/ À X/ ÐKÑ Ä Xs/ ÐKÑ
(resp. sobrejectiva). Sugestão: Verificar que a primeira pode ser obtida por
composição da segunda com dois isomorfismos, um à esquerda e outro à
direita.
s§I
s um morfismo de
s grupos de Lie e 0 À K Ä K
c) Sejam K § I e K
36
Cap. I. Medida e Integração em Variedades
grupos suave e sobrejectivo. Utilizar o teorema de Sard e a alínea precedente
s é sobrejectiva.
para deduzir que a aplicação linear H0/ À X/ ÐKÑ Ä Xs/ ÐKÑ
CAPÍTULO II
Tópicos de Álgebra Multilinear
§1. Relações entre espaços vectoriais reais e complexos.
II.1.1. Ao longo desta exposição, todos os espaços vectoriais que vamos
considerar serão espaços vectoriais reais ou complexos, e notaremos Š o
respectivo corpo dos escalares, que é portanto ‘ ou ‚. Por vezes será natural
considerar situações em que alguns dos espaços vectoriais de que falamos
podem ser reais ou complexos e outros, de modo mais ou menos
independente, podem também ser reais ou complexos. Para nos referirmos a
uma situação deste tipo, diremos que temos uns espaços vectoriais sobre Š e
outros espaços vectoriais sobre Šw . Num tal contexto, quando escrevermos
Š § Šw , queremos significar que, ou Š e Šw coincidem, ou Š œ ‘ e Šw œ ‚.
II.1.2. Se I é um espaço vectorial complexo, I pode ser também olhado, de
modo trivial, como espaço vectorial real. Basta, com efeito, ter em conta o
facto de cada número real poder ser olhado como um número complexo. Do
mesmo modo, se I e J são espaços vectoriais complexos, e se 0À I Ä J é
uma aplicação linear, então 0 é também uma aplicação linear, quando se
considera I e J como espaços vectoriais reais. Quando, ao falarmos de uma
aplicação linear, for importante explicitar se estamos a considerar os espaços
vectoriais envolvidos como sendo reais ou complexos, diremos respectivamente que temos uma aplicação linear real ou uma aplicação linear
complexa.
II.1.3. Suponhamos que I é um espaço vectorial complexo. Vamos chamar
aplicação de estrutura de I à aplicação linear N À I Ä I , definida por
N ÐBÑ œ 3B. Trata-se de uma aplicação linear complexa (portanto também
uma aplicação linear real), que verifica a condição N ‰ N œ M.I .
II.1.4. Suponhamos que I é um espaço vectorial real e que N À I Ä I é uma
aplicação linear (real, evidentemente), verificando N ‰ N œ M.I . Existe
então sobre I uma, e uma só, estrutura de espaço vectorial complexo, cuja
estrutura de espaço vectorial real associada seja a estrutura de partida e cuja
aplicação de estrutura seja N . Mais precisamente, para cada complexo
- œ + ,3, com +ß , − ‘, e cada B − I , tem-se -B œ +B ,N ÐBÑ.
Dem: É imediato constatar que a existir uma tal estrutura de espaço vectorial
complexo, a multiplicação de um complexo - œ + ,3 por um vector B − I
não pode deixar de ser igual a +B ,N ÐBÑ, o que implica em particular a
afirmação de unicidade do enunciado. Definindo a multiplicação de um
38
Cap. II. Tópicos de Álgebra Multilinear
complexo por um vector pela citada fórmula, a única propriedade um pouco
menos trivial que é necessário verificar para vermos que temos uma estrutura
de espaço vectorial complexo é a de que se tem -Ð- w BÑ œ Ð-- w ÑB. Ora, sendo
- œ + ,3 e - w œ +w ,w 3, obtemos
-Ð- w BÑ œ -Ð+w B ,w N ÐBÑÑ œ +Ð+w B ,w N ÐBÑ ,N Ð+w B ,w N ÐBÑÑ œ
œ ++w B +,w N ÐBÑ ,+w N ÐBÑ ,,w N ÐN ÐBÑÑ œ
œ Ð++w ,,w ÑB Ð+,w ,+w ÑN ÐBÑ œ
œ ÐÐ++w ,,w Ñ Ð+,w ,+w Ñ3ÑB œ Ð-- w ÑB.
É agora trivial constatar que a estrutura de espaço vectorial real associada a
esta estrutura de espaço vectorial complexo é a estrutura dada e que a
aplicação de estrutura é precisamente N .
II.1.5. Tendo em conta o que acabamos de ver, chama-se estrutura complexa de
um espaço vectorial real I a uma aplicação linear N À I Ä I , verificando
N ‰ N œ M.I . Concluímos portanto que é equivalente considerar um
espaço vectorial complexo ou um espaço vectorial real, munido de uma
estrutura complexa.
II.1.6. Sejam I e J espaços vectoriais complexos, com aplicações de estrutura
N e N w , respectivamente. Se 0À I Ä J é uma aplicação linear real, tem-se
que 0 é uma aplicação linear complexa se, e só se, para cada B − I , se tem
0ÐN ÐBÑÑ œ N w Ð0ÐBÑÑ.
Dem: A condição necessária é evidente e, quanto à condição suficiente, dado
um complexo - œ + ,3, vemos que
0Ð-BÑ œ 0Ð+B ,N ÐBÑÑ œ +0ÐBÑ ,0ÐN ÐBÑÑ œ
œ +0ÐBÑ ,N w Ð0ÐBÑÑ œ - 0ÐBÑ.
II.1.7. Suponhamos que I é um espaço vectorial complexo, com aplicação de
estrutura N À I Ä I . É então imediato constatar que a aplicação linear N é
também uma estrutura complexa sobre o espaço vectorial real associado. A
estrutura de espaço vectorial complexo, definida por N , diz-se conjugada
da de partida, e usa-se a notação I para notar o espaço vectorial complexo
conjugado de I . Repare-se que, como é imediato constatar, o produto de um
complexo - por um vector B, para a estrutura de I , é igual ao produto do
complexo conjugado - por B, para a estrutura de I . Por vezes será cómodo
usar a notação I , no caso em que I é um espaço vectorial real, como
significando o mesmo que I .
II.1.8. Se I é um espaço vectorial complexo, uma família ÐB4 Ñ4−N é linearmente
independente, é geradora, ou é base se, e só se, isso acontecer em relação ao
espaço vectorial complexo conjugado I . No caso em que a família é uma
base, as componentes de um vector B − I para a estrutura de I são os
§1. Relações entre espaços vectoriais reais e complexos
39
complexos conjugados das componentes para a estrutura de I .
Dem: Trata-se de uma consequência imediata das definições.
II.1.9. Dados os espaços vectoriais complexos I e J , com as aplicações de
estrutura N e N w , chama-se aplicação antilinear de I em J a uma aplicação
linear real 0À I Ä J , que verifica
0ÐN ÐBÑÑ œ N w Ð0ÐBÑÑ.
É imediato constatar que as aplicações antilineares de I em J são precisamente a mesma coisa que as aplicações lineares complexas de I em J e que
as aplicações lineares complexas de I em J . Em particular, uma aplicação
linear real 0À I Ä J é uma aplicação antilinear se, e só se, ela verifica
0Ð-BÑ œ - 0ÐBÑ, para cada - − ‚ e cada B − I .
II.1.10. Seja I um espaço vectorial complexo, de dimensão finita ou infinita, e
seja ÐB4 Ñ4−N uma família de vectores de I . Tem-se então que esta família é
linearmente independente, é geradora, ou é uma base, se, e só se, o mesmo
acontecer à família formada pelos B4 e pelos 3B4 , relativamente à estrutura de
espaço vectorial real associada de I . Em particular, se I tiver dimensão
finita 8, como espaço vectorial complexo, então I tem dimensão #8, como
espaço vectorial real.
Dem: Trata-se de uma consequência imediata das definições.
II.1.11. (Corolário) Se I é um espaço vectorial real de dimensão 8, então I
admite uma estrutura complexa se, e só se, 8 é par.
Dem: Pelo que acabámos de ver, se I tivesse dimensão infinita, como
espaço vectorial complexo, então I tinha dimensão infinita, como espaço
vectorial real, e se I tivesse dimensão 5 , como espaço vectorial complexo,
então I tinha dimensão #5 , como espaço vectorial real. Concluímos portanto
que, se I admite uma estrutura complexa, então tem que ser 8 œ #5 , pelo
que 8 é par. Reciprocamente, se I tem dimensão #5 , podemos considerar
uma base B" ß á ß B#5 e definir uma aplicação linear N À I Ä I por
N ÐB#4" Ñ œ B#4 e N ÐB#4 Ñ œ B#4" (lembrar que uma aplicação linear fica
determinada, se dermos de modo arbitrário as imagens dos elementos de uma
base), aplicação que se verifica imediatamente ser uma estrutura complexa de
I.
§2. Espaços de aplicações multilineares.
II.2.1. Sejam I e J espaços vectoriais. Para cada : ", notaremos P: ÐIà J Ñ o
espaço vectorial cujos elementos são as aplicações :-lineares 0À I : Ä J , isto
é, as aplicações que, quando se fixam os valores de : " das variáveis, são
lineares na restante variável. É claro que, no caso em que : œ ", o espaço
vectorial P" ÐIà J Ñ não é mais do que o espaço das aplicações lineares de I
40
Cap. II. Tópicos de Álgebra Multilinear
em J , espaço que será notado também PÐIà J Ñ. Para : œ !, pomos, por
convenção, P! ÐIà J Ñ œ J . Será útil olhar para esta convenção como um
caso particular da definição geral, tendo em conta as seguintes observações:
I ! é um conjunto com um único elemento (a família vazia de vectores de I )
e qualquer aplicação de I ! em J vai ser !-linear; podemos portanto
identificar uma aplicação !-linear de I ! em J com o elemento de J ,
imagem do único elemento de I ! por essa aplicação.
Nas observações que acabamos de fazer, admitimos três situações:
a) I e J são espaços vectoriais reais; nesse caso P: ÐIà J Ñ é um espaço
vectorial real;
b) I e J são espaços vectoriais complexos; nesse caso P: ÐIà J Ñ é um espaço vectorial complexo;
c) I é um espaço vectorial real e J é um espaço vectorial complexo; neste
caso, P: ÐIà J Ñ é o espaço das aplicações multilineares, no sentido real, mas
tem uma estrutura natural de espaço vectorial complexo, que resulta da
estrutura complexa de J (de facto, temos um subespaço vectorial complexo
do espaço de todas as aplicações de I : em J ).
II.2.2. Quando quisermos tornar mais claro qual o sentido que se está a dar à
expressão P: ÐIà J Ñ, escreveremos P:‘ ÐIà J Ñ nos casos a) e c) e P:‚ ÐIà J Ñ
no caso b). Esta precisão é especialmente importante no caso em que I e J
são espaços vectoriais complexos: nesse quadro é frequente considerarmos,
para além do espaço das aplicações :-lineares complexas, o espaço das
aplicações :-lineares reais, isto é o espaço que se obtém quando se considera
I como espaço vectorial real; utilizamos então a notação P:‚ ÐIà J Ñ para o
primeiro espaço e a notação P:‘ ÐIà J Ñ para o segundo. É claro que
P:‚ ÐIà J Ñ vai ser um subespaço vectorial complexo de P:‘ ÐIà J Ñ.
II.2.3. Se nos quisermos referir, de uma forma abreviada, a uma situação em que
qualquer dos três casos a),b) e c), descritos em II.2.1, é permitido, diremos
que I é um espaço vectorial sobre Š e J um espaço vectorial sobre Šw , com
:
Š § Šw ; nesse caso, como dissémos, P: ÐIà J Ñ œ PŠ
ÐIà J Ñ é um espaço
w
vectorial sobre Š .
O resultado que apresentamos em seguida é a generalização natural, para
as aplicações multilineares, do resultado que diz que uma aplicação linear
fica determinada se dermos, de modo arbitrário, as imagens dos elementos
de uma dada base.
II.2.4. Sejam I e J espaços vectoriais, o primeiro dos quais munido de uma
base ÐB4 Ñ4−N . Sejam : " e ÐC4" ßáß4: Ñ uma família arbitrária de vectores de
J , indexada em N : . Existe então uma, e uma só, aplicação :-linear
0À I : Ä J tal que, quaisquer que sejam 4" ß á ß 4: em N ,
0ÐB4" ß á ß B4: Ñ œ C4" ßáß4: .
§2. Espaços de aplicações multilineares
41
Mais precisamente, dados A" ß á ß A: em I , com A5 œ ! +4ß5 B4 (para cada
4
5 , os +4ß5 são nulos, salvo para um número finito de valores de 4), tem-se
(*)
0ÐA" ß á ß A: Ñ œ " +4" ß" +4# ß# â +4: ß: C4" ß4# ßáß4: ,
4" ßáß4:
em que as parcelas do somatório anterior são nulas, salvo para um número
finito de valores de Ð4" ß á ß 4: Ñ.3
Dem: A unicidade de 0 e a fórmula (*) no enunciado resultam de que, se
0À I : Ä J é multilinear, e se A5 œ ! +4ß5 B4 , então tem-se sucessivamente
4
0ÐA" ß á ß A: Ñ œ " +4" ß" 0ÐB4" ß A# ß á ß A: Ñ œ
4"
œ " +4" ß" +4# ß# 0ÐB4" ß B4# ß á ß A: Ñ œ
4" ß4#
ã
œ " +4" ß" +4# ß# â +4: ß: 0ÐB4" ß B4# ß á ß B4: Ñ.
4" ßáß4:
Quanto à existência, definindo uma aplicação 0À I : Ä J pela igualdade (*)
no enunciado, é fácil constatar que temos uma aplicação multilinear e que
esta aplicação aplica ÐB4" ß á ß B4: Ñ em C4" ßáß4: (reparar que a decomposição
de B5 é B5 œ ! $4ß5 B4 ).
4
No que se segue, os espaços P: ÐIà J Ñ que teremos ocasião de aplicar
com mais frequência serão aqueles em que o espaço vectorial J é ‘ ou ‚.
Por esse motivo, e no sentido de aligeirar a exposição, vamos limitar o
nosso estudo ao desses casos particulares.
II.2.5. Suponhamos que I é um espaço vectorial de dimensão finita sobre Š,
com uma base ÐB4 Ñ4−N , e que Šw ¨ Š. Dado : ", notemos, para sistema
Ð4" ß á ß 4: Ñ de : índices de N , 04" ßáß4: À I : Ä Šw a aplicação :-linear definida
por
04" ßáß4: ÐB5" ß á ß B5: Ñ œ $4" ß5" ‚ â ‚ $4: ß5: ,
ou seja, 04" ßáß4: ÐB5" ß á ß B5: Ñ œ " se, e só se, 4" œ 5" , …, 4: œ 5: e
04" ßáß4: ÐB5" ß á ß B5: Ñ œ ! caso contrário.
3Para
quem não tenha medo de raciocinar com o conjunto vazio, este resultado é também
verdadeiro, e trivial, no caso em que : œ !. Comparar com as observações feitas em
II.2.1, a propósito de P! ÐIà J Ñ.
42
Cap. II. Tópicos de Álgebra Multilinear
Tem-se então que a família das aplicações lineares 04" ßáß4: é uma base do
espaço vectorial P: ÐIà Šw Ñ, sobre Šw (dita base associada às bases de
partida), e, para cada 0 − P: ÐIà Šw Ñ, tem-se
0 œ " 0ÐB4" ß á ß B4: Ñ 04" ßáß4: .
4" ßáß4:
Em particular, se I tem dimensão finita 7, P: ÐIà Šw Ñ tem dimensão 7: .4
Dem: Dado 0 − P: ÐIà Šw Ñ, o facto de se ter
0 œ " 0ÐB4" ß á ß B4: Ñ 04" ßáß4:
4" ßáß4:
resulta de que ambos os membros são aplicações multilineares de I : em Šw
que dão o mesmo resultado quando aplicados a qualquer ÐB5" ß á ß B5: Ñ
(reparar que a soma do segundo membro aplicada a este sistema de vectores
vai ter apenas uma parcela não nula, a correspondente a 4" œ 5" , …,
4: œ 5: ). A unicidade da decomposição resulta de modo análogo, se
repararmos que, se fosse
0 œ " +4" ßáß4: 04" ßáß4: ,
4" ßáß4:
concluíamos, aplicando ambos os membros a ÐB5" ß á ß B5: Ñ, que se tinha
0ÐB5" ß á ß B5: Ñ œ +5" ßáß5: .
II.2.6. Como caso particular do resultado precedente, se I é um espaço vectorial
de dimensão 7, sobre Š, com uma base ÐB4 Ñ4−N e se Šw ¨ Š, o espaço
vectorial PÐIà Šw Ñ, sobre Šw , tem dimensão 7 e uma base associada, constituída pelos 04 , com 4 − N onde a aplicação linear 04 À I Ä Š § Šw está
definida pela condição de aplicar B4 em " e todos os restantes B5 em !,
tendo-se, para cada 0 − PÐIà Šw Ñ, 0 œ ! 0ÐB4 Ñ 04 .
Uma interpretação importante das aplicações lineares 04 − PÐIà ŠÑ é a de
que, para cada B − I , os 04 ÐBÑ não são mais do que as componentes de B na
base dos B4 , isto é, que se tem
B œ " 04 ÐBÑ B4 .
Dem: Sendo B œ ! +4 B4 , vem
05 ÐBÑ œ " +4 05 ÐB4 Ñ œ " +4 $4ß5 œ +5 .
4Como
anteriormente, e desde que olhemos as coisas com suficiente cuidado, este
resultado é também válido, e trivial, para : œ !. A base correspondente de
P! ÐIà Šw Ñ œ Šw é simplesmente constituída pelo único elemento " − Šw .
§2. Espaços de aplicações multilineares
43
Como aplicação simples do resultado anterior, temos o resultado clássico
sobre a existência de um isomorfismo de qualquer espaço vectorial de
dimensão finita sobre o seu bidual.
II.2.7. Seja I um espaço vectorial sobre Š. Existe então uma aplicação linear
injectiva " À I Ä PÐPÐIà ŠÑà ŠÑ, de I no seu bidual, definida por
" ÐBÑÐ0Ñ œ 0ÐBÑ,
aplicação essa que é um isomorfismo, no caso em que I tem dimensão finita.
Dem: É imediato que " é uma aplicação linear. Para vermos que " é
injectiva, basta vermos que, dado B Á ! em I , existe 0 − PÐIà ŠÑ tal que
0ÐBÑ Á !, o que é uma consequência de II.2.4, visto que podemos considerar
uma base de I tendo B como um dos seus elementos e tomar para 0 a
aplicação linear definida pela condição de aplicar B em " e os restantes
elementos da base em !. Por fim, no caso em que I tem dimensão finita 7,
resulta do que vimos atrás que PÐPÐIà ŠÑà ŠÑ tem também dimensão 7,
pelo que a aplicação linear injectiva " tem que ser um isomorfismo.
II.2.8. Sejam I um espaço vectorial sobre Š, Šw ¨ Š e : ! e ; ! dois
inteiros. Existe então uma aplicação bilinear, entre espaços vectoriais
sobre Šw ,
Œ À P: ÐIà Šw Ñ ‚ P; ÐIà Šw Ñ Ä P:; ÐIà Šw Ñ,
que a cada par Ð0ß (Ñ de aplicações multilineares 0À I : Ä Šw e (À I ; Ä Šw ,
associa a aplicação multilinear 0 Œ (À I :; Ä Šw , definida por
0 Œ (ÐA" ß á ß A:; Ñ œ 0ÐA" ß á ß A: Ñ ‚ (ÐA:" ß á ß A:; Ñ.
Aos elementos de P: ÐIà ŠÑ, no caso em que Š é o corpo dos escalares de I ,
costuma-se dar o nome de tensores (mais precisamente, tensores covariantes)
de grau : sobre I . A 0 Π( costuma-se dar o nome de produto tensorial de 0
e (.
II.2.9. No caso particular em que : œ ! ou ; œ !, e portanto o correspondente
espaço é Šw , o produto tensorial não vai ser mais do que a multiplicação, à
esquerda ou à direita, pelos escalares. Esta afirmação será um caso particular
da definição anterior, se repararmos no modo como se identifica uma
aplicação de I ! em Šw com um elemento de Šw , ou poderá alternativamente
ser olhada como uma convenção por quem não se sentir bem com este tipo de
raciocínios.
II.2.10. (Associatividade) Sejam I um espaço vectorial sobre Š, Šw ¨ Š e
:ß ;ß < 0 três inteiros. Dados 0 − P: ÐIà Šw Ñ, ( − P; ÐIà Šw Ñ e
3 − P< ÐIà Šw Ñ, tem-se então
Ð0 Œ (Ñ Œ 3 œ 0 Œ Ð( Œ 3Ñ − P:;< ÐIà Šw Ñ.
44
Cap. II. Tópicos de Álgebra Multilinear
Dem: Basta reparar que ambos os membros dão o mesmo resultado, a saber,
0ÐA" ß á ß A: Ñ (ÐA:" ß á ß A:; Ñ 3ÐA:;" ß á ß A:;< Ñ,
quando aplicados a ÐA" ß á ß A:;< Ñ.
II.2.11. Como é usual, sempre que tem lugar uma propriedade associativa, faz
sentido referirmo-nos, sem parênteses, ao produto tensorial de 5 factores: Se,
para cada " Ÿ 4 Ÿ 5 , -4 − P:4 ÐIà Šw Ñ, fica bem definido um produto
tensorial
-" Œ -# Œ â Œ -5 − P:" :# â:5 ÐIà Šw Ñ.
II.2.12. No caso em que o espaço vectorial I tem dimensão finita e está munido
de uma base ÐB4 Ñ4−N , é imediato constatar que os elementos 04" ßáß4: da base
associada de P: ÐIà Šw Ñ estão também definidos por
04" ßáß4: œ 04" Œ â Œ 04: .
Note-se que, embora associativo, o produto tensorial não é, em geral,
comutativo. Por exemplo, se 0 e ( são tensores de grau ", tem-se, em
geral,
0 Œ (ÐBß CÑ œ 0ÐBÑ(ÐCÑ Á (ÐBÑ0ÐCÑ œ ( Œ 0ÐBß CÑ.
Tem-se, no entanto, 0 Œ ( œ ( Œ 0, no caso em que o grau de 0 é zero ou
o grau de ( é zero, visto que, em ambos os casos, temos a multiplicação
de um escalar por uma aplicação multilinear.
II.2.13. Sejam I e J espaços vectoriais sobre Š e -À I Ä J uma aplicação
linear. Se Šw ¨ Š, existe então, para cada : !, uma aplicação linear entre
espaços vectoriais sobre Šw ,
-‡ À P: ÐJ à Šw Ñ Ä P: ÐIà Šw Ñ,
definida por -‡ Ð0Ñ œ 0 ‰ -: , isto é,
-‡ Ð0ÑÐA" ß á ß A: Ñ œ 0Ð-ÐA" Ñß á ß -ÐA: ÑÑ.
Dizemos que -‡ Ð0Ñ é a imagem recíproca de 0 por meio de - e que -‡ é a
aplicação linear dual de -.5
II.2.14. Um caso particular trivial, mas importante, de imagem recíproca é aquele
em que I é um subespaço vectorial de J e tomamos para +À I Ä J a
aplicação linear inclusão. A imagem recíproca +‡ Ð0Ñ não é mais do que a
claro que, no caso em que : œ !, a aplicação linear -‡ não é mais do que a identidade
de Šw .
5É
§2. Espaços de aplicações multilineares
45
restrição de 0 a I : , restrição essa que é notada por vezes, um pouco
abusivamente, 0ÎI .
II.2.15. Nas condições de II.2.13, suponhamos que K é outro espaço vectorial
sobre Š, e que .À J Ä K é outra aplicação linear. É então imediato
constatar-se que, considerando a composição . ‰ -À I Ä K, tem-se
Ð. ‰ -ч œ -‡ ‰ .‡ À P: ÐKà Šw Ñ Ä P: ÐIà Šw Ñ.
Uma vez que é imediato que, considerando a aplicação idêntica M.I À I Ä I ,
ÐM.I ч À P: ÐIà Šw Ñ Ä P: ÐIà Šw Ñ é a aplicação idêntica, concluímos, com um
argumento do tipo usual, que, se -À I Ä J é um isomorfismo, então a
aplicação linear dual -‡ À P: ÐJ à Šw Ñ Ä P: ÐIà Šw Ñ é também um isomorfismo,
tendo Ð-" ч como isomorfismo inverso.
II.2.16. Sejam os espaços vectoriais I e J , sobre Š, e a aplicação linear
-À I Ä J . Sejam Šw ¨ Š e :ß ; !. Dados 0 − P: ÐJ à Šw Ñ e ( − P; ÐJ à Šw Ñ,
tem-se então
-‡ Ð0 Œ (Ñ œ -‡ Ð0Ñ Œ -‡ Ð(Ñ − P:; ÐIà Šw Ñ.
Dem: Basta reparar que ambos os membros dão o mesmo resultado, a saber,
0(-(w" Ñß á ß -ÐA: ÑÑ(Ð-ÐA:" Ñß á ß -ÐA:" ÑÑ, quando aplicados a um
elemento arbitrário ÐA" ß á ß A:; Ñ de I :; .
§3. Grupo simétrico e sinal de uma permutação.
II.3.1. Para cada inteiro 8 !, chama-se grupo simétrico de ordem 8 ao grupo
Æ8 das permutações de Ö"ß á ß 8×. Para cada 5 − Æ8 , isto é, para cada
bijecção 5 À Ö"ß á ß 8× Ä Ö"ß á ß 8×, define-se o número de inversões invÐ5 Ñ
como sendo o número de elementos do conjunto
ÖÐ4ß 5Ñ ± 4 5 e 5 Ð4Ñ 5 Ð5Ñ×.
A sgÐ5 Ñ œ Ð"ÑinvÐ5Ñ − Ö"ß "× dá-se o nome de sinal ou paridade da
permutação 5 .
II.3.2. Sejam 8 # e 4ß 5 dois elementos distintos de Ö"ß á ß 8×. Nota-se então
Ð4 † 5Ñ a permutação de Ö"ß á ß 8×, que aplica 4 em 5 , 5 em 4 e deixa fixos os
restantes elementos. Às permutações do tipo Ð4 † 5Ñ dá-se o nome de transposições, chamando-se transposições consecutivas aquelas que são da forma
Ð4 † 4 "Ñ.
II.3.3. Toda a permutação 5 − Æ8 pode ser obtida por composição de um
número finito de transposições (considerando a aplicação idêntica como a
composta da família vazia de transposições).
Dem: O resultado demonstra-se por indução em 5 , mostrando-se que ele é
46
Cap. II. Tópicos de Álgebra Multilinear
verdadeiro para toda a permutação 5 , que verifique 5Ð4Ñ œ 4, para cada
" Ÿ 4 Ÿ 8 5 . Para 5 œ !, isto é evidente. Suponhamos que o resultado é
verdadeiro para um certo 5 , e que a permutação 5 verifica 5 Ð4Ñ œ 4, para
cada " Ÿ 4 Ÿ 8 Ð5 "Ñ, assim como 5 Ð8 5Ñ Á 8 5 . Tem-se então que
3 œ Ð5 Ð8 5Ñ † 8 5Ñ ‰ 5 verifica 3Ð4Ñ œ 4, para cada " Ÿ 4 Ÿ 8 5 , e
tem-se 5 œ Ð5 Ð8 5Ñ † 8 5Ñ ‰ 3, pelo que, tendo em conta a hipótese de
indução, 5 é a composição de um número finito de transposições. Fazendo
5 œ 8, obtemos a afirmação do enunciado.
II.3.4. Toda a transposição é composição de um número ímpar de transposições
consecutivas.
Dem: Seja 5 œ Ð4 † 5Ñ, em que se pode já supor que 4 5. Façamos a
demonstração por indução em 5 4. O resultado é evidente, se 5 4 œ " e,
para a passagem de indução, basta atender a que, se 5 4 ", tem-se
Ð4 † 5Ñ œ Ð4 † 4 "Ñ ‰ Ð4 " † 5Ñ ‰ Ð4 † 4 "Ñ.
II.3.5. (Lema) Se 4 Á 5 , 5 − Æ8 e 3 œ Ð4 † 5Ñ ‰ 5 , tem-se sg(3) œ sg(5 ).
Dem: Tendo em conta o resultado anterior, podemos reduzir-nos ao caso em
que 5 œ 4 ". Ora, nesse caso, tem-se:
a) Se 5 " Ð4Ñ 5 " Ð4 "Ñ, então invÐ3Ñ œ invÐ5 Ñ ";
b) Se 5 " Ð4Ñ 5 " Ð4 "Ñ, então invÐ3Ñ œ invÐ5 Ñ ";
em qualquer dos casos sgÐ3Ñ œ sgÐ5 Ñ.
II.3.6. (Teorema de Bézout) O sinal da aplicação idêntica é " e o sinal de uma
transposição é ". Se 5 e 3 são permutações, então
sgÐ3 ‰ 5 Ñ œ sgÐ3Ñ sgÐ5 Ñ.
Se 5 é uma permutação, então sgÐ5 " Ñ œ sgÐ5 Ñ.
Dem: É imediato que o sinal da permutação idêntica é " e daqui resulta, pelo
lema anterior, que o sinal de uma transposição é ". Dadas agora duas
permutações 5 e 3, podemos, por II.3.3, escrever 3 œ 3" ‰ â ‰ 34 e
5 œ 5" ‰ â ‰ 55 , com os 3! e os 5" transposições; resulta então do lema
anterior que sgÐ3Ñ œ Ð"Ñ4 e sgÐ5 Ñ œ Ð"Ñ5 . Uma vez que
3 ‰ 5 œ 3" ‰ â ‰ 34 ‰ 5" ‰ â ‰ 55 ,
sai agora, pelo mesmo lema,
sgÐ3 ‰ 5 Ñ œ Ð"Ñ45 œ Ð"Ñ4 Ð"Ñ5 œ sgÐ3Ñ sgÐ5 Ñ.
Por fim, o facto de ser sgÐ5 " Ñ œ sgÐ5 Ñ vem de que se tem M. œ 5 ‰ 5 " ,
donde " œ sgÐM.Ñ œ sgÐ5 Ñ sgÐ5 " Ñ, e atendemos a que sgÐ5 Ñ é um elemento
de Ö"ß "×, logo igual ao seu inverso.
II.3.7. Suponhamos, mais geralmente, que N e O são dois conjuntos totalmente
ordenados com 8 elementos e que 5 À N Ä O é uma bijecção. Define-se
então o número de inversões invÐ5 Ñ e o sinal sgÐ5 Ñ pelas mesmas fórmulas
§3. Grupo simétrico e sinal de uma permutação
47
que em II.3.1. É então imediato que, sendo -À Ö"ß á ß 8× Ä N e
.À Ö"ß á ß 8× Ä O as bijecções estritamente crescentes, invÐ5 Ñ e sgÐ5 Ñ
coincidem com o número de inversões e o sinal da permutação
." ‰ 5 ‰ - − Æ8 . Resulta daqui imediatamente que, se N , O e P são
conjuntos totalmente ordenados com 8 elementos, e se 5 À N Ä O e
3À O Ä P são duas bijecções, é ainda verdade que
sgÐM.N Ñ œ ",
sgÐ3 ‰ 5 Ñ œ sgÐ3Ñ sgÐ5 Ñ,
sgÐ5 " Ñ œ sgÐ5 Ñ.
II.3.8. Seja N § Ö"ß á ß 8× um conjunto com 5 elementos. Definimos então o
sinal ou paridade de N , sgÐN Ñ, como sendo o elemento sgÐ5 Ñ − Ö"ß "×, em
que 5 − Æ8 é a permutação que aplica Ö"ß á ß 5× sobre N , de modo
crescente, e aplica Ö5 "ß á ß 8× sobre Ö"ß á ß 8× Ï N , também de modo
crescente.
Contando o número de inversões desta permutação 5 , vemos que, se
N œ Ö4" ß á ß 45 ×, com 4" â 45 , tem-se
sgÐN Ñ œ Ð"ÑÐ4" "ÑÐ4# #ÑâÐ45 5Ñ
(em particular, sgÐN Ñ não depende de 8!), sendo claro a posteriori que a
fórmula anterior é ainda válida no caso em que N œ Ö4" ß á ß 45 ×, com os 4!
distintos, mas não obrigatoriamente por ordem crescente.
Tem-se assim, por exemplo, sgÐgÑ œ ", sgÐÖ4×Ñ œ Ð"Ñ4" e, para 4 Á 5 ,
sgÐÖ4ß 5×Ñ œ Ð"Ñ45" .
II.3.9. Seja N § Ö"ß á ß 8× um conjunto com 5 elementos. Tem-se então
sgÐÖ"ß á ß 8× Ï N Ñ œ Ð"Ñ5Ð85Ñ sgÐN Ñ.
Dem: Seja 5À Ö"ß á ß 8× Ä Ö"ß á ß 8× a permutação que aplica Ö"ß á ß 5×
sobre N , de modo crescente, e que é também crescente em Ö5 "ß á ß 8×.
Do mesmo modo, seja 3 − Æ8 a permutação que aplica Ö"ß á ß 8 5× sobre
Ö"ß á ß 8× Ï N , de modo crescente, e que é também crescente em
Ö8 5 "ß á ß 8×. É então imediato constatar-se que se tem 3 œ 5 ‰ / ,
onde / é a permutação de Ö"ß á ß 8×, que aplica Ö"ß á ß 8 5× sobre
Ö5 "ß á ß 8×, de modo crescente, e aplica Ö8 5 "ß á ß 8× sobre
Ö"ß á ß 5×, também de modo crescente. Reparando que invÐ/ Ñ œ 5Ð8 5Ñ,
resulta agora, do teorema de Bézout, que
sgÐÖ"ß á ß 8× Ï N Ñ œ sgÐ3Ñ œ sgÐ5 Ñ sgÐ/ Ñ œ
œ Ð"Ñ5Ð85Ñ sgÐ5 Ñ œ Ð"Ñ5Ð85Ñ sgÐN Ñ.
II.3.10. Seja 5À Ö"ß á ß 7 8× Ä Ö"ß á ß 7 8× uma permutação. Vem então
sgÐ5 Ñ œ sgÐ5ÎÖ"ßáß7× Ñ sgÐ5ÎÖ7"ßáß78× Ñ sgÐÖ5 Ð"Ñß á ß 5 Ð7Ñ×Ñ.
Dem: O conjunto que define o número de inversões de 5 vai ser a união
disjunta de três subconjuntos, a saber:
48
Cap. II. Tópicos de Álgebra Multilinear
a) ÖÐ4ß 5Ñ − Ö"ß á ß 7×# ± 4 5 e 5 Ð4Ñ 5 Ð5Ñ×;
b) ÖÐ4ß 5Ñ − Ö7 "ß á ß 7 8×# ± 4 5 e 5 Ð4Ñ 5 Ð5Ñ×;
c) ÖÐ4Þ5Ñ − Ö"ß á ß 7× ‚ Ö7 "ß á ß 7 8× ± 5 Ð4Ñ 5 Ð5Ñ×.
Os números de elementos do primeiro e do segundo conjuntos são, respectivamente, invÐ5/Ö"ßáß7× Ñ e invÐ5/Ö7"ßáß78× Ñ. Ficamos portanto reduzidos a
provar que " elevado ao número de elementos do terceiro conjunto é igual
a sgÐÖ5 Ð"Ñß á ß 5 Ð7Ñ×Ñ. Escrevamos, para isso,
Ö5 Ð"Ñß á ß 5 Ð7Ñ× œ Ö5 Ð3" Ñß á ß 5 Ð37 Ñ×,
com 5 Ð3" Ñ â 5 Ð37 Ñ. Constatamos então que o número de pares Ð4ß 5Ñ
em c) com 4 œ 3" é 5 Ð3" Ñ " (correspondentes aos 5 tais que 5 Ð5Ñ está entre
" e 5 Ð3" Ñ, excluindo este), o número de pares com 4 œ 3# é 5 Ð3# Ñ #
(correspondentes aos 5 tais que 5 Ð5Ñ está entre " e 5 Ð3# Ñ, excluindo 5 Ð3" Ñ e
5Ð3# Ñ), e assim sucessivamente, pelo que o número de elementos do conjunto
em questão é igual a Ð5 Ð3" Ñ "Ñ Ð5 Ð3# Ñ #Ñ â Ð5 Ð37 Ñ 7Ñ e "
elevado a este número de elementos é, por II.3.8, igual a
sgÐÖ5 Ð"Ñß á ß 5 Ð7Ñ×Ñ.
§4. Aplicações multilineares alternadas. O determinante.
II.4.1. Sejam I um espaço vectorial sobre Š e J um espaço vectorial sobre
Šw ¨ Š. Para cada : ! e cada permutação 5 − Æ: , tem então lugar uma
aplicação linear entre espaços vectoriais sobre Šw ,
5
s À P: ÐIà J Ñ Ä P: ÐIà J Ñ,
definida por
5
sÐ0ÑÐA" ß á ß A: Ñ œ 0ÐA5Ð"Ñ ß á ß A5Ð:Ñ Ñ.
s P: ÐIà J Ñ Ä P: ÐIà J Ñ é
II.4.2. Sendo M. − Æ: a permutação idêntica, então M.À
a aplicação idêntica. Sendo 5 ß 3 − Æ: duas permutações, tem-se que
Ð5 ‰ 3Ñs œ 5
3À P: ÐIà J Ñ Ä P: ÐIà J Ñ.
s ‰s
Em consequência, tem-se Ð5 " Ñs œ 5
s " .
Dem: A primeira afirmação é trivial e a terceira é uma consequência das
duas primeiras. Quanto à segunda, dados A" ß á ß A: em I , podemos notar,
para cada " Ÿ 4 Ÿ :, C4 œ A5Ð4Ñ , e obtemos
5
3Ð0ÑÑÐA" ß á ß A: Ñ œ s
3Ð0ÑÐA5Ð"Ñ ß á ß A5Ð:Ñ Ñ œ s
3Ð0ÑÐC" ß á ß C: Ñ œ
sÐs
œ 0ÐC3Ð"Ñ ß á ß C3Ð:Ñ Ñ œ 0ÐA5Ð3Ð"ÑÑ ß á ß A5Ð3Ð:ÑÑ Ñ œ
œ Ð5 ‰ 3Ñs Ð0ÑÐA" ß á ß A: Ñ.
§4. Aplicações multilineares alternadas. O determinante
49
II.4.3. Dados os espaços vectoriais I e J e a aplicação :-linear 0À I : Ä J , são
equivalentes as três propriedades seguintes:
a) Para cada " Ÿ 4 Ÿ : ",
0ÐB" ß á ß B4" ß B4 ß B4" ß B4# ß á ß B: Ñ œ 0ÐB" ß á ß B4" ß B4" ß B4 ß B4# ß á ß B: Ñ,
quaisquer que sejam B" ß á ß B: em I ;
b) Para cada 4 5 ,
0ÐB" ß á ß B4 ß á ß B5 ß á ß B: Ñ œ 0ÐB" ß á ß B4" ß B5 ß B4" ß á ß B5" ß B4 ß B5" ß á ß ß B: Ñ,
quaisquer que sejam B" ß á ß B: em I ;
c) Para cada 5 − Æ: , tem-se 5
s Ð0Ñ œ sgÐ5 Ñ 0.
Dem: A propriedade a) é trivialmente um caso particular da propriedade b) e
esta última é trivialmente a tradução do caso particular de c) em que se toma
para 5 a transposição Ð4 † 5Ñ, que sabemos ter sinal ". Resta-nos portanto
supor que a propriedade a) é verificada e provar c). Para isso, consideremos o
conjunto das permutações 5 − Æ: , para as quais a igualdade de c) é verificada. É evidente que esse conjunto contém a permutação identidade, que tem
sinal ", e, por hipótese, ele contém as transposições consecutivas Ð4 † 4 "Ñ,
que têm sinal ". Por outro lado, se este conjunto contiver duas permutações
5 e 3, o resultado anterior e o teorema de Bézout mostram-nos que ele
contém também 5 ‰ 3. Uma vez que, por II.3.3 e II.3.4, toda a permutação é
composição de um número finito de transposições consecutivas, concluímos
que o conjunto em questão contém todas as permutações, o que mostra que a
propriedade c) é verificada.
II.4.4. Sejam I um espaço vectorial sobre Š e J um espaço vectorial sobre
Šw ¨ Š. Diz-se que uma aplicação :-linear 0À I : Ä J é alternada ou
anti-simétrica se ela verifica as propriedades equivalentes referidas em II.4.3
(reparar que estas propriedades se encontram automaticamente verificadas,
no caso em que : œ ! ou : œ "). Nota-se E: ÐIà J Ñ o subconjunto de
P: ÐIà J Ñ, formado pelas aplicações :-lineares alternadas, conjunto que é
trivialmente um subespaço vectorial sobre Šw .
Em particular, tem-se E! ÐIà J Ñ œ P! ÐIà J Ñ œ J e E" ÐIà J Ñ œ PÐIà J Ñ.
II.4.5. De modo análogo, e embora isso não vá ter grande interesse neste curso,
definem-se as aplicações :-lineares simétricas, como sendo as aplicações
:-lineares 0À I : Ä J , para as quais se tem 5
s Ð0Ñ œ 0, para cada permutação
5. Uma demonstração inteiramente análoga à de II.4.3 mostra também que a
condição anterior é equivalente a qualquer das propriedades, que se obtêm a
partir das propriedades b) e c) daquele resultado, omitindo o sinal menos no
segundo membro das respectivas igualdades. Usa-se a notação W : ÐIà J Ñ
para o subespaço vectorial de P: ÐIà J Ñ, cujos elementos são as aplicações
:-lineares simétricas. Como antes, tem-se W ! ÐIà J Ñ œ P! ÐIà J Ñ œ J e
W " ÐIà J Ñ œ PÐIà J Ñ.
50
Cap. II. Tópicos de Álgebra Multilinear
No nosso curso as aplicações multilineares alternadas jogarão um papel
muito mais importante que o das aplicações multilineares simétricas. No
entanto, muito do que for dito para as aplicações alternadas pode ser
adaptado de modo trivial ao caso das aplicações simétricas, a
demonstração vindo normalmente mesmo simplificada. Quando for esse o
caso, faremos referência a essas adaptações sem apresentar demonstração.
Os três resultados que seguem são contra-exemplos, em que a adaptação
referida não é possível.
II.4.6. Sejam 0À I : Ä J uma aplicação multilinear alternada e B" ß á ß B: − I
tais que exista 4 Á 5 , com B4 œ B5 . Tem-se então 0ÐB" ß á ß B: Ñ œ !.
Dem: Basta atender a que, pela propriedade b) de II.4.3, tem-se
0ÐB" ß á ß B: Ñ œ 0ÐB" ß á ß B: Ñ.
II.4.7. Seja 0À I : Ä J uma aplicação multilinear alternada, e seja B" ß á ß B: um
sistema linearmente dependente de vectores de I . Tem-se então
0ÐB" ß á ß B: Ñ œ !.
Dem: Podemos já eliminar os casos triviais em que : œ ! ou : œ ", visto
que, no primeiro caso, a família vazia de vectores é linearmente
independente, e, no segundo caso, a conclusão correspondente é
simplesmente que 0Ð!Ñ œ !, para cada aplicação linear 0À I Ä J . Supondo
portanto : #, vem que existe 4 tal que B4 seja combinação linear dos
restantes, e podemos então escrever, tendo em conta o resultado anterior,
0ÐB" ß á ß B: Ñ œ " +5 0ÐB" ß á ß B4" ß B5 ß B4" ß á ß B: Ñ œ !.
5Á4
II.4.8. (Corolário) Sejam I um espaço vectorial de dimensão 8, sobre Š, e J
um espaço vectorial sobre Šw ¨ Š. Para cada : 8, tem-se então
E: ÐIà J Ñ œ Ö!×.
Dem: Basta atender a que qualquer sistema de : vectores de I é linearmente
dependente.
Vamos agora estudar um operador, que a cada 0 − P: ÐIà J Ñ, associa uma
aplicação multilinear alternada AltÐ0Ñ − E: ÐIà J Ñ. Este operador vai ser
uma projecção, no sentido que, quando 0 já é alternado, AltÐ0Ñ œ 0 .
II.4.9. Sejam I um espaço vectorial sobre Š e J um espaço vectorial sobre
Šw ¨ Š. Para cada : !, tem então lugar uma aplicação linear
AltÀ P: ÐIà J Ñ Ä E: ÐIà J Ñ,
definida por
§4. Aplicações multilineares alternadas. O determinante
AltÐ0Ñ œ
51
"
" sgÐ5 Ñ 5
s Ð0Ñ.
:x 5−º
:
Para cada 0 − P: ÐIà J Ñ e 5 − Æ: , tem-se
AltÐ5
s Ð0ÑÑ œ 5
s ÐAltÐ0ÑÑ œ sgÐ5 Ñ AltÐ0Ñ,
e vem AltÐ0Ñ œ 0, para cada 0 − E: ÐIà J Ñ. Em particular, para : œ ! e
: œ ", Alt é a aplicação idêntica.
Dem: É imediato que Alt é uma aplicação linear de P: ÐIà J Ñ em P: ÐIà J Ñ.
O facto de se ter AltÐ0Ñ œ 0, para cada 0 − E: ÐIà J Ñ, vem de que Æ: tem :x
elementos e de que, para um tal 0, tem-se então 5
sÐ0Ñ œ sgÐ5 Ñ 0, para cada
5 − Æ: . Se atendermos agora a que, para cada 5 − Æ: , têm lugar bijecções
de Æ: sobre Æ: , que a cada 3 associam 3 ‰ 5 e 5 ‰ 3, respectivamente,
vemos que
AltÐ5
s Ð0ÑÑ œ
"
"
" sgÐ3Ñ s
3Ð5
s Ð0ÑÑ œ sgÐ5 Ñ " sgÐ3 ‰ 5 Ñ Ð3 ‰ 5 Ñs Ð0Ñ œ
:x 3−º
:x 3−º
:
:
"
œ sgÐ5 Ñ " sgÐ7 Ñ s7 Ð0Ñ œ sgÐ5 Ñ AltÐ0Ñ
:x 7 −º
:
e, do mesmo modo,
5
s ÐAltÐ0ÑÑ œ
"
"
" sgÐ3Ñ 5
3Ð0ÑÑ œ sgÐ5 Ñ " sgÐ5 ‰ 3Ñ Ð5 ‰ 3Ñs Ð0Ñ œ
s Ðs
:x 3−º
:x 3−º
:
:
"
œ sgÐ5 Ñ " sg(7 ) s7 Ð0Ñ œ sgÐ5 Ñ AltÐ0Ñ,
:x 7 −º
:
esta última igualdade implicando, em
AltÐ0Ñ − E: ÐIà J Ñ, para cada 0 − P: ÐIà J Ñ.
particular,
que
vem
De modo análogo se pode mostrar que tem lugar uma aplicação linear
SymÀ P: ÐIà J Ñ Ä W : ÐIà J Ñ,
definida por SymÐ0Ñ œ
:
"
:x
!5
s Ð0Ñ, a qual verifica SymÐ0Ñ œ 0, para cada
5
0 − W ÐIà J Ñ, tendo-se, para cada 0 − P: ÐIà J Ñ e cada 5 − Æ: ,
SymÐ5
s Ð0ÑÑ œ 5
s ÐSymÐ0ÑÑ œ SymÐ0Ñ.
II.4.10. (Lema) Sejam I um espaço vectorial de dimensão 7, sobre Š, com
uma base ÐB4 Ñ"Ÿ4Ÿ7 , e J um espaço vectorial sobre Šw ¨ Š. Consideremos
0ß ( − E: ÐIà J Ñ tais que, quaisquer que sejam os índices 4" 4# á 4:
em Ö"ß á ß 7×, se tenha
52
Cap. II. Tópicos de Álgebra Multilinear
0ÐB4" ß á ß B4: Ñ œ (ÐB4" ß á ß B4: Ñ.
Tem-se então 0 œ (.
Dem: Considerando a aplicação multilinear alternada 0 (, vemos que basta
demonstrar que, se 0 − E: ÐIà J Ñ é tal que, quaisquer que sejam
4" â 4: em Ö"ß á ß 7×, se tenha 0ÐB4" ß á ß B4: Ñ œ !, então 0 œ !.
Considerando um tal 0, sabemos, por II.2.4, que, para ver que 0 œ !, basta
ver que, quaisquer que sejam 4" ß á ß 4: em Ö"ß á ß 7×, se tem
0ÐB4" ß á ß B4: Ñ œ !. Ora, se os elementos 4! não forem todos distintos, isso é
uma consequência de II.4.6 e, se eles forem distintos, podemos escrever
Ö4" ß á ß 4: × œ Ö5" ß á ß 5: ×, com 5" â 5: , existindo então uma permutação 5 − Æ: tal que 4! œ 55Ð!Ñ , o que implica que
0ÐB4" ß á ß B4: Ñ œ sgÐ5 Ñ 0ÐB5" ß á ß B5: Ñ œ !
(fazer C! œ B5! ), e a demonstração está terminada.
Para as aplicações multilineares simétricas, vamos ter um resultado
correspondente ao anterior, mas em que devemos ser um pouco mais
cuidadosos, visto que já não é válido o resultado correspondente a II.4.6.
Adaptando convenientemente a demonstração anterior, o que se pode ver
é que, se 0ß ( em W : ÐIà J Ñ são tais que, quaisquer que sejam os índices
4" Ÿ â Ÿ 4: em Ö"ß á ß 7×, se tenha
0ÐB4" ß á ß B4: Ñ œ (ÐB4" ß á ß B4: Ñ,
então 0 œ (.
II.4.11. Seja I um espaço vectorial de dimensão 7 sobre Š, com uma base
ÐB4 Ñ"Ÿ4Ÿ7 . Sejam ! Ÿ : Ÿ 7 e Šw ¨ Š, e consideremos a correspondente
base de P: ÐIà Šw Ñ, constituída pelos 04" ßáß4: À I : Ä Šw , onde 4" ß á ß 4: −
Ö"ß á ß 7× (cf. II.2.5). Seja, para cada 4" â 4: em Ö"ß á ß 7×,
0•4" ßáß4: œ :x AltÐ04" ßáß4: Ñ − E: ÐIà Šw Ñ.
Tem-se então:
a) Dados 4" â 4: e 5" â 5: em Ö"ß á ß 7×,
0•4" ßáß4: ÐB5" ß á ß B5: Ñ œ $4" ß5" ‚ â ‚ $4: ß5: ;
b) Os 0•4" ßáß4: constituem uma base de E: ÐIà Šw Ñ, dita base associada à base
dada, e, para cada 0 − E: ÐIà Šw Ñ,
0 œ " 0ÐB4" ß á ß B4: Ñ 0•4" ßáß4:
4" â4:
(comparar com II.2.5);
§4. Aplicações multilineares alternadas. O determinante
c) Em particular, E: ÐIà Šw Ñ tem dimensão Š 7: ‹ œ
53
7x
:xÐ7:Ñx ;
d) Para : œ ", 0•4 œ 04 − E" ÐIà ŠÑ œ PÐIà ŠÑ.
Dem: Tendo em conta a definição da aplicação Alt, vemos que
0•4" ßáß4: ÐB5" ß á ß B5: Ñ œ " sgÐ5 Ñ04" ßáß4: ÐB55Ð"Ñ ß á ß B55Ð:Ñ Ñ œ
5
œ $4" ß5" ‚ â ‚ $4: ß5: ,
uma vez que, por as sucessões 4" ß á ß 4: e 5" ß á ß 5: serem estritamente crescentes, no somatório anterior só a parcela correspondente à permutação
5 œ M. pode ser eventualmente não nula e que, mesmo essa, só não é nula no
caso em que cada 43 œ 53 , caso em que ela é igual a ". Aplicando o lema
anterior, vemos agora que cada 0 − E: ÐIà Šw Ñ é combinação linear dos
0•4" ßáß4: , com os coeficientes definidos no enunciado, visto que ambos os
membros da igualdade respectiva são elementos de E: ÐIà Šw Ñ, que dão o
mesmo valor quando aplicados a cada ÐB5" ß á ß B5: Ñ, com 5" â 5: . A
unicidade de uma tal combinação linear estabelece-se do mesmo modo, pelo
que concluímos b). Por fim, c) resulta de que o número de sucessões
estritamente crescentes de elementos de Ö"ß á ß 7× é igual ao número de
combinações de 7 elementos, tomados : a :.
A versão do resultado anterior, para os espaços de aplicações
multilineares simétricas, é de enunciado mais complicado pelo que, uma
vez que não teremos ocasião de a utilizar, não a enunciamos aqui.
Vamos agora apresentar um resultado simples, em que se constata qual o
comportamento da operação de imagem recíproca, definida em II.2.13,
relativamente às projecções Alt e aos espaços E: ÐIà Šw Ñ. Estes resultados
têm versões correspondentes evidentes, que nos abstemos de enunciar,
para as projecções Sym e para os espaços W : ÐIà Šw Ñ.
II.4.12. Sejam I e J espaços vectoriais sobre Š e -À I Ä J uma aplicação
linear. Se Šw ¨ Š, a aplicação linear -‡ À P: ÐJ à Šw Ñ Ä P: ÐIà Šw Ñ verifica as
seguintes propriedades:
a) Para cada 0 − P: ÐJ à Šw Ñ e 5 − Æ: , 5
s Ð-‡ Ð0ÑÑ œ -‡ Ð5
s Ð0ÑÑ − P: ÐIà Šw Ñ;
b) Para cada 0 − P: ÐJ à Šw Ñ, Alt(-‡ Ð0ÑÑ œ -‡ ÐAltÐ0ÑÑ − E: ÐIà Šw Ñ;
c) Em particular, para cada 0 − A: ÐJ à Šw Ñ, vem também -‡ Ð0Ñ − E: ÐIà Šw Ñ.
Dem: Trata-se de uma consequência trivial das definições.
II.4.13. Tendo em conta o resultado anterior, para cada aplicação linear
-À I Ä J , notaremos ainda -‡ a aplicação linear E: ÐJ à Šw Ñ Ä E: ÐIà Šw Ñ,
restrição da aplicação -‡ À P: ÐJ à Šw Ñ Ä P: ÐIà Šw Ñ, sendo trivial que continua
a ser válida a propriedade correspondente à enunciada em II.2.15.
II.4.14. Um caso particular importante de II.4.11 é aquele em que temos um
espaço vectorial I , de dimensão 7 sobre Š, e consideramos Šw ¨ Š e o
54
Cap. II. Tópicos de Álgebra Multilinear
espaço vectorial sobre Šw , E7 ÐIà Šw Ñ (tomamos portanto : igual à dimensão
de I ). Concluímos então que este espaço tem dimensão " e que, a cada base
ÐB4 Ñ"Ÿ4Ÿ7 de I , fica associada uma base de E7 ÐIà Šw Ñ, formada por um
único vector 0•"ßáß7 .
II.4.15. Sejam I um espaço vectorial sobre Š, J um espaço vectorial sobre
Šw ¨ Š e 0 − E: ÐIà J Ñ. Sejam B" ß á ß B: e C" ß á ß C: dois sistemas de
vectores de I tais que, para uma certa matriz Ð+5ß4 Ñ de escalares, se tenha
C4 œ ! +5ß4 B5 . Tem-se então
5
0ÐC" ß á ß C: Ñ œ detÐÐ+5ß4 ÑÑ 0ÐB" ß á ß B: Ñ.
Dem: Tendo em conta a multilinearidade de 0, podemos escrever
0ÐC" ß á ß C: Ñ œ " +5" ß" â +5: ß: 0ÐB5" ß á ß B5: Ñ.
5" ßáß5:
Tendo em conta o facto de 0 ser alternada, vemos que todas as parcelas
correspondentes a um sistema de índices 5" ß á ß 5: com alguma repetição são
nulas, pelo que a expressão anterior pode ser escrita alternativamente na
forma
0ÐC" ß á ß C: Ñ œ " +5Ð"Ñß" â +5Ð:Ñß: 0ÐB5Ð"Ñ ß á ß B5Ð:Ñ Ñ.
5
e portanto, atendendo mais uma vez ao facto de 0 ser alternada,
0ÐC" ß á ß C: Ñ œ " +5Ð"Ñß" â +5Ð:Ñß: 5
s Ð0ÑÐB" ß á ß B: Ñ œ
5
œ " sgÐ5 Ñ +5Ð"Ñß" â +5Ð:Ñß: 0ÐB" ß á ß B: Ñ œ detÐÐ+5ß4 ÑÑ 0ÐB" ß á ß B: Ñ.
5
II.4.16. O caso particular de II.4.14 em que I œ Š7 e em que consideramos a
base canónica /" ß á ß /7 deste espaço é especialmente interessante. O
correspondente elemento 0•"ßáß7 − E7 Њ7 à ŠÑ toma o nome de função
determinante e será notado det.
A razão de ser desta nomenclatura está em que, dados os vectores
A" ß á ß A7 de Š7 , com
A4 œ Ð+"ß4 ß á ß +7ß4 Ñ œ +"ß4 /" â +7ß4 /7 ,
detÐA" ß á ß A7 Ñ vai ser o determinante da matriz dos +5ß4 (aquela cujas
colunas são os A4 ). Esta afirmação é clara para quem conheça a definição do
determinante a partir das aplicações multilineares alternadas e é uma
consequência do resultado precedente para quem prefira a definição mais
clássica (lembrar que se tem 0•"ßáß7 Ð/" ß á ß /7 Ñ œ ").
§4. Aplicações multilineares alternadas. O determinante
55
II.4.17. Seja I um espaço vectorial de dimensão 7 sobre Š, e sejam B" ß á ß B7
e C" ß á ß C7 duas bases de I , com C4 œ ! +5ß4 B5 . Notando então 0•"ßáß7 e
5
(•"ßáß7 os elementos das bases associadas de E7 ÐIà ŠÑ, tem-se
0•"ßáß7 œ detÐÐ+5ß4 ÑÑ (•"ßáß7 .
Dem: Aplicando II.4.11 e II.4.15, obtemos
0•"ßáß7 œ 0•"ßáß7 ÐC" ß á ß C7 Ñ (•"ßáß7 œ
œ detÐÐ+5ß4 ÑÑ 0•"ßáß7 ÐB" ß á ß B7 Ñ (•"ßáß7 œ
œ detÐÐ+5ß4 ÑÑ (•"ßáß7 .
II.4.18. Suponhamos que I é um espaço vectorial de dimensão " sobre Š. Para
cada aplicação linear -À I Ä I , existe então um, e um só, + − Š tal que
- œ + M.I , isto é, tal que -ÐBÑ œ +B, para cada B − I .
Dem: A unicidade de + nas condições do enunciado é trivial. Para provar a
existência, fixamos B! − I não nulo, constituindo portanto uma base de I , e
reparamos que se tem então -ÐB! Ñ œ +B! , para um certo + − Š. Para cada
B − I vai existir , − Š tal que B œ ,B! e podemos então escrever
-ÐBÑ œ -Ð,B! Ñ œ ,-ÐB! Ñ œ ,+B! œ +B,
o que termina a demonstração.
II.4.19. Seja I um espaço vectorial de dimensão 7, sobre Š, e seja -À I Ä I
uma aplicação linear. Tem-se então que E7 ÐIà ŠÑ é um espaço vectorial de
dimensão ", sobre Š, e ficamos com uma aplicação linear
-‡ À E7 ÐIà ŠÑ Ä E7 ÐIà ŠÑ. Define-se o determinante da aplicação linear -,
detÐ-Ñ, como sendo o elemento de Š associado à aplicação linear -‡ . Por
outras palavras, detÐ-Ñ é o único elemento de Š para o qual se tem
-‡ Ð0Ñ œ detÐ-Ñ 0,
para cada 0 − E7 ÐIà ŠÑ.
II.4.20. Seja I um espaço vectorial de dimensão 7 sobre Š, com uma base
B" ß á ß B7 . Seja -À I Ä I uma aplicação linear e sejam +5ß4 os elementos da
matriz de - na base considerada, isto é, os definidos por -ÐB4 Ñ œ ! +5ß4 B5 .
5
Tem-se então detÐ-Ñ œ detÐÐ+5ß4 ÑÑ.
Dem: Aplicando II.4.11 e II.4.15, obtemos
detÐ-Ñ0•"ßáß7 œ -‡ Ð0•"ßáß7 Ñ œ -‡ Ð0•"ßáß7 ÑÐB" ß á ß B7 Ñ 0•"ßáß7 œ
œ 0•"ßáß7 Ð-ÐB" Ñß á ß -ÐB7 ÑÑ 0•"ßáß7 œ
œ detÐÐ+5ß4 ÑÑ 0•"ßáß7 ÐB" ß á ß B7 Ñ 0•"ßáß7 œ
œ detÐÐ+5ß4 ÑÑ 0•"ßáß7 ,
donde o resultado.
56
Cap. II. Tópicos de Álgebra Multilinear
II.4.21. No caso em que I é um espaço vectorial de dimensão ! e -À I Ä I é a
única aplicação linear possível (a aplicação linear nula), tem-se
E! ÐIà ŠÑ œ Š e a aplicação linear -‡ À Š Ä Š é a aplicação idêntica, o que
nos permite concluir que detÐ-Ñ œ ". Isto está de acordo com o facto6 de o
determinante de uma matriz ! ‚ ! ser igual a ".
No caso em que o espaço vectorial I tem dimensão ", sabemos que, para
cada aplicação linear -À I Ä I , existe + − Š tal que -ÐBÑ œ +B, tendo-se
então, pelo resultado precedente, detÐ-Ñ œ +.
II.4.22. Sejam I um espaço vectorial de dimensão 7 sobre Š e -ß .À I Ä I
duas aplicações lineares. Tem-se então:
a) detÐM.I Ñ œ ";
b) detÐ. ‰ -Ñ œ detÐ.ÑdetÐ-Ñ;7
c) Se - é um isomorfismo, então detÐ-Ñ Á ! e detÐ-" Ñ œ det"Ð-Ñ .
Dem: A alínea a) é trivial e a alínea c) é uma consequência de a) e b), visto
que se tem -" ‰ - œ M.I . Resta-nos verificar b) e, para isso, basta
repararmos que, para cada 0 − E7 ÐIà ŠÑ, vem
Ð. ‰ -ч Ð0Ñ œ -‡ Ð.‡ Ð0ÑÑ œ detÐ-Ñ.‡ Ð0Ñ œ detÐ.ÑdetÐ-Ñ 0.
II.4.23. Sejam I um espaço vectorial sobre Š e J e K dois subespaços
vectoriais de I tais que tenha lugar a soma directa I œ J Š K. Seja
-À I Ä I uma aplicação linear tal que -ÐJ Ñ § J e -ÐKÑ § K . Tem-se
então
detÐ-Ñ œ detÐ-ÎJ Ñ detÐ-ÎK Ñ.
Dem: Sejam B" ß á ß B: uma base de J e B:" ß á ß B:; uma base de K.
Tem-se portanto que B" ß á ß B:; é uma base de I , e podemos considerar a
correspondente base de E:; ÐIà ŠÑ, formada pelo único elemento
0 œ 0•"ßáß:; . Sejam 0w − E: ÐJ à ŠÑ e 0ww − E; ÐKà ŠÑ as aplicações
multilineares alternadas definidas por
0w ÐA" ß á ß A: Ñ œ 0ÐA" ß á ß A: ß -ÐB:" Ñß á ß -ÐB:; ÑÑ,
0ww ÐA:" ß á ß A:; Ñ œ 0ÐB" ß á ß B: ß A:" ß á ß A:; Ñ.
Podemos então escrever
0Ð-ÐB" Ñß á ß -ÐB:; ÑÑ œ 0w Ð-ÐB" Ñß á ß -ÐB: ÑÑ œ
œ Ð-ÎJ ч Ð0w ÑÐB" ß á ß B: Ñ œ
œ detÐ-ÎJ Ñ 0w ÐB" ß á ß B: Ñ œ
œ detÐ-ÎJ Ñ 0ww Ð-ÐB:" Ñß á ß -ÐB:; ÑÑ œ
6Que, infelizmente, nem
7Para quem ainda o não
toda a gente considera como evidente.
soubesse, este resultado permite concluir que o determinante do
produto de duas matrizes é igual ao produto dos respectivos determinantes.
§4. Aplicações multilineares alternadas. O determinante
57
blablablablablablablaba œ detÐ-ÎJ Ñ Ð-ÎK ч Ð0ww ÑÐB:" ß á ß B:; Ñ œ
œ detÐ-ÎJ ÑdetÐ-ÎK Ñ 0ww ÐB:" ß á ß B:; Ñ œ
œ detÐ-ÎJ ÑdetÐ-ÎK Ñ 0ÐB" ß á ß B:; Ñ œ
œ detÐ-ÎJ ÑdetÐ-ÎK Ñ,
pelo que
-‡ Ð0Ñ œ -‡ Ð0ÑÐB" ß á ß B:; Ñ 0 œ 0Ð-ÐB" Ñß á ß -ÐB:; ÑÑ 0 œ
œ detÐ-ÎJ ÑdetÐ-ÎK Ñ 0,
donde o resultado.
§5. Produto exterior.
II.5.1. Sejam I um espaço vectorial sobre Š, Šw ¨ Š e p,q 0 dois inteiros.
Dados 0 − E: ÐIà Šw Ñ e ( − E; ÐIà Šw Ñ, definimos em II.2.8 o produto
tensorial 0 Œ ( − P:; ÐIà Šw Ñ, que, em geral, não será uma aplicação multilinear alternada. Define-se então o produto exterior 0 • ( − E:; ÐIà Šw Ñ,
como sendo a aplicação multilinear alternada
0•( œ
Ð: ;Ñx
AltÐ0 Œ (Ñ.8
:x ;x
É imediato que fica assim definida uma aplicação bilinear
• À E: ÐIà Šw Ñ ‚ E; ÐIà Šw Ñ Ä E:; ÐIà Šw Ñ.
II.5.2. No caso em que : œ ! ou ; œ !, sabemos que o produto tensorial não é
mais do que a multiplicação pelos escalares. Uma vez que !x œ " e que o
produto de uma aplicação multilinear alternada por um escalar é ainda uma
aplicação multilinear alternada, concluímos que, neste caso, o produto
exterior é também a multiplicação pelos escalares.
Quando se estudou o produto tensorial, viu-se que esta operação é, em
geral, não comutativa. Vamos agora ver que, nesse aspecto, o produto
exterior comporta-se bastante melhor: Embora ele não seja propriamente
comutativo, pode-se dizer que é mais ou menos comutativo, no sentido
que precisaremos adiante. Comecemos por provar o seguinte lema:
é muito clara qual a necessidade de introduzir o factor multiplicativo Ð:;Ñx
:x ;x nesta
definição, e, de facto, alguns autores (e. g. Kobayashi e Nomizu) não o introduzem. A sua
utilização vai, no entanto, contribuir para simplificar algumas fórmulas mais adiante e,
talvez por esse motivo, a convenção que seguimos parece estar de acordo com a tendência
actual.
8Não
58
Cap. II. Tópicos de Álgebra Multilinear
II.5.3. (Lema) Dados 0 − P: ÐIà Šw Ñ e ( − P; ÐIà Šw Ñ, tem-se
AltÐ( Œ 0Ñ œ Ð"Ñ:; AltÐ0 Œ (Ñ.
Dem: Dados B" ß á ß B:; em I , vem
( Œ 0ÐB" ß á ß B:; Ñ œ (ÐB" ß á ß B; Ñ 0ÐB;" ß á ß B:; Ñ œ
œ 0ÐB5Ð"Ñ ß á ß B5Ð:Ñ Ñ (ÐB5Ð:"Ñ ß á ß B5Ð:;Ñ Ñ œ
œ 0 Œ (ÐB5Ð"Ñ ß á ß B5Ð:;Ñ Ñ œ 5
s Ð0 Œ (ÑÐB" ß á ß B:; Ñ,
onde 5 − Æ:; é a permutação definida por 5 Ð"Ñ œ ; ", …, 5 Ð:Ñ œ : ; ,
5 Ð: "Ñ œ ", …, 5 Ð: ;Ñ œ ; . Tem-se portanto ( Œ 0 œ 5
s Ð0 Œ (Ñ e,
contando o número de inversões de 5 , constata-se que sgÐ5 Ñ œ Ð"Ñ:; , pelo
que o resultado é uma consequência de II.4.9.
II.5.4. (±-comutatividade) Dados 0 − E: ÐIà Šw Ñ e ( − E; ÐIà Šw Ñ, tem-se
( • 0 œ Ð"Ñ:; 0 • (.
Dem: Trata-se de uma consequência imediata da definição e do lema anterior.
Tal como acontecia na secção anterior, a definição e os resultados precedentes estendem-se naturalmente ao quadro das aplicações multilineares
simétricas, com enunciados que vêm eventualmente ainda mais simples.
Em vez do produto exterior, temos uma aplicação bilinear
À W : ÐIà Šw Ñ ‚ W ; ÐIà Šw Ñ Ä W :; ÐIà Šw Ñ,
chamada produto tensorial simétrico, definida por
0( œ
Ð: ;Ñx
SymÐ0 Œ (Ñ,
:x ;x
esta operação sendo mesmo comutativa, no sentido que se tem
0 ( œ ( 0. Do mesmo modo, mais geralmente, para 0 − P: ÐIà Šw Ñ e
( − P; ÐIà Šw Ñ, tem-se SymÐ( Œ 0Ñ œ SymÐ0 Œ (Ñ.
A propriedade associativa, que vimos ser válida para o produto tensorial,
continua a ser válida para o produto exterior, mas agora com uma
demonstração muito menos trivial. Começamos por demonstrar o seguinte
lema:
II.5.5. (Lema) Sejam 0 − P: ÐIà Šw Ñ e ( − P; ÐIà Šw Ñ, tais que, ou AltÐ0Ñ œ !,
ou AltÐ(Ñ œ !. Tem-se então AltÐ0 Œ (Ñ œ !.
Dem: Vamos começar por demonstrar o resultado no caso em que
AltÐ(Ñ œ !. Temos que provar que AltÐ0 Œ (ÑÐB" ß á ß B:; Ñ œ !, ou seja,
que
§5. Produto exterior
59
! œ " sgÐ5 Ñ 0ÐB5Ð"Ñ ß á ß B5Ð:Ñ Ñ (ÐB5Ð:"Ñ Ñß á ß B5Ð:;Ñ Ñ.
5
Para cada aplicação injectiva 5! À Ö"ß á ß :× Ä Ö"ß á ß : ;×, notemos Æw a
parte de Æ:; , constituída pelas bijecções 5 , cuja restrição a Ö"ß á ß :× seja
5! ; para demonstrar a igualdade anterior, basta evidentemente demonstrar
que, para cada 5! , é nulo o somatório em questão, quando estendido apenas
às permutações 5 − Æw , para o que será suficiente ver que se tem
! œ " sgÐ5 Ñ (ÐB5Ð:"Ñ ß á ß B5Ð:;Ñ Ñ.
5 −Æw
Uma vez que, tendo em conta II.3.10, tem-se, para cada 5 − Æw ,
sgÐ5 Ñ œ sgÐ5! Ñ sgÐÖ5 Ð"Ñß á ß 5 Ð:Ñ×Ñ sgÐ5ÎÖ:"ßáß:;× Ñ,
vemos que a igualdade anterior é equivalente à igualdade
! œ " sgÐ5ÎÖ:"ßáß:;× Ñ (ÐB5Ð:"Ñ ß á ß B5Ð:;Ñ Ñ.
5 −Æw
Ora, fixado 5! , notemos 5 w Ð"Ñ â 5 w Ð;Ñ os elementos do conjunto
N œ Ö"ß á ß : ;× Ï Ö5! Ð"Ñß á ß 5! Ð:Ñ× e / a bijecção estritamente
crescente de Ö"ß á ß ;× sobre Ö: "ß á ß : ;×. Tem então lugar uma
bijecção de Æw sobre Æ; , que a cada 5 associa 5 w " ‰ 5ÎÖ:"ßáß:;× ‰ / . O
facto de 5 w e / serem crescentes, implica que
sgÐ5 w
"
‰ 5ÎÖ:"ßáß:;× ‰ / Ñ œ sgÐ5ÎÖ:"ßáß:;× Ñ,
pelo que, notando, para cada " Ÿ 4 Ÿ :, C4 œ B5w Ð4Ñ , obtemos
" sgÐ5ÎÖ:"ßáß:;× Ñ (ÐB5Ð:"Ñ ß á ß B5Ð:;Ñ Ñ œ
5 −Æw
œ " sgÐ5 w
"
‰ 5 ‰ / Ñ (ÐC5w " ‰5 ‰/ Ð"Ñ ß á ß C5w " ‰5 ‰/ Ð;Ñ Ñ œ
5 −Æw
œ ;x AltÐ(ÑÐC" ß á ß C; Ñ œ !,
o que termina a demonstração, no caso em que AltÐ(Ñ œ !. O caso em que
AltÐ0Ñ œ ! reduz-se ao caso já estudado, visto que, por II.5.3, tem-se
AltÐ0 Œ (Ñ œ Ð"Ñ:; AltÐ( Œ 0Ñ.
II.5.6. (Associatividade) Sejam I um espaço vectorial sobre Š, Šw ¨ Š, e os
tensores alternados 0 − E: ÐIà Šw Ñ, ( − E; ÐIà Šw Ñ e ' − E< ÐIà Šw Ñ. Tem-se
então
Ð0 • (Ñ • ' œ 0 • Ð( • ' Ñ œ
Ð: ; <Ñx
AltÐ0 Œ ( Œ ' Ñ − E:;< ÐIà Šw Ñ.
:x ;x <x
60
Cap. II. Tópicos de Álgebra Multilinear
Dem: Vamos demonstrar que se tem
Ð0 • ( Ñ • ' œ
Ð: ; <Ñx
AltÐÐ0 Œ (Ñ Œ ' Ñ.
:x ;x <x
De maneira análoga se demonstraria que
0 • Ð( • ' Ñ œ
Ð: ; <Ñx
AltÐ0 Œ Ð( Œ ' ÑÑ,
:x ;x <x
pelo que o resultado será então uma consequência da associatividade do
produto tensorial. Ora, tem-se
Ð: ; <Ñx
AltÐÐ0 • (Ñ • ' Ñ œ
Ð: ;Ñx <x
Ð: ; <Ñx
œ
AltÐAltÐ0 Œ (Ñ Œ ' ÑÑ,
:x ;x <x
Ð0 • ( ) • ' œ
pelo que, para provarmos a igualdade referida, tudo o que temos que ver é
que
AltÐÐ0 Œ (Ñ Œ ' Ñ œ AltÐAltÐ0 Œ (Ñ Œ ' Ñ,
ou seja, que
AltÐÐÐ0 Œ (Ñ AltÐ0 Œ (ÑÑ Œ ' Ñ œ !.
Mas isto é uma consequência do lema anterior, visto que
AltÐÐ0 Œ (Ñ AltÐ0 Œ (ÑÑ œ AltÐ0 Œ (Ñ AltÐAltÐ0 Œ (ÑÑ œ
œ AltÐ0 Œ (Ñ AltÐ0 Œ (Ñ œ !
(lembrar que AltÐ0 Œ (Ñ é alternado e que Alt é a identidade no espaço dos
tensores alternados).
II.5.7. O facto de ser válida a propriedade associativa permite-nos, dados, para
cada " Ÿ 4 Ÿ 8, 04 − E:4 ÐIà Šw Ñ, definir um produto exterior, sem parênteses,
0" • â • 08 − E:" â:8 ÐIà Šw Ñ.
Tem então lugar a seguinte fórmula explícita para esse produto exterior:
0" • â • 08 œ
Ð:" â :8 Ñx
AltÐ0" Œ â Œ 08 Ñ.
:" xâ:8 x
Dem: A demonstração faz-se por indução em 8. O caso 8 œ " é trivial e o
caso 8 œ # não é mais do que a definição do produto exterior. Supondo que
o resultado é válido para 8 factores, a demonstração de que ele é válido para
8 " factores é decalcada pelo que fizémos na demonstração precedente (o
§5. Produto exterior
61
que aí fizémos foi mostrar que o resultado era válido para 3 factores, a partir
do facto de ele ser válido para 2 factores).
II.5.8. Um caso particular importante da fórmula anterior é aquele em que todos
os :4 são ". Dado portanto, para cada " Ÿ 4 Ÿ 8, 04 − E" ÐIà Šw Ñ, obtemos a
seguinte fórmula para o tensor alternado 0" • â • 08 − E8 ÐIà Šw Ñ:
0" • â • 08 œ 8x AltÐ0" Œ â Œ 08 Ñ.
Com demonstração análoga se verificaria que o produto tensorial
simétrico é associativo, começando-se naturalmente por estabelecer o
análogo do lema II.5.5: Se 0 − P: ÐIà Šw Ñ e ( − P; ÐIà Šw Ñ são tais que,
ou SymÐ0Ñ œ !, ou SymÐ(Ñ œ !, então SymÐ0 Œ (Ñ œ !. Do mesmo
modo, dado, para cada " Ÿ 4 Ÿ 8, 04 − W :4 ÐIà Šw Ñ, tem-se a fórmula
análoga à de II.5.7:
0" â 08 œ
Ð:" â :8 Ñx
SymÐ0" Œ â Œ 08 Ñ.
:" xâ:8 x
II.5.9. Seja I um espaço vectorial de dimensão 7 sobre Š, com uma base
ÐB4 Ñ"Ÿ4Ÿ7 e seja Šw ¨ Š. Dado ! Ÿ : Ÿ 7, podemos então considerar a
base associada de E" ÐIà Šw Ñ œ PÐIà Šw Ñ, constituída pelos 04 , e a base
associada de E: ÐIà Šw Ñ, constituída pelos 0•4" ßáß4: , com 4" â 4: em
Ö"ß á ß 7×. Tem-se então
0•4" ßáß4: œ 04" • â • 04: .
Dem: Uma vez que, como se viu em II.2.12,
04" ßáß4: œ 04" Œ â Œ 04: ,
o resultado é uma consequência da definição dada em II.4.11 e da fórmula
para o produto exterior de tensores alternados de grau 1, apresentada em
II.5.8.
O resultado que se segue é mais um exemplo das relações dos
determinantes com os espaços de aplicações multilineares alternadas.
Nele se dá mais uma caracterização do produto exterior de 8 tensores
alternados de grau ".
II.5.10. Sejam I um espaço vectorial sobre Š, Šw ¨ Š e, para cada " Ÿ 4 Ÿ 8,
04 − E" ÐIà Šw Ñ œ PÐIà Šw Ñ. Dados B" ß á ß B8 − I , tem-se então
Ð0" • â • 08 ÑÐB" ß á ß B8 Ñ œ detÐÐ04 ÐB5 ÑÑ.
Dem: Tendo em conta a fórmula para o produto exterior, apresentada em
II.5.8, e a definição da aplicação Alt, obtemos
62
Cap. II. Tópicos de Álgebra Multilinear
Ð0" • â • 08 ÑÐB" ß á ß B8 Ñ œ " sgÐ5 Ñ 5
s Ð0" Œ â Œ 08 ÑÐB" ß á ß B8 Ñ œ
5
œ " sgÐ5 Ñ Ð0" Œ â Œ 08 ÑÐB5Ð"Ñ ß á ß B5Ð8Ñ Ñ œ
5
œ " sgÐ5 Ñ 0" ÐB5Ð"Ñ Ñ â 08 ÐB5Ð8Ñ Ñ œ detÐÐ04 ÐB5 ÑÑ.
5
Vamos agora estabelecer uma fórmula alternativa para o produto exterior
de dois tensores alternados de graus : e ; , em cuja demonstração será
claro qual a utilidade do factor Ð:;Ñx
:x ;x na definição do produto exterior.
Começamos, como é habitual, por apresentar um lema:
II.5.11. (Lema) Sejam I um espaço vectorial sobre Š e J um espaço vectorial
sobre Šw ¨ Š, e consideremos 0 − P:; ÐIà J Ñ, que seja alternado, tanto nas
primeiras : variáveis, como nas últimas ; variáveis, isto é, tal que se
verifiquem as duas condições seguintes:
a) Dados B:" ß á ß B:; − I , é alternada a aplicação multilinear de I : em
J , definida por
ÐB" ß á ß B: Ñ È 0ÐB" ß á ß B: ß B:" ß á ß B:; Ñ;
b) Dados B" ß á ß B: − I , é alternada a aplicação multilinear de I ; em J ,
definida por
ÐB:" ß á ß B:; Ñ È 0ÐB" ß á ß B: ß B:" ß á ß B:; Ñ;
(reparar que 0 não será, em geral, alternada). Para cada sucessão estritamente
crescente 4" â 4: de elementos do conjunto Ö"ß á ß : ;×, notemos
4:" â 4:; a sucessão estritamente crescente dos restantes elementos
daquele conjunto. Tem-se então
AltÐ0ÑÐB" ß á ß B: ß B:" ß á ß B:; Ñ œ
:x ;x
" sgÐÖ4" ß á ß 4: ×Ñ 0ÐB4" ß á ß B4: ß B4:" ß á ß B4:; Ñ.
œ
Ð: ;Ñx 4" â4:
Dem: Dado 5 − Æ:; , notemos 5 w a permutação em Æ:; , que aplica
Ö"ß á ß :× em Ö5 Ð"Ñß á ß 5 Ð:Ñ×, de modo crescente, e aplica, também de
modo crescente Ö: "ß á ß : ;× em Ö5 Ð: "Ñß á ß 5 Ð: ;Ñ×. Tem-se
então, utilizando o facto de 0 ser alternado, tanto nas primeiras : variáveis
como nas ; últimas,
§5. Produto exterior
63
0ÐB5Ð"Ñ ß á ß B5Ð:Ñ ß B5Ð:"Ñ ß á ß B5Ð:;Ñ Ñ œ
œ sgÐ5ÎÖ"ßáß:× Ñ sgÐ5ÎÖ:"ßáß:;× Ñ 0ÐB5w Ð"Ñ ß á ß B5w Ð:Ñ ß B5w Ð:"Ñ ß á ß B5w Ð:;Ñ Ñ
(pensar em notar C4 œ B5w Ð4Ñ e D5 œ B5w Ð:5Ñ …), pelo que, tendo em conta
II.3.10,
sgÐ5 Ñ 0ÐB5Ð"Ñ ß á ß B5Ð:;Ñ Ñ œ sgÐÖ5 Ð"Ñß á ß 5 Ð:Ñ×Ñ 0ÐB5w Ð"Ñ ß á ß B5w Ð:;Ñ Ñ.
Se atendermos agora a que, para cada sucessão estritamente crescente
4" â 4: em Ö"ß á ß : ;×, há exactamente :x ;x permutações 5 , tais
que Ö5 Ð"Ñß á ß 5 Ð:Ñ× œ Ö4" ß á ß 4: ×, concluímos que
AltÐ0ÑÐB" ß á ß B:; Ñ œ
"
" sgÐ5 Ñ 0ÐB5Ð"Ñ ß á ß B5Ð:Ñ ß B5Ð:"Ñ ß á ß B5Ð:;Ñ Ñ œ
œ
Ð: ;Ñx 5
:x ;x
" sgÐÖ4" ß á ß 4: ×Ñ 0ÐB4" ß á ß B4: ß B4:" ß á ß B4:; Ñ.
œ
Ð: ;Ñx 4" â4:
II.5.12. (Fórmula alternativa para o produto exterior) Sejam 0 − E: ÐIà Šw Ñ e
( − E; ÐIà Šw Ñ. Tem-se então, com as notações do lema anterior,
0 • (ÐB" ß á ß B:; Ñ œ
œ
" sgÐÖ4" ß á ß 4: ×Ñ 0ÐB4" ß á ß B4: Ñ (ÐB4:" ß á ß B4:; Ñ.
4" â4:
Dem: Uma vez que 0 Œ ( − P:; ÐIà Šw Ñ verifica trivialmente as hipóteses
do lema anterior, o resultado é uma consequência imediata deste e da
definição do produto exterior.
II.5.13. A aplicação da fórmula para o produto exterior, obtida no resultado anterior, é especialmente cómoda nos casos em que : (ou ; ) é pequeno. Por
exemplo, nos casos : œ " e : œ #, obtemos, respectivamente
0 • (ÐB" ß á ß B;" Ñ œ
œ " Ð"Ñ4" 0ÐB4 Ñ (ÐB" ß á ß B4" ß B4" ß á ß B;" Ñ,
4
0 • (ÐB" ß á ß B;# Ñ œ
œ " Ð"Ñ45" 0ÐB4 ß B5 Ñ (ÐB" ß á ß B4" ß B4" ß á ß B5" ß B5" ß á ß B;# Ñ.
45
O lema II.5.11 e a fórmula obtida em II.5.12 têm versões correspondentes,
com as aplicações multilineares simétricas no papel das alternadas.
64
Cap. II. Tópicos de Álgebra Multilinear
Assim, se 0 − W : ÐIà Šw Ñ e ( − W ; ÐIà Šw Ñ, ver-se-ia facilmente que
0 (ÐB" ß á ß B:; Ñ œ
" 0ÐB4" ß á ß B4: Ñ (ÐB4:" ß á ß B4:; Ñ.
4" â4:
II.5.14. (Compatibilidade com as imagens recíprocas) Sejam I e J espaços
vectoriais sobre Š, -À I Ä J uma aplicação linear e Šw ¨ Š. Dados
0 − E: ÐJ à Šw Ñ e ( − E; ÐJ à Šw Ñ, tem-se então
-‡ Ð0 • (Ñ œ -‡ Ð0Ñ • -‡ Ð(Ñ − E:; ÐIà Šw Ñ.
Dem: Trata-se de uma consequência trivial de II.2.16 e de II.4.12, tendo em
conta a definição do produto exterior.
§6. Produto interior.
II.6.1. Sejam I um espaço vectorial sobre Š, J um espaço vectorial sobre
Šw ¨ Š e B − I . Para cada : ", tem então lugar uma aplicação linear
intB À P: ÐIà J Ñ Ä P:" ÐIà J Ñ, chamada produto interior por B, definida por
intB Ð0ÑÐB" ß á ß B:" Ñ œ 0ÐBß B" ß á ß B:" Ñ.
No caso em que : œ ", tem-se P:" ÐIà J Ñ œ J , e a aplicação
intB À PÐIà J Ñ Ä J é simplesmente a aplicação definida por intB Ð0Ñ œ 0ÐBÑ.
Repare-se que, não só cada intB é uma aplicação linear, como tem lugar uma
aplicação bilinear, que a ÐBß 0Ñ associa intB Ð0Ñ (mais precisamente, esta aplicação é Š-linear na primeira variável e Šw -linear na segunda).
Resulta facilmente da definição que a aplicação intB vai aplicar E: ÐIà J Ñ
em E:" ÐIà J Ñ. Vamos necessitar, mais geralmente, de fórmulas que
relacionem o produto interior com as aplicações Alt. Para enunciar essas
relações, temos necessidade de fixar a seguinte notação:
II.6.2. Dados : " e " Ÿ 4 Ÿ :, vamos notar 74 − Æ: a permutação que aplica
"ß á ß : sucessivamente em #ß á ß 4ß "ß 4 "ß á ß :, por outras palavras, a
definida por
Ú5 "
74 Ð5Ñ œ Û "
Ü5
se 5 4
se 5 œ 4.
se 5 4
Repare-se que, contando o número de inversões, constata-se imediatamente
que sgÐ74 Ñ œ Ð"Ñ4" .
§6. Produto interior
65
II.6.3. (Lema) Dados : " e 0 − P: ÐIà J Ñ, tem-se, para cada B − I ,
"
" Ð"Ñ4" AltÐintB Ðs7 4 Ð0ÑÑÑ.
: 4œ"
:
intB ÐAltÐ0ÑÑ œ
Dem: Escrevendo, por conveniência de notações, B œ B" , vem
:x intB ÐAltÐ0ÑÑÐB# ß á ß B: Ñ œ :x AltÐ0ÑÐB" ß á ß B: Ñ œ
œ " sgÐ5 Ñ 0ÐB5Ð"Ñ ß á ß B5Ð:Ñ Ñ.
5
O somatório anterior é igual à soma de : somatórios, a saber, os correspondentes, para os diferentes " Ÿ 4 Ÿ :, às permutações 5 que verificam
5Ð4Ñ œ ". O resultado ficará portanto provado, se virmos que, para cada 4, o
somatório anterior, quando estendido apenas às permutações 5 , que
verificam 5 Ð4Ñ œ ", é igual a Ð: "Ñx Ð"Ñ4" AltÐintB Ðs7 4 Ð0ÑÑÑÐB# ß á ß B: Ñ.
Fixemos portanto um tal 4. Reparemos que existe uma correspondência
biunívoca entre o conjunto das permutações 5 − Æ: , que verificam 5 Ð4Ñ œ ",
e o conjunto Æ:" , correspondência que a cada 5 associa a permutação
5 w À Ö"ß á ß : "× Ä Ö"ß á ß : "×, definida por
5 w Ð5Ñ œ œ
5 Ð5Ñ "
5 Ð5 "Ñ "
se 5 4
.
se 5 4
Além disso, contando o número de inversões, constata-se imediatamente que
sgÐ5 Ñ œ Ð"Ñ4" sgÐ5 w Ñ. Se notarmos C5 œ B5Ð5Ñ e D5 œ B5" , e se reparamos
que 0 œ Ð74" Ñs Ðs7 4 Ð0ÑÑ, vemos que, se 5 Ð4Ñ œ ",
sgÐ5 Ñ 0ÐB5Ð"Ñ ß á ß B5Ð:Ñ Ñ œ sgÐ5 Ñ 0ÐC" ß á ß C: Ñ œ
œ sgÐ5 Ñ s7 4 Ð0ÑÐC4 ß C" ß á ß C4" ß C4" ß á ß C: Ñ œ
œ sgÐ5 Ñ s7 4 Ð0ÑÐB" ß B5Ð"Ñ ß á ß B5Ð4"Ñ ß B5Ð4"Ñ ß á ß B5Ð:Ñ Ñ œ
œ sgÐ5 Ñ intB Ðs7 4 Ð0ÑÑÐD5w Ð"Ñ ß á ß D5w Ð:"Ñ Ñ,
donde
" sgÐ5 Ñ 0ÐB5Ð"Ñ ß á ß B5Ð:Ñ Ñ œ
5 Ð4Ñœ"
œ Ð"Ñ4" " sgÐ5 w Ñ intB Ðs7 4 Ð0ÑÑÐD5w Ð"Ñ ß á ß D5w Ð:"Ñ Ñ œ
5w
4"
œ Ð"Ñ Ð: "Ñx AltÐintB Ðs7 4 Ð0ÑÑÑÐD" ß á ß D:" Ñ œ
œ Ð"Ñ4" Ð: "Ñx AltÐintB Ðs7 4 Ð0ÑÑÑÐB# ß á ß B: Ñ,
como queríamos.
II.6.4. Em particular, se 0 − E: ÐIà J Ñ, com : ", e se B − I , tem-se
intB Ð0Ñ − E:" ÐIà J Ñ.
66
Cap. II. Tópicos de Álgebra Multilinear
Dem: Embora este resultado tenha uma demonstração directa trivial, ele é
também uma consequência do resultado anterior, visto que, uma vez que 0 é
alternado, tem-se AltÐ0Ñ œ 0 e s7 4 Ð0Ñ œ Ð"Ñ4" 0.
II.6.5. (Lema) Sejam I um espaço vectorial sobre Š e Šw ¨ Š. Dados
0 − P: ÐIà Šw Ñ, ( − P; ÐIà Šw Ñ e B − I , tem-se então:
a) Se " Ÿ 4 Ÿ :,
intB Ðs7 4 Ð0 Œ (ÑÑ œ intB Ðs7 4 Ð0ÑÑ Œ (;
b) Se : " Ÿ 4 Ÿ : ; ,
intB Ðs7 4 Ð0 Œ (ÑÑ œ 0 Œ intB Ðs7 4: Ð(ÑÑ.
Dem: Demonstremos apenas a alínea b), visto que a demonstração de a) é do
mesmo tipo (e até um pouco mais simples). Escrevendo B œ B" , vem, para
cada 4 entre : " e : ; ,
intB Ðs7 4 Ð0 Œ (ÑÑÐB# ß á ß B:; Ñ œ s7 4 Ð0 Œ (ÑÐB" ß á ß B8 Ñ œ
œ 0 Œ (ÐB# ß á ß B4 ß B" ß B4" ß á ß B:; Ñ œ
œ 0ÐB# ß á ß B:" Ñ (ÐB:# ß á ß B4 ß B" ß B4" ß á ß B:; Ñ œ
œ 0ÐB# ß á ß B:" Ñ s7 4: Ð(ÑÐB" ß B:# ß á ß B:; Ñ œ
œ 0ÐB# ß á ß B:" Ñ intB Ðs7 4: Ð(ÑÑÐB:# ß á ß B:; Ñ œ
œ 0 Œ intB Ðs7 4: Ð(ÑÑÐB# ß á ß B:; Ñ
(na passagem da terceira para a quarta linha, pensar talvez em pôr C" œ B" e,
para # Ÿ 5 Ÿ ; , C5 œ B:5 …).
II.6.6. (Resultado fundamental) Sejam I um espaço vectorial sobre Š e
Šw ¨ Š. Se 0 − E: ÐIà Šw Ñ e ( − E; ÐIà Šw Ñ, com :ß ; ", então
intB Ð0 • (Ñ œ intB Ð0Ñ • ( Ð"Ñ: 0 • intB Ð(Ñ.
§6. Produto interior
67
Dem: Tendo em conta os resultados anteriores,
intB Ð0 • (Ñ œ
Ð: ;Ñx
intB ÐAltÐ0 Œ (ÑÑ œ
:x ;x
Ð: ; "Ñx
" Ð"Ñ4" AltÐintB Ðs7 4 Ð0 Œ (ÑÑÑ œ
:x ;x
4œ"
:;
œ
Ð: ; "Ñx
" Ð"Ñ4" AltÐintB Ðs7 4 Ð0ÑÑ Œ (Ñ
:x ;x
4œ"
:
œ
Ð: ; "Ñx
" Ð"Ñ4" AltÐ0 Œ intB Ðs7 4: Ð(ÑÑÑ œ
:x ;x
4œ:"
:;
œ
Ð: ; "Ñx
" Ð"Ñ4" Ð"Ñ4" AltÐintB Ð0Ñ Œ (Ñ
:x ;x
4œ"
:
œ
Ð: ; "Ñx
" Ð"Ñ4" Ð"Ñ4:" Alt(0 Œ 38>B Ð(ÑÑ œ
:x ;x
4œ:"
:;
œ
Ð: ; "Ñx
Ð: ; "Ñx
AltÐintB Ð0Ñ Œ (Ñ Ð"Ñ:
Alt(0 Œ 38>B Ð(ÑÑ œ
Ð: "Ñx ;x
:x Ð; "Ñx
œ intB Ð0Ñ • ( Ð"Ñ: 0 • intB Ð(Ñ.
œ
II.6.7. Sejam I um espaço vectorial sobre Š e J um espaço vectorial sobre
Šw ¨ Š. Seja 0 − E: ÐIà J Ñ, com : #. Dados Bß C − I , tem-se então
intB ÐintC Ð0ÑÑ œ intC ÐintB Ð0ÑÑ, em particular, vem intB ÐintB Ð0ÑÑ œ !.
Dem: Basta vermos que ambos os membros dão o mesmo resultado, quando
aplicados a ÐA" ß á ß A:# Ñ, e isso é uma consequência imediata da
caracterização das aplicações multilineares alternadas, apresentada em
II.4.3.
§7. Orientação de espaços vectoriais reais.
II.7.1. (Revisão) Lembremos que, se I é um espaço vectorial real de dimensão
8 e se B" ß á ß B8 e C" ß á ß C8 são duas bases de I , diz-se que elas estão
positivamente relacionadas se, considerando a matriz de mudança de base,
cujos elementos +5ß4 estão definidos por C4 œ ! +5ß4 B5 , tem-se
5
detÐÐ+5ß4 ÑÑ !; caso contrário, isto é, se se tiver detÐÐ+5ß4 ÑÑ !, dizemos
que elas estão negativamente relacionadas.9
9A
razão porque só faz sentido apresentar esta noção para os espaços vectoriais reais está
em que, no caso dos espaços vectoriais complexos, o determinante da matriz de mudança
de base será, em geral, um número complexo, não fazendo portanto sentido pedir que ele
68
Cap. II. Tópicos de Álgebra Multilinear
A relação de duas bases serem positivamente relacionadas é uma relação de
equivalência, que tem a propriedade especial de podermos garantir que duas
bases estão positivamente relacionadas desde que exista uma terceira com a
qual nenhuma delas esteja positivamente relacionada.
Chama-se orientação de I a uma aplicação ! do conjunto das bases de I
(indexadas em Ö"ß á ß 8×) no conjunto Ö"ß "× com a propriedade de se ter
!ÐB" ß á ß B8 Ñ œ !ÐC" ß á ß C8 Ñ se, e só se, as duas bases estiverem positivamente relacionadas. Chama-se espaço vectorial orientado a um espaço vectorial real de dimensão finita, no qual se fixou uma orientação e, relativamente
a um tal espaço, chamam-se bases positivas ou directas àquelas cuja imagem
é " e bases negativas ou retrógradas àquelas cuja imagem é ".
Fixada uma base B" ß á ß B8 de I e um número & − Ö"ß "×, existe uma, e
uma só, orientação ! de I tal que !ÐB" ß á ß B8 Ñ œ &; em particular cada
espaço vectorial I tem duas, e só duas, orientações, uma simétrica da outra.
II.7.2. Seja I um espaço vectorial real de dimensão 8 e seja 0 um elemento não
nulo do espaço vectorial real E8 ÐIà ‘Ñ, de dimensão ". Tem-se então:
a) Se B" ß á ß B8 é um sistema de vectores de I , então este sistema é uma
base se, e só se, 0ÐB" ß á ß B8 Ñ Á !.
b) Duas bases B" ß á ß B8 e C" ß á ß C8 de I estão positivamente relacionadas
se, e só se, os números reais não nulos 0ÐB" ß á ß B8 Ñ e 0ÐC" ß á ß C8 Ñ têm o
mesmo sinal.
Dem: Se o sistema B" ß á ß B8 não é uma base, ele é linearmente dependente
pelo que, como vimos em II.4.7, 0ÐB" ß á ß B8 Ñ œ !. Se o sistema for uma
base, podemos considerar a base associada de E8 ÐIà ‘Ñ, formada por um
único elemento 0•"ßáß8 , para o qual se tem 0•"ßáß8 ÐB" ß á ß B8 Ñ œ ". Uma vez
que E8 ÐIà ‘Ñ tem dimensão ", vem 0 œ + 0•"ßáß8 , com + Á !, bastando
agora reparar que se tem 0ÐB" ß á ß B8 Ñ œ + Á !. A alínea b) é uma
consequência imediata de II.4.15.
II.7.3. (Corolário) Nas condições anteriores, dada uma base B" ß á ß B8 de I ,
esta base está negativamente relacionada com as bases que se obtêm trocando
a posição de dois dos vectores ou multiplicando um dos vectores por um
número real negativo.
Em geral, se I é um espaço vectorial real de dimensão 8, não existe sobre
I uma orientação que seja melhor que a outra, pelo que orientar um
espaço resultará normalmente de uma escolha mais ou menos arbitrária.
Uma excepção é a dos espaços vectoriais de dimensão !:
seja positivo ou negativo. Repare-se também que, nesta definição, é importante a ordem
pela qual consideramos os elementos da base, ordem que está implícita ao considerarmos
as bases indexadas em Ö"ß á ß 8×. Não faz sentido falar de bases positiva ou
negativamente relacionadas, quando estas estiverem indexadas em conjuntos arbitrários.
§7. Orientação de espaços vectoriais reais
69
II.7.4. Se I é um espaço vectorial de dimensão !, I admite uma única base, a
saber, a família vazia de vectores. Chamamos orientação positiva de I à
orientação relativamente à qual essa base é directa e damos à outra orientação
o nome de orientação negativa.
II.7.5. Chama-se orientação canónica de ‘8 a orientação relativamente à qual a
base canónica /" ß á ß /8 é directa. Quando não referimos explicitamente qual
a orientação que consideramos em ‘8 , é esta a que está implícita.
II.7.6. Se I é um espaço vectorial real de dimensão ", uma base de I é a mesma
coisa que um vector não nulo, e dadas duas bases B e C, tem-se B œ +C, para
um certo + − ‘ Ï Ö!×, e então que elas são positivamente relacionadas se, e
só se, + !. Dar uma orientação de I é portanto dar uma aplicação
sgÀ I Ï Ö!× Ä Ö"ß "×, tal que, sendo B œ +C, se tenha sgÐBÑ œ sgÐCÑ se, e
só se, + !. Aos vectores não nulos cuja imagem é " costuma-se dar o nome
de vectores positivos e àqueles cuja imagem é " o de vectores negativos (é
claro que não havia inconveniente em chamá-los respectivamente de vectores
directos e vectores retrógrados).
II.7.7. Por exemplo, para ‘, com a sua orientação canónica, os elementos
+ − ‘ Ï Ö!× positivos (resp. negativos) são aqueles que são maiores que !
(resp. menores que !), o que mostra que a nomenclatura utilizada não conduz
a confusões.10 É esta a orientação que se considera em ‘, salvo aviso em
contrário. A aplicação sgÀ ‘ Ï Ö!× Ä Ö"ß "× é portanto a aplicação sinal
usual, definida por sgÐBÑ œ ", se B !, e sgÐBÑ œ ", se B ! ou,
equivalentemente, por
B
sgÐBÑ œ
.
lBl
II.7.8. Lembrando a definição de orientação, vemos que, se ! é uma orientação
do espaço vectorial real I , de dimensão 8, então, dadas duas bases
B" ß á ß B8 e C" ß á ß C8 de I , com C5 œ ! +4ß5 B4 , tem-se
4
!ÐC" ß á ß C8 Ñ œ sgÐdetÐÐ+4ß5 ÑÑÑ !ÐB" ß á ß B8 Ñ,
ou, por outras palavras, sendo -À I Ä I o isomorfismo definido por
-ÐB4 Ñ œ C4 ,
!ÐC" ß á ß C8 Ñ œ sgÐdetÐ-ÑÑ !ÐB" ß á ß B8 Ñ.
II.7.9. Seja I um espaço vectorial real de dimensão 8, e consideremos o correspondente espaço vectorial de dimensão ", E8 ÐIà ‘Ñ. Para cada orientação de
I existe então uma, e uma só, orientação de E8 ÐIà ‘Ñ, dita orientação asso10No
entanto, também se pode considerar em ‘ a outra orientação, e aí os núneros
positivos são os que são menores que ! e os negativos os que são maiores que !.
70
Cap. II. Tópicos de Álgebra Multilinear
ciada, tal que, quaisquer que sejam a base B" ß á ß B8 de I e o elemento não
nulo 0 de E8 ÐIà ‘Ñ, se tenha
sgÐ0ÐB" ß á ß B8 ÑÑ œ sgÐ0Ñ !ÐB" ß á ß B8 Ñ.
Além disso, se trocarmos a orientação de I , a orientação associada de
E8 ÐIà ‘Ñ vem também trocada. Fica assim estabelecida uma bijecção entre o
conjunto das orientações de I e o das orientações de E8 ÐIà ‘Ñ.
Dem: Fixemos uma base C" ß á ß C8 de I e um elemento não nulo ( de
E8 ÐIà ‘Ñ. Sabemos que existe então sobre E8 ÐIà ‘Ñ uma, e uma só, orientação, que no elemento particular ( tome o valor sgÐ(Ñ − Ö"ß "× que
verifica
sgÐ(ÐC" ß á ß C8 ÑÑ œ sgÐ(Ñ !ÐC" ß á ß C8 Ñ.
É imediato que, para cada elemento não nulo 0 de E8 ÐIà ‘Ñ, tem-se ainda
sgÐ0ÐC" ß á ß C8 ÑÑ œ sgÐ0Ñ !ÐC" ß á ß C8 Ñ.
O facto de, para uma base arbitrária B" ß á ß B8 de I se verificar ainda
sgÐ0ÐB" ß á ß B8 ÑÑ œ sgÐ0Ñ !ÐB" ß á ß B8 Ñ
é agora uma consequência de II.7.2. Ficou portanto estabelecida a existência
de uma orientação em E8 ÐIà ‘Ñ, verificando a propriedade do enunciado, e a
unicidade desta orientação é imediata, assim como o facto de ela vir trocada
quando se troca a orientação de I .
II.7.10. (Corolário) Em particular, dada uma base B" ß á ß B8 de I , tem-se, para
a base associada 0•"ßáß8 de E8 ÐIà ‘Ñ,
sgÐ0•"ßáß8 Ñ œ !ÐB" ß á ß B8 Ñ.
Dem: Basta atender a que 0•"ßáß8 ÐB" ß á ß B8 Ñ œ ".
II.7.11. No caso em que I é um espaço vectorial de dimensão !, tem-se
E! ÐIà ‘Ñ œ ‘ e verifica-se imediatamente que, à orientação positiva de I
(cf. II.7.4) fica associada a orientação canónica de ‘.
II.7.12. Considerando em ‘8 a orientação canónica, a orientação associada de
E8 Б8 à ‘Ñ é aquela para a qual o elemento det − E8 Б8 à ‘Ñ é positivo.
Dem: Basta atender a que det é o elemento 0•"ßáß8 , da base associada à base
canónica /" ß á ß /8 de ‘8 .
II.7.13. Sejam I e J espaços vectoriais reais de dimensão 8, munidos de
orientações ! e " , e -À I Ä J um isomorfismo. Existe então um, e um só,
sgÐ-Ñ − Ö"ß "× tal que, qualquer que seja a base B" ß á ß B8 de I , se tenha
" Ð-ÐB" Ñß á ß -ÐB8 ÑÑ œ sgÐ-Ñ !ÐB" ß á ß B8 Ñ.
Além disso, se trocarmos a orientação de I ou se trocarmos a orientação de
J , sgÐ-Ñ vem trocado.
§7. Orientação de espaços vectoriais reais
71
Dem: Fixando uma base C" ß á ß C8 de I , podemos definir sgÐ-Ñ pela condição de ser " Ð-ÐC" Ñß á ß -ÐC8 ÑÑ œ sgÐ-Ñ !ÐC" ß á ß C8 Ñ. Para verificarmos a
igualdade do enunciado, para uma base arbitrária B" ß á ß B8 , basta
repararmos que, se for C4 œ ! +5ß4 B5 , tem-se também -ÐC4 Ñ œ ! +5ß4 -ÐB5 Ñ.
5
5
Ficou portanto provada a existência de sgÐ-Ñ, nas condições do enunciado. A
unicidade, assim como o facto de sgÐ-Ñ vir trocado, se trocarmos uma das
orientações, de I ou de J , é trivial.
II.7.14. Nas condições anteriores, diz-se que sgÐ-Ñ é o sinal do isomorfismo -,
entre os espaços vectoriais reais de dimensão finita e orientados I e J . Se é um isomorfismo tal que sgÐ-Ñ œ ", diz-se que - é um isomorfismo positivo, ou que conserva as orientações. Dos outros isomorfismos, diz-se que
são negativos, ou que invertem as orientações.
II.7.15. Sejam I , J e K espaços vectoriais reais orientados de dimensão 8 e
-À I Ä J e .À J Ä K dois isomorfismos. Tem-se então:
a) O isomorfismo M.I À I Ä I conserva as orientações, isto é, sgÐM.I Ñ œ ".
b) sgÐ. ‰ -Ñ œ sgÐ.Ñ sgÐ-Ñ.
c) sgÐ-" Ñ œ sgÐ-Ñ.
Dem: A alínea a) é trivial e a alínea c) é uma consequência de a) e b). Para
verificarmos b), basta fixar uma base B" ß á ß B8 de I e verificar que,
notando !, " e # as orientações de I , J e K, respectivamente,
sgÐ. ‰ -Ñ !ÐB" ß á ß B8 Ñ œ # Ð.Ð-ÐB" ÑÑß á ß .Ð-ÐB8 ÑÑÑ œ
œ sgÐ.Ñ " Ð-ÐB" Ñß á ß -ÐB8 ÑÑ œ sgÐ.Ñ sgÐ-Ñ !ÐB" ß á ß B8 Ñ.
II.7.16. Se I é um espaço vectorial real orientado de dimensão 8 e se -À I Ä I
é um isomorfismo, então tem-se sgÐ-Ñ œ sgÐdetÐ-ÑÑ, em particular sgÐ-Ñ não
depende da orientação considerada em I .
Dem: Trata-se de uma consequência imediata da caracterização das bases
positiva e negativamente relacionadas, apresentada em II.7.2, visto que,
dados uma base B" ß á ß B8 de I e um elemento não nulo 0 − E8 ÐIà ‘Ñ,
tem-se -‡ Ð0Ñ œ detÐ-Ñ 0, donde
0Ð-ÐB" Ñß á ß -ÐB8 ÑÑ œ detÐ-Ñ 0ÐB" ß á ß B8 Ñ.
II.7.17. Sejam I e J espaços vectoriais reais de dimensão 8, munidos de
orientações ! e " , e consideremos nos espaços vectoriais reais de dimensão
", E8 ÐIà ‘Ñ e E8 ÐJ à ‘Ñ as orientações associadas. Seja -À I Ä J um
isomorfismo,
e
consideremos
o
isomorfismo
associado
-‡ À E8 ÐJ à ‘Ñ Ä E8 ÐIà ‘Ñ. Tem-se então sgÐ-‡ Ñ œ sgÐ-Ñ.
Dem: Fixando um elemento não nulo 0 − E8 ÐJ à ‘Ñ e uma base B" ß á ß B8
72
Cap. II. Tópicos de Álgebra Multilinear
de I , podemos escrever
sgÐ-‡ Ñ sgÐ0Ñ !ÐB" ß á ß B8 Ñ œ sgÐ-‡ Ð0ÑÑ !ÐB" ß á ß B8 Ñ œ
œ " Ð-‡ Ð0ÑÐB" ß á ß B8 ÑÑ œ " Ð0Ð-ÐB" Ñß á ß -ÐB8 ÑÑÑ œ
œ sgÐ0Ñ " Ð-ÐB" Ñß á ß -ÐB8 ÑÑ œ sgÐ0Ñ sgÐ-Ñ !ÐB" ß á ß B8 Ñ.
Vamos agora estudar situações em que, a partir de orientações em certos
espaços vectoriais, é possivel construir orientações associadas noutros
espaços vectoriais. As situações são principalmente duas, e dizem respeito
à noção de orientação induzida num subespaço vectorial e à de orientação
produto num produto cartesiano de espaços vectoriais reais. Uma maneira
de atacar ao mesmo tempo estas duas situações, e de apanhar de passagem
outras que têm também algum interesse, é a de estudar o que se passa
quando temos uma sucessão exacta curta de espaços vectoriais.
II.7.18. Dados três espaços vectoriais sobre Š, I , J e K, e duas aplicações
.
-
lineares -À I Ä J e .À J Ä K , diz-se que I Ä J Ä K é uma sucessão
exacta se se tem -ÐIÑ œ kerÐ.Ñ. Mais geralmente, diz-se que uma sucessão
do tipo
-"
-#
-$
-8#
-8"
I" Ä I# Ä I$ Ä â Ä I8" Ä I8
é uma sucessão exacta, se isso acontecer, para cada " Ÿ 3 Ÿ 8 #, à
sucessão
-3"
-3
I3 Ä I3" Ä I3#
(é claro que esta definição pode ser apresentada, com adaptações triviais,
para sucessões que sejam infinitas à esquerda, à direita, ou de ambos os
lados).
-
II.7.19. Por exemplo, dizer que uma sucessão Ö!× Ä I Ä J é exacta é o
mesmo que dizer que -À I Ä J é uma aplicação linear injectiva, dizer que
-
uma sucessão I Ä J Ä Ö!× é exacta é o mesmo que dizer que -À I Ä J é
-
uma aplicação linear sobrejectiva e dizer que Ö!× Ä I Ä J Ä Ö!× é uma
sucessão exacta é o mesmo que dizer que -À I Ä J é um isomorfismo.
-
.
Repare-se que, se uma sucessão I Ä J Ä K é exacta, tem-se, em
particular, . ‰ - œ !; esta última condição é aliás equivalente ao facto de se
ter -ÐIÑ § kerÐ.Ñ.
II.7.20. Dizer que uma sucessão do tipo
-
.
Ö!× Ä I Ä J Ä K Ä Ö!×
é uma sucessão exacta equivale a dizer que se verificam as três condições
§7. Orientação de espaços vectoriais reais
73
seguintes:
a) -À I Ä J é uma aplicação linear injectiva;
b) .À J Ä K é uma aplicação linear sobrejectiva;
c) -ÐIÑ œ kerÐ.Ñ.
Às sucessões exactas deste tipo costuma-se dar o nome de sucessões exactas
curtas.
II.7.21. Como exemplos típicos de sucessões exactas curtas temos:
a) Se I e J são espaços vectoriais, podemos considerar o produto cartesiano
I ‚ J , assim com as projecções canónicas
1" À I ‚ J Ä I ,
1# À I ‚ J Ä J ,
definidas por 1" ÐBß CÑ œ B e 1# ÐBß CÑ œ C, e as injecções canónicas
+" À I Ä I ‚ J ,
+# À J Ä I ‚ J ,
definidas por +" ÐBÑ œ ÐBß !Ñ e +# ÐCÑ œ Ð!ß CÑ. É então imediato verificar-se
que têm lugar as sucessões exactas curtas
+"
1#
+#
1"
Ö!× Ä I Ä I ‚ J Ä J Ä Ö!×
Ö!× Ä J Ä I ‚ J Ä I Ä Ö!×.
b) Se o espaço vectorial K , sobre Š, é soma directa dos subespaços vectoriais I e J , e se +" À I Ä K e +# À J Ä K são as inclusões e 1" À K Ä I e
1# À K Ä J são as projecções associadas à soma directa, têm lugar as
sucessões exactas curtas
+"
1#
+#
1"
Ö!× Ä I Ä K Ä J Ä Ö!×
Ö!× Ä J Ä K Ä I Ä Ö!×.
c) Se -À I Ä J é uma aplicação linear injectiva, podemos considerar o
subespaço vectorial -ÐIÑ de J e o espaço vectorial quociente J Î-ÐIÑ e,
notando 1À J Ä J Î-ÐIÑ a projecção canónica, vai ter lugar a sucessão
exacta curta
-
1
Ö!× Ä I Ä J Ä
J
Ä Ö!×.
-ÐIÑ
Em particular, se I é um subespaço vectorial de J , e se notarmos +À I Ä J
a inclusão, tem lugar uma sucessão exacta curta
+
1
Ö!× Ä I Ä J Ä
J
Ä Ö!×.
I
d) Se .À I Ä J é uma aplicação linear sobrejectiva, e se +À kerÐ.Ñ Ä I é a
74
Cap. II. Tópicos de Álgebra Multilinear
inclusão, tem lugar uma sucessão exacta curta
.
+
Ö!× Ä kerÐ.Ñ Ä I Ä J Ä Ö!×.
II.7.22. Consideremos uma sucessão exacta curta de espaços vectoriais sobre Š,
.
-
Ö!× Ä I Ä J Ä K Ä Ö!×
assim como uma base ÐB4 Ñ4−N de I e uma base ÐD5 Ñ5−O de K. Para cada
5 − O , escolhamos C5 − J tal que .ÐC5 Ñ œ D5 . Tem-se então que a família
formada pelos C5 e pelos -ÐB4 Ñ é uma base de J . Em particular, J tem
dimensão finita se, e só se, I e K têm dimensões finitas e, nesse caso, tem-se
dimÐJ Ñ œ dimÐIÑ dimÐKÑ.
Dem: Para verificarmos a independência linear, suponhamos que se tinha
" +4 -ÐB4 Ñ " ,5 C5 œ !.
4
5
Aplicando . a ambos os membros, e atendendo a que . ‰ - œ !, obtemos
! œ " +4 .Ð-ÐB4 ÑÑ " ,5 .ÐC5 Ñ œ " ,5 D5 ,
4
5
5
donde, pela independência linear dos D5 , ,5 œ !, para cada 5 ; podemos então
reescrever a primeira igualdade na forma na forma ! œ -Ð! +4 B4 Ñ, donde,
por - ser uma aplicação linear injectiva, ! œ ! +4 B4 , e a independência
linear dos B4 garante que +4 œ !, para cada 4. Seja agora C − J arbitrário.
Tem-se .ÐCÑ − J , pelo que podemos escrever .ÐCÑ œ ! ,5 D5 œ .Ð! ,5 C5 Ñ;
sai então .ÐC ! ,5 C5 Ñ œ !, pelo que C ! ,5 C5 − kerÐ.Ñ œ -ÐIÑ, isto é,
C ! ,5 C5 œ -Ð! +4 B4 Ñ, e portanto C œ ! +4 -ÐB4 Ñ ! ,5 C5 .
II.7.23. Consideremos uma sucessão exacta curta de espaços vectoriais reais de
dimensão finita
-
.
Ö!× Ä I Ä J Ä K Ä Ö!×
Diz-se que um sistema de orientações !, de I , " , de J e # , de K é
compatível com a sucessão exacta se, qualquer que seja a base B" ß á ß B7 de
I , a base D" ß á ß D8 de K e os vectores C" ß á ß C8 de J , tais que .ÐC5 Ñ œ D5 ,
se tem, para a base C" ß á ß C8 -ÐB" Ñß á ß -ÐB7 Ñ de J (por esta ordem11),
" ÐC" ß á ß C8 ß -ÐB" Ñß á ß -ÐB7 ÑÑ œ !ÐB" ß á ß B7 Ñ # ÐD" ß á ß D8 Ñ.
11A
ordenação dos elementos desta base não parece talvez a mais natural, mas é a que se
revela mais útil nas aplicações.
§7. Orientação de espaços vectoriais reais
75
II.7.24. Consideremos uma sucessão exacta curta de espaços vectoriais reais de
dimensão finita
-
.
Ö!× Ä I Ä J Ä K Ä Ö!×
Dadas orientações em dois destes espaços, existe então uma, e uma só, orientação no terceiro (dita orientação associada às outras duas e à sucessão exacta
curta) tal que o sistema das três orientações fique compatível.
Dem: Suponhamos que dois dos espaços estão orientados. Fixemos uma base
B" ß á ß B7 de I , uma base D" ß á ß D8 de K e vectores C" ß á ß C8 em J tais
que .ÐC5 Ñ œ D5 . Sabemos que C" ß á ß C8 ß -ÐB" Ñß á ß -ÐB7 Ñ é uma base de J ,
pelo que podemos fixar uma orientação no terceiro espaço, pela condição de
se ter
(1)
" ÐC" ß á ß C8 ß -ÐB" Ñß á ß -ÐB7 ÑÑ œ !ÐB" ß á ß B7 Ñ # ÐD" ß á ß D8 Ñ.
Para verificarmos que o sistema das três orientações fica compatível com a
sucessão exacta (a unicidade da orientação do terceiro espaço nestas
condições é então imediata), fixemos um elemento não nulo 0 em
E78 ÐJ à ‘Ñ, e comecemos por mostrar que, se D"w ß á ß D8w é outra base de K e
se os vectores C"w ß á ß C8w em J são escolhidos de modo que .ÐC5w Ñ œ D5w ,
então tem-se ainda
(2)
" ÐC"w ß á ß C8w ß -ÐB" Ñß á ß -ÐB7 ÑÑ œ !ÐB" ß á ß B7 Ñ # ÐD"w ß á ß D8w Ñ.
Ora, sendo D5w œ ! ,jß5 Dj , vem .ÐC5w ! ,jß5 Cj Ñ œ 0, donde a existência de
Bww5 − I tais que
j
j
C5w " ,jß5 Cj œ -ÐBww5 Ñ,
j
e o facto de uma aplicação multilinear alternada se anular quando aplicada a
um sistema linearmente dependente permite-nos escrever, por -ÐIÑ ter
dimensão 7 e portanto qualquer sistema que contenha mais que 7 elementos
deste espaço ser linearmente dependente,
0ÐC"w ß á ß C8w ß -ÐB" Ñß á ß -ÐB7 ÑÑ œ
œ 0Ð" ,jß" Cj -ÐBww" Ñß á ß " ,jß8 Cj -ÐB8ww Ñß -ÐB" Ñß á ß -ÐB7 ÑÑ œ
j
j
œ 0Ð" ,jß" Cj ß á ß " ,jß8 Cj ß -ÐB" Ñß á ß -ÐB7 ÑÑ,
j
j
portanto, uma vez que é trivialmente multilinear alternada a aplicação de J 8
em ‘, que a ÐC"w ß á ß C8w Ñ associa 0ÐC"w ß á ß C8w ß -ÐB" Ñß á ß -ÐB7 ÑÑ, podemos
escrever, tendo em conta II.4.15,
0ÐC"w ß á ß C8w ß -ÐB" Ñß á ß -ÐB7 ÑÑ œ detÐÐ,jß5 ÑÑ 0ÐC" ß á ß C8 ß -ÐB" Ñß á ß - ÐB7 ÑÑ.
76
Cap. II. Tópicos de Álgebra Multilinear
Uma vez que se tem também
# ÐD"w ß á ß D8w Ñ œ detÐÐ,jß5 ÑÑ # ÐD" ß á ß D8 Ñ,
vemos que (2) vai ser uma consequência de (1) e destas duas últimas
w
fórmulas, tendo em conta II.7.2. Vejamos agora que, sendo Bw" ß á ß B7
outra
base de I , tem-se ainda
(3)
w
w
" ÐC"w ß á ß C8w ß -ÐB"w Ñß á ß -ÐB7
ÑÑ œ !ÐB"w ß á ß B7
Ñ # ÐD"w ß á ß D8w Ñ,
o que acabará a demonstração. Para isso, reparamos que, sendo
Bw4 œ ! +3ß4 B3 , sabemos que se tem
3
w
!ÐBw" ß á ß B7
Ñ œ detÐÐ+3ß4 ÑÑ !ÐB" ß á ß B7 Ñ,
e, uma vez que -ÐBw4 Ñ œ ! +3ß4 -ÐB3 Ñ e que é multilinear alternada a
3
‘,
aplicação
de
I7
em
w
w
w
w
ÐB" ß á ß B7 Ñ È 0ÐC" ß á ß C8w ß -ÐB"w Ñß á ß -ÐB7
ÑÑ,
definida
por
w
0ÐC"w ß á ß C8w ß -ÐB"w Ñß á ß -ÐB7
ÑÑ œ detÐÐ+3ß4 ÑÑ 0ÐC"w ß á ß C8w ß -ÐB" Ñß á ß -ÐB7 ÑÑ,
pelo que (3) vai ser uma consequência de (2) e das duas igualdades
anteriores, tendo mais uma vez em conta II.7.2.
Vejamos agora alguns exemplos importantes da situação tratada anteriormente.
II.7.25. Sejam I e J espaços vectoriais reais, com dimensões 7 e 8, munidos
de orientações ! e " respectivamente. Chama-se então orientação produto de
I ‚ J à orientação # associada às orientações de I e de J e à sucessão
exacta curta
+#
1"
Ö!× Ä J Ä I ‚ J Ä I Ä Ö!×.12
É claro que esta orientação vem trocada, desde que se troque a orientação de
I ou a de J . Examinando as definições, vemos que, se B" ß á ß B7 é uma
base de I e C" ß á ß C8 é uma base de J , tem-se, para a correspondente base
12Mais
uma vez, a ordem dos termos nesta sucessão exacta é a inversa daquela que
pareceria mais natural, o que se destina a compensar o atropelo à ordem natural feito na
definição II.7.23. Esta segunda inversão permite que a caracterização do sinal das bases
naturais do produto cartesiano seja aquela que seria de esperar. É claro que, se tivéssemos
usado uma ordem diferente, tanto em II.7.23 como aqui, obteríamos o mesmo resultado
de um modo aparentemente mais elegante, mas isso ir-nos-ia criar problemas nas outras
aplicações da situação geral descrita em II.7.23.
§7. Orientação de espaços vectoriais reais
77
do produto I ‚ J ,
# ÐÐB" ß !Ñß á ß ÐB7 ß !Ñß Ð!ß C" Ñß á ß Ð!ß C8 ÑÑ œ
œ !ÐB" ß á ß B7 Ñ " ÐC" ß á ß C8 Ñ.
II.7.26. Sejam I um espaço vectorial real de dimensão 8 e J § I um
hiperplano, isto é, um subespaço vectorial de dimensão 8 ". O conjunto
diferença I Ï J vai ser então união disjunta de dois subconjuntos abertos,
chamados semi-espaços abertos determinados por J , definidos do seguinte
modo: O espaço vectorial quociente IÎJ tem dimensão " e, fixando uma
orientação neste espaço, os semi-espaços vão ser o conjunto dos vectores de
I cuja classe de equivalência é positiva e o daqueles cuja classe de
equivalência é negativa (é claro que, se tivéssemos trocado a orientação do
quociente, estes dois conjuntos viriam simplesmente trocados entre si). Dito
isto, é imediato que dar uma orientação a IÎJ é equivalente a escolher um
dos semi-espaços, como sendo aquele cujos elementos são os vectores cujas
classes de equivalência devem ser positivas (costuma-se então dizer que este
é o semi-espaço positivo associado a essa orientação e que o outro é o
semi-espaço negativo). A uma orientação de IÎJ também se costuma dar o
nome de orientação transversa a J .
II.7.27. Suponhamos que I é um espaço vectorial real de dimensão 8 e que
1À I Ä ‘ é uma aplicação linear não nula. Tem-se então que J œ kerÐ1Ñ é
um hiperplano de I e os semi-espaços abertos associados são o conjunto dos
B − I tais que 1ÐBÑ ! e o conjunto daqueles tais que 1ÐBÑ !.
Dem: Uma vez que a imagem de uma aplicação linear é um subespaço
vectorial, 1ÐIÑ, sendo não nulo, tem que ser igual a ‘. Concluímos portanto
que 1 é sobrejectiva, pelo que se obtém por passagem ao quociente, um
isomorfismo 1 de IÎJ sobre ‘, que à classe de equivalência de B associa
1ÐBÑ. Basta agora reparar que, escolhendo uma das orientações de IÎJ , ou o
isomorfismo 1 aplica o conjunto dos vectores positivos sobre o conjunto dos
números positivos e o dos vectores negativos sobre o dos números negativos
(se 1 for um isomorfismo positivo), ou vice-versa.
II.7.28. Seja I um espaço vectorial real orientado de dimensão 8, seja J § I
um hiperplano, e suponhamos fixada uma orientação transversa de J , isto é,
uma orientação de IÎJ , ou, equivalentemente, a escolha de um dos
semi-espaços abertos para semi-espaço positivo. Define-se então a
orientação induzida no hiperplano J como sendo a associada às orientações
de I e de IÎJ e à sucessão exacta curta
+
1
Ö!× Ä I Ä J Ä
I
Ä Ö!×,
J
onde + e 1 são a inclusão e a projecção canónica sobre o quociente.
Examinando as definições, vemos que, se B for um vector do semi-espaço
78
Cap. II. Tópicos de Álgebra Multilinear
aberto positivo (resp. negativo), então uma base B" ß á ß B8" de J é directa
se, e só se, a base Bß B" ß á ß B8" de I for directa (resp. retrógrada).
O resultado que se segue descreve a situação em que duas sucessões
exactas curtas estão ligadas por um sistema compatível de isomorfismos.
II.7.29. Dadas duas sucessões exactas curtas de espaços vectoriais sobre Š
-
.
Ö!× Ä I Ä J Ä K Ä Ö!×,
-w
.w
Ö!× Ä I w Ä J w Ä Kw Ä Ö!×,
diz-se que um sistema de aplicações lineares, 3À I Ä I w , 5 À J Ä J w e
7 À K Ä Kw é compatível com as sucessões exactas se se tem 5 ‰ - œ -w ‰ 3 e
7 ‰ . œ .w ‰ 5 , o que também costuma exprimir-se dizendo que o diagrama
-
.
-w
.w
Ö!× Ä I Ä J Ä K Ä Ö!×
3Æ3
5Æ5
7 Æ7
Ö!× Ä I w Ä J w Ä Kw Ä Ö!×
é comutativo.
II.7.30. Sob as hipóteses de II.7.29, suponhamos que todos os espaços vectoriais
são reais, de dimensão finita e munidos de orientações e que estas são
compatíveis com cada uma das sucessões exactas. Suponhamos ainda que as
aplicações lineares 3À I Ä I w , 5 À J Ä J w e 7 À K Ä Kw são isomorfismos13.
Tem-se então
sgÐ3Ñ sgÐ5 Ñ sgÐ7 Ñ œ ".
Dem: Notemos !, " , # , !w , " w , # w as orientações dos espaços vectoriais I , J ,
K, I w , J w , Kw . Consideremos uma base B" ß á ß B7 de I e uma base
D" ß á ß D8 de K, e sejam C" ß á ß C8 vectores de J tais que .ÐC5 Ñ œ D5 . Temos
então uma base C" ß á ß C8 ß -ÐB" Ñß á ß -ÐB7 Ñ de I , para a qual
" ÐC" ß á ß C8 ß -ÐB" Ñß á ß -ÐB7 ÑÑ œ !ÐB" ß á ß B7 Ñ # ÐD" ß á ß D8 Ñ.
Definindo então ?4 œ 3ÐB4 Ñ − I w , A5 œ 7 ÐD5 Ñ − Kw e @5 œ 5 ÐC5 Ñ − J w ,
tem-se que ?" ß á ß ?7 é uma base de I w , A" ß á ß A8 é uma base de Kw e os
vectores @5 verificam
.w Ð@5 Ñ œ .w Ð5 ÐC5 ÑÑ œ 7 Ð.ÐC5 ÑÑ œ 7 ÐD5 Ñ œ A5 ,
pelo que temos uma base @" ß á ß @8 ß -w Ð?" Ñß á ß -w Ð?7 Ñ de J w , para a qual
13Pode-se
provar que, se duas delas o forem, a terceira também o é (cf. o exercício II.27),
mas isso não nos vai interessar de momento.
§7. Orientação de espaços vectoriais reais
79
" w Ð@" ß á ß @8 ß -w Ð?" Ñß á ß -w Ð?7 ÑÑ œ !w Ð?" ß á ß ?7 Ñ # w ÐA" ß á ß A8 Ñ.
Tem-se
!w Ð?" ß á ß ?7 Ñ œ sgÐ3Ñ !ÐB" ß á ß B7 Ñ,
# w ÐA" ß á ß A8 Ñ œ sgÐ7 Ñ # ÐD" ß á ß D8 Ñ
e, uma vez que -w Ð?4 Ñ œ -w Ð3ÐB4 ÑÑ œ 5 Ð-ÐB4 ÑÑ,
" w Ð@" ß á ß @8 ß -w Ð?" Ñß á ß -w Ð?7 ÑÑ œ sgÐ5 Ñ " ÐC" ß á ß C8 ß -ÐB" Ñß á ß -ÐB7 ÑÑ,
pelo que o resultado é uma consequência de multiplicar termo a termo estas
três últimas fórmulas, tendo em conta as obtidas anteriormente.
§8. Elemento de volume e operadores ‡.
II.8.1. Se I é um espaço euclidiano orientado de dimensão ", existe em I um, e
um só, vector B, verificando mBm œ " e constituindo uma base directa14.
Dizemos então que B é o vector unitário positivo de I .
Dem: Se C for um vector não nulo de I , o vector B œ CÎmCm verifica a
condição mBm œ ". Para cada D − I , tem-se D œ +B, e então
mDm œ l+lmBm œ l+l, pelo que o únicos vectores de I de norma " são B e B
e, destes dois, há um, e um só, que constitui uma base directa.
II.8.2. Seja I um espaço euclidiano orientado de dimensão 8. Existe então um, e
um só elemento Z 96I − E8 ÐIà ‘Ñ, a que se dá o nome de elemento de
volume de I , tal que, para cada base ortonormada B" ß á ß B8 de I , com o
correspondente elemento 0•"ßáß8 da base de E8 ÐIà ‘Ñ, se tenha
Z 96I œ œ
0•"ßáß8 ,
0•"ßáß8 ,
se a base é directa
se a base é retrógrada.
Tem-se então que Z 96I é um elemento positivo do espaço vectorial
E8 ÐIà ‘Ñ, de dimensão ", relativamente à orientação associada deste espaço.
Dem: A unicidade é uma consequência trivial de I admitir pelo menos uma
base ortonormada. Para demonstrarmos a existência, fixamos uma base ortonormada C" ß á ß C8 , com a correspondente base de E8 ÐIà ‘Ñ, constituída
pelo único elemento (•"ßáß8 , e definimos
(
,
Z 96I œ œ •"ßáß8
(•"ßáß8 ,
se a base é directa
se a base é retrógrada,
e ficamos então reduzidos a provar que a condição do enunciado se verifica
14Por
outras palavras, existe uma única base ortonormada directa.
80
Cap. II. Tópicos de Álgebra Multilinear
para qualquer base ortonormada B" ß á ß B8 , com o correspondente elemento
0•"ßáß8 da base de E8 ÐIà ‘Ñ. Ora, isso é uma consequência de II.4.17 visto
que, sendo C4 œ ! +5ß4 B5 , o facto de termos duas bases ortonormadas
5
implica que a matriz dos +5ß4 é uma matriz ortogonal, tendo portanto
determinante igual a „". O facto de Z 96I ser um elemento positivo de
E8 ÐIà ‘Ñ, relativamente à orientação associada, é uma consequência
imediata de II.7.10.
II.8.3. Seja I um espaço euclidiano de dimensão 8, munido de uma orientação
!, e seja B" ß á ß B8 uma base ortonormada de I . Para cada 0 − E8 ÐIà ŠÑ,
tem-se então
0 œ !ÐB" ß á ß B8 Ñ 0ÐB" ß á ß B8 Ñ Z 96I .
Dem: Trata-se de uma mera reformulação de II.4.11.
II.8.4. No caso em que o espaço euclidiano orientado I tem dimensão !, o elemento de volume Z 96I − E! ÐIà ‘Ñ œ ‘ vai ser " ou ", conforme a
orientação de I seja a positiva ou a negativa.
Dem: Basta atender a que " − ‘ œ E! ÐIà ‘Ñ é trivialmente a base associada
à única base de I (o sistema vazio de vectores).
Lembremos que, se I é um espaço euclidiano de dimensão 8, então tem
lugar um isomorfismo )À I Ä PÐIà ‘Ñ (o isomorfismo canónico),
definido por
)ÐBÑÐCÑ œ ØCß BÙ.
II.8.5. Seja I um espaço euclidiano e seja B" ß á ß B8 uma base ortonormada de
I. Tem-se então que os elementos da base associada de
PÐIà ‘Ñ œ E" ÐIà ‘Ñ são )ÐB" Ñß á ß )ÐB8 Ñ. Em particular, no caso em que I
é orientado e de dimensão " e B é o vector unitário positivo de I , o elemento
de volume Z 96I é igual a )ÐBÑ.
Dem: Basta atender a que )ÐB4 ÑÐB5 Ñ œ ØB5 ß B4 Ù œ $4ß5 .
II.8.6. Considerando em ‘8 as suas estrutura euclidiana e orientação canónicas,
o elemento de volume de ‘8 não é mais do que o elemento det − E8 Б8 à ‘Ñ
(cf. II.4.16).
II.8.7. Sejam I e J espaços euclidianos orientados de dimensão 8, e seja
-À I Ä J um isomorfismo, com coeficiente de dilatação -- . Tem-se então
-‡ ÐZ 96J Ñ œ sgÐ-Ñ -- Z 96I .
Dem: Fixemos bases ortonormadas B" ß á ß B8 e C" ß á ß C8 para I e J ,
respectivamente. Podemos então escrever -ÐB4 Ñ œ ! +5ß4 C5 e então, tendo
5
§8. Elemento de volume e operadores ‡
81
em conta I.1.14, -- œ ldetÐÐ+5ß4 ÑÑl. Vem agora, tendo em conta II.4.11 e
II.4.15,
-‡ ÐZ 96J Ñ œ „-‡ ÐZ 96J ÑÐB" ß á ß B8 Ñ Z 96I œ
œ „Z 96J Ð-ÐB" Ñß á ß -ÐB8 ÑÑ Z 96I œ
œ „detÐÐ+5ß4 ÑÑ Z 96J ÐC" ß á ß C8 Ñ Z 96I œ
œ „-- Z 96I œ „sgÐ-Ñ -- Z 96I ,
bastando atender por fim a que, tendo em conta II.7.17, ambos os membros
da igualdade do enunciado são elementos positivos de E8 ÐIà ‘Ñ, se conservar as orientações, e elementos negativos deste espaço, se - inverter as
orientações.
II.8.8. O resultado precedente permite apresentar uma justificação para a
denominação “elemento de volume” dada à aplicação multilinear alternada
Z 96I À I 8 Ä ‘, quando I é um espaço euclidiano munido de uma
orientação !. Com efeito, dada uma base arbitrária B" ß á ß B8 de I , podemos
definir o paralelipípedo associado a esta base como sendo o conjunto T dos
elementos B − I que se podem escrever na forma ! >4 B4 , com >4 − Ò!ß "Ó, e
4
então, sendo .I a medida de Lebesgue nos borelianos de I , Z 96I aplica
ÐB" ß á ß B8 Ñ em „.I ÐT Ñ, mais precisamente,
Z 96I ÐB" ß á ß B8 Ñ œ !ÐB" ß á ß B8 Ñ .I ÐT Ñ.
Dem: Sendo -À ‘8 Ä I o isomorfismo definido por -Ð/4 Ñ œ B4 , vemos que
T œ -ÐÒ!ß "Ó8 Ñ, donde, uma vez que .8 ÐÒ!ß "Ó8 Ñ œ ", .E ÐT Ñ œ -- e podemos
escrever
Z 96I ÐB" ß á ß B8 Ñ œ -‡ ÐZ 96I ÑÐ/" ß á ß /8 Ñ œ
œ sgÐ-Ñ -- Z 96‘8 Ð/" ß á ß /8 Ñ œ
œ sgÐ-Ñ -- œ !ÐB" ß á ß B8 Ñ .I ÐT Ñ.
II.8.9. Sejam I um espaço euclidiano orientado de dimensão 8 e Š um dos
corpos ‘ ou ‚. Para cada ! Ÿ : Ÿ 8, existe então uma aplicação linear
‡À E: ÐIà ŠÑ Ä E8: ÐIà ŠÑ,
definida por
Ї0ÑÐB" ß á ß B8: Ñ Z 96I œ 0 • )ÐB" Ñ • â • )ÐB8: Ñ,
onde )À I Ä PÐIà ‘Ñ œ E" ÐIà ‘Ñ é o isomorfismo associado à estrutura
euclidiana de I .
Dem: Dados 0 − E: ÐIà ŠÑ e B" ß á ß B8: arbitrários em I , vemos que
0 • )ÐB" Ñ • â • )ÐB8: Ñ − E8 ÐIà ŠÑ,
pelo que, uma vez que este espaço vectorial sobre Š tem dimensão " e
82
Cap. II. Tópicos de Álgebra Multilinear
admite Z 96I como base, fica bem definido um elemento
Ї0ÑÐB" ß á ß B8: Ñ − Š, pela igualdade do enunciado. É imediato que a
aplicação ‡0À I 8: Ä Š, assim definida, é multilinear e o facto de ela ser
alternada é uma consequência da caracterização destas dada na alínea a) de
II.4.3 e da anti-simetria do produto exterior de tensores alternados de grau
ímpar. A linearidade da aplicação ‡À E: ÐIà ŠÑ Ä E8: ÐIà ŠÑ, que a 0
associa ‡0, é imediata.
II.8.10. É imediato que, se trocarmos a orientação de um espaço euclidiano
orientado I , o seu elemento de volume vem multiplicado por " e portanto
a aplicação linear ‡ vem também multiplicada por ".
II.8.11. (Lema) Seja I um espaço euclidiano de dimensão 8, munido de uma
orientação !. Dados B" ß á ß B8 em I , tem-se então
Z 96I ÐB" ß á ß B8 Ñ Z 96I œ )ÐB" Ñ • â • )ÐB8 Ñ.
Dem: Uma vez que ambos os membros da igualdade do enunciado, quando
considerados como funções de ÐB" ß á ß B8 Ñ, são aplicações multilineares
alternadas de I 8 em E8 ÐIà ‘Ñ, resulta de II.4.10 que, para demonstrar essa
igualdade, basta mostrar que ela se verifica quando B" ß á ß B8 for uma base
ortonormada de I . Ora, nesse caso, verificámos em II.8.5 que os )ÐB4 Ñ são
os elementos 04 da base associada de E" ÐIà ‘Ñ, pelo que, tendo em conta
II.5.9,
)ÐB" Ñ • â • )ÐB8 Ñ œ 0•"ßáß8 œ !ÐB" ß á ß B8 Ñ Z 96I ,
que é igual ao primeiro membro da igualdade, uma vez que
Z 96I ÐB" ß á ß B8 Ñ œ !ÐB" ß á ß B8 Ñ 0•"ßáß8 ÐB" ß á ß B8 Ñ œ !ÐB" ß á ß B8 Ñ.
II.8.12. Vejamos o que são as aplicações lineares ‡À E: ÐIà ŠÑ Ä E8: ÐIà ŠÑ
nos casos particulares em que : œ ! e : œ 8:
a) Se 0 − E8 ÐIà ŠÑ, tem-se que ‡0 − E! ÐIà ŠÑ œ Š é a componente de 0 na
base Z 96I , isto é, 0 œ Ї0Ñ Z 96I . Em particular, ‡ÐZ 96I Ñ œ ".
b) Se + − Š œ E! ÐIà ŠÑ, tem-se ‡+ œ + Z 96I − E8 ÐIà ŠÑ. Em particular,
‡" œ Z 96I .
Dem: A alínea a) não é mais do que um caso particular trivial da definição,
podendo ser olhada como uma convenção pelos inimigos do conjunto vazio.
Quanto à alínea b), utilizando o lema anterior, obtemos
Ї+ÑÐB" ß á ß B8 Ñ Z 96I œ + )ÐB" Ñ • â • )ÐB8 Ñ œ + Z 96I ÐB" ß á ß B8 Ñ Z 96I ,
donde Ї+ÑÐB" ß á ß B8 Ñ œ + Z 96I ÐB" ß á ß B8 Ñ.
O resultado anterior mostra que a aplicação linear ‡, de E! ÐIà ŠÑ para
E8 ÐIà ŠÑ, é um isomorfismo, tendo como inverso a aplicação linear ‡ de
E8 ÐIà ŠÑ para E! ÐIà ŠÑ. Vamos agora ver que, a menos de sinal, o
mesmo vai acontecer com as aplicações lineares ‡ nos espaços E: ÐIà ŠÑ.
§8. Elemento de volume e operadores ‡
83
II.8.13. Seja I um espaço euclidiano de dimensão 8, munido de uma orientação
!, e seja B" ß á ß B8 uma base ortonormada de I . Para cada ! Ÿ : Ÿ 8,
tem-se então:
a) A aplicação linear ‡À E: ÐIà ŠÑ Ä E8: ÐIà ŠÑ é um isomorfismo, tendo
como isomorfismo inverso o produto de Ð"Ñ:Ð8:Ñ pela aplicação linear
‡À E8: ÐIà ŠÑ Ä E: ÐIà ŠÑ.
b) Notando, para cada 4" â 4: em Ö"ß á ß 8×, 4:" â 48 os
restantes elementos de Ö"ß á ß 8×, tem-se, para os elementos das bases
associadas de E: ÐIà ŠÑ e E8: ÐIà ŠÑ,
‡ 0•4" ßáß4: œ sgÐÖ4" ß á ß 4: ×Ñ !ÐB" ß á ß B8 Ñ 0•4:" ßáß48 .
Dem: Dados 5:" â 58 em Ö"ß á ß 8×, tem-se
‡ 0•4" ßáß4: ÐB5:" ß á ß B58 Ñ Z 96I œ 0•4" ßáß4: • )ÐB5:" Ñ • â • )ÐB58 Ñ œ
œ )ÐB4" Ñ • â • )ÐB4: Ñ • )ÐB5:" Ñ • â • )ÐB58 Ñ,
expressão que será nula se Ö4" ß á ß 4: × e Ö5:" ß á ß 58 × tiverem algum elemento em comum e que, caso contrário, isto é, quando 5:" œ 4:" ,…,
58 œ 48 , é igual a
sgÐÖ4" ß á ß 4: ×Ñ )ÐB" Ñ • â • )ÐB8 Ñ œ sgÐÖ4" ß á ß 4: ×Ñ !ÐB" ß á ß B8 Ñ Z 96I .
Podemos portanto escrever
‡ 0•4" ßáß4: œ "
‡ 0•4" ßáß4: ÐB5:" ß á ß B58 Ñ 0•5:" ßáß58 œ
5:" â58
œ sgÐÖ4" ß á ß 4: ×Ñ !ÐB" ß á ß B8 Ñ 0•4:" ßáß48 ,
o que termina a demonstração de b). Reparemos agora que a composta
‡
Ð"Ñ:Ð8:Ñ ‡
E: ÐIà ŠÑ qqqqqp E8: ÐIà ŠÑ qqqqqp E: ÐIà ŠÑ
vai aplicar cada elemento 0•4" ßáß4: da base de E: ÐIà ŠÑ em
Ð"Ñ:Ð8:Ñ sgÐÖ4" ß á ß 4: ×Ñ sgÐÖ4:" ß á ß 48 ×Ñ 0•4" ßáß4: œ 0•4" ßáß4:
(cf. II.3.9), pelo que esta composta é igual à aplicação identidade. Do mesmo
modo se verifica que a composta
Ð"Ñ:Ð8:Ñ ‡
‡
E8: ÐIà ŠÑ qqqqqp E: ÐIà ŠÑ qqqqqp E8: ÐIà ŠÑ
é igual à aplicação identidade, o que termina a demonstração de a).
II.8.14. (Corolário) Nas hipóteses do resultado anterior, dados ( − E: ÐIà ŠÑ e
4" â 4: em Ö"ß á ß 8×, vem, notando 4:" â 48 os restantes
índices de Ö"ß á ß 8×,
84
Cap. II. Tópicos de Álgebra Multilinear
Ї(ÑÐB4:" ß á ß B48 Ñ œ sgÐÖ4" ß á ß 4: ×Ñ !ÐB" ß á ß B8 Ñ (ÐB4" ß á ß B4: Ñ.
Dem: Uma vez que
( œ " (ÐB4" ß á ß B4: Ñ 0•4" ßáß4: ,
4" â4:
vemos que
‡( œ " (ÐB4" ß á ß B4: ÑЇ 0•4" ßáß4: Ñ œ
4" â4:
œ " (ÐB4" ß á ß B4: Ñ sgÐÖ4" ß á ß 4: ×Ñ !ÐB" ß á ß B8 Ñ 0•4:" ßáß48
4" â4:
e daqui resulta a fórmula do enunciado, tendo em conta a caracterização das
componentes de um elemento de E8: ÐIà ŠÑ na base associada a
B" ß á ß B8 .
II.8.15. Seja I um espaço euclidiano orientado de dimensão 8 e seja B" ß á ß B8
uma base ortonormada de I . Dados 0ß ( − E: ÐIà ŠÑ, com ! Ÿ : Ÿ 8,
tem-se então
0 • Ї(Ñ œ ( • Ї0Ñ œ " 0ÐB4" ß á ß B4: Ñ (ÐB4" ß á ß B4: Ñ Z 96I .
4" â48
Dem: Utilizando a fórmula para o produto exterior apresentada em II.5.12,
obtemos, tendo em conta o corolário anterior,
Ð0 • ‡(ÑÐB" ß á ß B8 Ñ œ " sgÐÖ4" ß á ß 4: ×Ñ 0ÐB4" ßáß B4: Ñ Ð‡(ÑÐB4:" ß á ß B48 Ñ œ
4" â4:
œ " !ÐB" ß á ß B8 Ñ 0ÐB4" ß á ß B4: Ñ (ÐB4" ß á ß B4: Ñ
4" â4:
pelo que, para deduzir a fórmula para 0 • Ї(Ñ no enunciado, basta reparar
que
0 • Ї(Ñ œ Ð0 • ‡(ÑÐB" ß á ß B8 Ñ 0•"ßáß8 œ
œ Ð0 • ‡(ÑÐB" ß á ß B8 Ñ !ÐB" ß á ß B8 Ñ Z 96I .
A fórmula para ( • Ї0Ñ resulta da anterior por simetria dos papéis de 0 e
(.
O comportamento das aplicações lineares ‡À E: ÐJ à ŠÑ Ä E8: ÐJ à ŠÑ,
relativamente às imagens recíprocas por meio de aplicações lineares
-À I Ä J , não é muito fácil de descrever em geral. Vamos no entanto
verificar que a situação simplifica-se consideravelmente no caso em que
-À I Ä J é um isomorfismo ortogonal.
§8. Elemento de volume e operadores ‡
85
II.8.16. Sejam I e J espaços euclidianos orientados de dimensão 8 e seja
-À I Ä J um isomorfismo ortogonal. Para cada 0 − E: ÐJ à ŠÑ, tem-se então
‡ -‡ Ð0Ñ œ sgÐ-Ñ -‡ Ї0Ñ − E8: ÐIà ŠÑ.
Dem: Uma vez que - é um isomorfismo ortogonal, tem-se, para o coeficiente
de dilatação, -- œ " pelo que, por II.8.7, -‡ ÐZ 96J Ñ œ sgÐ-Ñ Z 96I . Mais uma
vez por - ser um isomorfismo ortogonal, dado B − I , tem-se, para cada
C − I,
)ÐBÑÐCÑ œ ØCß BÙ œ Ø-ÐCÑß -ÐBÑÙ œ )Ð-ÐBÑÑÐ-ÐCÑÑ œ -‡ Ð) Ð- ÐBÑÑÑÐCÑ,
ou seja, )ÐBÑ œ -‡ Ð)Ð-ÐBÑÑÑ. Podemos agora escrever, quaisquer que sejam
B" ß á ß B8: − I ,
Ї-‡ Ð0ÑÑÐB" ß á ß B8: Ñ Z 96I œ -‡ Ð0Ñ • )ÐB" Ñ • â • )ÐB8: Ñ œ
œ -‡ Ð0Ñ • -‡ Ð)Ð-ÐB" ÑÑÑ • â • -‡ Ð)Ð-ÐB8: ÑÑÑ œ
œ -‡ Ð0 • )Ð-ÐB" ÑÑ • â • )Ð-ÐB8: ÑÑÑ œ
œ -‡ ÐЇ0ÑÐ-ÐB" Ñß á ß -ÐB8: ÑÑ Z 96J Ñ œ
œ Ї0ÑÐ-ÐB" Ñß á ß -ÐB8: ÑÑ -‡ ÐZ 96J Ñ œ
œ sgÐ-Ñ Ð‡0ÑÐ-ÐB" Ñß á ß -ÐB8: ÑÑ Z 96I
donde
Ї-‡ Ð0ÑÑÐB" ß á ß B8: Ñ œ sgÐ-Ñ Ð‡0ÑÐ-ÐB" Ñß á ß -ÐB8: ÑÑ œ
œ sgÐ-Ñ -‡ Ї0ÑÐB" ß á ß B8: Ñ.
II.8.17. Sejam I um espaço euclidiano orientado de dimensão 8 e B − I um
elemento fixado. Tem-se então:
a) Se 0 − E: ÐIà ŠÑ, com ! Ÿ : 8,
‡Ð0 • )ÐBÑÑ œ intB Ї0Ñ − E8:" ÐIà ŠÑ.
b) Se 0 − E: ÐIà ŠÑ, com ! : Ÿ 8,
‡ intB Ð0Ñ œ Ð"Ñ8" Ї0Ñ • )ÐBÑ − E8:" ÐIà ŠÑ.
Dem: Quaisquer que sejam B" ß á ß B8:" − I , vem
ЇÐ0 • )ÐBÑÑÑÐB" ß á ß B8:" Ñ Z 96I œ 0 • )ÐBÑ • )ÐB" Ñ • â • )ÐB8:" Ñ œ
œ Ї0ÑÐBß B" ß á ß B8:" Ñ Z 96I œ
œ intB Ї0ÑÐB" ß á ß B8:" Ñ Z 96I ,
o que prova a). Quanto a b), podemos aplicar a conclusão a que acabamos de
chegar a ‡0 − E8: ÐIà ŠÑ e concluir que
Ð"Ñ:Ð8:Ñ intB Ð0Ñ œ intB Ї‡0Ñ œ ‡ÐЇ0Ñ • )ÐBÑÑ,
donde, aplicando ‡ a ambos os membros,
86
Cap. II. Tópicos de Álgebra Multilinear
Ð"Ñ:Ð8:Ñ ‡ intB Ð0Ñ œ Ð"ÑÐ8:"ÑÐ:"Ñ Ð‡0Ñ • )ÐBÑ,
e o resultado fica demonstrado se repararmos que,
Ð"ÑÐ8:"ÑÐ:"Ñ:Ð8:Ñ œ Ð"Ñ8" .
II.8.18. (Corolário) Seja I um espaço euclidiano orientado de dimensão 8 ".
Tem-se então:
a) Para cada B − I ,
‡ )ÐBÑ œ intB ÐZ 96I Ñ,
por outras palavras,
Ї)ÐBÑÑÐB" ß á ß B8" Ñ œ Z 96I ÐBß B" ß á ß B8" Ñ.
b) Para cada 0 − E" ÐIà ŠÑ e B − I ,
0 • ‡)ÐBÑ œ 0ÐBÑ Z 96I .
Dem: A alínea a) não é mais do que o caso particular 0 œ 1 − E! ÐIà ŠÑ da
alínea a) do resultado anterior, visto que ‡" œ Z 96I . Por outro lado, a alínea
b) do resultado anterior permite-nos escrever, tendo em conta II.8.15,
0ÐBÑ Z 96I œ 0ÐBÑ Ð‡"Ñ œ ‡ 0ÐBÑ œ ‡ intB Ð0Ñ œ Ð"Ñ8" Ї0Ñ • )ÐBÑ œ
œ )ÐBÑ • Ї0Ñ œ 0 • Ї)ÐBÑÑ.
II.8.19. Um isomorfismo que aparece com suficiente frequência para merecer um
nome é o composto dos isomorfismos )À I Ä PÐIà ‘Ñ œ E" ÐIà ‘Ñ e
‡À E" ÐIà ‘Ñ Ä E8" ÐIà ‘Ñ, quando I é um espaço euclidiano orientado de
dimensão 8. Vamos notar
)˜À I Ä E8" ÐIà ‘Ñ
esse isomorfismo. Recorde-se que, como vimos no resultado anterior, tem-se
)˜ÐBÑ œ intB ÐZ 96I Ñ.
Uma primeira situação em que o isomorfismo )˜ intervém é na definição
do produto externo num espaço euclidiano orientado de dimensão 8,
generalizando o bem conhecido produto externo de dois vectores de ‘$
(ou, mais geralmente, de um espaço euclidiano orientado de dimensão $).
Repare-se desde já que, enquanto que em ‘$ se define o produto externo
de dois vectores, num espaço euclidiano orientado de dimensão 8 apenas
se define o produto externo de 8 " vectores. Em consequência, apenas
na dimensão $ se tem uma operação no sentido estrito da palavra.
§8. Elemento de volume e operadores ‡
87
II.8.20. Seja E um espaço euclidiano orientado de dimensão 8 ". Dados 8 "
vectores B" ß á ß B8" − I , define-se o produto externo B" ‚ â ‚ B8" − I
pela igualdade
"
B" ‚ â ‚ B8" œ )˜ Ð)ÐB" Ñ • â • )ÐB8" ÑÑ.
II.8.21. Tendo em conta a anti-simetria do produto exterior de tensores
alternados de grau 1, assim como a caracterização das aplicações alternadas
dada na alínea a) de II.4.3, deduzimos imediatamente que tem lugar uma
aplicação multilinear alternada
I 8" Ä I ,
ÐB" ß á ß B8" Ñ È B" ‚ â ‚ B8" ,
em particular, tem-se B" ‚ â ‚ B8" œ !, sempre que estes vectores sejam
linearmente dependentes.
O resultado que segue dá uma caracterização alternativa do produto
exterior, a qual mostra, em particular, que, no caso de ‘$ , a definição que
estamos a usar é equivalente à clássica (lembrar o conceito de produto
mistoá ).
II.8.22. Seja I um espaço euclidiano orientado de dimensão 8 ". Dados
B" ß á ß B8" − I , tem-se, para cada C − I ,
ØCß B" ‚ â ‚ B8" Ù œ Z 96I ÐCß B" ß á ß B8" Ñ.
Dem: Tendo em conta o lema II.8.11 e a alínea b) de II.8.18, vem
ØCß B" ‚ â ‚ B8" Ù Z 96I œ )ÐCÑÐB" ‚ â ‚ B8" Ñ Z 96I œ
œ )ÐCÑ • ‡Ð)ÐB" ‚ â ‚ B8" ÑÑ œ
œ )ÐCÑ • )ÐB" Ñ • â • )ÐB8" Ñ œ
blablablablablablaba œ Z 96I ÐCß B" ß á ß B8" Ñ Z 96I ,
donde o resultado.
II.8.23. (Corolário) Sejam I um espaço euclidiano orientado de dimensão
8 " e B" ß á ß B8" um sistema linearmente independente de vectores de I .
Existe então um, e um só, vector C − I , de norma ", ortogonal a cada um
dos B4 e tal que Cß B" ß á ß B8" seja uma base directa de I , e tem-se então
B" ‚ â ‚ B8" œ + C,
onde
+ œ mB" ‚ â ‚ B8" m œ Z 96I ÐCß B" ß á ß B8" Ñ !.
Dem: Dizer que um vector C é ortogonal a cada B4 é equivalente a dizer que
C pertence ao complementar ortogonal do subespaço vectorial de dimensão
88
Cap. II. Tópicos de Álgebra Multilinear
8 " gerado pelos B4 , complementar ortogonal esse que é um subespaço
vectorial de dimensão ", tendo portanto dois, e só dois, vectores de norma ",
que são simétricos um do outro; destes é evidente que um, e um só, verifica a
condição de Cß B" ß á ß B8" ser uma base directa de I (ver, por exemplo,
II.7.3). Uma vez que
ØB4 ß B" ‚ â ‚ B8" Ù œ Z 96I ÐB4 ß B" ß á ß B8" Ñ œ !,
concluímos que B" ‚ â ‚ B8" é ortogonal a cada B4 , e portanto tem-se
B" ‚ â ‚ B8" œ + C, para um certo + − ‘. Uma vez que Z 96I é positivo,
obtemos agora
+ œ ØCß + CÙ œ ØCß B" ‚ â ‚ B8" Ù œ Z 96I ÐCß B" ß á ß B8" Ñ !
e a igualdade B" ‚ â ‚ B8" œ + C, com mCm œ " implica finalmente que se
tem mB" ‚ â ‚ B8" m œ +.
II.8.24. Em particular, no caso em que I é um espaço euclidiano orientado de
dimensão ", podemos falar do produto externo da família vazia de vectores,
que não vai ser mais do que o vector unitário positivo de I .
EXERCÍCIOS
Ex II.1 Sejam I e J espaços vectoriais complexos, e notemos I o espaço
vectorial complexo, conjugado de I , isto é, aquele que coincide com I
como espaço vectorial mas em que a multiplicação de + − ‚ por B − I é
igual a +B, no sentido da multiplicação de I . Reparemos que as aplicações
anti-lineares de I para J não são mais do que as aplicações lineares
complexas de I para J . Mostrar que o espaço vectorial complexo P‘ ÐIà J Ñ
é soma directa dos seus subespaços vectoriais complexos P‚ ÐIà J Ñ e
P‚ ÐIà J Ñ e dizer quais as projecções associadas a esta soma directa.
Ex II.2 Lembrar que, se I é um espaço vectorial sobre Š, o seu dual é o espaço
vectorial PÐIà ŠÑ e o seu bidual é o dual deste último, isto é, o espaço
vectorial PÐPÐIà ŠÑà ŠÑ, tendo lugar uma aplicação linear injectiva
" À I Ä PÐPÐIà ŠÑà ŠÑ,
definida por " ÐBÑÐ0Ñ œ 0ÐBÑ, a qual é um isomorfismo se I tiver dimensão
finita (cf. II.2.7).
Mostrar que, se I tem dimensão infinita, então a aplicação linear " não é
sobrejectiva. Sugestão: Supondo que I tem dimensão infinita, considerar
uma base ÐB4 Ñ4−N de I . Considerar os 04 − PÐIà ŠÑ definidos pela condição
de se ter 04 ÐB4 Ñ œ " e, para cada 5 Á 4, 04 ÐB5 Ñ œ !. Mostrar que os 04 são
linearmente independentes e, completando-os numa base de PÐIà ŠÑ,
Exercícios
89
mostrar a existência de F − PÐPÐIà ŠÑà ŠÑ tal que FÐ04 Ñ œ ", para cada 4.
Mostrar que F não pode estar na imagem de " .
Ex II.3 Sejam I um espaço vectorial de dimensão 8 sobre Š, com duas bases
ÐB4 Ñ"Ÿ4Ÿ8 e ÐA5 Ñ"Ÿ5Ÿ8 , e consideremos os escalares +4ß5 definidos por
A5 œ " +4ß5 B4
8
4œ"
(os elementos da matriz de mudança da primeira para a segunda base).
Consideremos as bases associadas de P: ÐIà ŠÑ, formadas pelos 04" ßáß4: , para
a primeira base, e pelos (5" ßáß5: , para a segunda base. Mostrar que, se
- − P: ÐIà ŠÑ, com
- œ " ,4" ßáß4: 04" ßáß4: œ " -5" ßáß5: (5" ßáß5: ,
4" ßáß4:
5" ßáß5:
então as componentes de - nas duas bases associadas estão relacionadas por
-5" ßáß5: œ " +4" ß5" â +4: ß5: ,4" ßáß4:
4" ßáß4:
(Nota: Por este motivo, os elementos de P: ÐIà ŠÑ costumam ser chamados
tensores : vezes covariantes). Mostrar que, em consequência,
04" ßáß4: œ " +4" ß5" â +4: ß5: (5" ßáß5: .
5" ßáß5:
Ex II.4 Seja I um espaço vectorial de dimensão 8 sobre Š, com uma base
ÐB4 Ñ"Ÿ4Ÿ8 , e consideremos as bases associadas em P: ÐIà ŠÑ, P; ÐIà ŠÑ e
P:; ÐIà ŠÑ. Dados 0 − P: ÐIà ŠÑ e ( − P; ÐIà ŠÑ, exprimir as componentes
de 0 Œ ( − P:; ÐIà ŠÑ a partir das componentes de 0 e de (.
Ex II.5 Seja N um conjunto com 8 elementos, não munido a priori de nenhuma
ordem total. Mostrar que, para cada bijecção 5À N Ä N , pode-se definir o
sinal sgÐ5 Ñ de 5 , como sendo o sinal de 5 quando se considera em N uma
ordem total arbitrária. Mostrar que a noção de sinal assim definida verifica
ainda as propriedades enunciadas no teorema de Bézout. Por que razão não é
possível fazer o mesmo para bijecções entre dois conjuntos distintos com 8
elementos, não munidos a priori de ordens totais?
Ex II.6 Sejam I e J espaços vectoriais e 0À I : Ä J uma aplicação multilinear,
tal que se tenha 0ÐB" ß á ß B: Ñ œ !, sempre que exista 3 : tal que B3 œ B3" .
Mostrar que 0 é uma aplicação multilinear alternada. Sugestão: Utilizar a
condição a) de II.4.3, partindo do facto que, para cada sistema arbitrário de
90
Cap. II. Tópicos de Álgebra Multilinear
vectores B" ß á ß B: ,
! œ 0ÐB" ß á ß B3" ß B3 B3" ß B3 B3" ß B3# ß á ß B: Ñ.
Ex II.7 Sejam I um espaço vectorial sobre Š e J um espaço vectorial sobre
Šw ¨ Š. Mostrar que tem então lugar uma soma directa
P# ÐIà J Ñ œ W # ÐIà J Ñ Š E# ÐIà J Ñ
e dizer quais as projecções associadas a esta soma directa.
Ex II.8 Sejam I um espaço vectorial de dimensão 8 sobre Š e B" ß á ß B: um
sistema de : vectores de I . Mostre que este sistema é linearmente
independente se, e só se, existe 0 − E: ÐIà ŠÑ tal que 0ÐB" ß á ß B: Ñ Á !.
Ex II.9 Sejam I um espaço vectorial de dimensão 8 sobre o corpo Š e
-À I Ä I uma aplicação linear. Mostrar que - é um isomorfismo se, e só se,
detÐ-Ñ Á !.
Ex II.10 a) Verificar que o resultado II.4.22 pode servir para demonstrar o facto
de o determinante do produto de duas matrizes do tipo 8 ‚ 8 ser igual ao
produto dos determinantes destas.
b) Mostrar que o resultado II.4.23 permite demonstrar que, dadas duas
matrizes E, do tipo : ‚ :, e F , do tipo ; ‚ ; , o determinante da matriz
E
”!
!
F•
é igual a detÐEÑ ‚ detÐFÑ.
Ex II.11 (Generalização de II.4.23) Sejam I um espaço vectorial de dimensão
finita sobre Š e J e K dois subespaços vectoriais de I , tais que tenha lugar
a soma directa I œ J Š K. Seja -À I Ä I uma aplicação linear, tal que
-ÐJ Ñ § J , mas não obrigatoriamente -ÐKÑ § K. Sendo 1K À I Ä K a
segunda projecção associada à soma directa, mostrar que se tem
detÐ-Ñ œ detÐ-ÎJ Ñ ‚ detÐ1K ‰ -ÎK Ñ
e utilizar este facto para deduzir o seguinte resultado sobre determinantes de
matrizes: Dadas as matrizes E, de tipo : ‚ :, F , de tipo ; ‚ ; , e G , de tipo
: ‚ ; , o determinante da matriz, de tipo Ð: ;Ñ ‚ Ð: ;Ñ,
E
”!
G
F•
é igual ao produto dos determinantes das matrizes E e F . Sugestão: Notando
1J À I Ä J a primeira projecção associada à soma directa e -w À I Ä I a
aplicação linear definida por
Exercícios
91
-w ÐBÑ œ -Ð1J ÐBÑÑ 1K Ð-Ð1K ÐBÑÑ,
verificar que detÐ-Ñ œ detÐ-w Ñ e aplicar II.4.23 a -w .
Ex II.12 Sejam I um espaço vectorial complexo de dimensão 8 e -À I Ä I
uma aplicação linear. Sabemos que também podemos olhar para I como
espaço vectorial real de dimensão #8 e então -À I Ä I é também uma
aplicação linear no sentido real. Notemos det‚ Ð-Ñ e det‘ Ð-Ñ o determinante
de -, quando se olha para I como espaço vectorial complexo, e o determinante de -, quando se olha para I como espaço vectorial real15. Verificar
que se tem
det‘ Ð-Ñ œ ldet‚ Ð-Ñl# .
Sugestão: Fazer a demonstração por indução em 8, lembrando que, se
8 ", - admite um valor próprio complexo e aplicando em seguida o
exercício anterior.
Ex II.13 a) Lembrar que, se G é uma matriz quadrada, com elementos -4ß5 ,
define-se o traço de G , trÐGÑ, como sendo o escalar ! -4ß4 . Mostrar que, se
4
E é uma matriz do tipo 7 ‚ 8 e se F é uma matriz do tipo 8 ‚ 7, então
trÐE ‚ FÑ œ trÐF ‚ EÑ.
b) Sejam I um espaço vectorial de dimensão 8 sobre Š e -À I Ä I uma
aplicação linear. Mostrar que se pode definir um escalar trÐ-Ñ − Š, chamado
ainda traço da aplicação linear -, pela condição de se ter, para cada base
B" ß á ß B8 de I , para a qual -ÐB5 Ñ œ ! -4ß5 B4 , trÐ-Ñ œ ! -4ß4 .
4
4
c) Sejam I e J espaços vectoriais sobre Š, com dimensões 7 e 8,
respectivamente, e -À I Ä J e .À J Ä I duas aplicações lineares. Mostrar
que se tem
trÐ- ‰ .Ñ œ trÐ. ‰ -Ñ.
d) Sejam I um espaço vectorial complexo e -À I Ä I uma aplicação linear.
No mesmo espírito que no exercício II.12, notemos tr‚ Ð-Ñ − ‚ o traço de -,
quando olhamos para I como espaço vectorial complexo, e tr‘ Ð-Ñ − ‘ o
traço de -, quando olhamos para I como espaço vectorial real. Mostrar que
se tem
tr‘ Ð-Ñ œ # dÐtr‚ Ð-ÑÑ
(onde notamos dÐ-Ñ a parte real de um complexo - ).
15Tem-se,
portanto, det‚ Ð-Ñ − ‚ e det‘ Ð-Ñ − ‘.
92
Cap. II. Tópicos de Álgebra Multilinear
Ex II.14 Sejam I um espaço vectorial de dimensão finita sobre Š e J e K dois
subespaços vectoriais tais que tenha lugar a soma directa I œ J Š K e
notemos 1J À I Ä J e 1K À I Ä K as projecções associadas a esta soma
directa. Se -À I Ä I é uma aplicação linear, mostrar que, considerando as
aplicações lineares 1J ‰ -ÎJ À J Ä J e 1K ‰ -ÎK À K Ä K , tem-se
trÐ-Ñ œ trÐ1J ‰ -ÎJ Ñ trÐ1K ‰ -ÎK Ñ
(comparar com a conclusão do exercício II.11).
Ex II.15 Sejam I um espaço vectorial de dimensão 8 sobre o corpo Š e
-À I Ä I uma aplicação linear e consideremos a correspondente aplicação
linear -‡ À E8 ÐIà ŠÑ Ä E8 ÐIà ŠÑ, entre espaços vectoriais de dimensão ".
Mostrar que se tem detÐ-Ñ œ trÐ-‡ Ñ.
Ex II.16 a) O “teorema” que enunciamos em seguida é falso. Apresentar um
contra-exemplo e descobrir onde é que falha a demonstração que
apresentamos.
“Teorema” Sejam I e J espaços vectoriais de dimensões 7 e 8, respectivamente, sobre o corpo Š, e sejam -À I Ä J e .À J Ä I duas
aplicações lineares. Tem-se então, para as aplicações lineares
. ‰ -À I Ä I e - ‰ .À J Ä I , detÐ. ‰ -Ñ œ detÐ- ‰ .Ñ.
“Dem”: Tendo em conta o exercício II.15 e a alínea c) do exercício II.13,
podemos escrever
detÐ. ‰ -Ñ œ trÐÐ. ‰ -ч Ñ œ trÐ-‡ ‰ .‡ Ñ œ
œ trÐ.‡ ‰ -‡ Ñ œ trÐÐ- ‰ .ч Ñ œ detÐ- ‰ .Ñ.
b) Verificar que o “teorema” em questão já é válido desde que se faça a
exigência de se ter 7 œ 8.
Ex II.17 Sejam I um espaço vectorial sobre Š e Šw ¨ Š. Mostrar que, para
cada
: !,
tem
lugar
uma
aplicação
:-linear
alternada,
PÐIà Šw Ñ: Ä E: ÐIà Šw Ñ, que a cada Ð0" ß á ß 0: Ñ associa 0" • â • 0: .
Sugestão: Utilizar a caracterização dada na alínea a) de II.4.3.
Ex II.18 Diz-se que um elemento 0 − E: ÐIà Šw Ñ é decomponível se existirem
0" ß á ß 0: em PÐIà Šw Ñ tais que se tenha 0 œ 0" • â • 0: . Seja I um espaço
vectorial de dimensão %, sobre Š, com uma base B" ß B# ß B$ ß B% , e sejam 04 os
elementos da base associada de PÐIà ŠÑ. Sendo então 0 o elemento
0" • 0# 0$ • 0% − E# ÐIà ŠÑ, mostrar que 0 • 0 Á ! e deduzir daqui que 0
não é decomponível.
Ex II.19 (Alguns resultados auxiliares de Álgebra Linear)
a) Sejam I um espaço vectorial sobre Š e 0" ß á ß 0: : elementos de
PÐIà ŠÑ. Mostrar que aqueles elementos são linearmente independentes se, e
só se, a aplicação linear 0À I Ä Š: , definida por
Exercícios
93
0ÐBÑ œ Ð0" ÐBÑß á ß 0: ÐBÑÑ,
é sobrejectiva. Sugestão: Considerar em Š: o produto interno canónico (real
ou complexo) e verificar que aquele sistema é linearmente dependente se, e
só se, existe um vector não nulo de Š: , que seja ortogonal ao subespaço
vectorial 0ÐIÑ de Š: .
b) Mostrar que um sistema de elementos 0" ß á ß 0: de PÐIà ŠÑ é linearmente
independente se, e só se, existem elementos B" ß á ß B: de I , tais que
04 ÐB5 Ñ œ $4ß5 , e verificar que, nesse caso, os elementos B" ß á ß B: têm que ser
linearmente independentes.
c) Utilizar a alínea b) para provar que, dados elementos arbitrários
(" ß á ß (: − PÐIà ŠÑ, um elemento 0 − PÐIà ŠÑ pertence ao subespaço
vectorial gerado pelos (4 se, e só se, 0ÐBÑ œ !, para cada B que verifique
(4 ÐBÑ œ !, para todo o 4.
Sugestão: Mostrar que se pode já supor que os elementos (" ß á ß (: são
linearmente independentes.
Ex II.20 Seja I um espaço vectorial sobre Š.
a) Dados 0" ß á ß 0: − PÐIà ŠÑ, mostrar que estes elementos são linearmente
independentes se, e só se, o elemento 0" • â • 0: − E: ÐIà ŠÑ é diferente de
!.
Sugestão: Se os elementos forem linearmente independentes, considerar
B" ß á ß B: − I tais que 04 ÐB5 Ñ œ $4ß5 e calcular 0" • â • 0: ÐB" ß á ß B: Ñ.
Para a recíproca, ter em conta o exercício II.17.
b) Dados dois sistemas linearmente independentes de elementos de PÐIà ŠÑ,
0" ß á ß 0: e (" ß á ß (: , mostrar que estes dois sistemas geram o mesmo
subespaço vectorial de PÐIà ŠÑ se, e só se, existe + − Š, tal que
0" • â • 0: œ + (" • â • (: . Sugestão: Se eles gerarem o mesmo
subespaço, cada 04 é combinação linear dos (5 ; se eles não geram o mesmo
subespaço, existe (5 que não é combinação linear dos 04 e então
(5 • Ð0" • â • 0: Ñ Á !, mas (5 • Ð(" • â • (: Ñ œ !.
Ex II.21 Seja I um espaço vectorial sobre Š. Dado 0 − E: ÐIà ŠÑ, com : ",
chama-se subespaço associado a 0 o conjunto
I w œ ÖB − I ±
a
B# ßáßB:
0ÐBß B# ß á ß B: Ñ œ !×,
conjunto que se verifica trivialmente ser um subespaço vectorial de I .
Mostrar que, se 0" ß á ß 0: é um sistema linearmente independente de elementos de PÐIà ŠÑ, então o subespaço associado a 0" • â • 0: é o conjunto dos
vectores B − I tais que 04 ÐBÑ œ !, para cada " Ÿ 4 Ÿ :.
Sugestão: Considerar vectores C" ß á ß C: − I , tais que 04 ÐC5 Ñ œ $4ß5 . Se
B − I é tal que 0" ÐBÑ Á !, utilizar II.5.10 e o exercício II.11 para mostrar
que 0" • â • 0: ÐBß C# ß á ß C: Ñ œ 0" ÐBÑ Á !. Se B − I é tal que 04 ÐBÑ œ !,
94
Cap. II. Tópicos de Álgebra Multilinear
para cada 4, utilizar II.5.10 para mostrar que, quaisquer que sejam B# ß á ß B: ,
0" • â • 0: ÐBß B# ß á ß B: Ñ œ !.
Ex II.22 Sejam I e J espaços vectoriais de dimensão !, munidos de orientações
(cf. II.7.4). Seja -À I Ä J a única aplicação linear, a qual é evidentemente
um isomorfismo. Discutir em que casos é que - conserva ou inverte as
orientações.
Ex II.23 Seja /" ß á ß /8 a base canónica de ‚8 , como espaço vectorial complexo.
Vamos chamar orientação canónica de ‚8 , como espaço vectorial real,
aquela para a qual a base /" ß 3/" ß /# ß 3/# ß á ß /8 ß 3/8 é directa.
a) Mostrar que, se -À ‚8 Ä ‚8 é um isomorfismo de espaços vectoriais
complexos, então, quando consideramos - como isomorfismo para as
estruturas reais associadas, - conserva as orientações. Sugestão: Ter em
conta II.7.16 e o exercício II.12.
b) Seja I um espaço vectorial complexo de dimensão 8. Mostrar que existe
sobre I , considerado como espaço vectorial real de dimensão #8, uma, e
uma só, orientação (a que daremos o nome de orientação canónica), tal que,
qualquer que seja o isomorfismo complexo -À ‚8 Ä I , - conserva as
orientações, quando se considera em ‚8 a orientação canónica.
c) Mostrar que, se I é um espaço vectorial complexo, com uma base
B" ß á ß B8 , então considerando a orientação canónica de I , como espaço
vectorial real, a base B" ß 3B" ß á ß B8 ß 3B8 é directa.
d) Mostrar que, se I e J são espaços vectoriais complexos de dimensão 8, e
se -À I Ä J é um isomorfismo complexo, então, considerando I e J como
espaços vectoriais reais, com as orientações canónicas, - conserva as orientações.
e) Alguns autores definem a orientação canónica de ‚8 como sendo aquela
para a qual a base e" ß á ß /8 ß 3/" ß á ß 3/8 é directa. Que relação existe entre a
orientação definida deste modo e aquela que definimos no início?
Ex II.24 Consideremos uma sucessão exacta curta de espaços vectoriais sobre Š
-
.
Ö!× Ä I Ä J Ä K Ä Ö!×,
com I de dimensão 7 e K de dimensão 8.
a) Mostrar que existe uma aplicação linear 3À J Ä I tal que 3 ‰ - œ M.I .
b) Sendo Šw ¨ Š, mostrar que se pode definir uma aplicação bilinear de
A8 ÐKà Šw Ñ ‚ E7 ÐIà Šw Ñ em E78 ÐJ à Šw Ñ, que notaremos Ð(ß 0Ñ È ( ‚ 0,
por ( ‚ 0 œ .‡ Ð(Ñ • 3‡ Ð0Ñ, onde 3À J Ä I é uma aplicação linear arbitrária,
verificando 3 ‰ - œ M.I (estamos evidentemente a afirmar que este resultado
não depende da escolha de 3).
c) Nas condições de b), mostrar que, se ( Á ! e 0 Á !, então ( ‚ 0 Á !;
d) Sendo B" ß á ß B7 uma base de I e D" ß á ß D8 uma base de K, e escolhendo C" ß á ß C8 em J , tais que .ÐC4 Ñ œ D4 , mostrar que se tem
Exercícios
95
( ‚ 0ÐC" ß á ß C8 ß -ÐB" Ñß á ß -ÐB7 ÑÑ œ (ÐD" ß á ß D8 Ñ 0ÐB" ß á ß B7 Ñ.
Sugestão: Para demonstrar a independência da escolha de 3 e a conclusão de
c), basta demonstrar d). Para esse efeito, utilizar a fórmula para o produto
exterior descrita em II.5.12.
Ex II.25 Nas condições do exercício anterior, suponhamos que Š œ Šw œ ‘, e
que I , J e K estão orientados, com orientações compatíveis com a referida
sucessão exacta curta. Considerando as orientações associadas em E7 ÐIà ‘Ñ,
E8 ÐKà ‘Ñ e E78 ÐJ à ‘Ñ, mostrar que, para cada par de elementos não nulos
0 − E7 ÐIà ‘Ñ e ( − E8 ÐKà ‘Ñ, tem-se sgÐ( ‚ 0Ñ œ sgÐ(Ñ sgÐ0Ñ.
Ex II.26 Sejam I , J e K espaços vectoriais complexos e -À I Ä J e .À J Ä K
aplicações lineares complexas tais que tenha lugar a sucessão exacta curta
-
.
Ö!× Ä I Ä J Ä K Ä Ö!×.
Consideremos sobre I , J e K, olhados como espaços vectoriais reais, as
orientações canónicas (cf. a alínea b) do exercício II.23). Mostrar que o
sistema das três orientações é então compatível com a sucessão exacta curta.
Ex II.27 a) Consideremos o seguinte diagrama comutativo de espaços vectoriais
sobre Š e de aplicações lineares:
-
.
-w
.w
I Ä J Ä K Ä Ö!×
3Æ3
5Æ5
,
I w Ä J w Ä Kw Ä Ö!×
em que as duas linhas são exactas. Mostrar que existe uma, e uma só,
aplicação linear 7 À K Ä Kw , tal que 7 ‰ . œ .w ‰ 5 ,16 e que essa aplicação
linear é um isomorfismo se isso acontecer a 3 e a 5 .
b) Consideremos o seguinte diagrama comutativo de espaços vectoriais sobre
Š e de aplicações lineares:
-
Ö!× Ä I Ä
-w
.
J Ä K
5Æ5
7 Æ7,
.w
Ö!× Ä I w Ä J w Ä Kw
em que as duas linhas são exactas. Mostrar que existe uma, e uma só,
aplicação linear 3À I Ä I w tal que 5 ‰ - œ -w ‰ 3 e que esta aplicação linear
é um isomorfismo se isso acontecer a 5 e a 7 .
c) Consideremos o seguinte diagrama comutativo de espaços vectoriais sobre
Š e de aplicações lineares:
16Por
deste.
outras palavras que permita prolongar o diagrama sem perda da comutatividade
96
Cap. II. Tópicos de Álgebra Multilinear
-
.
-w
.w
Ö!× Ä I Ä J Ä K Ä Ö!×
3Æ3
5Æ5
7 Æ7
,
Ö!× Ä I w Ä J w Ä Kw Ä Ö!×
em que as duas linhas são exactas. Mostrar que, se 3 e 7 são isomorfismos, o
mesmo vai acontecer a 5 . Nota: Esta conclusão é um caso particular do chamado “Lema dos Cinco”.17
Ex II.28 Seja I um espaço euclidiano orientado de dimensão 8. Dados dois
sistemas de 8 vectores de I , B" ß á ß B8 e C" ß á ß C8 , mostrar que se tem
detÐÐØB4 ß C5 ÙÑÑ œ Z 96I ÐB" ß á ß B8 Ñ Z 96I ÐC" ß á ß C8 Ñ.
Sugestão: Aplicando duas vezes o lema II.4.10, mostrar que é suficiente
provar o resultado no caso particular em que ambos os sistemas coincidem
com uma mesma base ortonormada A" ß á ß A8 .
Ex II.29 Seja I um espaço euclidiano de dimensão !, sobre o qual se considera
uma das suas orientações (a positiva ou a negativa). Sendo Š igual a ‘ ou
‚, o que será o isomorfismo ‡À Š œ E! ÐIà ŠÑ Ä E! ÐIà ŠÑ œ Š?
Ex II.30 Seja I um espaço euclidiano orientado de dimensão # e consideremos o
correspondente isomorfismo )À I Ä PÐIà ‘Ñ œ E" ÐIà ‘Ñ.
a) Dado B − I Ï Ö!×, mostrar que se tem ‡)ÐBÑ œ )ÐCÑ, onde C é o único
vector de I tal que ØBß CÙ œ !, mCm œ mBm e Bß C é uma base directa.
Sugestão: Por linearidade, basta considerar o caso em que mBm œ ".
b) Dado B − I Ï Ö!×, mostrar que o produto externo da família formada pelo
único vector B é o vector C que verifica as três condições ØBß CÙ œ !,
mCm œ mBm e Cß B é uma base directa.
Ex II.31 Seja I um espaço euclidiano orientado de dimensão 8 e sejam
B" ß á ß B8" e C" ß á ß C8" dois sistemas de 8 " vectores de I . Mostrar
que se tem
Z 96I ÐB" ‚ â ‚ B8" ß C" ß á ß C8" Ñ œ detÐÐØB4 ß C5 ÙÑÑ
e deduzir daqui que
ØB" ‚ â ‚ B8" ß C" ‚ â ‚ C8" Ù œ detÐÐØB4 ß C5 ÙÑÑ.
Sugestão: Recordar a caracterização do isomorfismo )˜À I Ä E8" ÐIà ŠÑ
referida em II.8.19 e ter em conta II.5.10.
Ex II.32 Seja I um espaço euclidiano orientado de dimensão $.
a) Dados Bß C − I , mostrar que se tem
17Cf.
IV.5.14 adiante.
Exercícios
97
)ÐB ‚ CÑ œ intC Ї)ÐBÑÑ.
Sugestão: Aplicar ‡ a ambos os membros da igualdade
‡)ÐB ‚ CÑ œ )ÐBÑ • )ÐCÑ
e utilizar a alínea a) de II.8.17.
b) Deduzir de a) e de II.6.6 que, dados Bß Cß D − I , tem-se
)ÐÐB ‚ CÑ ‚ DÑ œ intD Ð)ÐBÑÑ • )ÐCÑ )ÐBÑ • intD Ð)ÐCÑÑ
e concluir daqui que
ÐB ‚ CÑ ‚ D œ ØBß DÙC ØCß DÙB.
Ex II.33 Seja I um espaço euclidiano de dimensão 8, munido de uma orientação
!, e seja A" ß á ß A8 uma base ortonormada de I . Mostrar que se tem
A" ‚ â ‚ A4" ‚ A4" ‚ â ‚ A8 œ !ÐA" ß á ß A8 Ñ Ð"Ñ4" A4 .
Sugestão: Utilizar a alínea b) de II.8.13.
Ex II.34 Seja I um espaço euclidiano orientado de dimensão 8.
a) Mostrar que, para cada ! Ÿ : Ÿ 8, pode-se definir um produto interno no
espaço vectorial E: ÐIà ‘Ñ pela condição de se ter, para 0ß ( − E: ÐIà ‘Ñ,
0 • Ї(Ñ œ Ø0ß (Ù Z 96I .
Sugestão: Ter em conta II.8.15.
b) Mostrar que o produto interno anterior não depende da orientação que se
considera em I .
c) Mostrar que, se B" ß á ß B8 é uma base ortonormada de I , então a base
associada de E: ÐIà ‘Ñ é também ortonormada. Deduzir, em particular, que
Z 96I é o único elemento positivo de norma " de E8 ÐIà ‘Ñ.
d) Mostrar que são ortogonais os isomorfismos ‡À E: ÐIà ‘Ñ Ä E8: ÐIà ‘Ñ
e )À I Ä E" ÐIà ‘Ñ.
Ex II.35 Seja I um espaço euclidiano orientado de dimensão 8 ". Dados
- − E" ÐIà ŠÑ e ? − I , mostrar que
- • ‡)Ð?Ñ œ -Ð?Ñ Z 96I .
Sugestão: Fixar uma base ortonormada directa A" ß á ß A8 de I tal que
? œ + A" e determinar - • ‡)Ð?ÑÐA" ß á ß A8 Ñ, utilizando a caracterização do
produto externo em II.5.12.
CAPÍTULO III
Formas Diferenciais e Teorema de Stokes
§1. Campos tensorais e formas diferenciais.
III.1.1. Sejam I um espaço vectorial real de dimensão finita e Q § I uma
variedade. Dado um espaço vectorial J sobre o corpo Š (igual a ‘ ou ‚),
vamos chamar campo tensorial (covariante) de grau : sobre Q com valores
em J (ou, abreviadamente, J -campo tensorial sobre Q ) a uma família
0 œ Ð0B ÑB−Q , em que, para cada B − Q , 0B − P: ÐXB ÐQ Ñà J Ñ é uma
aplicação multilinear de XB ÐQ Ñ: em J . É costume omitir a referência a J ,
ou falar de campo tensorial real, no caso em que J œ ‘, e falar de campo
tensorial complexo no caso em que J œ ‚.
III.1.2. É claro que, no caso em que : œ !, um campo tensorial, com valores em
J , não é mais do que uma aplicação de Q em J .
No que se segue, teremos necessidade de nos referirmos a campos
tensoriais suaves. Temos que ser cuidadosos com o que queremos
significar com uma tal afirmação, uma vez que, embora um campo
tensorial seja uma aplicação de domínio Q , trata-se de uma aplicação
que, em geral, não está a tomar valores num espaço vectorial fixado (os
diferentes espaços de aplicações multilineares P: ÐXB ÐQ Ñà J ÑÑ não aparecem naturalmente como subespaços vectoriais de um mesmo espaço
vectorial).
III.1.3. Sejam Q § I uma variedade e J um espaço vectorial de dimensão
finita sobre Š. Vamos dizer que um J -campo tensorial de grau :,
0 œ Ð0B ÑB−Q é suave se existir uma aplicação suave 0 œ Ð0B ÑB−Q , de Q em
P: ÐIà J Ñ, tal que, para cada B − Q , 0B − P: ÐXB ÐQ Ñà J Ñ seja uma restrição
de 0B − P: ÐIà J Ñ (dizemos então que 0 é um prolongamento suave de 0).
III.1.4. É claro que dizer que um campo tensorial de grau !, com valores em J , é
suave é o mesmo que dizer que o é como aplicação de Q em J (o
prolongamento 0 de 0 é neste caso único, e igual ao próprio 0).
Na mesma ordem de ideias, se a variedade Q § I é tal que, para cada
B − Q , XB ÐQ Ñ œ I (é o que acontece se Q for um aberto de I ou, mais
geralmente, uma variedade, possivelmente com bordo, com dimensão em
cada ponto igual à de I ), então um campo tensorial de grau : sobre Q , com
valores em J , não é mais do que uma aplicação de Q em P: ÐIà J Ñ e o
100
Cap. III. Formas diferenciais e teorema de Stokes
campo tensorial é suave se, e só se, o for como aplicação (mais uma vez, o
prolongamento 0 de 0 é único e igual ao próprio 0).
III.1.5. Sejam I w § I dois espaços vectoriais de dimensão finita e Q § I w uma
variedade. Se 0 œ Ð0B ÑB−Q é um campo tensorial de grau :, sobre Q , com
valores no espaço vectorial J , tem-se que 0 é suave, quando se considera Q
como parte de I w , se, e só se, isso acontece quando se considera Q como
parte de I .
Dem: Suponhamos que 0 é suave, quando se considera Q como parte de I .
Podemos então considerar uma aplicação suave 0 œ Ð0B ÑB−Q , de Q em
P: ÐIà J Ñ, tal que cada 0B seja uma restrição de 0B , e, compondo com a
aplicação linear de P: ÐIà J Ñ em P: ÐI w à J Ñ, que a cada ( associa a restrição
de ( a I w : , obtemos um prolongamento suave de 0 com valores em
P: ÐI w à J Ñ, o que mostra que 0 é suave, quando se considera Q como parte
de I w . Suponhamos, reciprocamente, que 0 é suave, quando se considera Q
como parte de I w . Seja s0 œ Ðs0B ÑB−Q uma aplicação suave de Q em
P: ÐI w à J Ñ, tal que cada 0B seja uma restrição de s0B . Escolhamos uma
aplicação linear 1À I Ä I w , tal que 1Ð?Ñ œ ?, para cada ? − I w (por
exemplo, a projecção ortogonal, para um produto interno que se fixe em I ).
Podemos então considerar a aplicação linear imagem recíproca
1‡ À P: ÐI w à J Ñ Ä P: ÐIà J Ñ e verifica-se imediatamente que a família
Ð1‡ Ðs0B ÑÑB−Q é um prolongamento suave de 0, quando se considera Q como
parte de I .
III.1.6. Sejam Q § I uma variedade, J um espaço vectorial de dimensão finita
sobre Š e J w § J um subespaço vectorial. Seja 0 œ Ð0B ÑB−Q um campo
tensorial de grau :, sobre Q , com valores em J w . Tem-se então que 0 é
também um campo tensorial com valores em J e 0 é suave como campo
tensorial com valores em J se, e só se, o for como campo tensorial com
valores em J w .
Dem: A demonstração tem o mesmo espírito que a do resultado precedente:
Uma das implicações é trivial e resulta simplesmente de que P: ÐIà J w Ñ é um
subespaço vectorial de P: ÐIà J Ñ; Para a outra implicação, consideramos uma
aplicação linear 1À J Ä J w , tal que 1Ð@Ñ œ @, para cada @ − J w , e reparamos
que, se s0 œ Ðs0B ÑB−Q for um prolongamento suave de 0, com valores em
P: ÐIà J Ñ, a família dos 1 ‰ s0B é um prolongamento suave de 0, com valores
em P: ÐIà J w Ñ.
Por definição, um campo tensorial é suave se admitir um prolongamento
suave, mas em geral haverá muitos prolongamentos nessas condições. Em
certos casos é cómodo termos um prolongamento suave definido
explicitamente. O resultado que se segue mostra uma maneira de
conseguir isso, no caso em que fixamos um produto interno no espaço
vectorial ambiente da variedade.
§1. Campos tensoriais e formas diferenciais
101
III.1.7. Sejam I um espaço vectorial de dimensão finita, munido de um produto
interno e Q § I uma variedade. Para cada B − Q , seja 1B À I Ä XB ÐQ Ñ a
projecção ortogonal. Se 0 œ Ð0B ÑB−Q é um campo tensorial suave de grau :
sobre Q , com valores em J , tem lugar uma aplicação suave s0 œ Ðs0B ÑB−Q de
Q em P: ÐIà J Ñ, definida por s0B œ 1B‡ Ð0B Ñ œ 0B ‰ 1B: , a qual constitui um
prolongamento suave de 0 (diremos que s0 é o prolongamento euclidiano de
0).
Dem: O facto de Q ser uma variedade, que implica que o fibrado tangente
X ÐQ Ñ œ ÐXB ÐQ ÑÑB−Q é um fibrado vectorial, mostra-nos que é suave a
aplicação de Q em PÐIà IÑ, que a B associa 1B . Por outro lado, vai existir,
por definição, uma aplicação suave 0 œ Ð0B ÑB−Q , de Q em P: ÐIà J Ñ tal que
cada 0B − P: ÐXB ÐQ Ñà J Ñ seja uma restrição de 0B . Uma vez que tem lugar
uma aplicação multilinear, em particular suave,
P: ÐIà J Ñ ‚ PÐIà IÑ ‚ â ‚ PÐIà IÑ Ä P: ÐIà J Ñ,
Ð.ß -" ß á ß -: Ñ È . ‰ Ð-" ‚ â-: Ñ,
concluímos que tem lugar a aplicação suave de Q em P: ÐIà J Ñ, que a B
associa 0B ‰ 1B: œ 0B ‰ 1B: , a qual vai ser trivialmente ainda um prolongamento de 0.
III.1.8. Sejam I um espaço vectorial real de dimensão finita e Q § I uma
variedade. Se J é um espaço vectorial, real ou complexo, de dimensão finita,
chamamos forma diferencial de grau :, com valores em J a um campo
tensorial Ð0B ÑB−Q , de grau : e com valores em J , tal que, para cada B − Q ,
a aplicação :-linear 0B À XB ÐQ Ñ: Ä J seja alternada, isto é, que, para cada
B − Q , 0B − E: ÐXB ÐQ Ñà J Ñ. Uma tal forma diferencial diz-se suave se o for
enquanto campo tensorial. Como anteriormente, nos casos em que J œ ‘ ou
J œ ‚, falamos também de formas diferenciais reais (ou, simplesmente,
formas diferenciais) e de formas diferenciais complexas.
É claro que, nos casos em que : œ ! e : œ ", uma forma diferencial de grau
: é o mesmo que um campo tensorial de grau : e portanto, no primeiro caso,
o mesmo que uma aplicação Q Ä J .
III.1.9. Sejam Q § I uma variedade e 0 œ Ð0B ÑB−Q uma forma diferencial
suave de grau : sobre Q , com valores em J . Existe então uma aplicação
suave 0 œ Ð0B ÑB−Q , de Q em E: ÐIà J Ñ, tal que, para cada B − Q , 0B seja
uma restrição de 0B .
Dem: Basta considerar um produto interno em I e tomar para 0 o prolongamento euclidiano de 0, tendo em conta III.1.7.
Como no capítulo precedente, e uma vez que esse será o quadro que nos
vai interessar principalmente, vamos, a partir de agora, concentrar a nossa
atenção no caso dos campos tensoriais e formas diferenciais reais ou
complexos.
102
Cap. III. Formas diferenciais e teorema de Stokes
s §I
s e Q § I duas variedades e 0 À Q
s Ä Q uma aplicação
III.1.10. Sejam Q
suave. Se 0 œ Ð0C ÑC−Q é um campo tensorial de grau : sobre Q , real ou
s , a aplicação linear
complexo, podemos considerar, para cada B − Q
s
H0B À XB ÐQ Ñ Ä X0 ÐBÑ ÐQ Ñ, e portanto, por ser 00 ÐBÑ − P: ÐX0 ÐBÑ ÐQ Ñà ŠÑ, a
s Ñà ŠÑ. Ficamos portanto
respectiva imagem recíproca H0B‡ Ð00 ÐBÑ Ñ − P: ÐXB ÐQ
s
com um campo tensorial de grau : sobre Q , também real ou complexo,
0 ‡ 0 œ ÐH0B‡ Ð00 ÐBÑ ÑÑB−Qs ,
a que se dá o nome de imagem recíproca de 0 por meio de 0 . É claro que, se
0 fosse uma forma diferencial, o mesmo ia acontecer a 0 ‡ 0.
Repare-se que, examinando a definição de imagem recíproca por meio de
uma aplicação linear, se constata imediatamente que
Ð0 ‡ 0ÑB Ð?" ß á ß ?: Ñ œ 00 ÐBÑ ÐH0B Ð?" Ñß á ß H0B Ð?: ÑÑ.
III.1.11. Nas condições anteriores, se o campo tensorial 0, sobre Q , fosse suave,
s.
o mesmo ia acontecer ao campo tensorial imagem recíproca 0 ‡ 0, sobre Q
:
Dem: Seja 0 œ Ð0C ÑC−Q uma aplicação suave de Q em P ÐIà ŠÑ, tal que,
s um
para cada C − Q , 0C − P: ÐXC ÐQ Ñà ŠÑ seja uma restrição de 0C . Sejam Y
s , contendo Q
s , e s0 À Y
s Ä I uma aplicação suave cuja restrição a
aberto de I
s seja 0 . Tem-se então uma aplicação suave de Y
s em PÐIà
s IÑ, definida por
Q
s
s
s Ñ Ä X0 ÐBÑ ÐQ Ñ
B È H0 B , e, para cada B − Q , a aplicação linear H0B À XB ÐQ
s BÀ I
s Ä I . Considerando a aplicação multilinear, em
é uma restrição de H0
particular suave,
s IÑ ‚ â ‚ PÐIà
s IÑ Ä P: ÐIà
s ŠÑ,
P: ÐIà ŠÑ ‚ PÐIà
Ð.ß -" ß á ß -: Ñ È . ‰ Ð-" ‚ â-: Ñ,
s em P: ÐIà
s ŠÑ, que a B associa
obtemos uma aplicação suave de Q
:
s B , aplicação essa que vai constituir trivialmente um prolongamento
00 ÐBÑ ‰ H0
suave para 0 ‡ 0.
III.1.12. Um caso particular importante de imagem recíproca é aquele em que
s § Q e 0À Q
s Ä Q é a inclusão, definida por 0 ÐBÑ œ B. A imagem
Q
recíproca 0 ‡ 0, do campo tensorial 0 de grau : sobre Q , costuma então ser
s . Repare-se
notada 0ÎQs e ser chamada de restrição do campo tensorial 0 a Q
que se trata, em geral, não de uma restrição no sentido estrito, mas de uma
s e por
espécie de dupla restrição: Por um lado restringimos a aplicação 0 a Q
s , restringimos o valor 0B − P: ÐXB ÐQ Ñà ŠÑ, de
outro lado, para cada B − Q
s Ñà ŠÑ. De qualquer modo, podemos
modo a obter um elemento de P: ÐXB ÐQ
s
s Ñ, a fórmula tranquilizadora
escrever, para cada B − Q e ?" ß á ß ?: em XB ÐQ
Ð0ÎQs ÑB Ð?" ß á ß ?: Ñ œ 0B Ð?" ß á ß ?: Ñ.
§1. Campos tensoriais e formas diferenciais
103
Como casos particulares em que se obtêm verdadeiras restrições, temos
(comparar com o que se disse em III.1.4):
a) O caso em que : œ !; neste caso temos simplesmente a restrição de uma
s em Š;
aplicação de Q em Š, que vai ser uma aplicação de Q
s
s
b) O caso em que, para cada B − Q , XB ÐQ Ñ œ XB ÐQ Ñ; é o que acontece se
s for um aberto de Q ou, mais geralmente, se a variedade Q
s tem em cada
Q
ponto dimensão igual à de Q .
s §I
s eQ §I
III.1.13. Dentro do mesmo espírito que na alínea a) atrás, se Q
s
são variedades e 0 À Q Ä Q é uma aplicação suave, então, para cada campo
tensorial : sobre Q , de grau !, real ou complexo, : é simplesmente uma
aplicação de Q em Š e a forma diferencial imagem recíproca 0 ‡ : não é
s Ä Š.
mais do que a aplicação composta : ‰ 0 À Q
III.1.14. A noção de campo tensorial, ou forma diferencial, imagem recíproca foi
definida a partir da noção algébrica de imagem recíproca de um elemento de
s em I . Citamos em seguida
P: ÐIà ŠÑ por meio de uma aplicação linear de I
algumas das propriedades desta noção que se deduzem trivialmente das propriedades correspondentes no quadro algébrico.
s §I
s e Q § I três variedades e 0 À Q˜ Ä Q
s e
a) Sejam Q˜ § I˜ , Q
s
1À Q Ä Q duas aplicações suaves. Para cada campo tensorial 0 œ Ð0D ÑD−Q
sobre Q , tem-se então
Ð1 ‰ 0 ч 0 œ 0 ‡ Ð1‡ 0Ñ
(atender a II.2.15 e ao facto de se ter HÐ1 ‰ 0 ÑB œ H10 ÐBÑ ‰ H0B ). Em consequência, e uma vez que se tem evidentemente
‡
0 œ 0,
M.Q
s Ä Q fosse um difeomorfismo, então
concluímos que, se 1À Q
‡
1" Ð1‡ 0Ñ œ 0.
s §I
s e Q § I variedades, 0 À Q
s Ä Q uma aplicação suave,
b) Sendo Q
0 œ Ð0B ÑB−Q e ( œ Ð(B ÑB−Q campos tensoriais de grau : sobre Q e + − Š,
tem-se
0 ‡ Ð0 (Ñ œ 0 ‡ 0 0 ‡ (,
0 ‡ Ð+ 0Ñ œ + 0 ‡ 0.
s §I
s e Q § I variedades, 0 À Q
s Ä Q uma aplicação suave e
c) Sendo Q
0 œ Ð0B ÑB−Q e ( œ Ð(B ÑB−Q campos tensoriais de graus : e ; sobre Q ,
tem-se
0 ‡ Ð0 Œ (Ñ œ 0 ‡ 0 Œ 0 ‡ (
(cf. II.2.16).
s §I
s e Q § I variedades, 0 À Q
s Ä Q uma aplicação suave e
d) Sendo Q
0 œ Ð0B ÑB−Q e ( œ Ð(B ÑB−Q formas diferenciais de graus : e ; sobre Q ,
104
Cap. III. Formas diferenciais e teorema de Stokes
tem-se
0 ‡ Ð0 • (Ñ œ 0 ‡ 0 • 0 ‡ (
(cf. II.5.14).
O resultado que se segue exprime o facto de a noção de campo tensorial
suave ser local.
III.1.15. Sejam Q § I uma variedade e ÐY4 Ñ4−N uma família de abertos de Q
de união Q . Seja 0 œ Ð0B ÑB−Q um campo tensorial de grau :, sobre Q , real
ou complexo, tal que, para cada 4 − N , a restrição 0ÎY4 seja um campo
tensorial suave sobre Y4 . Tem-se então que 0 é suave.
Dem: Considerando o prolongamento euclidiano de 0, relativamente a um
certo produto interno de I , ficamos reduzidos a provar que, se s0 é uma
aplicação de Q em P: ÐIà ŠÑ, cuja restrição a cada Y4 seja suave, então s0 é
uma aplicação suave e isso é uma consequência de a suavidade de uma
aplicação ser uma questão local.
O passo seguinte é reparar que as diferentes operações algébricas
envolvendo os espaços de aplicações multilineares ou de aplicações
multilineares alternadas conduzem, quando aplicadas fibra a fibra, de
campos tensoriais ou formas diferenciais suaves a campos tensoriais ou
formas diferenciais suaves. Em muitos casos omitiremos as demonstrações que resultem trivialmente de considerar os prolongamentos
euclidianos dos campos tensoriais envolvidos.
III.1.16. Sejam Q § I uma variedade e : !. Tem-se então que o conjunto
dos campos tensoriais de grau : sobre Q , com valores em Š, tem uma
estrutura natural de espaço vectorial sobre Š e este espaço vectorial admite
como subespaços vectoriais:
a) O conjunto das formas diferenciais de grau :;
b) O conjunto dos campos tensoriais suaves de grau :;
c) O conjunto das formas diferenciais suaves de grau :.
III.1.17. Sejam Q § I uma variedade e 0 œ Ð0B ÑB−Q e ( œ Ð(B ÑB−Q campos
tensoriais suaves de graus : e ; , sobre Q , com valores em ŠÞ É então
também suave o campo tensorial de grau : ; , sobre Q
0 Œ ( œ Ð0B Œ (B ÑB−Q . Em particular, se 0 À Q Ä Š é uma aplicação suave
(isto é, um campo tensorial suave de grau !), vem também suave o campo
tensorial 0 0 œ Ð0 ÐBÑ 0B ÑB−Q .
III.1.18. Sejam Q § I uma variedade e 0 œ Ð0B ÑB−Q um campo tensorial suave
de grau : sobre Q , com valores em Š. tem-se então:
a) Para cada permutação 5 − Æ: , vem suave o campo tensorial
§1. Campos tensoriais e formas diferenciais
105
5
s Ð0Ñ œ Ð5
s Ð0B ÑÑB−Q ;
b) Tem lugar uma forma diferencial suave
AltÐ0Ñ œ ÐAltÐ0B ÑÑB−Q .
III.1.19. Sejam Q § I uma variedade e 0 œ Ð0B ÑB−Q e ( œ Ð(B ÑB−Q formas
diferenciais suaves de graus : e ; , sobre Q , com valores em ŠÞ É então
também suave a forma diferencial de grau : ; , sobre a variedade Q
0 • ( œ Ð0B • (B ÑB−Q .
III.1.20. Sejam I um espaço euclidiano e Q § I uma variedade. Para cada
B − Q , temos então um isomorfismo )B À XB ÐQ Ñ Ä PÐXB ÐQ Ñà ‘Ñ, definido
por )B Ð@ÑÐ?Ñ œ Ø?ß @Ù. Para cada campo vectorial \ œ Ð\B ÑB−Q sobre Q ,
isto é, para cada família de vectores de I , tal que, para cada B − Q ,
\B − XB ÐQ Ñ, notamos então )Ð\Ñ a família Ð)B Ð\B ÑÑB−Q , que é portanto
uma forma diferencial de grau " com valores em ‘. Do mesmo modo, para
cada forma diferencial de grau ", = œ Ð=B ÑB−Q , com valores em ‘, notamos
)" Ð=Ñ a família Ð)B" Ð=B ÑÑB−Q , que é portanto um campo vectorial sobre Q .
Fica assim estabelecida uma correspondência biunívoca entre campos
vectorais e formas diferenciais de grau ", com valores em ‘.
III.1.21. Sejam I um espaço euclidiano e Q § I uma variedade. Se
\ œ Ð\B ÑB−Q é um campo vectorial sobre Q , tem-se que \ é suave se, e só
se, a forma diferencial )Ð\Ñ œ Ð)B Ð\B ÑÑB−Q é suave.
Dem: Comecemos por supor que \ é um campo vectorial suave, ou seja, que
é uma aplicação suave de Q em I . Por composição com o isomorfismo
)À I Ä PÐIà ‘Ñ, obtemos uma aplicação suave = œ Ð=B ÑB−Q de Q para
PÐIà ‘Ñ, definida por =B œ )Ð\B Ñ, e é trivial que cada aplicação linear
)B Ð\B Ñ − PÐXB ÐQ Ñà ‘Ñ é uma restrição de PÐIà ‘Ñ, o que mostra que )Ð\Ñ
é uma forma diferencial suave. Suponhamos agora, reciprocamente, que )(X)
é uma forma diferencial suave. Seja B! − Q arbitrário. Seja Y um aberto de
Q , com B! − Y , tal que exista um campo de referenciais ortonormado
\" ß á ß \7 sobre Y , constituído portanto por aplicações suaves de Y em I .
É então imediato que, para cada " Ÿ 4 Ÿ 7, temos uma aplicação suave de
Y em ‘, que a B associa )B Ð\B ÑÐ\4 B Ñ œ Ø\B ß \4 B Ù, pelo que o facto de se
ter
\B œ " Ø\B ß \4 B Ù \4 B
7
4œ"
mostra que é suave a restrição de \ a Y . Tendo em conta o facto de a noção
de aplicação suave ser local, concluímos finalmente que \ é uma aplicação
suave de Q em I .
106
Cap. III. Formas diferenciais e teorema de Stokes
Examinamos, nos dois resultados seguintes, exemplos importantes da
situação que temos estado a estudar.
III.1.22. Sejam Q § I uma variedade e 0 À Q Ä Š uma aplicação suave. Tem
então lugar uma forma diferencial suave de grau ", H0 œ ÐH0B ÑB−Q .
Dem: Uma vez que, para cada B − Q , H0B é uma aplicação linear de
XB ÐQ Ñ em ‘, vemos que H0 é realmente uma forma diferencial de grau ".
Por outro lado, podemos considerar um aberto Y de I , contendo Q , e um
prolongamento suave 0 À Y Ä Š de 0 e tem então lugar uma aplicação suave
H0 À Y Ä PÐIà ŠÑ. Uma vez que, para cada B − Q , H0B À XB ÐQ Ñ Ä Š é
uma restrição de H0 B À I Ä Š, concluímos que a forma diferencial H0 é
suave.
III.1.23. (Corolário) Sejam I um espaço euclidiano, Q § I uma variedade e
0 À Q Ä ‘ uma aplicação suave. Tem então lugar um campo vectorial suave,
gradÐ0 Ñ sobre Q , a que se dá o nome de gradiente de 0 , definido por
gradÐ0 Ñ œ )" ÐH0 Ñ, ou seja, por
Ø?ß gradÐ0 ÑB Ù œ H0B Ð?Ñ,
para cada B − Q e ? − XB ÐQ Ñ.
III.1.24. Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7, suavemente orientada. Tem então lugar uma forma diferencial suave de
grau 7, com valores em ‘, Z 96 œ ÐZ 96B ÑB−Q , chamada forma diferencial
elemento de volume, em que, para cada B − Q , Z 96B − E7 ÐXB ÐQ Ñà ‘Ñ é o
elemento de volume do espaço euclidiano orientado XB ÐQ Ñ.
Dem: Seja B! − Q arbitrário. Seja Y um aberto de Q , com B! − Y , tal que
exista sobre Y um campo de referenciais ortonormado suave \" ß á ß \7 . O
facto de a orientação de Q ser suave implica que, se necessário restringindo
os campos vectoriais a um aberto mais pequeno que ainda contenha B! ,
pode-se já supor que os campos vectoriais constituem em cada B − Y uma
base directa de XB ÐQ Ñ ou constituem em cada B − Q uma base retrógrada
de
XB ÐQ Ñ.
Vem
então
ou,
para
cada
B − Y,
Z 96B œ )B Ð\" B Ñ • â • )B Ð\7 B Ñ
ou,
para
cada
B − Y,
Z 96B œ )B Ð\" B Ñ • â • )B Ð\7 B Ñ, pelo que ÐZ 96B ÑB−Y é uma forma
diferencial suave sobre Y . Tendo em conta III.1.15, concluímos finalmente
que Z 96 é uma forma diferencial suave.
III.1.25. Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 suavemente orientada. Sejam ! Ÿ : Ÿ 7 e = œ Ð=B ÑB−Q uma forma
diferencial suave de grau :, com valores em Š. Sendo, para cada B − Q ,
‡=B a imagem do tensor alternado =B − E: ÐXB ÐQ Ñà ŠÑ pelo isomorfismo
‡À E: ÐXB ÐQ Ñà ŠÑ Ä E7: ÐXB ÐQ Ñà ŠÑ,
tem-se então que a forma diferencial ‡= œ Ї=B ÑB−Q , de grau 7 :, é tam-
§1. Campos tensoriais e formas diferenciais
107
bém suave.
Dem: Seja B! − Q arbitrário. Seja Y um aberto de Q , com B! − Y , tal que
exista sobre Y um campo de referenciais ortonormado suave \" ß á ß \7 . O
facto de a orientação de Q ser suave implica que, se necessário restringindo
os campos vectoriais a um aberto mais pequeno que ainda contenha B! ,
pode-se já supor que os campos vectoriais constituem em cada B − Y uma
base directa de XB ÐQ Ñ ou constituem em cada B − Q uma base retrógrada
de XB ÐQ Ñ. Notemos & œ ", no primeiro caso, e & œ ", no segundo. Uma
vez que, tendo em conta II.8.5 e II.5.9, os elementos da base de
E: ÐXB ÐQ Ñà ŠÑ associados à base \" B ß á ß \7 B de XB ÐQ Ñ são os
)B Ð\3" B Ñ • â • )B Ð\3: B Ñ, sabemos que se tem, para cada B − Y ,
=B œ " =B Ð\3" B ß á ß \3: B Ñ )B Ð\3" B Ñ • â • )B Ð\3: B Ñ,
3" â3:
onde, para cada 3" â 3: é trivialmente suave a aplicação Y Ä Š,
B È =B Ð\3" B ß á ß \3: B Ñ.
Tendo em conta a alínea b) de II.8.13, tem-se, notando, como é usual, para
cada 3" â 3: em Ö"ß á ß 7×ß 3:" â 37 os restantes índices,
‡=B œ " & sgÐÖ3" ß á ß 3: ×Ñ =B Ð\3" B ß á ß \3: B Ñ )B Ð\3:" B Ñ • â • )B Ð\37 B Ñ,
3" â3:
o que mostra que a restrição de ‡= a Y é suave. Podemos aplicar agora
III.1.15 para garantir que ‡= é suave.
§2. Derivada exterior duma forma diferencial.
III.2.1. Recordemos que, se Q § I é uma variedade e se \ œ Ð\B ÑB−Q e
] œ Ð]B ÑB−Q são campos vectoriais suaves, então, embora os vectores
H]B Ð\B Ñ e H\B Ð]B Ñ de I não pertençam, em geral, a XB ÐQ Ñ, a diferença
Ò\ß ] ÓB œ H]B Ð\B Ñ H\B Ð]B Ñ
já pertence a XB ÐQ Ñ, o que nos permite considerar um novo campo vectorial
suave Ò\ß ] Ó sobre Q , o parêntesis de Lie de \ e ] , que a cada B associa
Ò\ß ] ÓB .
III.2.2. Seja Q § I uma variedade e seja = œ Ð=B ÑB−Q uma forma diferencial
suave de grau :, real ou complexa. Existe então uma, e uma só, forma
diferencial . =, de grau : ", a que daremos o nome de derivada exterior de
=, tal que, qualquer que seja a aplicação suave = œ Ð=B ÑB−Q , de Q em
E: ÐIà ŠÑ, com cada =B restrição de =B , se tenha
108
Cap. III. Formas diferenciais e teorema de Stokes
Ð. =ÑB Ð?" ß á ß ?:" Ñ œ
œ " Ð"Ñ4" H=B Ð?4 ÑÐ?" ß á ß ?4" ß ?4" ß á ß ?:" Ñ.
:"
4œ"
Além disso, se, para cada " Ÿ 4 Ÿ : ", \4 œ Ð\4 B ÑB−Q é um campo
vectorial suave sobre Q , tem-se
Ð. =ÑÐ\" ß á ß \:" Ñ œ
œ " Ð"Ñ4" HÐ=Ð\" ß á ß \4" ß \4" ß ß á ß \:" ÑÑÐ\4 Ñ
:"
4œ"
œ " Ð"Ñ45 =ÐÒ\4 ß \5 Óß \" ß á ß \4" ß \4" ß á ß \5" ß \5" ß á ß \:" ÑÞ18
45
Dem: A unicidade de uma forma diferencial .=, verificando a condição do
enunciado, resulta de existência de pelo menos uma aplicação suave = de Q
em E: ÐIà ŠÑ, tal que cada =B seja uma restrição de =B (cf. III.1.9).
Suponhamos agora que B! − Q e que ?" ß á ß ?:" − XB! ÐQ Ñ. Podemos
então considerar campos vectoriais suaves \" ß á ß \:" , com \4 B! œ ?4
(tomar, por exemplo, \4 B œ 1B Ð?4 Ñ). Vamos mostrar que, quaisquer que
sejam os \4 nestas condições, e qualquer que seja a aplicação suave
= œ (=B ÑB−Q , de Q em E: ÐIà ŠÑ, com cada =B restrição de =B , tem-se
" Ð"Ñ4" H=B! Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ œ
:"
4œ"
œ " Ð"Ñ4" HÐ=Ð\" ß á ß \s4 ß ß á ß \:" ÑÑB! Ð?4 Ñ
:"
4œ"
œ " Ð"Ñ45 =B! ÐÒ\4 ß \5 ÓB! ß ?" ß á ß ?s4 ß á ß ?s5 ß á ß ?:" Ñ;
45
Se o fizermos, ficará provado que o segundo membro da primeira igualdade
do enunciado não depende da escolha de =, o que nos dá um elemento bem
18Neste
enunciado, como em várias ocasiões adiante, aparecem expressões em que
figuram os elementos de uma certa sucessão indexada de " a 8, com a excepção de um ou
mais. Uma convenção que se utiliza com frequência e que se revela mais económica no
que diz respeito ao comprimento das expressões escritas, consiste em escrever com um
“s” em cima dos termos que são omitidos. Assim, por exemplo, em vez de
H=B Ð?4 ÑÐ?" ß á ß ?4" ß ?4" ß á ß ?:" Ñ,
podemos escrever
H=B Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ.
§2. Derivada exterior duma forma diferencial
109
definido Ð. =ÑB! − P: ÐXB! ÐQ Ñà ŠÑ, e ao mesmo tempo ficará demonstrada a
segunda igualdade do enunciado19. Ora, vem
" Ð"Ñ4" HÐ=Ð\" ß á ß \s4 ß ß á ß \:" ÑÑB! Ð?4 Ñ œ
:"
4œ"
œ " Ð"Ñ4" HÐ=Ð\" ß á ß \s4 ß ß á ß \:" ÑÑB! Ð?4 Ñ œ
:"
4œ"
œ " Ð"Ñ4" H=B! Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ
:"
4œ"
œ " Ð"Ñ4" " =B! Ð?" ß á ß ?5" ß H\5 B! Ð?4 Ñß ?5" ß á ß ?s4 ß á ß ?:" Ñ
:"
4œ"
54
œ " Ð"Ñ4" " =B! Ð?" ß á ß ?s4 ß á ß ?5" ß H\5 B! Ð?4 Ñß ?5" ß á ß ?:" Ñ œ
:"
4œ"
54
œ " Ð"Ñ4" H=B! Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ
:"
4œ"
œ " Ð"Ñ4" Ð"Ñ5" =B! ÐH\5 B! Ð?4 Ñß ?" ß á ß ?s5 ß á ß ?s4 ß á ß ?:" Ñ
54
œ " Ð"Ñ4" Ð"Ñ5# =B! ÐH\5 B! Ð?4 Ñß ?" ß á ß ?s4 ß á ß ?s5 ß á ß ?:" Ñ.
54
Trocando no penúltimo somatório os índices 4 e 5 , podemos portanto
escrever
" Ð"Ñ4" HÐ=Ð\" ß á ß \s4 ß ß á ß \:" ÑÑB! Ð?4 Ñ œ
:"
4œ"
œ " Ð"Ñ4" H=B! Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ
:"
4œ"
œ " Ð"Ñ45 =B! ÐH\5 B! Ð?4 Ñ H\4 B! Ð?5 Ñß ?" ß á ß ?s4 ß á ß ?s5 ß á ß ?:" Ñ œ
45
œ " Ð"Ñ4" H=B! Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ
:"
4œ"
œ " Ð"Ñ45 =B! ÐÒ\4 ß \5 ÓB! ß ?" ß á ß ?s4 ß á ß ?s5 ß á ß ?:" Ñ,
45
o que estabelece a igualdade pretendida. Resta-nos agora verificar que, para
19O
raciocínio aqui é aquele que leva a concluir que, se tivermos duas aplicações
0 À E Ä G e 1À F Ä G tais que, quaisquer que sejam B − E e C − F , 0 ÐBÑ œ 1ÐCÑ, então
0 e 1 são constantes e com um valor constante comum.
110
Cap. III. Formas diferenciais e teorema de Stokes
cada B! − Q , a aplicação multilinear Ð. =ÑB! − P: ÐXB! ÐQ Ñà ŠÑ, definida pela
primeira igualdade do enunciado, pertence mesmo a E: ÐXB! ÐQ Ñà ŠÑ. Ora,
considerando o elemento
H=B! − PÐXB! ÐQ Ñà E: ÐIà ŠÑÑ,
podemos notar 3 o elemento de P:" ÐXB! ÐQ Ñà ŠÑ, definido por
3Ð?" ß á ß ?:" Ñ œ H=B! Ð?" ÑÐ?# ß á ß ?:" Ñ,
elemento esse que é portanto alternado nas últimas : variáveis, pelo que,
tendo em conta o lema II.5.11, concluímos que
Ð. =ÑB! œ Ð: "Ñ AltÐ3Ñ,
em particular Ð. =ÑB! é alternado.
III.2.3. Tal como se disse em III.1.4, há duas situações em que, nas condições
anteriores, o prolongamento = é único, e coincide com o próprio =:
a) A primeira situação é aquela em que : œ !; a forma diferencial de grau ! é
simplesmente uma aplicação suave 0 À Q Ä Š e a identidade que nos serviu
para definir .= escreve-se simplesmente
.0B Ð?Ñ œ H0B Ð?Ñ,
por outras palavras a forma diferencial de grau ", com valores em Š, .0 , não
é mais do que a forma diferencial H0 , referida em III.1.22.
b) A segunda situação é aquela em que, para cada B − Q , XB ÐQ Ñ œ I ; é o
que acontece no caso em que Q é um aberto de I ou, mais geralmente, uma
variedade, possivelmente com bordo, com dimensão em cada ponto igual à
de I . Nesse caso a fórmula de definição escreve-se simplesmente
Ð. =ÑB Ð?" ß á ß ?:" Ñ œ
œ " Ð"Ñ4" H=B Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ.
:"
4œ"
III.2.4. (Lema) Sejam Q § I uma variedade e = œ Ð=B ÑB−Q uma forma
diferencial suave de grau :, real ou complexa. Existe então um aberto Y de
I , com Q § Y , e uma forma diferencial suave =˜ œ Ð=˜B ÑB−Y , de grau :, tal
que = œ =˜ÎQ (restrição enquanto forma diferencial, cf. III.1.12). Além disso,
qualquer que seja =˜ nestas condições, tem-se que . = œ Ð. =˜ÑÎQ .
Dem: Trata-se de um resultado essencialmente trivial, que resulta de notar
que dizer que =˜ é uma forma diferencial sobre um aberto Y de I , contendo
Q , tal que =˜ÎQ œ =, é o mesmo que dizer que =˜ é um prolongamento suave
a Y de uma aplicação suave = œ Ð=B ÑB−Q , de Q em E: ÐIà ŠÑ, tal que cada
=B seja uma restrição de =B .
§2. Derivada exterior duma forma diferencial
111
O lema anterior permite reduzir de forma trivial a demonstração de várias
propriedades da derivação exterior ao caso em que as formas diferenciais
estão definidas num aberto de I , quadro em que é desnecessário
considerar prolongamentos para as formas diferenciais. Como primeiro
exemplo, temos:
III.2.5. Sejam Q § I uma variedade e = œ Ð=B ÑB−Q uma forma diferencial
suave de grau :, real ou complexa. Tem-se então que a forma diferencial .=,
de grau : ", é também suave.
Dem: Tendo em conta o resultado anterior, basta demonstrar isto no caso
particular em que Q é um aberto de I . Nesse caso, = é simplesmente uma
aplicação suave de Q em E: ÐIà ŠÑ, a partir da qual obtemos uma aplicação
suave H=À Q Ä PÐIà E: ÐIà ŠÑÑ. Compondo H= com o isomorfismo canónico de PÐIà P: ÐIà ŠÑÑ sobre P:" ÐIà ŠÑ e com a aplicação linear de
P:" ÐIà ŠÑ em P:" ÐIà ŠÑ, que a cada - associa a aplicação multilinear
definida por
Ð?" ß á ß ?:" Ñ È " Ð"Ñ4" -Ð?4 ß ?" ß á ß ?s4 ß á ß ?:" Ñ,
:"
4œ"
obtemos precisamente a forma diferencial .=, o que mostra que esta é
suave.
III.2.6. Sejam Q § I uma variedade, = œ Ð=B ÑB−Q e 5 œ Ð5B ÑB−Q duas
formas diferenciais suaves de grau :, com valores em Š e + − Š. Tem-se
então
.Ð= 5 Ñ œ . = . 5 ,
.Ð+ =Ñ œ + . =.
Dem: Como anteriormente, podemos reduzir-nos ao caso em que Q é um
aberto de I e nesse caso a demonstração é trivial.
s §I
s e Q § I duas variedades e 0 À Q
s Ä Q uma aplicação
III.2.7. Sejam Q
suave. Se = œ Ð=C ÑC−Q é uma forma diferencial de grau :, sobre Q , com
valores em Š, tem-se então
.Ð0 ‡ =Ñ œ 0 ‡ Ð. =Ñ.
se
Dem: Comecemos por demonstrar o resultado no caso particular em que Q
s e de I , respectivamente. Uma vez que
Q são abertos de I
Ð. =ÑC ÐA" ß á ß A:" Ñ œ " Ð"Ñ4" H=C ÐA4 ÑÐA" ß á ß As4 ß á ß A:" Ñ,
4
podemos escrever
112
Cap. III. Formas diferenciais e teorema de Stokes
Ð0 ‡ Ð. =ÑÑB Ð?" ß á ß ?:" Ñ œ Ð. =Ñ0 ÐBÑ ÐH0B Ð?" Ñß á ß H0B Ð?:" ÑÑ œ
s
œ " Ð"Ñ4" H=0 ÐBÑ ÐH0B Ð?4 ÑÑÐH0B Ð?" Ñß á ß H0B Ð?4 Ñß á ß H0B Ð?:" ÑÑ.
4
Por outro lado,
Ð.Ð0 ‡ =ÑÑB Ð?" ß á ß ?:" Ñ œ " Ð"Ñ4" HÐ0 ‡ =ÑB Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ œ
4
œ " Ð"Ñ4" HÐÐ0 ‡ =ÑÐ?" ß á ß ?s4 ß á ß ?:" ÑÑB Ð?4 Ñ,
4
pelo que, uma vez que
Ð0 ‡ =ÑB Ð?" ß á ß ?s4 ß á ß ?:" Ñ œ
s
œ =0 ÐBÑ ÐH0B Ð?" Ñß á ß H0B Ð?4 Ñß á ß H0B Ð?:" ÑÑ,
podemos escrever
Ð.Ð0 ‡ =ÑÑB Ð?" ß á ß ?:" Ñ œ
s
œ " Ð"Ñ4" H=0 ÐBÑ ÐH0B Ð?4 ÑÑÐH0B Ð?" Ñß á ß H0B Ð?4 Ñß á ß H0B Ð?:" ÑÑ
4
s
" Ð"Ñ4" " =0 ÐBÑ ÐH0B Ð?" Ñß á ß H# 0B Ð?4 ß ?5 Ñß á ß H0B Ð?4 Ñß á ß H0B Ð?:" ÑÑ
4
" Ð"Ñ
4"
4
54
" =0 ÐBÑ ÐH0B Ð?" Ñß á ß H0BsÐ?4 Ñß á ß H# 0B Ð?4 ß ?5 Ñß á ß H0B Ð?:" ÑÑ œ
54
s
œ " Ð"Ñ4" H=0 ÐBÑ ÐH0B Ð?4 ÑÑÐH0B Ð?" Ñß á ß H0B Ð?4 Ñß á ß H0B Ð?:" ÑÑ
4
s
s
" Ð"Ñ45# =0 ÐBÑ ÐH# 0B Ð?4 ß ?5 Ñß H0B Ð?" Ñß á ß H0B Ð?5 Ñß á ß H0B Ð?4 Ñß á ß H0B Ð?:" ÑÑ
54
s
s
" Ð"Ñ45$ =0 ÐBÑ ÐH# 0B Ð?4 ß ?5 Ñß H0B Ð?" Ñß á ß H0B Ð?4 Ñß á ß H0B Ð?5 Ñß á ß H0B Ð?:" ÑÑ.
54
Trocando 4 com 5 no último somatório, e tendo em conta o facto de H# 0B ser
uma aplicação bilinear simétrica, constatamos que os dois últimos somatórios
são simétricos um do outro pelo que, comparando com a fórmula para
Ð0 ‡ Ð. =ÑÑB Ð?" ß á ß ?:" Ñ obtida acima, temos o resultado demonstrado neste
s e Q são variedades
caso particular. Passemos agora ao caso geral em que Q
quaisquer. Podemos então começar por considerar um aberto Z de I , com
Q § Z , e uma forma diferencial suave =˜, de grau :, sobre Z , tal que
s , com Q
s § Y , e 0˜ À Y Ä I um
= œ =˜ÎQ . Sejam Y um aberto de I
prolongamento suave da aplicação 0 . A continuidade de 0˜ mostra-nos que, se
necessário substituindo Y por um aberto mais pequeno e 0˜ pela sua restrição,
pode-se já supor que 0̃ ÐY Ñ § Z . O caso particular já demonstrado
‡
‡
garante-nos que .Ð0˜ =˜Ñ œ 0˜ Ð. =˜Ñ e basta agora repararmos que, por um
§2. Derivada exterior duma forma diferencial
113
‡
s (trivial ou, se preferirmos, podemos
lado, 0 ‡ = é a restrição de 0˜ =˜ a Q
reparar que a restrição é a mesma coisa que a imagem recíproca pela
‡
s
inclusão), e portanto, pelo lema III.2.4, .Ð0 ‡ =Ñ é a restrição de .Ð0˜ =˜Ñ a Q
‡
e, por outro lado, . = é a restrição de . =˜ a Q e portanto 0 Ð. =Ñ é a restrição
‡
s .
de 0˜ Ð. =˜Ñ a Q
III.2.8. Sejam Q § I uma variedade e = œ Ð=B ÑB−Q uma forma diferencial
suave de grau :. Tem-se então .Ð. =Ñ œ !.
Dem: Como anteriormente, é suficiente fazer a demonstração no caso
particular em que Q é um aberto de I . Podemos então escrever
Ð.Ð. =ÑÑB Ð?" ß á ß ?:# Ñ œ
œ " Ð"Ñ4" HÐ. =ÑB Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:# Ñ œ
:#
4œ"
œ " Ð"Ñ4" HÐ. =Ð?" ß á ß ?s4 ß á ß ?:# ÑÑB Ð?4 Ñ.
:#
4œ"
Uma vez que se tem
Ð. =ÑB Ð?" ß á ß ?s4 ß á ß ?:# Ñ œ
œ " Ð"Ñ5" H=B Ð?5 ÑÐ?" ß á ß ?s5 ß á ß ?s4 ß á ß ?:# Ñ
54
œ " Ð"Ñ5# H=B Ð?5 ÑÐ?" ß á ß ?s4 ß á ß ?s5 ß á ß ?:# Ñ,
54
obtemos agora
Ð.Ð. =ÑÑB Ð?" ß á ß ?:# Ñ œ
œ " Ð"Ñ45# H# =B Ð?4 ß ?5 ÑÐ?" ß á ß ?s5 ß á ß ?s4 ß á ß ?:# Ñ
54
œ " Ð"Ñ45$ H# =B Ð?4 ß ?5 ÑÐ?" ß á ß ?s4 ß á ß ?s5 ß á ß ?:# Ñ œ !,
54
visto que os dois somatórios são simétricos um do outro, como se reconhece
se trocarmos 4 com 5 no segundo somatório e repararmos que H# =B é uma
aplicação bilinear simétrica.
Vamos agora estabelecer uma fórmula, do tipo regra de Leibnitz, para a
derivada exterior do produto exterior de duas formas diferenciais.
Começamos, para isso, com um lema, em que a primeira forma diferencial
tem grau !, isto é, é uma função.
114
Cap. III. Formas diferenciais e teorema de Stokes
III.2.9. (Lema) Sejam Q § I uma variedade, = œ Ð=B ÑB−Q uma forma
diferencial suave de grau :, com valores em Š, e 0 À Q Ä Š uma aplicação
suave. Tem-se então, para a forma diferencial suave 0 = œ 0 • =,
.Ð0 =Ñ œ 0 . = Ð.0 Ñ • =.
Dem: Como habitualmente, podemo-nos reduzir ao caso em que Q é um
aberto de I . Obtemos então
Ð.Ð0 =ÑÑB Ð?" ß á ß ?:" Ñ œ
œ " Ð"Ñ4" HÐ0 =ÑB Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ œ
4
œ 0B " Ð"Ñ4" H=B Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ
4
œ " Ð"Ñ4" H0B Ð?4 Ñ =B Ð?" ß á ß ?s4 ß á ß ?:" Ñ œ
4
œ Ð0 . =ÑB Ð?" ß á ß ?s4 ß á ß ?:" Ñ Ð.0 • =ÑB Ð?" ß á ß ?s4 ß á ß ?:" Ñ,
onde, para a interpretação do último somatório, tivémos em conta a caracterização do produto exterior referida em II.5.12.
III.2.10. Sejam Q § I uma variedade e = œ Ð=B ÑB−Q e 5 œ Ð5B ÑB−Q duas
formas diferenciais suaves, de graus : e ; , respectivamente, com valores em
Š. Tem-se então
.Ð= • 5 Ñ œ Ð. =Ñ • 5 Ð"Ñ: = • Ð. 5 Ñ.
Dem: Mais uma vez, basta demonstrar o resultado no caso particular em que
Q é um aberto de I . Fixando uma base A" ß á ß A8 de I , sabemos que, para
cada B − Q , =B − E: ÐIà ŠÑ e 5B − E; ÐIà ŠÑ se decompôem nas bases
associadas daqueles espaços:
=B œ " =B ÐA4" ß á ß A4: Ñ 0•4" ßáß4: ,
4" â4:
5B œ " 5B ÐA5" ß á ß A5: Ñ 0•5" ßáß5: .
5" â5;
O que nos interessa da decomposição anterior é saber que existem conjuntos
finitos de índices, E e F , e, para cada ! − E e " − F , formas diferenciais
constantes -+ , de grau :, e ." , de grau ; (portanto, trivialmente, com
. -! œ ! e . ." œ !), e aplicações suaves 0! À Q Ä Š e 1" À Q Ä Š, de
modo que se tenha
= œ " 0! -! ,
!
5 œ " 1" . " .
"
Tendo em conta o lema precedente, a propriedade algébrica de ±-comutativi-
§2. Derivada exterior duma forma diferencial
115
dade do produto exterior e a regra de Leibnitz para a derivação do produto de
duas funções, podemos agora escrever
.Ð= • 5 Ñ œ .Ð" 0! 1" Ð-+ • ." Ñ œ " .Ð0! 1" Ñ • -! • ." œ blablabla
!ß "
!ß "
œ " 0! .1" • -! • ." " 1" .0! • -! • ." œ
!ß "
!ß "
œ Ð"Ñ: " Ð0! -! Ñ • Ð.1" • ." Ñ " Ð.0! • -! Ñ • Ð1" ." Ñ œ
!ß "
!ß "
œ Ð "Ñ: Ð" 0! -! Ñ • Ð" .1" • ." Ñ Ð" .0! • -! Ñ • Ð" 1" ." Ñ œ
!
"
!
"
œ Ð "Ñ: = • Ð. 5 Ñ Ð. =Ñ • 5,
donde o resultado.
Vamos agora verificar como o operador de diferenciação exterior .
intervém na definição dos operadores clássicos do cálculo vectorial. Um
primeiro exemplo disso foi já apresentado, quando nos referimos em
III.1.23 à definição do gradiente duma função suave, com valores reais.
III.2.11. Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 " que, para simplificar, suporemos suavemente orientada. Dado um
campo vectorial suave \ œ Ð\B ÑB−Q , define-se então uma aplicação suave
divÐ\ÑÀ Q Ä ‘, chamada divergência de \ , por
divÐ\Ñ œ ‡Ð.Ї)Ð\ÑÑÑ.20
A razão por que exigimos que a variedade Q estivesse suavemente
orientada foi para podermos utilizar os operadores ‡. No entanto, uma vez
que estes aparecem duas vezes na definição e que eles vêm multiplicados
por " quando se troca a orientação de um espaço euclidiano,
constatamos que, se trocássemos a orientação em todos os espaços
vectoriais tangentes, o operador de divergência obtido não se alterava.
Raciocinando na vizinhança de cada ponto de Q , poderíamos concluir
que a definição da divergência é independente da orientação suave que se
considera em Q e poderia mesmo ser dada para uma variedade que não
admitisse nenhuma orientação suave (localmente todas as variedades são
orientáveis). Não detalhamos mais estas observações para não tornar o
texto mais pesado, mas o leitor poderá facilmente fazê-lo.
20Repare-se
que )Ð\Ñ é uma forma diferencial real suave de grau " pelo que ‡)Ð\Ñ é
uma forma diferencial suave de grau 7 ", .Ї)Ð\ÑÑ é uma forma diferencial suave de
grau 7 e, finalmente, ‡Ð.Ї)Ð\ÑÑÑ é uma forma diferencial suave de grau !, isto é, uma
aplicação suave Q Ä ‘.
116
Cap. III. Formas diferenciais e teorema de Stokes
III.2.12. Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 " que, mais uma vez para simplificar, suporemos suavemente orientada.
Se 0 À Q Ä Š é uma aplicação suave, define-se o seu laplaciano como sendo
a aplicação suave ?0 À Q Ä Š,
?0 œ ‡.Ї.0 Ñ.21
Repare-se que, no caso particular em que Š œ ‘, tem-se .0 œ )ÐgradÐ0 ÑÑ
pelo que a definição anterior pode ser reescrita na forma
?0 œ divÐgradÐ0 ÑÑ.
III.2.13. Sejam I um espaço euclidiano e Q § I uma variedade de dimensão $
suavemente orientada. Se \ œ Ð\B ÑB−Q é um campo vectorial suave sobre
Q , define-se o seu rotacional rotÐ\Ñ como sendo o campo vectorial suave
rotÐ\Ñ œ )" Ї.Ð)Ð\ÑÑÑ.22
Vamos agora apresentar fórmulas alternativas para os operadores
diferenciais que estudámos atrás, no caso particular em que a variedade
Q é um aberto de I ou, mais geralmente, tem dimensão igual à de I em
todos os pontos. Isso permitir-nos-á, em particular, reconhecer as definições destes operadores, porventura já encontradas no quadro do Cálculo
Vectorial clássico. Com frequência, o espaço euclidiano I , a que nos
referiremos, será ‘7 e a base ortonormada considerada será a base
canónica. Nesse caso, as derivadas duma função na direcção dos vectores
da base serão evidentemente as derivadas parciais usuais.
III.2.14. Sejam I um espaço euclidiano, com uma base ortonormada
A" ß á ß A7 , e Q § I um aberto ou, mais geralmente, uma variedade com
dimensão 7 em cada ponto. Seja 0 À Q Ä Š uma aplicação suave. Tem-se
então, para cada B − Q ,
.0B œ " H0B ÐA4 Ñ )ÐA4 Ñ
7
4œ"
e, no caso em que Š œ ‘,
21Repare-se
que .0 é uma forma diferencial suave de grau ", com valores em Š, pelo que
‡.0 é uma forma diferencial suave de grau 7 "ß .Ї.0 Ñ é uma forma diferencial suave
de grau 7 e, finalmente, ‡.Ї.0 Ñ é uma forma diferencial de grau !, isto é, uma
aplicação suave Q Ä Š.
22Ao contrário do que sucedia com a divergência e o laplaciano, a orientação de Q é
essencial para a definição do rotacional. Repare-se que )Ð\Ñ é uma forma diferencial
suave de grau ", pelo que .Ð)Ð\ÑÑ é uma forma diferncial suave de grau #, ‡.Ð)Ð\ÑÑ é
uma forma diferencial suave de grau $ # œ " e, finalmente, )" Ї.Ð)Ð\ÑÑÑ é um
campo vectorial suave sobre Q .
§2. Derivada exterior duma forma diferencial
117
gradÐ0 ÑB œ " H0B ÐA4 Ñ A4 .
7
4œ"
Em particular, no caso em que I œ ‘7 e A" ß á ß A7 é a base canónica,
podemos escrever, respectivamente,
.0B œ "
7
4œ"
`0
ÐBÑ )ÐA4 Ñ,
`B4
gradÐ0 ÑB œ Ð
`0
`0
ÐBÑß á ß
ÐBÑÑ.
`B"
`B7
Dem: Uma vez que a base é ortonormada, sabemos que os )ÐA4 Ñ são os
elementos da base de PÐIà ŠÑ associada à base A" ß á ß A7 de I pelo que,
uma vez que .0B ÐA4 Ñ œ H0B ÐA4 Ñ, a primeira fórmula é simplesmente um
caso particular de II.2.5. A segunda fórmula resulta da primeira por aplicação
do isomorfismo )" a ambos os membros desta.
III.2.15. (Nota) Ainda no caso em que I œ ‘7 e a base considerada é a
canónica, é costume usar as notações .B" ß á ß .B7 em vez de
)ÐA" Ñß á ß )ÐA7 Ñ. Estas notações, cujas motivações seria longo discutir,
podem ser justificadas no quadro anterior desde que olhemos para cada B4
como sendo a aplicação linear que a cada B − ‘7 associa a sua componente
de ordem 4, visto que o respectivo diferencial .B4 é então igual, em cada
ponto, a )ÐA4 Ñ. Com estas notações pode-se portanto escrever a fórmula
clássica
.0B œ "
7
4œ"
`0
ÐBÑ .B4 .
`B4
No caso em que 7 é pequeno usam-se formulações particulares como, no
caso de ‘$ ,
.0 œ
`0
`0
`0
.B
.C
.D .
`B
`C
`D
III.2.16. Seja I um espaço euclidiano, com dimensão 7 ", com uma base
ortonormada A" ß á ß A7 , e seja Q § I um aberto ou, mais geralmente, uma
variedade com dimensão 7 em cada ponto. Seja \ œ Ð\B ÑB−Q um campo
vectorial suave sobre Q e sejam 04 À Q Ä ‘ as funções suaves componentes
de \ , definidas por \B œ ! 04 ÐBÑ A4 . Considerando então em Q a
orientação associada a uma das orientações de I , tem-se
divÐ\ÑB œ " H04 B ÐA4 Ñ.
7
4œ"
118
Cap. III. Formas diferenciais e teorema de Stokes
Em particular, no caso em que I œ ‘7 , sendo \B œ Ð0" ÐBÑß á ß 07 ÐBÑÑ,
vem
divÐ\ÑB œ "
7
4œ"
`04
ÐBÑ.
`B4
Dem: Seja & − Ö"ß "× a orientação da base A" ß á ß A7 de I e
consideremos em Q a orientação suave correspondente (lembrar que
XB ÐQ Ñ œ I , para cada B − Q ). Uma vez que )ÐA" Ñß á ß )ÐA7 Ñ é a base de
PÐIà ‘Ñ associada à base ortonormada A" ß á ß A7 de I , vemos que
‡)Ð\B Ñ œ " 04 ÐBÑ ‡)ÐA4 Ñ œ
7
4œ"
7
s
œ " & Ð"Ñ4" 04 ÐBÑ )ÐA" Ñ • â • )ÐA4 Ñ • â • )ÐA7 Ñ,
4œ"
donde
s
.Ї)Ð\ÑÑB œ " & Ð"Ñ4" .04 B • )ÐA" Ñ • â • )ÐA4 Ñ • â • ) ÐA7 Ñ œ
7
4œ"
s
œ " & Ð"Ñ4" " H04 B ÐA5 Ñ )ÐA5 Ñ • )ÐA" Ñ • â • )ÐA4 Ñ • â • )ÐA7 Ñ œ
7
7
4œ"
7
5œ"
s
œ " & Ð"Ñ4" H04 B ÐA4 Ñ )ÐA4 Ñ • )ÐA" Ñ • â • )ÐA4 Ñ • â • )ÐA7 Ñ œ
4œ"
7
7
4œ"
4œ"
œ " & H04 B ÐA4 Ñ )ÐA" Ñ • â • )ÐA4 Ñ œ Ð" H04 B ÐA4 ÑÑ Z 96I ,
o que implica finalmente que
divÐ\ÑB œ ‡.Ї)Ð\ÑÑB œ " H04 B ÐA4 Ñ.
7
4œ"
III.2.17. Seja I um espaço euclidiano, com dimensão 7 ", com uma base
ortonormada A" ß á ß A7 , e seja Q § I um aberto ou, mais geralmente, uma
variedade com dimensão 7 em cada ponto. Seja 0 À Q Ä Š uma aplicação
suave. Considerando então em Q a orientação associada a uma das
orientações de I , tem-se
?0B œ " H# 0B ÐA4 ß A4 Ñ.
7
4œ"
Em particular, no caso em que I œ ‘7 , tem-se
§2. Derivada exterior duma forma diferencial
?0B œ "
7
4œ"
119
` #0
ÐBÑ.23
`B4 `B4
Dem: No caso em que Š œ ‘, o resultado é uma consequência imediata de
III.2.14 e de III.2.16. Para o caso geral, tudo o que temos que fazer é unir as
respectivas demonstrações e fazer um pequeno curto-circuito: Notemos,
como anteriormente, & − Ö"ß "× a orientação da base A" ß á ß A7 . Uma vez
que .0B œ ! H0B ÐA4 Ñ )ÐA4 Ñ, obtemos
‡.0B œ " H0B ÐA4 Ñ ‡)ÐA4 Ñ œ
7
4œ"
7
s
œ " & Ð"Ñ4" H0B ÐA4 Ñ )ÐA" Ñ • â • )ÐA4 Ñ • â • )ÐA7 Ñ
4œ"
donde
.Ї.0 ÑB œ
s
œ " & Ð"Ñ4" " H# 0B ÐA5 ß A4 Ñ )ÐA5 Ñ • )ÐA" Ñ • â • )ÐA4 Ñ • â • )ÐA7 Ñ œ
7
7
4œ"
7
5œ"
s
œ " & Ð"Ñ4" H# 0B ÐA4 ß A4 Ñ )ÐA4 Ñ • )ÐA" Ñ • â • )ÐA4 Ñ • â • )ÐA7 Ñ œ
4œ"
7
7
4œ"
4œ"
œ " & H# 0B ÐA4 ß A4 Ñ )ÐA" Ñ • â • )ÐA7 Ñ œ " H# 0B ÐA4 ß A4 Ñ Z 96I ,
?0B œ ‡.Ї.0 ÑB œ " H# 0B ÐA4 ß A4 Ñ.
7
4œ"
III.2.18. Seja I um espaço euclidiano orientado de dimensão $, com uma base
ortonormada directa A" ß A# ß A$ , e seja Q § I um aberto ou, mais
geralmente, uma variedade com dimensão $ em cada ponto. Seja
\ œ Ð\B ÑB−Q um campo vectorial suave e sejam 0" ß 0# ß 0$ À Q Ä ‘ as
aplicações suaves componentes de \ , definidas por
\B œ 0" ÐBÑ A" 0# ÐBÑ A# 0$ ÐBÑ A$ .
Tem-se então, para cada B − Q ,
23A
definição de derivada de segunda ordem de uma função num ponto costuma por
vezes ser apresentada apenas no caso em que o domínio da função é um conjunto aberto.
É no entanto imediato constatar-se que essa definição faz perfeitamente sentido no caso
mais geral em que o domínio é total, no sentido que o espaço vectorial tangente a este em
cada um dos seus pontos é o espaço todo, visto que isso garante que a primeira derivada é
uma aplicação suave com valores num espaço vectorial fixado.
120
Cap. III. Formas diferenciais e teorema de Stokes
rotÐ\ÑB œ ÐH0$ B ÐA# Ñ H0# B ÐA$ ÑÑ A" ÐH0" B ÐA$ Ñ H0$ B ÐA" ÑÑ A#
ÐH0# B ÐA" Ñ H0" B ÐA# ÑÑ A$ .
Em particular, no caso em que I œ ‘$ , sendo \B œ Ð0" ÐBÑß 0# ÐBÑß 0$ ÐBÑÑ,
tem-se
rotÐ\Ñ œ Ð
`0$
`0# `0"
`0$ `0#
`0"
ß
ß
Ñ.
`B#
`B$ `B$
`B" `B"
`B#
Dem: Vem
)Ð\B Ñ œ 0" ÐBÑ )ÐA" Ñ 0# ÐBÑ )ÐA# Ñ 0$ ÐBÑ )ÐA$ Ñ,
pelo que
.Ð)Ð\ÑÑB œ " H0" B ÐA4 Ñ )ÐA4 Ñ • )ÐA" Ñ " H0# B ÐA4 Ñ )ÐA4 Ñ • ) ÐA# Ñ
$
$
4œ"
4œ"
œ " H0$ B ÐA4 Ñ )ÐA4 Ñ • )ÐA$ Ñ œ
$
4œ"
œ H0" B ÐA# Ñ )ÐA# Ñ • )ÐA" Ñ H0" B ÐA$ Ñ )ÐA$ Ñ • )ÐA" Ñ
œ H0# B ÐA" Ñ )ÐA" Ñ • )ÐA# Ñ H0# B ÐA$ Ñ )ÐA$ Ñ • )ÐA# Ñ
œ H0$ B ÐA" Ñ )ÐA" Ñ • )ÐA$ Ñ H0$ B ÐA# Ñ )ÐA# Ñ • )ÐA$ Ñ œ
œ ÐH0# B ÐA" Ñ H0" B ÐA# ÑÑ )ÐA" Ñ • )ÐA# Ñ
œ ÐH0" B ÐA$ Ñ H0$ B ÐA" ÑÑ )ÐA" Ñ • )ÐA$ Ñ
œ ÐH0$ B ÐA# Ñ H0# B ÐA$ ÑÑ )ÐA# Ñ • )ÐA$ Ñ
e daqui resulta a conclusão pretendida tendo em conta a caracterização do
rotacional em III.2.13 e o facto de se ter
‡Ð)ÐA" Ñ • )ÐA# ÑÑ œ sgÐÖ"ß #×Ñ )ÐA$ Ñ œ )ÐA$ Ñ,
‡Ð)ÐA" Ñ • )ÐA$ ÑÑ œ sgÐÖ"ß $×Ñ )ÐA# Ñ œ )ÐA# Ñ,
‡Ð)ÐA# Ñ • )ÐA$ ÑÑ œ sgÐÖ#ß $×Ñ )ÐA" Ñ œ )ÐA" Ñ.
§3. Derivada de Lie duma forma diferencial.
III.3.1. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q um campo vectorial suave
e 0 œ Ð0B ÑB−Q um campo tensorial suave de grau :, com valores em Š.
Existe então um, e um só, campo tensorial _\ Ð0Ñ, de grau : e com valores
em Š, a que se dá o nome de derivada de Lie de 0 na direcção de \ , tal que,
qualquer que seja a aplicação suave 0 œ Ð0B ÑB−Q , de Q em P: ÐIà ŠÑ, com
cada 0B restrição de 0B , se tenha
§3. Derivada de Lie duma forma diferencial
121
_\ Ð0ÑB Ð?" ß á ß ?: Ñ œ H0B Ð\B ÑÐ?" ß á ß ?: Ñ
" 0B Ð?" ß á ß ?4" ß H\B Ð?4 Ñß ?4" ß á ß ?: Ñ.
:
4œ"
Além disso, se, para cada " Ÿ 4 Ÿ :, \4 œ Ð\4 B ÑB−Q é um campo vectorial
suave sobre Q , tem-se
_\ Ð0ÑÐ\" ß á ß \7 Ñ œ HÐ0Ð\" ß á ß \7 ÑÑÐ\Ñ
" 0Ð\" ß á ß \4" ß Ò\ß \4 Óß \4" ß á ß \: Ñ.
:
4œ"
Dem: A demonstração tem o mesmo espírito que a de III.2.2. Começamos
por notar que a unicidade de um campo tensorial _\ Ð0Ñ, verificando a
condição do enunciado, resulta da existência de pelo menos uma aplicação
suave 0, de Q em P: ÐIà ŠÑ, tal que cada 0B seja uma restrição de 0B .
Suponhamos agora que B! − Q e que ?" ß á ß ?: − XB! ÐQ Ñ. Podemos então
considerar, tal como na demonstração referida, campos vectoriais suaves
\" ß á ß \: , com \4 B! œ ?4 e vamos mostrar que, quaisquer que sejam os \4
nestas condições, e qualquer que seja a aplicação suave 0 œ Ð0B ÑB−Q , de Q
em P: ÐIà ŠÑ, com cada 0B restrição de 0B , tem-se
H0B! Ð\B! ÑÐ?" ß á ß ?: Ñ " 0B! Ð?" ß á ß H\B! Ð?4 Ñß á ß ?: Ñ œ
:
4œ"
œ HÐ0Ð\" ß á ß \: ÑÑB! Ð\B! Ñ " 0B! Ð?" ß á ß Ò\ß \4 ÓB! ß á ß ?: Ñ;
:
4œ"
Se o fizermos, ficará provado que o segundo membro da primeira igualdade
do enunciado não depende da escolha de 0, o que nos dá um elemento bem
definido _\ Ð0ÑB! − P: ÐXB! ÐQ Ñà ŠÑ, e ao mesmo tempo ficará demonstrada a
segunda igualdade do enunciado. Ora, vem
HÐ0Ð\" ß á ß \: ÑÑB! Ð\B! Ñ œ HÐ0Ð\" ß á ß \: ÑÑB! Ð\B! Ñ œ
œ H0B! Ð\B! ÑÐ?" ß á ß ?: Ñ " 0B! Ð?" ß á ß H\4 B! Ð\B! Ñß á ß ?: Ñ œ
:
4œ"
:
œ H0B! Ð\B! ÑÐ?" ß á ß ?: Ñ " 0B! Ð?" ß á ß H\4 B! Ð\B! Ñ H\B! Ð\4 B! Ñß á ß ?: Ñ
4œ"
:
" 0B! Ð?" ß á ß H\B! Ð?4 Ñß á ß ?: Ñ œ
4œ"
122
Cap. III. Formas diferenciais e teorema de Stokes
œ H0B! Ð\B! ÑÐ?" ß á ß ?: Ñ " 0B! Ð?" ß á ß Ò\ß \4 ÓB! ß á ß ?: Ñ blablblablablabla
:
4œ"
" 0B! Ð?" ß á ß H\B! Ð?4 Ñß á ß ?: Ñ,
:
4œ"
o que termina a demonstração.
III.3.2. Tal como se disse em III.1.4, há duas situações em que, nas condições
anteriores, o prolongamento 0 é único, e coincide com o próprio 0:
a) A primeira situação é aquela em que : œ !; o campo tensorial de grau ! é
simplesmente uma aplicação suave 0 À Q Ä Š e a identidade que nos serviu
para definir _\ Ð0Ñ escreve-se simplesmente
_\ Ð0 ÑB œ H0B Ð\B Ñ,
por outras palavras, a derivada de Lie de 0 na direcção de \ não é mais do
que a derivada usual de 0 , aplicada a \ .
b) A segunda situação é aquela em que, para cada B − Q , XB ÐQ Ñ œ I ; é o
que acontece no caso em que Q é um aberto de I ou, mais geralmente, uma
variedade, possivelmente com bordo, com dimensão em cada ponto igual à
de I . Nesse caso a fórmula de definição escreve-se simplesmente
_\ Ð0ÑÐ?" ß á ß ?: Ñ œ H0B Ð\B ÑÐ?" ß á ß ?: Ñ
" 0B Ð?" ß á ß ?4" ß H\B Ð?4 Ñß ?4" ß á ß ?: Ñ.
:
4œ"
III.3.3. (Lema) Sejam Q § I uma variedade, 0 œ Ð0B ÑB−Q um campo tensorial
suave de grau :, com valores em Š, e \ œ ÐXB ÑB−Q um campo vectorial
suave. Existe então um aberto Y de I , com Q § Y , um campo tensorial
suave de grau :, com valores em Š, 0˜ œ Ð0˜B ÑB−Y , e um campo vectorial
suave, \˜ œ Ð\˜ B ÑB−Y , tais que 0 œ 0˜ÎQ (restrição enquanto campo tensorial,
cf. III.1.12) e \ œ \˜ ÎQ . Além disso, quaisquer que sejam 0˜ e \˜ nestas
condições, tem-se que _\ Ð0Ñ œ _\˜ Ð0˜ÑÎQ .
Dem: A justificação, que é trivial, é a mesma que a dada para o resultado
correspondente, para a derivação exterior, III.2.4.
O lema anterior permite reduzir de forma trivial a demonstração de várias
propriedades da derivação de Lie ao caso em que os campos tensoriais e
os campos vectoriais estão definidos num aberto de I , quadro em que é
desnecessário considerar prolongamentos para estes. Como primeiro
exemplo, temos:
III.3.4. Sejam Q § I uma variedade, 0 œ Ð0B ÑB−Q um campo tensorial suave
de grau :, com valores em Š, e \ œ Ð\B ÑB−Q um campo vectorial suave.
§3. Derivada de Lie duma forma diferencial
123
Tem-se então que a derivada de Lie _\ Ð0Ñ é um campo tensorial suave.
Dem: Tendo em conta o resultado anterior, basta fazer a demonstração no
caso particular em que Q é um aberto de I . Nesse caso, temos uma
aplicação suave H0À Q Ä PÐIà P: ÐIà ŠÑÑ pelo que H0Ð\Ñ é uma aplicação
suave de Q em P: ÐIà ŠÑ, e ficamos reduzidos a provar que, para cada 4, é
suave a aplicação de Q em P: ÐIà ŠÑ, que a cada B − Q associa a aplicação
multilinear definida por Ð?" ß á ß ?: Ñ È 0B Ð?" ß á ß H\B Ð?4 Ñß á ß ?: Ñ. Ora,
isso é uma consequência da suavidade das aplicações de Q em P: ÐIà ŠÑ e
em PÐIà IÑ, que a B associam 0B e H\B , respectivamente, se repararmos
que tem lugar uma aplicação bilinear de P: ÐIà ŠÑ ‚ PÐIà IÑ em P: ÐIà ŠÑ,
que a Ð(ß -Ñ associa a aplicação multilinear definida por
Ð?" ß á ß ?: Ñ È (Ð?" ß á ß -Ð?4 Ñß á ß ?: Ñ.
III.3.5. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q e ] œ Ð]B ÑB−Q dois
campos vectoriais suaves, 0 œ Ð0B ÑB−Q e ( œ Ð(B ÑB−Q dois campos
tensoriais suaves de grau :, com valores em Š, + − ‘ e , − Š. Tem-se então
_\] Ð0Ñ œ _\ Ð0Ñ _] Ð0Ñ,
_\ Ð0 (Ñ œ _\ Ð0Ñ _\ Ð(Ñ,
_+\ Ð0Ñ œ +_\ Ð0Ñ,
_\ Ð,0Ñ œ ,_\ Ð0Ñ.
Dem: Trata-se de uma consequência imediata da definição.
Se em III.3.5 substituirmos as constantes + e , por funções suaves,
obtemos o seguinte resultado:
III.3.6. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q um campo vectorial suave
e 0 œ Ð0B ÑB−Q um campo tensorial suave de grau :, com valores em Š.
Sejam 0 À Q Ä ‘ e 1À Q Ä Š duas aplicações suaves. Tem-se então
_0 \ Ð0ÑB Ð?" ß á ß ?: Ñ œ 0 ÐBÑ _\ Ð0ÑB Ð?" ß á ß ?: Ñ
" H0B Ð?4 Ñ 0B Ð?" ß á ß ?4" ß \B ß ?4" ß á ß ?: Ñ,
:
4œ"
_\ Ð10ÑB Ð?" ß á ß ?: Ñ œ 1ÐBÑ _\ Ð0ÑB Ð?" ß á ß ?: Ñ H1B Ð\B Ñ 0B Ð?" ß á ß ?: Ñ.
Dem: Reduzindo-nos, como anteriormente, ao caso particular em que Q é
um aberto de I , temos em ambos os casos de uma consequência imediata da
definição, por aplicação da regra de Leibnitz para a derivação de um
produto.
A segunda fórmula no resultado anterior pode ser generalizada numa
fórmula para a derivada de Lie de um produto tensorial de campos
tensoriais:
124
Cap. III. Formas diferenciais e teorema de Stokes
III.3.7. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q um campo vectorial suave
e 0 œ Ð0B ÑB−Q e ( œ Ð(B ÑB−Q dois campos vectoriais suaves de graus : e ; ,
com valores em Š. Tem-se então
_\ Ð0 Œ (Ñ œ _\ Ð0Ñ Œ ( 0 Œ _\ Ð(Ñ.
Dem: Como anteriormente, basta considerarmos o caso particular em que Q
é um aberto de I . Tem-se então
_\ Ð0 Œ (ÑB Ð?" ß á ß ?:; Ñ œ HÐ0 Œ (ÑB Ð\B ÑÐ?" ß á ß ?:; Ñ
" 0B Œ (B Ð?" ß á ß H\B Ð?4 Ñß á ß ?:; Ñ œ
:;
4œ"
œ H0B Ð\B Ñ Œ (B Ð?" ß á ß ?:; Ñ 0B Œ H(B Ð\B ÑÐ?" ß á ß ?:; Ñ
" 0B Ð?" ß á ß H\B Ð?4 Ñß á ß ?: Ñ (B Ð?:" ß á ß ?:; Ñ
:
4œ"
" 0B Ð?" ß á ß ?: Ñ (Ð?:" ß á ß H\B Ð?4 Ñß á ß ?:; Ñ œ
:;
4œ:"
œ H0B Ð\B ÑÐ?" ß á ß ?: Ñ (B Ð?:" ß á ß ?:; Ñ
0B Ð?" ß á ß ?: Ñ H(B Ð\B ÑÐ?:" ß á ß ?:; Ñ
" 0B Ð?" ß á ß H\B Ð?4 Ñß á ß ?: Ñ (B Ð?:" ß á ß ?:; Ñ
:
4œ"
" 0B Ð?" ß á ß ?: Ñ (Ð?:" ß á ß H\B Ð?4 Ñß á ß ?:; Ñ œ
:;
4œ:"
œ _\ Ð0ÑB Ð?" ß á ß ?: Ñ (B Ð?:" ß á ß ?:; Ñ
0B Ð?" ß á ß ?: Ñ _\ Ð(ÑB Ð?:" ß á ß ?:; Ñ œ
œ Ð_\ Ð0ÑB Œ (B 0B Œ _\ Ð(ÑB ÑÐ?" ß á ß ?:; Ñ,
donde o resultado.
III.3.8. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q um campo vectorial suave
e 0 œ Ð0B ÑB−Q um campo tensorial suave de grau :, com valores em Š.
Tem-se então:
a) Para cada permutação 5 − Æ: , _\ Ð5
s Ð0ÑÑ œ 5
s Ð_\ Ð0ÑÑ;
b) _\ ÐAltÐÐ0ÑÑ œ AltÐ_\ Ð0ÑÑ;
c) Em particular, se 0 é uma forma diferencial de grau :, com valores em Š,
também _\ Ð0Ñ é uma forma diferencial.
Dem: Como anteriormente, basta considerarmos o caso particular em que Q
é um aberto de I . Notando @4 œ ?5Ð4Ñ , vem
§3. Derivada de Lie duma forma diferencial
125
_\ Ð5
s Ð0ÑÑB Ð?" ß á ß ?: Ñ œ H5
s Ð0ÑB Ð\B ÑÐ?" ß á ß ?: Ñ blablablablablblabla
"5
s Ð0B ÑÐ?" ß á ß ?4" ß H\B Ð?4 Ñß ?4" ß á ß ?: Ñ œ
:
4œ"
œ HÐ5
s Ð0ÑÐ?" ß á ß ?: ÑÑB Ð\B Ñ
" 0B Ð?5Ð"Ñ ß á ß ?5Ð5" Ð4Ñ"Ñ ß H\B Ð?5Ð5" Ð4ÑÑ Ñß ?5Ð5" Ð4Ñ"Ñ ß á ß ?5Ð:Ñ Ñ œ
:
4œ"
œ H0Ð@" ß á ß @: ÑB Ð\B Ñ
" 0B Ð@" ß á ß @5" Ð4Ñ" ß H\B Ð@5" Ð4Ñ Ñß @5" Ð4Ñ" ß á ß @: Ñ œ
:
4œ"
œ H0Ð@" ß á ß @: ÑB Ð\B Ñ
" 0B Ð@" ß á ß @5 ß H\B Ð@5 Ñß @5" ß á ß @: Ñ œ
:
5œ"
œ _\ Ð0ÑB Ð@" ß á ß @: Ñ œ 5
s Ð_\ Ð0ÑB ÑÐ?" ß á ß ?: Ñ,
o que prova a). A alínea b) resulta de a), tendo em conta a definição do
operador Alt de antissimetrização, e a alínea c) é uma consequência simples
de b).
III.3.9. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q um campo vectorial suave
e = œ Ð=B ÑB−Q e 3 œ Ð3B ÑB−Q duas formas diferenciais suaves de grau :,
com valores em Š. Tem-se então
_\ Ð= • 3Ñ œ _\ Ð=Ñ • 3 = • _\ Ð3Ñ.
Dem: Trata-se de uma consequência de III.3.7 e da alínea b) de III.3.9, tendo
em conta a fórmula
=•3 œ
Ð: ;Ñx
AltÐ= • 3Ñ.
:x ;x
s §I
s e Q § I duas variedades e 0 À Q
s Ä Q uma aplicação
III.3.10. Sejam Q
suave. Sejam \ œ Ð\B ÑB−Qs e ] œ Ð]C ÑC−Q dois campos vectoriais suaves
s , ]0 ÐBÑ œ H0B Ð\B Ñ. Para
0 -relacionados, isto é, tais que, para cada B − Q
cada campo tensorial suave de grau :, 0 œ Ð0C ÑC−Q , com valores em Š,
tem-se então
0 ‡ _] Ð0Ñ œ _\ Ð0 ‡ 0Ñ.
Dem: Seja 0 œ Ð0C ÑC−Q uma aplicação suave de Q em P: ÐIà ŠÑ tal que
s , contendo Q
s, e
cada 0C seja uma restrição de 0C . Sejam Y um aberto de I
0 À Y Ä I um prolongamento suave de 0 . Uma vez que tem lugar uma
s em PÐIà
s IÑ, que a B associa H0 B , podemos
aplicação suave de Q
126
Cap. III. Formas diferenciais e teorema de Stokes
s em P: ÐIà
s ŠÑ ,
considerar uma aplicação suave de Q
‡
0 ‡ 0 œ ÐH0 B 00 ÐBÑ ÑB−Qs œ Ð00 ÐBÑ ‰ ÐH0 B ‚ â ‚ H0 B ÑÑB−Qs ,
tendo-se, é claro, que cada Ð0 ‡ 0ÑB œ H0B‡ Ð00 ÐBÑ Ñ é uma restrição de Ð0 ‡ 0ÑB .
Podemos portanto escrever, tendo em conta a fórmula
Ð0 ‡ 0ÑB Ð?" ß á ß ?: Ñ œ 00 ÐBÑ ÐH0 B Ð?" Ñß á ß H0 B Ð?: ÑÑ,
_\ Ð0 ‡ 0ÑB Ð?" ß á ß ?: Ñ œ HÐ0 ‡ 0ÑB Ð\B ÑÐ?" ß á ß ?: Ñ
" Ð0 ‡ 0ÑB Ð?" ß á ß H\B Ð?4 Ñß á ß ?: Ñ œ
:
4œ"
œ H00 ÐBÑ ÐH0B Ð\B ÑÑÐH0B Ð?" Ñß á ß H0B Ð?: ÑÑ
" 00 ÐBÑ ÐH0 B Ð?" Ñß á ß H# 0 B Ð\B ß ?4 Ñß á ß H0 B Ð?: ÑÑ
:
4œ"
:
" 00 ÐBÑ ÐH0 B Ð?" Ñß á ß H0 B ÐH\B Ð?4 ÑÑß á ß H0 B Ð?: ÑÑ.
4œ"
Uma vez que ]0 ÐBÑ œ H0B Ð\B Ñ œ H0 B Ð\B Ñ, e portanto, por derivação de
ambos os membros,
H]0 ÐBÑ ÐH0B Ð?4 ÑÑ œ H# 0 B Ð?4 ß \B Ñ H0 B ÐH\B Ð?4 ÑÑ,
obtemos, a partir da fórmula anterior, e tendo em conta a simetria da
aplicação bilinear H# 0 B ,
_\ Ð0 ‡ 0ÑB Ð?" ß á ß ?: Ñ œ H00 ÐBÑ Ð]0 ÐBÑ ÑÐH0B Ð?" Ñß á ß H0B Ð?: ÑÑ
" 00 ÐBÑ ÐH0B Ð?" Ñß á ß H]0 ÐBÑ ÐH0B Ð?4 ÑÑß á ß H0B Ð?: ÑÑ œ
:
4œ"
œ _] Ð0Ñ0 ÐBÑ ÐH0B Ð?" Ñß á ß H0B Ð?: ÑÑ œ Ð0 ‡ _] Ð0ÑÑB Ð?" ß á ß ?: Ñ,
o que termina a demonstração.
A propriedade que apresentamos em seguida estuda o que se passa quando
aplicamos sucessivamente dois operadores de derivação de Lie.
III.3.11. Sejam Q § I uma variedade e \ œ Ð\B ÑB−Q e ] œ Ð]B ÑB−Q dois
campos vectoriais suaves. Se 0 œ Ð0B ÑB−Q é um campo tensorial suave de
grau :, com valores em Š, tem-se
_\ Ð_] Ð0ÑÑ _] Ð_\ Ð0ÑÑ œ _Ò\ß] Ó Ð0Ñ.
§3. Derivada de Lie duma forma diferencial
127
Dem: Tendo em conta o lema III.3.3, podemos já supor que Q é um aberto
de I . Tem-se então
_] Ð0ÑÐ?" ß á ß ?: Ñ œ H0Ð] ÑÐ?" ß á ß ?: Ñ
" 0Ð?" ß á ß H] Ð?4 Ñß á ß ?: Ñ,
:
4œ"
pelo que
_\ Ð_] Ð0ÑÑÐ?" ß á ß ?: Ñ œ HÐ_] Ð0ÑÐ?" ß á ß ?: ÑÑÐ\Ñ
" _] Ð0ÑÐ?" ß á ß H\Ð?5 Ñß á ß ?: Ñ œ
:
5œ"
œ H# 0Ð\ß ] ÑÐ?" ß á ß ?: Ñ H0ÐH] Ð\ÑÑÐ?" ß á ß ?: Ñ
" H0Ð\ÑÐ?" ß á ß H] Ð?4 Ñß á ß ?: Ñ 0Ð?" ß á ß H# ] Ð\ß ?4 Ñß á ß ?: Ñ
:
4œ"
:
" H0Ð] ÑÐ?" ß á ß H\Ð?5 Ñß á ß ?: Ñ
5œ"
" 0Ð?" ß á ß H] Ð?4 Ñß á ß H\Ð?5 Ñß á ß ?: Ñ
45
:
" 0Ð?" ß á ß H] ÐH\Ð?5 ÑÑß á ß ?: Ñ
5œ"
" 0Ð?" ß á ß H\Ð?5 Ñß á ß H] Ð?4 Ñß á ß ?: Ñ.
45
Trocando \ com ] na fórmula anterior e subtraindo daquela a fórmula assim
obtida, vem, tendo em conta a simetria da aplicação bilinear H# 0,
_\ Ð_] Ð0ÑÑÐ?" ß á ß ?: Ñ _] Ð_\ Ð0ÑÑÐ?" ß á ß ?: Ñ œ
œ H0ÐH] Ð\Ñ H\Ð] ÑÑÐ?" ß á ß ?: Ñ
" 0Ð?" ß á ß H# ] Ð\ß ?4 Ñ H# \Ð] ß ?4 Ñß á ß ?: Ñ
:
4œ"
:
" 0Ð?" ß á ß H] ÐH\Ð?5 ÑÑ H\ÐH] Ð?5 ÑÑß á ß ?: Ñ œ
5œ"
œ H0ÐÒ\ß ] ÓÑÐ?" ß á ß ?: Ñ
" 0Ð?" ß á ß H# ] Ð\ß ?4 Ñ H# \Ð] ß ?4 Ñ H] ÐH\Ð?4 ÑÑ H\ÐH] Ð?4 ÑÑß á ß ?: Ñ.
:
5œ"
Mas, por derivação de ambos os membros da identidade
Ò\ß ] Ó œ H] Ð\Ñ H\Ð] Ñ,
obtemos
128
Cap. III. Formas diferenciais e teorema de Stokes
HÒ\ß ] ÓÐ?4 Ñ œ H# ] Ð?4 ß \Ñ H] ÐH\Ð?4 ÑÑ H# \Ð?4 ß ] Ñ H\ÐH] Ð?4 ÑÑ,
o que, substituído na última fórmula e tendo em conta a simetria das aplicações bilineares H# \ e H# ] , dá
_\ Ð_] Ð0ÑÑÐ?" ß á ß ?: Ñ _] Ð_\ Ð0ÑÑÐ?" ß á ß ?: Ñ œ
œ H0ÐÒ\ß ] ÓÑÐ?" ß á ß ?: Ñ " 0Ð?" ß á ß HÒ\ß ] ÓÐ?4 Ñß á ß ?: Ñ œ
:
4œ"
œ _Ò\ß] Ó Ð0ÑÐ?" ß á ß ?: Ñ.
III.3.12. (Corolário) Em particular, tomando para 0 um campo tensorial de grau
!, vemos que, se 0 À Q Ä Š é uma aplicação suave, então
H0 ÐÒ\ ,] ÓÑ œ HÐH0 Ð] ÑÑÐ\Ñ œ HÐH0 Ð\ÑÑÐ] Ñ.
É clássico utilizar a notação \ † 0 para H0 Ð\Ñ, pelo que a fórmula anterior é
então escrita do seguinte modo:
Ò\ß ] Ó † 0 œ \ † Ð] † 0 Ñ ] † Ð\ † 0 Ñ.
III.3.13. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q um campo vectorial
suave e 0 œ Ð0B ÑB−Q um campo tensorial suave de grau : " e com valores
em Š. Tem então lugar um campo tensorial suave de grau : "
int\ Ð0Ñ œ Ðint\B Ð0B ÑÑB−Q ,
onde int\B Ð0B ÑÐ?" ß á ß ?:" Ñ œ 0B Ð\B ß ?" ß á ß ?:" Ñ.
Dem: Seja 0 œ Ð0B ÑB−Q uma aplicação suave de Q em P: ÐIà ŠÑ, tal que
cada 0B seja uma restrição de 0B . Considerando a aplicação bilinear de
P: ÐIà ŠÑ ‚ I em P:" ÐIà ŠÑ, que a Ð-ß AÑ associa intA Ð-Ñ, vemos que vai
ter lugar uma aplicação suave de Q em P:" ÐIà ŠÑ, que a B associa
int\B Ð0B Ñ, sendo trivial que cada int\B Ð0B Ñ é uma restrição de int\B Ð0B Ñ.
III.3.14. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q e ] œ Ð]B ÑB−Q campos
vectoriais suaves e 0 œ Ð0B ÑB−Q um campo tensorial suave de grau : " e
com valores em Š. Tem-se então
_\ Ðint] Ð0ÑÑ int] Ð_\ Ð0ÑÑ œ intÒ\ß] Ó Ð0Ñ.
Dem: Como usualmente, podemos já supor que Q é um aberto de I . Uma
vez que
Ðint] Ð0ÑÑB Ð?" ß á ß ?:" Ñ œ 0B Ð]B ß ?" ß á ß ?:" Ñ,
obtemos
§3. Derivada de Lie duma forma diferencial
129
_\ Ðint] Ð0ÑÑB Ð?" ß á ß ?:" Ñ œ HÐint] Ð0ÑÐ?" ß á ß ?:" ÑÑB Ð\B Ñ blablabla
" int] Ð0ÑB Ð?" ß á ß H\B Ð?4 Ñß á ß ?:" Ñ œ
:"
4œ"
œ H0B Ð\B ÑÐ]B ß ?" ß á ß ?:" Ñ 0B ÐH]B Ð\B Ñß ?" ß á ß ?:" Ñ
" 0B Ð]B ß ?" ß á ß H\B Ð?4 Ñß á ß ?:" Ñ œ
:"
4œ"
œ 0B ÐH]B Ð\B Ñ H\B Ð]B Ñß ?" ß á ß ?:" Ñ H0B Ð\B ÑÐ]B ß ?" ß á ß ?:" Ñ
0B ÐH\B Ð]B Ñß ?" ß á ß ?:" Ñ " 0B Ð]B ß ?" ß á ß H\B Ð?4 Ñß á ß ?:" Ñ œ
:"
4œ"
œ 0B ÐÒ\ß ] ÓB ß á ß ?" ß á ß ?:" Ñ _\ Ð0ÑB Ð]B ß ?" ß á ß ?:" Ñ œ
œ intÒ\ß] ÓB Ð0B ÑÐ?" ß á ß ?:" Ñ int]B Ð_\ Ð0ÑB ÑÐ?" ß á ß ?:" Ñ,
donde o resultado
Nos resultados anteriores a derivada de Lie foi aplicada a um campo
tensorial suave arbitrário, que pode evidentemente ser, em particular, uma
forma diferencial. Nos três resultados que se seguem, o primeiro dos quais
é simplesmente uma reformulação de III.3.6, já é essencial termos uma
forma diferencial.
III.3.15. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q um campo vectorial
suave, = œ Ð=B ÑB−Q uma forma diferencial suave de grau : " e com
valores em Š e 0 À Q Ä ‘ uma aplicação suave. Tem-se então
_0 \ Ð=Ñ œ 0 _\ Ð=Ñ .0 • int\ Ð=Ñ.
Dem: Tendo em conta a primeira fórmula de III.3.6, vem
_0 \ Ð=ÑB Ð?" ß á ß ?: Ñ œ 0 ÐBÑ _\ Ð=ÑB Ð?" ß á ß ?: Ñ
" H0B Ð?4 Ñ =B Ð?" ß á ß ?4" ß \B ß ?4" ß á ß ?: Ñ œ
:
4œ"
œ 0 ÐBÑ _\ Ð=ÑB Ð?" ß á ß ?: Ñ
" Ð"Ñ4" H0B Ð?4 Ñ int\B Ð=B ÑÐ?" ß á ß ?4" ß ?4" ß á ß ?: Ñ œ
:
4œ"
œ 0 ÐBÑ _\ Ð=ÑB Ð?" ß á ß ?: Ñ .0B • int\B Ð=B ÑÐ?" ß á ß ?: Ñ.
III.3.16. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q um campo vectorial
suave e = œ Ð=B ÑB−Q uma forma diferencial suave de grau : ", com
valores em Š. Tem-se então
130
Cap. III. Formas diferenciais e teorema de Stokes
int\ Ð. =Ñ . int\ Ð=Ñ œ _\ Ð=Ñ.
Dem: Podemos já supor que Q é um aberto de I . Tem-se então
int\ Ð=ÑB Ð?" ß á ß ?s4 ß á ß ?: Ñ œ =B Ð\B ß ?" ß á ß ?s4 ß á ß ?: Ñ,
pelo que
. int\ Ð=ÑB Ð?" ß á ß ?: Ñ œ " Ð"Ñ4" HÐint\ Ð=ÑÑB Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?: Ñ œ
:
4œ"
œ " Ð"Ñ4" ˆH=B Ð?4 ÑÐ\B ß ?" ß á ß ?s4 ß á ß ?: Ñ =B ÐH\B Ð?4 Ñß ?" ß á ß ?s4 ß á ß ?: щ œ
:
4œ"
œ Ð. =ÑB Ð\B ß ?" ß á ß ?: Ñ H=B Ð\B ÑÐ?" ß á ß ?: Ñ
" =B Ð?" ß á ß H\B Ð?4 Ñß á ß ?: Ñ œ
:
4œ"
œ int\ Ð. =ÑB Ð?" ß á ß ?: Ñ _\ Ð=ÑB Ð?" ß á ß ?: Ñ,
donde o resultado.
III.3.17. (Nota) No resultado anterior exigimos que o grau : da forma diferencial = fosse maior ou igual a ", sem o que int\ Ð=Ñ não fazia sentido. É no
entanto imediato constatar que, no caso em que temos uma forma diferencial
de grau !, isto é, uma aplicação suave 0 À Q Ä Š, tem-se
int\ Ð.0 Ñ œ _\ Ð0 Ñ,
pelo que tudo se passa como se o resultado anterior fosse ainda válido para as
formas diferenciais de grau ! desde que, para uma tal forma diferencial, se
defina int\ Ð=Ñ œ !.
III.3.18. Sejam Q § I uma variedade, \ œ Ð\B ÑB−Q um campo vectorial
suave e = œ Ð=B ÑB−Q uma forma diferencial suave de grau :, com valores
em Š. Tem-se então
. _\ Ð=Ñ œ _\ Ð. =Ñ œ . int\ Ð. =Ñ.
Dem: No caso em que : ", sai, tendo em conta III.3.16 e III.2.8,
d_\ Ð=Ñ œ .Ðint\ Ð. =Ñ . int\ Ð=ÑÑ œ . int\ Ð. =Ñ œ
œ . int\ Ð. =Ñ int\ Ð.. =Ñ œ _\ Ð. =Ñ.
O caso : œ ! é análogo, tendo em conta a fórmula trivial referida na nota
anterior,
. _\ Ð0 Ñ œ . int\ Ð.0 Ñ œ . int\ Ð.0 Ñ int\ Ð..0 Ñ œ _\ Ð.0 Ñ.
§4. Integral duma forma diferencial
131
§4. Integral duma forma diferencial.
III.4.1. Sejam I um espaço vectorial de dimensão finita, munido de um produto
interno, e Q § I uma variedade de dimensão 7, suavemente orientada24.
Seja = œ Ð=B ÑB−Q uma forma diferencial suave de grau 7, com valores em
Š. Tem então lugar uma aplicação suave 0 À Q Ä Š, definida por 0 ÐBÑ œ ‡
=B (cf. III.1.25), ou seja, por
=B œ 0 ÐBÑ Z 96B ,
onde Z 96B − E7 ÐXB ÐQ Ñà ‘Ñ é o elemento de volume do espaço euclidiano
orientado XB ÐQ Ñ. Dizemos então que a forma diferencial = é integrável se a
aplicação suave 0 À Q Ä Š for integrável, relativamente à medida .Q
(associada a Q como subvariedade do espaço euclidiano I ), e, nesse caso,
define-se o integral de =, 'Q = ou, simplesmente, ' =, como sendo o
elemento de Š
( = œ ( 0 ÐBÑ . .Q ÐBÑ.25
Q
Q
Mais geralmente, se E § Q é um boreliano, diz-se que = é integrável sobre
E se a aplicação 0 for integrável sobre E e, nesse caso, define-se
( = œ ( 0 ÐBÑ . .Q ÐBÑ.
E
E
III.4.2. Nas condições anteriores, se trocarmos a orientação de Q , o elemento de
volume vem multiplicado por " pelo que o facto de = ser ou não integrável
não muda e o integral de =, quando esta forma diferencial for integrável, vem
multiplicado por ".
s §I
s e Q § I , suavemente
III.4.3. Dadas as variedades de dimensão 7, Q
s Ä Q conserva (resp.
orientadas, diz-se que um difeomorfismo :À Q
s , o isomorfismo
inverte) as orientações se, para cada B − Q
s Ñ Ä X:ÐBÑ ÐQ Ñ
H:B À XB ÐQ
conserva (resp. inverte) as orientações.
24Veremos
adiante que esta definição não depende do produto interno que se considera
em I , pelo que ela fará sentido no quadro de uma subvariedade suavemente orientada de
um espaço vectorial de dimensão finita, não forçosamente dotado a priori de um produto
interno.
25Repare-se que só se define o integral de uma forma diferencial cujo grau seja igual à
dimensão da variedade.
132
Cap. III. Formas diferenciais e teorema de Stokes
s espaços euclidianos, Q
s §I
s e Q § I duas variedades de
III.4.4. Sejam I e I
s
dimensão 7, suavemente orientadas, e :À Q Ä Q um difeomorfismo que
conserve as orientações ou inverta as orientações e notemos & œ " no
primeiro caso e & œ " no segundo. Seja = œ Ð=B ÑB−Q uma forma
diferencial suave com valores em Š. Tem-se então que a forma diferencial
s é integrável se, e só se, = o for e, nesse caso,
suave :‡ = sobre Q
‡
( : = œ & ( =.
s
Q
Q
s§Q
s , :‡ = é integrável
s é um boreliano e E œ :ÐEÑ
Mais geralmente, se E
s
sobre E se, e só se, = for integrável sobre E e, nesse caso,
‡
( : = œ & ( =.26
s
E
E
Dem: Tendo em conta III.4.2, podemos já supor que o difeomorfismo : conserva as orientações. Reparemos agora que, sendo 0 À Q Ä Š a aplicação
suave definida por =C œ 0 ÐCÑ Z 96C , vai-se ter, tendo em conta II.8.7,
Ð:‡ =ÑB œ H:B‡ Ð=:ÐBÑ Ñ œ 0 Ð:ÐBÑÑ H:B‡ ÐZ 96:ÐBÑ Ñ œ 0 Ð:ÐBÑÑ -H:ÐBÑ Z 96B .
s em Š associada a :‡ = está defiConcluímos portanto que a aplicação de Q
nida por B È -H:ÐBÑ 0 Ð:ÐBÑÑ, sendo portanto uma aplicação suave que, de
acordo com I.3.5, vai ser integrável, relativamente à medida .Qs , se, e só se,
isso acontecer a 0 , relativamente à medida .Q , tendo-se, nesse caso,
‡
( : = œ ( 0 Ð:ÐBÑÑ -H:ÐBÑ . .Qs ÐBÑ œ ( 0 ÐCÑ . .Q ÐCÑ œ ( =.
s
Q
s
Q
Q
Q
Tendo em conta o facto de o integral de uma função sobre um subconjunto
boreliano ser igual ao integral sobre o espaço todo do produto desta pela
função característica do boreliano, o argumento anterior implica também a
afirmação sobre os integrais em subconjuntos borelianos.
III.4.5. (Corolário) Sejam I um espaço vectorial de dimensão finita, sobre o
qual consideramos dois produtos internos, e Q § I uma variedade de
dimensão 7 suavemente orientada. Se = œ Ð=B ÑB−Q é uma forma diferencial
suave de grau 7, com valores em Š, = é integrável relativamente a um dos
produtos internos se, e só se, o for relativamente ao outro e então o integral é
o mesmo nos dois casos. Podemos assim falar de formas diferenciais
integráveis e do integral de uma tal forma diferencial mesmo no caso em que
o espaço ambiente não está munido a priori de nenhum produto interno.
26Doravante,
e com o objectivo de não tornar os enunciados pesados, não enunciaremos
explicitamente os resultados envolvendo os integrais de formas diferenciais sobre
subconjuntos borelianos, quando for claro que estes são generalizações imediatas dos
resultados correspondentes para os integrais sobre toda a variedade.
§4. Integral duma forma diferencial
133
Dem: Basta aplicar o resultado anterior à aplicação identidade de Q ,
considerando no domínio um dos produtos internos e no espaço de chegada o
outro.
III.4.6. Seja Q § I uma variedade de dimensão 7 suavemente orientada.
Dadas as formas diferenciais integráveis de grau 7, reais ou complexas,
= œ Ð=B ÑB−Q e 5 œ Ð5B ÑB−Q e o escalar + − Š, tem-se que = 5 e + = são
integráveis e
( = 5 œ ( = ( 5,
Q
Q
Q
( + = œ + ( =.
Q
Q
Dem: Trata-se de uma consequência imediata da correspondente propriedade
para o integral de uma função relativamente a uma medida.
III.4.7. Seja Q § I uma variedade de dimensão 7 suavemente orientada. Seja
= œ Ð=B ÑB−Q uma forma diferencial suave de grau 7, com valores em Š, e
de suporte compacto, isto é, tal que exista um conjunto compacto O § Q tal
que =B œ !, para cada B  O . Tem-se então que = é integrável.
Repare-se que a condição de a forma diferencial = ter suporte compacto
encontra-se trivialmente verificada sempre que a variedade Q for compacta.
Dem: Sendo 0 À Q Ä Š a aplicação contínua definida por 0 ÐBÑ œ ‡=B ,
tem-se evidentemente que 0 é nula fora de O . Uma vez que a função
contínua, que a B associa l0 ÐBÑl, admite um máximo , sobre O e que
.Q ÐOÑ _, concluímos agora que
( l0 ÐBÑl . .Q ÐBÑ œ ( l0 ÐBÑl . .Q ÐBÑ Ÿ , .Q ÐOÑ _,
Q
O
o que mostra que 0 , e portanto =, é integrável.
§5. Teorema de Stokes.
Vamos começar por examinar o modo como uma orientação numa
variedade induz uma orientação no seu bordo de índice ".
III.5.1. Seja Q § I uma variedade de dimensão 7. Para cada B no bordo de
índice ", `" ÐQ Ñ, tem-se então que XB Ð`" ÐQ ÑÑ é um hiperplano de XB ÐQ Ñ e
os semi-espaços abertos correspondentes (cf. II.7.26) são o conjunto
XB ÐQ Ñ Ï tB ÐQ Ñ dos vectores que são tangentes, mas não estritamente tangentes a Q em B e o conjunto tB ÐQ Ñ Ï XB Ð`" ÐQ ÑÑ dos vectores que são
estritamente tangentes a Q no ponto B, mas não são tangentes a `" ÐQ Ñ
nesse ponto.
Dem: Sejam Y um aberto de ‘7" ‚ Ò!ß _Ò, com ! − Y , Z um aberto de
134
Cap. III. Formas diferenciais e teorema de Stokes
Q , com B − Z , e :À Y Ä Z um difeomorfismo com :Ð!Ñ œ B. Tem-se
então que a restrição de :
é um difeomorfismo de
Y Б7" ‚ Ö!×Ñ œ `" ÐY Ñ sobre Z `" ÐQ Ñ œ `" ÐZ Ñ, pelo que H:! vai
ser um isomorfismo de ‘7 sobre XB ÐQ Ñ, aplicando ‘7" ‚ Ò!ß _Ò sobre
tB ÐQ Ñ e ‘7" ‚ Ö!× sobre XB Ð`" ÐQ ÑÑ. Uma vez que ‘7" ‚ Ö!× é um
hiperplano de ‘7 , com os semi-espaços abertos ‘7" ‚ Ó!ß _Ò e
‘7" ‚ Ó_ß !Ò (cf., por exemplo, II.7.27), concluímos imediatamente que
XB Ð`" ÐQ ÑÑ é um hiperplano de XB ÐQ Ñ, tendo como semi-espaços abertos
H:! Б7" ‚ Ó!ß _ÒÑ œ tB ÐQ Ñ Ï XB Ð`" ÐQ ÑÑ,
H:! Б7" ‚ Ó_ß !ÒÑ œ XB ÐQ Ñ Ï tB ÐQ Ñ.
III.5.2. Nas condições anteriores, vamos chamar orientação transversa canónica
de XB Ð`" ÐQ ÑÑ em XB ÐQ Ñ (cf. II.7.26) aquela cujo semi-espaço positivo é
XB ÐQ Ñ Ï tB ÐQ Ñ (o conjunto dos vectores tangentes que apontam para fora).
III.5.3. Seja Q § I uma variedade de dimensão 7 suavemente orientada.
Chama-se então orientação induzida da variedade `" ÐQ Ñ, de dimensão
7 ", a definida pela condição de, para cada B − `" ÐQ Ñ, o hiperplano
XB Ð`" ÐQ ÑÑ de XB ÐQ Ñ ter a orientação induzida pela orientação de XB ÐQ Ñ e
pela orientação transversa canónica de XB Ð`" ÐQ ÑÑ em XB ÐQ Ñ (cf. II.7.28).
Por outras palavras, para cada base A" ß á ß A7" de XB Ð`" ÐQ ÑÑ e cada
vector A − XB ÐQ Ñ Ï tB ÐQ Ñ, a base Aß A" ß á ß A7" de XB ÐQ Ñ tem a mesma
orientação que a base A" ß á ß A7" de XB Ð`" ÐQ ÑÑ.
É a orientação induzida a que se considera sempre, salvo aviso em contrário,
sobre o bordo de índice " de uma variedade suavemente orientada.
s §I
s e Q § I duas variedades de dimensão 7 suavemente
III.5.4. Sejam Q
s
orientadas e :À Q Ä Q um difeomorfismo que conserva (resp. inverte) as
s Ñ sobre
orientações. Tem-se então que o difeomorfismo restrição, de `" ÐQ
`" ÐQ Ñ, também conserva (resp. inverte) as orientações.
s Ñ podemos fixar A − XB ÐQ
s Ñ Ï tB ÐQ
s Ñ, tendo-se
Dem: Para cada B − `" ÐQ
então H:B ÐAÑ − X:ÐBÑ ÐQ Ñ Ï t:ÐBÑ ÐQ Ñ; dada uma base A" ß á ß A7" de
s ÑÑ, tem-se que
XB Ð`ÐQ
s ÑÑ Ä X:ÐBÑ Ð`" ÐQ ÑÑ
HÐ:Î`" ÐQs Ñ ÑB À XB Ð`" ÐQ
s ÑÑ, e
conserva as orientações se, e só se, as bases A" ß á ß A7" , de XB Ð`" ÐQ
H:B ÐA" Ñß á ß H:B ÐA7" Ñ, de X:ÐBÑ Ð`" ÐQ ÑÑ, tiverem a mesma orientação,
s Ñ, e
ou seja, se, e só se, as bases Aß A" ß á ß A7" , de XB ÐQ
H:B ÐAÑß H:B ÐA" Ñß á ß H:B ÐA7" Ñ, de X:ÐBÑ ÐQ Ñ, tiverem a mesma
s Ñ Ä X:ÐBÑ ÐQ Ñ conservar as
orientação, isto é, se, e só se, H:B À XB ÐQ
orientações.
II.5.5 Seja Q § I uma variedade de dimensão 7 suavemente orientada.
Tem-se então que a orientação induzida em `" ÐQ Ñ é também suave.
§5. Teorema de Stokes
135
Dem: Seja B! − `" ÐQ Ñ arbitrário. Sejam Y um aberto de ‘7" ‚ Ò!ß _Ò,
com ! − Y , Z um aberto de Q , com B! − Z , e :À Y Ä Z um
difeomorfismo com :Ð!Ñ œ B! . Tem-se então que a restrição de : é um
difeomorfismo de Y Б7" ‚ Ö!×Ñ œ `" ÐY Ñ sobre Z `" ÐQ Ñ œ `" ÐZ Ñ,
pelo que H:! vai ser um isomorfismo de ‘7 sobre XB! ÐQ Ñ, aplicando
‘7" ‚ Ò!ß _Ò sobre tB! ÐQ Ñ e ‘7" ‚ Ö!× sobre XB! Ð`" ÐQ ÑÑ. Sendo
/" ß á ß /7 a base canónica de ‘7 , tem-se que, para cada
C − Y Б7" ‚ Ö!×Ñ, /7 − XC ÐY Ñ Ï tC ÐY Ñ, portanto
H:C Ð/7 Ñ − X:ÐCÑ ÐQ Ñ Ï t:ÐCÑ ÐQ Ñ.
Podemos então considerar os campos vectoriais suaves sobre Z , que a cada B
associam H::" ÐBÑ Ð/4 Ñ, os quais vão constituir para cada B uma base de
XB ÐQ Ñ pelo que, se necessário substituindo Z por um aberto mais pequeno
contendo ainda B! e : por uma sua restrição, podemos já supor que, ou para
todo o B − Z a base
H::" ÐBÑ Ð/7 Ñß H::" ÐBÑ Ð/" Ñß á ß H::" ÐBÑ Ð/7" Ñ
de XB ÐQ Ñ é directa, ou para todo o B − Z aquela base é retrógrada, o que
implica que, ou para cada B − Z `" ÐQ Ñ a base
H::" ÐBÑ Ð/" Ñß á ß H::" ÐBÑ Ð/7" Ñ
de XB Ð`" ÐQ ÑÑ é directa, ou para cada B − Z `" ÐQ Ñ aquela base é retrógrada.
Estamos agora em condições de enunciar, como lema, uma primeira
versão particular do teorema de Stokes, em que a variedade considerada é
um produto de intervalos.
III.5.6. (Lema) Sejam 7 " e, para cada " Ÿ 4 Ÿ 7, +4 ,4 dois reais e
consideremos a variedade compacta de dimensão 7,
Q œ $ Ò+4 ß ,4 Ó,
4
sobre a qual se toma a orientação constante, correspondente à orientação
canónica de ‘7 (reparar que se tem XB ÐQ Ñ œ ‘7 , para cada B − Q ). Se
= œ Ð=B ÑB−Q é uma forma diferencial suave de grau 7 ", com valores em
Š, tem-se então que
136
Cap. III. Formas diferenciais e teorema de Stokes
( .= œ (
Q
`" ÐQ Ñ
=Î`" ÐQ Ñ .27
Dem: Para cada " Ÿ 4 Ÿ 7, notemos
Q4 œ Ó+" ß ," Ò ‚ â ‚ Ó+4" ß ,4" Ò ‚ Ö+4 × ‚ Ó+4" ß ,4" Ò ‚ â ‚ Ó+7 ß ,7 Ò,
Q4w œ Ó+" ß ," Ò ‚ â ‚ Ó+4" ß ,4" Ò ‚ Ö,4 × ‚ Ó+4" ß ,4" Ò ‚ â ‚ Ó+7 ß ,7 Ò,
e reparemos que `" ÐQ Ñ é a união disjunta das subvariedades abertas Q4 e
Q4w . Notemos que num ponto de Q4 o vector /4 é tangente mas não
estritamente tangente a Q e que num ponto de Q4w isso acontece ao vector /4 .
Considerando o aberto E4 de ‘7" , definido por
E4 œ Ó+" ß ," Ò ‚ â ‚ Ó+4" ß ,4" Ò ‚ Ó+4" ß ,4" Ò ‚ â ‚ Ó+7 ß ,7 Ò,
com a orientação canónica de ‘7" , podemos considerar os difeomorfismos
:4 À E4 Ä Q4 e :4w À E4 Ä Q4w , definidos por
:4 ÐB" ß á ß B4" ß B4" ß á ß B7 Ñ œ ÐB" ß á ß B4" ß +4 ß B4" ß á ß B7 Ñ,
:4w ÐB" ß á ß B4" ß B4" ß á ß B7 Ñ œ ÐB" ß á ß B4" ß ,4 ß B4" ß á ß B7 Ñ,
e, reparando que tanto H:4 ÐBÑ como H:4w ÐBÑ aplicam a base canónica de
‘7" em /" ß á ß /4" ß /4" ß á ß /7 , constatamos, tendo em conta a definição
da orientação induzida no bordo de índice " de Q , que, se 4 é ímpar, :4
inverte as orientações e :4w conserva as orientações e, se 4 é par, :4 conserva
as orientações e :jw inverte as orientações (para :4 temos que ver o que
acontece ao sinal da base /4 ß /" ß á ß /4" ß /4" ß á ß /7 e para :4w o que
acontece ao sinal da base /4 ß /" ß á ß /4" ß /4" ß á ß /7 ). Reparemos também
que, para os elementos 0•"ßáß5"ß5"ßáß7 da base associada de E7" Б7 à ŠÑ,
tem-se
:4‡ Ð0•"ßáß5"ß5"ßáß7 Ñ œ :4‡ Ð0•"ßáß5"ß5"ßáß7 ÑÐ/" ß á ß /7" Ñ Z 96‘7" œ
œ 0•"ßáß5"ß5"ßáß7 Ð/" ß á ß /4" ß /4" ß á ß /7 Ñ Z 96‘7" œ $4ß5 Z 96‘7"
e, do mesmo modo,
‡
:4w Ð0•"ßáß5"ß5"ßáß7 Ñ œ $4ß5 Z 96‘7" .
Podemos agora escrever
27Repare-se
que a forma diferencial . = é automaticamente integrável, por ser suave e Q
ser compacta, mas o mesmo não se poderia dizer a priori sobre a forma diferencial
=Î`" ÐQ Ñ , visto que a variedade `" ÐQ Ñ não é em geral compacta. O facto de esta última
forma ser integrável é parte da conclusão do lema.
§5. Teorema de Stokes
137
=B œ " 05 ÐBÑ 0•"ßáß5"ß5"ßáß7 ,
7
5œ"
onde as aplicações suaves 05 À Q Ä Š estão definidas por
05 ÐBÑ œ =B Ð/" ß á ß /5" ß /5" ß á ß /7 Ñ,
e o que vimos atrás permite-nos então escrever
Ð:4‡ =ÑB œ 04 Ð:4 ÐBÑÑ Z 96‘7" ,
‡
Ð:4w =ÑB œ 04 Ð:4w ÐBÑÑ Z 96‘7" .
Por diferenciação exterior, obtemos
Ð. =ÑB œ " .05 B • 0•"ßáß5"ß5"ßáß7 .
7
5œ"
Uma vez que
0•"ßáß5"ß5"ßáß7 œ )Ð/" Ñ • â • )Ð/5" Ñ • )Ð/5" Ñ • â • )Ð/7 Ñ
e que
.05 B œ "
7
4œ"
`05
ÐBÑ )Ð/4 Ñ,
`B4
a fórmula precedente vai-nos dar
. =B œ " .05 B • )Ð/" Ñ • â • )Ð/5" Ñ • )Ð/5" Ñ • â • )Ð/7 Ñ œ
7
5œ"
7
œ"
5œ"
7
`05
ÐBÑ )Ð/5 Ñ • )Ð/" Ñ • â • )Ð/5" Ñ • )Ð/5" Ñ • â • )Ð/7 Ñ œ
`B5
œ " Ð"Ñ5"
5œ"
e portanto
`05
ÐBÑ Z 96‘7
`B5
138
Cap. III. Formas diferenciais e teorema de Stokes
5"
( . = œ ( " Ð"Ñ
7
Q
Q 5œ"
œ " Ð"Ñ5" (
7
5œ"
7
E5
5œ"
7
E5
5œ"
7
E5
œ " Ð"Ñ5" (
œ " Ð"Ñ5" (
Ð(
,5
+5
`05
ÐBÑ .B œ
`B5
`05
ÐBÑ .B5 Ñ .ÐB" ß á ß B5" ß B5" ß á ß B7 Ñ œ
`B5
05 ÐB" ß á ß ,5 ß á ß B7 Ñ 05 ÐB" ß á ß +5 ß á ß B7 Ñ .ÐB" ß á ß Bs5 ß á ß B7 Ñ œ
œ " Ð"Ñ5" Ð(
05 ‰ :5w ÐCÑ 05 ‰ :5 ÐCÑ .C œ 28
5œ"
7
E5
:5w Ð=Ñ (
5œ"
Q5w
=Î`" ÐQ Ñ (
œ " Ð"Ñ5" Ð(
‡
E5
:5‡ Ð=Ñ œ
Q5
=Î`" ÐQ Ñ Ñ œ (
`" ÐQ Ñ
=Î`" ÐQ Ñ .
s §I
s e Q § I duas variedades suavemente orientadas
III.5.7. (Lema) Sejam Q
s Ä Q um difeomorfismo. Para cada B! − Q
s , existe então um aberto
e :À Q
s de Q
s , com B! − Y
s , tal que a restrição de : a Y
s seja um difeomorfismo
Y
que ou conserva ou inverte as orientações.
s um aberto de Q
s , contendo B! , tal que exista um campo de
Dem: Seja Y
s
referenciais suave de X ÐQ ÑÎYs , isto é, que existam campos vectoriais
s tais que, para cada B − Y
s , \" B ß á ß \7 B seja uma base
\" ß á ß \7 sobre Y
s
s
de XB ÐQ Ñ. A suavidade da orientação de Q implica que, se necessário subs por um aberto mais pequeno, contendo ainda B! , pode-se já
stituindo Y
supor que ou aquelas bases são todas directas ou elas são todas retrógradas.
s Ñ, que é um aberto de Q contendo :ÐB! Ñ, podemos
Sendo Y œ :ÐY
considerar os campos vectoriais suaves ]" ß á ß ]7 sobre Y , definidos por
]4 C œ H::" ÐCÑ Ð\4 :" ÐCÑ Ñ
s contendo Y
s ). A
(considerar um prolongamento de : a um aberto de I
suavidade da orientação de Q implica que, se necessário substituindo Y por
s pela imagem recíproca
um aberto mais pequeno, ainda contendo :ÐB! Ñ, Y
deste aberto e : pela sua restrição, pode-se já supor que as bases
]" C ß á ß ]7 C são ou todas directas ou todas retrógradas. É agora imediato que
ou o difeomorfismo : conserva as orientações ou ele inverte as
orientações.
28Nesta
igualdade sabemos que a diferença de duas funções é integrável em E5 e estamos
a afirmar que o integral dessa diferença é igual à diferença dos dois integrais. Este
raciocínio poderia ser incorrecto se nada nos garantisse que cada uma das duas funções é
integrável em E5 . Isso acontece, no entanto, visto que estas funções são restrições de
funções contínuas sobre a aderência de E5 , que é compacta.
§5. Teorema de Stokes
139
III.5.8. (Teorema de Stokes) Seja Q § I uma variedade de dimensão 7 ",
suavemente orientada, e seja = œ Ð=B ÑB−Q uma forma diferencial suave de
grau 7 ", com valores em Š e com suporte compacto. Tem-se então
( .= œ (
Q
`" ÐQ Ñ
=Î`" ÐQ Ñ .29
Repare-se que a condição de a forma diferencial = ter suporte compacto encontra-se automaticamente verificada no caso em que a variedade Q é compacta.
Dem: Vamos demonstrar o resultado com hipóteses suplementares sucessivamente mais fracas, até chegar ao resultado geral.
a) Vamos começar por supor que Q é um aberto de
7:
‚ Ò!ß _Ò: , com a orientação correspondente à orientação
‘7
: œ‘
canónica de ‘7 . Seja O § Q um compacto fora do qual = se anula e seja =
o prolongamento de = a ‘7
: que se anula fora de Q . Este prolongamento é
ainda suave por ter restrições suaves aos abertos Q e ‘7
: Ï O , cuja união é
7
‘: (a segunda restrição é identicamente nula). É claro que . = vai ser um
prolongamento suave de . =, que se anula fora de O . Seja , ! tal que
O § Ó,ß ,Ò7 e apliquemos o lema anterior ao produto cartesiano de
intervalos Q w œ Ò,ß ,Ó7: ‚ Ò!ß ,Ó: , que contém O e está contido em ‘7
: .
Reparando que = se anula nos pontos deste produto de intervalos em que
pelo menos uma das coordenadas é , ou , , obtemos agora
( .= œ (
Q
œ(
‘7
:
.= œ (
`" Б7
: Ñ
Qw
.Ð=ÎQ w Ñ œ (
=Î`" Б7: Ñ œ (
`" ÐQ w Ñ
`" ÐQ Ñ
=Î`" ÐQ w Ñ œ
=Î`" ÐQ Ñ .
b) Vamos supor agora que, mais geralmente, a variedade Q é tal que existe
um aberto Y de ‘7
: e um difeomorfismo :À Y Ä Q que ou conserva ou
inverte as orientações. Uma vez que, se o teorema é válido para Q com uma
certa orientação, é-o trivialmente também para Q com a outra orientação (a
orientação induzida no bordo vem também trocada pelo que ambos os
membros da igualdade vêm multiplicados por "), podemos já supor que :
conserva as orientações. Obtemos agora, uma vez que o difeomorfismo
:Î`" ÐY Ñ À `" ÐY Ñ Ä `" ÐQ Ñ também conserva as orientações,
29Tal
como anteriormente, o facto de a forma diferencial . = sobre Q ser integrável é
uma consequência de ela ser suave e de suporte compacto. Já a restrição de = a `" ÐQ Ñ
não terá a priori suporte compacto (tê-lo-ia se a variedade Q não tivesse cantos visto que
nesse caso `" ÐQ Ñ era fechado em Q ). O facto de esta restrição ser integrável é parte do
enunciado do teorema.
140
Cap. III. Formas diferenciais e teorema de Stokes
‡
‡
( . = œ ( : Ð. =Ñ œ ( . : Ð=Ñ œ (
Q
œ(
Y
Y
`" ÐY Ñ
Ð:Î`" ÐY Ñ Ñ Ð=Î`" ÐQ Ñ Ñ œ (
Ð:‡ =ÑÎ`" ÐY Ñ œ
‡
`" ÐY Ñ
`" ÐQ Ñ
=Î`" ÐQ Ñ .
c) Vamos supor agora, ainda mais geralmente, que a variedade Q é
arbitrária, mas que a forma diferencial = é tal que existe um compacto O ,
contido num aberto Z de Q que seja difeomorfo a um aberto de ‘7
: por um
difeomorfismo que conserve ou inverta as orientações, tal que = se anula fora
de O . É claro que . = ainda se anula fora de O pelo que podemos escrever
( . = œ ( . =ÎZ œ (
Q
Z
`" ÐZ Ñ
=Î`" ÐZ Ñ œ (
`" ÐQ Ñ
=Î`" ÐQ Ñ .
d) Passemos por fim à demonstração no caso geral. Seja O § Q um
compacto fora do qual = se anula. Para cada B − O , existe um aberto ZB de
Q contendo B que seja difeomorfo a um aberto de ‘7
: e, se necessário
substituindo esse aberto por um aberto mais pequeno, pode-se já supor que o
difeomorfismo em questão ou conserva ou inverte as orientações. Uma vez
que o compacto O vai estar contido na união dos abertos ZB , vai existir uma
parte finita N de O tal que O esteja contido na união dos conjuntos ZB , com
B − N . Pelo teorema da partição da unidade, podemos considerar aplicações
suaves !B À Q Ä Ò!ß "Ó, onde B − N , tais que cada !B seja nula fora de uma
parte GB de ZB , fechada em Q e que, para cada C − O , ! !B ÐCÑ œ "
B−N
(considerar a cobertura aberta de Q formada pelos ZB , com B − N , e por
Q Ï O e deitar fora a função da partição da unidade correspondente a este
último aberto). Sendo, para cada B − N , =ÐBÑ a forma diferencial suave !B =,
tem-se que =ÐBÑ é nula fora do compacto O GB contido em ZB e vem, para
cada C − Q , =C œ ! =ÐBÑ , visto que ambos os membros da igualdade são
C
nulos se C  O e, para C − O , ! !ÐBÑ ÐCÑ œ ". Tem-se então . = œ ! . =ÐBÑ
B−N
B−N
B−N
pelo que escrevemos finalmente
( . = œ " ( . =ÐBÑ œ " (
Q
B−N
Q
B−N
`" ÐQ Ñ
=ÐBÑ Î`" ÐQ Ñ œ (
`" ÐQ Ñ
=Î`" ÐQ Ñ .
III.5.9. (Corolário) Seja Q § I uma variedade sem bordo, de dimensão
7 ", suavemente orientada. Se = œ Ð=B ÑB−Q é uma forma diferencial
suave de grau 7 " com suporte compacto (condição que se encontra
automaticamente verificada se a variedade Q é compacta), então
( . = œ !.
Q
§5. Teorema de Stokes
141
Note-se que a condição de a forma diferencial = ter suporte compacto é
essencial para a validade do teorema de Stokes. De facto, considerando
uma variedade Q e uma forma diferencial = de suporte compacto tal que
o integral da restrição de = a `" ÐQ Ñ seja não nulo, é imediato que a
igualdade do teorema de Stokes é falsa quando considerarmos como
variedade `! ÐQ Ñ e como forma diferencial a restrição de = (reparar que
.Q ÐQ Ï `! ÐQ ÑÑ œ !).
§6. Versões clássicas do teorema de Stokes.
III.6.1. (Lema) Seja I um espaço euclidiano orientado de dimensão 7 " e
seja J § I um subespaço vectorial de dimensão 7 ", munido de uma
orientação transversa e da orientação induzida (cf. II.7.28). Seja Z 96J o elemento de volume de J . Existe então um, e um só, vector D − I , com norma
", ortogonal a J e pertencente ao semi-espaço positivo, a que damos o nome
de normal unitária positiva, e então, para cada B − I ,
Ї)ÐBÑÑÎJ œ ØBß DÙ Z 96J − E7" ÐJ à ‘Ñ.
Dem: A existência e unicidade de D nas condições do enunciado vem de que
o complementar ortogonal J ¼ de J em I tem dimensão ", pelo que possui
dois, e só dois, vectores de norma ", um simétrico do outro, e destes um vai
estar no semi-espaço positivo e outro no negativo. Seja A" ß á ß A7" uma
base ortonormada, por exemplo directa, de J . Tendo em conta a definição da
orientação induzida, Dß A" ß á ß A7" é uma base ortonormada directa de I e
vem
B œ ØBß DÙ D " ØBß A4 Ù A4 .
4
Obtemos agora, notando Z 96I o elemento de volume de I e tendo em conta
a alínea a) de II.8.18,
‡) ÐBÑÐA" ß á ß A7" Ñ œ Z 96I ÐBß A" ß á ß A7" Ñ œ
œ ØBß DÙ Z 96I ÐDß A" ß á ß A7" Ñ " ØBß A4 Ù Z 96I ÐA4 A" ß á ß A7" Ñ œ
4
œ ØBß DÙ,
e portanto
Ї)ÐBÑÑÎJ œ ‡)ÐBÑÐA" ß á ß A7" Ñ Z 96J œ ØBß DÙ Z 96J .
142
Cap. III. Formas diferenciais e teorema de Stokes
III.6.2. (Teorema da divergência) Sejam I um espaço euclidiano e Q § I
uma variedade de dimensão 7 ", suavemente orientada30. Seja
\ œ Ð\B ÑB−Q um campo vectorial suave, nulo fora de uma certa parte
compacta O de Q . Para cada B − `" ÐQ Ñ, existe então um, e um só, vector
^B − XB ÐQ Ñ Ï tB ÐQ Ñ, com norma " e ortogonal a XB Ð`" ÐQ ÑÑ, a que
daremos o nome de normal unitária exterior e vem
( divÐ\ÑB . .Q ÐBÑ œ (
Q
`" ÐQ Ñ
Ø\B ß ^B Ù . .`" ÐQ Ñ ÐBÑ,
em que as funções integrandas são suaves.31
Dem: A existência e unicidade de ^B , nas condições do enunciado, é uma
consequência do lema anterior e da caracterização do semi-espaço positivo
para a orientação transversa. Seja = œ Ð=B ÑB−Q a forma diferencial real
suave de grau 7 ", definida por =B œ ‡)Ð\B Ñ forma essa que é
evidentemente nula fora do compacto O § Q . Aplicando o teorema de
Stokes, podemos portanto escrever
( .= œ (
Q
`" ÐQ Ñ
=Î`" ÐQ Ñ ,
e o que vamos fazer é interpretar os dois membros desta igualdade em termos
de integrais de funções para as medidas .Q e .`" ÐQ Ñ . Em primeiro lugar,
tendo em conta o lema anterior, tem-se, para cada B em `" ÐQ Ñ,
=B ÎXB Ð`" ÐQ ÑÑ œ Ø\B ß ^B Ù Z 96wB ,
onde Z 96wB é o elemento de volume de XB Ð`" ÐQ ÑÑ, pelo que a suavidade da
forma diferencial =Î`" ÐQ Ñ , de grau 7 ", garante a suavidade da aplicação
de `" ÐQ Ñ em ‘, que a B associa Ø\B ß ^B Ù (cf. III.1.25), concluindo-se em
seguida, por definição, que
(
`" ÐQ Ñ
=Î`" ÐQ Ñ œ (
`" ÐQ Ñ
Ø\B ß ^B Ù . .`" ÐQ Ñ ÐBÑ.
Por outro lado, pela definição da divergência em III.2.11, tem-se, notando
Z 96B o elemento de volume de XB ÐQ Ñ,
. =B œ ‡divÐ\ÑB œ divÐ\ÑB Z 96B ,
30Pode-se
demonstrar este resultado sem a hipótese de Q estar suavemente orientada (cf.
as observações feitas a seguir a III.2.11) mas não temos então um simples corolário do
teorema de Stokes e somos obrigados a repetir parte da respectiva demonstração,
nomeadamente o argumento de partição da unidade para passar do local para o global.
Com o objectivo de manter a exposição mais simples, preferimos fazer aqui a exigência
simplificadora.
31De facto, e embora isso não nos vá fazer falta, pode-se ver mesmo que é suave a
aplicação de `" ÐQ Ñ em I , que a B associa ^B .
§6. Versões clássicas do teorema de Stokes
143
donde, finalmente
( . = œ ( divÐ\ÑB . .Q ÐBÑ.
Q
Q
III.6.3. (Teorema de Stokes clássico) Sejam I um espaço euclidiano e Q § I
uma variedade de dimensão $, suavemente orientada32. Seja \ œ Ð\B ÑB−Q
um campo vectorial suave sobre Q . Seja Q w § Q uma variedade compacta
de dimensão #, suavemente orientada. Tem-se então:
a) Para cada B − Q w , existe um, e um só, vector ^B − XB ÐQ Ñ, que seja ortogonal a XB ÐQ w Ñ, tenha norma " e pertença ao semi-espaço positivo, para a
orientação transversa de XB ÐQ w Ñ em XB ÐQ Ñ que induz em XB ÐQ w Ñ a orientação dada (diremos que ^B é a normal unitária positiva).
b) Para cada B − `" ÐQ w Ñ, existe um, e um só, vector [B − XB Ð`" ÐQ w ÑÑ, que
tenha norma " e constitua uma base directa para a orientação de `" ÐQ w Ñ
como bordo de Q w (diremos que [B é a tangente unitária positiva).
c) Tem-se
(
Qw
ØrotÐ\B Ñß ^B Ù . .Q w ÐBÑ œ (
`" ÐQ w Ñ
Ø\B ß [B Ù . .`" ÐQ w Ñ ÐBÑ,
onde as funções integrandas são aplicações suaves.33
Dem: A existência e unicidade de ^B nas condições de a) resulta de que o
complementar ortogonal de XB ÐQ w Ñ em XB ÐQ Ñ tem dimensão ", pelo que
tem dois, e só dois, vectores de norma ", um simétrico do outro, e destes vai
haver um, e um só, que seja positivo para a orientação transversa. Do mesmo
modo, a existência e unicidade de [B nas condições de b) resulta de que
XB Ð`" ÐQ w ÑÑ é um espaço vectorial de dimensão ". Considerando a forma
diferencial suave de grau ", sobre Q , )Ð\Ñ, podemos aplicar o teorema de
Stokes à sua restrição a Q w , para concluir que se tem
(
Qw
. )Ð\ÑÎQ w œ (
`" ÐQ w Ñ
)Ð\ÑÎ`" ÐQ w Ñ ,
e tudo o que temos que fazer, tal como no resultado anterior, é interpretar
ambos os membros desta igualdade em termos de integrais de funções
relativamente às medidas .Q w e .`" ÐQ w Ñ . Pela definição do rotacional, em
III.2.13, tem-se . )Ð\Ñ œ ‡)ÐrotÐ\ÑÑ pelo que o lema III.6.1 garante que,
para cada B − Q w ,
Ð. )Ð\ÑÑB ÎXB ÐQ w Ñ œ ØrotÐ\ÑB ß ^B Ù Z 96B ,
caso mais clássico, Q é um aberto de ‘$ ou, mais geralmente, dum espaço
euclidiano orientado de dimensão $.
33Tal como no resultado anterior, pode-se provar que são mesmo suaves as aplicações de
Q w em I e de `" ÐQ w Ñ em I , que a B associam ^B e [B , respectivamente.
32No
144
Cap. III. Formas diferenciais e teorema de Stokes
onde Z 96B é o elemento de volume de XB ÐQ w Ñ. Resulta daqui a suavidade da
aplicação de Q w em ‘, que a B associa ØrotÐ\ÑB ß ^B Ù, e a fórmula
(
Qw
. )Ð\ÑÎQ w œ (
Qw
ØrotÐ\ÑB ß ^B Ù . .Q w ÐBÑ.
Por outro lado, para cada B − `" ÐQ w Ñ, o facto de [B constituir uma base
ortonormada directa de XB Ð`" ÐQ w ÑÑ implica que a componente de
)Ð\B ÑÎXB Ð`" ÐQ w ÑÑ no elemento de volume Z 96wB de XB Ð`" ÐQ w ÑÑ é igual a
)Ð\B ÑÐ[B Ñ œ Ø\B ß [B Ù, o que nos permite concluir a suavidade da
aplicação de `" ÐQ w Ñ em ‘, que a B associa Ø\B ß [B Ù assim como o facto de
se ter
(
`" ÐQ w Ñ
)Ð\ÑÎ`" ÐQ w Ñ œ (
`" ÐQ w Ñ
Ø\B ß [B Ù . .`" ÐQ w Ñ .
§7. Operador prismático e lema de Poincaré.
Um resultado clássico, sobre a derivação do integral paramétrico, diz-nos
que, se N é um intervalo aberto de números reais, Y um aberto num
espaço vectorial de dimensão finita I , J um espaço vectorial de
dimensão finita e 0 À N ‚ Y Ä J uma aplicação de classe G 5 , onde
5 !, então, para cada par de reais +ß , − N , tem lugar uma aplicação de
classe G 5 , 1À Y Ä J , definida por
1ÐBÑ œ ( 0 Ð>ß BÑ .>,
,
+
e que, no caso em que 5 ",
H1B Ð?Ñ œ ( H# 0Ð>ßBÑ Ð?Ñ .>.
,
+
Vamos necessitar de uma versão mais geral deste resultado, em que o
aberto Y é substituído por uma variedade e o intervalo N não é
obrigatoriamente aberto.
III.7.1. Sejam I e J espaços vectoriais de dimensão finita, M § ‘ um intervalo,
Q § I uma variedade e 0 À M ‚ Q Ä J uma aplicação de classe G 5 . Dados
+ß , − M , tem então lugar uma aplicação de classe G 5 , 1À Q Ä J , definida
por
1ÐBÑ œ ( 0 Ð>ß BÑ .>,
,
+
§7. Operador prismático e lema de Poincaré
145
e, no caso em que 5 ", tem-se, para cada ? − XB ÐQ Ñ,
H1B Ð?Ñ œ ( H# 0Ð>ßBÑ Ð?Ñ .>.
,
+
Dem: Seja N um intervalo aberto de ‘, contendo M e tal que M seja fechado
em N ; basta tomarmos para extremidade esquerda de N a de M , no caso em
que esta não pertence a M , e _, caso contrário, e tomar para extremidade
direita de N a de M , no caso em que esta não pertence a M , e _, caso
contrário. Seja Y um aberto de I tal que a variedade Q seja fechada em Y
(toda a variedade é localmente compacta e, portanto, localmente fechada em
I ). Tem-se então que M ‚ Q é fechado em N ‚ Y pelo que, pelo método da
partição da unidade, podemos considerar um prolongamento de classe G 5 de
0 , 0 À N ‚ Y Ä J . Aplicando o resultado conhecido a 0 , obtemos uma aplicação de classe G 5 , 1À Y Ä J , definida por
1ÐBÑ œ ( 0 Ð>ß BÑ .>,
,
+
a qual é evidentemente um prolongamento de 1 e, no caso em que 5 ",
tem-se, para cada ? − XB ÐQ Ñ,
H1B Ð?Ñ œ H 1B Ð?Ñ œ ( H# 0 Ð>ßBÑ Ð?Ñ .> œ ( H# 0Ð>ßBÑ Ð?Ñ .>.
,
,
+
+
III.7.2. Sejam Q § I uma variedade, : ! e = œ Ð=Ð>ßBÑ ÑÐ>ßBÑ−Ò!ß"Ó‚Q uma
forma diferencial suave de grau : ", real ou complexa, sobre a variedade
Ò!ß "Ó ‚ Q . Tem então lugar uma forma diferencial suave de grau : sobre a
variedade Q , T = œ ÐT =B ÑB−Q , definida por
T =B Ð?" ß á ß ?: Ñ œ (
"
=Ð>ßBÑ ÐÐ"ß !Ñß Ð!ß ?" Ñß á ß Ð!ß ?: ÑÑ .>.
!
Dem: Considerando o prolongamento euclidiano de =, sabemos que existe
uma aplicação suave = œ Ð=Ð>ßBÑ ÑÐ>ßBÑ−Ò!ß"Ó‚Q , de Ò!ß "Ó ‚ Q em
E:" Б ‚ Ià ŠÑ, tal que cada =Ð>ßBÑ − E:" Б ‚ XB ÐQ Ñà ŠÑ seja uma
restrição de =Ð>ßBÑ . Pelo resultado precedente, vai ter lugar uma aplicação
suave 0 œ Ð0B ÑB−Q , de Q em E:" Б ‚ Ià ŠÑ, definida por
0B œ (
"
=Ð>ßBÑ .>,
!
e, por composição com as aplicações lineares
intÐ"ß!Ñ À E:" Б ‚ Ià ŠÑ Ä E: Б ‚ Ià ŠÑ
e
146
Cap. III. Formas diferenciais e teorema de Stokes
+‡ À E: Б ‚ Ià ŠÑ Ä E: ÐIà ŠÑ
(onde +À I Ä ‘ ‚ I é a aplicação linear, +ÐBÑ œ Ð!ß BÑ), obtemos uma
aplicação suave T =, de Q em E: ÐIà ŠÑ, onde
T =B Ð?" ß á ß ?: Ñ œ 0B ÐÐ"ß !Ñß Ð!ß ?" Ñß á ß Ð!ß ?: ÑÑ œ
œ(
"
=Ð>ßBÑ ÐÐ"ß !Ñß Ð!ß ?" Ñß á ß Ð!ß ?: ÑÑ .>.
!
Vemos assim que cada T =B é uma restrição de T =B , o que mostra que T = é
uma forma diferencial suave.
III.7.3. À aplicação T , que, a cada forma diferencial suave =, de grau : "
sobre Ò!ß "Ó ‚ Q , associa a forma diferencial suave T =, de grau : sobre Q ,
costuma-se dar o nome de operador prismático, por analogia com um
operador com o mesmo nome que é utilizado nas teorias da homologia e da
cohomologia singular, e que joga aí um papel semelhante ao deste.
Repare-se que, como é imediato, T é uma aplicação linear.
III.7.4. Nas condições de III.7.2, notemos :! ß :" À Q Ä Ò!ß "Ó ‚ Q as aplicações
suaves definidas por
:! ÐBÑ œ Ð!ß BÑ,
:" ÐBÑ œ Ð"ß BÑ.
Se = œ Ð=Ð>ßBÑ ÑÐ>ßBÑ−Ò!ß"Ó‚Q é uma forma diferencial suave de grau : " sobre
Ò!ß "Ó ‚ Q , real ou complexa, tem-se então
.T = T . = œ :"‡ = :!‡ =.
Se = œ Ð=Ð>ßBÑ ÑÐ>ßBÑ−Ò!ß"Ó‚Q é uma forma diferencial suave de grau ! sobre
Ò!ß "Ó ‚ Q , real ou complexa, tem-se então
T . = œ :"‡ = :!‡ =.
Dem: Comecemos por tratar o caso em que a forma diferencial = tem grau
: ", com : !. Seja = œ Ð=Ð>ßBÑ ÑÐ>ßBÑ−Ò!ß"Ó‚Q uma aplicação suave de
Ò!ß "Ó ‚ Q em E:" Б ‚ Ià ŠÑ, tal que cada =Ð>ßBÑ seja uma restrição de
=Ð>ßBÑ . Podemos então considerar, como na demonstração de III.7.2, uma
aplicação suave T =, de Q em E: ÐIà ŠÑ, definida por
T =B Ð?" ß á ß ?: Ñ œ (
"
=Ð>ßBÑ ÐÐ"ß !Ñß Ð!ß ?" Ñß á ß Ð!ß ?: ÑÑ .>,
!
tendo-se que cada T =B − E: ÐXB ÐQ Ñà ŠÑ vai ser uma restrição de T =B . A
definição do operador de derivação exterior permite-nos agora escrever
§7. Operador prismático e lema de Poincaré
147
Ð.T =ÑB Ð?" ß á ß ?:" Ñ œ " Ð"Ñ4" HÐT =ÑB Ð?4 ÑÐ?" ß á ß ?s4 ß á ß ?:" Ñ œ
:"
œ " Ð"Ñ4" (
4œ"
:"
4œ"
"
s
H# =Ð>ßBÑ Ð?4 ÑÐÐ"ß !Ñß Ð!ß ?" Ñß á ß Ð!ß ?4 Ñß á ß Ð!ß ?:" ÑÑ .>.
!
Por outro lado,
ÐT .=ÑB Ð?" ß á ß ?:" Ñ œ
œ(
œ(
"
Ð. =ÑÐ>ßBÑ ÐÐ"ß !Ñß Ð!ß ?" Ñß á ß Ð!ß ?:" ÑÑ .> œ
!
"
H=Ð>ßBÑ ÐÐ"ß !ÑÑÐÐ!ß ?" Ñß á ß Ð!ß ?:" ÑÑ .>
!
œ " Ð"Ñ4 (
:"
4œ"
"
s
H=Ð>ßBÑ ÐÐ!ß ?4 ÑÑÐÐ"ß !Ñß Ð!ß ?" Ñß á ß Ð!ß ?4 Ñß á ß Ð!ß ?:" ÑÑ .>
!
pelo que, somando as igualdades anteriores e atendendo a que
`
H# =Ð>ßBÑ Ð?4 Ñ œ H=Ð>ßBÑ ÐÐ!ß ?4 ÑÑ e H=Ð>ßBÑ ÐÐ"ß !ÑÑ œ `>
=Ð>ßBÑ , obtemos
Ð.T = T . =ÑB Ð?" ß á ß ?:" Ñ œ
"
`
œ(
=Ð>ßBÑ ÐÐ!ß ?" Ñß á ß Ð!ß ?:" ÑÑ .> œ
! `>
œ =Ð"ßBÑ ÐÐ!ß ?" Ñß á ß Ð!ß ?:" ÑÑ =Ð!ßBÑ ÐÐ!ß ?" Ñß á ß Ð!ß ?:" ÑÑ œ
œ Ð:"‡ = :!‡ =ÑB Ð?" ß á ß ?:" Ñ,
o que termina a demonstração, para as formas de grau maior ou igual a ". O
caso em que = é uma forma de grau !, portanto uma aplicação de Ò!ß "Ó ‚ Q
em Š, é do mesmo tipo, mas mais simples: Vem
ÐT . =ÑB œ (
"
!
. =Ð>ßBÑ ÐÐ"ß !ÑÑ .> œ (
œ =Ð"ßBÑ =Ð!ßBÑ
"
`
=Ð>ßBÑ .> œ
! `>
œ Ð:"‡ = :!‡ =ÑB .
s espaços vectoriais de dimensão finita e Q § I e Q
s §I
s
III.7.5. Sejam I e I
s Ä Q são suaveduas variedades. Diz-se que duas aplicações suaves 0 ß 1À Q
s Ä Q , tal
mente homotópicas se existir uma aplicação suave LÀ Ò!ß "Ó ‚ Q
s,
que, para cada B − Q
LÐ!ß BÑ œ 0 ÐBÑ,
LÐ"ß BÑ œ 1ÐBÑ.
Diz-se então que L é uma homotopia suave de 0 para 1.
s §I
s duas variedades e 0 ß 1À Q
s Ä Q duas
III.7.6. Sejam Q § I e Q
aplicações suaves, suavemente homotópicas. Seja = œ Ð=C ÑC−Q uma forma
diferencial suave de grau : sobre Q , que seja fechada, isto é, que verifique
148
Cap. III. Formas diferenciais e teorema de Stokes
s:
. = œ !. Tem-se então, para as correspondentes imagens recíprocas sobre Q
‡
‡
a) Se : œ !, então 0 = œ 1 =;
s , isto
b) Se : ", então 1‡ = 0 ‡ = é uma forma diferencial exacta sobre Q
s,
é, existe uma forma diferencial suave de grau : ", 5 œ Ð5B ÑB−Qs , sobre Q
tal que 1‡ = 0 ‡ = œ . 5 .
Dem: Nas notações de III.7.4, sendo L uma homotopia suave de 0 para 1, L
s em Q , tal que L ‰ :! œ 0 e
é uma aplicação suave de Ò!ß "Ó ‚ Q
L ‰ :" œ 1. O facto de se ter . = œ ! implica que
T .L ‡ = œ T L ‡ . = œ !.
Podemos aplicar agora III.7.4 para escrever, se : œ !,
1‡ = 0 ‡ = œ :"‡ L ‡ = :!‡ L ‡ = œ T .L ‡ = œ !,
e, se : ",
1‡ = 0 ‡ = œ :"‡ L ‡ = :!‡ L ‡ = œ T .L ‡ = .T L ‡ = œ . 5,
desde que se tome 5 œ T L ‡ =, que é uma forma diferencial suave de grau
s .
: " sobre Q
III.7.7. Diz-se que uma variedade Q § I é suavemente contráctil se a aplicação
identidade de Q é suavemente homotópica a uma aplicação constante de Q
em Q , isto é, se existem B! − Q e uma aplicação suave
LÀ Ò!ß "Ó ‚ Q Ä Q tais que, para cada B − Q ,
LÐ!ß BÑ œ B,
LÐ"ß BÑ œ B! .
III.7.8. Como exemplos de variedades suavemente contrácteis, temos:
a) Se Q § I é uma variedade estrelada relativamente a um dos seus pontos
B! , então Q é suavemente contráctil. Em particular, toda a variedade, que
seja um conjunto convexo e não vazio, é suavemente contráctil.
s §I
s duas variedades difeomorfas, então, se Q é
b) Sendo Q § I e Q
s é também suavemente contráctil.
suavemente contráctil, Q
c) Se Q § I é uma variedade arbitrária, então cada ponto B! − Q admite
um sistema fundamental de vizinhanças abertas que são variedades suavemente contrácteis.
Dem: Para a), podemos considerar a aplicação suave LÀ Ò!ß "Ó ‚ Q Ä Q ,
definida por
LÐ>ß BÑ œ Ð" >Ñ B > B! ,
que verifica LÐ!ß BÑ œ B e LÐ"ß BÑ œ B! .
Para provar b), seja LÀ Ò!ß "Ó ‚ Q Ä Q uma homotopia suave de M.Q para
s um difeomorfismo.
a aplicação constante de valor B! − Q e seja 0 À Q Ä Q
s
s ÄQ
s por
Podemos então definir uma aplicação suave LÀ Ò!ß "Ó ‚ Q
§7. Operador prismático e lema de Poincaré
149
s CÑ œ 0 ÐLÐ>ß 0 " ÐCÑÑÑ,
LÐ>ß
s CÑ œ C e LÐ"ß
s CÑ œ 0 ÐB! Ñ, pelo que L
s é uma
aplicação que verifica LÐ!ß
homotopia suave de M.Qs para a aplicação constante de valor 0 ÐB! Ñ.
Relativamente a c), reparamos que o ponto B! admite um sistema
fundamental de vizinhanças abertas, que são difeomorfas à intersecção de um
sector de um espaço vectorial de dimensão finita com uma bola aberta de
centro em ! (relativamente a uma certa norma), bastando então reparar que
uma tal intersecção é estrelada relativamente a ! (aliás é mesmo convexa).
III.7.9. Sejam Q § I uma variedade e = œ Ð=B ÑB−Q uma forma diferencial
suave de grau :. Como referimos atrás, diz-se que = é fechada se se tem
. = œ ! e, no caso em que : ", diz-se que = é exacta se existe uma forma
diferencial suave 5 œ Ð5B ÑB−Q , de grau : ", tal que = œ . 5 . A identidade
.. 5 œ ! mostra-nos que toda a forma diferencial exacta é fechada. O lema
de Poincaré, que demonstramos em seguida, diz-nos que a recíproca é
também verdadeira, no caso em que a variedade Q é suavemente contráctil.
Apresentamos a seguir um exemplo de uma situação em que essa recíproca
não é verdadeira, o que nos dará, em particular, um exemplo de uma
variedade que não é suavemente contráctil.
III.7.10. (Lema de Poincaré) Sejam Q § I uma variedade suavemente
contráctil e = œ Ð=B ÑB−Q uma forma diferencial suave, de grau : ",
verificando . = œ !. Existe então uma forma diferencial suave de grau : ",
5 œ Ð5B ÑB−Q , tal que = œ . 5 .
Dem: Uma vez que a aplicação M.Q À Q Ä Q é suavemente homotópica a
uma aplicação constante 0 À Q Ä Q , vimos em III.7.6 que existe uma forma
‡
diferencial suave 5 , de grau : ", tal que 0 ‡ = M.Q
= œ . 5 . O facto de se
ter : " e H0B œ !, para cada B − Q , implica que
Ð0 ‡ =ÑB Ð?" ß á ß ?: Ñ œ =0 ÐBÑ ÐH0B Ð?" Ñß á ß H0B Ð?: ÑÑ œ !,
‡
portanto 0 ‡ = œ !. Uma vez que M.Q
= œ =, a igualdade que referimos atrás
pode ser escrita na forma = œ . 5 , portanto = œ .Ð5 Ñ.
III.7.11. Seja Q § I uma variedade de dimensão 7, compacta, sem bordo,
orientável e não vazia. Existe então sobre Q uma forma diferencial suave de
grau 7, que é fechada mas não exacta, a saber, a forma diferencial elemento
de volume, Z 96 œ ÐZ 96B ÑB−Q , associada a uma orientação suave e a um
produto interno de I . Em particular, no caso em que 7 ", a variedade Q
não é suavemente contráctil.
Dem: Fixemos um produto interno em I e consideremos sobre Q uma
orientação suave. Sabemos então que Z 96 œ ÐZ 96B ÑB−Q é uma forma
diferencial suave de grau 7, que vai ser automaticamente fechada, uma vez
que sobre uma variedade de dimensão 7 todas as formas diferenciais de grau
maior que 7 são identicamente nulas. Vamos demonstrar, por absurdo, que a
forma diferencial Z 96 não é exacta. Suponhamos assim que existia uma
150
Cap. III. Formas diferenciais e teorema de Stokes
forma diferencial suave = de grau 7 ", tal que Z 96 œ . =. Sendo .Q a
medida de Lebesgue de Q , o teorema de Stokes permitia-nos escrever então
.Q ÐQ Ñ œ ( " . .Q ÐBÑ œ ( Z 96 œ ( . = œ (
Q
Q
Q
`" ÐQ Ñ
=Î`" ÐQ Ñ œ !,
o que é absurdo.
III.7.12. Como exemplo de variedade nas condições anteriores, temos a hipersuperfície esférica W de um espaço euclidiano I , com dimensão 8 " (8 !),
W œ ÖB − I ± mBm œ "×.
O facto de W ser orientável vem de que podemos considerar em W a
orientação que resulta de W ser o bordo de índice " da bola fechada
F œ ÖB − I ± mBm Ÿ "×,
que é uma variedade de dimensão 8 ", sobre a qual podemos considerar
uma orientação constante.
§8. Aplicação à demonstração de resultados topológicos.
III.8.1. Dados um conjunto Q e um subconjunto W § Q , chama-se retracção
de Q sobre W a uma aplicação 0 À Q Ä W que prolongue a identidade de W ,
isto é, que verifique 0 ÐBÑ œ B, para cada B − W . Por outras palavras, dizer
que 0 À Q Ä W é uma retracção de Q sobre W é o mesmo que dizer que se
tem 0 ‰ + œ M.W , onde +À W Ä Q é a inclusão.
III.8.2. Se Q é um espaço topológico separado e se 0 é uma retracção contínua
de Q sobre um subconjunto W , então W é fechado em Q .
Dem: Basta atender a que W œ ÖB − Q ± 0 ÐBÑ œ B×.
III.8.3. (Inexistência de retracções suaves sobre o bordo) Sejam I um espaço
euclidiano e Q § I uma variedade de dimensão 7, compacta, orientável e
não vazia. Não existe então nenhuma retracção suave de Q sobre o bordo
`" ÐQ Ñ.
Dem: Suponhamos que 0 À Q Ä W era uma retracção suave de Q sobre o
bordo W œ `" ÐQ Ñ, e consideremos sobre W a orientação induzida por uma
das orientações suaves de Q . Tem-se, é claro, 7 ", visto que não existe
nenhuma aplicação de Q no conjunto vazio. A variedade W tem dimensão
7 " e podemos considerar sobre W a forma diferencial elemento de
volume Z 96 œ ÐZ 96B ÑB−W , que é uma forma diferencial suave de grau 7 ".
Uma vez que numa variedade de dimensão 7 " todas as formas
diferenciais de grau 7 são nulas, tem-se . Z 96 œ !. Consideremos a forma
diferencial suave de grau 7 ", 0 ‡ Z 96, sobre Q , para a qual se tem ainda
§8. Aplicação à demonstração de resultados topológicos
151
.0 ‡ Z 96 œ 0 ‡ . Z 96 œ !.
Aplicando o teorema de Stokes, vem
! œ ( .0 ‡ Z 96 œ ( Ð0 ‡ Z 96ÑÎW .
Q
W
Mas, sendo +À W Ä Q a inclusão, tem-se
‡
‡ ‡
‡
( Ð0 Z 96ÑÎW œ ( + 0 Z 96 œ ( Ð0 ‰ +Ñ Z 96 œ
W
W
W
œ ( M.W‡ Z 96 œ ( Z 96 œ .W ÐWÑ Á !,
W
W
pelo que fomos conduzidos a um absurdo (repare-se que W não é vazio, mais
uma vez por não existir nenhuma aplicação de Q no conjunto vazio).
III.8.4. (Corolário) Sejam I um espaço euclidiano de dimensão 8, F a bola
fechada,
F œ ÖB − I ± mBm Ÿ "×,
e W § F a hipersuperfície esférica,
W œ ÖB − I ± mBm œ "×.
Não existe então nenhuma retracção suave de F sobre W .
Nas condições do corolário precedente pode-se provar a afirmação mais
forte, que garante que não existe nenhuma retracção contínua de F sobre
W. Para provarmos isso, apresentamos dois resultados sobre aproximação
de funções contínuas por aplicações suaves, resultados que são úteis em
várias situações em que se pretende generalizar resultados sobre aplicações suaves para obter outros sobre aplicações contínuas.
III.8.5. Sejam I e J espaços vectoriais de dimensão finita, o segundo dos quais
munido duma norma, Q § I um conjunto fechado e 0 À Q Ä J uma
aplicação contínua. Para cada $ !, existe então uma aplicação suave
1À I Ä J , tal que, para cada B − Q , m1ÐBÑ 0 ÐBÑm $ .34
Dem:35 Seja $ ! e consideremos, para cada C − Q , o aberto YC de Q ,
YC œ ÖB − Q ± m0 ÐCÑ 0 ÐBÑm $ ×,
s C de I , tal
que contém C. Para cada C − Q , podemos considerar um aberto Y
s C Q e, aplicando o teorema da partição da unidade à cobertura
que YC œ Y
34Ver o exercício III.41 adiante para generalizações deste resultado.
35Esta demonstração é baseada na de um resultado análogo que encontrámos
em [14].
152
Cap. III. Formas diferenciais e teorema de Stokes
s C e por I Ï Q , e ignorando a função corresaberta de I constituída pelos Y
pondente a este último aberto, concluímos a existência de uma família
localmente finita Ð:C ÑC−Q , de aplicações suaves :C À I Ä Ò!ß "Ó tais que :C se
s C fechada em I , que, para cada B − I ,
anula fora de uma certa parte de Y
! :C ÐBÑ Ÿ " e que, para cada B − Q , ! :C ÐBÑ œ ". Seja 1À I Ä J a
C−Q
C−Q
aplicação suave definida por
1ÐBÑ œ " :C ÐBÑ 0 ÐCÑ
C−Q
(soma de uma família localmente finita de aplicações suaves). Seja B − Q .
Notemos QB o conjunto finito dos C − Q tais que :C ÐBÑ Á ! e reparemos
s C Q œ YC , donde m0 ÐCÑ 0 ÐBÑm $ Þ
que, para cada C − QB , vem B − Y
Tem-se portanto
m1ÐBÑ 0 ÐBÑm œ m" :C ÐBÑ 0 ÐCÑ " :C ÐBÑ 0 ÐBÑm œ
C−QB
C−QB
œ m" :C ÐBÑ Ð0 ÐCÑ 0 ÐBÑÑm Ÿ
C−QB
Ÿ " :C ÐBÑ m0 ÐCÑ 0 ÐBÑm " :C ÐBÑ $ œ $ .
C−QB
C−QB
III.8.6. Sejam I e J espaços vectoriais de dimensão finita, o segundo dos quais
munido de uma norma, Q § I um conjunto fechado e W uma parte fechada
de Q . Seja 0 À Q Ä J uma aplicação contínua tal que a restrição
0ÎW À W Ä ‘ seja suave. Para cada $ ! existe então uma aplicação suave
1À I Ä J tal que 1ÎW œ 0ÎW e que m1ÐBÑ 0 ÐBÑm $ , para cada B − Q .
Dem: O facto de 0ÎW ser uma aplicação suave, com domínio W fechado em
I , garante-nos a existência de uma aplicação suave s0 À I Ä J , prolongando
0ÎW (corolário do teorema da partição da unidade). Pelo resultado precedente,
podemos considerar uma aplicação suave s1À I Ä J tal que, para cada
B − Q , m1ÐBÑ
0 ÐBÑm $ . Consideremos o aberto Y de Q , contendo W ,
s
s ÐBÑ 0 ÐBÑm $ ×,
Y œ ÖB − Q ± m0
s um aberto de I , tal que Y œ Y
s Q . Pelo teorema da partição da
e seja Y
s e I Ï W,
unidade, relativo à apresentação de I como união dos abertos Y
podemos considerar uma aplicação suave :À I Ä Ò!ß "Ó tal que :ÐBÑ œ ",
s . Consideremos finalmente a
para cada B − W , e :ÐBÑ œ !, para cada B  Y
aplicação suave 1À I Ä J , definida por
1ÐBÑ œ :ÐBÑ s0 ÐBÑ Ð" :ÐBÑÑ s1ÐBÑ.
§8. Aplicação à demonstração de resultados topológicos
153
Se B − W , vem :ÐBÑ œ ", portanto 1ÐBÑ œ s0 ÐBÑ œ 0 ÐBÑ. Se B − Q , duas
hipóteses são possíveis: Se B  Y , tem-se :ÐBÑ œ !, donde
m1ÐBÑ 0 ÐBÑm œ m1ÐBÑ
0 ÐBÑm $;
s
se
B − Y,
tem-se
simultaneamente
m1ÐBÑ
0 ÐBÑm $, pelo que, mais uma vez,
s
s ÐBÑ 0 ÐBÑm $
m0
e
s ÐBÑ 0 ÐBÑÑ Ð" :ÐBÑÑÐ1ÐBÑ
m1ÐBÑ 0 ÐBÑm œ m:ÐBÑÐ0
0 ÐBÑÑm Ÿ
s
s ÐBÑ 0 ÐBÑm Ð" :ÐBÑÑm1ÐBÑ
Ÿ :ÐBÑm0
0 ÐBÑm
s
:ÐBÑ $ Ð" :ÐBÑÑ $ œ $.
III.8.7. (Corolário) Sejam I um espaço euclidiano de dimensão 8, F a bola
fechada,
F œ ÖB − I ± mBm Ÿ "×,
e W § F a hipersuperfície esférica,
W œ ÖB − I ± mBm œ "×.
Não existe então nenhuma retracção contínua de F sobre W .
Dem: Suponhamos que 0 À F Ä W era uma retracção contínua de F sobre W .
A restrição de 0 a W era a identidade de W , em particular suave, pelo que,
pelo resultado precedente, ia existir uma aplicação suave 1À I Ä I tal que
1ÎW œ 0ÎW œ M.W e que, para cada B − F , m1ÐBÑ 0 ÐBÑm ", o que implica,
em particular, por ser m0 ÐBÑm œ ", que 1ÐBÑ Á !. A aplicação 1 não tinha que
tomar valores em W , mas podemos considerar a aplicação suave 2À F Ä W ,
definida por 2ÐBÑ œ 1ÐBÑÎm1ÐBÑm. Esta aplicação ia ser uma retracção suave
de F sobre W , o que contrariava a conclusão de III.8.4.
III.8.8. (Teorema do ponto fixo de Brouwer) Sejam I um espaço euclidiano e
F § I a bola fechada,
F œ ÖB − I ± mBm Ÿ "×.
Se 0 À F Ä F é uma aplicação contínua, existe então B − F tal que
0 ÐBÑ œ B.
Dem: Notemos W œ ÖB − I ± mBm œ "×. Vamos supor que, para cada
B − F , 0 ÐBÑ Á B e tentar chegar a um absurdo, construindo uma aplicação
contínua 1À F Ä W que seja uma retracção de F sobre W . Geometricamente,
a aplicação 1 associa a cada B − F um dos pontos de intersecção de W com a
recta determinada por B e 0 ÐBÑ, a saber o que está do lado de B. Por outras
palavras, vai-se ter 1ÐBÑ œ B :ÐBÑ Ð0 ÐBÑ BÑ, onde a aplicação :À F Ä ‘
deve verificar as condições :ÐBÑ Ÿ ! e
ØB :ÐBÑ Ð0 ÐBÑ BÑß B :ÐBÑ Ð0 ÐBÑ BÑÙ œ ".
154
Cap. III. Formas diferenciais e teorema de Stokes
Figura 4
Esta última condição é equivalente à equação do segundo grau em :ÐBÑ
Ø0 ÐBÑ Bß 0 ÐBÑ BÙ :ÐBÑ# # Ø0 ÐBÑ Bß BÙ :ÐBÑ Ð" ØBß BÙÑ œ !.
Reparemos que, se B − W , a desigualdade de Cauchy-Schwartz garante-nos
que
Ø0 ÐBÑß BÙ Ÿ lØ0 ÐBÑß BÙl Ÿ m0 ÐBÑm Ÿ " œ ØBß BÙ
e que, se fosse Ø0 ÐBÑß BÙ œ ØBß BÙ, 0 ÐBÑ e B seriam linearmente dependentes
e ter-se-ia m0 ÐBÑm œ ", pelo que, uma vez que, por hipótese, 0 ÐBÑ Á B, viria
0 ÐBÑ œ B, o que era absurdo, por se ter então Ø0 ÐBÑß BÙ œ " Á
" œ ØBß BÙ. Concluímos assim que, se B − W , tem-se Ø0 ÐBÑß BÙ ØBß BÙ,
portanto Ø0 ÐBÑ Bß BÙ !. Podemos agora examinar de novo a equação do
segundo grau em :ÐBÑ atrás referida para concluir que, se B − W , aquela
equação admite uma solução nula e a outra estritamente positiva e que, se
B − F Ï W, aquela equação admite duas raízes reais, uma estritamente
positiva e a outra estritamente negativa; em qualquer caso, existe uma única
solução menor ou igual a !, a saber,
:ÐBÑ œ
Ø0 ÐBÑ Bß BÙ ÈØ0 ÐBÑ Bß BÙ# Ð" mBm# Ñm0 ÐBÑ Bm#
.
m0 ÐBÑ Bm#
A aplicação :À F Ä ‘, assim definida, é contínua, ficando portanto contínua
a correspondente aplicação 1À F Ä W , definida por
1ÐBÑ œ B :ÐBÑ Ð0 ÐBÑ BÑ,
aplicação que vai ser uma retração de F sobre W , visto que, para cada B − W ,
tem-se :ÐBÑ œ !, portanto 1ÐBÑ œ B.
III.8.9. (Teorema da esfera despenteada) Seja I um espaço euclidiano de
dimensão 8 ímpar e seja W § I a hipersuperfície esférica,
§8. Aplicação à demonstração de resultados topológicos
155
W œ ÖB − I ± mBm œ "×.
Se \À W Ä I é uma aplicação suave, então existe B − W tal que \B − ‘B.
Em particular, se \ œ Ð\B ÑB−W é um campo vectorial suave sobre W , então
existe B − W tal que \B œ !.
Dem: Pode-se evidentemente já supor que a dimensão 8 de I é maior que ",
sem o que o resultado é trivial. Suponhamos que \À W Ä I é uma aplicação
suave tal que, para cada B − W , \B Â ‘B, isto é, B e \B são linearmente
independentes. Podemos então considerar uma aplicação suave
LÀ Ò!ß "Ó ‚ W Ä W, definida por
LÐ>ß BÑ œ
cosÐ1>Ñ B sinÐ1>Ñ \B
,
mcosÐ1>Ñ B sinÐ1>Ñ \B m
a qual verifica LÐ!ß BÑ œ B e LÐ"ß BÑ œ B, sendo portanto uma homotopia
suave de M.W para M.W . Fixemos uma orientação de I e consideremos
sobre W a orientação suave que lhe vem de ser o bordo da bola
F œ ÖB − I ± mBm Ÿ "×,
com a orientação constante. O facto de a dimensão de I ser ímpar implica
que o isomorfismo M.I À I Ä I inverte as orientações, visto que, se
A" ß á ß A8 for uma base directa de I , a base A" ß á ß A8 de I vai ser
retrógrada. Segue-se daqui que M.F À F Ä F é um difeomorfismo
invertendo as orientações, pelo que o difeomorfismo M.W À W Ä W também
inverte as orientações (cf. III.5.4). Sendo Z 96 a forma diferencial elemento
de volume de W , que, por ter grau igual à dimensão de W vai ser
automaticamente fechada, podemos aplicar III.7.6 para garantir a existência
de uma forma diferencial suave 5 , de grau 8 # sobre W , tal que
M.W‡ Z 96 ÐM.W ч Z 96 œ . 5.
Tendo em conta o teorema de Stokes, assim como III.4.4, podemos agora
escrever
.W ÐWÑ œ ( Z 96 œ ( M.W‡ Z 96 ( . 5 œ
W
W
W
œ ( ÐM.W Ñ Z 96 œ ( Z 96 œ .W ÐWÑ,
‡
W
W
o que é absurdo por ser .W ÐWÑ Á !. Por fim, no caso em que \ é um campo
vectorial suave, tem-se Ø\B ß BÙ œ !, pelo que a condição \B − ‘B implica
\B œ !.
III.8.10. (Corolário) Seja I um espaço euclidiano de dimensão ímpar e seja
W § I a hipersuperfície esférica,
W œ ÖB − I ± mBm œ "×.
156
Cap. III. Formas diferenciais e teorema de Stokes
Se \À W Ä I é uma aplicação contínua, então existe B − W tal que
\B − ‘B. Em particular, no caso em que \ é um campo vectorial contínuo
sobre W , existe B − W tal que \B œ !.
Dem: Suponhamos que \À W Ä I era uma aplicação contínua tal que, para
cada B − W , \B Â ‘B. Resulta daqui que o subconjunto compacto E de
I ‚ I , constituído pelos ÐBß \B Ñ, com B − \ , não intersectava o
subconjunto fechado F de I ‚ I , formado pelos pares ÐBß AÑ, com B − W e
A − ‘B (reparar que, para B − W , esta última condição é equivalente a
A œ ØAß BÙB). Podíamos então considerar a distância estritamente positiva $ ,
do compacto E ao fechado F , em que consideramos, para fixar ideias, a
norma do máximo em I ‚ I . Tendo em conta o resultado de aproximação
III.8.5, podíamos considerar uma aplicação suave ] À W Ä I tal que, para
cada B − W , m]B \B m $ , o que implicava que
mÐBß ]B Ñ ÐBß \B Ñm $,
portanto ÐBß ]B Ñ Â F, ou seja ]B Â ‘B. Chegámos assim a uma contradição
com a conclusão do resultado precedente.
III.8.11. (Nota) Uma maneira de olhar intuitivamente para os resultados precedentes é imaginar que a hipersuperfície esférica é cabeluda e que a tentamos
pentear de maneira suave ou simplesmente contínua. Podemos então garantir
que há pelo menos um ponto onde o cabelo tem que ficar em pé.
Repare-se também que a condição de I ter dimensão ímpar é essencial. Por
exemplo, em ‘2 , a aplicação suave de W em ‘# , que a ÐBß CÑ associa ÐCß BÑ,
é um campo vectorial suave que nunca se anula e um exemplo análogo pode
ser apresentado em cada espaço ‘#8 .
§9. Teorema de Stokes singular. Ângulo sólido orientado.
III.9.1. Seja Q § I uma variedade. Vamos chamar variedade singular de
s é uma variedade de
dimensão 8 em Q a um par ÐEß 0 Ñ, em que E § I
dimensão 8 suavemente orientada e 0 À E Ä Q é uma aplicação contínua.
Dizemos que a variedade singular é compacta se isso acontecer a E e que ela
é sem bordo se E é uma variedade sem bordo. Chamamos bordo da
variedade singular à variedade singular determinada pelo bordo `" ÐEÑ, com a
orientação induzida, e pela restrição da aplicação 0 a esse bordo, restrição
que será notada simplesmente `Ð0 Ñ. Dizemos que a variedade singular é
suave se isso acontecer à aplicação 0 .
III.9.2. Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma forma diferencial
suave de grau 8, com valores em Š. Se ÐEß 0 Ñ é uma variedade singular
suave de dimensão 8 em Q , podemos considerar a forma diferencial suave
0 ‡ =, de grau 8 sobre E, e diz-se que = é integrável em ÐEß 0 Ñ se 0 ‡ = for
integrável em E, definindo-se nesse caso o integral de = em ÐEß 0 Ñ como
§9. Teorema de Stokes singular
157
sendo igual ao integral de 0 ‡ = em E:
(
ÐEß0 Ñ
= œ ( 0 ‡ =.
E
Quando não houver risco de confusão sobre qual a variedade orientada E que
se considera, usa-se também a notação
( =œ(
0
=.
ÐEß0 Ñ
III.9.3. Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma forma diferencial
suave de grau 8, com valores em Š. Se ÐEß 0 Ñ é uma variedade singular
suave, compacta, de dimensão 8 em Q , então = é integrável em ÐEß 0 Ñ.
Dem: Trata-se de uma consequência de III.4.7, visto que 0 ‡ = vai ser uma
forma diferencial suave de grau 8, sobre a variedade compacta suavemente
orientada E, com dimensão 8.
III.9.4. (Exemplo) Sejam Q § I uma variedade e 1À Q Ä Š uma aplicação
suave, portanto também uma forma diferencial suave de grau !, com valores
s um conjunto finito, que é portanto uma variedade
em Š. Seja E § I
compacta de dimensão !, e consideremos uma orientação sobre E
(automaticamente suave), notando, para cada B − E, &B œ " ou &B œ ",
conforme a orientação do espaço vectorial, de dimensão !, XB ÐEÑ seja a
canónica ou não. Se 0 À E Ä Q é uma aplicação arbitrária (automaticamente
suave), tem-se então que
( 1 œ " &B 1Ð0 ÐBÑÑ.
0
B−E
Dem: A forma diferencial 0 ‡ 1, de grau !, sobre E, não é mais do que a
função composta 1 ‰ 0 À E Ä Š. Uma vez que o elemento de volume do
espaço vectorial XB ÐEÑ, de dimensão !, é &B , podemos escrever
Ð1 ‰ 0 ÑB œ &B 1Ð0 ÐBÑ Z 96B
e portanto, uma vez que a medida de Lebesgue sobre E é a medida de
contagem,
‡
( 1 œ ( 0 1 œ ( &B 1Ð0 ÐBÑÑ . .E ÐBÑ œ " &B 1Ð0 ÐBÑÑ.
0
E
E
B−E
III.9.5. Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma forma diferencial
suave de grau 8 ", com valores em Š. Se ÐEß 0 Ñ é uma variedade singular
de dimensão 8 em Q , com 0 aplicação constante, tem-se então que = é
integrável em ÐEß 0 Ñ e 'ÐEß0 Ñ = œ !.
158
Cap. III. Formas diferenciais e teorema de Stokes
Dem: O facto de 0 ser constante implica que, para cada B − E, H0B œ !
donde, uma vez que 8 ", Ð0 ‡ =ÑB œ H0B‡ =0 ÐBÑ œ !.
s §I
s duas variedades, 1À Q
s Ä Q uma aplicação
III.9.6. Sejam Q § I e Q
suave e = œ Ð=D ÑD−Q uma forma diferencial suave de grau 8, com valores
s,
em Š. Se ÐEß 0 Ñ é uma variedade singular suave de dimensão 8 em Q
ÐEß 1 ‰ 0 Ñ vai ser uma variedade singular suave de dimensão 8 em Q e = é
integrável em ÐEß 1 ‰ 0 Ñ se, e só se, 1‡ = for integrável em ÐEß 0 Ñ, tendo-se,
nesse caso,
(
1‰0
= œ ( 1‡ =.
0
Dem: Trata-se de uma consequência imediata da definição, se repararmos
que Ð1 ‰ 0 ч = œ 0 ‡ 1‡ =.
III.9.7. (Reparametrização) Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma
s
forma diferencial suave de grau 8, com valores em Š. Sejam E e E
s Ä E um
variedades de dimensão 8 suavemente orientadas e 0 À E
difeomorfismo conservando (resp. invertendo) as orientações. Se ÐEß 1Ñ é
uma variedade singular suave em Q , tem-se que = é integrável em ÐEß 1Ñ se,
s 1 ‰ 0 Ñ e, nesse caso,
e só se, = é integrável em ÐEß
(
ÐEß1Ñ
=œ(
s
ÐEß1‰0
Ñ
=
(resp. (
ÐEß1Ñ
= œ (
s
ÐEß1‰0
Ñ
=).
Dem: Trata-se de uma consequência imediata da definição e de III.4.4, se
repararmos que Ð1 ‰ 0 ч = œ 0 ‡ 1‡ =.
III.9.8. Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma forma diferencial
suave de grau 8, real ou complexa. Sejam F § Q uma variedade de dimensão 8, suavemente orientada, e ÐEß 0 Ñ uma variedade singular de dimensão 8
em Q , tal que 0 seja um difeomorfismo de E sobre F conservando (resp.
invertendo) as orientações. Tem-se então que = é integrável em ÐEß 0 Ñ se, e
só se, =ÎF é integrável em F e, nesse caso,
( = œ ( =ÎF
0
F
(resp. ( = œ ( =ÎF ).
0
F
Dem: Trata-se de uma consequência imediata da definição e de III.4.4, se
repararmos que 0 ‡ = œ 0 ‡ Ð=ÎF Ñ.
III.9.9. (Teorema de Stokes singular) Sejam Q § I uma variedade e
= œ Ð=C ÑC−Q uma forma diferencial suave de grau 8 sobre Q , real ou
complexa. Seja ÐEß 0 Ñ uma variedade singular, compacta, suave, de
dimensão 8 ", em Q . Tem-se então que . = é integrável em ÐEß 0 Ñ, = é
integrável em Ð`" ÐEÑß `Ð0 ÑÑ e
§9. Teorema de Stokes singular
159
( .= œ (
0
=.
`Ð0 Ñ
Dem: Este resultado vai ser uma consequência simples do teorema de Stokes,
demonstrado em III.5.8. Com efeito, esse resultado, aplicado à forma diferencial suave de grau 8 sobre E, 0 ‡ =, garante-nos que se tem
‡
( .0 = œ (
E
`" ÐEÑ
Ð0 ‡ =ÑÎ`" ÐEÑ ,
em que, em particular, as formas diferenciais .0 ‡ = e 0 ‡ = são integráveis
sobre as variedades respectivas. Basta agora repararmos que .0 ‡ = œ 0 ‡ . =, e
portanto
‡
( .0 = œ ( . =,
E
0
e que, notando +À `" ÐEÑ Ä E a inclusão,
(
`" ÐEÑ
Ð0 ‡ =ÑÎ`" ÐEÑ œ (
`" ÐEÑ
+‡ 0 ‡ = œ (
`" ÐEÑ
`Ð0 ч = œ (
=.
`0
III.9.10. (Exemplo) Dada uma variedade Q § I , um exemplo importante, e
muito frequente, de variedade singular em Q é o constituído pelos caminhos
ou trajectórias em Q , isto é, pelos pares ÐÒ+ß ,Óß 0 Ñ, com + e , números reais,
verificando + ,, e 0 À Ò+ß ,Ó Ä Q aplicação contínua. Trata-se de
variedades singulares de dimensão ", estando implícito que a orientação que
se considera em Ò+ß ,Ó é a que provém da orientação canónica de ‘.
Repare-se que `" ÐÒ+ß ,ÓÑ œ Ö+ß ,× e que, como se reconhece imediatamente, a
orientação associada de Ö+ß ,× é aquela para a qual X, ÐÖ+ß ,×Ñ œ Ö!× tem a
orientação canónica e X+ ÐÖ+ß ,×Ñ œ Ö!× tem a orientação não canónica. O
teorema de Stokes singular pode, neste caso particular, ser enunciado do
seguinte modo:
Sejam Q § I uma variedade e 1À Q Ä Š uma aplicação suave. Se
0 À Ò+ß ,Ó Ä Q é uma trajectória suave, tem-se
( .1 œ 1Ð0 Ð,ÑÑ 1Ð0 Ð+ÑÑ.
0
É claro que este resultado tem também uma justificação trivial, independente
do teorema de Stokes geral.
Vamos agora verificar que, quando a forma diferencial é fechada, o
integral sobre duas variedades singulares suavemente homotópicas é o
mesmo. Mais precisamente, começamos por estabelecer este resultado
para as variedades singulares sem bordo e vemos em seguida que ele é
160
Cap. III. Formas diferenciais e teorema de Stokes
ainda válido para as variedades singulares com bordo, mediante uma
condição restritiva sobre as homotopias.
III.9.11. Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma forma diferencial
suave, de grau 8, real ou complexa, que seja fechada, isto é, que verifique
.= œ !. Seja E uma variedade compacta, sem bordo, suavemente orientada e
de dimensão 8 e sejam 0 ß 1À E Ä Q duas aplicações suaves que sejam
suavemente homotópicas. Tem-se então
( = œ ( =.
0
1
Dem: Tendo em conta III.7.6, vemos que, se 8 œ !, o resultado é uma
consequência trivial de se ter 0 ‡ = œ 1‡ = e que, se 8 !, existe uma forma
diferencial suave 5 , de grau 8 " sobre E, tal que 1‡ = 0 ‡ = œ . 5 e tem-se
então, tendo em conta o teorema de Stokes e o facto de a variedade E não ter
bordo,
‡
‡
( = ( = œ ( 1 = 0 = œ ( .5 œ (
1
0
E
E
`" ÐEÑ
5Î`" ÐEÑ œ !,
donde o resultado.
Do ponto de vista formal o resultado anterior é inútil, visto que ele é uma
caso particular do que apresentamos em seguida. Pareceu-nos útil
começar por esse caso particular, tendo em conta a sua simplicidade e o
facto de conter as ideias que nos conduzirão ao caso geral.
III.9.12. Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma forma diferencial
suave, fechada e de grau 8, com valores em Š. Seja E uma variedade
compacta, eventualmente com bordo, suavemente orientada e de dimensão 8
e sejam 0 ß 1À E Ä Q duas aplicações suaves com a mesma restrição a `" ÐEÑ
e que sejam suavemente homotópicas com bordo fixo, isto é, tais que exista
uma aplicação suave LÀ Ò!ß "Ó ‚ E Ä Q , verificando as condições
LÐ!ß BÑ œ 0 ÐBÑ,
LÐ"ß BÑ œ 1ÐBÑ,
LÐ>ß BÑ œ 0 ÐBÑ œ 1ÐBÑ,
para B − E,
para B − E,
para B − `" ÐEÑ e > − Ò!ß "Ó.
Tem-se então
( = œ ( =.
0
1
Dem: No caso em que 8 œ !, sabemos, por III.7.6, que 0 ‡ = œ 1‡ =, o que
implica trivialmente o resultado (é claro que, neste caso, `" ÐEÑ œ g, pelo que
§9. Teorema de Stokes singular
161
a hipótese suplementar sobre a homotopia é vazia e não temos nada de novo
em relação ao resultado precedente). Suponhamos agora que 8 ! e, em vez
de aplicar III.7.6, reexaminemos a respectiva demonstração. Sendo T o
operador prismático, temos, como então, T .L ‡ = œ T L ‡ . = œ !, pelo que,
aplicando III.7.4, obtemos
1‡ = 0 ‡ = œ :"‡ L ‡ = :!‡ L ‡ = œ T .L ‡ = .T L ‡ = œ .T L ‡ =.
Reparemos agora que T L ‡ = é uma forma diferencial suave de grau 8 "
sobre E, cuja restrição a `" ÐEÑ é nula, visto que, se B − `" ÐEÑ e
A" ß á ß A8" são tangentes a `" ÐEÑ em B, sai
ÐT L ‡ =ÑB ÐA" ß á ß A8" Ñ œ
(
"
ÐL ‡ =ÑÐ>ßBÑ ÐÐ"ß !Ñß Ð!ß A" Ñß á ß Ð!ß A8" ÑÑ .> œ
!
œ(
"
=LÐ>ßBÑ ÐHLÐ>ßBÑ ÐÐ"ß !ÑÑß HLÐ>ßBÑ ÐÐ!ß A" ÑÑß á ß HLÐ>ßBÑ ÐÐ!ß A8" ÑÑÑ .> œ !,
!
visto que a identidade LÐ>ß BÑ œ 0 ÐBÑ, para cada B − `" ÐEÑ e > − Ò!ß "Ó,
implica que HLÐ>ßBÑ ÐÐ"ß !ÑÑ œ !. Obtemos agora, tendo em conta o teorema
de Stokes,
‡
‡
‡
( = ( = œ ( 1 = 0 = œ ( .T L = œ (
1
0
E
E
`" ÐEÑ
T L ‡ =Î`" ÐEÑ œ !,
donde o resultado.
III.9.13. Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma forma diferencial
suave, fechada e de grau 8, com valores em Š. Seja ÐEß 0 Ñ uma variedade
singular suave, sem bordo, de dimensão 8 em Q . Suponhamos que existe
uma variedade compacta F , de dimensão 8 " e suavemente orientada, tal
que E œ `" ÐFÑ e que a orientação de E seja a induzida pela de F , e que
existe um prolongamento suave s0 À F Ä Q de 0 . Tem-se então
(
= œ !.
ÐEß0 Ñ
Dem: Trata-se de uma consequência do teorema de Stokes singular, visto
que, uma vez que . = œ !, sai
( =œ(
0
s
`0
= œ ( . = œ !.
s0
III.9.14. (Teorema da variedade esburacada) Seja F uma variedade de dimensão 8 e sejam G" ß á ß G: variedades sem cantos, de dimensão 8, contidas em
`! ÐFÑ, fechadas em F e disjuntas duas a duas. Seja
162
Cap. III. Formas diferenciais e teorema de Stokes
s œ F Ï . `! ÐG5 Ñ.
F
5
Figura 5
s é uma variedade de
Tem-se então que cada `! ÐG5 Ñ é aberto em F e que F
dimensão 8, fechada em F , para a qual se tem
s œ `! ÐFÑ Ï . G5 ,
`! ÐFÑ
5
s œ `" ÐFÑ . `" ÐG5 Ñ
`" ÐFÑ
5
s œ `; ÐFÑ. Além disso, supondo que F está munido
e, para cada ; #, `; ÐFÑ
s e em cada G5 a orientação
de uma orientação suave e que se considera em F
s
s , e XB ÐG5 Ñ œ XB ÐFÑ,
induzida pela de F (XB ÐFÑ œ XB ÐFÑ, para cada B − F
para cada B − G5 ), tem-se então que, para cada B − `" ÐG5 Ñ, a orientação
s pela orientação de G5 é a oposta da
induzida em XB Ð`" ÐG5 ÑÑ œ XB Ð`" ÐFÑÑ
s e, para cada B − `" ÐFÑ, a orientação induzida
induzida pela orientação de F
s pela orientação de F coincide com a induzida pela
em XB ÐFÑ œ XB ÐFÑ
s.
orientação de F
Dem: O facto de cada `! ÐG5 Ñ ser aberto em F é uma consequência imediata
de aplicarmos o teorema da função inversa à inclusão de `! ÐG5 Ñ em `! ÐFÑ,
que é aberto em F (a respectiva derivada em cada ponto vai ser a aplicação
s vai ser a união
identidade do espaço vectorial tangente comum). Vem que F
disjunta de F Ï G5 com cada um dos `" ÐG5 Ñ. Para cada B − F Ï -G5 ,
s , pelo que F
s vai ser no ponto B uma variedade com a
tem-se B − intF ÐFÑ
mesma dimensão e índice que F . Do mesmo modo, no caso em que F está
orientada, é evidente que, para B − `" ÐFÑ, a orientação induzida em
s pela orientação de F coincide com a induzida pela
XB ÐFÑ œ XB ÐFÑ
s . Resta-nos examinar o que sucede a F
s num ponto
orientação de F
B! − `" ÐG5 Ñ.
Aplicando o resultado bem conhecido que caracteriza o modo como uma
subvariedade, eventualmente com bordo, está inserida dentro da variedade
sem bordo ambiente, à variedade G5 contida em `! ÐFÑ, concluímos a
existência de um espaço vectorial J , com uma base A" ß á ß A8 , de um aberto
§9. Teorema de Stokes singular
163
Z de `! ÐFÑ, com B! − Z , de um aberto Y de J , com ! − Y e de um
difeomorfismo <À Y Ä Z , com <Ð!Ñ œ B! , de modo que, sendo N o sector
de J , constituído pelos vectores com a última componente naquela base
maior ou igual a !, <" ÐZ G5 Ñ œ Y N . Se necessário reduzindo estes
abertos, pode-se já supor que Z não intersecta nenhum dos restantes G5w .
Tem-se então que <" ÐZ `" ÐG5 ÑÑ é constituído pelos pontos de Y N
onde N é uma variedade de índice ", isto é, por aqueles cuja última
componente é nula e daqui deduzimos que, sendo N o sector de J
constituído pelos vectores com última componente menor ou igual a !,
s œ Y N . Obtemos portanto, por restrição de <, um difeomor<" ÐZ FÑ
s , o que mostra que F
s é, no ponto B! , uma
fismo de Y N sobre Z F
variedade de dimensão 8 e índice ". Além disso, uma vez que A8 é tangente,
mas não estritamente tangente, a N e A8 é tangente, mas não estritamente
tangente, a N , concluímos que H<! ÐA8 Ñ é tangente, mas não estritamente
s e que H<! ÐA8 Ñ é tangente, mas não estritamente tangente a
tangente a F
G5 e daqui deduzimos imediatamente que, no caso em que F está orientada,
s pelas orientações de
as orientações induzidas em XB Ð`" ÐG5 ÑÑ œ XB Ð`" ÐFÑÑ
s
G5 e de F são opostas.
III.9.15. Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma forma diferencial
suave, fechada e de grau 8, com valores em Š. Sejam F uma variedade
compacta, suavemente orientada, de dimensão 8 ", e G" ß á ß G:
variedades compactas, sem cantos, de dimensão 8 ", contidas em `! ÐFÑ e
s œ F Ï - `! ÐG5 Ñ, seja s0 À F
s Ä Q uma aplidisjuntas duas a duas e, sendo F
cação suave. Considerando então em `" ÐFÑ e em cada `" ÐG5 Ñ as orientações
induzidas pelas de F e G5 , respectivamente, tem-se
(
= œ "(
:
s Î` ÐFÑ Ñ
Ð`" ÐFÑß0
"
5œ"
s Î` ÐG Ñ Ñ
Ð`" ÐG5 Ñß0
" 5
=.
s é uma variedade compacta, de
Dem: Tendo em conta o teorema anterior, F
s é a união disjunta de `" ÐFÑ e
dimensão 8 ", suavemente orientada e `" ÐFÑ
s œ XB Ð`" ÐFÑÑ
dos `" ÐG5 Ñ, para cada B − `" ÐFÑ, a orientação de XB Ð`" ÐFÑÑ
s
induzida pela de F coincidindo com a induzida pela de F e, para cada
s œ XB Ð`" ÐG5 ÑÑ induzida pela de F
s
B − `" ÐG5 Ñ, a orientação de XB Ð`" ÐFÑÑ
sendo a oposta da induzida pela de G5 . Tem-se então, tendo em conta
III.9.13,
(
s s
Ð`" ÐFÑß0
Î`
= œ !,
s Ñ
" ÐFÑ
164
Cap. III. Formas diferenciais e teorema de Stokes
bastando agora repararmos que se tem
(
s s
Ð`" ÐFÑß0
Î`
s Ñ
" ÐFÑ
=œ(
= "(
:
s Î` ÐFÑ Ñ
Ð`" ÐFÑß0
"
5œ"
s Î` ÐG Ñ Ñ
Ð`" ÐG5 Ñß0
" 5
=.
Um exemplo de forma diferencial fechada, cujo integral sobre uma
variedade singular suave vai ter um significado geométrico importante, é
a forma diferencial ângulo sólido, que definimos em seguida. Ela vai
permitir generalizar, para dimensões superiores, o conceito de ângulo
orientado descrito por um caminho plano em torno da origem (cf. a figura
a seguir). Repare-se que, mesmo neste caso particular, a definição desse
conceito envolve alguma delicadeza.
Caminho 1:
Caminho 2:
Caminho 3:
Caminho 4:
1
$
1
$
1
$
1
$
radianos
radianos
#1 radianos
%1 radianos
Figura 6
III.9.16. Seja I um espaço euclidiano orientado de dimensão 8 ". Notemos
W § I a hipersuperfície esférica de centro ! e raio ",
W œ ÖB − I ± mBm œ "×,
que é uma variedade sem bordo, com dimensão 8 ", sobre a qual
consideramos a orientação suave que lhe vem de ser o bordo de índice " de
F œ ÖB − I ± mBm œ "× (onde consideramos a orientação constante que lhe
vem de I ). Vamos notar Z 96W a forma diferencial elemento de volume de W
e 3À I Ï Ö!× Ä W a aplicação suave definida por 3ÐBÑ œ BÎmBm. Vamos
chamar forma diferencial ângulo sólido de I a forma diferencial suave de
grau 8 " sobre I Ï Ö!×, HÀ I Ï Ö!× Ä E8" ÐIà ‘Ñ, imagem recíproca de
Z 96W por meio de 3, H œ 3‡ Z 96W .
III.9.17. Nas condições anteriores, a forma diferencial ângulo sólido
HÀ I Ï Ö!× Ä E8" ÐIà ‘Ñ é uma forma diferencial fechada cuja restrição a
§9. Teorema de Stokes singular
165
W é Z 96W .
Dem: Uma vez que, sobre a variedade W , de dimensão 8 ", todas as
formas diferenciais de grau 8 são nulas, vemos que . Z 96W œ !; daqui se
deduz que . H œ . 3‡ Z 96W œ 3‡ . Z 96W œ !, o que mostra que a forma
diferencial H é fechada. Por fim, sendo +À W Ä I Ï Ö!× a inclusão, tem-se
3 ‰ + œ M.W , pelo que
HÎW œ +‡ 3‡ Z 96W œ Ð3 ‰ +ч Z 96W œ M.W‡ Z 96W œ Z 96W .
III.9.18. Seja I um espaço euclidiano orientado de dimensão 8 " e seja
ÐEß 0 Ñ uma variedade singular suave, de dimensão 8 ", em I Ï Ö!×
(portanto E é uma variedade de dimensão 8 ", suavemente orientada e
0 À E Ä I Ï Ö!× é uma aplicação suave). Diz-se que ÐEß 0 Ñ tem ângulo
sólido se a forma diferencial H for integrável em ÐEß 0 Ñ e define-se então o
ângulo sólido orientado de ÐEß 0 Ñ (subentendido, em torno de ! − I ) como
sendo o número real
nÐEß 0 Ñ œ (
H,
ÐEß0 Ñ
que será notado simplesmente nÐ0 Ñ quando não houver perigo de confusão
sobre qual a variedade orientada E que se considera. É claro que, se a
variedade singular E é compacta, e é esse o caso que usualmente terá mais
interesse, ela vai ter automaticamente ângulo sólido. Repare-se que este
ângulo depende quer da orientação de E quer da de I , vindo multiplicado
por " sempre que se troca uma daquelas orientações.
Um caso particular importante é aquele em que E é uma subvariedade
compacta de dimensão 8 " de I Ï Ö!×, suavemente orientada. Define-se
então o ângulo sólido orientado de E, nÐEÑ, como sendo o ângulo sólido
orientado da variedade singular ÐEß +Ñ, onde +À E Ä I Ï Ö!× é a inclusão.
Tem-se portanto, neste caso,
nÐEÑ œ ( HÎE .
E
A razão pela qual se utiliza a expressão “ângulo sólido orientado” decorre
intuitivamente da propriedade seguinte, que caracteriza o valor deste no caso
particular em que a composição 3 ‰ 0 é um difeomorfismo de E sobre uma
subvariedade de W , que ou conserva ou inverte as orientações. Relembrar, a
propósito, o que se disse no exercício I.8.
III.9.19. Seja I um espaço euclidiano orientado de dimensão 8 " e seja
ÐEß 0 Ñ uma variedade singular suave de dimensão 8 " em I Ï Ö!×, tal que
3 ‰ 0 seja um difeomorfismo de E sobre um subconjunto F de W , que
conserve (resp. inverta) as orientações. Tem-se então que ÐEß 0 Ñ tem ângulo
sólido e nÐEß 0 Ñ é igual a .W ÐFÑ (resp. igual a .W ÐFÑ).
Dem: Seja & œ " no caso em que 3 ‰ 0 conserva as orientações e & œ " no
166
Cap. III. Formas diferenciais e teorema de Stokes
caso em que 3 ‰ 0 inverte as orientações. Tem-se então, tendo em conta
III.4.4,
nÐEß 0 Ñ œ ( 0 ‡ H œ ( 0 ‡ 3‡ Z 96W œ ( Ð3 ‰ 0 ч Z 96W ÎF œ
E
E
œ & ( Z 96W ÎF œ & .W ÐFÑ.
E
F
Figura 7
As hipóteses do resultado anterior são, de algum modo, excepcionais e,
em casos mais gerais, podemos, quando muito, tentar obter uma
decomposição do domínio como união de um conjunto de medida nula
com um número finito de subconjuntos abertos disjuntos, onde a restrição
de 0 verifique as condições anteriores; o ângulo sólido orientado de 0
pode então ser calculado como soma dos ângulos sólidos orientados das
restrições de 0 a esses abertos. É com uma decomposição deste tipo que
determinámos intuitivamente os ângulos sólidos orientados dos caminhos
na figura 6. Estas decomposições não são sempre possíveis e a sua
utilização nos casos em que I tem dimensão maior que # não será em
geral cómoda. Em qualquer caso não as poderemos utilizar para inferir
resultados sobre variedades singulares gerais, sendo apenas úteis em
justificações heurísticas, que nos ajudem a intuir o que se está a passar.
Os exemplos apresentados na figura 6 sugerem que, dados dois caminhos
com as mesmas extremidades, a diferença dos respectivos ângulos sólidos
orientados é um múltiplo inteiro de #1. Os próximos resultados conduzirão à demonstração deste facto e da respectiva generalização para um
espaço euclidiano I de dimensão 8 e variedades singulares compactas de
dimensão 8 " com mesma restrição ao bordo, em que a quantidade #1 é
§9. Teorema de Stokes singular
167
substituída pela medida 58" da hipersuperfície esférica unitária de
dimensão 8 ".
III.9.20. Seja I um espaço euclidiano orientado de dimensão 8 ". Sejam F
uma variedade compacta, suavemente orientada, de dimensão 8 e s0 À F Ä I
uma aplicação suave tal que, para cada B em `ÐFÑ œ - `4 ÐFÑ, s0 ÐBÑ Á !.
4 "
Supohamos ainda que ! é um valor regular da restrição s0 Î`! ÐFÑ À `! ÐFÑ Ä I .
"
Então s0 ÐÖ!×Ñ é um subconjunto finito ÖB" ß á ß B: × de `! ÐFÑ, tal que, para
s B À XB5 ÐFÑ Ä I é um isomorfismo e, notando &5 œ " ou
cada " Ÿ 5 Ÿ :, H0
5
&5 œ ", conforme este isomorfismo conserve ou inverta as orientações,
tem-se que o ângulo sólido orientado de s0 Î`" ÐFÑ À `" ÐFÑ Ä I Ï Ö!× é igual a
58" ! &5 .
:
5œ"
"
Dem: Vem que s0 ÐÖ!×Ñ é um subconjunto fechado de F , e portanto um
compacto. Por outro lado, o facto de supormos s0 ÐBÑ Á !, para cada
B − `ÐFÑ implica que aquele compacto está contido em `! ÐFÑ. O facto de !
"
ser um valor regular da restrição de s0 a `! ÐFÑ implica agora que s0 ÐÖ!×Ñ é
uma variedade de dimensão !, a qual, sendo compacta, vai ser um conjunto
finito ÖB" ß á ß B: × (a família dos conjuntos unitários vai ser uma cobertura
aberta, de onde se pode extrair uma subcobertura finita). Pelo teorema da
função inversa, podemos escolher, para cada " Ÿ 5 Ÿ :, um aberto Y5 de
`! ÐFÑ, com B5 − Y5 , e um aberto Z5 de I , com ! − Z5 , tal que 0ÎY5 seja um
difeomorfismo de Y5 sobre Z5 e, se necessário reduzindo estes abertos,
podemos já supor que os Y5 são disjuntos dois a dois e que cada um dos
difeomorfismos 0ÎY5 À Y5 Ä Z5 ou conserva ou inverte as orientações (cf.
III.5.7). Vem que +Z5 é um aberto de I , contendo !, pelo que existe < !
tal que a bola fechada F < Ð!Ñ esteja contida naquela intersecção. Sendo
W< œ ÖC − I ± mCm œ <×, que é uma variedade de dimensão 8 ",
consideramos em W< a orientação que lhe vem de ser o bordo de F < Ð!Ñ e
reparamos que a restrição de 3 a W< , definida por 3ÐCÑ œ CÎ<, vai ser um
difeomorfismo de W< sobre W œ W" , que conserva as orientações, por ser a
restrição do difeomorfismo de F < Ð!Ñ sobre F " Ð!Ñ, definido pela mesma
fórmula, que conserva claramente as orientações.
Notemos, para cada 5 , G5 œ Ð0ÎY5 Ñ" ÐF < Ð!ÑÑ, que é portanto uma variedade
compacta, sem cantos, de dimensão 8, contida em Y5 . Uma vez que a aplis œ F Ï - `! ÐG5 Ñ em I Ï Ö!×, podemos
cação suave s0 À F Ä I aplica F
5
deduzir de III.9.15 que o ângulo sólido orientado da restrição de s0 a `" ÐFÑ é
igual à soma dos ângulos sólidos orientados das restrições de s0 aos `" ÐG5 Ñ e
tudo o que temos que demonstrar é que o ângulo sólido orientado da restrição
de s0 a cada `" ÐG5 Ñ é &5 58" . Ora, tendo em conta o facto de a restrição de s0
168
Cap. III. Formas diferenciais e teorema de Stokes
a G5 ser um difeomorfismo de G5 sobre F < Ð!Ñ, que conserva ou inverte as
orientações conforme &5 œ " ou &5 œ ", deduzimos que a restrição de s0 a
`" ÐG5 Ñ é um difeomorfismo de `" ÐG5 Ñ sobre W< , que conserva ou inverte as
orientações conforme &5 œ " ou &5 œ ", e portanto que a restrição de 3 ‰ s0
a `" ÐG5 Ñ é um difeomorfismo de `" ÐG5 Ñ sobre W , que conserva ou inverte as
orientações conforme &5 œ " ou &5 œ ". Aplicando III.9.19, concluímos
portanto que o ângulo sólido orientado da restrição de s0 a `" ÐG5 Ñ é
efectivamente &5 58" .
III.9.21 (Corolário) Seja I um espaço euclidiano orientado de dimensão 8 "
e F § I uma variedade compacta de dimensão 8, tal que !  `ÐFÑ œ
- `4 ÐFÑ, sobre a qual se considera a orientação induzida. Considerando em
4 "
`" ÐFÑ a orientação induzida pela de F , tem-se então que o ângulo sólido
orientado de `" ÐFÑ é ! ou 58" , conforme se tenha ! Â F ou ! − `! ÐFÑ.
Dem: Basta aplicar o resultado anterior à inclusão de F em I .
III.9.22 Seja I um espaço euclidiano orientado de dimensão 8 ". Sejam F
uma variedade compacta, suavemente orientada, de dimensão 8 e s0 À F Ä I
uma aplicação suave tal que, para cada B em `ÐFÑ œ - `4 ÐFÑ, s0 ÐBÑ Á !.
4 "
Tem-se então que o ângulo sólido orientado da restrição de s0 a `" ÐFÑ é um
múltiplo inteiro de 58" .
Dem: É claro que, se ! fosse um valor regular da restrição de s0 a `! ÐFÑ,
tínhamos uma consequência trivial de III.9.20.
Vamos começar por demonstrar o resultado com a hipótese suplementar de a
variedade F não ter cantos, caso em que `" ÐFÑ, sendo uma subvariedade
fechada de F , é uma variedade compacta e sem bordo. Seja < ! tal que a
bola aberta F< Ð!Ñ não intersecte o compacto s0 Ð`" ÐFÑÑ. Pelo corolário do
teorema de Sard (cf. I.5.8), podemos considerar C − F< Ð!Ñ, que seja um valor
regular da restrição de s0 a `! ÐFÑ e então, sendo 0˜ À F Ä I a aplicação suave
definida por 0˜ ÐBÑ œ s0 ÐBÑ C, tem-se que !  0˜ Ð`" ÐFÑÑ e ! é um valor
regular da restrição de 0̃ a `! ÐFÑ, o que, por III.9.20, implica que o ângulo
sólido orientado da restrição de 0̃ a `" ÐFÑ é um múltiplo inteiro de 58" .
Mas, tem lugar uma aplicação suave LÀ Ò!ß "Ó ‚ `" ÐFÑ Ä I Ï Ö!×, definida
por LÐ>ß BÑ œ s0 ÐBÑ >C, para a qual se tem LÐ!ß BÑ œ s0 ÐBÑ e
LÐ"ß BÑ œ 0˜ ÐBÑ, pelo que deduzimos de III.9.11 que o ângulo sólido
orientado da restrição de s0 a `" ÐFÑ coincide com o da restrição de 0˜ , sendo
assim um múltiplo inteiro de 58" .
Passemos, por fim, à demonstração do caso geral em que a variedade F pode
ter cantos. Seja O œ ÖB − F ± s0 ÐBÑ œ !×, que é um conjunto compacto
contido em `! ÐFÑ. O facto de `! ÐFÑ ser localmente compacto implica a
existência de um aberto Y de `! ÐFÑ, contendo O e contido numa parte
compacta O w de `! ÐFÑ; pelo teorema da partição da unidade, relativo à
cobertura de F formada pelos abertos Y e F Ï O , podemos considerar uma
§9. Teorema de Stokes singular
169
aplicação suave :À F Ä Ò!ß "Ó, nula fora de Y e tal que :ÐBÑ œ ", para cada
B − O. Outra vez pelo mesmo corolário do teorema de Sard, podemos considerar um valor regular = − Ó!ß "Ò da restrição de : a `! ÐFÑ. Seja
G œ ÖB − F ± :ÐBÑ =× œ ÖB − `! ÐFÑ ± :ÐBÑ =×.
Vem que G vai ser uma variedade compacta, sem cantos, com dimensão 8,
contida em `! ÐFÑ, tendo como bordo `" ÐGÑ œ ÖB − F ± :ÐBÑ œ =×. Uma
vez que O § `! ÐGÑ, e portanto a aplicação suave s0 À F Ä I aplica
F Ï `! ÐGÑ em I Ï Ö!×, concluímos de III.9.15 que o ângulo sólido orientado
da restrição de s0 a `" ÐFÑ coincide com o da sua restrição a `" ÐGÑ, o qual,
pelo caso particular estudado no início, é um múltiplo inteiro de 58" .
III.9.23 Seja I um espaço euclidiano orientado de dimensão 8 ". Seja E uma
variedade compacta, suvemente orientada, de dimensão 8 " e sejam
0 ß 1À E Ä I Ï Ö!× duas aplicações suaves tais que, para cada B − `" ÐEÑ,
0 ÐBÑ œ 1ÐBÑ. Tem-se então que nÐ1Ñ nÐ0 Ñ é um múltiplo inteiro de 58" .
Dem: Comecemos por notar que, por continuidade, tem-se ainda
0 ÐBÑ œ 1ÐBÑ, para cada B − `ÐEÑ œ - `4 ÐEÑ. Consideremos a variedade
4 "
compacta de dimensão 8, F œ Ò!ß "Ó ‚ E. Para cada Ð>ß BÑ − F , tem-se
XÐ>ßBÑ ÐFÑ œ ‘ ‚ XB ÐEÑ
e podemos considerar neste espaço vectorial a orientação produto, isto é,
aquela para a qual cada base A" ß á ß A8" de XB ÐEÑ tem a mesma orientação
que a base Ð"ß !Ñß Ð!ß A" Ñß á ß Ð!ß A8" Ñ de ‘ ‚ XB ÐEÑ. Ficamos assim com
uma orientação da variedade F , orientação que se verifica imediatamente ser
suave (dado um campo de referenciais sobre um aberto Y de E, obtemos, a
partir dele, um campo de referenciais sobre Ò!ß "Ó ‚ Y , com a mesma orientação). Seja LÀ F Ä I a aplicação suave definida por
LÐ>ß BÑ œ Ð" >Ñ0 ÐBÑ >1ÐBÑ.
Se Ð>ß BÑ − `ÐFÑ œ - `4 ÐFÑ, então, ou > − Ö!ß "×, e então LÐ>ß BÑ œ 0 ÐBÑ
4 "
ou LÐ>ß BÑ œ 1ÐBÑ, portanto LÐ>ß BÑ − I Ï Ö!×, ou B − `ÐEÑ, e então
0 ÐBÑ œ 1ÐBÑ, donde LÐ>ß BÑ œ 0 ÐBÑ, portanto ainda LÐ>ß BÑ − I Ï Ö!×.
Podemos assim aplicar o resultado precedente para garantir que o ângulo
sólido orientado da restrição de L a `" ÐFÑ é um múltiplo inteiro de 58" e
vamos agora mostrar que esse ângulo sólido orientado é igual a
nÐ1Ñ nÐ0 Ñ, o que terminará a demonstração. Vem que `" ÐFÑ é a união
disjunta das três variedades de dimensão 8 ", Ó!ß "Ò ‚ `" ÐEÑ, Ö!× ‚ `! ÐEÑ
e Ö"× ‚ `" ÐEÑ, pelo que o ângulo sólido orientado da restrição da L a `" ÐFÑ
é a soma dos ângulos sólidos orientados das restrições de L a estas três
variedades. Uma vez que, para cada Ð>ß BÑ − Ó!ß "Ò ‚ `" ÐEÑ, LÐ>ß BÑ œ 0 ÐBÑ,
vemos que a imagem recíproca da forma diferencial H pela restrição de L a
Ó!ß "Ò ‚ `" ÐEÑ é igual à imagem recíproca por meio da projecção de
170
Cap. III. Formas diferenciais e teorema de Stokes
Ó!ß "Ò ‚ `" ÐEÑ sobre `" ÐEÑ, da imagem recíproca de H pela restrição de 0 a
`" ÐEÑ, imagem recíproca essa que é nula por se tratar de uma forma
diferencial de grau 8 " sobre a variedade `" ÐEÑ de dimensão 8 #.
Concluímos assim que o ângulo sólido orientado da restrição de L a
Ó!ß "Ò ‚ `" ÐEÑ é !. Consideremos agora os difeomorfismos
:! À `! ÐEÑ Ä Ö!× ‚ `! ÐEÑ,
:" À `! ÐEÑ Ä Ö"× ‚ `! ÐEÑ
definidos por
:! ÐBÑ œ Ð!ß BÑ,
:" ÐBÑ œ Ð"ß BÑ.
Considerando nos contradomínios as orientações induzidas no bordo pela
orientação produto de Ò!ß "Ó ‚ E, tem-se que :! inverte as orientações e :"
conserva as orientações, visto que, dada uma base A" ß á ß A8" de XB ÐEÑ, as
imagens destes vectores, tanto por H:! B como por H:" B , são
Ð!ß A" Ñß á ß Ð!ß A8" Ñ e que, no ponto Ð"ß BÑ, o vector Ð"ß !Ñ é tangente, mas
não estritamente tangente, a Ò!ß "Ó ‚ E e, no ponto Ð!ß BÑ, é o vector Ð"ß !Ñ
que está nessas condições. Tendo em conta III.9.7, concluímos que os
ângulos sólidos orientados das restrições de L a Ö!× ‚ `! ÐEÑ e a
Ö"× ‚ `! ÐEÑ são iguais respectivamente ao simétrico do ângulo sólido
orientado de L ‰ :! À `! ÐEÑ Ä I Ï Ö!× e ao ângulo sólido orientado de
L ‰ :" À `! ÐEÑ Ä I Ï Ö!×, bastando reparar, por fim, que estas composições
não são mais do que as restrições de 0 e 1, respectivamente, e que E Ï `! ÐEÑ
tem medida nula, por ser união das variedades `4 ÐEÑ, com 4 ", que têm
dimensão inferior à de E.
III.9.24 (Corolário) Seja I um espaço euclidiano orientado de dimensão 8 #.
Seja E uma variedade compacta, suvemente orientada, de dimensão 8 " e
seja 0 À E Ä I Ï Ö!× uma aplicação suave cuja restrição a `" ÐEÑ seja
constante (é o que acontece, automaticamente, no caso em que a variedade E
não tem bordo). Tem-se então que o ângulo sólido orientado de 0 é um
múltiplo inteiro de 58" .36
Dem: Trata-se de uma consequência do resultado precedente, se repararmos
que, tendo em conta III.9.5, uma aplicação constante de E em I Ï Ö!× tem
ângulo sólido orientado nulo.
36Repare-se
que, ao contrário dos resultados anteriores, é necessário exigir aqui que I
tenha dimensão pelo menos #. No caso em que I tem dimensão ", obtém-se um contra-exemplo simples tomando para E um conjunto unitário.
Exercícios
171
EXERCÍCIOS
Ex III.1 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 ", suavemente orientada e munida de uma estrutura riemaniana suave.
Dados 7 " campos vectoriais suaves sobre Q , \" ß á ß \7" , mostrar
que, considerando, para cada B − Q , o produto externo \" B ‚ â ‚ \7" B ,
tem lugar um campo vectorial suave
\" ‚ â ‚ \7" œ Ð\" B ‚ â ‚ \7" B ÑB−Q .
Ex III.2 Comecemos com algumas observações sobre notações muito utilizadas
na prática. Suponhamos que Q é uma variedade de dimensão 7 e que : é
um difeomorfismo de Q sobre um aberto Z num sector de ‘7 , ou, mais
geralmente, sobre um subconjunto (automaticamente total) de ‘7 (é claro
que tais difeomorfismos só existem, em geral, localmente e, nesse caso, as
observações seguintes só se aplicam a abertos convenientes de Q ). Notamos
então :" ß á ß :7 as componentes de :, isto é, as aplicações suaves de Q em
‘ definidas por
:ÐCÑ œ Ð:" ÐCÑß á ß :7 ÐCÑÑ.
a) Mostrar que têm lugar campos vectoriais suaves
" Ÿ 4 Ÿ 7, definidos por
Ð
`
`:4
sobre Q , onde
`
ÑC œ H::"ÐCÑ Ð/4 Ñ,
`:4
em que /" ß á ß /7 é a base canónica de ‘7 . Por outras palavras, estes são os
campos vectoriais sobre Q que estão :-relacionados com os campos
vectoriais constantes /4 sobre Z .
b) Mostrar que, para cada C − Q , os vectores Ð ``:4 ÑC constituem uma base de
XC ÐQ Ñ e que os elementos da base associada de PÐXC ÐQ Ñà ‘Ñ são
. :" C ß á ß . :7 C .
c) Se = œ Ð=C ÑC−Q é uma forma diferencial de grau : sobre Q , com valores
em Š, mostrar que se pode escrever
=C œ " 04" ßáß4: ÐCÑ . :4" C • â • . :4: C
4" â4:
e que então = é suave se, e só se cada aplicação 04" ßáß4: À Q Ä Š é suave.
d) Mostrar, por indução em :, que se tem
172
Cap. III. Formas diferenciais e teorema de Stokes
.Ð. :4" • â • . :4: Ñ œ !
e deduzir daqui que, se = é uma forma diferencial suave de grau :, com
valores em Š, com uma decomposição como em c), então
. =C œ " " HÐ04" ßáß4: ÑC ÐÐ
4" â4:
4
`
ÑC Ñ . :4 C • . :4" C • â • . :4: C .
` :4
Nota: É frequente e clássico utilizar as notações
.B" ß á ß .B7
em vez de . :" ß á ß . :7
e as notações
`
`
ßáß
`B"
`B7
em vez de
`
`
.
ßáß
` :"
` :7
Estas últimas apresentam a seguinte particularidade: Se 0 À Q Ä Š é uma
aplicação suave, a fórmula de derivação das funções compostas mostra-nos
que
H0C ÐÐ
`
` (0 ‰ :" )
ÑC Ñ œ HÐ0 ‰ :" Ñ:ÐCÑ Ð/4 Ñ œ
Ð:ÐCÑÑ.
`B4
`B4
Ex III.3 (Formas diferenciais e funções de variável complexa) Neste exercício
vamos notar D e D as aplicações suaves de ‚ em ‚, que a cada complexo D
associam respectivamente D e o seu conjugado D , e notamos B e C as
aplicações suaves de ‚ em ‘, que a cada complexo D œ B 3C , com
Bß C − ‘, associam respectivamente B e C .
a) Reparar que, com estas notações, as formas diferenciais de grau " sobre
‚ œ ‘# , .B e .C são precisamente as referidas na nota no fim do exercício
precedente e que se tem
.D œ .B 3 .C,
.D œ .B 3 .C.
Mostrar que .D e .D constituem uma base do espaço vectorial complexo de
dimensão # P‘ Ð‚à ‚Ñ e que .D é uma base do subespaço P‚ Ð‚à ‚Ñ e .D é
uma base do subespaço P‚ Ð‚à ‚Ñ. Para cada 0 − P‘ Ð‚à ‚Ñ, dizer quais as
componentes de 0 na base .D , .D .
b) Dados um aberto Y de ‚ e uma aplicação suave 0 À Y Ä ‚, nota-se
`0
ÐDÑ œ H0D Ð/" Ñ œ H0D Ð"Ñ,
`B
e definem-se aplicações suaves
`0
`D
e
`0
`D ,
`0
ÐDÑ œ 1 ÐH0D ÑÐ"Ñ,
`D
`0
ÐDÑ œ H0D Ð/# Ñ œ H0D Ð3Ñ
`C
de Y em ‚, por
`0
ÐDÑ œ 1 ÐH0D ÑÐ"Ñ,
`D
Exercícios
173
onde H0D − P‘ Ð‚à ‚Ñ e
1 À P‘ Ð‚à ‚Ñ Ä P‚ Ð‚à ‚Ñ,
1 À P‘ Ð‚à ‚Ñ Ä P‚ Ð‚à ‚Ñ
são as projecções associadas à soma directa
P‘ Ð‚à ‚Ñ œ P‚ Ð‚à ‚Ñ Š P‚ Ð‚à ‚Ñ
(cf. o exercício II.1).
Mostrar que a aplicação 0 é holomorfa (no sentido que, para cada D , a
aplicação linear real H0D é mesmo uma aplicação linear complexa) se, e só
se, `0
`D œ ! e que 0 é anti-holomorfa (no sentido que, para cada D , H0D é
antilinear) se, e só se, `0
`D œ !.
Mostrar que se tem
`0
" `0
`0
œ Ð
3
Ñ,
`D
# `B
`C
`0
" `0
`0
œ Ð
3
Ñ,
`D
# `B
`C
`0
`0
.0 œ
.D
.D .
`D
`D
c) Mostrar que se tem .D • .D œ #3 .B • .C e deduzir daqui que .D • .D é
uma base do espaço vectorial complexo A#‘ Ð‚à ‚Ñß de dimensão ".
d) Mostrar que a forma diferencial =, de grau ", definida por =D œ 0 ÐDÑ .D , é
fechada, isto é, verifica . = œ !, se, e só se, a aplicação 0 é holomorfa.
e) Quando a aplicação 0 é holomorfa, define-se 0 w ÐDÑ œ H0D Ð"Ñ − ‚.
Mostrar que se tem então .0D œ 0 w ÐDÑ .D .
Ex III.4 Sejam Y um aberto num sector de ‘$ e 0 ß 1ß 2À Y Ä ‚ três aplicações
suaves. Seja = a fórmula diferencial de grau # sobre Y , definida por
=ÐBßCßDÑ œ 0 ÐBß Cß DÑ .C • .D 1ÐBß Cß DÑ .B • .D 2ÐBß Cß DÑ .B • .C.
Mostrar que se tem
.= œ Ð
`0
`1 `2
Ñ .B • .C • .D .
`B `C
`D
Ex III.5 Seja = a forma diferencial de grau " em ‘# Ï Ö!×, definida por
C
B
=ÐBßCÑ œ #
.B #
.C.
#
B C
B C#
a) Mostrar que se tem . = œ 0.
b) Seja ‘ § ‘# a semi-recta Ò!ß _Ò ‚ Ö!× e seja !À ‘# Ï ‘ Ä Ó!ß #1Ò a
aplicação suave que a cada par ÐBß CÑ associa o seu argumento. Mostrar que
. ! é a restrição de = a ‘# Ï ‘ .
c) Por que razão a conclusão de b) pode explicar a de a)?
174
Cap. III. Formas diferenciais e teorema de Stokes
d) Mostrar que não existe nenhuma função 0 À ‘# Ï Ö!× Ä ‘ tal que .0 œ =.
Sugestão: A restrição de uma tal função a ‘# Ï ‘ teria de diferir de ! por
uma constante.
s espaços euclidianos, Q § I e Q
s §I
s variedades de
Ex III.6 Sejam I e I
s Ä Q uma isometria suave, isto é, um difeomorfismo tal
dimensão 7 e 0 À Q
s , a aplicação linear H0B À XB ÐQ
s Ñ Ä X0 ÐBÑ ÐQ Ñ, seja um
que, para cada B − Q
isomorfismo ortogonal. Nas alíneas b) e seguintes supomos ainda que Q e
s estão suavemente orientadas e que o difeomorfismo 0 conserva as
Q
orientações.
s Ä ‘ é uma aplicação suave, então
a) Mostrar que, se 1À Q
gradÐ1 ‰ 0 ÑB œ ÐH0B Ñ" ÐgradÐ1Ñ0 ÐBÑ Ñ,
por outras palavras, os campos vectoriais gradÐ1 ‰ 0 Ñ e gradÐ1Ñ estão 0 -relacionados.
b) Supondo 7 ", sejam \ œ Ð\B ÑB−Qs e ] œ Ð]C ÑC−Q campos vectoriais
suaves 0 -relacionados, isto é, tais que ]0 ÐBÑ œ H0B Ð\B Ñ. Mostrar que, para
s , tem-se divÐ] Ñ0 ÐBÑ œ divÐ\ÑB .
cada B − Q
c) Supondo 7 ", mostrar que, se 1À Q Ä Š é uma aplicação suave, então,
s
para cada B − Q
?Ð1 ‰ 0 ÑB œ ?10 ÐBÑ .
s têm dimensão 3. Mostrar que, se \ œ Ð\B Ñ s
d) Suponhamos que Q e Q
B−Q
e ] œ Ð]C ÑC−Q são campos vectoriais 0 -relacionados, então os campos
vectoriais rotÐ\Ñ e rotÐ] Ñ são também 0 -relacionados.
Sugestão: Para as três últimas alíneas, ter em conta o resultado II.8.16.
Ex III.7 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 ", suavemente orientada, e seja Z 96 œ ÐZ 96B ÑB−Q a forma diferencial
de grau 7 elemento de volume. Dado um campo vectorial suave
\ œ Ð\B ÑB−Q , mostrar que tem lugar a seguinte fórmula para a divergência
de \ , que não faz intervir explicitamente os operadores ‡:
. int\ ÐZ 96Ñ œ divÐ\Ñ Z 96.
Sugestão: Ter em conta a alínea a) de II.8.18.
Ex III.8 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7. Dado um campo vectorial suave \ œ Ð\B ÑB−Q , como se poderia definir
a divergência de \ , divÐ\ÑÀ Q Ä ‘, de modo a generalizar a definição que
apresentámos, no caso em que Q estava suavemente orientada (cf. III.2.11)?
Sugestão: Raciocinar localmente, reparando que a divergência não se altera
quando se troca a orientação em todos os pontos de uma variedade.
Ex III.9 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão $,
suavemente orientada. Mostrar que:
Exercícios
175
a) Para cada aplicação suave 0 À Q Ä ‘, tem-se rotÐgradÐ0 ÑÑ œ !;
b) Para cada campo vectorial suave \ œ Ð\B ÑB−Q , tem-se divÐrotÐ\ÑÑ œ !.
Ex III.10 Sejam I um espaço euclidiano e Q § I uma variedade. Dadas as
aplicações suaves 0 ß 1À Q Ä ‘, mostrar que se tem
gradÐ0 1Ñ œ 0 gradÐ1Ñ gradÐ0 Ñ 1.
Ex III.11 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
$, suavemente orientada. Consideremos uma aplicação suave 0 À Q Ä ‘ e
\ œ Ð\B ÑB−Q um campo vectorial suave. Mostrar que se tem
rotÐ0 \Ñ œ 0 rotÐ\Ñ gradÐ0 Ñ ‚ \ .
Ex III.12 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 ", suavemente orientada. Consideremos uma aplicação suave
0 À Q Ä ‘ e \ œ Ð\B ÑB−Q um campo vectorial suave. Mostrar que se tem
divÐ0 \Ñ œ 0 divÐ\Ñ ØgradÐ0 Ñß \Ù.
Sugestão: Ter em conta o exercício II.35.
Ex III.13 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 ", suavemente orientada. Sejam 0 ß 1À Q Ä ‘ duas aplicações suaves.
Mostrar que se tem
?Ð0 1Ñ œ 0 Ð?1Ñ Ð?0 Ñ1 #ØgradÐ0 Ñß gradÐ1ÑÙ.
Ex III.14 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
$, suavemente orientada. Sejam \ œ Ð\B ÑB−Q e ] œ Ð]B ÑB−Q dois campos
vectoriais suaves. Mostrar que se tem então
divÐ\ ‚ ] Ñ œ ØrotÐ\Ñß ] Ù Ø\ß rotÐ] ÑÙ.
Sugestão: Ter em conta o exercício II.35.
Ex III.15 Seja I um espaço euclidiano de dimensão 7 ", sobre o qual
consideramos a norma associada, e seja + − I fixado.
a) Sendo \ œ Ð\B ÑB−I o campo vectorial suave definido por \B œ B +,
mostrar que se tem divÐ\Ñ œ 7. Deduzir daqui que, sendo ] œ Ð]B ÑB−IÏÖ+×
o campo vectorial suave definido por
B+
]B œ
,
mB +m7
tem-se divÐYÑB œ !, para cada B.
b) Sendo :À Ó!ß _Ò Ä ‘ uma aplicação suave, seja 0 À I Ï Ö+× Ä ‘ a
aplicação suave definida por
0 ÐBÑ œ :ÐmB +mÑ.
176
Cap. III. Formas diferenciais e teorema de Stokes
Mostrar que se tem
gradÐ0 ÑB œ
:w ÐmB +mÑ
ÐB +Ñ,
mB +m
?0B œ :ww ÐmB +mÑ Ð7 "Ñ
:w ÐmB +mÑ
.
mB +m
c) Chamam-se funções harmónicas as funções cujo laplaciano é
identicamente nulo. Determinar as funções suaves :À Ó!ß _Ò Ä ‘ para as
quais a correspondente função 0 À I Ï Ö+× Ä ‘, definida em b), é harmónica.
Ex III.16 Seja I um espaço euclidiano e seja Q § I uma variedade de
dimensão 7 ", suavemente orientada. Seja \ œ Ð\B ÑB−Q um campo
vectorial suave. Mostrar que, se A" ß á ß A7 é uma base ortonormada de
XB! ÐQ Ñ, então
divÐ\ÑB! œ " ØH\B! ÐA4 Ñß A4 Ù.
7
4œ"
Sugestão: Se necessário substituindo Q por um aberto contendo B! , pode-se
já supor que existem campos vectoriais suaves [" ß á ß [7 tais que
[4 B! œ A4 e que, para cada B − Q , os [4 B constituam uma base
ortonormada directa de XB ÐQ Ñ. Começar por demonstrar o resultado no caso
particular em que \ é um dos campos vectoriais [5 , utilizando para isso a
segunda caracterização da derivada exterior em III.2.2. Passar ao caso geral
por linearidade e utilizando o exercício III.12.
Ex III.17 Sejam Q § I uma variedade sem bordo, \ œ Ð\B ÑB−Q um campo
vectorial suave e =À H Ä Q o respectivo fluxo. Recordemos que H é um
aberto de ‘ ‚ Q e que, para cada B − Q , NB œ Ö> − ‘ ± Ð>ß BÑ − H× é um
intervalo aberto contendo ! e que a aplicação
NB Ä Q ,
> È =Ð>ß BÑ,
é a solução máxima da equação diferencial
`
=Ð>ß BÑ œ \=Ð>ßBÑ ,
`>
com a condição inicial =Ð!ß BÑ œ B. Para cada = − ‘, seja Y= o aberto de Q
constituído pelos B tais que Ð=ß BÑ − H e seja := À Y= Ä Y= o difeomorfismo
definido por := ÐBÑ œ =Ð=ß BÑ. Seja 0 œ Ð0B ÑB−Q um campo tensorial suave
de grau :, real ou complexo.
a) Mostrar que se tem, para cada B − Q ,
Ð:=‡ Ð0ÎY= ÑÑB 0B
.
=Ä!
=
_\ Ð0ÑB œ lim
Deduzir daqui que, se, qualquer que seja = − ‘ suficientemente pequeno,
Exercícios
177
:=‡ Ð0ÎY= Ñ œ 0ÎYB , então _\ Ð0Ñ œ !.
Sugestão: Começar por notar que basta fazer a demonstração no caso em que
Q é um aberto de I . Nesse caso verificar que o segundo membro, aplicado a
Ð?" ß á ß ?: Ñ, é igual a 1w Ð!Ñ, onde
1Ð=Ñ œ 0:= ÐBÑ ÐH:= B Ð?" Ñß á ß H:= B Ð?: ÑÑ œ
œ 0=Ð=ßBÑ ÐH=Ð=ßBÑ Ð!ß ?" Ñß á ß H=Ð=ßBÑ Ð!ß ?: ÑÑ,
lembrando que H# =Ð!ßBÑ é uma aplicação bilinear simétrica e que se tem
H=Ð!ßBw Ñ Ð"ß !Ñ œ \Bw .
b) Mostrar que se tem, mais geralmente, para cada > − ‘ tal que Ð>ß BÑ − H,
‡
Ð:=>
Ð0ÎY=> ÑÑB Ð:>‡ Ð0ÎY> ÑÑB
=Ä!
=
:>‡ Ð_\ Ð0ÑÎY> ÑB œ lim
e deduzir daqui que, se _\ Ð0Ñ œ !, então, para cada > − ‘, :>‡ Ð0ÎY> Ñ œ 0ÎY> .
Sugestão: Aplicar a alínea anterior com :> ÐBÑ no lugar de B e aplicar em
seguida H:> ‡B a ambos os membros, atendendo a igualdades do tipo
:=> œ := ‰ :> (válida numa vizinhança aberta de B). Para a última afirmação, verificar que a aplicação 1, referida na sugestão de a), tem derivada
identicamente nula.
Nota: Nas condições anteriores suponhamos que o espaço ambiente I da
variedade sem bordo Q está munido de um produto interno e seja
0 œ Ð0B ÑB−Q o campo tensorial suave de grau #, com valores em ‘, em que,
para cada B − Q , 0B é o produto interno de XB ÐQ Ñ induzido pelo de I . Aos
campos vectoriais suaves \ tais que _\ Ð0Ñ œ ! dá-se o nome de campos
vectoriais de Killing. Tendo em conta o que vimos neste exercício, os
campos vectoriais de Killing são caracterizados pela propriedade de cada
difeomorfismo :> À Y> Ä Y> ser uma isometria (ou seja, de cada
isomorfismo H:> B À XB ÐQ Ñ Ä X:> ÐBÑ ÐQ Ñ ser ortogonal).
Ex III.18 Sejam Q § I uma variedade e \ œ Ð\B ÑB−Q e ] œ Ð]B ÑB−Q dois
campos vectoriais suaves sobre Q . O parênteses de Lie Ò\ß ] Ó é por vezes
também notado _\ Ð] Ñ e toma o nome de derivada de Lie de ] na direcção
de \ . Mostrar que, para cada aplicação suave 0 À Q Ä ‘, têm lugar os
seguintes resultados correspondentes às conclusões de III.3.6:
_0 \ Ð] Ñ œ 0 _\ Ð] Ñ H0 Ð] Ñ \ ,
_\ Ð0 ] Ñ œ 0 _\ Ð] Ñ H0 Ð\Ñ ] .
Ex III.19 a) Utilizar o corolário III.3.12 para demonstrar a identidade de Jacobi:
Se \ , ] e ^ são campos vectoriais suaves sobre a variedade Q § I , então
ÒÒ\ß ] Óß ^Ó ÒÒ] ß ^Óß \Ó ÒÒ^ß \Óß ] Ó œ !.
Sugestão: Mostrar que, se [ é um campo vectorial sobre Q tal que, para
cada aplicação suave 0 À Q Ä ‘, [ † 0 œ !, então [ œ !.
178
Cap. III. Formas diferenciais e teorema de Stokes
b) Mostrar que a conclusão da alínea a) pode ser também escrita, com a
notação do exercício anterior, na forma
_Ò\ß] Ó Ð^Ñ œ _\ Ð_] Ð^ÑÑ _] Ð_\ Ð^ÑÑ,
forma essa em que é claro um parentesco com a fórmula de III.3.11.
Ex III.20 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 ", suavemente orientada e seja Z 96 œ ÐZ 96B ÑB−Q a forma diferencial
elemento de volume de Q . Seja \ œ Ð\B ÑB−Q um campo vectorial suave.
Mostrar que se tem
_\ ÐZ 96Ñ œ divÐ\Ñ Z 96.
Sugestão: Ter em conta III.3.16 e o exercício III.7.
Nota: Supondo que a variedade Q não tem bordo, podemos, para cada
> − ‘, notar :> À Y> Ä Y> o difeomorfismo definido a partir do fluxo de \ ,
tal como no exercício III.17. Tendo em conta o que se viu nesse exercício,
concluímos que se tem divÐ\Ñ œ ! se, e só se, :>‡ ÐZ 96ÎY> Ñ œ Z 96ÎY> . Uma
vez que, como se verifica facilmente, por um argumento de continuidade, os
difeomorfismos :> conservam as orientações, podemos concluir das observações precedentes que todo o campo vectorial de Killing tem divergência nula.
Pode-se também verificar facilmente que a condição de se ter
:>‡ ÐZ 96ÎY> Ñ œ Z 96ÎY>
é equivalente à de exigir que cada isomorfismo H:> B À XB ÐQ Ñ Ä X:> ÐBÑ ÐQ Ñ
tenha coeficiente de dilatação igual a ", condição que se pode verificar, por
um argumento de teoria da medida, ser equivalente à de se ter
.Q Ð:> ÐEÑÑ œ .Q ÐEÑ, para cada boreliano E § Y> , o que nos dá uma nova
interpretação geométrica da condição de um campo vectorial \ verificar
divÐ\Ñ œ !.
Ex III.21 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
$, suavemente orientada. Sejam \ œ Ð\B ÑB−Q e ] œ Ð]B ÑB−Q dois campos
vectoriais suaves. Mostrar que se tem
rotÐ\ ‚ ] Ñ œ divÐ] Ñ \ divÐ\Ñ ] Ò\ß ] Ó.
Sugestão: Partir da identidade
)ÐrotÐ\ ‚ ] ÑÑ œ ‡.Ð)Ð\ ‚ ] ÑÑ œ ‡.‡Ð)Ð\Ñ • )Ð] ÑÑ,
e atender às igualdades já conhecidas
‡Ð= • ) Ð] ÑÑ œ int] Ї=Ñ,
‡) Ð\Ñ œ int\ ÐZ 96Ñ,
_] ÐZ 96Ñ œ divÐ] Ñ Z 96,
. int] Ð=Ñ œ _] Ð.=Ñ int] Ð.=Ñ,
.‡) Ð\Ñ œ divÐ\Ñ Z 96,
_] Ðint\ ÐZ 96ÑÑ œ int\ Ð_] ÐZ 96ÑÑ intÒ] ß\Ó ÐZ 96Ñ.
Exercícios
179
Ex III.22 Verificar o que afirma o teorema de Stokes no caso em que a variedade
Q , com dimensão ", é um intervalo fechado e limitado Ò+ß ,Ó ou um intervalo
do tipo Ò+ß _Ò.
Ex III.23 Seja F § I uma variedade compacta, de dimensão ", suavemente
orientada. Mostrar que `" ÐFÑ é constituído por um número par de pontos,
havendo tantos pontos em `" ÐFÑ onde a orientação induzida é a canónica
como pontos em que a orientação induzida é a não canónica.
Sugestão: Considerar a aplicação 0 À F Ä ‘ de valor constante " e aplicar o
teorema de Stokes.
Ex III.24 Mostrar que o seguinte Teorema de Green no plano é uma
consequência do teorema de Stokes: Sejam Y § ‘# um aberto e 0 ß 1À Y Ä ‚
duas aplicações suaves. Dada uma variedade compacta de dimensão #,
Q § Y , tem-se
(
`" ÐQ Ñ
0 ÐBß CÑ .B 1ÐBß CÑ .C œ (
Q
`1
`0
ÐBß CÑ
ÐBß CÑ .B .C,
`B
`C
em que o integral do primeiro membro é o de uma forma diferencial e o do
segundo é o de uma função para a medida de Lebesgue.
Ex III.25 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 ". Seja, para cada B − `" ÐQ Ñ, JB o complementar ortogonal de
XB Ð`" ÐQ ÑÑ em XB ÐQ Ñ.
a) Mostrar que a família dos JB é um fibrado vectorial de dimensão " de base
`" ÐQ Ñ e que este fibrado vectorial fica suavemente orientado pela condição
de A − JB ser uma base directa se, e só se, A Â tB ÐQ Ñ. Sugestão: Relacionar
a projecção ortogonal de I sobre JB com as projecções ortogonais de I
sobre XB ÐQ Ñ e XB Ð`" ÐQ ÑÑ.
b) Deduzir de a) que tem lugar uma secção suave do referido fibrado que a
cada B − `" ÐQ Ñ associa a normal unitária exterior ^B .
Ex III.26 Mostrar que, nas condições de III.6.3, são suaves as aplicações de Q w
em I , que a B associa a normal unitária positiva ^B , e de `" ÐQ w Ñ em I , que
a B associa a tangente unitária positiva [B .
Ex III.27 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 ", suavemente orientada, e seja, para cada B − `" ÐQ Ñ, ^B a normal
unitária exterior (cf. III.6.2). Dada uma aplicação suave 0 À Q Ä Š, nula fora
duma parte compacta O de Q , mostrar que se tem
( ?0B . .Q ÐBÑ œ (
Q
`" ÐQ Ñ
H0B Ð^B Ñ . .`" ÐQ Ñ ÐBÑ
(a função integranda do segundo membro costuma ser chamada de derivada
normal de 0 e ser notada `0
`8 ÐBÑ). Sugestão: No caso em que Š œ ‘, o resul-
180
Cap. III. Formas diferenciais e teorema de Stokes
tado é uma consequência trivial do teorema da divergência. No caso geral,
considerar a parte real e a parte imaginária de 0 .
Ex III.28 (Fórmula de Green) Sejam I um espaço euclidiano e Q § I uma
variedade de dimensão 7 ", suavemente orientada, e seja, para cada
B − `" ÐQ Ñ, ^B a normal unitária exterior (cf. III.6.2).
a) Dadas duas aplicações suaves 0 ß 1À Q Ä ‘, uma das quais nula fora duma
certa parte compacta O de Q , mostrar que se tem
( 0B ?1B ?0B 1B . .Q ÐBÑ œ (
Q
`" ÐQ Ñ
0B H1B Ð^B Ñ H0B Ð^B Ñ 1B . .`" ÐQ Ñ ÐBÑ.
Sugestão: Aplicar o teorema da divergência ao campo vectorial
0 gradÐ1Ñ 1 gradÐ0 Ñ,
tendo em conta o exercício II.13.
b) Generalizar a conclusão de a) ao caso em que 0 e 1 podem tomar valores
em ‚.
Ex III.29 Sejam I um espaço euclidiano de dimensão 7 ", Y § I um
conjunto aberto e 0 À Y Ä Š uma função harmónica, isto é, uma aplicação
suave tal que ?0B œ !, para cada B − Y .
Para cada + − I e > !, notemos
F > Ð+Ñ œ ÖB − I ± mB +m Ÿ >×,
W> Ð+Ñ œ ÖB − I ± mB +m œ >×
(a bola fechada e a hipersuperfície esférica de centro + e raio >).
a) Para cada + − Y e cada > !, tal que F > Ð+Ñ § Y , seja
:Ð>Ñ œ
"
0 ÐBÑ . .W> Ð+Ñ ÐBÑ − Š.
(
>7" W> Ð+Ñ
Mostrar que se tem :w Ð>Ñ œ !. Sugestão: Fazer uma mudança de variáveis
para reduzir os integrais sobre W> Ð+Ñ a integrais sobre W" Ð!Ñ, utilizar o
teorema de derivação do integral paramétrico, regressar a W> Ð+Ñ com uma
nova mudança de variáveis e ter em conta o exercício III.27.
b) Utilizar a alínea anterior para provar a primeira propriedade da média das
funções harmónicas: Se < ! é tal que F < Ð+Ñ § Y , então 0 Ð+Ñ é a média de
0 sobre W< Ð+Ñ, isto é,
0 Ð+Ñ œ
"
0 ÐBÑ . .W< Ð+Ñ ÐBÑ.
(
.W< Ð+Ñ ÐW< Ð+ÑÑ W< Ð+Ñ
c) Utilizar a alínea b) para provar a segunda propriedade da média das
funções harmónicas: Se < ! é tal que F < Ð+Ñ § Y , então 0 Ð+Ñ é a média de
Exercícios
181
0 sobre F < Ð+Ñ, isto é,
0 Ð+Ñ œ
"
0 ÐBÑ . .I ÐBÑ.
(
.I ÐF < Ð+ÑÑ F < Ð+Ñ
Ex III.30 Seja I um espaço euclidiano de dimensão 7 ", sobre o qual
consideramos a norma associada. Seja + − I e notemos 0+ À I Ä ‘ a
aplicação que se anula em + e que nos pontos de I Ï Ö+× está definida por
57" mB+m
0+ ÐBÑ œ Ð7#Ñ
"
ln
ÐmB
+Ñm,
#1
"
7#
,
se 7 Á #
se 7 œ #
,
onde 57" é a medida da hipersuperfície esférica unitária de I ).
a) Mostrar que 0+ é uma função localmente integrável e que a restrição de 0+
a I Ï Ö+× é harmónica (cf. o exercício III.15).
b) Mostrar que, para cada função suave de suporte compacto :À I Ä ‚,
tem-se
( 0+ ÐBÑ ?:B . .I ÐBÑ œ :Ð+Ñ,
I
conclusão que se pode exprimir dizendo que o laplaciano de 0+ no sentido
das distribuições é igual à distribuição de Dirac centrada em +.
Sugestão: Aplicar a fórmula de Green, estabelecida no exercício III.28, à
variedade I Ï F< Ð+Ñ (onde F< Ð+Ñ é a bola aberta de centro + e raio <) e fazer
em seguida < tender para !.
Ex III.31 Seja I um espaço euclidiano de dimensão 7 ", sobre o qual
consideramos a norma associada. Seja Q § I uma variedade compacta de
dimensão 7 e notemos, para cada B − `" ÐQ Ñ, ^B a normal unitária exterior.
Mostrar que, se + Â Q , então
(
`" ÐQ Ñ
Ø^B ß B +Ù
. .`" ÐQ Ñ ÐBÑ œ !
mB +m7
e que, se + − `! ÐQ Ñ,
(
`" ÐQ Ñ
Ø^B ß B +Ù
. .`" ÐQ Ñ ÐBÑ œ 57" .
mB +m7
Sugestão: Aplicar o teorema da divergência, isolando, no segundo caso, o
ponto + por uma pequena bola de centro +.
Ex III.32 (Uma versão da fórmula integral de Cauchy) Sejam Y § ‚ um
aberto e 0 À Y Ä ‚ uma função holomorfa. Seja Q § Y uma variedade
compacta de dimensão #, sobre a qual se considera a orientação
correspondente à orientação canónica de ‚ œ ‘# , e considere-se no bordo
`" ÐQ Ñ a orientação induzida. Utilizar o teorema de Stokes para mostrar que:
182
Cap. III. Formas diferenciais e teorema de Stokes
a) Se + − ‚ Ï Q , então
(
`" ÐQ Ñ
0 ÐDÑ
.D œ !.
D+
b) Se + − `! ÐQ Ñ, então
(
`" ÐQ Ñ
0 ÐDÑ
.D œ #130 Ð+Ñ
D+
ÐDÑ
Sugestão: A aplicação 1ÐDÑ œ 0D+
é holomorfa em Y Ï Ö+×. Para a alínea b)
convirá retirar à variedade Q uma bola aberta de centro + e raio < e fazer em
seguida < tender para !.
Ex III.33 Sejam Y § ‚ um aberto e 0 À Y Ä ‚ uma aplicação suave. Seja
Q § Y uma variedade compacta de dimensão #, sobre a qual se considera a
orientação correspondente à orientação canónica de ‚ œ ‘# , e considere-se
no bordo `" ÐQ Ñ a orientação induzida.
a) Mostrar que, com as notações do exercício III.3, tem-se
(
`" ÐQ Ñ
0 ÐDÑ .D œ #3(
Q
`0
ÐBß CÑ .B .C.
`D
Sugestão: Ter em conta as conclusões das diferentes alíneas do referido
exercício.
b) Sendo + − `! ÐQ Ñ, mostrar que tem lugar a seguinte fórmula integral de
Cauchy, que generaliza a obtida na alínea b) do exercício anterior,
(
`" ÐQ Ñ
0 ÐDÑ
" `0
.D #3(
ÐDÑ .B .C œ #130 Ð+Ñ,
D+
Q D + `D
Sugestão: A mesma que para a alínea b) do exercício anterior, reparando
ÐDÑ
`1
" `0
que, sendo 1ÐDÑ œ 0D+
, tem-se `D
œ D+
`D .
Ex III.34 Relembrando a possibilidade de definir a divergência de um campo
vectorial suave cujo domínio seja uma variedade não obrigatoriamente
orientada (cf. o exercício III.8), enunciar e demonstrar uma versão do
teorema da divergência (cf. III.6.2) no quadro das variedades não orientadas.
s §I
s , mostrar que a relação entre
Ex III.35 Dadas as variedades Q § I e Q
s
aplicações suaves de Q em Q , definida por 0 µ 1, se, e só se, 0 e 1 são
suavemente homotópicas, é uma relação de equivalência. Sugestão: Para a
transitividade, e no sentido de arredondar os cantos, trabalhar com uma
aplicação suave !À ‘ Ä Ò!ß "Ó tal que !Ð>Ñ œ !, sempre que > Ÿ "$ , e que
!Ð>Ñ œ ", sempre que > #$ . Para construir uma tal função utilizar a técnica
das partições da unidade.
Exercícios
183
Ex III.36 Seja Q § I uma variedade suavemente contráctil. Mostrar que, se
s §I
s é uma variedade e se 0 ß 1À Q
s Ä Q são aplicações suaves
Q
arbitrárias, então 0 e 1 são suavemente homotópicas. Sugestão: As duas
aplicações vão ser suavemente homotópicas a uma mesma aplicação
constante.
Ex III.37 Mostrar que, se Q § I é uma variedade suavemente contráctil, então
Q é conexa por arcos suaves.
Ex III.38 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
$, suavemente orientada. Supondo que Q é suavemente contráctil, mostrar
que:
a) Se \ œ Ð\B ÑB−Q é um campo vectorial suave sobre Q tal que
rotÐ\Ñ œ !, então existe uma aplicação suave 0 À Q Ä ‘, para a qual
\ œ gradÐ0 Ñ;
b) Se \ œ Ð\B ÑB−Q é um campo vectorial suave sobre Q tal que
divÐ\Ñ œ !, então existe um campo vectorial suave ] œ Ð]B ÑB−Q , tal que
\ œ rotÐ] Ñ.
Ex III.39 Seja I um espaço euclidiano de dimensão 8 " e notemos ‘ o
intervalo Ò!ß _Ò e W œ ÖB − I ± mBm œ "×.
a) Dado B − I Ï Ö!×, mostrar que o complementar I Ï ‘ B da semirecta
gerada por B é suavemente contráctil. Sugestão: Este conjunto é estrelado
relativamente a B.
b) Dado B − W , mostrar que W Ï ÖB× é suavemente contráctil.
Sugestão: Projectar sobre W a restrição da homotopia que se considera em a).
c) Dado B − W , e sendo J o subespaço vectorial de dimensão 8 " de I ,
constituído pelos vectores ortogonais a B, mostrar que existe um difeomorfismo 0 À W Ï ÖB× Ä J (a projecção estereográfica), definido por
0 ÐCÑ œ
ØCß BÙ
"
B
C,
" ØCß BÙ
" ØCß BÙ
Figura 8
deduzindo daí, mais uma vez, o facto de a variedade W Ï ÖB× ser suavemente
contráctil.
184
Cap. III. Formas diferenciais e teorema de Stokes
Ex III.40 (Um rotacional alternativo)
a) Sejam J é um espaço euclidiano e P++ ÐJ à J Ñ é o espaço vectorial das
aplicações lineares anti-autoadjuntas de J em J . Mostrar que existe um isomorfismo # À P++ ÐJ à J Ñ Ä E# ÐJ à ‘Ñ, definido por # Ð-ÑÐBß CÑ œ Ø-ÐBÑß CÙ.
b) Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
arbitrária, não obrigatoriamente orientada. Seja \ œ Ð\B ÑB−Q um campo
vectorial suave sobre Q . Podemos então considerar a forma diferencial
suave )Ð\Ñ, de grau ", e o respectivo diferencial exterior, a forma diferencial
suave de grau # . )Ð\Ñ. Para cada B − Q , vamos definir o rotacional
alternativo de \ , rotÐ\ÑB (a definição e a notação são não standard) como
sendo a aplicação linear anti-autoadjunta de XB ÐQ Ñ em XB ÐQ Ñ definida por
rotÐ\ÑB œ # " Ð. )Ð\ÑB Ñ.
Mostrar que:
b1 ) Se existe uma aplicação suave 0 À Q Ä ‘, tal que \ œ gradÐ0 Ñ, então
rotÐ\Ñ œ !;
b2 ) Se a variedade Q é suavemente contráctil e se rotÐ\Ñ œ !, então existe
uma aplicação suave 0 À Q Ä ‘, tal que \ œ gradÐ0 Ñ.
c) Se I é um espaço euclidiano, Q § I é uma variedade e \ œ Ð\B ÑB−Q é
um campo vectorial suave, define-se, para cada B − Q , a derivada covariante de \ no ponto B como sendo a aplicação linear f\B À XB ÐQ Ñ Ä XB ÐQ Ñ
definida por f\B Ð?Ñ œ 1B ÐH\B Ð?ÑÑ, onde 1B À I Ä XB ÐQ Ñ é a projecção
ortogonal. Mostrar que o rotacional alternativo de \ , definido na alínea
precedente, é dado por
rotÐ\ÑB œ fÐ\ÑB fÐ\чB .37
Deduzir que, no caso em que Q é suavemente contráctil, uma condição
necessária e suficiente para a existência de uma aplicação suave 0 À Q Ä ‘,
tal que \ œ gradÐ0 Ñ é que a aplicação linear f\B À XB ÐQ Ñ Ä XB ÐQ Ñ seja
autoadjunta, para cada B − Q .
d) No caso em que J é um espaço euclidiano de dimensão arbitrária, não
obrigatoriamente orientado, pode-se definir analogamente, para Bß C − J , um
produto externo alternativo B ‚ C − P++ ÐJ à J Ñ, pela igualdade
B ‚ C œ # " Ð)Ð\Ñ • )Ð] ÑÑ.
Mostrar que se tem
B ‚ CÐDÑ œ ØBß DÙ C ØCß DÙ B.
e) No caso em que J é um espaço euclidiano orientado de dimensão $,
mostrar que tem lugar um isomorfismo +.À J Ä P++ ÐJ à J Ñ, que a cada
B − J associa o elemento +.B − P++ ÐJ à J Ñ definido pela condição de se ter
a notar -‡ a aplicação linear adjunta de uma aplicação linear
-À TB ÐQ Ñ Ä XB ÐQ Ñ.
37Estamos
Exercícios
185
Ø+.B ÐCÑß DÙ œ Z 96J ÐBß Cß DÑ,
quaisquer que sejam Cß D − J , ou, equivalentemente,
+.B ÐCÑ œ B ‚ C,
onde ‚ nota o produto externo usual em J .
Mostrar que este isomorfismo permite relacionar naturalmente o produto
externo usual com o produto externo alternativo e o rotacional usual com o
rotacional alternativo.
Deduzir as fórmulas
+.B‚C œ +.B ‰ +.C +.C ‰ +.B œ B ‚ C
(cf. o exercício II.32) assim como, no quadro das variedades de dimensão $
suavemente orientadas,
f\B Ð@Ñ f\B‡ Ð@Ñ œ rotÐ\ÑB ‚ @,
Øf\B Ð@Ñß AÙ Øf\B ÐAÑß @Ù œ Z 96ÐrotÐ\ÑB ß @ß AÑ,
quaisquer que sejam @ß A − XB ÐQ Ñ e o campo vectorial suave \ , esta última
fórmula podendo ser escrita de modo equivalente,
ØH\B Ð@Ñß AÙ ØH\B ÐAÑß @Ù œ Z 96ÐrotÐ\ÑB ß @ß AÑ,
o que está no mesmo espírito da caracterização da divergência encontrada no
exercício III.16.
Ex III.41 (Complementos ao teorema de aproximação por aplicações suaves)
Sejam I e J espaços vectoriais de dimensão finita, o segundo dos quais
munido de uma norma.
a) Verificar que, adaptando trivialmente a demonstração de III.8.5, se pode
obter a seguinte generalização desse resultado:
Sejam Y § I um conjunto aberto (por exemplo Y œ I …), Q § Y um
subconjunto fechado em Y , G § J um subconjunto convexo não vazio (por
exemplo G œ J …), 0 À Q Ä J uma aplicação contínua, tal que 0 ÐQ Ñ § G ,
e $À Q Ä Ó!ß _Ò uma aplicação contínua (por exemplo, uma constante…).
Existe então uma aplicação suave 1À Y Ä J tal que 1ÐY Ñ § G e que, para
cada B − Q , m1ÐBÑ 0 ÐBÑm $ ÐBÑ.
Sugestão: Por translação, reduzir o resultado ao caso em que ! − G .
b) Concluir de a) que, se Q § I é uma variedade, eventualmente com
bordo, e se 0 À Q Ä J é uma aplicação contínua, então, para cada $ !,
existe uma aplicação suave 1À Q Ä J tal que, para cada B − Q ,
m1ÐBÑ 0 ÐBÑm $.
Sugestão: Atender a que toda a variedade Q § I é um espaço topológico
localmente compacto e deduzir daí que Q se pode escrever como intersecção
de um aberto de I com um fechado de I (este último igual à aderência de
Q em I ).
c) Utilizar a conclusão de a) para mostrar que, se G § J é um conjunto
186
Cap. III. Formas diferenciais e teorema de Stokes
convexo e fechado e se 0 À G Ä G é uma aplicação contínua sem ponto fixo
(isto é, tal que 0 ÐBÑ Á B, para todo o B), então existe uma aplicação suave
sem ponto fixo 1À G Ä G . Sugestão: Tomar $ ÐBÑ œ m0 ÐBÑ Bm.
Ex III.42 a) Sejam \ um espaço topológico e ] § \ um subconjunto tais que
exista um espaço euclidiano I , com a bola F œ ÖB − I ± mBm Ÿ "× e a
hipersuperfície esférica W œ ÖB − I ± mBm œ "×, e um homeomorfismo
:À \ Ä F , com :Ð] Ñ œ W (pode-se dizer que Ð\ß ] Ñ é um par bola-esfera
topológico). Mostrar que não existe nenhuma retracção contínua de \ sobre
].
b) Seja I um espaço vectorial de dimensão finita, munido de uma norma,
notada m mw , não obrigatoriamente proveniente dum produto interno, e
notemos
F w œ ÖB − I ± mBmw Ÿ "×,
W w œ ÖB − I ± mBmw œ "×.
Mostrar que ÐF w ß W w Ñ é um par bola-esfera topológico.
Sugestão: Considerando em I uma norma m m, proveniente dum produto
interno, com os correspondentes
F œ ÖB − I ± mBm Ÿ "×,
W œ ÖB − I ± mBm œ "×,
mostrar que existe um homeomorfismo 0 À I Ä I , aplicando F w sobre F e
W w sobre W , definido por
0 ÐBÑ œ
mBmw B
mBm ,
!,
se B Á !
.
se B œ !
Ex III.43 Demonstrar, sem utilizar o teorema da não existência de retracção da
bola sobre a esfera, a seguinte versão suave do teorema do ponto fixo de
Brouwer (cf. III.8.8): Sendo I um espaço euclidiano e 0 À F Ä F uma
aplicação suave, onde F œ ÖB − I ± mBm Ÿ "×, existe B − F tal que
0 ÐBÑ œ B.
Sugestão: Supondo que isso não acontecia, considerar
W œ ÖB − I ± mBm œ "×
e mostrar que se pode considerar uma aplicação suave LÀ Ò!ß "Ó ‚ W Ä W ,
definida por
LÐ>ß BÑ œ
B >0 ÐBÑ
,
mB >0 ÐBÑm
a qual vai ser uma homotopia de M.W para a aplicação 1À W Ä W , definida por
Exercícios
187
1ÐBÑ œ
B 0 ÐBÑ
.
mB 0 ÐBÑm
Sendo Z 96 a forma diferencial elemento de volume de W , utilizar III.7.6 e o
teorema de Stokes para a variedade sem bordo W , para deduzir que
.W ÐWÑ œ ( 1‡ Z 96;
W
reparando que 1 é a restrição de uma aplicação suave 1À F Ä W , definida
pela mesma fórmula, utilizar mais uma vez o teorema de Stokes, para a
variedade F com bordo W , para deduzir que
‡
‡
( 1 Z 96 œ ( 1 Z 96 œ !,
W
W
pelo que se foi conduzido a um absurdo.
Ex III.44 Mostrar que a conclusão de III.8.4 (não existência de retracção suave
da bola sobre a esfera) pode ser deduzida directamente da conclusão do
exercício anterior. Sugestão: Se 0 fosse uma retracção suave de F sobre W , o
que aconteceria à aplicação suave 1À F Ä F , definida por 1ÐBÑ œ 0 ÐBÑ?
Ex III.45 Sejam Y § ‚ um aberto e 0 À Y Ä ‚ uma aplicação suave e consideremos a forma diferencial suave =, de grau ", definida por =D œ 0 ÐDÑ .D (cf.
o exercício III.3). Dados + , em ‘ e a aplicação suave # À Ò+ß ,Ó Ä Y ,
mostrar que o integral de = sobre a variedade singular ÐÒ+ß ,Óß # Ñ é dado por
w
( = œ ( 0 Ð# Ð>ÑÑ # Ð>Ñ .>,
,
#
+
pelo que não é mais do que o que em Análise Complexa é notado
( 0 ÐDÑ .D.
#
Ex III.46 a) Nas condições de III.9.11, mostrar que, se a forma diferencial =
fosse exacta, então
( = œ !,
0
pelo que a conclusão desse resultado era trivial.
b) Nas condições de III.9.12, mostrar que, se a forma diferencial = fosse
exacta, então o integral de = sobre a variedade singular ÐEß 0 Ñ só dependia
da restrição de 0 ao bordo `" ÐEÑ, pelo que a conclusão desse resultado era
trivial.
188
Cap. III. Formas diferenciais e teorema de Stokes
Ex III.47 Apresentar uma nova demonstração de III.9.12, sem utilizar o operador
prismático, seguindo o seguinte caminho:
a) Considerar sobre a variedade compacta Ò!ß "Ó ‚ E, de dimensão 8 ", a
orientação que associa a cada espaço vectorial tangente
XÐ>ßBÑ ÐÒ!ß "Ó ‚ EÑ œ ‘ ‚ XB ÐEÑ
a orientação produto da orientação canónica de ‘ pela orientação dada de
XB ÐEÑ.
b) Aplicar o teorema de Stokes à forma diferencial L ‡ =, de grau 8 sobre
Ò!ß "Ó ‚ E.
c) Verificar que os integrais das restrições de L ‡ = às subvariedades abertas
de `" ÐÒ!ß "Ó ‚ EÑ, Ö!× ‚ `! ÐEÑ e Ö"× ‚ `! ÐEÑ, com a orientação induzida no
bordo, são iguais respectivamente a '0 = e '1 =.
d) Verificar que o integral da restrição de L ‡ = à subvariedade aberta
Ó!ß "Ò ‚ `" ÐEÑ de `" ÐÒ!ß "Ó ‚ EÑ, com a orientação induzida no bordo, é nulo.
Ex III.48 Seja I um espaço euclidiano orientado de dimensão 8 ", seja W a
respectiva hipersuperfície esférica de centro ! e raio " e seja 3À I Ï Ö!× Ä W
B
a aplicação suave definida por 3ÐBÑ œ mBm
. Seja E § I Ï Ö!× uma variedade
sem bordo tal que 3ÎE seja um homeomorfismo de E sobre um subconjunto
F de W . Mostrar que 3ÎE é um difeomorfismo de E sobre F se, e só se, para
cada B − E, B Â XB ÐEÑ. Sugestão: Verificar que esta condição é equivalente
à de exigir que a restrição de H3B a XB ÐEÑ seja injectiva.
Ex III.49 Seja I um espaço euclidiano orientado de dimensão 8 " e consideremos sobre W œ ÖB − I ± mBm œ "× a orientação que lhe vem de ser bordo
da bola fechada ÖB − I ± mBm Ÿ "×. Notemos Z 96I o elemento de volume
de I e Z 96W a forma diferencial elemento de volume da variedade W . Seja
HÀ I Ï Ö!× Ä E8" ÐIà ‘Ñ a forma diferencial ângulo sólido.
a) Mostrar que, para cada C − W e A" ß á ß A8" − XC ÐWÑ, tem-se
Z 96W C ÐA" ß á ß A8" Ñ œ Z 96I ÐCß A" ß á ß A8" Ñ.
b) Mostrar que, para cada B − I Ï Ö!× e D" ß á ß D8" − I , tem-se
HB ÐD" ß á ß D8" Ñ œ
"
Z 96I ÐBß D" ß á ß D8" Ñ.
mBm8
c) No caso particular em que I œ ‘8 , com o produto interno e orientação
usuais, mostrar que, notando, como é usual, .B" ß á ß .B8 a base de
E" Б8 à ‘Ñ associada à base canónica de ‘8 , sai, para cada
B œ ÐB" ß á ß B8 Ñ − ‘8 Ï Ö!×,
HB œ " Ð"Ñ4"
8
4œ"
ˆÈB#"
B4
8 .B" • â • .B4" • .B4" • â • .B8 .
â B#8 ‰
Exercícios
189
Aproveitar este resultado para reconhecer a forma diferencial sobre ‘# Ï Ö!×
referida no exercício III.5.
Ex III.50 Sejam I um espaço euclidiano orientado de dimensão 8 ", W a
respectiva hipersuperfície esférica unitária de centro !, H a forma diferencial
ângulo sólido em I Ï Ö!× e 3À I Ï Ö!× Ä W a projecção, definida por
3ÐBÑ œ BÎmBm. Seja E uma variedade de dimensão 8 ", suavemente
orientada.
a) Se 0 À E Ä W é uma aplicação suave, mostrar que 0 tem ângulo sólido se,
e só se, a forma diferencial, de grau 8 ", Z 96W for integrável em ÐEß 0 Ñ e
que, nesse caso, n0 œ 'ÐEß0 Ñ Z 96W .
b) Se 0 À E Ä I Ï Ö!× é uma aplicação suave, mostrar que 0 tem ângulo
sólido se, e só se 3 ‰ 0 À E Ä W tem ângulo sólido e que, nesse caso,
n0 œ nÐ3 ‰ 0 Ñ.
Ex III.51 Seja I um espaço euclidiano orientado de dimensão 8 " e seja
E § I uma variedade de dimensão 8 ", suavemente orientada, tal que
! Â E. Para cada B − E seja ^B a normal unitária positiva, isto é, o único
vector de I ortogonal a XB ÐEÑ, de norma " e tal que a orientação induzida
em XB ÐEÑ, pela orientação de I e pela orientação transversa definida por ^B ,
seja a orientação dada. Mostrar que E tem ângulo sólido se, e só se, a
"
aplicação de E em ‘, que a B associa mBm
8 Ø^B ß BÙ, é integrável para a medida
.E e que, nesse caso,
nÐEÑ œ (
E
"
Ø^B ß BÙ . .E ÐBÑ.
mBm8
Utilizar esta conclusão para reintrepretar a conclusão do exercício III.31, à
luz de III.9.21. Sugestão: Utilizar a caracterização de HB dada na alínea b)
do exercício III.49.
Ex III.52 No caso em que I é um espaço euclidiano orientado de dimensão ",
explicitar o que é o ângulo sólido orientado de uma variedade singular
compacta de dimensão !, ÐEß 0 Ñ, onde 0 é uma aplicação de E em I Ï Ö!×.
Ex III.53 Consideremos em ‚ o seu produto interno e a sua orientação canónicos
(‚ œ ‘# ).
a) Mostrar que a forma diferencial ângulo sólido
HÀ ‚ Ï Ö!× Ä E" Ð‚à ‘Ñ
está definida por
A
HD ÐAÑ œ eÐ Ñ.
D
onde eÐAÑ denota a parte imaginária de um número complexo A.
Sugestão: Utilizar a caracterização de H dada na alínea b) do exercício
III.49.
190
Cap. III. Formas diferenciais e teorema de Stokes
b) Mostrar que, se E é uma variedade compacta e suavemente orientada, de
dimensão ", e se 0 À E Ä ‚ Ï Ö!× é uma aplicação suave, então o ângulo
sólido orientado de 0 é dado por
nÐ0 Ñ œ eÐ(
ÐEß0 Ñ
"
.DÑ.
D
c) Sendo :À ‚ Ï Ö!× Ä ‘ a aplicação suave definida por
:ÐDÑ œ logÐlDlÑ,
mostrar que se tem
A
. :D ÐAÑ œ dÐ Ñ.
D
Deduzir daqui que, se 0 À Ò+ß ,Ó Ä ‚ Ï Ö!× é uma aplicação suave, tem-se
(
0
"
0 Ð,Ñ
.D œ logÐl
lÑ 3 nÐ0 Ñ.
D
0 Ð+Ñ
Ex III.54 Seja I um espaço euclidiano orientado de dimensão 8 #, seja E
uma variedade compacta, suavemente orientada, de dimensão 8 ", e seja
0 À E Ä I Ï Ö!× uma aplicação suave, cuja restrição a `" ÐEÑ seja constante e
tal que, para um certo C − I Ï Ö!×, 0 ÐEÑ § I Ï Ð‘ CÑ (ou seja, tal que
3 ‰ 0 À E Ä W não seja sobrejectiva). Mostrar que se tem então nÐ0 Ñ œ !.
Sugestão: Tendo em conta o exercício III.39, deduzir a existência de uma
forma diferencial =, de grau 8 #, sobre I Ï Ð‘ CÑ, tal que . = seja a
restrição de H, aplicando em seguida o teorema de Stokes singular. No caso
8 œ #, lembrar o exercício III.23.
Ex III.55 (O teorema fundamental da Álgebra) Para cada < !, seja W< § ‚
o conjunto dos números complexos de módulo <.
a) Sendo, para cada 8 − ™, 08 À ‚ Ï Ö!× Ä ‚ Ï Ö!× a aplicação suave
definida por 08 ÐDÑ œ D 8 , verificar que 08‡ H œ 8 H e deduzir daí que, para
cada < !, nÐ0 Ñ œ #81.
b) Sejam 8 " e 0 À ‚ Ä ‚ uma aplicação polinomial da forma
0 ÐDÑ œ D 8 +" D 8" +# D 8# â +8" D +8 ,
com os +4 números complexos. Mostrar que, para < !, suficientemente
grande, 0 aplica W< em ‚ Ï Ö!× e a restrição de 0 a W< é suavemente
homotópica à restrição de 08 a W< (enquanto aplicações W< Ä ‚ Ï Ö!×);
deduzir daqui que nÐ0ÎW< Ñ œ #81 e, portanto, que existe D − ‚, com lDl <,
tal que 0 ÐDÑ œ !.
Ex III.56 (Integração ao longo de uma variedade singular parametrizada)
Sejam Q § I uma variedade e = œ Ð=C ÑC−Q uma forma diferencial suave
s uma variedade compacta, suavede grau 8, real ou complexa. Sejam E § I
Exercícios
191
mente orientada, de dimensão 8, F § I˜ uma variedade e 0 À E ‚ F Ä Q
uma aplicação suave. Para cada C − F , seja 0C À E Ä Q a aplicação suave
definida por 0C ÐBÑ œ 0 ÐBß CÑ. Mostrar que tem lugar uma aplicação suave
1À F Ä Š, definida por
1ÐCÑ œ (
=.
ÐEß0C Ñ
Sugestão: Mostrar que tem lugar uma aplicação suave 2À E ‚ F Ä Š,
definida por Ð0C‡ =ÑB œ 2ÐBß CÑ Z 96B , aplicando em seguida o exercício I.17.
Ex III.57 (O ângulo sólido em torno dum ponto) Seja I um espaço euclidiano
orientado de dimensão 8 ". Sendo E uma variedade suavemente orientada
de dimensão 8 " e 0 À E Ä I uma aplicação suave, diz-se que ÐEß 0 Ñ tem
ângulo sólido em torno do ponto C − I Ï 0 ÐEÑ se, sendo 0C À E Ä I Ï Ö!× a
aplicação suave definida por 0C ÐBÑ œ 0 ÐBÑ C, ÐEß 0C Ñ tem ângulo sólido;
nesse caso, define-se o ângulo sólido orientado de ÐEß 0 Ñ em torno de C ,
notado nC ÐEß 0 Ñ ou, simplesmente, nC Ð0 Ñ, como sendo o ângulo sólido
orientado de ÐEß 0C Ñ. No caso em que E § I e 0 À E Ä I é a inclusão,
usa-se também a notação nC ÐEÑ em vez de nC ÐEß 0 Ñ.
a) Supondo que a variedade E é compacta, utilizar o exercício anterior para
deduzir que tem lugar uma aplicação suave de I Ï 0 ÐEÑ em ‘, que a cada C
associa nC ÐEß 0 Ñ.
b) Suponhamos que 8 #, que a variedade E é compacta e que a restrição
de 0 a `" ÐEÑ é constante (é o que acontece, evidentemente, se a variedade E
não tem bordo). Mostrar que a aplicação que a C associa nC ÐEß 0 Ñ é
constante sobre cada componente conexa do aberto I Ï 0 ÐEÑ, sendo nula na
componente conexa ilimitada deste aberto. Sugestão: Temos uma aplicação
suave que toma valores num conjunto discreto. Ter também em conta o
exercício III.54.
Ex III.58 (O que se passa quando atravessamos a variedade) Seja I um
espaço euclidiano orientado de dimensão 8 " e seja E § I uma variedade
compacta, sem bordo, de dimensão 8 ", suavemente orientada. Seja + − E.
Consideremos um aberto Y de I , com + − Y , e uma aplicação suave
0 À Y Ä ‘, tal que H0+ Á ! e que E Y œ ÖB − Y ± 0 ÐBÑ œ !×. Se
necessário substituindo 0 por 0 , pode-se já supor que a orientação de
X+ ÐEÑ é a induzida pela orientação de I e pela orientação transversa para a
qual gradÐ0 Ñ+ é um vector positivo. Se necessário reduzindo o aberto Y ,
pode-se já supor que, para cada B − Y , H0B Á ! e que, para cada
B − Y E, a orientação de XB ÐEÑ é a induzida pela de I e pela orientação
transversa para a qual gradÐ0 ÑB é um vector positivo.
a) Sendo $ œ mgradÐ0 Ñ+ m !, mostrar que se pode fixar & ! tal que a bola
aberta F& Ð+Ñ esteja contida em Y , que, para cada B − F& Ð+Ñ,
192
Cap. III. Formas diferenciais e teorema de Stokes
mgradÐ0 ÑB gradÐ0 Ñ+ m
$
#
e que, para cada B − F& Ð+Ñ E, com B Á +, exista A − X+ ÐEÑ com mAm œ "
e
m
B+
"
Am ,
mB +m
#
deduzindo daqui que, sempre que B − F& Ð+Ñ E, com B Á +,
$
mB +m,
#
lØgradÐ0 ÑB ß B +Ùl $ mB +m,
lØgradÐ0 Ñ+ ß B +Ùl
donde gradÐ0 ÑB Â ‘ÐB +Ñ.
b) Sendo & ! escolhido nas condições de a), mostrar que existe ! &w &
tal que, quaisquer que sejam ,ß - − F&w Ð+Ñ, tais que 0 Ð,Ñ ! e 0 Ð-Ñ !, se
tenha
n, ÐEÑ œ n- ÐEÑ 58" .
Sugestão: Fixar ! < &. Mostrar que E fica união disjunta das duas
subvariedades abertas de dimensão 8 ",
E! œ ÖB − E ± mB +m <×,
E" œ ÖB − E ± mB +m <×,
e do conjunto de medida .E nula ÖB − E ± mB +m œ <×.
A
Figura 9
Considerar então a variedade compacta de dimensão 8
F œ ÖB − Y ± mB +m Ÿ <, 0 ÐBÑ Ÿ !×,
Exercícios
193
para a qual `" ÐFÑ é a união disjunta dos subconjuntos abertos E" e
F! œ ÖB − Y ± mB +m œ <, 0 ÐBÑ !×.
Tendo em conta III.9.21, mostrar que, se ,ß - − F< Ð+Ñ verificam 0 Ð,Ñ ! e
0 Ð-Ñ !, então n, ÐF! Ñ n, ÐE" Ñ œ 58" e que n- ÐF! Ñ n- ÐE" Ñ œ !,
donde
n, ÐEÑ œ n, ÐE! Ñ n, ÐF! Ñ 58" ,
n- ÐEÑ œ n- ÐE! Ñ n- ÐF! Ñ,
e atender a que os primeiros membros são múltiplos inteiros de 58" , assim
como à continuidade em + da aplicação que a B associa
s! Ñ nB ÐF
s ! Ñ,
nB ÐE! Ñ nB ÐF! Ñ œ nB ÐE
s ! são variedades compactas convenientes, que diferem de E! e
s! e F
onde A
de F! por conjuntos de medida nula.
c) Deduzir que o conjunto aberto I Ï E tem, pelo menos, duas componentes
conexas.
Ex III.59 (O ângulo sólido de uma aplicação contínua) Seja I um espaço
euclidiano orientado de dimensão 8 ". Seja E uma variedade compacta,
suavemente orientada, de dimensão 8 " e notemos `ÐEÑ a união dos
bordos `4 ÐEÑ, com 4 ", que é um subconjunto compacto de E (o
complementar do aberto `! ÐEÑ de E). Seja 0 À E Ä I Ï Ö!× uma aplicação
contínua tal que 0Î`ÐEÑ À `ÐEÑ Ä I Ï Ö!× seja uma aplicação suave (esta
última condição está automaticamente verificada se 8 Ÿ # ou se a variedade
E não tem bordo). Mostrar que:
a) Existe uma aplicação suave 2À E Ä I Ï Ö!×, tal que a restrição de 2 a
`ÐEÑ coincida com a de 0 e que, para cada B − E,
m2ÐBÑ 0 ÐBÑm m0 ÐBÑm. Sugestão: Lembrar III.8.6.
s E Ä I Ï Ö!×, cujas restrições a `ÐEÑ
b) Dadas duas aplicações suaves 2ß 2À
coincidam com a de 0 e tais que, para cada B − E,
m2ÐBÑ 0 ÐBÑm m0 ÐBÑm,
s
m2ÐBÑ
0 ÐBÑm m0 ÐBÑmß
s . Sugestão: Definir
tem-se que nÐEß 2Ñ œ nÐEß 2Ñ
s
LÐ>ß BÑ œ Ð" >Ñ 2ÐBÑ > 2ÐBÑ
e ter em conta III.9.12.
Nota: Nas condições anteriores, define-se o ângulo sólido orientado de
ÐEß 0 Ñ, notado ainda nÐEß 0 Ñ ou, simplesmente nÐ0 Ñ, como sendo igual a
nÐEß 2Ñ, qualquer que seja a aplicação suave 2À E Ä I Ï Ö!×, cuja restrição
a `ÐEÑ coincida com a de 0 e tal que, para cada B − E, se tenha
m2ÐBÑ 0 ÐBÑm m0 ÐBÑm. É claro que esta noção de ângulo sólido orientado
generaliza a já conhecida no caso em que a aplicação 0 é suave.
194
Cap. III. Formas diferenciais e teorema de Stokes
Ex III.60 Sejam I um espaço euclidiano orientado de dimensão 8 " e E § I
uma variedade compacta, suavemente orientada, de dimensão 8 ". Sendo
0 ß 1À E Ä I Ï Ö!× duas aplicações contínuas, com uma mesma restrição
suave a `ÐEÑ, mostrar que nÐ1Ñ nÐ0 Ñ é um múltiplo inteiro de 58" . Além
disso, se elas forem continuamente homotópicas com bordo fixo, isto é tais
que exista uma aplicação contínua LÀ Ò!ß "Ó ‚ E Ä I Ï Ö!×, verificando
LÐ!ß BÑ œ 0 ÐBÑ, LÐ"ß BÑ œ 1ÐBÑ e, para cada > − Ò!ß "Ó e B − `ÐEÑ,
LÐ>ß BÑ œ 0 ÐBÑ, mostrar que se tem mesmo nÐ0 Ñ œ nÐ1Ñ. Sugestão: Tendo
s Ò!ß "Ó ‚ E Ä I Ï Ö!×,
em conta III.8.6, considerar uma aplicação suave LÀ
coincidindo com L em Ò!ß "Ó ‚ `ÐEÑ e para a qual se verifique a condição
s BÑ LÐ>ß BÑm mLÐ>ß BÑm, para cada Ð>ß BÑ − E, e aplicar, em
mLÐ>ß
seguida, III.9.12.
Ex III.61 (A variedade esburacada) Seja I um espaço euclidiano orientado de
dimensão 8 ". Seja F uma variedade sem cantos, suavemente orientada,
de dimensão 8 e sejam G" ß á ß G: variedades compactas, sem cantos, de
dimensão 8, contidas em `! ÐFÑ e disjuntas duas a duas (: !). Sendo
s œ F Ï - `! ÐG5 Ñ, seja s0 À F
s Ä I Ï Ö!× uma aplicação contínua. Mostrar
F
5
que se tem então
nÐ`" ÐFÑß 0Î`" ÐFÑ Ñ œ " nÐ`" ÐG5 Ñß 0Î`" ÐG5 Ñ Ñ.
5
É claro que o caso particular em que : œ ! afirma que, se 0 À F Ä I Ï Ö!× é
uma aplicação contínua, então
nÐ`" ÐFÑß 0Î`" ÐFÑ Ñ œ !.
s e I espaços vectoriais orientados de dimensão 8 ", o
Ex III.62 Sejam I
s um aberto limitado
segundo dos quais munido de um produto interno. Seja Y
s e notemos frÐY
s Ñ a respectiva fronteira. Seja 0 À frÐY
s Ñ Ä I Ï Ö!× uma
de I
aplicação de classe G ! (ou, equivalentemente, para quem conheça o teorema
de extensão de Tietze-Urysohn, uma aplicação contínua).
s Ñ Ä I , prolongando
a) Mostrar que existe uma aplicação contínua s0 À adÐY
s
s
s,
0 . Dado um tal prolongamento 0 , seja O o subconjunto compacto de Y
s
constituído pelos pontos B tais que 0 ÐBÑ œ ! e considerar, tendo em conta a
aplicação do teorema de Sard estudada no exercício I.19, uma variedade
s §Y
s , tal que O
s § `! ÐQ
s Ñ.
compacta, sem cantos, com dimensão 8, Q
s Ñß s0
Mostrar que o valor do ângulo sólido orientado nÐ`" ÐQ
Ñ
não
sÑ
Î`" ÐQ
s , nas condições anteriores. Sugestão:
depende da escolha da variedade Q
s e Q
s w nas codições referidas, considerar uma
Dadas duas variedades Q
s ww , compacta, sem cantos, com dimensão 8, tal que
terceira variedade Q
Exercícios
195
s § `! ÐQ
s ww Ñ § `! ÐQ
s Ñ `! ÐQ
s w Ñ,
O
aplicando em seguida o exercício anterior.
b) Tendo em conta o que se viu em a), a cada aplicação contínua
s0 À adÐY
s Ñ Ä I , prolongando 0 , ficou associado um número, a saber, o
s Ñ, para uma variedade
ângulo sólido orientado da restrição de s0 a `" ÐQ
s e contendo
compacta, sem cantos, com dimensão 8, arbitrária, contida em Y
s
s
s
O œ ÖB − Y ± 0 ÐBÑ œ !×. Mostrar que este número também não depende do
prolongamento s0 escolhido (ele depende portanto apenas da aplicação
s Ñ Ä I Ï Ö!×, e do aberto Y
s que se está a considerar).
0 À frÐY
s Ñ Ä I , com os
Sugestão: Dados dois prolongamentos contínuos s0 ß 0˜ À adÐY
˜
s
correspondentes compactos O e O , considerar & !, tal que m0 ÐBÑm &,
s Ñ, e tomar o compacto O , contendo O
s e O˜ e contido em
para todo o B − frÐY
s ÐBÑm Ÿ & e m0˜ ÐBÑm Ÿ &.
s , constituído pelos pontos B − adÐY
s Ñ tais que m0
Y
s §Y
s , de modo que se tenha O § `! ÐQ
s Ñ, mostrar
Tomando a variedade Q
˜
s
s
que as restrições de 0 e 0 a `" ÐQ Ñ são continuamente homotópicas, como
s Ñ em I Ï Ö!×, aplicando em seguida o exercício III.59.
aplicações de `" ÐQ
c) O número que nas alíneas anteriores foi associado a cada aplicação
s Ñ Ä I Ï Ö!× costuma ser ainda notado nÐ0 Ñ (ou nÐY
s ß 0 Ñ,
contínua 0 À frÐY
se quisermos ser mais precisos). Mostrar que esta notação é compatível com
a utilizada anteriormente, no caso particular em que é dada uma variedade
s§I
s , e se toma Y
s œ `! ÐFÑ
s (porcompacta, sem cantos, de dimensão 8, F
s Ñ œ `" ÐFÑ
s ).
tanto frÐY
CAPÍTULO IV
Introdução à Cohomologia de de Rham
§1. Cohomologia de de Rham.
IV.1.1. Sejam Q § I uma variedade e Š um dos corpos, ‘ ou ‚. Para cada
: !, vamos notar H:Š ÐQ Ñ, ou H: ÐQ à ŠÑ, o conjunto das formas
diferenciais suaves de grau : sobre Q , conjunto que é trivialmente um
espaço vectorial sobre Š. Será cómodo notarmos, para cada : !, H:Š ÐQ Ñ,
ou H: ÐQ à ŠÑ, um espaço vectorial Ö!×, reduzido ao vector nulo. Com
frequência, omitiremos a referência ao corpo Š na notação quando estiver
implícito qual o corpo Š que se está a considerar ou quando se tratar de
resultados gerais válidos para cada um dos corpos (estará então implícito que
o corpo Š é o mesmo ao longo do enunciado). Para cada : !, a
diferenciação exterior, definida em III.2.2, é uma aplicação linear
.À H: ÐQ Ñ Ä H:" ÐQ Ñ,
aplicação que será notada, mais precisamente, . : quando for importante
explicitar qual o valor de : que se está a considerar. Será cómodo extender
esta definição, notando . : À H: ÐQ Ñ Ä H:" ÐQ Ñ a aplicação linear nula, no
caso em que : ! (trata-se, aliás, da única aplicação linear possível). Além
disso, tendo em conta III.2.8, para cada : − ™, é nula a aplicação composta
.
.
H: ÐQ Ñ Ä H:" ÐQ Ñ Ä H:# ÐQ Ñ,
isto é, tem-se . :" ‰ . : œ !.
IV.1.2. Em geral, chama-se complexo de cocadeias a um par G ñ , formado por
uma família de espaços vectoriais38 ÐG : Ñ:−™ e uma família de aplicações
lineares . : À G : Ä G :" (os operadores de cobordo), tal que, para cada
: − ™, . :" ‰ . : œ !À G : Ä G :# .
No quadro geral dum complexo de cocadeias G ñ , chamam-se cociclos de
grau : aos elementos B − G : tais que . : ÐBÑ œ ! e cobordos de grau : aos
elementos B − G : tais que exista C − G :" tal que B œ . :" ÐCÑ. Nota-se
^ : ÐG ñ Ñ § G : e F : ÐG ñ Ñ § G : os subespaços vectoriais cujos elementos são,
respectivamente, os cociclos e os cobordos de grau : (o núcleo e a imagem
de duas aplicações lineares) e a igualdade . : ‰ . :" œ ! implica trivialmente
38Ou,
mais geralmente, de módulos sobre um anel, mas o caso dos espaços vectoriais é o
que nos interessa de momento.
198
Cap. IV. Introdução à cohomologia de de Rham
que se tem F : ÐG ñ Ñ § ^ : ÐG ñ Ñ, o que nos permite considerar o espaço
vectorial quociente
L : ÐG ñ Ñ œ
^ : ÐG ñ Ñ
,
F : ÐG ñ Ñ
a que se dá o nome de espaço de cohomologia de grau : do complexo de
cocadeias G ñ . Se B − ^ : ÐG ñ Ñ, notaremos usualmente ÒBÓ a classe de
equivalência de B em L : ÐG ñ Ñ.
IV.1.3. Tendo em conta o que dissémos atrás, se Q § I é uma variedade,
fica-lhe associado um complexo de cocadeias HñŠ ÐQ Ñ, constituído pela
família dos espaços vectoriais H:Š ÐQ Ñ e pela dos operadores de
diferenciação exterior . : À H:Š ÐQ Ñ Ä H:"
Š ÐQ Ñ, complexo de cocadeias ao
qual se dá o nome de complexo de de Rham39 da variedade Q . Aos cociclos
e aos cobordos deste complexo de cocadeias dá-se, respectivamente, o nome
de formas diferenciais fechadas e de formas diferenciais exactas, por outras
palavras, e como já referimos ocasionalmente, uma forma diferencial suave
=, de grau :, diz-se fechada se verificar a condição . = œ ! e diz-se exacta se
for da forma . 5 , para alguma forma diferencial suave 5 , de grau : " (ou se
:
for !, no caso em que : œ !). Notamos simplesmente ^Š: ÐQ Ñ e FŠ
ÐQ Ñ os
ñ
ñ
espaços vectoriais ^ : ÐHŠ
ÐQ ÑÑ e F : ÐHŠ
ÐQ ÑÑ e
LŠ: ÐQ Ñ œ
^Š: ÐQ Ñ
:
FŠ
ÐQ Ñ
ñ
os espaços de cohomologia L : ÐHŠ
ÐQ ÑÑ, a que se dá o nome de espaços de
cohomologia de de Rham da variedade Q . Como anteriormente, omitimos
com frequência das notações a referência ao corpo Š, quando daí não advier
perigo de confusão.
A importância dos espaços de cohomologia de de Rham vem de que,
como veremos adiante, eles têm frequentemente dimensão finita e a
respectiva dimensão é um invariante topológico da variedade Q . Isto
apesar de, na maior parte dos casos os espaços vectoriais H: ÐQ Ñ, ^ : ÐQ Ñ
e F : ÐQ Ñ, enquanto espaços de funções, serem espaços vectoriais de
dimensão infinita. Reparemos também que o lema de Poincaré,
demonstrado em III.7.10, diz-nos que, quando a variedade Q é
suavemente contráctil, toda a forma diferencial suave de grau : " que
seja fechada é exacta, isto é, que, para cada : ", F : ÐQ Ñ œ ^ : ÐQ Ñ ou,
equivalentemente, L : ÐQ Ñ œ Ö!×. A dimensão de um espaço de
cohomologia de de Rham L : ÐQ Ñ, com : ", pode portanto ser olhada
intuitivamente como uma medida da “complicação” da variedade Q .
Neste momento, podemos apenas caracterizar um dos espaços de cohomologia não trivial, nomeadamente, o de grau !.
39A
repetição da palavra “de” não é um engano. A referência é a um matemático de nome
“de Rham”.
§1. Cohomologia de de Rham
199
IV.1.4. Seja Q § I uma variedade. Tem-se então:
a) Para cada : !, L : ÐQ Ñ œ Ö!×;
b) Se Q tem dimensão 7, para cada : 7, L : ÐQ Ñ œ Ö!×;
c) F ! ÐQ Ñ œ Ö!× e ^ ! ÐQ Ñ é o espaço vectorial das aplicações 0 À Q Ä Š
que são constantes sobre cada componente conexa de Q ;
d) Seja ÐQ3 Ñ3−M a família das componentes conexas de Q e consideremos,
para cada 3 a aplicação suave 03 À Q Ä Š, de valor constante " nos pontos de
Q3 e que se anula nas restantes componentes conexas. Tem-se então que as
classes de equivalência Ò03 Ó − L ! ÐQ Ñ são linearmente independentes e, no
caso em que M é finito, constituem uma base de L ! ÐQ Ñ. Em particular, se a
variedade Q tem um número finito 5 de componentes conexas, então o
espaço de cohomologia L ! ÐQ Ñ tem dimensão 5 e, caso contrário, L ! ÐQ Ñ
tem dimensão infinita.
Dem: As conclusões de a) e b) resultam imediatamente de que, nas
condições referidas, tem-se H: ÐQ Ñ œ Ö!×, donde também ^ : ÐQ Ñ œ Ö!× e
portanto L : ÐQ Ñ œ Ö!× (lembrar que, se Q tem dimensão 7, então XB ÐQ Ñ
é um espaço vectorial de dimensão 7, e portanto E: ÐXB ÐQ Ñà ŠÑ œ Ö!×, para
cada : 7). O facto de se ter F ! ÐQ Ñ œ Ö!× vem de que se trata da imagem
da aplicação linear . " À H" ÐQ Ñ Ä H! ÐQ Ñ, cujo domínio é Ö!×. Uma vez
que H! ÐQ Ñ é o espaço das aplicações suaves 0 À Q Ä Š e que a diferencial
exterior de uma tal aplicação suave coincide com a derivação usual, vemos
que ^ ! ÐQ Ñ é o espaço das aplicações suaves 0 À Q Ä Š com derivada
identicamente nula e, tendo em conta o facto de as componentes conexas de
uma variedade serem subconjuntos abertos desta, em particular variedades e
de toda a aplicação definida numa variedade conexa e com derivada
identicamente nula ser constante, vemos que ^ ! ÐQ Ñ pode ser caracterizado
alternativamente como o espaço das aplicações 0 À Q Ä Š que são
constantes em cada componente conexa. Considerando as aplicações 03
definidas no enunciado, vemos que elas são elementos independentes de
^ ! ÐQ Ñ, uma vez que, se ! +3 03 œ !, obtemos +3 œ ! ao aplicarmos ambos
os membros a um ponto B − Q3 . Além disso, no caso em que M é finito, se
0 − ^ ! ÐQ Ñ toma o valor constante +3 em Q3 , é imediato que, para todo o
B − Q , 0 ÐBÑ œ ! +3 03 ÐBÑ,40 o que mostra que temos uma base de ^ ! ÐQ Ñ.
O facto de se ter F ! ÐQ Ñ œ Ö!× implica que a aplicação canónica
^ ! ÐQ Ñ Ä L ! ÐQ Ñ œ
^ ! ÐQ Ñ
F ! ÐQ Ñ
é um isomorfismo, donde a conclusão de d).
IV.1.5. Suponhamos que temos dois complexos de cocadeias G ñ e G w ñ , constituídos respectivamente pelos espaços vectoriais G : , com os operadores de
40No
caso em que M é infinito, o problema está em que esta soma não tem que ter apenas
um número finito de parcelas não nulas.
200
Cap. IV. Introdução à cohomologia de de Rham
cobordo . : À G : Ä G :" , e pelos espaços vectoriais G w : , com os operadores
de cobordo . w : À G w : Ä G w :" . Dá-se o nome de morfismo de complexos de
cocadeias de G ñ para G w ñ a uma família -ñ œ Ð-: Ñ:−™ de aplicações lineares
-: À G : Ä G w : tal que, para cada :, . w : ‰ -: œ -:" ‰ . : , o que se costuma
também traduzir com a afirmação de que tem lugar um diagrama comutativo
G:
- Æ-
Ä
.
G :"
-Æ-
G w:
Ä
.w
G w :"
(repare-se que omitimos os expoentes : e : " nos símbolos das aplicações
lineares no diagrama, uma vez que eles são determinados pelos respectivos
domínios).
IV.1.6. Se -ñ œ Ð-: Ñ:−™ é um morfismo de complexos de cocadeias de G ñ para
G w ñ , então, para cada :, a aplicação linear -: À G : Ä G w : aplica ^ : ÐG ñ Ñ em
^ : ÐG w ñ Ñ e F : ÐG ñ Ñ em F : ÐG w ñ Ñ e define portanto, por passagem ao quociente,
uma aplicação linear
ñ
L : Ð-ñ ÑÀ L : ÐG ñ Ñ Ä L : ÐG w Ñ
por
L : Ð-ñ ÑÐÒBÓÑ œ Ò-: ÐBÑÓ.
Têm, além disso, lugar as seguintes propriedades de functorialidade41:
a) A família M.G ñ das aplicações lineares identidade M.G : À G : Ä G : é um
morfismo de complexos de cocadeias de G ñ para G ñ e, para cada :,
L : ÐM.G ñ ÑÀ L : ÐG ñ Ñ Ä L : ÐG ñ Ñ
é a aplicação linear identidade;
b) Se -ñ é um morfismo de complexos de cocadeias de G ñ para G w ñ e se .ñ é
um morfismo de complexos de cocadeias de G w ñ para G ww ñ , então a família
.ñ ‰ -ñ œ Ð.: ‰ -: Ñ:−™ é um morfismo de complexos de cocadeias de G ñ
para G ww ñ e, para cada :,
ñ
L : Ð.ñ ‰ -ñ Ñ œ L : Ð.ñ Ñ ‰ L : Ð-ñ ÑÀ L : ÐG ñ Ñ Ä L : ÐG ww Ñ.
c) Se -ñ œ Ð-: Ñ:−™ é um morfismo de complexos de cocadeias de G ñ para
G w ñ , tal que, para cada :, -: À G : Ä G w : seja um isomorfismo (dizemos então
que -ñ é um isomorfismo de complexos de cocadeias de G ñ para G w ñ ), então a
família -ñ " œ ÐÐ-: Ñ" Ñ:−™ é um morfismo de complexos de cocadeias de
G w ñ para G ñ e, para cada :,
41Quem
conheça as noções de categoria e de functor compreenderá a razão desta
designação. Preferimos, no entanto, não alongar este texto, entrando na discussão desses
conceitos.
§1. Cohomologia de de Rham
201
ñ
L : Ð-ñ " Ñ œ L : Ð-ñ Ñ" À L : ÐG w Ñ Ä L : ÐG ñ Ñ.
Dem: Se B − ^ : ÐG ñ Ñ, tem-se . : ÐBÑ œ !, donde
:
. w Ð-: ÐBÑÑ œ -:" Ð. : ÐBÑÑ œ -:" Ð!Ñ œ !,
o que mostra que -: ÐBÑ − ^ : ÐG w ñ Ñ. Do mesmo modo, se B − F : ÐG ñ Ñ, tem-se
B œ . :" ÐCÑ, para um certo C − G :" , e então
:
-: ÐBÑ œ -: Ð. :" ÐCÑÑ œ . w Ð-:" ÐCÑÑ,
o que mostra que -: ÐBÑ − F : ÐG w ñ Ñ. O facto de -: aplicar ^ : ÐG ñ Ñ em
^ : ÐG w ñ Ñ e F : ÐG ñ Ñ em F : ÐG w ñ Ñ implica que fica bem definida pela fórmula
do enunciado a aplicação L : Ð-ñ ÑÀ L : ÐG ñ Ñ Ä L : ÐG w ñ Ñ. A propriedade
referida em a) resulta trivialmente das definições, tal como resulta a
igualdade L : Ð.ñ ‰ -ñ Ñ œ L : Ð.ñ Ñ ‰ L : Ð-ñ Ñ, se repararmos que o facto de
.ñ ‰ -ñ ser um morfismo de complexos de cocadeias resulta de que
:
:
. ww ‰ .: ‰ -: œ .:" ‰ . w ‰ -: œ .:" ‰ -:" ‰ . : .
Quanto à conclusão de c), começamos por reparar que, de se ter
. w : ‰ -: œ -:" ‰ . : , deduzimos, compondo ambos os membros à esquerda
com Ð-:" Ñ" e à direita com Ð-: Ñ" , Ð-:" Ñ" ‰ . w : œ . : ‰ Ð-: Ñ" , o que
mostra que -ñ " é efectivamente um morfismo de complexos de cocadeias, e
deduzimos então, de se ter -ñ " ‰ -ñ œ M.G ñ e -ñ ‰ -ñ " œ M.G w ñ , tendo em
conta as conclusões de b) e c), que se tem
L : Ð-ñ " Ñ ‰ L : Ð-ñ Ñ œ M.L : ÐG ñ Ñ ,
L : Ð-ñ Ñ ‰ L : Ð-ñ " Ñ œ M.L : ÐG w ñ Ñ ,
o que mostra que L : Ð-ñ Ñ é um isomorfismo, tendo L : Ð-ñ " Ñ como isomorfismo inverso.
IV.1.7. Sejam Q § I e Q w § I w duas variedades e 0 À Q w Ä Q uma aplicação
suave. Tendo em conta III.2.7, a família 0 ‡ das aplicações lineares
0 ‡ À H: ÐQ Ñ Ä H: ÐQ w Ñ
(se quiséssemos ser mais precisos deveríamos tê-las notado 0 ‡ : ) constitui um
morfismo de complexos de cocadeias de Hñ ÐQ Ñ para Hñ ÐQ w Ñ pelo que,
tendo em conta o que dissémos atrás, ficam-lhe associadas aplicações
lineares
L : Ð0 ‡ ÑÀ L : ÐQ Ñ Ä L : ÐQ w Ñ,
que notaremos simplesmente L : Ð0 Ñ, por
L : Ð0 ÑÐÒ=ÓÑ œ Ò0 ‡ =Ó.
IV.1.8. Tendo em conta a alínea a) de III.1.14, deduzimos que:
a) Sendo Q § I uma variedade, e M.Q À Q Ä Q a aplicação identidade, o
202
Cap. IV. Introdução à cohomologia de de Rham
‡
morfismo de complexos de cocadeias M.Q
À Hñ ÐQ Ñ Ä Hñ ÐQ Ñ é o morfismo
:
identidade, e portanto também cada L ÐM.Q ÑÀ L : ÐQ Ñ Ä L : ÐQ Ñ é a aplicação linear identidade.
b) Se Q § I , Q w § I w e Q ww § I ww são variedades e 0 À Q ww Ä Q w e
1À Q w Ä Q são aplicações suaves, o morfismo de complexos de cocadeias
Ð1 ‰ 0 ч À Hñ ÐQ Ñ Ä Hñ ÐQ ww Ñ coincide com o composto 0 ‡ ‰ 1‡ dos
morfismos de complexos de cocadeias 1‡ À Hñ ÐQ Ñ Ä Hñ ÐQ w Ñ e
0 ‡ À Hñ ÐQ w Ñ Ä Hñ ÐQ ww Ñ, e portanto, para cada :,
L : Ð1 ‰ 0 Ñ œ L : Ð0 Ñ ‰ L : Ð1ÑÀ L : ÐQ Ñ Ä L : ÐQ ww Ñ.
c) Em consequência, se 1À Q w Ä Q é um difeomorfismo, então
1‡ À Hñ ÐQ Ñ Ä Hñ ÐQ w Ñ é um isomorfismo de complexos de cocadeias e
portanto, para cada :, L : Ð1ÑÀ L : ÐQ Ñ Ä L : ÐQ w Ñ é um isomorfismo, tendo
L : Ð1" Ñ como isomorfismo inverso.42
IV.1.9. Lembremos que, como se definiu em III.7.5, dadas duas variedades
Q § I e Q w § I w , diz-se que duas aplicações suaves 0 ß 1À Q w Ä Q são
suavemente
homotópicas
se
existir
uma
aplicação
suave
LÀ Ò!ß "Ó ‚ Q w Ä Q tal que LÐ!ß BÑ œ 0 ÐBÑ e LÐ"ß BÑ œ 1ÐBÑ, dizendo-se
então que L é uma homotopia suave de 0 para 1.43
IV.1.10. A relação de homotopia suave é uma relação de equivalência na classe
das aplicações suaves de Q w para Q .
Dem: A reflexividade e a simetria desta relação são essencialmente triviais:
se 0 À Q w Ä Q é uma aplicação suave, então a aplicação suave definida por
LÐ>ß BÑ œ 0 ÐBÑ é uma homotopia de 0 para 0 e se LÀ Ò!ß "Ó ‚ Q w Ä Q é
uma homotopia suave de 0 para 1, obtemos, a partir dela, uma homotopia
s Ò!ß "Ó ‚ Q w Ä Q ,
suave
LÀ
de
1
para
0,
definida
por
s BÑ œ LÐ" >ß BÑ. Para a transitividade é que temos que ser um pouco
LÐ>ß
mais cuidadosos para evitar os cantos que poderiam destruir a suavidade.
Suponhamos então que 0 ß 1ß 2À Q w Ä Q são aplicações suaves, que a
aplicação LÀ Ò!ß "Ó ‚ Q w Ä Q é uma homotopia suave de 0 para 1 e que a
s Ò!ß "Ó ‚ Q w Ä Q é uma homotopia suave de 1 para 2. Com o
aplicação LÀ
s para obtermos uma
objectivo de combinarmos as homotopias L e L
homotopia suave de 0 para 2, começamos por reparar que, aplicando o
teorema da partição da unidade à cobertura aberta de Ò!ß "Ó constituída pelos
42Para
quem conheça a linguagem da teoria das categorias, as alíneas a) e b) mostram
que, no quadro da cohomologia de de Rham de grau :, estamos em presença de um
functor contravariante da categoria das variedades para a dos espaços vectoriais e a
conclusão principal de c) é um caso particular do resultado geral que nos garante que um
functor aplica isomorfismos em isomorfismos.
43Para cada > − Ò!ß "Ó, ficamos com uma aplicação suave L À Q w Ä Q , definida por
>
L> ÐBÑ œ LÐ>ß BÑ, tendo-se, em particular, L! œ 0 e L" œ 1. Intuitivamente, é instrutivo
olhar para a homotopoia suave, como sendo a família das aplicações suaves L> , que
constitui uma espécie de deformação suave de 0 em 1.
§1. Cohomologia de de Rham
203
intervalos Ò!ß #Î$Ò e Ó"Î$ß "Ó, podemos deduzir a existência de uma aplicação
suave :À Ò!ß "Ó Ä Ò!ß "Ó tal que :Ð>Ñ œ !, para cada > Ÿ "Î$, e :Ð>Ñ œ ", para
cada > #Î$ (a função da partição da unidade correspondente ao segundo
aberto). Definimos então uma aplicação L̃À Ò!ß "Ó ‚ Q w Ä Q por
˜ BÑ œ
LÐ>ß
LÐ:Ð#>Ñß BÑ,
s :Ð#> "Ñß BÑ,
LÐ
se > Ÿ
se >
"
#
"
#
,
˜ BÑ œ 1ÐBÑ, visto que,
reparando, desde já, que, para cada > − Ò"Î$ß #Î$Ó, LÐ>ß
˜ BÑ œ LÐ:Ð#>Ñß BÑ œ LÐ"ß BÑ œ 1ÐBÑ, ou > "Î# e
ou > Ÿ "Î# e então LÐ>ß
s :Ð#> "Ñß BÑ œ LÐ!ß
s BÑ œ 1ÐBÑ. Podemos agora
então L̃Ð>ß BÑ œ LÐ
garantir que a aplicação L̃ é suave, por ter restrições suaves a cada um dos
três abertos Ò!ß "Î#Ò ‚ Q w , Ó"Î#ß "Ó ‚ Q w e Ó"Î$ß #Î$Ò ‚ Q w de Ò!ß "Ó ‚ Q w ,
˜ BÑ œ LÐ!ß BÑ œ 0 ÐBÑ
cuja união é Ò!ß "Ó ‚ Q w e, reparando que se tem LÐ!ß
s
e L̃Ð"ß BÑ œ LÐ"ß BÑ œ 1ÐBÑ, concluímos que 0 e 2 são realmente
suavemente homotópicas.
IV.1.11. Sejam Q § I , Q w § I w e Q ww § I ww variedades, 0 ß s0 À Q ww Ä Q w
aplicações suaves, suavemente homotópicas e 1ß s1À Q w Ä Q aplicações
suaves, suavemente homotópicas. Tem-se então que as aplicações suaves
1 ‰ 0 À Q ww Ä Q e s1 ‰ s0 À Q ww Ä Q são também suavemente homotópicas.
Dem: Sejam LÀ Ò!ß "Ó ‚ Q ww Ä Q w uma homotopia suave de 0 para s0 e
s Ò!ß "Ó ‚ Q w Ä Q uma homotopia suave de 1 para s1. Podemos então
LÀ
considerar a aplicação suave L̃À Ò!ß "Ó ‚ Q ww Ä Q definida por
˜ BÑ œ LÐ>ß
s LÐ>ß BÑÑ,
LÐ>ß
a qual vai constituir uma homotopia suave de 1 ‰ 0 para s1 ‰ s0 .
IV.1.12. Sejam Q § I e Q w § I w variedades e 0 ß 1À Q w Ä Q duas aplicações
suaves, suavemente homotópicas.Tem-se então
L : Ð0 Ñ œ L : Ð1ÑÀ L : ÐQ Ñ Ä L : ÐQ w Ñ.
Dem: Temos essencialmente uma reformulação das conclusões de III.7.6,
visto que, dado Ò=Ó − L : ÐQ Ñ, tem-se = − ^ : ÐQ Ñ, isto é, . = œ ! e então
esse resultado garante-nos a existência de 5 − H:" ÐQ w Ñ tal que
1‡ = 0 ‡ = œ . 5 , por outras palavras que 1‡ = 0 ‡ = − F : ÐQ w Ñ, o que
mostra que
Ò0 ‡ =Ó œ Ò1‡ =Ó −
^ : ÐQ w Ñ
œ L : ÐQ w Ñ.
F : ÐQ w Ñ
IV.1.13. Recordemos que uma variedade Q § I é dita suavemente contráctil se
existir B! − Q tal que M.Q À Q Ä Q seja suavemente homotópica à aplicação constante de valor B! (cf. III.7.7). Para uma tal variedade podemos
determinar explicitamente todos os espaços de cohomologia de de Rham,
204
Cap. IV. Introdução à cohomologia de de Rham
nomeadamente, tem-se L : ÐQ Ñ œ Ö!× para todo o : Á !, e L ! ÐQ Ñ é um
espaço vectorial de dimensão ", admitindo uma base formada pela classe de
equivalência da aplicação Q Ä ‘ de valor constante igual a ".
Dem: O facto de se ter L : ÐQ Ñ œ Ö!× para cada : !, é um resultado trivial
válido em qualquer variedade. O facto de se ter L : ÐQ Ñ œ Ö!×, para cada
: !, não é mais do que uma reformulação do lema de Poincaré (cf.
III.7.10), que afirma que, neste caso, F : ÐQ Ñ œ ^ : ÐQ Ñ. Por fim, a
conclusão sobre L ! ÐQ Ñ vai ser uma consequência da alínea d) de IV.1.4,
desde que mostremos que a variedade Q é conexa, visto que ela é
trivialmente não vazia. Ora, sendo LÀ Ò!ß "Ó ‚ Q Ä Q uma homotopia
suave entre M.Q e a aplicação de valor constante B! , vemos que, para cada
B − Q , B e B! pertencem à mesma componente conexa de Q por
pertencerem ambos ao conjunto conexo formado pelos pontos da forma
LÐ>ß BÑ, com > − Ò!ß "Ó.
Por vezes é cómodo sabermos que, numa variedade suavemente contráctil,
não só a aplicação identidade é suavemente homotópica a uma certa
aplicação constante, como podemos mesmo garantir que ela é suavemente
homotópica a qualquer aplicação constante. De facto, podemos afirmar
mesmo mais:
IV.1.14. Sejam Q § I uma variedade suavemente contráctil e Q w § I uma
variedade arbitrária. Se 0 ß 1À Q w Ä Q são aplicações suaves arbitrárias,
então 0 e 1 são suavemente homotópicas. Em particular, M.Q À Q Ä Q é
suavemente homotópica a qualquer aplicação constante Q Ä Q .
Dem: Seja B! − Q tal que a aplicação 2! À Q Ä Q , de valor constante B! ,
seja suavemente homotópica a M.Q À Q Ä Q . Sejam Q w uma variedade e
0! À Q w Ä Q a aplicação de valor constante B! . Tendo em conta IV.1.11,
para cada aplicação suave 0 À Q w Ä Q , 0 œ M.Q ‰ 0 é suavemente
homotópica a 0! œ 2! ‰ 0 . Por transitividade (cf. IV.1.10), concluímos
finalmente que, se 0 ß 1À Q w Ä Q são aplicações suaves, 0 e 1 são
suavemente homotópicas por serem ambas suavemente homotópicas a 0! .
§2. Produtos e somas de complexos de cocadeias.
IV.2.1. Sejam ÐI4 Ñ4−N uma família de espaços vectoriais, I um espaço vectorial
e, para cada 4 − N , 1
s4 À I Ä I4 uma aplicação linear. Vamos dizer que I é
um produto da família dos I4 , definido pelas projecções 1
s4 , se, qualquer que
§2. Produtos e somas de complexos de cocadeias
205
seja a família ÐB4 Ñ4−N de elementos B4 − I4 , existe um, e um só B − I tal
que, para cada 4, 1
s4 ÐBÑ œ B4 .44
IV.2.2. Dada uma família ÐI4 Ñ4−N de espaços vectoriais, o produto cartesiano
# I5 , com a estrutura usual de espaço vectorial, é, evientemente, um
5−N
produto daquela família, no sentido da definição anterior, definido pelas
projecções canónicas usuais 14 À # I5 Ä I4 . Para além disso, dados um
5−N
espaço vectorial I e aplicações lineares 1
s4 À I Ä I4 , ficamos com uma
#
aplicação linear .À I Ä
I5 , definida por .ÐBÑ œ Ð1
s5 ÐBÑÑ5−N (a única que
5−N
verifica 14 ‰ . œ 1
s4 ), sendo imediato constatar, a partir da definição, que I é
um produto dos I4 , definido pelas projecções 1
s4 , se, e só se, a aplicação
linear . é um isomorfismo de I sobre # I5 . Em particular, e de forma
5−N
menos precisa, podemos dizer que os produtos de uma família de espaços
vectoriais são precisamente os espaços vectoriais que são isomorfos ao
produto cartesiano usual dessa família.
O interesse da definição geral de produto, que apresentámos atrás, está na
possibilidade de descrever, de forma precisa, situações frequentes na
prática em que aparecem espaços vectoriais que, não sendo o produto
cartesiano de uma certa família são naturalmente isomorfos a esse produto
(por vezes costuma dizer-se uma frase do tipo “pode ser identificado ao
produto…”. Por exemplo, dados três espaços vectoriais I" ß I# ß I$ , o
produto ÐI" ‚ I# Ñ ‚ I$ não é o mesmo que o produto I" ‚ I# ‚ I$ ,
mas é comum dizer-se que se identifica com este; o que se passa é que
ÐI" ‚ I# Ñ ‚ I$ é um produto dos espaços vectoriais I" ß I# ß I$ , com as
projecções 1
s 4 À ÐI" ‚ I# Ñ ‚ I$ Ä I4 definidas por
1" ÐÐB" ß B# Ñß B$ Ñ œ B" ,
s
1
s # ÐÐB" ß B# Ñß B$ Ñ œ B# ,
1
s $ ÐÐB" ß B# Ñß B$ Ñ œ B$ .
Encontraremos adiante outros exemplos de situações deste tipo.
IV.2.3. Seja N um conjunto de índices e seja, para cada 4 − N , G4ñ um complexo
de cocadeias, definido pelos espaços vectoriais G4: , com : − ™, e pelas
aplicações lineares cobordo .4: À G4: Ä G4:" . Suponhamos que, para cada
: − ™, se considera um produto G : da família dos G4: , definido pelas projec:
:
ções 1
s4 À G : Ä G4 . Existe então uma, e uma só, maneira de definir
aplicações lineares . : À G : Ä G :" , de modo a obter um complexo de
cocadeias G ñ , constituído pelos espaços vectoriais G : e pelas aplicações
lineares de cobordo . : , para o qual, para cada 4 − N , a família de aplicações
44Quem
conhecer os fundamentos da Teoria das Categorias reconhecerá facilmente que
esta definição é equivalente à que se enquadra na noção geral de produto numa categoria.
206
Cap. IV. Introdução à cohomologia de de Rham
:
lineares 1
sñ4 œ Ð1
s4 Ñ:−™ constitua um morfismo de complexos de cocadeias de
ñ
G ñ para G4 . Mais precisamente, para cada B − G : , . : ÐBÑ é o único elemento
de G :" tal que, para cada 4,
:"
: :
:"
1
s4 Ð. : ÐBÑÑ œ .4 Ð1
s4 ÐBÑÑ − G4 .
Dem: Para cada B − G : , a existência e unicidade de um elemento
. : ÐBÑ − G :" verificando a condição acima é uma consequência do facto de
:"
G :" ser um produto dos G4:" , definido pelas projecções 1
s4 e é trivial a
verificação de que a aplicação . : À G : Ä G :" , assim definida, é
efectivamente linear. O facto de, para cada 4 − N , ser
:#
:" :" :
:" : :
1
s4 Ð. :" Ð. : ÐBÑÑ œ .4 Ð1
s4 Ð. ÐBÑÑÑ œ .4 Ð.4 Ð1
s4 ÐBÑÑÑ œ !,
implica, pela parte de unicidade na definição de produto, que
. :" Ð. : ÐBÑÑ œ !, o que mostra que se obteve efectivamente um complexo de
cocadeias G ñ . A condição de definição de . : ÐBÑ no enunciado exprime
:
exactamente o facto de cada família 1
sñ4 œ Ð1
s4 Ñ:−™ ser um morfismo de
complexos de cocadeias de G ñ para G4ñ e isso mostra, ao mesmo tempo, que a
definição apresentada para as aplicações lineares . : é efectivamente a única
que faz com que aquelas famílias constituam complexos de cocadeias.
IV.2.4. Nas condições anteriores, dizemos que G ñ é um complexo de cocadeias
produto dos complexos de cocadeias G4ñ , definido pelas projecções
:
1
sñ4 œ Ð1
s4 Ñ:−™ , de G ñ para G4ñ .
Repare-se que, no caso em que, para cada :, tomamos para G : o produto
cartesiano dos G4: , com as projecções canónicas usuais, as aplicações
cobordo . : À G : Ä G :" não são mais do que as aplicações produto
cartesiano dos .4: .
IV.2.5. (Compatibilidade dos produtos com a cohomologia) Nas condições
anteriores, para cada : − ™, L : ÐG ñ Ñ é um produto da família dos L : ÐG4ñ Ñ,
definido pelas projecções
L : Ð1
sñ4 ÑÀ L : ÐG ñ Ñ Ä L : ÐG4ñ Ñ.45
Mais precisamente, dados ÒB4 Ó − L : ÐG4ñ Ñ, onde B4 − ^ : ÐG4ñ Ñ, sendo B − G :
:
o único elemento que verifica as condições 1
s4 ÐBÑ œ B4 , tem-se B − ^ : ÐG ñ Ñ e
ÒBÓ é o único elemento de L : ÐG ñ Ñ cuja imagem por cada L : Ð1
sñ4 Ñ é ÒB4 Ó.
Dem: Consideremos uma família arbitrária de elementos ÒB4 Ó − L : ÐG4ñ Ñ,
que, mesmo no caso em que cada G : é o produto cartesiano dos G4: , definido
pelas projecções canónicas, L : ÐG ñ Ñ não será, em geral, o produto cartesiano dos L : ÐG4ñ Ñ,
embora este resultado garanta que é isomorfo a este produto cartesiano. É a existência de
fenómenos deste tipo que nos levou a discutir a noção geral de produto que apresentámos
atrás.
45Repare-se
§2. Produtos e somas de complexos de cocadeias
207
onde B4 − ^ : ÐG4ñ Ñ, isto é, B4 − G4: e .4: ÐB4 Ñ œ !. Seja B − G : o único
:
elemento que verifica as condições 1
s4 ÐBÑ œ B4 . Tem-se então
:"
: :
:
1
s4 Ð. : ÐBÑÑ œ .4 Ð1
s4 ÐBÑÑ œ .4 ÐB4 Ñ œ !,
pelo que, pela parte de unicidade na definição de produto, tem-se . : ÐBÑ œ !,
isto é, B − ^ : ÐG ñ Ñ, o que nos permite considerar o elemento ÒBÓ − L : ÐG ñ Ñ,
:
para o qual se tem L : Ð1
sñ4 ÑÐÒBÓÑ œ Ò1
s4 ÐBÑÓ œ ÒB4 Ó. Resta-nos mostrar a unici:
dade, para o que tomamos ÒCÓ − L : ÐG ñ Ñ com ÒB4 Ó œ L : Ð1
sñ4 ÑÐÒCÓÑ œ Ò1
s4 ÐCÑÓ,
:
:
ñ
para cada 4 − N . Para cada 4 tem-se então 1
s4 ÐCÑ B4 − F ÐG4 Ñ, por outras
:"
:
palavras, existe um elemento D4 − G4 tal que .4:" ÐD4 Ñ œ 1
s4 ÐCÑ B4 . Seja
:"
D − G :" tal que, para cada 4, 1
s4 ÐDÑ œ D4 . Tem-se então, para cada 4,
:
:" :"
:"
1
s4 Ð. :" ÐDÑÑ œ .4 Ð1
s4 ÐDÑÑ œ .4 ÐD4 Ñ œ
:
:"
:
œ1
s4 ÐCÑ B4 œ .4 ÐD4 Ñ œ 1
s4 ÐC BÑ,
donde C B œ .:" ÐDÑ, o que mostra que ÒBÓ œ ÒCÓ em L : ÐG ñ Ñ.
IV.2.6. Sejam Q § I uma variedade e ÐY4 Ñ4−N uma família de abertos de Q
disjuntos dois a dois e de união Q . Notando +4 À Y4 Ä Q as inclusões,
definidas por +4 ÐBÑ œ B, tem-se então que o complexo de cocadeias Hñ ÐQ Ñ é
um produto dos complexos de cocadeias Hñ ÐY4 Ñ, tendo como projecções as
famílias de aplicações lineares +4‡ À H: ÐQ Ñ Ä H: ÐY4 Ñ. Em consequência, para
cada :, L : ÐQ Ñ é um produto dos L : ÐY4 Ñ, definido pelas projecções L : Ð+4 Ñ,
que associam a cada Ò=Ó as classes Ò=ÎY4 Ó.
Dem: Uma vez que, para cada 4, a família dos +4‡ À H: ÐQ Ñ Ä H: ÐY4 Ñ
constitui um morfismo de complexos de cocadeias de Hñ ÐQ Ñ para Hñ ÐY4 Ñ,
ficamos reduzidos a provar que, para cada :, H: ÐQ Ñ é um produto dos
H: ÐY4 Ñ com as projecções +4‡ À H: ÐQ Ñ Ä H: ÐY4 Ñ, ou seja, que, dados
=4 − H: ÐY4 Ñ, existe um, e um só, = − H: ÐQ Ñ tal que, para cada 4, =4 œ =ÎY4
e isso é trivial, se nos lembrarmos que a suavidade de uma forma diferencial
é uma questão local e que, para cada B − Y4 , XB ÐY4 Ñ œ XB ÐQ Ñ.
Repare-se que, fora do caso trivial em que não exista mais do que um
aberto Y4 não vazio, as hipóteses do resultado anterior só podem
verificar-se se a variedade Q não é conexa. De facto um caso frequente
de aplicação deste resultado é aquele em que os Y4 são precisamente as
componentes conexas de Q (lembrar que uma variedade é sempre
localmente conexa e que, portanto, as suas componentes conexas são
conjuntos abertos), caso em que o resultado mostra que, para
determinarmos os espaços de cohomologia, apenas temos que nos
preocupar como o que acontece no caso das variedades conexas.
208
Cap. IV. Introdução à cohomologia de de Rham
IV.2.7. Dada uma família ÐI4 Ñ4−N de espaços vectoriais, vamos dizer que uma
família ÐB4 Ñ4−N , com B4 − I4 , é essencialmente finita se se tem B4 œ !, com
um número finito de excepções possíveis, isto é, se existe uma parte finita N!
de N tal que B4 œ !, para cada 4  N! . Repare-se também que, no caso em
que todos os I4 são iguais a um mesmo espaço vectorial I , para cada família
essencialmente finita ÐB4 Ñ4−N de vectores de I fica bem definida a sua soma
! B4 que é, por definição, a soma dos vectores não nulos da família e
portanto também igual a ! B4 , onde N! é uma parte finita arbitrária de N , tal
4−N
4−N!
que B4 œ !, para cada 4  N! .
Repare-se que, como é trivial, quando o conjunto N é finito, toda a família
indexada em N é essencialmente finita e, quando todos os espaços vectoriais
coincidem, a sua soma, no sentido anterior, coincide com a sua soma, no
sentido usual.
IV.2.8. Sejam ÐI4 Ñ4−N uma família de espaços vectoriais, I um espaço vectorial
e, para cada 4 − N , s+4 À I4 Ä I uma aplicação linear. Vamos dizer que I é
uma soma da família dos I4 , definida pelas injecções s+4 , se, qualquer que
seja B − I , existe uma, e uma só, família essencialmente finita ÐB4 Ñ4−N , com
B4 − I4 , tal que B œ ! s+4 ÐB4 Ñ. É imediato constatar-se que esta condição
4−N
pode ser enunciada, de modo equivalente, exigindo que cada s+4 seja uma
aplicação linear injectiva e que I seja soma directa dos seus subespaços
vectoriais s+4 ÐI4 Ñ.
IV.2.9. Como primeiro exemplo, trivial, de soma, no sentido anterior, temos as
somas directas usuais de subespaços vectoriais: Se ÐI4 Ñ4−N é uma família de
subespaços vectoriais de I e se +4 À I4 Ä I são as inclusões, então I é uma
soma dos I4 ß com as injecções +4 se, e só se I é soma directa dos I4 .
Vamos agora estudar as relações que existem entre as noções de soma e
de produto de espaços vectoriais e que mostrarão que, no caso em que o
conjunto de índices é finito, dar uma soma é equivalente a dar um
produto. Em qualquer caso, e como vamos ver, a partir de um produto é
sempre possível construir uma soma.
IV.2.10. Sejam ÐI4 Ñ4−N uma família de espaços vectoriais e I um produto desta
família, com as projecções 1
s4 À I Ä I4 . Têm então lugar um subespaço
vectorial I! § I , constituído pelos B − I tais que a família Ð1
s4 ÐBÑÑ4−N seja
essencialmente finita, e aplicações lineares s+4 À I4 Ä I! § I , definidas pela
condição de, para cada C − I4 , se ter
1
s5 Ðs+4 ÐCÑÑ œ œ
C,
!,
se 5 œ 4
se 5 Á 4,
§2. Produtos e somas de complexos de cocadeias
209
e I! é uma soma dos I4 com as injecções s+4 (dizemos que os s+4 são as
injecções associadas às projecções 1
s4 ). Mais precisamente, para cada B − I ,
existe uma única família essencialmente finita ÐB4 Ñ4−N , com B4 − I4 , tal que
B œ !s+4 ÐB4 Ñ, a saber, a definida por B4 œ 1
s4 ÐBÑ.
Dem: O facto de I! ser efectivamente um subespaço vectorial é de
verificação simples, se repararmos que a união de dois conjuntos finitos é
ainda um conjunto finito. É também imediato verificar-se que as aplicações
s+4 À I4 Ä I! , definidas no enunciado são efectivamente lineares. Reparemos
agora que, se B − I! e se ÐB4 Ñ4−N é uma família essencialmente finita tal que
B œ !s+4 ÐB4 Ñ então, aplicando 1
s5 a ambos os membros, obtemos
1
s5 ÐBÑ œ B5 , o que nos mostra a unicidade de uma possível decomposição.
Por fim, dado B − I! arbitrário, pondo B4 œ 1
s4 ÐBÑ − I4 , a família ÐB4 Ñ4−N
vai ser, por definição, essencialmente finita e o facto de se ter, para cada 5 ,
1
s5 Ð"s+4 ÐB4 ÑÑ œ " 1
s5 Ðs+4 ÐB4 ÑÑ œ B5 œ 1
s5 ÐBÑ
4
4
implica, pela parte de unicidade na definição de produto, que se tem
B œ !s+4 ÐB4 Ñ.
IV.2.11. Sejam ÐI4 Ñ4−N uma família de espaços vectoriais e I um espaço
vectorial soma desta família, com as injecções s+4 À I4 Ä I . Existem então
aplicações lineares 1
s4 À I Ä I4 , a que daremos o nome de projecções
associadas, definidas pela condição de, para cada B − I , se ter 1
s4 ÐBÑ œ B4 ,
onde ÐB4 Ñ4−N é a única família essencialmente finita, com B4 − I4 , tal que
B œ !s+4 ÐB4 Ñ.
Estas projecções verificam então as seguintes condições:
a) Para cada C − I4 , tem-se
1
s5 Ðs+4 ÐCÑÑ œ œ
C,
!,
se 5 œ 4
se 5 Á 4.
b) Para cada B − I , a família Ðs+4 Ð1
s4 ÐBÑÑÑ4−N , de vectores de I , é essencialmente finita e
B œ "s+4 Ð1
s4 ÐBÑÑ.
4−N
Dem: A verificação de que cada aplicação 1
s4 À I Ä I4 é efectivamente linear
é trivial e a conclusão de b) é essencialmente apenas uma reformulação da
definição das aplicações 1
s4 . A alínea a) resulta também da definição das
210
Cap. IV. Introdução à cohomologia de de Rham
projecções, se repararmos que, para cada C − I4 , se pode escrever
s+4 ÐCÑ œ s+4 ÐCÑ "s+5 Ð!Ñ.
5Á4
IV.2.12. Suponhamos, reciprocamente, que ÐI4 Ñ4−N é uma família de espaços
vectoriais, que I é um espaço vectorial e que, para cada 4 − N , temos aplicações lineares 1
s4 À I Ä I4 e s+4 À I4 Ä I , verificando as condições:
a) Para cada C − I4 , tem-se
1
s5 Ðs+4 ÐCÑÑ œ œ
C,
!,
se 5 œ 4
se 5 Á 4.
b) Para cada B − I , a família Ðs+4 Ð1
s4 ÐBÑÑÑ4−N , de vectores de I , é essencialmente finita e
B œ "s+4 Ð1
s4 ÐBÑÑ.
4−N
Tem-se então que I é uma soma da família dos I4 , com as injecções s+4 , e as
aplicações lineares 1
s4 são as projecções associadas.
Dem: O facto de se ter, por a), 1
s4 ‰s+4 œ M.I4 implica que cada aplicação
linear s+4 À I4 Ä I é injectiva e deduz-se então de b) que, para cada B − I , a
família dos B4 œ 1
s4 ÐBÑ − I4 é essencialmente finita e é tal que B œ !
s+4 ÐB4 Ñ. Quanto à unicidade, se fosse B œ !s+4 ÐC4 Ñ, com a família dos C4 − I4
essencialmente finita, obtínhamos, aplicando 1
s5 a ambos os membros e tendo
em conta a), B5 œ 1
s5 ÐBÑ œ C5 . Ficou assim provado que I é uma soma dos
I4 , com as injecções s+4 e resulta imediatamente de b) que os 1
s4 são as
projecções associadas.
No caso em que o conjunto dos índices N é finito46, todas as famílias são
essencialmente finitas e podemos enunciar resultados correspondentes aos
dois anteriores para os produtos, o que mostra, em particular a equivalência essencial entre as noções de soma e de produto.
IV.2.13. Seja ÐI4 Ñ4−N uma família finita de espaços vectoriais e seja I um
produto dos I4 , com as projecções 1
s4 À I Ä I4 . Sendo s+4 À I4 Ä I as
injecções associadas (cf. IV.2.10), são então verificadas as propriedades:
a) Para cada C − I4 , tem-se
46Ou,
mais geralmente, N pode ser infinito, mas I4 œ Ö!×, salvo para um número finito
de índices.
§2. Produtos e somas de complexos de cocadeias
1
s5 Ðs+4 ÐCÑÑ œ œ
b) Para cada B − I ,
C,
!,
211
se 5 œ 4
se 5 Á 4.
B œ "s+4 Ð1
s4 ÐBÑÑ.
4−N
Em particular, I também é uma soma dos I4 , com as injecções s+4 À I4 Ä I ,
e os 1
s4 são as projecções associadas.
Dem: A conclusão de a) é simplesmente a definição das injecções associadas
a um produto. Quanto a b), a igualdade resulta da parte de unicidade na
definição de produto, uma vez que, para cada 5 − N , e tendo em conta a),
1
s5 ˆ"s+4 Ð1
s4 ÐBÑщ œ 1
s5 ÐBÑ.
4−N
O facto de I ser uma soma dos I4 , com as injecções s+4 , e de as projecções
associadas a esta soma serem os 1
s4 , é agora uma consequência de IV.2.12.
IV.2.14. Suponhamos, reciprocamente, que ÐI4 Ñ4−N é uma família finita de
espaços vectoriais, que I é um espaço vectorial e que, para cada 4 − N ,
1
s4 À I Ä I4 e s+4 À I4 Ä I são aplicações lineares verificando as condições:
a) Para cada C − I4 , tem-se
1
s5 Ðs+4 ÐCÑÑ œ œ
b) Para cada B − I ,
C,
!,
se 5 œ 4
se 5 Á 4.
B œ "s+4 Ð1
s4 ÐBÑÑ.
4−N
Tem-se então que I é um produto dos I4 , com a projecções 1
s4 , e os s+4 são as
injecções associadas.
Em particular, tendo em conta IV.2.11, se I é uma soma da família finita dos
I4 , com as injecções s+4 À I4 Ä I , e se 1
s4 À I Ä I4 são as projecções
associadas, então I é um produto dos I4 , com as projecções 1
s4 e as
injecções associadas são os s+4 .
Dem: Seja ÐB4 Ñ4−N uma família arbitrária, com B4 − I4 . Se B − I é tal que,
para cada 4, 1
s4 ÐBÑ œ B4 , deduzimos de b) que
B œ "s+4 Ð1
s4 ÐBÑÑ œ "s+4 ÐB4 Ñ.
4−N
4−N
Por outro lado, se definirmos B œ !s+4 ÐB4 Ñ, resulta de a) que, para cada 5 ,
212
Cap. IV. Introdução à cohomologia de de Rham
1
s5 ÐBÑ œ B5 . Ficou assim provado que I é efectivamente um produto dos I4 ,
com as projecções 1
s4 À I Ä I4 , e o facto de as injecções associadas serem os
s+4 é uma mera reformulação de a).
IV.2.15. Seja N um conjunto de índices e seja, para cada 4 − N , G4ñ um
complexo de cocadeias, definido pelos espaços vectoriais G4: , com : − ™, e
pelas aplicações lineares cobordo .4: À G4: Ä G4:" . Suponhamos que, para
cada : − ™, se considera uma soma G : da família dos G4: , definida pelas
injecções s+:4 À G4: Ä G : . Existe então uma, e uma só, maneira de definir
aplicações lineares . : À G : Ä G :" , de modo a obter um complexo de
cocadeias G ñ , constituído pelos espaços vectoriais G : e pelas aplicações
lineares de cobordo . : , para o qual, para cada 4 − N , a família de aplicações
lineares s+ñ4 œ Ðs+:4 Ñ:−™ constitua um morfismo de complexos de cocadeias de
G4ñ para G ñ . Mais precisamente, para cada B − G : , com B œ !s+:4 ÐB4 Ñ, onde
B4 − G4: , . : ÐBÑ é o elemento de G :" ,
:
. : ÐBÑ œ "s+:"
4 Ð.4 ÐB4 ÑÑ.
4
Dem: Por definição de soma, cada B − G : pode-se escrever de maneira
única na forma B œ !s+:4 ÐB4 Ñ, com a família dos B4 − G4: essencialmente
finita, de onde resulta trivialmente que a família dos .4: ÐB4 Ñ − G4:" é
também essencialmente finita, o que nos permite concluir que fica bem
definida uma aplicação . : À G : Ä G :" por
:
. : ÐBÑ œ "s+:"
4 Ð.4 ÐB4 ÑÑ,
4
sendo trivial verificar que esta aplicação é linear. É também imediato
verificar que se tem . :" Ð. : ÐBÑÑ œ !, pelo que obtivémos assim
efectivamente um complexo de cocadeias G ñ . Se C − G4: , podemos escrever
s+4 ÐCÑ œ !s+5 ÐB5 Ñ, com B4 œ C e B5 œ !, para cada 5 Á 4, pelo que vem
:
:" :
. : Ðs+4 ÐCÑÑ œ "s+:"
5 Ð.5 ÐB5 ÑÑ œ s+ 4 Ð.4 ÐCÑÑ,
5
Ðs+:4 Ñ:−™
o que mostra que s+ñ4 œ
constitui um morfismo de complexos de cocadeias de G4ñ para G ñ . Quanto à unicidade, basta repararmos que, dados
morfismos . : À G : Ä G :" , definindo uma estrutura de complexo de
cocadeias, relativamente à qual os s+ñ4 œ Ðs+:4 Ñ:−™ constituissem morfismos de
§2. Produtos e somas de complexos de cocadeias
213
complexos de cocadeias, não podia deixar de ser, para cada B œ !s+:4 ÐB4 Ñ,
. : ÐBÑ œ " . : Ðs+:4 ÐB4 ÑÑ œ "s+4:" Ð.4: ÐB4 ÑÑ.
4
4
IV.2.16. Nas condições anteriores, dizemos que G ñ é um complexo de cocadeias
soma dos complexos de cocadeias G4ñ , definido pelas injecções s+4ñ œ Ðs+:4 Ñ:−™ ,
de G4ñ para G ñ .
IV.2.17. (Compatibilidade das somas com a cohomologia) Nas condições
anteriores, para cada : − ™, L : ÐG ñ Ñ é uma soma da família dos L : ÐG4ñ Ñ,
definida pelas injecções L : Ðs+ñ4 ÑÀ L : ÐG4ñ Ñ Ä L : ÐG ñ Ñ. Além disso, sendo,
:
para cada : − ™ e 4 − N , 1
s4 À G : Ä G4 as projecções associadas à
:
:
apresentação de G : como soma dos G4 , tem-se que as famílias 1
sñ4 œ Ð1
s4 Ñ:−™
vão constituir morfismos de complexos de cocadeias de G ñ para G4ñ e as
aplicações lineares L : Ð1
sñ4 ÑÀ L : ÐG ñ Ñ Ä L : ÐG4ñ Ñ são as projecções associadas
à apresentação de L : ÐG ñ Ñ como soma dos L : ÐG4ñ Ñ.
Dem: Para cada B − G : , podemos escrever B œ !s+:4 ÐB4 Ñ, com a família dos
B4 − G4: essencialmente finita, tendo-se então . : ÐBÑ œ !s+4:" Ð.4: ÐB4 ÑÑ, pelo
que
:"
:
: :
1
s4 Ð. : ÐBÑÑ œ .4 ÐB4 Ñ œ .4 Ð1
s4 ÐBÑÑ,
o que mostra que 1
sñ4 é efectivamente um morfismo de complexos de
ñ
cocadeias de G para G4ñ . Tendo em conta IV.2.11, sabemos que, para cada :,
tem-se, para C − G4: ,
: :
1
s5 Ðs+4 ÐCÑÑ œ œ
e que, para cada B − G : ,
C,
!,
se 5 œ 4
se 5 Á 4
:
B œ "s+:4 Ð1
s4 ÐBÑÑ,
4
:
dos s+:4 Ð1
s4 ÐBÑÑ
com a família
essencialmente finita e daqui resulta imediatamente que, para cada ÒCÓ − L : ÐG4ñ Ñ
L : Ð1
sñ4 ÑÐL : Ðs+4ñ ÑÐÒCÓÑÑ œ œ
e que, para cada ÒBÓ − L : ÐG ñ Ñ,
ÒCÓ,
!,
se 5 œ 4
se 5 Á 4
214
Cap. IV. Introdução à cohomologia de de Rham
ÒBÓ œ " L : Ðs+ñ4 ÑÐL : Ð1
s4ñ ÑÐÒBÓÑÑ,
4
com a família dos L : Ðs+ñ4 ÑÐL : Ð1
s4ñ ÑÐÒBÓÑÑ essencialmente finita. Tendo em
conta IV.2.12, deduzimos daqui que L : ÐG4ñ Ñ é efectivamente uma soma dos
L : ÐG4ñ Ñ, com as injecções L : Ðs+ñ4 ÑÀ L : ÐG4ñ Ñ Ä L : ÐG ñ Ñ, e que as projecções
associadas são os L : Ð1
sñ4 ÑÀ L : ÐG ñ Ñ Ä L : ÐG4ñ Ñ.
IV.2.18. (O dual duma soma é um produto) Seja ÐI4 Ñ4−N uma família de
espaços vectoriais sobre Š e seja I uma soma desta família, com as
injecções s+4 À I4 Ä I . Seja Šw ¨ Š e consideremos, para cada 4, a aplicação
linear dual s+‡4 À PÐIà Šw Ñ Ä PÐI4 à Šw Ñ, definida por s+4‡ Ð!Ñ œ ! ‰s+4 (cf.
II.2.13). Tem-se então que PÐIà Šw Ñ é um produto da família dos PÐI4 à Šw Ñ,
com as projecções s+‡4 À PÐIà Šw Ñ Ä PÐI4 à Šw Ñ.47
Dem: Seja, para cada 4 − N , !4 − PÐI4 à Šw Ñ. Para cada B − I , existe, por
definição, uma, e uma só, família essencialmente finita ÐB4 Ñ4−N , com B4 − I4 ,
tal que B œ !s+4 ÐB4 Ñ e então a família dos elementos !4 ÐB4 Ñ de Šw é também
essencialmente finita, o que nos permite definir um elemento !ÐBÑ − Šw por
!ÐBÑ œ ! !4 ÐB4 Ñ. É trivial verificar que a aplicação !À I Ä Šw , assim definida, é linear, ou seja, que ! − PÐIà Šw Ñ. Para cada 4, tem-se ! ‰s+4 œ !4 ,
visto que, se Bw − I4 , tem-se s+4 ÐBw Ñ œ !s+5 ÐB5 Ñ, com B4 œ Bw e B5 œ !, para
cada 5 Á 4, donde !Ðs+4 ÐBw ÑÑ œ !4 ÐBw Ñ. Por fim, se " − PÐIà Šw Ñ é tal que,
para cada 4, " ‰s+4 œ !4 , obtemos, para cada B − I , com a decomposição
acima indicada,
" ÐBÑ œ " Ð"s+4 ÐB4 ÑÑ œ " " Ðs+4 ÐB4 ÑÑ œ " !4 ÐB4 Ñ œ !ÐBÑ.
4
4
4
IV.2.19. (O dual dum produto finito é uma soma) Seja ÐI4 Ñ4−N uma família
finita de espaços vectoriais sobre Š e seja I um produto desta família, com
as projecções 1
s4 À I Ä I4 . Seja Šw ¨ Š e consideremos, para cada 4 − N , a
aplicação linear dual 1
s‡4 À PÐI4 à Šw Ñ Ä PÐIà Šw Ñ. Tem-se então que PÐIà Šw Ñ
é uma soma da família dos PÐI4 à Šw Ñ, tendo como injecções as aplicações
lineares 1
s‡4 À PÐI4 à Šw Ñ Ä PÐIà Šw Ñ e, sendo s+4 À I4 Ä I as injecções associadas ao produto referido, as projecções associadas a esta soma são as aplicações lineares s+‡4 À PÐIà Šw Ñ Ä PÐI4 à Šw Ñ.
Dem: Por IV.2.13, tem-se 1
s4 ‰s+4 œ M.À I4 Ä I4 , 1
s4 ‰s+5 œ !, se 4 Á 5 , e
47Pelo
contrário, em geral, o dual dum produto não será uma soma. Isso acontece, no
entanto, no caso em que N é finito (cf. o próximo resultado).
§2. Produtos e somas de complexos de cocadeias
215
!s+4 ‰ 1
s4 œ M.À I Ä I . Daqui se deduz que
s+‡4 ‰ 1
s4‡ œ Ð1
s4 ‰s+4 ч œ M.À PÐI4 à Šw Ñ Ä PÐI4 à Šw Ñ,
s+‡5 ‰ 1
s‡4 œ Ð1
s4 ‰s+5 ч œ !, se 4 Á 5 ,
‡
"1
s‡4 ‰s+4‡ œ ˆ"s+4 ‰ 1
s4 ‰ œ M.À PÐIà Šw Ñ Ä PÐIà Šw Ñ,
4
4
o que implica o resultado, tendo em conta IV.2.12.
§3. Sucessão exacta de Mayer-Vietoris.
Se uma variedade Q é união disjunta de dois subconjuntos abertos Y e
Z , então, como vimos em IV.2.6, L : ÐQ Ñ é um produto de L : ÐY Ñ e
L : ÐZ Ñ, com as projecções L : Ð+" Ñ e L : Ð+# Ñ, onde +" À Y Ä Q e
+# À Z Ä Q são as inclusões, e portanto existe um isomorfismo
L : ÐQ Ñ Ä L : ÐY Ñ ‚ L : ÐZ Ñ, definido por Ò=Ó È ÐÒ=ÎY Óß Ò=ÎZ ÓÑ. No caso
em que Q é união de dois subconjuntos abertos Y e Z , não
obrigatoriamente disjuntos, ficamos ainda com uma aplicação linear
L : ÐQ Ñ Ä L : ÐY Ñ ‚ L : ÐZ Ñ, definida pela mesma fórmula, mas essa
aplicação não tem que ser injectiva nem sobrejectiva. A sucessão exacta
de Mayer-Vietoris, que estudamos nesta secção, permite relacionar aquela
aplicação linear com outras, que fazem intervir a cohomologia de Y Z ,
e é um processo extremamente importante para ajudar ao cálculo efectivo
de alguns espaços de cohomologia. Começamos por estudar o que
podemos fazer quando temos, em geral, uma sucessão exacta de
complexos de cocadeias (relembrar a discussão sobre a noção de sucessão
exacta apresentada de II.7.18 a II.7.22).
IV.3.1. Consideremos três complexos de cocadeias G ñ , G w ñ e G ww ñ e dois
morfismos de complexos de cocadeias -ñ , de G ñ para G w ñ , e .ñ , de G w ñ para
G ww ñ . Diz-se que aqueles morfismos definem uma sucessão exacta curta de
complexos de cocadeias, ou que
-ñ
ñ
ñ .
ñ
! Ä G ñ Ä G w Ä G ww Ä !
é uma sucessão exacta curta de complexos de cocadeias se, para cada : − ™,
-:
:
: .
:
Ö!× Ä G : Ä G w Ä G ww Ä Ö!×
é uma sucessão exacta curta de espaços vectoriais (cf. II.7.20).
216
Cap. IV. Introdução à cohomologia de de Rham
Nas condições anteriores, ficamos, para cada : − ™, com aplicações
lineares L : Ð-ñ ÑÀ L : ÐG ñ Ñ Ä L : ÐG w ñ Ñ e L : Ð.ñ ÑÀ L : ÐG w ñ Ñ Ä L : ÐG ww ñ Ñ e
poderíamos ser levados a pensar que ficássemos com sucessões exactas
curtas
L : Ð- ñ Ñ
: ñ
ñ L Ð. Ñ
ñ
Ö!× p L : ÐG ñ Ñ qqp L : ÐG w Ñ qqp L : ÐG ww Ñ p Ö!×.
Tal não é o caso e, como veremos no próximo resultado, tudo o que
podemos afirmar é que a sucessão anterior é exacta em L : ÐG w ñ Ñ, no
sentido de ser exacta a sucessão
L : Ð- ñ Ñ
: ñ
ñ L Ð. Ñ
ñ
L : ÐG ñ Ñ qqp L : ÐG w Ñ qqp L : ÐG ww Ñ,
e que existem certas “aplicações lineares de conexão” que ligam estas
sucessões exactas para os diferentes valores de : e que permitem obter
uma sucessão exacta indefinidamente prolongável nos dois sentidos.
IV.3.2. (Lema da Serpente48) Seja
-ñ
ñ
ñ .
ñ
! Ä G ñ Ä G w Ä G ww Ä !
uma sucessão exacta curta de complexos de cocadeias. Para cada : − ™ tem
então lugar uma aplicação linear ` : À L : ÐG ww ñ Ñ Ä L :" ÐG ñ Ñ (a aplicação
linear de conexão), definida do seguinte modo:
Seja ÒBww Ó − L : ÐG ww ñ Ñ, onde Bww − ^ : ÐG ww ñ Ñ; podemos então escolher Bw − G w :
tal que .: ÐBw Ñ œ Bww e B − G :" tal que -:" ÐBÑ œ . w : ÐBw Ñ e então
B − ^ :" ÐG ñ Ñ e a sua classe de equivalência ÒBÓ − L :" ÐG ñ Ñ não depende
das escolhas feitas para Bww (na respectiva classe de equivalência), para Bw e
para B; pomos então, por definição, ` : ÐÒBww ÓÑ œ ÒBÓ. Tem então lugar, para
cada :, uma sucessão exacta
L : Ð-ñ Ñ
: ñ
ñ L Ð. Ñ
ñ
`:
L :" Ð-ñ Ñ
ñ
L : ÐG ñ Ñ qqp L : ÐG w Ñ qqp L : ÐG ww Ñ qqp L :" ÐG ñ Ñ qqp L :" ÐG w Ñ,
que pode ser indefinidamente prolongada nos dois sentidos, e a que se dá o
nome de sucessão exacta de cohomologia associada à sucessão exacta curta
de complexos de cocadeias.
Dem: Com o fim de melhor sistematizarmos a demonstração, que é um
pouco longa, vamos dividir esta em várias alíneas, começando por apresentar
um diagrama que pode ajudar a nos situarmos ao longo desta.
48A
explicação para o nome “Lema da Serpente” está no diagrama que apresentamos no
início da demonstração e no modo como nos movimentamos ao longo dele no decurso
desta.
§3. Sucessão exacta de Mayer-Vietoris
217
Ö!×
qp
G :"
Æ .:"
qqp
-:"
G w :"
Æ .w :"
qqp
.:"
G ww :"
Æ .ww :"
qp
Ö!×
Ö!×
qp
G :"
Æ .:"
qqp
-:
G w :"
Æ .w :"
qqp
.:
G ww :"
Æ .ww :"
qp
Ö!×
Ö!×
qp
G :"
Æ .:"
qqp
-:"
G w :"
Æ .w :"
qqp
.:"
G ww :"
Æ .ww :"
qp
Ö!×
Ö!×
qp
G :#
qqp
-:#
G w :#
qqp
.:#
G ww :#
qp
Ö!×
a) Vamos começar por verificar que as aplicações lineares de conexão estão
bem definidas. Seja então ÒBww Ó − L : ÐG ww ñ Ñ, onde Bww − ^ : ÐG ww ñ Ñ. A possibilidade de escolher Bw − G w : tal que .: ÐBw Ñ œ Bww é garantida pelo facto de
.: À G w : Ä G ww : ser uma aplicação linear sobrejectiva. Podemos então
escrever
:
:
:
.:" Ð. w ÐBw ÑÑ œ . ww Ð.: ÐBw ÑÑ œ . ww ÐBww Ñ œ !,
pelo que . w : ÐBw Ñ pertence ao núcleo da aplicação linear .:" que é, por
hipótese, igual à imagem da aplicação linear -:" , o que garante a existência
de B − G :" tal que -:" ÐBÑ œ . w : ÐBw Ñ. Tem-se então
-:# Ð. :" ÐBÑÑ œ . w
:"
Ð-:" ÐBÑÑ œ . w
:"
:
Ð. w ÐBw ÑÑ œ !
o que, por a aplicação linear -:# ser injectiva, implica que . :" ÐBÑ œ !, isto
é, que se tem B − ^ :" ÐG ñ Ñ. Provemos agora que o elemento
ÒBÓ − L :" ÐG ñ Ñ não depende das escolhas feitas. Consideramos, para isso,
Cww − ^ : ÐG ww ñ Ñ tal que ÒCww Ó œ ÒBww Ó − L : ÐG ww ñ Ñ, e escolhemos Cw − G w : tal que
.: ÐCw Ñ œ Cww e C − G :" tal que -:" ÐCÑ œ . w : ÐCw Ñ. Tem-se então
Cww Bww − F : ÐG ww ñ Ñ, o que implica a existência de D ww − G ww :" tal que
Cww Bww œ . ww :" ÐD ww Ñ. O facto de a aplicação linear .:" ser sobrejectiva
garante a existência de D w − G w :" tal que .:" ÐD w Ñ œ D ww . Tem-se então
.: ÐCw Bw . w
:"
ÐD w ÑÑ œ Cww Bww . ww
:"
Ð.:" ÐD w ÑÑ œ !
pelo que, uma vez que o núcleo da aplicação linear .: coincide com a
imagem da aplicação linear -: , podemos concluir a existência de D − G : tal
que -: ÐDÑ œ Cw Bw . w :" ÐD w Ñ. Tem-se então
:
:
:"
:
:
-:" Ð. : ÐDÑÑ œ . w Ð-: ÐDÑÑ œ . w ÐCw Bw . w ÐD w ÑÑ œ . w ÐCw Ñ .w ÐBw Ñ œ
œ -:" ÐCÑ -:" ÐBÑ œ -:" ÐC BÑ,
o que, por a aplicação linear -:" ser injectiva, implica que . : ÐDÑ œ C B,
ou seja, que ÒBÓ œ ÒCÓ em L :" ÐG ñ Ñ. Ficámos assim com uma aplicação bem
definida ` : À L : ÐG ww ñ Ñ Ä L :" ÐG ñ Ñ, sendo trivial a verificação de que esta
aplicação é linear.
218
Cap. IV. Introdução à cohomologia de de Rham
b) Vamos agora verificar a exactidão da sucessão exacta de cohomologia em
L : ÐG w ñ Ñ, isto é, que a imagem da aplicação L : Ð-ñ ÑÀ L : ÐG ñ Ñ Ä L : ÐG w ñ Ñ
coincide com o núcleo da aplicação L : Ð.ñ ÑÀ L : ÐG w ñ Ñ Ä L : ÐG ww ñ Ñ.
O facto de se ter .: ‰ -: œ ! implica trivialmente que se tem
L : Ð.ñ Ñ ‰ L : Ð-ñ Ñ œ !, e portanto que a imagem está contida no núcleo.
Suponhamos, reciprocamente, que ÒBw Ó − L : ÐG w ñ Ñ, com Bw − ^ : ÐG w ñ Ñß
pertence ao núcleo de L : Ð.ñ Ñ, isto é, que se tem .: ÐBw Ñ − F : ÐG ww ñ Ñ, ou seja,
que existe Bww − G ww :" tal que . ww :" ÐBww Ñ œ .: ÐBw Ñ. O facto de a aplicação
linear .:" ser sobrejectiva garante a existência de Cw − G w :" tal que
.:" ÐCw Ñ œ Bww . Podemos então escrever
.: ÐBw . w
:"
ÐCw ÑÑ œ . ww
:"
ÐBww Ñ . ww
:"
Ð.:" ÐCw ÑÑ œ !,
ou seja, Bw . w :" ÐCw Ñ pertence ao núcleo da aplicação linear .: , que é igual
à imagem de -: , pelo que podemos considerar B − G : tal que
Bw . w :" ÐCw Ñ œ -: ÐBÑ. Tem-se então
:
:
-:" Ð. : ÐBÑÑ œ . w Ð-: ÐBÑÑ œ . w ÐBw . w
:"
:
ÐCw ÑÑ œ . w ÐBw Ñ œ !
pelo que, por a aplicação linear -:" ser injectiva, tem-se . : ÐBÑ œ !, ou seja,
B − ^ : ÐG ñ Ñ. Podemos assim considerar o elemento ÒBÓ − L : ÐG ñ Ñ e vem
L : Ð-ñ ÑÐÒBÓÑ œ Ò-: ÐBÑÓ œ ÒBw . w
:"
ÐC w ÑÓ œ ÒBw Ó,
o que mostra que ÒBw Ó pertence à imagem de L : Ð-ñ Ñ.
c) Vamos agora verificar a exactidão da sucessão exacta de cohomologia em
L : ÐG ww ñ Ñ, isto é, que a imagem da aplicação L : Ð.ñ ÑÀ L : ÐG w ñ Ñ Ä L : ÐG ww ñ Ñ
coincide com o núcleo da aplicação de conexão ` : À L : ÐG ww ñ Ñ Ä L :+1 ÐG ñ Ñ.
Um elemento da imagem de L : Ð.ñ Ñ é um elemento da forma Ò.: ÐBw ÑÓ, com
Bw − ^ : ÐG w ñ Ñ, e o facto de se ter -:" Ð!Ñ œ ! œ . : ÐBw Ñ implica, por
definição, que ` : ÐÒ.: ÐBw ÑÓÑ œ !.
Suponhamos, reciprocamente, que ÒBww Ó − L : ÐG ww ñ Ñ é tal que ` : ÐÒBww ÓÑ œ !.
Sendo então Bw − G w : tal que .: ÐBw Ñ œ Bww e B − G :" tal que
-:" ÐBÑ œ . w : ÐBw Ñ, tem-se ! œ ÒBÓ, ou seja existe C − G : tal que . : ÐCÑ œ B.
Tem-se então
:
:
. w ÐBw -: ÐCÑÑ œ . w ÐBw Ñ -:" Ð. : ÐCÑÑ œ !,
o que mostra que Bw -: ÐCÑ − ^ : ÐG w ñ ÑÑ e, para o correspondente elemento
ÒBw -: ÐCÑÓ − L : ÐG w ñ Ñ, vem
L : Ð.ñ ÑÐÒBw -: ÐCÑÓÑ œ Ò.: ÐBw Ñ .: Ð-: ÐCÑÑÓ œ ÒBww Ó,
o que mostra que ÒBww Ó está na imagem de L : Ð.ñ Ñ.
d) Vamos verificar, por fim, a exactidão da sucessão exacta de cohomologia
em L :" ÐG ñ Ñ, isto é, que a imagem de ` : À L : ÐG ww ñ Ñ Ä L :+1 ÐG ñ Ñ coincide
com o núcleo de L :" Ð-ñ ÑÀ L :" ÐG ñ Ñ Ä L :" ÐG w ñ Ñ.
§3. Sucessão exacta de Mayer-Vietoris
219
Um elemento de L :+1 ÐG ñ Ñ na imagem de ` : vai ser um elemento da forma
ÒBÓ, para o qual existe Bww − ^ : ÐG ww ñ Ñ e Bw − G w : , tais que .: ÐBw Ñ œ Bww e
-:" ÐBÑ œ . w : ÐBw Ñ, tendo-se então
:
L :" Ð-ñ ÑÐÒBÓÑ œ Ò-:" ÐBÑÓ œ Ò. w ÐBw ÑÓ œ !,
o que mostra que ele está no núcleo de L :" Ð-ñ Ñ.
Suponhamos, reciprocamente, que ÒBÓ − L :+1 ÐG ñ Ñ pertence ao núcleo de
L :" Ð-ñ Ñ, portanto que se tem Ò-:" ÐBÑÓ œ !, ou seja, que existe Bw − G w : tal
que -:" ÐBÑ œ . w : ÐBw Ñ. Tem-se então
:
:
. ww Ð.: ÐBw ÑÑ œ .:" Ð. w ÐBw ÑÑ œ .:" Ð-:" ÐBÑÑ œ !,
ou seja, .: ÐBw Ñ − ^ : ÐG ww ñ Ñ, e, pela definição de ` : , vem, para o
correspondente Ò.: ÐBw ÑÓ − L : ÐG ww ñ Ñ, ` : ÐÒ.: ÐBw ÑÓÑ œ ÒBÓ, o que mostra que ÒBÓ
pertence à imagem de ` : .
IV.3.3. (Nota) Para quem encontra estes assuntos pela primeira vez, talvez valha
a pena explicar melhor a razão por que afirmamos que a sucessão exacta de
cohomologia pode ser prolongada indefinidamente nos dois sentidos. O que
se passa é que, por definição, o facto de uma sucessão “longa” ser exacta
reduz-se à exactidão de cada sucessão associada a duas aplicações lineares
consecutivas e, como é imediato realizar, essas sucessões de duas aplicações
lineares consecutivas que aparecem na sucessão referida no enunciado,
quando se consideram os diferentes valores de : são exactamente as mesmas
que aparecem quando se considera uma única sucessão, indefinidamente
prolongada nos dois sentidos. Nesta ordem de ideias, o resultado anterior
ficaria enunciado de modo equivalente se tivéssemos, por exemplo, afirmado
a exactidão, para cada :, da sucessão
ñ
L : Ð-ñ Ñ
` :"
: ñ
ñ L Ð. Ñ
ñ
`:
L :" ÐG ww Ñ qqp L : ÐG ñ Ñ qqp L : ÐG w Ñ qqp L : ÐG ww Ñ qqp L :" ÐG ñ Ñ.
IV.3.4. Sejam Q § I uma variedade e Y e Z abertos de Q tais que
Y Z œ Q . Notemos Hñ ÐY Ñ ‚ Hñ ÐZ Ñ o complexo de cocadeias produto de
Hñ ÐY Ñ e Hñ ÐZ Ñ construído a partir dos produtos cartesianos
H: ÐY Ñ ‚ H: ÐZ Ñ. Tem então lugar uma sucessão exacta curta de complexos
de cocadeias
-ñ
.ñ
! qp Hñ ÐQ Ñ qqp Hñ ÐY Ñ ‚ Hñ ÐZ Ñ qqp Hñ ÐY Z Ñ qp !
em que as aplicações lineares
-: À H: ÐQ Ñ Ä H: ÐY Ñ ‚ H: ÐZ Ñ
.: À H: ÐY Ñ ‚ H: ÐZ Ñ Ä H: ÐY Z Ñ
estão definidas por -: Ð=Ñ œ Ð=ÎY ß =ÎZ Ñ, .: Ð!ß " Ñ œ "ÎY Z !ÎY Z .
Dem: Do facto de, para cada Ð!ß " Ñ − H: ÐY Ñ ‚ H: ÐZ Ñ, se ter . : Ð!ß " Ñ œ
Ð. : Ð!Ñß . : Ð" ÑÑ, deduz-se imediatamente que -ñ e .ñ são efectivamente
220
Cap. IV. Introdução à cohomologia de de Rham
morfismos de complexos de cocadeias. O facto de cada -: ser uma aplicação
linear injectiva resulta de que, se = œ Ð=B ÑB−Q é uma forma diferencial de
grau : tal que =B œ !, para cada B − Y e para cada B − Z , então =B œ !,
para cada B − Q , isto é, = œ !. Uma vez que, para cada = − H: ÐQ Ñ, as
formas diferenciais =ÎY e =ÎZ têm a mesma restrição =ÎY Z a Y Z ,
concluímos que se tem .: ‰ -: œ !, e portanto que a imagem da aplicação
linear -: está contida no núcleo da aplicação linear .: . Reciprocamente, se
.: Ð!ß " Ñ œ !, tem-se !B œ "B , para cada B − Y Z o que nos garante que
se pode definir uma forma diferencial = sobre Q pela condição de se ter
=B œ !B , para cada B − Y , e =B œ "B , para cada B − Z , a suavidade de =
resultando então do facto de a suavidade ser uma questão local; tem-se então
Ð!ß " Ñ œ -: Ð=Ñ, o que mostra que Ð!ß " Ñ pertence à imagem de -: . Resta-nos
provar que a aplicação linear .: é sobrejectiva, para o que recorremos ao
teorema da partição da unidade. Por este resultado, podemos considerar duas
aplicações suaves :ß <À Q Ä Ò!ß "Ó, a primeira nula fora de um certo
subconjunto E de Y , fechado em Q , e a segunda nula fora de um certo
subconjunto F de Z , também fechado em Q , tais que, para cada B − Q ,
:ÐBÑ <ÐBÑ œ ". Seja então # − H: ÐY Z Ñ e definamos formas
diferenciais ! − H: ÐY Ñ e " − H: ÐZ Ñ por
!B œ œ
<ÐBÑ #B ,
!,
se B − Z
se B Â Z
"B œ œ
:ÐBÑ #B ,
!,
se B − Y
se B Â Y
(a suavidade de ! resulta de que ela tem restrições suaves aos abertos Y Z
e Y ÐQ Ï FÑ de Y , com união Y , a segunda por ser identicamente nula, e
a suavidade de " tem justificação análoga). Uma vez que, para cada
B−Y Z,
"B !B œ :ÐBÑ #B <ÐBÑ #B œ #B ,
concluímos que .: Ð!ß " Ñ œ # , o que termina a demonstração.
IV.3.5. Nas hipóteses de IV.3.4, à sucessão exacta curta de complexos de cocadeias aí referida fica associada a correspondente sucessão exacta de cohomologia, indefinidamente prolongável nos dois sentidos,
` :"
L : Ð-ñ Ñ
L : Ð.ñ Ñ
`:
L :" ÐY Z Ñ qqp L : ÐQ Ñ qqp L : ÐHñ ÐY Ñ ‚ Hñ ÐZ ÑÑ qqp L : ÐY Z Ñ qqp L :" ÐQ Ñ,
a que se dá o nome de sucessão exacta de Mayer-Vietoris associada aos
abertos Y e Z de Q (repare-se que utilizámos a “secção representativa” da
sucessão exacta de cohomologia referida na nota IV.3.349). Lembremos, a
propósito, que, de acordo com IV.2.5, o espaço de cohomologia
L : ÐHñ ÐY Ñ ‚ Hñ ÐZ ÑÑ é um produto de L : ÐY Ñ e L : ÐZ Ñ, com as projecções
naturalmente definidas, e portanto é isomorfo ao produto cartesiano
L : ÐY Ñ ‚ L : ÐZ Ñ, pelo isomorfismo que associa ÐÒ!Óß Ò" ÓÑ a ÒÐ!ß " ÑÓ.
49Por
razões exclusivamente tipográficas…
§3. Sucessão exacta de Mayer-Vietoris
221
Uma das aplicações típicas da sucessão exacta de Mayer-Vietoris é a
possibilidade de calcular explicitamente os espaços de cohomologia de
certas variedades, como, por exemplo, as hipersuperfícies esféricas.
Começamos por fazer algumas observações preliminares sobre as
projecções estereográficas.
IV.3.6. Sejam I um espaço euclidiano de dimensão 8 " e W § I a
hipersuperfície esférica de centro ! e raio ",
W œ ÖB − I ± mBm œ "×.
Sejam C − W fixado e J § I o subespaço vectorial de dimensão 8 " complementar ortogonal de ‘C. Tem-se então um difeomorfismo
0 À W Ï ÖC× Ä J (a projecção estereográfica a partir de C ), definido por
0 ÐBÑ œ C
"
ÐB CÑ, 50
" ØBß CÙ
o difeomorfismo inverso sendo a aplicação 1À J Ä W Ï ÖC×, definida por
1ÐDÑ œ C
#
ÐD CÑ.
" ØDß DÙ
Dem: Comecemos por reparar que, se Bß C − W , a desigualdade de
Cauchy-Schwarz implica que lØBß CÙl Ÿ " e que lØBß CÙl œ " se, e só se,
B œ „C , em particular ØBß CÙ œ " se, e só se, B œ C . Fica assim bem definida
uma aplicação suave 0 À W Ï ÖC× Ä I pela fórmula do enunciado e
verifica-se facilmente que 0 ÐBÑ − J e, mais precisamente, que 0 ÐBÑ é o
único elemento de J da forma C >ÐB CÑ, para algum > − ‘, isto é, o
único elemento de J que pertence à recta afim que contém B e C (resolver a
equação linear ØÐ" >ÑC >Bß CÙ œ !ÑÞ Reparemos agora que, para cada
D − J , existe um único elemento de W Ï ÖC× na recta afim que contém C e D ,
nomeadamente o elemento 1ÐDÑ definido no enunciado. Para isso, tudo o que
temos que reparar é que a equação
ØÐ" =ÑC =Dß Ð" =ÑC =DÙ œ "
é uma equação do segundo grau em = que admite a solução !, correspondente
ao ponto C, e a solução #ÎÐ" ØDß DÙÑ, corrspondente ao ponto 1ÐDÑ. As
caracterizações geométricas de 0 e 1 atrás descritas mostram que a aplicação
0 é uma bijecção de W Ï ÖC× sobre J e que a sua inversa é 1, pelo que
concluímos, em particular, que 0 é um difeomorfismo.
IV.3.7. Como corolário do resultado precedente, podemos concluir que, para
cada C − W , W Ï ÖC× é uma variedade conexa e que, no caso em que 8 #, a
50Geometricamente,
ao subespaço J .
0 ÐBÑ é o único ponto da recta afim, que contém B e C , que pertence
222
Cap. IV. Introdução à cohomologia de de Rham
variedade W é também conexa.
Dem: O facto de a variedade W Ï ÖC× ser conexo vem de que é difeomorfa ao
espaço vectorial J , que é convexo, e portanto conexo. No caso em que
8 #, o facto de W ser conexa é uma consequência de W Ï ÖC× ser denso em
W, o que ficará provado se mostrarmos a existência de uma sucessão de
elementos de W Ï ÖC× convergente para C. Para o verificarmos, basta
considerar um vector A − W , com ØAß CÙ œ ! e definir a sucessão de termo
geral
"
"
C8 œ cosÐ Ñ C sinÐ Ñ A.
8
8
IV.3.8. Consideremos agora o caso particular em que I œ ‘8 , onde 8 "ß com
o produto interno usual, caso em que a hipersuperfície esférica é
habitualmente notada W 8" . Notando, como é usual, /" ß á ß /8 a base
canónica de ‘8 , é frequente neste caso considerar-se as projecções
estereográficas realtivas ao “polo norte” /8 e ao “polo sul” /8 , as quais,
identificando, como é usual, ‘8 ao produto ‘8" ‚ ‘, vão ter ambas com
contradomínio o espaço vectorial ‘8" ‚ Ö!×. Compondo estas projecções
com o isomorfismo natural de ‘8" ‚ Ö!× sobre ‘8" , definido por
ÐBß !Ñ È B, obtemos então difeomorfismos, chamados ainda de projecções
estereográficas,
0 À W 8" Ï Ö/8 × Ä ‘8" ,
0 À W 8" Ï Ö/8 × Ä ‘8" ,
que se verifica facilmente estarem definidos por
B
B
0 ÐBß >Ñ œ
, 0 ÐBß >Ñ œ
,
">
">
as respectivas inversas,
1 À ‘8" Ä W 8" Ï Ö/8 ×,
1 À ‘8" Ä W 8" Ï Ö/8 ×,
estando definidas por
1 ÐDÑ œ ˆ
#D
ØDß DÙ "
‰,
ß
" ØDß DÙ " ØDß DÙ
1 ÐDÑ œ ˆ
#D
" ØDß DÙ
‰.
ß
" ØDß DÙ " ØDß DÙ
Podemos agora passar ao cálculo dos espaços de cohomologia das hipersuperfícies esféricas, começando com o caso trivial, mas diferente dos
outros, de W ! .
IV.3.9. Considerando a hipersuperfície esférica W ! œ Ö"ß "× § ‘, tem-se
L : ÐW ! Ñ œ Ö!×, para cada : Á !, e L ! ÐW ! Ñ é um espaço vectorial de
dimensão #, admitindo uma base Ò: Óß Ò: Ó, onde : ß : À Ö"ß "× Ä ‘ são
as aplicações definidas por : Ð"Ñ œ ", : Ð"Ñ œ !, : Ð"Ñ œ !,
§3. Sucessão exacta de Mayer-Vietoris
223
: Ð"Ñ œ ".
Dem: Este resultado não é mais do que um caso particular de IV.1.4, se
repararmos que W ! é uma variedade de dimensão !, cujas componentes
conexas são Ö"× e Ö"×.
IV.3.10. Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7 compacta, sem bordo, suavemente orientada. Sendo Š, igual a ‘ ou ‚, o
corpo dos escalares que se está a considerar, existe então uma aplicação
linear ë À L 7 ÐQ Ñ Ä Š, definida por ë ÐÒ=ÓÑ œ 'Q =. Se Q Á g, esta
aplicação é sobrejectiva, em particular, L 7 ÐQ Ñ Á Ö!×.
Dem: O facto de a variedade Q ser compacta e suavemente orientada
implica que, para cada = − H7 ÐQ Ñ œ ^ 7 ÐHñ ÐQ ÑÑ, está bem definido o
integral 'Q = − Š. Por outro lado, se for Ò=Ó œ Ò=w Ó em L 7 ÐQ Ñ, existe
3 − H7" ÐQ Ñ tal que =w = œ . 3 e então, pelo teorema de Stokes e uma
vez que `" ÐQ Ñ œ g,
w
( = ( = œ ( .3 œ (
Q
Q
Q
`" ÐQ Ñ
3Î`" ÐQ Ñ œ !,
donde 'Q = œ 'Q =w . Fica assim bem definida a aplicação ë À L 7 ÐQ Ñ Ä Š,
sendo trivial constatar que se trata de uma aplicação linear. Por fim, se
Q Á g, a sobrejectividade desta aplicação linear resulta de que, sendo
Z 96Q − H7 ÐQ Ñ œ ^ 7 ÐHñ ÐQ ÑÑ o elemento de volume de Q , tem-se
ë ÐÒZ 96Q ÓÑ=( Z 96Q œ ( " . .Q ÐBÑ œ .Q ÐQ Ñ Á !.
Q
Q
IV.3.11. (Lema) a) Dada uma sucessão exacta de espaços vectoriais do tipo
.
-
I qp J qp K,
com I e K com dimensões finitas : e ; , tem-se que J tem dimensão finita
menor ou igual a : ; .
b) Dados 8 " e uma sucessão exacta de espaços vectoriais do tipo
-"
-#
-$
-8#
-8"
Ö!× qp I" qp I# qp I$ qp â qp I8" qp I8 qp Ö!×,
onde cada I4 tem dimensão finita :4 , tem-se ! Ð"Ñ4 :4 œ !.
8
4œ"
Dem: a) Sendo J w § J o subespaço vectorial imagem de -, que coincide
com o núcleo de ., obtemos, por passagem ao quociente de ., uma aplicação
linear injectiva .
sÀ J ÎJ w Ä K, o que implica que J ÎJ w tem dimensão finita
menor ou igual a ; . O facto de J w ser a imagem da aplicação linear - implica
que J w tem dimensão finita menor ou igual a :. Considerando agora a
sucessão exacta curta
224
Cap. IV. Introdução à cohomologia de de Rham
Ö!× qp J w qp J qp J ÎJ w qp Ö!×,
deduzimos de II.7.22 que J tem dimensão finita igual à soma das dimensões
de J w e de J ÎJ w , portanto menor ou igual a : ; .
b) Comecemos por ver que esta afirmação é trivialmente verdadeira nos
casos em que 8 œ " ou 8 œ #, no primeiro caso, uma vez que, para uma
sucessão exacta do tipo Ö!× qp I" qp Ö!×, a segunda aplicação linear é
injectiva e portanto I" œ Ö!×, e, no segundo caso, uma vez que, para uma
-"
sucessão exacta do tipo Ö!× qp I" qp I# qp Ö!×, -" é um isomorfismo. A
afirmação é também verdadeira para 8 œ $, tendo em conta II.7.22. Façamos
então a demonstração por indução em 8, supondo que o resultado é válido
para um certo 8 $ e examinando o que sucede quando temos uma sucessão
exacta do tipo
-"
-#
-$
-8#
-8"
-8
Ö!× qp I" qp I# qp I$ qp â qp I8" qp I8 qp I8" qp Ö!×.
Consideramos então o subespaço vectorial I8w § I8 imagem da aplicação
linear -8" , que é também o núcleo da aplicação linear -8 , e reparamos que
se podem então considerar as sucessões exactas
-"
-#
+
-8
-$
-8#
-8"
Ö!× qp I" qp I# qp I$ qp â qp I8" qp I8w qp Ö!×
Ö!× qp I8w qp I8 qp I8" qp Ö!×.
Sendo :8w a dimensão de I8w , deduzimos, pela hipótese de indução, que se
tem Ð! Ð"Ñ4 :4 Ñ Ð"Ñ8 :8w œ ! e, tendo em conta, mais uma vez, II.7.22,
8"
4œ"
que :8w œ :8 :8" . Substituindo esta última igualdade na anterior, obtemos
finalmente o resultado.
IV.3.12. Seja 8 ! e consideremos na hipersuperfície esférica W 8 § ‘8" a
orientação suave que lhe vem de ser bordo da bola fechada de centro ! e raio
". Tem-se então:
a) Se 8 œ !, L ! ÐW ! Ñ œ L ! ÐÖ"ß "×Ñ é um espaço vectorial de dimensão #,
admitindo uma base Ò: Óß Ò: Ó, onde : ß : À W ! Ä ‘ são as aplicações
definidas por : Ð"Ñ œ : Ð"Ñ œ " e : Ð"Ñ œ : Ð"Ñ œ !.
b) Se 8 ", L ! ÐW 8 Ñ é um espaço vectorial de dimensão ", admitindo como
base a classe de equivalência da função W 8 Ä Š de valor constante ".
c) Se 8 ", L 8 ÐW 8 Ñ é um espaço vectorial de dimensão ", admitindo como
base a classe de equivalência do elemento de volume de W 8 e
ë À L 8 ÐW 8 Ñ Ä Š é um isomorfismo.
d) Para cada : Á !ß 8, L : ÐW 8 Ñ œ Ö!×.
Dem: A conclusão de a), tal como a conclusão de d), no caso em que 8 œ !,
já foi estabelecida em IV.3.9. Supomos assim, a partir de agora, que se tem
8 ". A conclusão de b) é uma consequência de W 8 ser uma variedade
conexa e não vazia, tendo em conta, IV.1.4. Reparemos também que, para a
§3. Sucessão exacta de Mayer-Vietoris
225
alínea c), tudo o que temos que verificar é que L 8 ÐW 8 Ñ tem dimensão ", visto
que o facto de a aplicação linear ë À L 8 ÐW 8 Ñ Ä Š ser sobrejectiva implica
então que ela é um isomorfismo e o facto de a classe de equivalência do
elemento de volume ser aplicada por ë em 58 Á ! implica então que essa
classe de equivalência constitui uma base. A fim de demonstrarmos as
alíneas c) e d), utilizando a sucessão exacta de Mayer-Vietoris, vamos olhar
para W 8 como união dos subconjuntos abertos W œ W 8 Ï Ö/8" × e
W œ W 8 Ï Ö/8" ×, que vão ser variedades contrácteis, por serem
difeomorfas a ‘8 através das projecções estereográficas 0 e 0 referidas em
IV.3.8 (cf. as alíneas a) e b) de III.7.8). Por IV.1.13, sabemos assim que
L ! ÐW Ñ e L ! ÐW Ñ são espaços vectoriais de dimensão " e que os restantes
espaços de cohomologia destas variedades são Ö!×. No que diz respeito à
intersecção W W œ W 8 Ï Ö/8 ß /8 ×, vemos que ela contém a variedade
W 8" ‚ Ö!×, naturalmente difeomorfa a W 8" , e vamos verificar que, para a
inclusão +À W 8" ‚ Ö!× Ä W W , cada
L : Ð+ÑÀ L : ÐW W Ñ Ä L : ÐW 8" ‚ Ö!×Ñ
é um isomorfismo, o que provará que cada L : ÐW W Ñ é isomorfo a
L : ÐW 8" Ñ. Para o verificarmos, identificamos, do modo usual, ‘8" a
‘8 ‚ ‘ e consideramos a aplicação suave 3À W W Ä W 8" ‚ Ö!×
B
definida por 3ÐBß >Ñ œ Ð mBm
ß !Ñ. Vem 3 ‰ + œ M.À W 8" ‚ Ö!× Ä W 8" ‚ Ö!×
e a aplicação + ‰ 3À W W Ä W W é suavemente homotópica à
identidade51, através da homotopia LÀ Ò!ß "Ó ‚ ÐW W Ñ Ä W W
definida por
LÐ=ß ÐBß >ÑÑ œ ˆ
BÈ" =# >#
ß =>‰.
mBm
Concluímos daqui que
L : Ð+Ñ ‰ L : Ð3Ñ œ L : Ð3 ‰ +ÑÀ L : ÐW 8" ‚ Ö!×Ñ Ä L : ÐW 8" ‚ Ö!×Ñ
L : Ð3Ñ ‰ L : Ð+Ñ œ L : Ð+ ‰ 3ÑÀ L : ÐW W Ñ Ä L : ÐW W Ñ
são as aplicações identidade, o que mostra que L : Ð+Ñ é realmente um isomorfismo, com inverso L : Ð3Ñ.
Podemos agora passar à demonstração de c) e d), que será feita por indução
em 8. Para 8 œ ", d) é trivial, tendo em conta IV.1.4, e, quanto a c),
podemos considerar a seguinte parte da sucessão exacta de Mayer-Vietoris
Ö!× Ä L ! ÐW " Ñ Ä L ! ÐHñ ÐW Ñ ‚ Hñ ÐW ÑÑ Ä L ! ÐW W Ñ Ä L " ÐW " Ñ Ä Ö!×
(lembrar que o espaço vectorial L " ÐHñ ÐW Ñ ‚ Hñ ÐW ÑÑ é isomorfo a
L " ÐW Ñ ‚ L " ÐW Ñ œ Ö!×), para a qual sabemos que L ! ÐW " Ñ tem dimensão
51Em
particular, a inclusão + é invertível, módulo homotopia suave, no sentido do
exercício IV.1 adiante.
226
Cap. IV. Introdução à cohomologia de de Rham
", que L ! ÐHñ ÐW Ñ ‚ Hñ ÐW ÑÑ, sendo isomorfo a L ! ÐW Ñ ‚ L ! ÐW Ñ, tem
dimensão # e que L ! ÐW W Ñ, sendo isomorfo a L ! ÐW ! Ñ œ L ! ÐÖ"ß "×Ñ,
tem dimensão #, o que nos permite deduzir, por IV.3.11, que L " ÐW " Ñ tem
efectivamente dimensão ". Suponhamos, por fim, que c) e d) são válidos para
um certo valor de 8 " e vejamos o que se passa com W 8" . Como no caso
de W " , podemos considerar a seguinte parte da sucessão exacta de
Mayer-Vietoris
Ö!× Ä L ! ÐW 8" Ñ Ä L ! ÐHñ ÐW Ñ ‚ Hñ ÐW ÑÑ Ä L ! ÐW W Ñ Ä L " ÐW 8" Ñ Ä Ö!×.
Como então L ! ÐW 8" Ñ tem dimensão " e L ! ÐHñ ÐW Ñ ‚ Hñ ÐW ÑÑ tem
dimensão #, mas já L ! ÐW W Ñ, sendo isomorfo a L ! ÐW 8 Ñ, vai agora ter
dimensão " pelo que o que concluímos de IV.3.11 é que L " ÐW 8" Ñ tem
dimensão !, ou seja, L " ÐW 8" Ñ œ Ö!×. Para cada : ", podemos escolher a
seguinte parte da sucessão exacta de Mayer-Vietoris
Ö!× Ä L :" ÐW W Ñ Ä L : ÐW 8" Ñ Ä Ö!×,
uma
vez
que
L : ÐHñ ÐW Ñ ‚ Hñ ÐW ÑÑ
é
isomorfo
a
:
:
L ÐW Ñ ‚ L ÐW Ñ œ Ö!× e que L :" ÐHñ ÐW Ñ ‚ Hñ ÐW ÑÑ é isomorfo a
L :" ÐW Ñ ‚ L :" ÐW Ñ œ Ö!×. Daqui se deduz que L : ÐW 8" Ñ é isomorfo a
L :" ÐW W Ñ que, como dissémos, é isomorfo a L :" ÐW 8 Ñ pelo que,
tendo em conta a hipótese de indução, L : ÐW 8" Ñ œ Ö!×, para cada
: Á 8 ", e L 8" ÐW 8" Ñ é um espaço vectorial de dimensão ".
IV.3.13. (Corolário) Seja 8 " e notemos +À W 8" Ä ‘8 Ï Ö!× a inclusão e
0 À ‘8 Ï Ö!× Ä W 8" a aplicação suave definida por 0 ÐBÑ œ BÎmBm. Tem-se
então:
a) Se 8 œ ", L : Б Ï Ö!×Ñ œ Ö!×, para cada : Á !, e L ! Б Ï Ö!×Ñ é um
espaço vectorial de dimensão #, admitindo uma base Ò: Óß Ò: Ó, onde
: ß : À ‘ Ï Ö!× Ä ‘ são as aplicações suaves que tomam, respectivamente,
o valor " no números positivos e o valor ! nos negativos e o valor " nos
números negativos e o valor ! nos positivos.
b) Se 8 #, L ! Б8 Ï Ö!×Ñ é um espaço vectorial de dimensão ", admitindo
como base a classe de equivalência da função de valor constante ".
c) Se 8 #, L 8" Б8 Ï Ö!×Ñ é um espaço vectorial de dimensão ",
admitindo como base ÒHÓ, onde H œ 0 ‡ Z 96W 8" é a forma diferencial ângulo
sólido (cf. III.9.16).
d) Para cada : Á !ß 8 ", L : Б8 Ï Ö!×Ñ œ Ö!×.
Dem: Trata-se de uma consequência do resultado anterior, se mostrarmos
que
L : Ð+ÑÀ L : Б8 Ï Ö!×Ñ Ä L : ÐW 8" Ñ
L : Ð0 ÑÀ L : ÐW 8" Ñ Ä L : Б8 Ï Ö!×Ñ
são isomorfismos inversos um do outro. Ora, tendo em conta a igualdade
0 ‰ + œ M.À W 8" Ä W 8" , vem
§3. Sucessão exacta de Mayer-Vietoris
227
L : Ð+Ñ ‰ L : Ð0 Ñ œ M.À L : ÐW 8" Ñ Ä L : ÐW 8" Ñ
e, uma vez que + ‰ 0 À ‘8 Ï Ö!× Ä ‘8 Ï Ö!× é suavemente homotópica à
identidade, pela homotopia LÀ Ò!ß "Ó ‚ Б8 Ï Ö!×Ñ Ä ‘8 Ï Ö!× definida por
B
LÐ=ß BÑ œ
,
" = =mBm
tem-se também
L : Ð0 Ñ ‰ L : Ð+Ñ œ M.À L : Б8 Ï Ö!×Ñ Ä L : Б8 Ï Ö!×Ñ,
donde o resultado.
§4. Cohomologia com suporte compacto.
IV.4.1. Seja Q § I uma variedade. Diz-se que uma forma diferencial suave de
grau :, = œ Ð=B ÑB−Q tem suporte compacto se existir um compacto O § Q
tal que =ÎÐQ ÏOÑ œ !. É claro que, quando a variedade Q for compacta, toda
a forma diferencial suave tem suporte compacto (tomar O œ Q ).
Para cada : !, notamos H:- ÐQ Ñ o subconjunto de H: ÐQ Ñ constituído pelas
formas diferenciais suaves de grau : com suporte compacto
(acrescentando-se uma referência a ‘ ou ‚ quando for importante sublinhar
qual o corpo que se está a considerar), sendo imediato realizar-se que H:- ÐQ Ñ
é um subespaço vectorial de H: ÐQ Ñ (lembrar que o vazio é um compacto
contido em Q e que a união de dois subconjuntos compactos de Q é ainda
um subconjunto compacto de Q ). Para cada : !, pomos, naturalmente,
H:- ÐQ Ñ œ H: ÐQ Ñ œ !.
Se = − H:- ÐQ Ñ, então . : Ð=Ñ − H-:" ÐQ Ñ, visto que, se O § Q é um
compacto tal que =ÎÐQ ÏOÑ œ !, tem-se também Ð. =ÑÎÐQ ÏOÑ œ
.Ð=ÎÐQ ÏOÑ Ñ œ !. Podemos assim considerar um novo complexo de cocadeias
Hñ- ÐQ Ñ definido pela família dos subespaços vectoriais H:- ÐQ Ñ § H: ÐQ Ñ e
pelos operadores de cobordo restrições dos operadores de cobordo
. : À H: ÐQ Ñ Ä H:" ÐQ Ñß 52 complexo de cocadeias a que se dá o nome de
complexo de de Rham com suporte compacto de Q . Os espaços vectoriais
^ : ÐH-ñ ÐQ ÑÑ, F : ÐH-ñ ÐQ ÑÑ e L : ÐH-ñ ÐQ ÑÑ são notados com frequência mais
simplesmente ^-: ÐQ Ñ, F-: ÐQ Ñ e L-: ÐQ Ñ e diz-se que os espaços vectoriais
L-: ÐQ Ñ são os espaços de cohomologia de de Rham com suporte compacto
da variedade Q .
É claro que, se Q tem dimensão 7 vem ainda L-: ÐQ Ñ œ Ö!×, para : 7 e
: !, e que, se Q é compacta, os espaços de cohomologia com suporte
52Temos
portanto um subcomplexo de cocadeias, noção cuja definição geral é evidente.
228
Cap. IV. Introdução à cohomologia de de Rham
compacto L-: ÐQ Ñ coincidem com os espaços de cohomologia ordinária
L : ÐQ Ñ.
IV.4.2. Do facto de se ter H:- ÐQ Ñ § H: ÐQ Ñ e de os operadores de cobordo de
Hñ- ÐQ Ñ serem restrições dos de Hñ ÐQ Ñ resulta trivialmente que se tem
também ^-: ÐQ Ñ § ^ : ÐQ Ñ e F-: ÐQ Ñ § F : ÐQ Ñ. Note-se, no entanto, que,
enquanto que ^-: ÐQ Ñ œ ^ : ÐQ Ñ H-: ÐQ Ñ, em geral F-: ÐQ Ñ estará estritamente contido em F : ÐQ Ñ H-: ÐQ Ñ. O que se passa é que se um elemento
= − H:- ÐQ Ñ for da forma . 3, nada nos garante que a forma diferencial 3
tenha suporte compacto.
IV.4.3. O que se disse atrás poder-nos-ia levar a pensar que L-: ÐQ Ñ § L : ÐQ Ñ.
É no entanto fácil de compreender que isso não tem nada de acontecer em
geral. De facto, existe uma aplicação linear canónica L-: ÐQ Ñ Ä L : ÐQ Ñ,
definida por Ò=Ó È Ò=Ó,53 para cada = − ^-: ÐQ Ñ § ^ : ÐQ Ñ, aplicação que
claramente não tem que ser sobrejectiva, mas que também não tem que ser
injectiva, na medida em que, para = − ^-: ÐQ Ñ pode-se ter Ò=Ó œ ! em
L : ÐQ Ñ e Ò=Ó Á ! em L-: ÐQ Ñ, pela razão já referida no fim de IV.4.2.
Ao contrário do que sucede com a cohomologia de de Rham usual, a
cohomologia com suporte compacto não se comporta bem com as
aplicações suaves gerais entre variedades. O problema está em que, se
0 À Q w Ä Q é uma aplicação suave entre variedades e = − H:- ÐQ Ñ, a
forma diferencial imagem recíproca 0 ‡ = − H: ÐQ w Ñ não tem que ter
suporte compacto (se O § Q é um compacto tal que =C œ !, para cada
C − Q Ï O , então Ð0 ‡ =ÑB œ !, para cada B − Q w Ï 0 " ÐOÑ, mas o
conjunto 0 " ÐOÑ, apesar de fechado em Q w , não tem que ser compacto).
Para podermos trabalhar com imagens recíprocas ao nível das formas
diferenciais de suporte compacto, temos que nos restringir a aplicações
suaves com uma propriedade especial.
IV.4.4. Sejam Q § I e Q w § I w duas variedades. Diz-se que uma aplicação
0 À Q w Ä Q é própria se é contínua e, para cada compacto O § Q , o
subconjunto 0 " ÐOÑ § Q w é também compacto.54 Como exemplos triviais
de aplicações próprias, temos os seguintes:
a) Se a variedade Q w é compacta, toda a aplicação contínua 0 À Q w Ä Q é
própria.55
b) Se 0 À Q w Ä Q é um homeomorfismo, então 0 é uma aplicação própria.
c) Se Q w é uma subvariedade fechada de Q , então a inclusão Q w Ä Q é
53É
54É
claro que a classe de equivalência de = é tomada em dois sentidos diferentes.
claro que esta definição pode ser apresentada, mais geralmente, no caso em que Q e
Q w são simplesmente espaços topológicos. As condições de termos um espaço separado
ou de termos um espaço localmente compacto seriam, no entanto, necessárias para a
validade de alguns dos resultados que referiremos.
55Pelo contrário, se a variedade Q w não é compacta, uma aplicação constante
0 À Q w Ä Q não é própria.
§4. Cohomologia com suporte compacto
229
uma aplicação própria.
d) Se as aplicações 1À Q ww Ä Q w e 0 À Q w Ä Q são próprias, então a
composta 0 ‰ 1À Q ww Ä Q é também própria.
Dem: Para alínea a), atendemos a que, se O § Q é compacto, então O é
fechado em Q pelo que 0 " ÐOÑ é fechado em Q w , e portanto compacto.
Para a alínea b), atendemos a que um conjunto homeomorfo a um compacto é
também compacto. Para a alínea c), atendemos a que, se O § Q é
compacto, então a sua imagem recíproca pela inclusão, Q w O , é fechada
em O , e portanto compacta. A alínea d) resulta trivialmente da transitividade
das imagens recíprocas.
IV.4.5. Sejam Q § I e Q w § I w duas variedades e 0 À Q w Ä Q uma aplicação
suave própria. Para cada : − ™ e = − H:- ÐQ Ñ, tem-se então 0 ‡ = − H-: ÐQ w Ñ,
pelo que, por restrição das aplicações lineares 0 ‡ À H: ÐQ Ñ Ä H: ÐQ w Ñ,
obtemos aplicações lineares, 0 ‡ À H:- ÐQ Ñ Ä H-: ÐQ w Ñ, ainda notadas com a
mesma letra, que vão definir trivialmente ainda um morfismo de complexos
de cocadeias de Hñ- ÐQ Ñ para H-ñ ÐQ w Ñ. As correspondentes aplicações lineares
ao nível da cohomologia serão notadas
L-: Ð0 ÑÀ L-: ÐQ Ñ Ä L-: ÐQ w Ñ.
IV.4.6. Tendo em conta a alínea a) de III.1.14, deduzimos que:
a) Sendo Q § I uma variedade, e M.Q À Q Ä Q a aplicação identidade, o
‡
morfismo de complexos de cocadeias M.Q
À Hñ- ÐQ Ñ Ä H-ñ ÐQ Ñ é o morfismo
identidade, e portanto também cada L-: ÐM.Q ÑÀ L-: ÐQ Ñ Ä L-: ÐQ Ñ é a
aplicação linear identidade.
b) Sendo Q § I , Q w § I w e Q ww § I ww variedades e 0 À Q ww Ä Q w e
1À Q w Ä Q aplicações suaves próprias, tem-se que 1 ‰ 0 À Q ww Ä Q é uma
aplicação suave própria e o morfismo de complexos de cocadeias
Ð1 ‰ 0 ч À Hñ- ÐQ Ñ Ä H-ñ ÐQ ww Ñ coincide com o composto 0 ‡ ‰ 1‡ dos
morfismos de complexos de cocadeias 1‡ À Hñ- ÐQ Ñ Ä H-ñ ÐQ w Ñ e
0 ‡ À Hñ- ÐQ w Ñ Ä H-ñ ÐQ ww Ñ, e portanto, para cada :,
L-: Ð1 ‰ 0 Ñ œ L-: Ð0 Ñ ‰ L-: Ð1ÑÀ L-: ÐQ Ñ Ä L-: ÐQ ww Ñ.
c) Em consequência, se 1À Q w Ä Q é um difeomorfismo, então
1‡ À Hñ- ÐQ Ñ Ä H-ñ ÐQ w Ñ é um isomorfismo de complexos de cocadeias e
portanto, para cada :, L-: Ð1ÑÀ L-: ÐQ Ñ Ä L-: ÐQ w Ñ é um isomorfismo, tendo
L-: Ð1" Ñ como isomorfismo inverso.
Se, como vimos, a cohomologia de de Rham com suporte compacto põe
alguns problemas na operação de imagem recíproca por aplicações suaves
arbitrárias, ela vai, em compensação, permitir uma outra operação importante, impossível ao nível de cohomologia de de Rham ordinária.
230
Cap. IV. Introdução à cohomologia de de Rham
IV.4.7. Sejam Q § I uma variedade e Y § I um subconjunto aberto. Para
cada = − H:- ÐY Ñ, podemos considerar uma forma diferencial de suporte
compacto =ÏQ , a que daremos o nome de extensão trivial de = a Q , definida
por
Ð=ÏQ ÑB œ œ
=B ,
!,
se B − Y
se B Â Y
(sendo O § Y um compacto fora do qual = se anule, a extensão trivial
também se anula fora de O e a sua suavidade resulta de ter restrições suaves
aos abertos Y e Q Ï O de Q , com união Q , a segunda por ser
identicamente nula). Ficamos assim com aplicações lineares injectivas
H:- ÐY Ñ Ä H-: ÐQ Ñ, que se definem também, de modo trivial, para : !, às
quais daremos o nome de injecções canónicas. Repare-se que, como se
realiza imediatamente, a derivada exterior da extensão trivial =ÏQ é a
extensão trivial da derivada exterior . =, ou seja .Ð=ÏQ Ñ œ Ð. =ÑÏQ .
Concluímos assim que a família das injecções canónicas (que são
trivialmente injectivas) constitui um morfismo de complexos de cocadeias de
Hñ- ÐY Ñ para H-ñ ÐQ Ñ, ao qual fica associada, para cada inteiro :, uma
aplicação linear L-: ÐY Ñ Ä L-: ÐQ Ñ, definida por Ò=Ó È Ò=ÏQ Ó, que, por
razões análogas às referidas em IV.4.3, não tem que ser injectiva nem
sobrejectiva.
IV.4.8. Sejam Q § I uma variedade e ÐY4 Ñ4−N uma família de abertos de Q
disjuntos dois a dois e de união Q . Notando +4 À Y4 Ä Q as inclusões, definidas por +4 ÐBÑ œ B, que são aplicações próprias, tem-se então que o complexo de cocadeias Hñ- ÐQ Ñ é uma soma dos complexos de cocadeias H-ñ ÐY4 Ñ,
tendo como injecções as famílias de injecções canónicas H:- ÐY4 Ñ Ä H-: ÐQ Ñ e
como projecções associadas as famílias das aplicações +4‡ À H-: ÐQ Ñ Ä H-: ÐY4 Ñ.
Em consequência, para cada :, L-: ÐQ Ñ é uma soma dos L-: ÐY4 Ñ, definida
pelas injecções L-: ÐY4 Ñ Ä L-: ÐQ Ñ, que estão associadas às injecções canónicas Hñ- ÐY4 Ñ Ä H-ñ ÐQ Ñ, que aplicam cada Ò=Ó na classe Ò=ÏQ Ó, as projecções
associadas sendo as aplicações lineares L-: Ð+4 ÑÀ L-: ÐQ Ñ Ä L-: ÐY4 Ñ, que aplicam Ò=Ó nas classes Ò=ÎY4 Ó.56
Dem: O facto de o complementar de cada Y4 ser a união dos restantes
abertos, e portanto um conjunto aberto, implica que cada Y4 é também
fechado em Q o que, pela alínea c) de IV.4.4, implica que cada inclusão
+4 À Y4 Ä Q é uma aplicação própria. Podemos assim considerar as
aplicações lineares associadas +4‡ À H-: ÐQ Ñ Ä H-: ÐY4 Ñ, definidas por
= È =ÎY4 , e sendo 54 À H:- ÐY4 Ñ Ä H-: ÐQ Ñ as injecções canónicas,
constatamos que, para cada = − H:- ÐY4 Ñ, +4‡ Ð54 Ð=ÑÑ œ = e, para 5 Á 4,
+5‡ Ð54 Ð=ÑÑ œ !. Além disso, se = − H-: ÐQ Ñ e se O § Q é um compacto fora
56Comparar
com IV.2.6 e com as observações feitas a seguir a este resultado.
§4. Cohomologia com suporte compacto
231
do qual = se anula o facto de o compacto O estar contido na união dos
abertos Y4 implica a existência de uma parte finita N w de N tal que O estaja
ainda contido na união dos Y4 com 4 − N w e daqui deduzimos que, para cada
4  N w , 54 Ð+4‡ Ð=ÑÑ œ !, verificando-se então facilmente que, para cada
B − Q,
" 54 Ð+4‡ Ð=ÑÑB œ =B
4−N w
(se B − Y5 com 5 Â N w , ambos os membros são ! e se B − Y5 com 5 − N w só
a parcela com 4 œ 5 do primeiro membro não é obrigatoriamente nula e essa
é igual a =B ). Podemos agora aplicar IV.2.12 para garantir que Hñ- ÐQ Ñ é uma
soma dos complexos de cocadeias Hñ- ÐY4 Ñ, tendo como injecções as famílias
de injecções canónicas 54 À H:- ÐY4 Ñ Ä H-: ÐQ Ñ e como projecções associadas
as famílias das aplicação lineares +4‡ À H-: ÐQ Ñ Ä H-: ÐY4 Ñ e resulta então de
IV.2.17 que L-: ÐQ Ñ é uma soma dos L-: ÐY4 Ñ, definida pelas injecções
L : Ð54ñ ÑÀ L-: ÐY4 Ñ Ä L-: ÐQ Ñ e que as aplicações L-: Ð+4 ÑÀ L-: ÐQ Ñ Ä L-: ÐY4 Ñ
são as projecções associadas.
IV.4.9. a) Seja Q uma variedade conexa, compacta, não vazia. Tem-se então
que L-! ÐQ Ñ é um espaço vectorial de dimensão ", admitindo como base a
classe de equivalência da aplicação Q Ä ‘ de valor constante ".
b) Seja Q uma variedade conexa, não compacta. Tem-se então
L-! ÐQ Ñ œ Ö!×.
c) Seja Q uma variedade e seja ÐQ4 Ñ4−N a família das componentes conexas
de Q . Seja N w o conjunto dos 4 − N tais que Q4 é compacto e seja, para cada
4 − N w , 04 À Q Ä ‘ a aplicação suave que toma o valor constante " em Q4 e
que é nula sobre as outras componentes conexas. Tem-se então que as classes
Ò04 Ó − L-! ÐQ Ñ, com 4 − N w , constituem uma base de L-! ÐQ Ñ, que tem
portanto dimensão igual a número de elementos de N w , se este é finito, e
dimensão infinita, caso contrário.
Dem: A alínea a) é uma consequência de IV.1.4, uma vez que, por a
variedade Q ser compacta, L-! ÐQ Ñ=L ! ÐQ Ñ. A alínea b) resulta de se ter
então ^-! ÐQ Ñ œ Ö!×, uma vez que, se 0 − ^-! ÐQ Ñ § ^ ! ÐQ Ñ, então
0 À Q Ä Š é uma aplicação constante e portanto tem que ser 0 œ ! sem o
que, por Q não ser compacta, 0 não se anulava fora duma parte compacta de
Q . Uma vez que as componentes conexas Q4 de Q são abertos disjuntos
dois a dois e com união Q , concluímos de IV.4.8 que L-! ÐQ Ñ é uma soma
dos L-! ÐQ4 Ñ, tendo como injecções as aplicações lineares associadas às
injecções canónicas H4- ÐQ4 Ñ Ä H4- ÐQ Ñ e então, por IV.2.8, essas injecções
são aplicações lineares injectivas e L-! ÐQ Ñ é soma directa dos subespaços
imagem destas injecções, o que implica a conclusão de c), tendo em conta a)
e b).
232
Cap. IV. Introdução à cohomologia de de Rham
Verificámos atrás que a cohomologia de de Rham de uma variedade
suavemente contráctil é isomorfa à cohomologia de um ponto, ou seja, é
nula nos graus diferentes de ! e com dimensão " no grau !. Para a
cohomologia de de Rham com suportes compactos já isso não se passa e,
como vamos ver, existem variedades contrácteis com espaços de
cohomologia muito diferentes. A razão da diferença de comportamento
está no facto de uma variedade contráctil ser uma variedade em que a
aplicação identidade é suavemente homotópica a uma aplicação constante
mas o facto de esta não ser em geral uma aplicação própria não nos
permite tirar partido desse facto para concluirmos alguma coisa sobre a
cohomologia com suporte compacto. São razões do mesmo tipo que
impedem aliás de aplicar no quadro da cohomologia com suporte
compacto outras construções que se utilizam no quadro da cohomologia
de de Rham usual.
IV.4.10. (Generalização de IV.3.10) Sejam I um espaço euclidiano e Q § I
uma variedade sem bordo de dimensão 7, suavemente orientada. Sendo Š,
igual a ‘ ou ‚, o corpo dos escalares que se está a considerar, existe então
uma aplicação linear ë À L-7 ÐQ Ñ Ä Š, definida por ë ÐÒ=ÓÑ œ 'Q =. Se
Q Á g, esta aplicação é sobrejectiva, em particular, L-7 ÐQ Ñ Á Ö!×.
7
Dem: O facto de cada = − H7
- ÐQ Ñ œ ^- ÐQ Ñ ser integrável é uma consequência de III.4.7. Por outro lado, se for Ò=Ó œ Ò=w Ó em L-7 ÐQ Ñ, existe
3 − H7"
ÐQ Ñ tal que =w = œ . 3 e então, pelo teorema de Stokes e uma
vez que `" ÐQ Ñ œ g,
w
( = ( = œ ( .3 œ (
Q
Q
Q
`" ÐQ Ñ
3Î`" ÐQ Ñ œ !,
donde 'Q = œ 'Q =w . Fica assim bem definida a aplicação ë À L-7 ÐQ Ñ Ä Š,
sendo trivial constatar que se trata de uma aplicação linear. Para verificarmos
que temos uma aplicação linear sobrejectiva, no caso em que Q Á g, basta
verificarmos que ela não é identicamente nula. Fixemos então B! − Q e uma
vizinhança compacta Z de B! em Q . Pelo teorema da partição da unidade
relativo à cobertura aberta de Q pelos abertos intÐZ Ñ e Q Ï ÖB! × (interior,
relativamente a Q ), podemos considerar uma aplicação suave :À Q Ä Ò!ß "Ó
tal que :ÐBÑ œ !, para cada B  Z e que :ÐB! Ñ œ " e, por :ÐBÑ ser estritamente positiva nalguma vizinhança aberta de B! , que tem portanto medida
7
não nula, vem 'Q :ÐBÑ . .Q ÐBÑ !. Sendo então = − H7
- ÐQ Ñ œ ^- ÐQ Ñ a
forma diferencial definida por =B œ :ÐBÑZ 96XB ÐQ Ñ , vem, para o correspondente Ò=Ó − L-7 ÐQ Ñ,
ë ÐÒ=ÓÑ œ ( = œ ( :ÐBÑ . .Q ÐBÑ !,
Q
o que termina a demonstração.
Q
§4. Cohomologia com suporte compacto
233
IV.4.11. Seja 8 !. Tem-se L-: Б8 Ñ œ Ö!×, para cada : Á 8, e L-8 Б8 Ñ é um
espaço vectorial de dimensão ", a aplicação linear ë À L-8 Б8 Ñ Ä Š sendo um
isomorfismo.
Dem: Vamos dividir a demonstração em várias partes:
a) Comecemos por notar que, uma vez que já sabemos que ë é uma aplicação
linear sobrejectiva, basta-nos, no caso : œ 8, mostrar uma das duas coisas:
ou que ë é uma aplicação linear injectiva, ou que L-8 Б8 Ñ tem dimensão ".
b) O caso em que 8 œ ! é trivial na medida em que ‘! é um espaço com um
único elemento, em particular compacto, pelo que já conhecemos a dimensão
de cada L-: Б! Ñ œ L : Б! Ñ. Podemos assim supor que 8 ".
c) Os casos em que : ! e : 8 são triviais e aquele em que : œ ! é uma
consequência de IV.4.9, visto que ‘8 é conexo e não compacto. Podemos
assim supor que " Ÿ : Ÿ 8.
d) Seja Ò=Ó − L-: Б8 Ñ, onde = − ^-: Б8 Ñ, um elemento arbitrário, se : Á 8,
ou, se : œ 8, um elemento tal que ë ÐÒ=ÓÑ œ !, isto é, tal que '‘8 = œ !.
Vamos mostrar que Ò=Ó œ !, isto é, que = − F-: Б8 Ñ, o que provará que
L-: Б8 Ñ œ Ö!×, para : Á 8, e que ë é uma aplicação linear injectiva, e terminará a demonstração.
e) O facto de a forma diferencial = ter suporte compacto implica a existência
de < ! tal que =B œ !, sempre que mBm <. O facto de se ter
L : Б8 Ñ œ Ö!×, por ‘8 ser contráctil, implica a existência de uma forma
diferencial, não obrigatoriamente de suporte compacto, ! − H:" Б8 Ñ tal
que = œ . !.
f) Seja
Y< œ ÖB − ‘8 ± mBm <×,
que é um aberto de ‘8 tal que .Ð!ÎY< Ñ œ =ÎY< œ !. Reparemos que, no caso
em que 8 #, Y< é conexo, por ser homeomorfo a W 8" ‚ Ó<ß _Ò, pelo
homeomorfismo W 8" ‚ Ó<ß _Ò Ä Y< definido por ÐBß >Ñ È >B, cujo
inverso está definido por C È ÐCÎmCmß mCmÑ.
g) Suponhamos que : œ ". A forma diferencial ! de grau ! é portanto uma
aplicação suave ‘8 Ä Š com derivada identicamente nula em Y< . No caso
em que 8 #, o facto de Y< ser conexo implica que ! toma um valor
constante - em Y< . Vamos ver que o mesmo acontece no caso em que 8 œ ",
com uma justificação um pouco mais completa. Ora, uma vez que Y< é a
união dos intervalos Ó_ß <Ò e Ó<ß _Ò, vemos que ! toma o valor
constante !Ð<Ñ no primeiro intervalo e o valor constante !Ð<Ñ no segundo
intervalo, pelo que o que temos que verificar é que !Ð<Ñ œ !Ð<Ñ e isso vai
ser uma consequência de que, pelo teorema de Stokes trivial, podemos
escrever
!œ( =œ(
‘
Ò<ß<Ó
.! œ (
!ÎÖ<ß<× œ !Ð<Ñ !Ð<Ñ.
`" ÐÒ<ß<ÓÑ
Provámos portanto, em qualquer caso, que ! toma um valor constante - em
234
Cap. IV. Introdução à cohomologia de de Rham
Y< e portanto que tem lugar uma aplicação suave " À ‘ Ä Š, identicamente
nula em Y< , e portanto de suporte compacto, definida por " Ð>Ñ œ !Ð>Ñ - ,
tendo-se assim " − H!- Ð‘Ñ e . " œ =, pelo que = − F-" БÑ, o que termina a
demonstração neste caso. Podemos assim, a partir de agora, supor que
8 : #.
h) Sejam 0 À W 8" Ä Y< e 1À Y< Ä W 8" as aplicações suaves definidas por
0 ÐBÑ œ #<B e 1ÐBÑ œ BÎmBm.57 Tem-se 1 ‰ 0 œ M. e 0 ‰ 1À Y< Ä Y< é
suavemente homotópica à identidade, pela homotopia suave
LÀ Ò!ß "Ó ‚ Y< Ä Y< definida por
LÐ>ß BÑ œ ˆ
#<Ð" >Ñ
>‰ B.
mBm
Daqui se deduz, para os correspondentes L : Ð0 ÑÀ L : ÐY< Ñ Ä L : ÐW 8" Ñ e
L : Ð1ÑÀ L : ÐW 8" Ñ Ä L : ÐY< Ñ, que L : Ð1Ñ ‰ L : Ð0 Ñ œ L : Ð0 ‰ 1Ñ é a
identidade de L : ÐY< Ñ e L : Ð0 Ñ ‰ L : Ð1Ñ œ L : Ð1 ‰ 0 Ñ é a identidade de
L : ÐW 8" Ñ, o que mostra que L : Ð0 ÑÀ L : ÐY< Ñ Ä L : ÐW 8" Ñ é um
isomorfismo,
tendo
como
isomorfismo
inverso
L : Ð1ÑÀ L : ÐW 8" Ñ Ä L : ÐY< Ñ.
i) Vamos mostrar a existência de " − H:# ÐY< Ñ tal que . " œ !ÎY< , ou seja,
uma vez que .Ð!ÎY< Ñ œ !, que se tem Ò!ÎY< Ó œ ! em L :" ÐY< Ñ. No caso em
que : 8, isso resulta de que L :" ÐY< Ñ é isomorfo a L :" ÐW 8" Ñ œ Ö!×.
Supondo então : œ 8, tendo em conta o isomorfismo referido em h), ficamos
reduzidos a provar que Ò0 ‡ Ð!ÎY< ÑÓ œ L :" Ð0 ÑÐÒ!ÎY< ÓÑ œ ! o que, tendo em
conta IV.3.12, é equivalente a provar que
(
W 8"
0 ‡ Ð!ÎY< Ñ œ !,
ou ainda, uma vez que 0 é um difeomorfismo, conservando as orientações,
de W 8" sobre W#< œ ÖB − ‘8 ± mBm œ #<×, considerado com a orientação
que lhe vem de ser bordo de índice " de F#< œ ÖB − ‘8 ± mBm Ÿ #<×, a
provar que
(
W#<
!ÎW#< œ !.
Mas isso é uma consequência do teorema de Stokes, visto que, por = ser nula
fora de F#< , podemos escrever
!œ(
‘8
=œ(
F#<
=œ(
F#<
.! œ (
W#<
!ÎW#< .
Ficou assim provada a existência pretendida da forma diferencial " .
j) Pelo teorema da partição da unidade, relativo à cobertura de ‘8 pelos
57Comparar
com a demonstração de IV.3.13.
§4. Cohomologia com suporte compacto
235
abertos Y< e ÖB − ‘8 ± mBm #<×, podemos considerar uma aplicação suave
:À ‘8 Ä Ò!ß "Ó, nula fora de um certo subconjunto G § Y< , fechado em ‘8 , e
s œ Ð"
s B ÑB−‘8 a forma
tal que :ÐBÑ œ ", para cada B com mBm #<. Seja "
diferencial suave de grau : # definida por
s B œ œ :ÐBÑ "B ,
"
!,
se B − Y<
,
se B Â Y<
s resultando de que ela vai ter restrições suaves aos abertos
a suavidade de "
8
Y< e ‘ Ï G , de união ‘8 , a segunda por ser identicamente nula. Sendo agora
s − H:" Б8 Ñ, tem-se ainda . !
s œ . ! œ = e, uma
!
s œ ! ."
s œ . ! .. "
8
s B œ "B , e
vez que, para cada B no aberto Y#< œ ÖB − ‘ ± mBm #<×, "
s
portanto também . " B œ . "B œ !B , concluímos que, para cada B − Y#< ,
8
!
sB œ !, o que mostra que !
s − H:"
- Б Ñ. Ficou assim provado que se tem
:
8
efectivamente = − F- Б Ñ, o que termina a demonstração.
O resultado anterior, caracterizando os espaços de cohomologia de de
Rham com suporte compacto de ‘8 , permite caracterizar também a das
variedades difeomorfas a ‘8 . Estas incluem, por exemplo, as bolas
abertas de um espaço euclidiano (cf. o exercício IV.21 adiante) mas, para
utilização futura, o exemplo seguinte vai ser especialmente importante.
IV.4.12. Sejam 8 " e, para cada " Ÿ 4 Ÿ 8, +4 ,4 em ‘. Tem-se então que o
aberto Q œ # Ó+4 ß ,4 Ò é difeomorfo a ‘8 e, em consequência, tem-se
8
4œ"
L-: ÐQ Ñ œ Ö!×, para cada : Á 8, e L-8 ÐQ Ñ é um espaço vectorial de
dimensão ", a aplicação linear ë À L-8 ÐQ Ñ Ä Š sendo um isomorfismo.
Dem: Começamos por notar que, para cada 4, existe um difeomorfismo
Ó"ß "Ò Ä Ó+4 ß ,4 Ò definido por
>È
+4 ,4
,4 +4
>
,
#
#
cujo inverso está definido por
=È
#= Ð+4 ,4 Ñ
.
,4 +4
Em seguida, reparamos que existe um difeomorfismo Ó"ß "Ò Ä ‘, definido
por
>È
cujo inverso está definido por
È" >#
>
,
236
Cap. IV. Introdução à cohomologia de de Rham
=È
=
.
È" =#
Por composição, concluímos a existência, para cada 4, de um difeomorfismo
:4 À Ó+4 ß ,4 Ò Ä ‘ e daqui se deduz a existência de um difeomorfismo :, de
Q œ # Ó+4 ß ,4 Ò sobre ‘8 , definido por
Ð>" ß á ß >8 Ñ È Ð:" Ð>" Ñß á ß :8 Ð>8 ÑÑ.
A existência deste difeomorfismo implica, por IV.4.6 e pelo resultado
precedente, que L-: ÐQ Ñ œ Ö!×, se : Á 8, e que L-8 ÐQ Ñ é um espaço
vectorial de dimensão " e o facto de ë ser um isomorfismo vem de que, por
IV.4.10, esta aplicação é uma aplicação linear sobrejectiva.
§5. Dualidade de Poincaré.
IV.5.1. Sejam I e J espaços vectoriais sobre o corpo Š e 0À I ‚ J Ä Š uma
aplicação bilinear. Vamos dizer que 0 define o primeiro espaço como dual do
segundo se a aplicação linear I È PÐJ à ŠÑ, que aplica B − I no elemento
C È 0ÐBß CÑ de PÐJ à ŠÑ, for um isomorfismo. Vamos dizer que 0 define o
segundo espaço como dual do primeiro, se a aplicação bilinear oposta,
s0À J ‚ I Ä Š, definida por s0ÐCß BÑ œ 0ÐBß CÑ definir o primeiro como dual
do segundo, isto é, se a aplicação linear J Ä PÐIà ŠÑ, que aplica C − J no
elemento B È 0ÐBß CÑ, for um isomorfismo. Quando as duas condições
anteriores forem verificadas, diremos simplesmente que 0 define cada um dos
espaços vectoriais como dual do outro.
IV.5.2. Lembremos que, se I é um espaço vectorial de dimensão finita 8, sobre
o corpo Š, então o dual PÐIà ŠÑ tem também dimensão 8 e que, mais
precisamente, se ÐB4 Ñ4−N é uma base de I , tem lugar uma base associada
Ð!4 Ñ4−N de PÐIà ŠÑ, definida por
!4 ÐB5 Ñ œ œ
",
!,
se 5 œ 4
.
se 5 Á 4
Para além disso, podemos mesmo afirmar que, se I tem dimensão infinita,
então PÐIà ŠÑ tem também dimensão infinita.
Dem: Basta repararmos que, se ÐB4 Ñ4−N é uma base de I , podemos definir as
aplicações lineares !4 − PÐIà ŠÑ, para cada 4 − N , pela mesma condição
que no caso da dimensão finita, e, embora estas não constituam uma base de
PÐIà ŠÑ, são, de qualquer modo, linearmente independentes, visto que, se
for ! +4 !4 œ !, aplicando ambos os membros a B5 , concluímos que
+5 œ !.
§5. Dualidade de Poincaré
237
IV.5.3. Como consequência do anterior, vemos que, se I e J são espaços
vectoriais sobre Š e se 0À I ‚ J Ä Š é uma aplicação bilinear definindo um
dos espaços como dual do outro, então, ou I e J têm a mesma dimensão
finita, ou ambos têm dimensão infinita.
IV.5.4. (Exemplos) a) Se I é um espaço vectorial sobre Š, tem lugar uma
aplicação bilinear PÐIà ŠÑ ‚ I Ä Š, definida por Ð-ß BÑ È -ÐBÑ, a qual
define o primeiro espaço como dual do segundo (trivialidade).
b) Se I é um espaço euclidiano, isto é, um espaço vectorial real, de
dimensão finita, munido de um produto interno, então o produto interno é
uma aplicação bilinear I ‚ I Ä ‘ que define cada um destes espaços
vectoriais como dual do outro (uma aplicação linear injectiva entre espaços
vectoriais com a mesma dimensão finita é um isomorfismo).
c) Analogamente, se I é um espaço hermitiano, isto é, um espaço vectorial
complexo, de dimensão finita, munido de um produto interno complexo,
então, notando I o espaço vectorial conjugado de I (cf. II.1.7), o produto
interno é uma aplicação bilinear I ‚ I Ä ‚ que define cada um destes
espaços vectoriais como dual do outro.
IV.5.5. Sejam I e J espaços vectoriais de dimensão finita e 0À I ‚ J Ä Š uma
aplicação bilinear, definindo um dos espaços I e J como dual do outro.
Tem-se então que 0 também define o outro espaço como dual deste.
Dem: Suponhamos que 0 define o primeiro espaço como dual do segundo.
Suponhamos que C − J , verifica C Á !. Escolhendo uma base de J tendo C
como um dos vectores, podemos construir uma aplicação linear ! − PÐJ à ŠÑ
tal que !ÐCÑ Á !. Por definição, vai existir B − I , cuja imagem pelo
isomorfismo I Ä PÐJ à ŠÑ seja !, tendo-se assim, em particular, 0ÐBß CÑ œ
!ÐCÑ Á !. Resulta daqui que a imagem de C pela aplicação linear
J Ä PÐIà ŠÑ, associada a 0, não é !. Ficou assim provado que a aplicação
linear J Ä PÐIà ŠÑß associada a 0, é injectiva pelo que, uma vez que, tendo
em conta IV.5.3, estes dois espaços têm a mesma dimensão finita, esta
aplicação linear é um isomorfismo, ou seja, 0 define o segundo espaço como
dual do primeiro. A recíproca é de demonstração análoga, ou reduz-se ao
caso já visto, por consideração da aplicação bilinear oposta s0À J ‚ I Ä Š.
O resultado anterior não se estende, de modo nenhum, à dimensão
infinita. De facto, podemos mesmo afirmar o seguinte:
IV.5.6. Sejam I e J espaços vectoriais sobre Š e 0À I ‚ J Ä Š uma aplicação
bilinear, definindo cada um dos espaços como dual do outro. Tem-se então
que I e J têm dimensão finita.
Dem: Tendo em conta IV.5.3, basta mostrarmos que J tem dimensão finita.
Suponhamos que isso não acontecia e seja ÐC4 Ñ4−N uma base de J , com N
conjunto infinito de índices. Consideremos, para cada 4 − N ß a aplicação
linear "4 − PÐJ à ŠÑ definida por
238
Cap. IV. Introdução à cohomologia de de Rham
"4 ÐC5 Ñ œ œ
",
!,
se 5 œ 4
.
se 5 Á 4
Trata-se de elementos linearmente independentes de PÐJ à ŠÑ, visto que, se
fosse ! ,4 "4 œ !, obtínhamos, aplicando ambos os membros a C5 , ,5 œ !.
Seja, para cada 4, B4 − I o elemento correspondente a "4 pelo inverso do
isomorfismo I Ä PÐJ à ŠÑ, associado a 0, ou seja, o definido pela condição
de se ter
0ÐB4 ß C5 Ñ œ œ
",
!,
se 5 œ 4
.
se 5 Á 4
Reparemos que, para cada C − J , vai ser finito o conjunto dos 4 − N tais que
0ÐB4 ß CÑ Á !, visto que, escrevendo C œ ! ,5 C5 , com a família dos ,5 essencialmente finita, a fórmula anterior implica que 0ÐB4 ß CÑ œ ,4 . Uma vez que
ÐB4 Ñ4−N é uma família linearmente independente de vectores de I , podemos
prolongá-la numa base de I e construir, a partir daí, uma aplicação linear
! − PÐIà ŠÑ tal que !ÐB4 Ñ œ ", para todo o 4. Seja C − J o elemento correspondente a ! pelo inverso do isomorfismo J Ä PÐIà ŠÑ associado a 0.
Tem-se assim, para cada 4, 0ÐB4 ß CÑ œ !ÐB4 Ñ œ ", o que é um absurdo, tendo
em conta a conclusão anterior de que devia ser finito o conjunto dos 4 com
esta propriedade.
IV.5.7. Seja Q uma variedade sem bordo, de dimensão 7, suavemente
orientada. Para cada ! Ÿ : Ÿ 7, tem então lugar uma aplicação bilinear
0: À L : ÐQ Ñ ‚ L-7: ÐQ Ñ Ä Š,
definida por
0: ÐÒ=Óß Ò3ÓÑ œ (
= • 3,
Q
a que daremos o nome de aplicação de Poincaré. Mais geralmente,
definimos ainda as aplicações bilineares 0: À L : ÐQ Ñ ‚ L-7: ÐQ Ñ Ä Š, para
: ! e para : 7 como sendo as únicas aplicações bilineares possíveis
(ambos os factores do domínio são Ö!×).
Dem: O resultado ficará demonstrado se verificarmos a existência de
aplicações bilineares (: À L : ÐQ Ñ ‚ L-7: ÐQ Ñ Ä L-7 ÐQ Ñ, definidas por
(: ÐÒ=Óß Ò3ÓÑ œ Ò= • 3Ó, visto que então as aplicações do enunciado não são
mais do que as compostas destas com a aplicação linear ë À L-7 ÐQ Ñ Ä Š,
referida em IV.4.10. Em primeiro lugar, sendo = − ^ : ÐQ Ñ e 3 − ^-7: ÐQ Ñ,
podemos considerar um compacto O § Q fora do qual 3 se anule e então
= • 3 anula-se fora de O e verifica .Ð= • 3Ñ œ . = • 3 Ð"Ñ: = • . 3 œ !,
o que mostra que = • 3 − ^-7 ÐQ Ñ. Sendo agora Ò=Ó œ Ò=w Ó, em L : ÐQ Ñ, e
§5. Dualidade de Poincaré
239
Ò3Ó œ Ò3w Ó, em L 7: ÐQ Ñ, tem-se =w œ = . ! e 3w œ 3 . " , com
! − H:" ÐQ Ñ e " − H-7:" ÐQ Ñ, e então, sendo O w § Q um compacto
fora do qual " , e portanto . " , se anule,
=w • 3w œ = • 3 . ! • Ð3 . " Ñ = • . " œ
œ = • 3 .Ð! • Ð3 . " Ñ Ð"Ñ: = • " Ñ,
com a forma diferencial ! • Ð3 . " Ñ Ð"Ñ: = • " , de grau 7 ", a
anular-se fora do compacto O O w § Q , o que mostra que
Ò= • 3Ó œ Ò=w • 3w Ó em L-7 ÐQ Ñ. Verificámos assim que estão bem definidas
as aplicações (: À L : ÐQ Ñ ‚ L-7: ÐQ Ñ Ä L-7 ÐQ Ñ, sendo imediato verificar
que elas são bilineares.
O teorema de dualidade de Poincaré, objectivo central desta secção, afirma-nos que, se Q é uma variedade sem bordo, de dimensão 7,
suavemente orientada, então, para cada :, 0: À L : ÐQ Ñ ‚ L-7: ÐQ Ñ Ä Š
define o primeiro espaço como dual do segundo. Uma vez que a
demonstração deste teorema vai ser longa, utilizando vários resultados
auxiliares, vamos apresentar uma definição auxiliar, a de variedade de
Poincaré, que perderá toda a utilidade no fim da secção, na medida em
que o teorema de Poincaré afirmará simplesmente que toda a variedade
sem bordo, de dimensão 7, suavemente orientada, é uma variedade de
Poincaré.
IV.5.8. Vamos chamar variedade de Poincaré de dimensão 7 a uma variedade
Q sem bordo, de dimensão 7, suavemente orientada, tal que, para cada :, a
aplicação de Poincaré 0: À L : ÐQ Ñ ‚ L-7: ÐQ Ñ Ä Š defina o primeiro
espaço como dual do segundo. Repare-se, desde já, que esta exigência é
trivial para : ! e : 7, na medida em que ambos os factores do domínio
são então iguais a Ö!×.
IV.5.9. São variedades de Poincaré de dimensão 7:
a) A variedade Q œ g;
b) Para cada 7 !, a variedade Q œ ‘7 e a variedade Q œ # Ó+3 ß ,3 Ò,
7
3œ"
onde, para cada " Ÿ 3 Ÿ 7, +3 ,3 são números reais, em ambos os casos
com a orientação canónica.
Dem: A alínea a) é trivial, na medida em que se tem L : ÐQ Ñ œ Ö!× e
L-7: ÐQ Ñ œ Ö!×, para cada :. Provemos então b). Uma vez que Q é
convexa em ‘7 e não vazia, e portanto suavemente contráctil, sabemos, por
IV.1.13, que se tem L : ÐQ Ñ œ Ö!× para cada : Á ! e que L ! ÐQ Ñ é um
espaço vectorial de dimensão ". Por outro lado, por IV.4.11 e IV.4.12,
sabemos que se tem L-7: ÐQ Ñ œ Ö!×, para : Á !, e que L-7 ÐQ Ñ é um
espaço vectorial de dimensão ", com ë À L-7 ÐQ Ñ Ä Š isomorfismo. A única
verificação não trivial que temos que fazer é portanto a de que a aplicação de
Poincaré 0! À L ! ÐQ Ñ ‚ L-7 ÐQ Ñ Ä Š define o primeiro espaço como dual do
240
Cap. IV. Introdução à cohomologia de de Rham
segundo e, uma vez que os dois factores do domínio têm dimensão ", basta
provarmos que a aplicação linear associada, de L ! ÐQ Ñ para PÐL-7 ÐQ Ñà ŠÑ,
não é identicamente nula. Ora, isso resulta de que, sendo 0 − ^ ! ÐQ Ñ a
aplicação de Q para Š identicamente igual a " e Ò=Ó − L-7 ÐQ Ñ um elemento
não nulo, tem-se
0! ÐÒ0 Óß Ò=ÓÑ œ ë ÐÒ=ÓÑ Á !.
IV.5.10. Se trocarmos a orientação em todos os pontos de uma variedade de
Poincaré de dimensão 7, obtemos ainda uma variedade de Poincaré de
dimensão 7.
Dem: Basta atendermos a que as aplicações de Poincaré vêm multiplicadas
por " e a que, multiplicando por " um isomorfismo, obtém-se ainda um
isomorfismo.
IV.5.11. Sejam Q e Q w variedades sem bordo, de dimensão 7, suavemente
orientadas e 0 À Q Ä Q w um difeomorfismo que conserve (resp. inverta) as
orientações. Se Q é uma variedade de Poincaré de dimensão 7, então o
mesmo acontece a Q w .
Dem: Tendo em conta o resultado precedente, podemos estudar apenas o
caso em que 0 conserva as orientações. Considerando os isomorfismos associados L : Ð0 ÑÀ L : ÐQ w Ñ Ä L : ÐQ Ñ e L-7: Ð0 ÑÀ L-7: ÐQ w Ñ Ä L-7: ÐQ Ñ,
assim como o isomorfismo dual
L-7: Ð0 ч À PÐL-7: ÐQ Ñà ŠÑ Ä PÐL-7: ÐQ w Ñà ŠÑ,
é então comutativo o diagrama
0:
L : ÐQ w Ñ ‚ L-7: ÐQ w Ñ qp
0 Ñ‚L-: Ð0 Ñ Æ L : Ð0 Ñ‚L-7: Ð0 Ñ
L : ÐQ Ñ ‚ L-7: ÐQ Ñ
Id
0:
Š
Æ Id ,
Š
qp
visto que, para cada ÐÒ=Óß Ò3ÓÑ − L : ÐQ w Ñ ‚ L-7: ÐQ w Ñ, tem-se
0: ÐL : Ð0 Ñ ‚ L-7: Ð0 ÑÐÒ=Óß Ò3ÓÑÑ œ ( Ð0 ‡ =Ñ • Ð0 ‡ 3Ñ œ ( 0 ‡ Ð= • 3Ñ œ
œ(
Q
Q
:
= • 3 œ 0 ÐÒ=Óß Ò3ÓÑ.
Qw
Daqui se deduz que a aplicação linear L : ÐQ w Ñ Ä PÐL-7: ÐQ w Ñà ŠÑ
associada a 0: é a composta dos isomorfismos
L : Ð0 Ñ
L : ÐQ w Ñ qp L : ÐQ Ñ qp PÐL-7: ÐQ Ñà ŠÑ
L-7: Ð0 ч
qp
PÐL-7: ÐQ w Ñà ŠÑ ,
o do meio por a variedade Q ser de Poincaré, o que prova que aquela aplicação linear é um isomorfismo, e portanto que a variedade Q w também é de
Poincaré.
§5. Dualidade de Poincaré
241
IV.5.12. Seja Q uma variedade sem bordo, de dimensão 7, suavemente
orientada e tal que exista uma família ÐY4 Ñ4−N de abertos de Q , disjuntos
dois a dois e de união Q , tal que cada Y4 , com a orientação correspondente,
seja uma variedade de Poincaré de dimensão 7. Tem-se então que Q é uma
variedade de Poincaré de dimensão 7.
Dem: Sendo +4 À Y4 Ä Q as inclusões, sabemos, por IV.2.6, que L : ÐQ Ñ é
um produto dos espaços vectoriais L : ÐY4 Ñ definido pelas projecções
L : Ð+4 ÑÀ L : ÐQ Ñ Ä L : ÐY4 Ñ. Por outro lado, tendo em conta IV.4.8, sabemos
que L-7: ÐQ Ñ é uma soma dos espaços L-7: ÐY4 Ñ com as injecções
54 À L-7: ÐY4 Ñ Ä L-7: ÐQ Ñ definidas por 54 ÐÒ=ÓÑ œ Ò=ÏQ Ó, onde =ÏQ é a
extensão a Q de = − H7:
ÐY4 Ñ, que se anula fora de Y4 (cf. IV.4.7), pelo
que, por IV.2.18, PÐL-7: ÐQ Ñà ŠÑ é um produto dos PÐL-7: ÐY4 Ñà ŠÑ com
as projecções
54‡ À PÐL-7: ÐQ Ñà ŠÑ Ä PÐL-7: ÐY4 Ñà ŠÑ.
Sendo, para cada 4, F4 À L : ÐY4 Ñ Ä PÐL-7: ÐY4 Ñà ŠÑ o isomorfismo
associado à aplicação bilinear 0: À L : ÐY4 Ñ ‚ L-7: ÐY4 Ñ Ä Š e sendo, do
mesmo modo FÀ L : ÐQ Ñ Ä PÐL-7: ÐQ Ñà ŠÑ a aplicação linear associada à
aplicação bilinear 0: À L : ÐQ Ñ ‚ L-7: ÐQ Ñ Ä Š, o facto de se ter, para cada
Ò=Ó − L : ÐQ Ñ e Ò3Ó − L-7: ÐY4 Ñ,
0: ÐL : Ð+4 ÑÐÒ=ÓÑß Ò3ÓÑ œ ( =ÎY4 • 3 œ ( = • 3ÏQ œ 0: ÐÒ=Óß 54 ÐÒ3ÓÑÑ,
Y4
Q
igualdade que também pode ser escrita na forma
F4 ÐL : Ð+4 ÑÐÒ=ÓÑÑÐÒ3ÓÑ œ FÐÒ=ÓÑÐ54 ÐÒ3ÓÑ œ 54‡ ÐFÐÒ=ÓÑÑÐÒ3ÓÑ,
implica que F4 ‰ L : Ð+4 Ñ œ 54‡ ‰ F.58 Estamos agora em condições de provar
que F é um isomorfismo, ou seja, que Q é uma variedade de Poincaré, como
queremos. Em primeiro lugar, se Ò=Ó − L : ÐQ Ñ é tal que FÐÒ=ÓÑ œ !, vem,
para cada 4, F4 ÐL : Ð+4 ÑÐÒ=ÓÑÑ œ 54‡ ÐFÐÒ=ÓÑÑ œ !, donde L : Ð+4 ÑÐÒ=ÓÑ œ !,
pelo que o facto de os L : Ð+4 Ñ definirem L : ÐQ Ñ como produto dos L : ÐY4 Ñ
implica que Ò=Ó œ !. Por outro lado, dado ! − PÐL-7: ÐQ Ñà ŠÑ arbitrário,
para cada 4 a sobrejectividade de F4 implica a existência de Ò=4 Ó − L : ÐY4 Ñ
tal que F4 ÐÒ=4 ÓÑ œ 54‡ Ð!Ñ e, sendo Ò=Ó − L : ÐQ Ñ o definido pela condição de
se ter L : Ð+4 ÑÐÒ=ÓÑ œ Ò=4 Ó, vemos que, para cada 4,
54‡ ÐFÐÒ=ÓÑÑ œ F4 ÐL : Ð+4 ÑÐÒ=ÓÑÑ œ F4 ÐÒ=4 ÓÑ œ 54‡ Ð!Ñ,
58Esta
igualdade exprime que a aplicação linear F é o produto das aplicações lineares F4 ,
no sentido do exercício IV.9 adiante, pelo que, se tivéssemos levado mais longe o estudo
geral da noção de produto, o resto da demonstração resumir-se-ia a aplicar um resultado
geral que garante que um produto de isomorfismos é um isomorfismo.
242
Cap. IV. Introdução à cohomologia de de Rham
o que, pelo facto de os 54‡ definirem PÐL-7: ÐQ Ñà ŠÑ como produto dos
PÐL-7: ÐY4 Ñà ŠÑ, implica que FÐÒ=ÓÑ œ !.
IV.5.13. (Corolário) Se Q é uma variedade orientada de dimensão !, então Q é
uma variedade de Poincaré.
Dem: Basta atender a que Q é a união disjunta dos seus subconjuntos
unitários, que são abertos e difeomorfos a ‘! .
O nosso próximo passo vai ser a prova que, se a variedade Q é união de
dois abertos Y e Z que sejam variedades de Poincaré e tais que Y Z
também seja uma variedade de Poincaré, então Q é uma variedade de
Poincaré. Para chegar aí, vamos precisar de um lema algébrico, o lema
dos cinco, de utilização muito frequente em Topologia Algébrica, e de
uma versão da sucessão exacta de Mayer-Vietoris, para a cohomologia de
de Rham com suporte compacto, que teremos ocasião de voltar a aplicar
na próxima secção.
IV.5.14. (Lema dos cinco) Consideremos o seguinte diagrama comutativo de
espaços vectoriais e aplicações lineares:
-"
I" qp
:" Æ :"
J"
."
qp
-#
I# qp
:# Æ :#
J#
.#
qp
-$
I$ qp
:$ Æ :$
J$
.$
qp
-%
I% qp
:% Æ :%
J%
.%
qp
I&
Æ :& .
:&
J&
Suponhamos que as duas linhas são sucessões exactas e que as aplicações
lineares :" , :# , :% e :& são isomorfismos. Tem-se então que :$ é também
um isomorfismo.59
Dem: Vamos começar por provar que a aplicação linear :$ é injectiva. Seja
então B$ − I$ tal que :$ ÐB$ Ñ œ !. Tem-se então
:% Ð-$ ÐB$ ÑÑ œ .$ Ð:$ ÐB$ ÑÑ œ !,
pelo que, por :% ser uma aplicação linear injectiva, -$ ÐB$ Ñ œ !; o facto de a
primeira linha ser exacta em I$ garante a existência de B# − I# tal que
-# ÐB# Ñ œ B$ e tem-se então
.# Ð:# ÐB# ÑÑ œ :$ Ð-# ÐB# ÑÑ œ :$ ÐB$ Ñ œ !,
pelo que o facto de a segunda linha ser exacta em J# garante a existência de
C" − J" tal que ." ÐC" Ñ œ :# ÐB# Ñ; uma vez que a aplicação linear :" é sobre59Este
resultado tem uma característica pouco comum em Matemática: As hipóteses que
fazemos podiam claramente ser enfraquecidas sem ter que mudar nada à demonstração
(por exemplo, bastaria pedir que a aplicação linear :" fosse sobrejectiva e a aplicação
linear :& fosse injectiva. A razão por que se procede deste modo é que o enunciado
apresentado é mais simples de ser fixado e as hipóteses feitas são as que se verificam nas
aplicações típicas deste lema em Topologia Algébrica.
§5. Dualidade de Poincaré
243
jectiva, existe B" − I" tal que :" ÐB" Ñ œ C" e vemos que
:# Ð-" ÐB" ÑÑ œ ." Ð:" ÐB" ÑÑ œ ." ÐC" Ñ œ :# ÐB# Ñ,
donde, por :# ser injectiva, -" ÐB" Ñ œ B# , e portanto
B$ œ -# ÐB# Ñ œ -# Ð-" ÐB" ÑÑ œ !,
o que prova a injectividade de :$ . Vamos provar agora que a aplicação linear
:$ é sobrejectiva. Seja então C$ − J$ arbitrário. O facto de a aplicação linear
:% ser sobrejectiva garante a existência de B% − I% tal que :% ÐB% Ñ œ .$ ÐC$ Ñ.
Vem então
:& Ð-% ÐB% ÑÑ œ .% Ð:% ÐB% ÑÑ œ .% Ð.$ ÐC$ ÑÑ œ !,
donde, por :& ser injectiva, -% ÐB% Ñ œ ! e a exactidão da primeira linha em
I% implica a existência de B$ − I$ tal que -$ ÐB$ Ñ œ B% ; vemos agora que
.$ ÐC$ :$ ÐB$ ÑÑ œ .$ ÐC$ Ñ :% Ð-$ ÐB$ ÑÑ œ .$ ÐC$ Ñ :% ÐB% Ñ œ !,
pelo que o facto de a primeira linha ser exacta em J$ implica a existência de
C# − J# tal que C$ :$ ÐB$ Ñ œ .# ÐC# Ñ; o facto de a aplicação linear :# ser
sobrejectiva permite fixar B# − I# tal que :# ÐB# Ñ œ C# e obtemos agora
:$ ÐB$ -# ÐB# ÑÑ œ :$ ÐB$ Ñ .# Ð:# ÐB# ÑÑ œ :$ ÐB$ Ñ .# ÐC# Ñ œ C$ ,
o que termina a prova da sobrejectividade de :$ .
IV.5.15. Sejam Q § I uma variedade e Y e Z abertos de Q tais que
Y Z œ Q . Notemos Hñ- ÐY Ñ ‚ H-ñ ÐZ Ñ o complexo de cocadeias produto de
Hñ- ÐY Ñ e H-ñ ÐZ Ñ construído a partir dos produtos cartesianos
H:- ÐY Ñ ‚ H-: ÐZ Ñ. Tem então lugar uma sucessão exacta curta de complexos
de cocadeias
.ñ
-ñ
! qp Hñ- ÐY Z Ñ qp H-ñ ÐY Ñ ‚ H-ñ ÐZ Ñ qp H-ñ ÐQ Ñ qp !,
em que as aplicações lineares
.: À H-: ÐY Z Ñ Ä H-: ÐY Ñ ‚ H-: ÐZ Ñ
-: À H-: ÐY Ñ ‚ H-: ÐZ Ñ Ä H-: ÐQ Ñ
estão definidas por .: Ð3Ñ œ Ð3ÏY ß 3ÏZ Ñ e -: Ð!ß " Ñ œ !ÏQ "ÏQ (notações
de IV.4.7).
Dem: Do facto de, para cada Ð!ß " Ñ − H:- ÐY Ñ ‚ H-: ÐZ Ñ, se ter .Ð!ß " Ñ œ
Ð. !ß . " Ñ deduz-se imediatamente que .ñ e -ñ são efectivamente morfismos
de complexos de cocadeias. O facto de cada aplicação linear .: ser injectiva
resulta de que já o é, por exemplo, a aplicação H:- ÐY Z Ñ Ä H-: ÐZ Ñ,
definida por .: Ð3Ñ œ 3ÏZ . O facto de se ter Ð3ÏY ÑÏQ œ 3ÏQ e
Ð3ÏZ ÑÏQ œ 3ÏQ implica que -: ‰ .: œ !, e portanto que a imagem de .: está
contida no núcleo de -: . Suponhamos, reciprocamente, que
244
Cap. IV. Introdução à cohomologia de de Rham
Ð!ß " Ñ − H:- ÐY Ñ ‚ H-: ÐZ Ñ pertence ao núcleo de -: , ou seja, que
!ÏQ "ÏQ œ !, e sejam O § Y e O w § Z compactos tais que ! se anule
em Y Ï O e " se anule em Z Ï O w ; da igualdade !ÏQ "ÏQ œ ! deduzimos
que se tem mesmo !B œ !, para cada B − Y Ï ÐO O w Ñ e "B œ !, para cada
B − Z Ï ÐO O w Ñ, e que "B œ !B , para cada B − Y Z , o que nos
permite definir 3 − H:- ÐY Z Ñ por 3B œ !B œ "B (3 anula-se fora do
compacto O O w § Y Z Ñ, para o qual se tem Ð!ß " Ñ œ .: Ð3Ñ. Resta-nos
provar que -: À H-: ÐY Ñ ‚ H-: ÐZ Ñ Ä H-: ÐQ Ñ é uma aplicação linear
sobrejectiva. Pelo teorema da partição da unidade, podemos considerar
aplicações suaves :ß <À Q Ä Ò!ß "Ó, a primeira nula fora do subconjunto
E § Y , fechado em Q , e a segunda nula fora do subconjunto F § Z ,
fechado em Q , e tais que, para cada B − Q , :ÐBÑ <ÐBÑ œ ". Dado
3 − H:- ÐQ Ñ, e sendo O § Q um compacto fora do qual 3 se anule, podemos
tomar ! − H:- ÐY Ñ e " − H-: ÐZ Ñ, definidos por !B œ :ÐBÑ 3B e "B œ <ÐBÑ 3B
(! anula-se fora do compacto O E § Y e " anula-se fora do compacto
O F § Z ), sendo imediato que as extensões !ÏQ e "ÏQ estão definidas
ainda por B È :ÐBÑ 3B e B È <ÐBÑ 3B , respectivamente, de onde se deduz
que -: Ð!ß " Ñ œ 3.
IV.5.16. Nas hipóteses de IV.5.15, à sucessão exacta curta de complexos de
cocadeias aí referida fica associada a correspondente sucessão exacta de
cohomologia, indefinidamente prolongável nos dois sentidos, de que
destacamos a seguinte “secção representativa”
` :"
L : Ð.ñ Ñ
L : Ð-ñ Ñ
`:
L-:" ÐQ Ñ qqp L-: ÐY Z Ñ qqp L : ÐH-ñ ÐY Ñ ‚ H-ñ ÐZ ÑÑ qqp L-: ÐQ Ñ qqp L-:" ÐY Z Ñ,
a que se dá o nome de sucessão exacta de Mayer-Vietoris com suporte compacto associada aos abertos Y e Z de Q (repare-se que utilizámos a “secção
representativa” da sucessão exacta de cohomologia referida na nota
IV.3.360). Lembremos, a propósito, que, de acordo com IV.2.5, o espaço de
cohomologia L : ÐH-ñ ÐY Ñ ‚ H-ñ ÐZ ÑÑ é um produto de L-: ÐY Ñ e L-: ÐZ Ñ, com
as projecções naturalmente definidas, e portanto é isomorfo ao produto
cartesiano L-: ÐY Ñ ‚ L-: ÐZ Ñ, pelo isomorfismo que associa ÐÒ!Óß Ò" ÓÑ a
ÒÐ!ß " ÑÓ.
IV.5.17. (Lema) Sejam 0" À I" ‚ J" Ä Š e 0# À I# ‚ J# Ä Š duas aplicações
lineares, cada uma das quais definindo o primeiro espaço como dual do
segundo. Seja I um produto de I" e I# , com as projecções 14 À I Ä I4 , e J
um produto de J" e J# , com as projecções 1
s4 À J Ä J4 . Tem então lugar uma
aplicação bilinear 0À I ‚ J Ä Š, definida por
0ÐBß CÑ œ 0" Ð1" ÐBÑß 1
s" ÐCÑÑ 0# Ð1# ÐBÑß 1
s# ÐCÑÑ,
a qual define também o primeiro espaço como dual do segundo.
Dem: Sejam F4 À I4 Ä PÐJ4 à ŠÑ as aplicações lineares associadas às aplica60Por
razões exclusivamente tipográficas…
§5. Dualidade de Poincaré
245
ções bilineares 04 , que, por hipótese, são isomorfismos e seja
FÀ I Ä PÐJ à ŠÑ a aplicação linear associada à aplicação bilinear 0, que
temos de demonstrar ser também um isomorfismo. Sejam s+4 À J4 Ä J as
injecções associadas à apresentação de J como produto dos J4 . Sendo B − I
tal que FÐBÑ œ !, tem-se, para cada 4 œ "ß # e cada C4 − J4 ,
! œ FÐBÑÐs+4 ÐC4 ÑÑ œ 0ÐBßs+4 ÐC4 ÑÑ œ
œ 0" Ð1" ÐBÑß 1
s" Ðs+4 ÐC4 ÑÑ 0# Ð1# ÐBÑß 1
s# Ðs+4 ÐC4 ÑÑ œ
œ 04 Ð14 ÐBÑß C4 Ñ œ F4 Ð14 ÐBÑÑÐC4 Ñ,
donde F4 Ð14 ÐBÑÑ œ ! e 14 ÐBÑ œ !, pelo que, por termos um produto, B œ !.
Para provarmos a sobrejectividade de F, consideremos " − PÐJ à ŠÑ
arbitrário. Para cada 4 œ "ß #, podemos considerar o elemento
" ‰s+4 − PÐJ4 à ŠÑ, e portanto também B4 − I tal que F4 ÐB4 Ñ œ " ‰s+4 . Seja
B − I tal que 14 ÐBÑ œ B4 . Para cada C − J , vem então
FÐBÑÐCÑ œ 0ÐBß CÑ œ 0" ÐB" ß 1
s" ÐCÑÑ 0# ÐB# ß 1
s# ÐCÑÑ œ
œ " ‰s+" Ð1
s" ÐCÑÑ " ‰s+# Ð1
s# ÐCÑÑ œ " ÐCÑ,
o que mostra que FÐBÑ œ " .
IV.5.18. Sejam I , J e K espaços vectoriais sobre Š e -À I Ä J e .À J Ä K
-
.
aplicações lineares tais que venha exacta a sucessão I qp J qp K . Sendo
Šw ¨ Š, é então também exacta a sucessão
.‡
-‡
PÐKà Šw Ñ qp PÐJ à Šw Ñ qp PÐIà Šw Ñ.61
Dem: O facto de se ter . ‰ - œ ! implica trivialmente que -‡ ‰ .‡ œ !, e
portanto que a imagem de .‡ está contida no núcleo de -‡ . Suponhamos,
reciprocamente, que ! − PÐJ à Šw Ñ pertence ao núcleo de -‡ , ou seja que
s À .ÐJ Ñ Ä Šw por
! ‰ - œ !. Pode-se então definir uma aplicação linear "
s Ð.ÐCÑÑ œ !ÐCÑ, visto que, se .ÐCÑ œ .ÐCw Ñ, vinha C Cw − kerÐ.Ñ œ -ÐIÑ,
"
ou seja, C Cw œ -ÐBÑ, e então !ÐCÑ !ÐCw Ñ œ !Ð-ÐBÑÑ œ !. Seja
1À K Ä .ÐJ Ñ uma aplicação linear tal que 1ÐDÑ œ D , para cada D − .ÐJ Ñ
(por exemplo, a projecção ortogonal sobre .ÐJ Ñ, associada a um produto
interno que se escolha em K , ou, alternativamente, uma aplicação linear
escolhida a partir da escolha de uma base de .ÐJ Ñ que se prolonga numa
61A
Álgebra Homológica é a parte da matemática que estuda, do ponto de vista geral os
complexos de cocadeias e os espaços de cohomologia associados, assim como outras
questões relacionadas. Nela se inserem naturalmente o estudo das sucessões exactas e
resultados como o lema da serpente ou o lema dos cinco. Em aplicações mais profundas
da Álgebra Homológica à Topologia Algébrica, revela-se necessário trabalhar, mais
geralmente, com módulos sobre um anel, em vez dos espaços vectoriais. Nesse quadro, o
resultado que acabamos de enunciar é, em geral, falso.
246
Cap. IV. Introdução à cohomologia de de Rham
base de K )62. Podemos então considerar " − PÐKà Šw Ñ, definida por
s ‰ 1, tendo-se, para cada C − J ,
"œ"
s Ð1Ð.ÐCÑÑÑ œ "
s Ð.ÐCÑÑ œ !ÐCÑ,
" Ð.ÐCÑÑ œ "
portanto ! œ .‡ Ð" Ñ.
IV.5.19. Sejam Q uma variedade sem bordo, de dimensão 7, suavemente orientada e Y e Z abertos de Q tais que Y Z œ Q . Suponhamos que Y , Z e
Y Z , com as orientações correspondentes, são variedades de Poincaré.
Tem-se então que Q é uma variedade de Poincaré.
Dem: Consideremos as secções das sucessões exactas de Mayer-Vietoris,
ordinária e de suporte compacto, associadas à cobertura de Q pelos abertos
Y e Z , representadas no diagrama 1 da página seguinte, a segunda das quais
está escrita da direita para a esquerda (cf. IV.3.5 e IV.5.16).
62É
aqui que aparece o problema, referido na nota anterior, se estivéssemos a trabalhar no
quadro dos módulos sobre um anel.
L :" ÐHñ ÐY Ñ ‚ Hñ ÐZ ÑÑ
L 7:" ÐHñ- ÐY Ñ ‚ Hñ- ÐZ ÑÑ
L :" Ð.ñ Ñ
qp
L 7:" Ð.ñ Ñ
oq
` :"
L : Ð-ñ Ñ
` 7:
L 7: Ð-ñ Ñ
L :" ÐY Z Ñ qp L : ÐQ Ñ
L-7:" ÐY Z Ñ oq L-7: ÐQ Ñ
L : ÐHñ ÐY Ñ ‚ Hñ ÐZ ÑÑ
qp
oq
L 7: ÐHñ- ÐY Ñ ‚ H-ñ ÐZ ÑÑ
L : Ð.ñ Ñ
qp
L 7: Ð.ñ Ñ
oq
L : ÐY Z Ñ
L-7: ÐY Z Ñ
Diagrama 1
L :" ÐHñ ÐY Ñ ‚ Hñ ÐZ ÑÑ
Æ Fs:"
L :" Ð.ñ Ñ
qp
L :" ÐY Z Ñ
Æ F:"
Ð"Ñ: ` :"
qp
L : ÐQ Ñ
Æ F:
L : Ð-ñ Ñ
qp
L : ÐHñ ÐY Ñ ‚ Hñ ÐZ ÑÑ
Æ Fs:
L : Ð.ñ Ñ
qp
L : ÐY Z Ñ
Æ F:
PÐL 7:" ÐHñ- ÐY Ñ ‚ Hñ- ÐZ ÑÑà ŠÑ qp PÐL-7:" ÐY Z Ñà ŠÑ qp PÐL-7: ÐQ Ñà ŠÑ qp PÐL 7: ÐHñ- ÐY Ñ ‚ H-ñ ÐZ ÑÑà ŠÑ qp PÐL-7: ÐY Z Ñà ŠÑ
Diagrama 2
248
Cap. IV. Introdução à cohomologia de de Rham
§5. Dualidade de Poincaré
249
Para cada par de espaços vectoriais na mesma coluna, temos uma aplicação
bilinear, do respectivo produto cartesiano para Š, nomeadamente a aplicação
de Poincaré, que notaremos 0, no caso da segunda, terceira e quinta colunas,
e a aplicação, que notaremos s0, construída a partir das aplicações de Poincaré
de Y e de Z , no caso da primeira e da quarta (cf. IV.5.17). Reparemos agora
que as referidas aplicações bilineares verificam as seguintes condições:
a) Para cada ÒÐ=ß 7 ÑÓ − L : ÐHñ ÐY Ñ ‚ Hñ ÐZ ÑÑ e Ò3Ó − L-7: ÐY Z Ñ,
:
0: ÐL : Ð.ñ ÑÐÒÐ=ß 7 ÑÓÑß Ò3ÓÑ œ s0 ÐÒ=ß 7 Óß L 7: Ð.ñ ÑÐÒ3ÓÑÑ
(e analogamente com : " no lugar de :). Com efeito, podemos escrever
0: ÐÒ7ÎY Z =ÎY Z Óß Ò3ÓÑ œ (
œ(
Ð7ÎY Z =ÎY Z Ñ • 3 œ
Y Z
Y Z
7ÎY Z • 3 (
=ÎY Z • 3 œ
Y Z
œ ( 7 • 3ÏZ ( = • 3ÏY œ
Z
Y
œ s0: ÐÒÐ=ß 7 ÑÓß ÒÐ3ÏY ß 3ÏZ ÑÓÑ.
b) Para cada Ò=Ó − L : ÐQ Ñ e ÒÐ3ß 5 ÑÓ − L 7: ÐHñ- ÐY Ñ ‚ H-ñ ÐZ ÑÑ,
s0: ÐL : Ð-ñ ÑÐÒ=ÓÑß ÒÐ3ß 5 ÑÓÑ œ 0: ÐÒ=Óß L 7: Ð.ñ ÑÐÒÐ3ß 5 ÑÓÑÑ.
Com efeito, podemos escrever
0: ÐÒ=ÎY Óß Ò3ÓÑ 0: ÐÒ=ÎZ Óß Ò5 ÓÑ œ ( =ÎY • 3 ( =ÎZ • 5 œ
Y
Z
œ ( = • 3ÏQ ( = • 5ÏQ œ
Q
Q
œ ( = • Ð3ÏQ 5ÏQ Ñ œ
Q
œ 0: ÐÒ=Óß ÒÐ3ÏQ 5ÏQ ÑÓÑ.
c) Para cada Ò=Ó − L :" ÐY Z Ñ e Ò3Ó − L-7: ÐQ Ñ, tem-se
0: Ð` :" ÐÒ=ÓÑß Ò3ÓÑ œ Ð"Ñ: 0:" ÐÒ=Óß ` 7: ÐÒ3ÓÑÑ.
Para o verificarmos, começamos por relembrar a definição explícita das
aplicações lineares de conexão ` :" e ` 7: (adaptar a definição geral em
IV.3.2 às duas sucessões exactas de complexos de cocadeias em questão):
Sabemos que existem formas diferenciais =" − H:" ÐY Ñ e =# − H:" ÐZ Ñ
tais que = œ =# ÎY Z =" ÎY Z e então ` :" ÐÒ=ÓÑ œ Ò7 Ó, onde 7 − H: ÐQ Ñ
verifica 7ÎY œ . =" e 7ÎZ œ . =# ; Sabemos que existem formas diferenciais
3" − H7:
ÐY Ñ e 3# − H7:
ÐZ Ñ tais que 3 œ 3" ÏQ 3# ÏQ e então tem-se
7:
`
ÐÒ3ÓÑ œ Ò5 Ó, onde a aplicação 5 − H7:"
ÐY Z Ñ verifica
5ÏY œ . 3" e 0ÏZ œ . 3# . Aplicando o teorema de Stokes às formas
250
Cap. IV. Introdução à cohomologia de de Rham
diferenciais de suporte compacto =" • 3" − H7"
ÐY Ñ e =# • 3# − H7"
ÐZ Ñ,
verificamos que
! œ ( .Ð=" • 3" Ñ œ ( Ð. =" • 3" Ð"Ñ:" =" • . 3" Ñ,
Y
Y
e analogamente para a outra forma diferencial, donde
:
( . =" • 3" œ Ð"Ñ ( =" • . 3" ,
Y
Y
:
( . =# • 3# œ Ð"Ñ ( =# • . 3# .
Z
Z
Podemos então escrever
0: Ð` :" ÐÒ=ÓÑß Ò3ÓÑ œ ( 7 • 3 œ ( 7 • 3" ÏQ ( 7 • 3# ÏQ œ
Q
Q
œ ( 7ÎY • 3" ( 7ÎZ • 3# œ
Y
Q
Z
œ ( . =" • 3" ( . =# • 3# œ
œ Ð"Ñ ( =" • . 3" ( =# • . 3# ‰ œ
Y
:ˆ
:ˆ
Z
œ Ð"Ñ ( =" • 5ÏY ( =# • 5ÏZ ‰ œ
œ Ð"Ñ: (
œ Ð"Ñ: (
Y
Y
Z
Z
Ð=" ÎY Z • 5 =# ÎY Z • 5 Ñ œ
Y Z
= • 5 œ 0:" ÐÒ=Óß ` 7: ÐÒ3ÓÑÑ,
Y Z
o que termina a verificação de c).
Podemos agora considerar o diagrama 2, na página 244, em que as aplicações
lineares da segunda linha são as duais das aplicações lineares na segunda
linha do diagrama 1, na mesma página, e as aplicações lineares verticais são
as associadas às aplicações bilineares atrás referidas. A segunda linha do
diagrama 2 é exacta, tendo em conta IV.5.18, e a primeira linha também o é,
uma vez que o facto de multiplicar uma aplicação linear por " não altera o
seu kernel nem a sua imagem. O que verificámos nas alíneas a), b) e c)
implica trivialmente a comutatividade do diagrama 2. Tendo em conta
IV.5.17 e o facto de Y , Z e Y Z serem variedades de Poincaré,
concluímos que as primeira, segunda, quarta e quinta aplicações lineares
verticais do diagrama 2 são isomorfismos. O lema dos cinco (IV.5.14)
permite-nos portanto concluir que a terceira aplicação linear vertical também
é um isomorfismo, o que mostra que Q é uma variedade de Poincaré.
Antes de passarmos, finalmente, à demonstração de que toda a variedade
sem bordo, de dimensão 7, suavemente orientada é uma variedade de
Poincaré, precisamos ainda de um resultado, de natureza topológica, sobre
§5. Dualidade de Poincaré
251
as variedades que, apesar de parecer eventualmente um pouco artificial,
pode ser aplicado na demonstração de vários teoremas profundos no
quadro destas.
IV.5.20. Lembremos que uma base de abertos de um espaço topológico \ é um
conjunto h de abertos de \ tal que todo o aberto Y de \ se possa escrever
como união de uma família de abertos pertencentes a h ou,
equivalentemente, tal que, para cada aberto Y de \ e cada B − Y , exista um
aberto Z − h tal que B − Z § Y . Vamos dizer que uma base de abertos h é
uma i-base de abertos se, sempre que Y ß Z − h , também Y Z − h .
Se h é uma base de abertos do espaço topológico \ (resp. uma i-base de
abertos) e se ] § \ é um subespaço topológico, então o conjunto hÎ] das
intersecções ] Y , com Y − h , é uma base de abertos (resp. uma i-base de
abertos) de ] .
IV.5.21. O espaço cartesiano ‘8 admite uma i-base de abertos contável63,
nomeadamente a constituída pelo conjunto vazio e pelos conjuntos da forma
$ Ó+4 ß ,4 Ò,
8
4œ"
onde, para cada " Ÿ 4 Ÿ 8, +4 ,4 são números racionais.64 Por homeomorfismo, todo o espaço vectorial I , de dimensão finita, vai admitir uma i-base
de abertos contável e portanto o mesmo acontece a todo o subespaço
topológico \ § I , em particular a toda a variedade.
IV.5.22. (Lema) Seja \ um espaço topológico localmente compacto e separado,
admitindo uma base de abertos contável (é o que acontece, em particular, se
\ § I é uma variedade, eventualmente com bordo). Existe então uma
sucessão de compactos de \ , ÐO8 Ñ8− , com \ œ - O8 e O8 § intÐO8" Ñ,
8
para cada 8.
Dem: Seja h uma base contável de abertos de \ e seja i a parte de h constituída pelos Z − h tais que adÐZ Ñ seja compacto. O conjunto i é ainda uma
base contável de abertos de \ , visto que, se Y é um aberto de \ e se B − Y ,
então existe uma vizinhança compacta E de B, com E § Y e o facto de
intÐEÑ ser um aberto de \ , contendo B, implica a existência de Z − h tal
que B − Z § intÐEÑ, em particular B − Z § Y , tendo-se então, por E ser
fechado, adÐZ Ñ § E e portanto adÐZ Ñ compacto, ou seja, Z − i .
Afastando já o caso trivial em que \ œ g, parametrizemos os conjuntos de i
como os termos de uma sucessão ÐZ8 Ñ8− . Definimos agora recursivamente
um compacto O8 , para cada 8 ", de modo que Z8 § O8 e que
63A palavra contável significa “finito ou numerável”.
64Reparar que a intersecção de dois intervalos Ó+ß ,Ò e
intervalo ÓmaxÐ+ß -Ñß minÐ,ß .ÑÒ.
Ó-ß .Ò de ‘, se não vazia, é igual ao
252
Cap. IV. Introdução à cohomologia de de Rham
O8 § intÐO8" Ñ, do seguinte modo: Pomos O" œ adÐZ" Ñ; supondo
construídos os O: , com : Ÿ 8, verificando as condições referidas,
atendemos a que o compacto O8 está contido na união de todos os Z4 , que é
igual a \ , pelo que podemos considerar R 8 " tal que O8 esteja
contido na união dos Z4 , com 4 Ÿ R , e definimos o compacto O8" como
sendo a união finita dos compactos adÐZ4 Ñ, com 4 Ÿ R ; o facto de se ter
O8 § intÐO8" Ñ vem de O8 estar contido na união dos abertos Z4 , com
4 Ÿ R , que está contida em O8" . O facto de se ter Z8 § O8 implica que a
união dos O8 contém a união dos Z8 , que é igual a \ .
IV.5.23. Sejam \ um espaço topológico e h uma base de abertos de \ .
a) Vamos notar h0 a base de abertos de \ , que contém h , formada por todas
as uniões finitas de conjuntos pertencentes a h . Repare-se que, se h é um
i-base de abertos, o mesmo acontece a h0 , visto que se tem
ˆ. Y3 ‰ ˆ. Z4 ‰ œ . ÐY3 Z4 Ñ.
3
4
3ß4
b) Vamos notar h= a base de abertos de \ , que contém h , formada por todas
as uniões contáveis de conjuntos pertencentes a h , disjuntos dois a dois.
Como anteriormente, se h é uma i-base de abertos, o mesmo acontece a h= .
IV.5.24. (Greub, Halperin e Vanstone, [7]) Seja \ um espaço topológico
localmente compacto, separado e admitindo uma base de abertos contável (é
o que acontece, em particular, se \ § I é uma variedade, eventualmente
com bordo). Seja h uma base arbitrária de abertos de \ . Tem-se então que
ÐÐh0 Ñ= Ñ0 é o conjunto de todos os abertos de \ .
Dem: Basta mostrarmos que \ − ÐÐh0 Ñ= Ñ0 , visto que então, dado um aberto
arbitrário Y de \ , Y é ainda um espaço topológico localmente compacto,
separado e com uma base de abertos contável, que admite uma base de
abertos h w , constituída pelos elementos de h que estão contidos em Y ,
tendo-se trivialmente ÐÐh0w Ñ= Ñ0 § ÐÐh0 Ñ= Ñ0 .
Tendo em conta IV.5.22, podemos considerar uma sucessão ÐO8 Ñ8− de
compactos de \ , com união \ , verificando a condição O8 § intÐO8" Ñ,
para cada 8, e ponhamos, por comodidade, O" œ O! œ g, o que é
compatível com a condição referida.
Para cada 8 ", consideremos um aberto Y8 − h0 , verificando
O8 Ï intÐO8" Ñ § Y8 § intÐO8" Ñ Ï O8# .
Para provarmos a existência de Y8 − h0 nessas condições, atendemos a que
O8 Ï intÐO8" Ñ é um compacto contido no aberto intÐO8" Ñ Ï O8# , escolhemos, para cada B nesse compacto, um aberto ZB − h tal que B − ZB §
intÐO8" Ñ Ï O8# e tomamos para Y8 uma união finita de tais abertos ZB ,
que ainda contenha o compacto.
Reparemos que a união dos abertos Y8 é \ , visto que, para cada B − \ ,
podemos considerar o menor dos naturais 8 tais que B − O8 , tendo-se então
§5. Dualidade de Poincaré
253
B Â O8" , portanto B − O8 Ï intÐO8" Ñ § Y8 .
Reparemos agora que, se 8 7 $, tem-se Y8 Y7 œ g, visto que se tem
Y8 O8# œ g e Y7 § O7" § O8# . Podemos assim considerar abertos
E" , E# e E$ , pertencentes a Ðh0 Ñ= , definidos por
E" œ . Y$8# œ Y" Y% Y( â
E# œ . Y$8" œ Y# Y& Y) â
8 "
E$ œ . Y$8# œ Y$ Y' Y* â,
8 "
8 "
e tem-se \ œ E" E# E$ , o que mostra que \ − ÐÐh0 Ñ= Ñ0 .
IV.5.25. (Teorema de dualidade de Poincaré) Se Q é uma variedade sem
bordo de dimensão 7, suavemente orientada, então Q é uma variedade de
Poincaré, isto é, para cada inteiro :, aplicação bilinear de Poincaré
0: À L : ÐQ Ñ ‚ L-7: ÐQ Ñ Ä Š define o primeiro espaço como dual do
segundo.
Dem: Para uma melhor sistematização, vamos dividir a demonstração em
várias partes:
a) Suponhamos que h é uma i-base de abertos de Q tal que cada Y − h seja
uma variedade de Poincaré. Vamos verificar que cada Y − h0 é uma
variedade de Poincaré, isto é, que qualquer conjunto aberto da forma
Y" Y# â Y8 , com Y4 − h , é uma variedade de Poincaré. Isso é trivial
se 8 œ ! ou 8 œ " e o caso geral prova-se por indução em 8, visto que
supondo o resultado verdadeiro para uniões de 8 conjuntos, a variedade
Y" â Y8" vai ser a união das variedades de Poincaré Y" â Y8
(hipótese de indução) e Y8" , cuja intersecção
ÐY" â Y8 Ñ Y8" œ ÐY" Y8" Ñ â ÐY8 Y8" Ñ
é também uma variedade de Poincaré (mais uma vez pela hipótese de
indução), o que, por IV.5.19, implica que Y" â Y8" é uma variedade
de Poincaré.
b) Suponhamos que h é uma i-base de abertos de Q tal que cada Y − h seja
uma variedade de Poincaré. Resulta então de IV.5.12 que cada Y − h= é uma
variedade de Poincaré.
c) Como referimos em IV.5.21, O espaço cartesiano ‘7 admite uma i-base
de abertos h , constituída pelo conjunto vazio e pelos conjuntos da forma
$ Ó+4 ß ,4 Ò,
7
4œ"
onde, para cada " Ÿ 4 Ÿ 7, +4 ,4 são números racionais. Uma vez que
cada um dos conjuntos de h , com a sua orientação canónica, é uma variedade
de Poincaré (cf. IV.5.9), concluímos de a) e b) e IV.5.24 que todos os abertos
254
Cap. IV. Introdução à cohomologia de de Rham
da i-base ÐÐh0 Ñ= Ñ0 , isto é, todos os abertos de ‘7 , são variedades de
Poincaré.
d) Seja h a classe dos abertos de Q difeomorfos a um aberto de ‘7 , por um
difeomorfismo que conserve, ou inverta, as orientações. Uma vez que cada
ponto B − Q pertence a um aberto da classe h e que toda a parte aberta de
um aberto pertencente a h pertence trivialmente a h , concluímos que h é
uma i-base de abertos de Q . Tendo em conta c) e IV.5.11, todos os abertos
pertencentes a h são variedades de Poincaré. Tendo em conta a) e b),
concluímos agora que todos os abertos da i-base ÐÐh0 Ñ= Ñ0 , isto é, todos os
abertos de Q , são variedades de Poincaré, em particular, Q é uma variedade
de Poincaré.
IV.5.26. (Corolário) Seja Q uma variedade sem bordo, de dimensão 7, suavemente orientada, conexa e não vazia. Tem-se então:
a) L-7 ÐQ Ñ é um espaço vectorial de dimensão " e ë À L-7 ÐQ Ñ Ä Š é um
isomorfismo.
b) Se Q não é compacta, então L 7 ÐQ Ñ œ Ö!× e se Q é compacta, então
L 7 ÐQ Ñ é um espaço vectorial de dimensão " e ë À L 7 ÐQ Ñ Ä Š é um
isomorfismo.
Dem: Pelo teorema de dualidade de Poincaré, sabemos que
0! À L ! ÐQ Ñ ‚ L-7 ÐQ Ñ Ä Š
define o primeiro espaço como dual do segundo pelo que, uma vez que
L ! ÐQ Ñ tem dimensão ", podemos concluir que L-7 ÐQ Ñ também tem
dimensão " e o facto de ë À L-7 ÐQ Ñ Ä Š ser uma aplicação linear
sobrejectiva (cf. IV.4.10) implica que ela é então um isomorfismo. Quanto a
b), apenas temos que examinar o que se passa quando Q não é compacta,
visto que, quando Q é compacta, temos um caso particular de a). Ora, tendo
em conta IV.4.9, sabemos que se tem então L-! ÐQ Ñ œ Ö!×, pela que a
conclusão resulta de que, pelo teorema de dualidade de Poincaré,
07 À L 7 ÐQ Ñ ‚ L-! ÐQ Ñ Ä Š
define o primeiro espaço como dual do segundo.
IV.5.27. (Corolário) Seja Q uma variedade compacta, sem bordo, de dimensão
7, suavemente orientada. Para cada :, o espaço vectorial L : ÐQ Ñ tem então
dimensão finita, igual à de L 7: ÐQ Ñ.65
Dem: O facto de a variedade Q ser compacta implica que L-7: ÐQ Ñ œ
L 7: ÐQ Ñ, pelo que o teorema da dualidade de Poincaré implica que
0: À L : ÐQ Ñ ‚ L 7: ÐQ Ñ Ä Š
65Com
técnicas um pouco mais elaboradas, pode-se provar que, mesmo que Q não seja
orientável, o facto de Q ser compacta e sem bordo implica que L : ÐQ Ñ tem dimensão
finita (cf., por exemplo [7]).
§5. Dualidade de Poincaré
255
define o primeiro espaço como dual do segundo. O mesmo teorema implica
que esta aplicação define o segundo espaço como dual do primeiro, visto que
a aplicação bilinear oposta L 7: ÐQ Ñ ‚ L : ÐQ Ñ Ä Š não é mais do que a
aplicação de Poincaré
07: À L 7: ÐQ Ñ ‚ L : ÐQ Ñ Ä Š,
multiplicada por Ð"Ñ:Ð7:Ñ œ „" (lembrar que, para = − H: ÐQ Ñ e
3 − H7: ÐQ Ñ, tem-se 3 • = œ Ð"Ñ:Ð7:Ñ = • 3). Aplicando IV.5.6 e
IV.5.3, deduzimos agora que L : ÐQ Ñ e L 7: ÐQ Ñ têm a mesma dimensão
finita.
§6. Aplicação à demonstração de resultados topológicos.
IV.6.1. Um espaço topológico \ diz-se uma 8-esfera topológica, ou uma esfera
topológica de dimensão 8, onde 8 !, se for homeomorfo à hipersuperfície
esférica W 8 § ‘8" . Um espaço topológico \ diz-se um 8-cubo topológico,
ou um cubo topológico de dimensão 8, onde 8 !, se for homeomorfo ao
cubo Ò!ß "Ó8 § ‘8 .
IV.6.2. Repare-se que uma !-esfera topológica é simplesmente um espaço
topológico com dois elementos e com a topologia discreta (a única topologia
separada) e que um !-cubo topológico é simplesmente um espaço topológico
com um único elemento. Repare-se também que toda a esfera topológica e
todo o cubo topológico são espaços topológicos compactos.
Note-se que, neste momento, era a priori possível um certo espaço
topológico ser simultneamente uma esfera topológica com dimensões
distintas, um cubo topológico com dimensões distintas ou uma esfera
topológica e um cubo topológico. O que vamos fazer nesta secção
implicará no entanto que isso não pode acontecer. Vamos começar por
apresentar exemplos importantes de cubos topológicos e de esferas
topológicas.
IV.6.3. a) Sejam 8 " e, para cada " Ÿ 4 Ÿ 8, +4 ,4 em ‘. Tem-se então que
\ œ $ Ò+4 ß ,4 Ó
8
4œ"
é um cubo topológico de dimensão 8 e
`Ð\Ñ œ ÖÐ>" ß á ß >8 Ñ − \ ± b >4 − Ö+4 ß ,4 ××
4
é uma esfera topológica de dimensão 8 ".
256
Cap. IV. Introdução à cohomologia de de Rham
b) Sejam 8 ", < ! e
F < œ ÖB − ‘8 ± mBm Ÿ <×,
W< œ ÖB − ‘8 ± mBm œ <×
(norma euclidiana). Tem-se então que F < é um cubo topológico de dimensão
8 e W< é uma esfera topológica de dimensão 8 ".
c) Sejam 8 " e " + ". Tem-se então que as calotes esféricas
\+ œ ÖÐBß >Ñ − ‘8 ‚ ‘ ± mÐBß >Ñm œ " • > +×
]+ œ ÖÐBß >Ñ − ‘8 ‚ ‘ ± mÐBß >Ñm œ " • > Ÿ +×
(norma euclidiana) são cubos topológicos de dimensão 8 e o bordo comum
^+ œ ÖÐBß >Ñ − ‘8 ‚ ‘ ± mÐBß >Ñm œ " • > œ +×
é uma esfera topológica de dimensão 8 ".
Dem: Nas condições de a), podemos considerar, para cada " Ÿ 4 Ÿ 8 um
homeomorfismo :4 À Ò!ß "Ó Ä Ò+4 ß ,4 Ó, definido por :4 Ð>Ñ œ +4 > Ð,4 +4 Ñ,
cujo inverso está definido por = È Ð= +4 ÑÎÐ,4 +4 Ñ, e então :" ‚ â ‚ :8
é um difeomorfismo de Ò!ß "Ó8 sobre # Ò+4 ß ,4 Ó, que aplica trivialmente
`ÐÒ!ß "Ó8 Ñ sobre `Ð# Ò+4 ß ,4 ÓÑ. Fica assim provado que # Ò+4 ß ,4 Ó é um cubo
topológico de dimensão 8 e concluímos que, para verificar que `Ð# Ò+4 ß ,4 ÓÑ
é uma esfera topológica de dimensão 8 ", basta verificá-lo para um sistema
particular de valores +4 ,4 , o que será feito adiante para +4 œ " e ,4 œ ".
Notemos agora m † m a norma euclidiana e | † | a norma do máximo de ‘8 .
Consideremos a aplicação contínua :À ‘8 Ä ‘8 definida por
!,
:ÐBÑ œ B lBl
mBm
,
se B œ !
se B Á !
(a continuidade em ! é implicada pela igualdade m:ÐBÑm œ lBl), aplicação
que vai ser um homeomorfismo por admitir o inverso bilateral <À ‘8 Ä ‘8
definido por
!,
<ÐBÑ œ BmBm
lBl
,
se B œ !
se B Á !
(a continuidade em ! é implicada pela igualdade l<ÐBÑl œ mBm). Nas
notações de b), o homeomorfismo : vai aplicar
Ò"ß "Ó8 œ ÖB − ‘8 ± lBl Ÿ "×
sobre F " œ ÖB − ‘8 ± mBm Ÿ "× e
`ÐÒ"ß "Ó8 Ñ œ ÖB − ‘8 ± lBl œ "×
§6. Aplicação à demonstração de resultados topológicos
257
sobre W" œ W 8" œ ÖB − ‘8 ± mBm œ "×, o que implica que F " é um cubo
topológico de dimensão 8 e que `ÐÒ"ß "Ó8 Ñ é uma esfera topológica de
dimensão 8 " (que é o que nos faltava para terminar a demonstração de a)).
A conclusão de b) é agora uma consequência de a homotetia B È < B, ser um
homeomorfismo de F " sobre F < , que aplica W" œ W 8" sobre W< .
Para verificarmos c), começamos por lembrar que, considerando
W 8 œ ÖÐBß >Ñ − ‘8 ‚ ‘ ± mÐBß >Ñm œ "×,
tem lugar o homeomorfismo 0 À W 8 Ï Ö/8" × Ä ‘8 (projecção estereográB
fica), definido por 0 ÐBß >Ñ œ ">
(cf. IV.3.8). Uma vez que
m0 ÐBß >Ñm# œ
mBm#
" >#
">
œ
œ
#
Ð" >Ñ
Ð" >Ñ#
">
#
e que a aplicação > È ">
"> tem derivada Ð">Ñ# e é, portanto, estritamente
decrescente, concluímos que, sendo <# œ "+
"+ , a restrição de 0 é um homeomorfismo de \+ sobre F + , que aplica ^+ sobre W< , o que mostra que \+ é
um 8-cubo topológico e que ^+ é uma Ð8 "Ñ-esfera topológica. A prova de
que ]+ é também um 8-cubo topológico pode ser feita, de modo análogo, por
consideração da projecção estereográfica 0 , ou, alternativamente, reduzir-se
ao já feito, reparando que ]+ é homeomorfo a \+ , pelo homeomorfismo
definido por ÐBß >Ñ È ÐBß >Ñ.
IV.6.4. (Um cubo dentro duma esfera) Seja 8 ! e consideremos a esfera
W 8 § ‘8" . Seja \ § W 8 um 5 -cubo topológico, com 5 !. Tem-se então
\ Á W 8 e, para os espaços de cohomologia de de Rham com suporte
compacto do aberto W 8 Ï \ , tem-se L-: ÐW 8 Ï \Ñ œ Ö!×, para cada : Á 8, e
L-8 ÐW 8 Ï \Ñ tem dimensão ". Em particular W 8 Ï \ é um aberto conexo não
vazio.66
Dem: Vamos dividir a demonstração em várias alíneas:
a) Consideremos em W 8 a sua orientação usual. Comecemos por reparar que,
se verificarmos que L-8 ÐW 8 Ï \Ñ tem dimensão " então, pelo teorema de
dualidade de Poincaré, L ! ÐW 8 Ï \Ñ também tem dimensão " pelo que, por
IV.1.4, a variedade W 8 Ï \ é conexa.
b) Vamos fazer a demonstração por indução na dimensão 5 do cubo
topológico \ § W 8 . Para 5 œ !, o resultado é verdadeiro visto que \ tem
um único elemento e portanto, por uma projecção esterográfica (cf. IV.3.6),
W 8 Ï \ é difeomorfo a um espaço vectorial de dimensão 8, e portanto a ‘8 ,
bastando então ter em conta IV.4.11. Vamos então supor que o resultado é
válido sempre que \ é um cubo topológico de dimensão 5 e verificar o que
acontece quando \ é um cubo topológico de dimensão 5 ".
c) Vamos fixar um homeomorfismo :À Ò!ß "Ó5" Ä \ e, para cada + Ÿ , em
caso em que 8 ", W 8 é, como sabemos, conexo e esta conclusão costuma ser
expressa pela afirmação de que um cubo topológico nunca destrói a conexão de W 8 .
66No
258
Cap. IV. Introdução à cohomologia de de Rham
Ò!ß "Ó, notar
\+ß, œ :ÐÒ!ß "Ó5 ‚ Ò+ß ,ÓÑ,
pondo, em particular
\+ œ \+ß+ œ :ÐÒ!ß "Ó5 ‚ Ö+×Ñ.
Reparemos que \+ é homeomorfo a Ò!ß "Ó5 ‚ Ö+×, e portanto a Ò!ß "Ó5 , sendo
portanto um cubo topológico de dimensão 5 .
d) Podemos já concluir que \ Á W 8 visto que, caso contrário, e contra a
hipótese de indução, W 8 Ï \"Î# não era conexo, por ser união dos abertos
disjuntos não vazios :ÐÒ!ß "Ó5 ‚ Ò!ß "Î#ÒÑ e :ÐÒ!ß "Ó5 ‚ Ó"Î#ß "ÓÑ.
e) Uma vez que, por IV.4.10, sabemos que tem lugar uma aplicação linear
sobrejectiva ë À L-8 ÐW 8 Ï \Ñ Ä Š, tudo o que temos que provar é que o
kernel desta aplicação é Ö!× e que L-: ÐW 8 Ï \Ñ œ Ö!×, para cada ! Ÿ : 8.
Seja então ! Ÿ : Ÿ 8 e Ò=Ó − L-: ÐW 8 Ï \Ñ, verificando, no caso em que
: œ 8, a condição 'W 8 Ï\ = œ !, e vamos mostrar que se tem então Ò=Ó œ !
em L-: ÐW 8 Ï \Ñ, o que terminará a demonstração.
f) Seja + − Ò!ß "Ó arbitrário. Pela hipótese de indução, sabemos que se tem
L-: ÐW 8 Ï \+ Ñ œ Ö!× e que ë À L-8 ÐW 8 Ï \+ Ñ Ä Š é um isomorfismo, por ser
uma aplicação linear sobrejectiva entre espaços com a mesma dimensão.
Uma vez que, para a extensão =ÏÐW 8 Ï\+ Ñ , que se anula fora de W 8 Ï \ , se tem
ainda, no caso em que : œ 8, 'W 8 Ï\+ =ÏÐW 8 Ï\+ Ñ œ !, podemos então concluir
que Ò=ÏÐW 8 Ï\+ Ñ Ó œ !, em L-: ÐW 8 Ï \+ Ñ.
g) Vamos melhorar um pouco a conclusão de f), mostrando que, para cada
+ − Ò!ß "Ó, existe um aberto M+ de Ò!ß "Ó, com + − M+ , tal que, com
s + œ :ÐÒ!ß "Ó5 ‚ M+ Ñ, se tenha já Ò= 8 s Ó œ ! em L-: ÐW 8 Ï \
s + Ñ.
\
ÏÐW Ï\ + Ñ
Para isso, começamos por reparar que o facto de se ter Ò=ÏÐW 8 Ï\+ Ñ Ó œ !, em
L-: ÐW 8 Ï \+ Ñ, garante a existência de 3 − H-:" ÐW 8 Ï \+ Ñ tal que
=ÏÐW 8 Ï\+ Ñ œ . 3, existindo portanto um compacto O § W 8 Ï \+ tal que
3B œ !, para cada B  O . Tem-se então \+ § W 8 Ï O pelo que o aberto
:" ÐW 8 Ï OÑ de Ò!ß "Ó5" contém o compacto Ò!ß "Ó5 ‚ Ö+×, o que nos
permite considerar & ! menor que o mínimo das distâncias dos pontos de
Ò!ß "Ó5 ‚ Ö+× ao complementar de :" ÐW 8 Ï OÑ (métrica do máximo de
Ò!ß "Ó5" ). Sendo
M+ œ Ö> − Ò!ß "Ó ± l> +l &×,
s + œ :ÐÒ!ß "Ó5 ‚ M+ Ñ § W 8 Ï O , ou
vem Ò!ß "Ó5 ‚ M+ § :" ÐW 8 Ï OÑ, donde \
8
8
s + , pelo que 3 8 s − H:"
s
seja, O § W Ï \
- ÐW Ï \ + Ñ vai verificar ainda
ÎÐW Ï\ + Ñ
=ÏÐW 8 Ï\s + Ñ œ .Ð3ÎÐW 8 Ï\s + Ñ Ñ, o que mostra que se tem Ò=ÏÐW 8 Ï\s + Ñ Ó œ ! em
s + Ñ, como queríamos.
L-: ÐW 8 Ï \
h) Seja $ ! um número de Lebesgue para a cobertura aberta do espaço
§6. Aplicação à demonstração de resultados topológicos
259
métrico compacto Ò!ß "Ó pelos conjuntos M+ .67 Seja R " tal que "ÎR $ .
Para cada ! Ÿ 4 Ÿ R , seja +4 œ 4ÎR − Ò!ß "Ó. Reparando que cada intervalo
Ò+4" ß +4 Ó tem diâmetro menor que $ , e está, portanto, contido nalgum dos
s + , e portanto
conjuntos M+ , concluímos que \+4" ß+4 § \
s + § W 8 Ï \+4" ß+4 ,
W8 Ï \
o que, tendo em conta a conclusão de g), implica que se tem ainda
Ò=ÏÐW 8 Ï\+4"ß+4 Ñ Ó œ ! − L-: ÐW 8 Ï \+4" ß+4 Ñ.
i) Vamos demonstrar, por indução em 4, que, para cada 4 ",
Ò=ÏÐW 8 Ï\!ß+4 Ñ Ó œ ! em L-: ÐW 8 Ï \!ß+4 Ñ. No caso em que 4 œ ", isso é uma
consequência de h), visto que +! œ !. Suponhamos então que isso é verdade
para um certo 4 8. Tem-se então que a união dos abertos W 8 Ï \!ß+4 e
W 8 Ï \+4 ß+4" de W 8 é o aberto W 8 Ï \+4 e a respectiva intersecção é o aberto
W 8 Ï \!ß+4" pelo que, uma vez que, pela hipótese de indução em 5 , e por ser
: " 8, tem-se L-:" ÐW 8 Ï \+4 Ñ œ Ö!×, podemos escrever a seguinte
porção da sucessão exacta de Mayer-Vietoris (cf. IV.5.16)
Ö!× œ L-:" ÐW 8 Ï \+4 Ñ Ä L-: ÐW 8 Ï \!ß+4" Ñ Ä L : ÐH-ñ ÐW 8 Ï \!ß+4 Ñ ‚ H-ñ ÐW 8 Ï \+4 ß+4" ÑÑ.
Esta sucessão exacta garante-nos que a segunda aplicação linear é injectiva.
A imagem do elemento Ò=ÏÐW 8 Ï\!ß+4" Ñ Ó − L-: ÐW 8 Ï \!ß+4" Ñ por essa aplicação
linear é o elemento ÒÐ=ÏÐW 8 Ï\!ß+4 Ñ ß =ÏÐW 8 Ï\+4ß+4" Ñ ÑÓ, o qual é !, tendo em conta
a caracterização de L : ÐH-ñ ÐW 8 Ï \!ß+4 Ñ ‚ H-ñ ÐW 8 Ï \+4 ß+4" ÑÑ como produto
de L-: ÐW 8 Ï \!ß+4 Ñ e L-: ÐW 8 Ï \+4 ß+4" Ñ e o facto de se ter Ò=ÏÐW 8 Ï\!ß+4 Ñ Ó œ !
em L-: ÐW 8 Ï \!ß+4 Ñ, tendo em conta a hipótese de indução, e
Ò=ÏÐW 8 Ï\+4ß+4" Ñ Ó œ ! em L-: ÐW 8 Ï \+4 ß+4" Ñ, pelo que vimos em h). A
injectividade da aplicação linear referida implica agora que
Ò=ÏÐW 8 Ï\!ß+4" Ñ Ó œ ! em L-: ÐW 8 Ï \!ß+4" Ñ, o que prova a asserção enunciada
nesta alínea.
j) O que estabelecemos em i), para todo o 4, reduz-se, no caso em que
4 œ R , e portanto +4 œ ", à conclusão que Ò=Ó œ ! em L-: ÐW 8 Ï \Ñ, o que,
de acordo com o que dissémos em e), termina a demonstração.
IV.6.5. (Corolário) Um espaço topológico não pode ser simultaneamente um
5 -cubo topológico e uma 8-esfera topológica.
Dem: Se isso acontecesse, W 8 seria um 5 -cubo topológico, contra a conclusão de que um 5 -cubo topológico contido em W 8 tem que ser distinto de
W 8 .
67Quem
não conhecer o teorema de existência de un número de Lebesgue para uma
cobertura aberta de um espaço métrico compacto poderá consultar o exercício IV.37, no
fim do capítulo.
260
Cap. IV. Introdução à cohomologia de de Rham
IV.6.6. (Jordan-Brouwer: uma esfera dentro duma esfera) Seja 8 ! e
consideremos a esfera W 8 § ‘8" . Seja \ § W 8 uma 5 -esfera topológica,
onde 5 !. Tem-se então:
1) 5 Ÿ 8.
2) 5 œ 8 se, e só se, \ œ W 8 .
3) Se 5 œ 8 ", então L-8 ÐW 8 Ï \Ñ tem dimensão # e L-: ÐW 8 Ï \Ñ œ Ö!×,
para cada : Á 8; em particular W 8 Ï \ tem duas componentes conexas.
4) Se 5 8 ", então L-8 ÐW 8 Ï \Ñ e L-5" ÐW 8 Ï \Ñ têm dimensão " e
L-: ÐW 8 Ï \Ñ œ Ö!×, para cada : Á 8ß 5 "; em particular W 8 Ï \ é conexo.
Dem: Vamos dividir a demonstração em várias alíneas:
a) Consideremos a orientação usual em W 8 . Comecemos por reparar que,
quando L-8 ÐW 8 Ï \Ñ tiver dimensão #, o teorema de dualidade de Poincaré
garante que L ! ÐW 8 Ï \Ñ tem dimensão # e portanto, por IV.1.4, W 8 Ï \ tem
duas componentes conexas. Do mesmo modo, quando L-8 ÐW 8 Ï \Ñ tiver
dimensão ", W 8 Ï \ vai ser conexo.
b) Vamos fazer a demonstração por indução em 5 , começando por examinar
o caso em que 5 œ !, e em que, portanto, \ é um conjunto formado por dois
elementos. As propriedades 1) e 2) do enunciado são triviais. Considerando a
projecção estereográfica a partir de um dos dois pontos de \ (cf. IV.3.6),
constatamos que W 8 Ï \ é difeomorfa ao complementar de um conjunto
unitário num espaço vectorial de dimensão 8 e portanto, por composição com
uma translação e um isomorfismo, W 8 Ï \ é difeomorfa a ‘8 Ï Ö!×. Em
particular, cada L-: ÐW 8 Ï \Ñ é isomorfo a L-: Б8 Ï Ö!×Ñ pelo que as
propriedades 3) e 4) do enunciado resultam de IV.3.13 e do teorema de
dualidade de Poincaré.
c) Vamos, a partir de agora, supor que o resultado é verdadeiro para um certo
5 ! e verificar o que sucede quando \ § W 8 é uma esfera topológica de
dimensão 5 ".
d) Consideremos a hipersuperfície esférica W 5" § ‘5# œ ‘5" ‚ ‘ e um
difeomorfismo :À W 5" Ä \ e definamos
\ œ :ÐÖÐBß >Ñ − W 5" ± > !×Ñ,
\ œ :ÐÖÐBß >Ñ − W 5" ± > Ÿ !×Ñ,
\! œ :ÐÖÐBß >Ñ − W 5" ± > œ !×Ñ,
reparando que, pela alínea c) de IV.6.3, \ e \ são cubos topológicos de
dimensão 5 " e \! é um esfera topológica de dimensão 5 .
Tem-se então que o aberto W 8 Ï \! é união dos abertos W 8 Ï \ e W 8 Ï \ ,
cuja intersecção é W 8 Ï \ , o que nos permitirá considerar adiante diferentes
porções da correspondente sucessão exacta de Mayer-Vietoris com suporte
compacto (cf. IV.5.16), relativamente à qual lembramos que cada
L : ÐH-ñ ÐW 8 Ï \ Ñ ‚ H-ñ ÐW 8 Ï \ ÑÑ
é isomorfo a L-: ÐW 8 Ï \ Ñ ‚ L-: ÐW 8 Ï \ Ñ (cf. IV.2.5), sendo portanto, por
IV.6.4, igual a Ö!×, se : 8, e de dimensão #, se : œ 8.
§6. Aplicação à demonstração de resultados topológicos
261
e) Uma vez que \! está contido estritamente em \ , e portanto em W 8 , a
hipótese de indução garante-nos que 5 8, e portanto que 5 " Ÿ 8, e
temos a propriedade 1) do enunciado.
f) Suponhamos que 5 " œ 8. Pela hipótese de indução, W 8 Ï \! tem duas
componentes conexas. Por IV.6.4, os abertos W 8 Ï \ e W 8 Ï \ , de união
W 8 Ï \! , são conexos o que implica que a sua intersecção W 8 Ï \ é vazia
(senão a união seria conexa), por outras palavras, tem-se \ œ W 8 .
Suponhamos agora que 5 " 8. Pela hipótese de indução W 8 Ï \! é
conexo pelo que, por ser união dos abertos não vazios W 8 Ï \ e W 8 Ï \ ,
estes não podem ser disjuntos, isto é W 8 Ï \ œ ÐW 8 Ï \ Ñ ÐW 8 Ï \ Ñ Á g,
ou seja, \ Á W 8 . Ficou assim provada a propriedade 2) do enunciado.
g) Suponhamos agora que 5 " œ 8 ". Pela hipótese de indução,
L-8" ÐW 8 Ï \! Ñ e L-8 ÐW 8 Ï \! Ñ têm dimensão " e L-: ÐW 8 Ï \! Ñ œ Ö!×, para
: Á 8ß 8 ". Consideremos a seguinte parte da sucessão exacta de
Mayer-Vietoris acima referida:
Ö!× Ä L-8" ÐW 8 Ï \! Ñ Ä L-8 ÐW 8 Ï \Ñ Ä X Ä L-8 ÐW 8 Ï \! Ñ Ä Ö!×,
onde notámos X œ L 8 ÐHñ- ÐW 8 Ï \ Ñ ‚ H-ñ ÐW 8 Ï \ ÑÑ, por razões tipográficas. Uma vez que o primeiro, o terceiro e o quarto espaços têm,
respectivamente, dimensões iguais a ", # e ", deduzimos de IV.3.11 que
L-8 ÐW 8 Ï \Ñ tem dimensão #. Por outro lado, para cada : 8, temos a parte
trivial de mesma sucessão exacta
Ö!× Ä L-: ÐW 8 Ï \Ñ Ä Ö!×,
que nos implica que L-: ÐW 8 Ï \Ñ œ Ö!×, igualdade que é trivialmente verdadeira para : 8. Ficou assim provada a propriedade 3) do enunciado.
h) Suponhamos, por fim, que 5 " 8 ". Pela hipótese de indução,
L-5" ÐW 8 Ï \! Ñ e L-8 ÐW 8 Ï \! Ñ têm dimensão " e L-: ÐW 8 Ï \! Ñ œ Ö!×, para
: Á 8ß 5 ". Consideremos as seguintes porções da sucessão exacta de
Mayer-Vietoris atrás referida
Ö!× Ä L-8 ÐW 8 Ï \Ñ Ä X Ä L-8 ÐW 8 Ï \! Ñ Ä Ö!×,
Ö!× Ä L-5" ÐW 8 Ï \! Ñ Ä L-5# ÐW 8 Ï \Ñ Ä Ö!×,
onde, mais uma vez, X œ L 8 ÐHñ- ÐW 8 Ï \ Ñ ‚ H-ñ ÐW 8 Ï \ ÑÑ. Utilizando,
mais uma vez, IV.3.11, do facto do segundo e terceiro termos da primeira
porção terem respectivamente dimensões # e " e do facto de o primeiro termo
da segunda porção ter dimensão " concluímos que L-8 ÐW 8 Ï \Ñ e
L 5# ÐW 8 Ï \Ñ têm dimensão ". Por outro lado, para cada : 8, distinto de
5 #, temos a parte trivial da mesma sucessão exacta
Ö!× Ä L-: ÐW 8 Ï \Ñ Ä Ö!×,
que nos implica que L-: ÐW 8 Ï \Ñ œ Ö!×, igualdade que é trivialmente verdadeira para : 8. Ficou assim provada a propriedade 4) do enunciado.
262
Cap. IV. Introdução à cohomologia de de Rham
IV.6.7. (Corolário) Um espaço topológico não pode ser simultaneamente uma
5 -esfera topológica e uma 8-esfera topológica, com 5 Á 8.
Dem: Se isso acontecesse, concluíamos que W 8 era uma 5 -esfera topológica,
o que contrariava a alínea 2) do resultado precedente.
IV.6.8. (Corolário) Se \ § ‘8 é uma 5 -esfera topológica, então 5 Ÿ 8 ".
Dem: Considerando a projecção estereográfica 0 À W 8 Ï Ö/8" × Ä ‘8 (cf.
IV.3.8), a imagem recíproca de \ ia ser uma 5 -esfera topológica contida
estritamente em W 8 , pelo que basta atender às alíneas 1) e 2) de IV.6.6.
IV.6.9. (Teorema da invariância da dimensão) Sejam Y § ‘7 um aberto não
vazio e 0 À Y Ä ‘8 uma aplicação contínua e injectiva. Tem-se então 7 Ÿ 8.
Em particular, um aberto não vazio de ‘7 não pode ser homeomorfo a um
aberto não vazio de ‘8 , com 7 Á 8.
Dem: Para a primeira afirmação do enunciado, escolhemos B! − Y e < !
tais que a bola fechada de centro B! e raio < estaja contida em Y e reparamos
então que a restrição de 0 ao compacto W< ÐB! Ñ œ ÖB − ‘7 ± mB B! m œ <×
vai ser um homeomorfismo sobre a sua imagem; uma vez que W< ÐB! Ñ é
homeomorfo, por translação, a W< Ð!Ñ que, por IV.6.3, é uma esfera
topológica de dimensão 7 ", deduzimos que 0 ÐW< ÐB! ÑÑ é uma esfera
topológica de dimensão 7 " contida em ‘8 o que, por IV.6.8, implica que
7 " Ÿ 8 ", ou seja, 7 Ÿ 8. A segunda afirmação resulta da primeira
visto que ficamos com uma aplicação contínua e injectiva de um aberto de
‘7 para ‘8 , cuja inversa é uma aplicação contínua e injectiva de um aberto
de ‘8 para ‘7 .
IV.6.10. (Corolário) Um espaço topológico não pode ser simultaneamente um
5 -cubo topológico e um 8-cubo topológico, com 5 Á 8.
Dem: Se isso acontecesse, e supondo já 5 8, existia um homeomorfismo
0 À Ò!ß "Ó8 Ä Ò!ß "Ó5 , cuja restrição ao aberto Ó!ß "Ò8 ia contrariar a conclusão
do resultado precedente.
IV.6.11. (Lema) Para cada 8 !, o espaço topológico W 8 § ‘8" é um espaço
topológico homogéneo, no sentido que, dados Bß C − W 8 , existe um homeomorfismo :À W 8 Ä W 8 tal que :ÐBÑ œ C.
Dem: Podemos considerar bases ortonormadas B" ß á ß B8" e C" ß á ß C8" de
‘8" , tais que B" œ B e C" œ C e o isomorfismo ortogonal :À ‘8" Ä ‘8"
definido pela condição de se ter :ÐB4 Ñ œ C4 , para cada 4. O facto de cada
vector e a sua imagem por : terem a mesma norma implica que :ÐW 8 Ñ œ W 8
pelo que obtemos, por restrição de :, um homeomorfismo :À W 8 Ä W 8 tal
que :ÐBÑ œ C.
IV.6.12. (Teorema de Jordan-Brouwer) Sejam 8 " e \ § W 8 uma esfera
topológica de dimensão 8 ". Tem-se então que W 8 Ï \ tem duas componentes conexas Y" e Y# , que são abertos de W 8 , verificando
frÐY" Ñ œ frÐY# Ñ œ \
§6. Aplicação à demonstração de resultados topológicos
263
(fronteiras relativas à topologia de W 8 ).
Dem: Tendo em conta a alínea 3) de IV.6.6, sabemos que W 8 Ï \ tem duas
componentes conexas Y" e Y# e o facto de W 8 Ï \ ser aberto, e portanto uma
variedade, implica que Y" e Y# são abertos. Resta-nos verificar que a
fronteira de cada um destes abertos é igual a \ , para o que basta examinar o
que se passa com Y" . O facto de os pontos de Y" serem interiores a Y" e de
Y# ser um aberto que não intersecta Y" , e portantos os pontos de Y# serem
exteriores a Y" , implica que frÐY" Ñ § \ . Resta-nos supor que se tinha
frÐY" Ñ Á \ e chegar a um absurdo. Seja então B! − \ tal que B! Â frÐY" Ñ, e
portanto B! − extÐY" Ñ. Seja Z um aberto de W 8 , com B! − Z , tal que
Z Y" œ g. Seja 0 À W 8" Ä \ um homeomorfismo. Tendo em conta o lema
anterior, concluímos que, se necessário compondo 0 com um
homeomorfismo conveniente de W 8" sobre W 8" , pode-se já supor que, para
o “polo norte” Ð!ß "Ñ − W 8" § ‘8" ‚ ‘, se tem 0 Ð!ß "Ñ œ B! . O facto de
0 " ÐZ Ñ ser um aberto de W 8" , contendo Ð!ß "Ñ permite-nos fixar ! Ÿ + "
tal que, para cada ÐCß >Ñ − W 8" , com > +, se tenha 0 ÐCß >Ñ − Z (reparar
que mCm# œ " ># Ÿ " +# ). Sejam então
\ œ 0 ÐÖÐCß >Ñ − W 8" ± > +×Ñ,
\ œ 0 ÐÖÐCß >Ñ − W 8" ± > Ÿ +×Ñ,
que, tendo em conta IV.6.3, são cubos topológicos de dimensão 8 ", contidos em \ e de união \ , o primeiro dos quais, pelo que dissémos atrás,
também contido em Z . Tendo em conta IV.6.4, W 8 Ï \ é conexo. Mas
W 8 Ï \ vai ser a união dos abertos disjuntos dois a dois, não vazios, Y" e
ÐÐW 8 Ï \ Ñ Z Ñ Y# , pelo que chegámos realmente a um absurdo.
Figura 10
264
Cap. IV. Introdução à cohomologia de de Rham
IV.6.13. (Nota) O teorema de Jordan-Brouwer foi enunciado originariamente
por Jordan, no caso em que 8 œ # e em que se considera ‘# em vez de W # ,
embora a sua primeira demonstração satisfatória só tenha aparecido mais
tarde, já neste século, e usando técnicas sofisticadas. A passagem do
resultado de W # para ‘# (ou, mais geralmente, de W 8 para ‘8 ) é
relativamente simples (cf. o exercício IV.42, no fim do capítulo). O resultado
parece intuitivamente evidente, quando pensamos na "-esfera topológica
como uma circunferência um pouco deformada, mas um exemplo como o
sugerido na figura 10 pode contribuir para enfraquecer um pouco essa
intuição.
IV.6.14. (Teorema de Brouwer da invariância do domínio) Sejam Y § ‘8
um conjunto aberto e 0 À Y Ä ‘8 uma aplicação contínua e injectiva.68
Tem-se então que 0 ÐY Ñ é um aberto de ‘8 e 0 é um homeomorfismo de Y
sobre 0 ÐY Ñ.
Dem: Basta verificarmos que se tem 0 ÐY Ñ aberto em ‘8 , visto que,
aplicando então esse resultado à restrição de 0 a cada aberto contido em Y ,
concluímos que 0 aplica abertos de Y em abertos de 0 ÐY Ñ. Considerando a
projecção estereográfica 0 À W 8 Ï Ö/8" × Ä ‘8 (cf. IV.3.8), que é um
homeomorfismo do aberto W 8 Ï Ö/8" × de W 8 sobre ‘8 , basta-nos provar
que 0" Ð0 ÐY ÑÑ é um conjunto aberto em W 8 . Seja então C! − 0" Ð0 ÐY ÑÑ
arbitrário, portanto C! œ 0" Ð0 ÐB! ÑÑ, para um certo B! − Y . Seja < ! tal
que a bola fechada,
F < ÐB! Ñ œ ÖB − ‘8 ± mB B! m Ÿ <×,
esteja contida em Y e notemos
F< ÐB! Ñ œ ÖB − ‘8 ± mB B! m <×,
W< ÐB! Ñ œ ÖB − ‘8 ± mB B! m œ <×.
Reparemos que F< ÐB! Ñ é convexo, e portanto conexo, e que, por translação,
F < ÐB! Ñ e W< ÐB! Ñ são respectivamente homeomorfos a F < Ð!Ñ e W< Ð!Ñ, e
portanto, por IV.6.3, são respectivamente um 8-cubo topológico e uma
Ð8 "Ñ-esfera topológica. Uma vez que a restrição de 0" ‰ 0 ao compacto
F < ÐB! Ñ, sendo contínua e injectiva, é um homeomorfismo sobre a sua imagem, concluímos que 0" Ð0 ÐF < ÐB! ÑÑÑ e 0" Ð0 ÐW< ÐB! ÑÑÑ são
respectivamente um 8-cubo topológico e uma Ð8 "Ñ-esfera topológica,
ambos contidos em W 8 . Tendo em conta IV.6.4 e IV.6.12,
W 8 Ï 0" Ð0 ÐF < ÐB! ÑÑÑ é conexo e W 8 Ï 0" Ð0 ÐW< ÐB! ÑÑÑ tem duas
componentes conexas, que são abertos de W 8 . Mas, como se realiza
facilmente,
W 8 Ï 0" Ð0 ÐW< ÐB! ÑÑÑ
é
a
união
dos
conexos
8
"
W Ï 0 Ð0 ÐF < ÐB! ÑÑÑ e 0" Ð0 ÐF< ÐB! ÑÑÑ, cada um dos quais vai estar contido
numa das componentes conexas e portanto ser igual a esta. Em particular,
68Comparar
com IV.6.9.
§6. Aplicação à demonstração de resultados topológicos
265
0" Ð0 ÐF< ÐB! ÑÑÑ é um aberto que contém C! e está contido em 0" Ð0 ÐY ÑÑ, o
que mostra que C! é interior a 0" Ð0 ÐY ÑÑ, e portanto que 0" Ð0 ÐY ÑÑ é
aberto.
§7. Invariância topológica da cohomologia.
As aplicações suavemente homotópicas entre variedades foram definidas
em III.7.5, tendo-se provado em IV.1.10 que se está em presença de uma
relação de equivalência na classe das aplicações suaves entre duas
variedades. Se abrirmos mão da suavidade, e exigirmos apenas a
continuidade, obtemos uma noção análoga, válida no quadro mais geral
dos espaços topológicos.
IV.7.1. Sejam \ e ] espaços topológicos. Diz-se que duas aplicações contínuas
0 ß 1À \ Ä ] são homotópicas se existir uma homotopia de 0 para 1, isto é,
uma aplicação contínua LÀ Ò!ß "Ó ‚ \ Ä ] tal que LÐ!ß BÑ œ 0 ÐBÑ e
LÐ"ß BÑ œ 1ÐBÑ.
IV.7.2. Se \ e ] são espaços topológicos, a relação atrás definida é uma relação
de equivalência na classe das aplicações contínuas de \ para ] .
Dem: A reflexividade e a simetria desta relação são essencialmente triviais:
se 0 À \ Ä ] é uma aplicação contínua, a aplicação definida por
LÐ>ß BÑ œ 0 ÐBÑ é uma homotopia de 0 para 0 e se LÀ Ò!ß "Ó ‚ \ Ä ] é uma
s Ò!ß "Ó ‚ \ Ä ] , de 1
homotopia de 0 para 1, obtemos uma homotopia LÀ
s BÑ œ LÐ" >ß BÑ. A prova da transitividade é mais
para 0 , definida por LÐ>ß
simples do que em IV.1.10, uma vez que não temos agora necessidade de
s Ò!ß "Ó ‚ \ Ä ] forem aplicações
“arredondar os cantos”. Ora, se Lß LÀ
s BÑ œ 1ÐBÑ e
contínuas, para as quais LÐ!ß BÑ œ 0 ÐBÑ, LÐ"ß BÑ œ 1ÐBÑ, LÐ!ß
˜ Ò!ß "Ó ‚ \ Ä ] por
s BÑ œ 2ÐBÑ, podemos definir uma aplicação LÀ
LÐ"ß
˜ BÑ œ
LÐ>ß
LÐ#>ß BÑ,
s
LÐ#>
"ß BÑ,
se > Ÿ
se > "
#
"
#
,
aplicação que é contínua por ter restrições contínuas aos dois subconjuntos
fechados Ò!ß "# Ó ‚ \ e Ò "# ß "Ó ‚ \ com união Ò!ß "Ó ‚ \ , e que verifica
˜ BÑ œ 0 ÐBÑ e LÐ"ß
˜ BÑ œ 2ÐBÑ.
LÐ!ß
É claro que, se Q w § I w e Q § I são variedades e se 0 ß 1À Q w Ä Q são
aplicações suaves suavemente homotópicas, então 0 e 1 são também
homotópicas no sentido da definição anterior. O nosso próximo objectivo
é a prova de que, reciprocamente, no caso em que a variedade Q w é
compacta e a variedade Q não tem bordo duas aplicações suaves que
266
Cap. IV. Introdução à cohomologia de de Rham
sejam homotópicas são também suavemente homotópicas. Para isso temos
necessidade de introduzir as vizinhanças tubulares de um subconjunto
compacto de uma variedade sem bordo.
IV.7.3. (Versão forte do teorema da aplicação inversa) Sejam Q § I e
s §I
s duas variedades sem bordo, com dimensão 8, O § Q um compacto
Q
s uma aplicação suave tal que 0ÎO À O Ä Q
s seja injectiva e que,
e 0À Q Ä Q
s Ñ seja um isomorfismo. Existe
para cada B − O , H0B À XB ÐQ Ñ Ä X0 ÐBÑ ÐQ
então um aberto Y de Q , com O § Y , tal que 0ÎY À Y Ä 0 ÐY Ñ seja um
s .69
difeomorfismo, com 0 ÐY Ñ aberto em Q
Dem: Podemos já afastar o caso trivial em que O œ g, em que podemos
tomar Y œ g. Para cada B − O , o teorema da aplicação inversa implica a
existência de um aberto YB de Q , com B − YB , tal que a restrição de 0 seja
s . Tem-se então que - YB
um difeomorfismo de YB sobre um aberto ZB de Q
B−O
é um aberto de Q , contendo O , e o resultado ficará provado se mostrarmos a
existência de um aberto Y de Q , com O § Y § - YB , tal que 0ÎY seja
s e a
injectiva, visto que então 0 ÐY Ñ œ - 0 ÐYB Y Ñ é um aberto de Q
B−O
B−O
aplicação inversa da bijecção 0ÎY À Y Ä 0 ÐY Ñ vem suave, por ter restrição
suave a cada um dos abertos 0 ÐYB Y Ñ § ZB (igual à restrição a esse aberto
de Ð0ÎYB Ñ" À ZB Ä YB ). Vamos então supor que não existia nenhum aberto
Y , com O § Y § - YB , tal que a restrição de 0 a Y seja injectiva e tentar
B−O
chegar a um absurdo. Para cada natural 8 ", podemos considerar então o
aberto
Y8 œ ÖC − . YB ± .ÐCß OÑ
B−O
"
×,
8
que contém O e está contido na união dos YB , pelo que a restrição de 0 a Y8
não é injectiva ou seja, existe B8 Á C8 em Y8 tais que 0 ÐB8 Ñ œ 0 ÐC8 Ñ. Pela
compacidade de O , que garante que as funções distância a B8 e a C8 atingem
aí um mínimo, podemos considerar Bw8 ß C8w − O tais que
.ÐB8 ß Bw8 Ñ œ .ÐB8 ß OÑ
"
,
8
.ÐC8 ß C8w Ñ œ .ÐC8 ß OÑ
"
,
8
em particular .ÐB8 ß Bw8 Ñ Ä ! e .ÐC8 ß C8w Ñ Ä !. A compacidade de O garante-nos que, se necessário substituindo todas as sucessões consideradas por
subsucessões correspondentes a um mesmo conjunto de índices, existe
ÐBw ß Cw Ñ em O tal que ÐB8w ß C8w Ñ Ä ÐBw ß Cw Ñ. O facto de se ter
69O
teorema da aplicação inversa usual não é mais do que o caso particular do resultado
anterior em que tomamos para O um conjunto reduzido a um elemento.
§7. Invariância topológica da cohomologia
.ÐB8 ß Bw Ñ Ÿ .ÐB8 ß B8w Ñ .ÐB8w ß Bw Ñ,
267
.ÐC8 ß Cw Ñ Ÿ .ÐC8 ß C8w Ñ .ÐC8w ß Cw Ñ,
garante que vem ainda .ÐB8 ß Bw Ñ Ä ! e .ÐC8 ß Cw Ñ Ä !, ou seja, B8 Ä Bw e
C8 Ä Cw . A continuidade de 0 garante agora que a sucessão 0 ÐB8 Ñ œ 0 ÐC8 Ñ
converge simultaneamente para 0 ÐBw Ñ e para 0 ÐCw Ñ, o que implica que
0 ÐBw Ñ œ 0 ÐCw Ñ. Pelo facto de a restrição de 0 a O ser injectiva, deduzimos
agora que Bw œ Cw e então, para 8 suficientemente grande, B8 e C8 são
elementos distintos de YBw com a mesma imagem por 0 , o que é absurdo,
tendo em conta o facto de a restrição de 0 a YBw ser injectiva.
IV.7.4. (Vizinhança tubular associada a um compacto) Sejam I um espaço
euclidiano, Q § I uma variedade sem bordo e O § Q um conjunto
compacto. Existe então um aberto [ de I , com O § [ , um aberto Y de
Q , com O § Y , e um real < ! tais que:
a) Para cada B − Y e A − XB ÐQ Ѽ , com mAm <, tem-se B A − [ , em
particular, Y § [ .
b) Para cada C − [ , existe um, e um só, B − Y tal que C B − XB ÐQ Ѽ e
mC Bm <, ou seja, existe um único ÐBß AÑ tal que B − Y , A − XB ÐQ Ѽ ,
mAm < e C œ B A.
c) É suave a aplicação FÀ [ Ä Y , definida pela condição de se ter, para
cada C − [ , C FÐCÑ − XFÐCÑ ÐQ Ѽ e mC FÐCÑm < (cf. a alínea b)),
aplicação que verifica a condição FÐBÑ œ B, para cada B − Y .
É costume dizer então que [ é uma vizinhança tubular de Y (cf. a figura
11).
Figura 11
Dem: Podemos afastar o caso trivial em que O œ g, caso em que podemos
tomar Y œ [ œ g e < ! arbitrário. Recordemos que, uma vez que Q é
uma variedade contida num espaço euclidiano de dimensão 8, podemos
considerar o fibrado vectorial de base Q , que a cada B − Q associa o
complementar ortogonal XB ÐQ Ѽ do espaço tangente, e que, por
conseguinte, o seu espaço total
268
Cap. IV. Introdução à cohomologia de de Rham
X ÐQ Ѽ œ ÖÐBß AÑ − I ‚ I ± B − Q , A − XB ÐQ Ѽ ×
é uma variedade sem bordo (cf., por exemplo [10]). Para além disso, sendo 8
a dimensão de I , se Q tem dimensão 7 em B, XB ÐQ Ѽ tem dimensão
8 7, pelo que X ÐQ Ѽ tem dimensão 8 em cada ÐBß AÑ. Recordemos ainda
que, por uma propriedade geral dos espaços totais dos fibrados vectoriais,
para um ponto de X ÐQ Ѽ da forma ÐBß !Ñ, tem-se
XÐBß!Ñ ÐX ÐQ Ѽ Ñ œ XB ÐQ Ñ ‚ XB ÐQ Ѽ
(cf., por exemplo, [10]). Podemos agora considerar a aplicação suave
GÀ X ÐQ Ѽ Ä I , definida por GÐBß AÑ œ B A. Para cada ponto do compacto O ‚ Ö!× § X ÐQ Ѽ , a aplicação linear
HGÐBß!Ñ À XB ÐQ Ñ ‚ XB ÐQ Ѽ Ä I
está definida por Ð?ß @Ñ È ? @ pelo que o facto de ter lugar a soma directa
I œ XB ÐQ Ñ Š XB ÐQ Ѽ implica que esta aplicação linear é um isomorfismo.
Uma vez que GÐBß !Ñ œ B, e portanto a restrição de G a O ‚ Ö!× é injectiva,
podemos aplicar IV.7.3 para concluir a existência de um aberto h w de
X ÐQ Ѽ , contendo O ‚ Ö!×, e de um aberto [ w de I tais que a restrição de
G seja um difeomorfismo de h w sobre [ w . Consideremos em I ‚ I a norma
do máximo e seja < ! menor que a distância estritamente positiva do
compacto
O ‚ Ö!×
ao
fechado
X ÐQ Ѽ Ï h w .70
Sendo
Y œ ÖB − Q ± .ÐBß OÑ <×, Y é um aberto de Q contendo O e, para cada
B − Y e A − XB ÐQ Ѽ , com mAm <, vem .ÐÐBß AÑß O ‚ Ö!×Ñ <, portanto
ÐBß AÑ − h w . Podemos então considerar o aberto
h œ ÖÐBß AÑ − X ÐQ Ѽ ± B − Y , mAm <×
de X ÐQ Ѽ , que contém O ‚ Ö!× e está contido em h w , e a restrição de G vai
ser um difeomorfismo de h sobre um aberto [ de I , contido em [ w , aberto
que contém Y , e portanto também O , uma vez que GÐBß !Ñ œ B. As alíneas
a) e b) do enunciado são agora triviais e a alínea c) resulta de que a aplicação
F não é mais do que a composta do difeomorfismo G" À [ Ä h com a
primeira projecção h Ä Y , desde que se repare que, para B − Y ,
GÐBß !Ñ œ B.
Quando a variedade sem bordo Q é compacta, podemos em IV.7.4 tomar
para compacto O o próprio Q e as respectivas conclusões podem então
ser enunciadas de modo mais completo.
IV.7.5. (Vizinhanças tubulares das variedades compactas) Sejam I um
espaço euclidiano e Q § I uma variedade compacta, sem bordo. Tendo em
70<
! arbitrário se fosse h w œ X ÐQ Ѽ .
§7. Invariância topológica da cohomologia
269
conta IV.7.4, podemos então garantir a existência de < ! e de um aberto [
de I , tais que:
a) Para cada B − Q e A − XB ÐQ Ѽ , com mAm <, tem-se B A − [ , em
particular, Q § [ .
b) Para cada C − [ , existe um, e um só, B − Q tal que C B − XB ÐQ Ѽ e
mC Bm <, ou seja, existe um único ÐBß AÑ tal que B − Q , A − XB ÐQ Ѽ ,
mAm < e C œ B A.
c) É suave a aplicação FÀ [ Ä Q , definida pela condição de se ter, para
cada C − [ , C FÐCÑ − XFÐCÑ ÐQ Ѽ e mC FÐCÑm <, aplicação que
verifica FÐBÑ œ B, para cada B − Q .
Neste caso podemos afirmar mais, nomeadamente:
d) [ é o conjunto dos C − I tais que .ÐCß Q Ñ < e, para cada C − [ ,
FÐCÑ é o único elemento de Q a distância mínima de C .71
Costuma-se então dizer que [ é uma vizinhança tubular de Q .
Dem: Podemos já afastar o caso trivial em que Q œ g, em que se toma
[ œ g e < ! arbitrário. Pela condição c), para cada C − [ , .ÐCß Q Ñ <.
Suponhamos agora que C − I é tal que .ÐCß Q Ñ < e que B! − Q é um
ponto a distância mínima de C , o que implica, em particular, que
mC B! m <. Sendo 0 À Q Ä ‘ a aplicação suave definida por
0 ÐBÑ œ mC Bm# œ ØC Bß C BÙ,
o facto de 0 atingir um mínimo em B! e de Q ser uma variedade sem bordo
implica que H0B! À XB! ÐQ Ñ Ä ‘ é a aplicação linear nula, isto é, que, para
cada A − XB! ÐQ Ñ,
! œ H0B! ÐAÑ œ #ØC B! ß AÙ.
Ficou assim provado que C B! − XB! ÐQ Ѽ , o que, por a), implica que
C œ B! ÐC B! Ñ − [ . Pela definição em c), vemos que B! œ FÐCÑ, o que
mostra que FÐCÑ é realmente o único ponto de Q a distância mínima de C .
IV.7.6. Sejam Q w § I w uma variedade compacta e Q § I uma variedade sem
bordo. Sejam 0 ß 1À Q w Ä Q duas aplicações suaves homotópicas. Tem-se
então que 0 e 1 são mesmo suavemente homotópicas.
Dem: Podemos já afastar o caso trivial em que Q w œ g. Seja então
LÀ Ò!ß "Ó ‚ Q w Ä Q uma aplicação contínua tal que LÐ!ß BÑ œ 0 ÐBÑ e
LÐ"ß BÑ œ 1ÐBÑ. Em particular a restrição de L ao subconjunto fechado
Ö!ß "× ‚ Q w de Ò!ß "Ó ‚ Q w é suave, por ter restrição suave a cada um dos
abertos Ö!× ‚ Q w e Ö"× ‚ Q w de Ö!ß "× ‚ Q w . Considerando o subconjunto
compacto LÐÒ!ß "Ó ‚ Q w Ñ de Q , deduzimos de IV.7.4 a existência de um
aberto [ de I , contendo esse compacto e de uma aplicação suave
FÀ [ Ä Q tal que, para cada C − LÐÒ!ß "Ó ‚ Q w Ñ, FÐCÑ œ C. Seja $ !
71Se
não quisermos afastar o caso trivial em que Q œ g, temos que usar a convenção que
a distância de C ao conjunto vazio é _ (o ínfimo do conjunto do vazio, sendo o máximo
dos seus minorantes, só pode ser olhado como _).
270
Cap. IV. Introdução à cohomologia de de Rham
menor que a distância estritamente positiva do compacto LÐÒ!ß "Ó ‚ Q w Ñ ao
fechado I Ï [ .72 Tendo em conta III.8.6, podemos considerar uma
s Ò!ß "Ó ‚ Q w Ä I tal que, para cada Ð>ß BÑ − Ò!ß "Ó ‚ Q w ,
aplicação suave LÀ
s BÑ LÐ>ß BÑm $,
mLÐ>ß
s BÑ − [ , e que, para cada Ð>ß BÑ − Ö!ß "× ‚ Q w , LÐ>ß
s BÑ œ
e portanto LÐ>ß
s
s
LÐ>ß BÑ, e portanto ainda LÐ!ß BÑ œ 0 ÐBÑ e LÐ"ß BÑ œ 1ÐBÑ. Podemos
finalmente considerar a aplicação suave L̃À Ò!ß "Ó ‚ Q w Ä Q definida por
˜ BÑ œ FÐLÐ>ß
˜ BÑ œ 0 ÐBÑ e
s BÑÑ, para a qual se vai ter ainda LÐ!ß
LÐ>ß
˜ BÑ œ 1ÐBÑ, o que mostra que 0 e 1 são suavemente homotópicas.
LÐ"ß
IV.7.7. Sejam Q w § I w uma variedade compacta e Q § I uma variedade sem
bordo. Se 0 À Q w Ä Q é uma aplicação contínua, então existe uma aplicação
suave 1À Q w Ä Q homotópica a 0 e, se 1ß s1À Q w Ä Q são aplicações suaves
homotópicas a 0 , então, para cada :,
L : Ð1Ñ œ L : Ð1ÑÀ
s L : ÐQ Ñ Ä L : ÐQ w Ñ.
Dem: Podemos já afastar o caso trivial em que Q w œ g. Considerando o
subconjunto compacto 0 ÐQ w Ñ de Q , deduzimos de IV.7.4 a existência de um
aberto [ de I , contendo esse compacto e de uma aplicação suave
FÀ [ Ä Q tal que, para cada C − 0 ÐQ w Ñ, FÐCÑ œ C . Seja $ ! menor que
a distância estritamente positiva do compacto 0 ÐQ w Ñ ao fechado I Ï [ .73
Tendo em conta III.8.5, podemos considerar uma aplicação suave 1̃À Q w Ä I
tal que, para cada B − Q w , m1ÐBÑ
0 ÐBÑm $ , e portanto 1ÐBÑ
− [ , pelo
˜
˜
que podemos definir uma aplicação suave 1À Q w Ä Q por 1ÐBÑ œ FÐ1ÐBÑÑ
.
˜
Seja L̃À Ò!ß "Ó ‚ Q w Ä I a aplicação contínua definida por
˜ BÑ œ 0 ÐBÑ >Ð1ÐBÑ
LÐ>ß
0 ÐBÑÑ,
˜
˜ BÑ œ 0 ÐBÑ e LÐ"ß
˜ BÑ œ 1ÐBÑ
para a qual se tem LÐ!ß
˜ . Para cada
Ð>ß BÑ − Ò!ß "Ó ‚ Q w , tem-se
˜ BÑ 0 ÐBÑm œ >m1ÐBÑ
mLÐ>ß
0 ÐBÑm $ ,
˜
pelo que L̃Ð>ß BÑ − [ , o que nos permite definir uma aplicação contínua
˜ BÑÑ. Tem-se então LÐ!ß BÑ œ
LÀ Ò!ß "Ó ‚ Q w Ä Q por LÐ>ß BÑ œ FÐLÐ>ß
FÐ0 ÐBÑÑ œ 0 ÐBÑ e LÐ"ß BÑ œ FÐ1ÐBÑÑ
œ 1ÐBÑ, o que mostra que a aplicação
˜
contínua 0 À Q w Ä Q é realmente homotópica à aplicação suave
1À Q w Ä Q . Por fim, se 1ß s1À Q w Ä Q são duas aplicações suaves, ambas
homotópicas a 0 , concluíamos, por transitividade, que 1 e s1 são homotópicas
e portanto, por IV.7.6, também suavemente homotópicas o que, por IV.1.12,
implica que, para cada :, L : Ð1Ñ œ L : Ð1ÑÀ
s L : ÐQ Ñ Ä L : ÐQ w Ñ.
72No
73No
caso em que fosse [ œ I , tomávamos $ ! arbitrário.
caso em que fosse [ œ I , tomávamos $ ! arbitrário.
§7. Invariância topológica da cohomologia
271
IV.7.8. Sejam Q w § I w uma variedade compacta e Q § I uma variedade sem
bordo. Se 0 À Q w Ä Q é uma aplicação contínua, define-se, para cada :, uma
aplicação linear L : Ð0 ÑÀ L : ÐQ Ñ Ä L : ÐQ w Ñ, pondo L : Ð0 Ñ œ L : Ð1Ñ, onde
1À Q w Ä Q é uma aplicação suave homotópica a 0 arbitrária.
É claro que, no caso em que a aplicação contínua 0 é suave, a definição
anterior coincide com a já conhecida, uma vez que podemos tomar para 1 o
próprio 0 .
IV.7.9. Sejam Q w § I w uma variedade compacta e Q § I uma variedade sem
bordo. Se 0 ß 1À Q w Ä Q são aplicações contínuas homotópicas, então
L : Ð0 Ñ œ L : Ð1ÑÀ L : ÐQ Ñ Ä L : ÐQ w Ñ.
Dem: Basta atender a que, se 2À Q w Ä Q é uma aplicação suave
homotópica a 0 , então 2 é também homotópica a 1.
Os dois resultados anteriores exprimem a invariância topológica da
cohomologia de de Rham, no quadro particular em que o domínio é uma
variedade compacta e o espaço de chegada é uma variedade sem bordo.
Com técnicas mais elaboradas de aproximação, como por exemplo as
descritas em [5], pode-se estudar essa invariância num quadro mais geral.
O facto de termos reduzido o nosso estudo ao quadro particular referido,
obriga-nos a enunciar a propriedade de functorialidade como três
resultados distintos.
IV.7.10. (Functorialidade) a) Sejam Q ww § I ww uma variedade compacta,
Q w § I w e Q § I variedades sem bordo, 0 À Q ww Ä Q w uma aplicação
contínua e 1À Q w Ä Q uma aplicação suave. Para cada :, tem-se então
L : Ð1 ‰ 0 Ñ œ L : Ð0 Ñ ‰ L : Ð1ÑÀ L : ÐQ Ñ Ä L : ÐQ ww ÑÞ
b) Sejam Q ww § I ww e Q w § I w variedades compactas, Q § I uma
variedade sem bordo, 0 À Q ww Ä Q w uma aplicação suave e 1À Q w Ä Q uma
aplicação contínua. Para cada :, tem-se então
L : Ð1 ‰ 0 Ñ œ L : Ð0 Ñ ‰ L : Ð1ÑÀ L : ÐQ Ñ Ä L : ÐQ ww ÑÞ
c) Sejam Q ww § I ww uma variedade compacta, Q w § I w uma variedade
compacta e sem bordo, Q § I uma variedade sem bordo e 0 À Q ww Ä Q w e
1À Q w Ä Q aplicações contínuas. Para cada :, tem-se então
L : Ð1 ‰ 0 Ñ œ L : Ð0 Ñ ‰ L : Ð1ÑÀ L : ÐQ Ñ Ä L : ÐQ ww ÑÞ
Dem: Para a alínea a), consideramos uma aplicação suave s0 À Q ww Ä Q w e
uma aplicação contínua LÀ Ò!ß "Ó ‚ Q ww Ä Q w tal que LÐ!ß BÑ œ 0 ÐBÑ e
LÐ"ß BÑ œ s0 ÐBÑ e reparamos que tem então lugar uma aplicação contínua
˜ Ò!ß "Ó ‚ Q ww Ä Q definida por LÐ>ß
˜ BÑ œ 1ÐLÐ>ß BÑÑ, para a qual se tem
LÀ
˜
˜
s
LÐ!ß BÑ œ 1 ‰ 0 ÐBÑ e LÐ"ß BÑ œ 1 ‰ 0 ÐBÑ, de onde deduzimos que
272
Cap. IV. Introdução à cohomologia de de Rham
s Ñ ‰ L : Ð1Ñ œ L : Ð0 Ñ ‰ L : Ð1Ñ.
L : Ð1 ‰ 0 Ñ œ L : Ð1 ‰ s0 Ñ œ L : Ð0
Para a alínea b), consideramos uma aplicação suave s1À Q w Ä Q e uma
s Ò!ß "Ó ‚ Q w Ä Q tal que LÐ!ß
s CÑ œ 1ÐCÑ e
aplicação contínua LÀ
s
LÐ"ß CÑ œ s1ÐCÑ e reparamos que tem então lugar uma aplicação contínua
˜ Ò!ß "Ó ‚ Q ww Ä Q definida por LÐ>ß
˜ BÑ œ LÐ>ß
s 0 ÐBÑÑ, para a qual se tem
LÀ
˜ BÑ œ 1 ‰ 0 ÐBÑ e LÐ"ß
˜ BÑ œ s1 ‰ 0 ÐBÑ, de onde deduzimos que
LÐ!ß
L : Ð1 ‰ 0 Ñ œ L : Ð1
s ‰ 0 Ñ œ L : Ð0 Ñ ‰ L : Ð1Ñ
s œ L : Ð0 Ñ ‰ L : Ð1Ñ.
Para a alínea c), combinamos os processos anteriores, considerando aplicações suaves s0 À Q ww Ä Q w e s1À Q w Ä Q e aplicações contínuas
LÀ Ò!ß "Ó ‚ Q ww Ä Q w ,
s Ò!ß "Ó ‚ Q w Ä Q ,
LÀ
s CÑ œ 1ÐCÑ e LÐ"ß
s CÑ œ
verificando LÐ!ß BÑ œ 0 ÐBÑ, LÐ"ß BÑ œ s0 ÐBÑ, LÐ!ß
s1ÐCÑ e reparamos que tem então lugar uma aplicação contínua
˜ Ò!ß "Ó ‚ Q ww Ä Q ,
LÀ
˜ BÑ œ LÐ>ß
s LÐ>ß BÑÑ,
LÐ>ß
˜ BÑ œ 1 ‰ 0 ÐBÑ e LÐ"ß
˜ BÑ œ s1 ‰ s0 ÐBÑ, de onde
para a qual se tem LÐ!ß
deduzimos que
s Ñ ‰ L : Ð1Ñ
L : Ð1 ‰ 0 Ñ œ L : Ð1
s ‰ s0 Ñ œ L : Ð0
s œ L : Ð0 Ñ ‰ L : Ð1Ñ.
IV.7.11. (Corolário) Sejam Q w § I w e Q § I variedades compactas e sem
bordo e 0 À Q w Ä Q um homeomorfismo. Para cada :, tem-se então que
L : Ð0 ÑÀ L : ÐQ Ñ Ä L : ÐQ w Ñ
é um isomorfismo e L : Ð0 Ñ" œ L : Ð0 " Ñ.
Dem: Aplicando a alínea c) de IV.7.10 às aplicações contínuas 0 À Q w Ä Q
e 0 " À Q Ä Q w , concluímos que
M.L : ÐQ Ñ œ L : ÐM.Q Ñ œ L : Ð0 ‰ 0 " Ñ œ L : Ð0 " Ñ ‰ L : Ð0 Ñ,
M.L : ÐQ w Ñ œ L : ÐM.Q w Ñ œ L : Ð0 " ‰ 0 Ñ œ L : Ð0 Ñ ‰ L : Ð0 " Ñ,
donde o resultado.
EXERCÍCIOS
Ex IV.1 Sejam Q § I e Q w § I w duas variedades e 0 À Q w Ä Q uma
aplicação suave. Diz-se que uma aplicação suave 1À Q Ä Q w é um inverso
esquerdo de 0 , módulo homotopia suave (respectivamente um inverso direito
de 0 , módulo homotopia suave) se 1 ‰ 0 À Q w Ä Q w é suavemente
Exercícios
273
homotópico a M.Q w (respectivamente se 0 ‰ 1À Q Ä Q é suavemente
homotópico a M.Q ). Diz-se que uma aplicação suave 1À Q Ä Q w é um
inverso de 0 , módulo homotopia suave, se for simultaneamente um inverso
esquerdo e um inverso direito, em ambos os casos módulo homotopia suave,
e, quando existir uma tal aplicação 1, diz-se que 0 é invertível, módulo
homotopia suave. Diz-se que as variedades Q e Q w são homotopicamente
equivalentes se existir 0 À Q w Ä Q invertível, módulo homotopia suave.
a) Mostrar que, se 0 À Q w Ä Q é um difeomorfismo, então 0 é invertível,
módulo homotopia suave, e 0 " À Q Ä Q w é um inverso de 0 , módulo
homotopia suave. Em particular duas variedades difeomorfas também são
homotopicamente equivalentes.
b) Mostrar que, se 0 À Q ww Ä Q w e 1À Q w Ä Q são aplicações suaves invertíveis, módulo homotopia suave, então 1 ‰ 0 À Q ww Ä Q é também invertível,
módulo homotopia suave. Deduzir daqui que a relação “homotopicamente
equivalente” é uma relação de equivalência nas classe das variedades.
c) Mostrar que, se 1ß s1À Q Ä Q w são suavemente homotópicas e se 1 é um
inverso esquerdo (respectivamente um inverso direito) de 0 módulo homotopia suave, então o mesmo acontece a s1.
d) Mostrar que, se uma aplicação suave 0 À Q w Ä Q admite um inverso
esquerdo 1À Q Ä Q w , módulo homotopia suave, e um inverso direito
s1À Q Ä Q w , módulo homotopia suave, então 1 e s1 são suavemente
homotópicas, e portanto 1 (tal como s1) é um inverso de 0 , módulo homotopia
suave. Sugestão: Lembrar a demonstração, por certo já encontrada no quadro
dos semi-grupos com elemento neutro, de que se um elemento possui um
inverso direito e um inverso esquerdo, então estes são iguais.
e) Mostrar que, se 0 À Q w Ä Q é invertível, módulo homotopia suave, então,
para cada :, L : Ð0 ÑÀ L : ÐQ Ñ Ä L : ÐQ w Ñ é um isomorfismo.
Ex IV.2 (Só para quem conheça os fundamentos da Teoria das Categorias)
a) Mostrar que se pode considerar naturalmente uma categoria cujos objectos
são as variedades e cujos morfismos entre duas variedades são as classes de
equivalência de aplicações suaves para a relação de “homotopia suave”.
Verificar que, para cada inteiro :, a cohomlogia de de Rham de grau : pode
ser olhada como um functor contravariante da categoria anterior para a dos
espaços vectoriais e reinterpretar o exercício IV.1 sob este ponto de vista.
b) Mostrar que as variedades suavemente contrácteis são precisamente
aquelas que são isomorfas a variedades reduzidas a um ponto, na categoria
atrás referida e reobter, a partir daí, a caracterização dos espaços de cohomologia de de Rham de uma tal variedade, obtida em IV.1.13.
Ex IV.3 Sejam Q § I uma variedade suavemente contráctil e Q w § I w uma
variedade conexa. Mostrar que quaisquer aplicações suaves 0 ß 1À Q Ä Q w
são suavemente homotópicas (comparar com IV.1.14). Sugestão: Utilizar a
hipótese de Q w ser conexa para mostrar que duas aplicações constantes
Q Ä Q w são sempre suavemente homotópicas. Utilizar IV.1.11 para
274
Cap. IV. Introdução à cohomologia de de Rham
mostrar que qualquer aplicação suave Q Ä Q w é suavemente homotópica a
uma certa aplicação constante.
Ex IV.4 O que será um produto de uma família de espaços vectoriais constituída
por um único elemento (isto é, em que o conjunto dos índices seja unitário)?
E um produto de uma família vazia de espaços vectoriais?
Ex IV.5 Sejam ÐI4 Ñ4−N uma família de espaços vectoriais, I um espaço
vectorial e, para cada 4 − N , 1
s4 À I Ä I4 uma aplicação linear.
a) Suponhamos que I é um produto dos I4 , com as projecções 1
s4 . Mostrar
que, dados um espaço vectorial J , e, para cada 4, uma aplicação linear
-4 À J Ä I4 , existe uma, e uma só, aplicação linear -À J Ä I tal que, para
cada 4, 1
s4 ‰ - œ -4 .74
b) Suponhamos que, quaisquer que sejam o espaço vectorial J e as
aplicações lineares -4 À J Ä I4 , existe uma, e uma só, aplicação linear
-À J Ä I tal que, para cada 4, 1
s4 ‰ - œ -4 . Mostrar que I é um produto dos
I4 , com as projecções 1
.
Sugestão:
Sendo .À I Ä # I4 a aplicação linear
s4
definida por .ÐBÑ œ Ð1
s4 ÐBÑÑ4−N , utilizar a hipótese para definir uma
aplicação linear -À # I4 Ä I , que se mostrará ser um inverso bilateral de ..
Ex IV.6 O que será uma soma de uma família de espaços vectoriais constituída
por um único elemento (isto é, em que o conjunto dos índices seja unitário)?
E uma soma de uma família vazia de espaços vectoriais?
Ex IV.7 Sejam ÐI4 Ñ4−N uma família de espaços vectoriais, I um espaço
vectorial e, para cada 4 − N , s+4 À I4 Ä I uma aplicação linear.
a) Suponhamos que I é uma soma dos I4 , com as injecções s+4 . Mostrar que,
dados um espaço vectorial J e, para cada 4, uma aplicação linear
-4 À I4 Ä J , existe uma, e uma só, aplicação linear -À I Ä J tal que, para
cada 4, - ‰s+4 œ -4 , nomeadamente a definida por
-Ð" +4 ÐB4 ÑÑ œ " -4 ÐB4 Ñ,
4
4
onde ÐB4 Ñ4−N é uma família essencialmente finita, com B4 − I4 .75
b) Suponhamos que, quaisquer que sejam o espaço vectorial J e as
aplicações lineares -4 À I4 Ä J , existe uma, e uma só, aplicação linear
-À I Ä J tal que, para cada 4, - ‰s+4 œ -4 . Mostrar que I é uma soma dos
s § # I4 a soma construída a
I4 , com as injecções s+4 . Sugestão: Sendo I
partir do produto cartesiano pelo método descrito em IV.2.10, considerar a
s Ä I definida por .ÐÐB4 Ñ4−N Ñ œ !s+4 ÐB4 Ñ e utilizar a
aplicação linear .À I
74Esta
condição exprime que, no sentido da teoria das categorias, I é um produto dos I4 ,
com as projecções 1
s 4 À I Ä I4 .
75Esta condição exprime que, no sentido da teoria das categorias, I é uma soma dos I ,
4
com as injecções s+4 À I4 Ä I .
Exercícios
275
s , que se mostrará ser um
hipótese para definir uma aplicação linear -À I Ä I
inverso bilateral de ..
Ex IV.8 Enunciar de forma precisa, e demonstrar, o facto de a soma de espaços
vectoriais, tal como o produto, estar definida a menos de isomorfismo.
Ex IV.9 Sejam ÐI4 Ñ4−N e ÐJ4 Ñ4−N famílias de espaços vectoriais e, para cada
4 − N , -4 À I4 Ä J4 uma aplicação linear. Se I e J são produtos daquelas
famílias, com as projecções 1
s4 À I Ä I4 e 1˜4 À J Ä J4 , respectivamente, define-se o produto das aplicações lineares -4 como sendo a única aplicação
linear -À I Ä J tal que, para cada 4, 1˜4 ‰ - œ -4 ‰ 1
s4 (cf. o exercício IV.5).
Do mesmo modo, se I w e J w são somas daquelas famílias, com as injecções
s+4 À I4 Ä I e +˜4 À J4 Ä J , respectivamente, define-se a soma das aplicações
lineares -4 como sendo a única aplicação linear -w À I w Ä J w tal que, para
cada 4, +˜4 ‰ -4 œ -w ‰s+4 (cf. o exercício IV.7).
a) No caso em que I e J são os produtos cartesianos das famílias ÐI4 Ñ4−N e
ÐJ4 Ñ4−N e as projecções consideradas são as projecções canónicas, verificar
que o produto das aplicações lineares -4 é o produto cartesiano usual de
aplicações.
b) Verificar que a soma de aplicações lineares, definida acima, é dada, mais
explicitamente por -w ÐBÑ œ ! +˜4 Ð-4 ÐB4 ÑÑ, onde ÐB4 Ñ4−N é uma família essen-
cialmente finita de vectores B4 − I4 tal que B œ !s+4 ÐB4 Ñ, ou seja, por outras
palavras, por
-w ÐBÑ œ " +˜4 Ð-4 Ð1
s4 ÐBÑÑÑ,
4−N
onde os 1
s4 À I w Ä I4 são as projecções associadas à soma (cf. IV.2.11).
c) Suponhamos que o conjunto de índices N é finito e que I e J são
produtos das famílias ÐI4 Ñ4−N e ÐJ4 Ñ4−N , com as projecções 1
s4 À I Ä I4 e
1̃4 À J Ä J4 , respectivamente, e consideremos as injecções associadas
s+4 À I4 Ä I e +˜4 À J4 Ä J , que sabemos definirem I e J como somas
daquelas famílias (cf. IV.2.13). Mostrar que a soma das aplicações lineares
-4 coincide então com o respectivo produto.
d) Generalizar a conclusão de c) ao caso em que o conjunto dos índices é
infinito, considerando, nas condições de IV.2.10, os subespaços soma
I! § I e J! § J .
Ex IV.10 Seja N um conjunto de índices e seja, para cada 4 − N , G4ñ um
complexo de cocadeias, definido pelos espaços vectoriais G4: , com : − ™, e
pelas aplicações lineares cobordo .4: À G4: Ä G4:" . Suponhamos que, para
cada : − ™, se considera um produto G : da família dos G4: , definido pelas
:
:
projecções 1
s4 À G : Ä G4 e consideremos o correspondente complexo de
cocadeias produto G ñ (cf. IV.2.4). Considerando, para cada :, as injecções
276
Cap. IV. Introdução à cohomologia de de Rham
associadas s+:4 À G4: Ä G : , mostrar que os s+ñ4 œ Ðs+4: Ñ:−™ são morfismos de
complexos de cocadeias de G4ñ para G ñ e que os correspondentes
L : Ðs+ñ4 ÑÀ L : ÐG4ñ Ñ Ä L : ÐG ñ Ñ são as injecções associadas à apresentação de
L : ÐG ñ Ñ como produto dos L : ÐG4ñ Ñ (cf. IV.2.5).
Ex IV.11 Sejam Q § I uma variedade e ÐY4 Ñ4−N uma família de abertos de Q
disjuntos dois a dois e de união Q . Notando +4 À Y4 Ä Q as inclusões,
definidas por +4 ÐBÑ œ B, viu-se em IV.2.6 que o complexo de cocadeias
Hñ ÐQ Ñ é um produto dos complexos de cocadeias Hñ ÐY4 Ñ, tendo como
projecções as famílias de aplicações lineares +4‡ À H: ÐQ Ñ Ä H: ÐY4 Ñ e que, em
consequência, para cada :, L : ÐQ Ñ é um produto dos L : ÐY4 Ñ, definido pelas
projecções L : Ð+4 Ñ, que associam a cada Ò=Ó as classes Ò=ÎY4 Ó. Determinar o
que são as injecções associadas H: ÐY4 Ñ Ä H: ÐQ Ñ e, consequentemente, as
injecções associadas L : ÐY4 Ñ Ä L : ÐQ Ñ.
Ex IV.12 a) Consideremos os espaços vectoriais e aplicações lineares
representados no seguinte diagrama
-
I
!Æ!
qp
Iw
qp
.
J
" Æ"
qp
Jw
qp
-w
#
.w
K
Æ#
Kw
e suponhamos que !, " e # são isomorfismos, que a primeira linha é uma
sucessão exacta e que o diagrama é comutativo, no sentido de se ter
" ‰ - œ -w ‰ ! e # ‰ . œ .w ‰ " . Mostrar que a segunda linha é então
também exacta.
b) Utilizar a conclusão de a) para mostrar que, nas hipóteses de IV.3.4 e
IV.3.5, tem também lugar, com morfismos convenientes, uma sucessão
exacta (dita também de Mayer-Vietoris)
` :"
`:
L :" ÐY Z Ñ qqp L : ÐQ Ñ qqp L : ÐY Ñ ‚ L : ÐZ Ñ qqp L : ÐY Z Ñ qqp L :" ÐQ Ñ.
Ex IV.13 Consideremos a circunferência W " § ‘# , com a orientação que lhe
vem de ser bordo da bola fechada de centro ! e raio ", e os subconjuntos
abertos W e W de W " , com união W " , definidos na demonstração de
IV.3.12. Consideremos a porção da sucessão exacta de Mayer-Vietoris
correspondente
L ! Ð.ñ Ñ
`!
L ! ÐHñ ÐW Ñ ‚ Hñ ÐW ÑÑ qqp L ! ÐW W Ñ qqp L " ÐW " Ñ qqp Ö!×.
Reparemos que W W é o conjunto dos ÐBß CÑ − W " tais que B Á !, tendo
assim duas componentes conexas
W. œ ÖÐBß CÑ − W " ± B !Ñ,
W/ œ ÖÐBß CÑ − W " ± B !×,
ambas naturalmente difeomorfas a Ó"ß "Ò pela projecção no segundo factor.
Exercícios
277
Sendo 0. ß 0/ À W W Ä ‘ as aplicações com valores constantes " em W. e
! em W/ e com valores constantes ! em W. e " em W/ , respectivamente,
sabemos portanto que L ! ÐW W Ñ é um espaço vectorial de dimensão #,
admitindo uma base formada pelas classes de equivalência Ò0. Ó e Ò0/ Ó.
a)
Verificar
para
que
escalares
+ß , − Š
a
classe
+Ò0. Ó ,Ò0/ Ó − L ! ÐW W Ñ pertence à imagem da aplicação linear
L ! Ð.ñ Ñ.
"
b) Sendo Z 96 o elemento de volume de W " , verificar que ` ! ÐÒ0. ÓÑ œ #1
ÒZ 96Ó
"
e ` ! ÐÒ0/ ÓÑ œ #1 ÒZ 96Ó.
Sugestão: A conclusão de a) é simples e, tendo em conta esta e a exactidão
"
da sucessão, é fácil de ver que, de b), basta provar que ` ! ÐÒ0. ÓÑ œ #1
ÒZ 96Ó.
Proceder então do seguinte modo:
1) Considerar a aplicação :À ‘ Ä W " , definida por :Ð>Ñ œ ÐcosÐ>Ñß sinÐ>ÑÑ e
verificar que as restrições de : são difeomorfismos Ó $#1 ß 1# Ò Ä W e
Ó 1# ß $#1 Ò Ä W .
2) Por um argumento de partição da unidade, mostrar a existência de uma
aplicação suave !À ‘ Ä Ò!ß _Ò, nula fora de uma parte de Ó 1# ß 1# Ò fechada
em ‘ e tal que '‘ !Ð>Ñ .> œ ".
3) Verificar que 0. œ .! Ð1ß 2Ñ, onde 1À W Ä ‘ e 2À W Ä ‘ estão
definidas por
1Ð:Ð>ÑÑ œ " (
>
1#
!Ð?Ñ .?,
2Ð:Ð=ÑÑ œ (
=
$#1
!Ð?Ñ .? ,
para cada > − Ó 1# ß $#1 Ò e = − Ó $#1 ß 1# Ò.
4) Verificar que existe = − H" ÐW " Ñ tal que =Ð:Ð>ÑÑ œ !Ð>Ñ Z 96:Ð>Ñ , para cada
> − Ó 1# ß 1# Ò e =ÐBßCÑ œ !, nos restantes pontos de W " e que = coincide com .1
em W e com .2 em W .
5) Lembrar que ë À L " ÐW " Ñ Ä Š é um isomorfismo.
Ex IV.14 Sejam Q § I e Q w § I w duas variedades, a segunda das quais suavemente contráctil. Sejam 1" À Q ‚ Q w Ä Q a projecção no primeiro factor e,
para cada C − Q w , 5C À Q Ä Q ‚ Q w a aplicação suave definida por
5C ÐBÑ œ ÐBß CÑ. Mostrar que, para cada :, L : Ð1" ÑÀ L : ÐQ Ñ Ä L : ÐQ ‚ Q w Ñ
é um isomorfismo, tendo como inverso L : Ð5C ÑÀ L : ÐQ ‚ Q w Ñ Ä L : ÐQ Ñ.
Deduzir, em particular, que a aplicação linear L : Ð5C Ñ não depende da escolha de C. Sugestão: Verificar que 1" ‰ 5C œ M.Q e que 5C ‰ 1" é suavemente
homotópico a M.Q ‚Q w , neste último caso utilizando IV.1.14.
Ex IV.15 Nas notações do exercício IV.13, consideremos “ œ W " ‚ W " § ‘% ,
que é portanto uma variedade compacta, sem bordo, de dimensão #, sobre a
qual consideramos a orientação produto (cf. II.7.25), que se verifica
facilmente ser suave.76 Verificar que:
76A
“ costuma-se dar o nome de toro (de dimensão #).
278
Cap. IV. Introdução à cohomologia de de Rham
a) L ! Ð“Ñ é um espaço vectorial de dimensão ", admitindo como base a
classe de equivalência da aplicação “ Ä ‘ de valor constante ".
b) L " Ð“Ñ é um espaço vectorial de dimensão #.
c) L # Ð“Ñ é um espaço vectorial de dimensão ", admitindo uma base formada
pela classe de equivalência do elemento de volume de “, e a aplicação linear
ë À L # Ð“Ñ Ä Š é um isomorfismo.
d) L : Ð“Ñ œ Ö!×, para os restantes valores de :.
Sugestão: A alínea a) resulta de “ ser conexo e, da alínea c), basta mostrar
que L # Ð“Ñ tem dimensão ". Nas notações do exercício IV.13, considerar os
abertos “ œ W " ‚ W e “ œ W " ‚ W de “, com união “ e reparar que o
exercício IV.14 permite calcular a dimensão dos espaços vectoriais L : Г Ñ,
L : Г Ñ e L : Г “ Ñ, este último por ser isomorfo ao espaço
L : ÐW " ‚ W. Ñ ‚ L : ÐW " ‚ W/ Ñ. Considerar a porção seguinte de sucessão
exacta de Mayer-Vietoris (já na versão referida no exercício IV.12)
Ö!× Ä L ! Ð“Ñ Ä L ! Г Ñ ‚ L ! Г Ñ Ä L ! Г “ Ñ Ä L " Ð“Ñ Ä
Ä L " Г Ñ ‚ L " Г Ñ Ä L " Г “ Ñ Ä L # Ð“Ñ Ä Ö!×,
a qual tem dois termos de dimensões ainda não conhecidas pelo que, por si
só, não determina essas dimensões. Estas ficam, no entanto determinadas, se,
por um estudo mais aprofundado da aplicação linear entre espaços vectoriais
de dimensão #, L " Г Ñ ‚ L " Г Ñ Ä L " Г “ Ñ, se concluir que esta
aplicação linear tem um núcleo com dimensão ". Nesse estudo atender ao
exercício anterior que garante que, se = é o elemento de volume de W " , para
cada variedade suavemente contráctil Q w , com projecção 3À W " ‚ Q w Ä W " ,
Ò3‡ =Ó constitui uma base de L " ÐW " ‚ Q w Ñ.
Ex IV.16 Continuemos a considerar a variedade W " § ‘# , com a orientação
usual, e, para simplificar as notações, identifiquemos, do modo usual, ‘# a
‚.
Consideremos,
como
no
exercício
precedente,
o
toro
“ œ W " ‚ W " § ‚ ‚ ‚. O objectivo deste exercício é a obtenção de uma
informação mais completa sobre o espaço de cohomologia L " ГÑ. Notemos
1" ß 1# À “ Ä W " as projecções, definidas por 1" ÐBß CÑ œ B e 1# ÐBß CÑ œ C, e
5" ß 5# À W " Ä “ as “injecções”, definidas por 5" ÐBÑ œ ÐBß "Ñ e 5# ÐCÑ œ Ð"ß CÑ.
Notemos Z 96 − H" ÐW " Ñ a forma diferencial elemento de volume de W " .
a) Verificar que se pode definir uma aplicação linear 0À L " Ð“Ñ Ä ‘# por
0ÐÒ=ÓÑ œ Š( 5"‡ = ß ( 5#‡ =‹.
W"
W"
b) Verificar que a aplicação linear 0À L " Ð“Ñ Ä ‘# é um isomorfismo, que as
formas diferenciais =" œ 1"‡ ÐZ 96Ñ e =# œ 1#‡ ÐZ 96Ñ, pertencentes a H" ГÑ,
são fechadas e que as classes de equivalência Ò=" Ó e Ò=# Ó constituem uma base
do espaço vectorial L " ГÑß de dimensão #.
Sugestão: Verificar que 0ÐÒ=" ÓÑ œ Ð#1ß !Ñ e que 0ÐÒ=# ÓÑ œ Ð!ß #1Ñ.
Exercícios
279
Ex IV.17 Sejam Q § I e Q w § I w variedades e 0 À Q w Ä Q uma aplicação
própria.
a) Mostrar que 0 é uma aplicação fechada, isto é, que, para cada conjunto
fechado E § Q w , o conjunto 0 ÐEÑ § Q é também fechado. Sugestão: Ter
em conta o facto de cada ponto , de Q possuir uma vizinhança compacta Z
e reparar que, se , é aderente a 0 ÐEÑ, então , é também aderente ao conjunto
Z 0 ÐEÑ œ 0 Ð0 " ÐZ Ñ EÑ.
b) Mostrar que, se a aplicação 0 é injectiva, então é um homeomorfismo de
Q w sobre um subconjunto fechado de Q .
c) Deduzir, em particular, que, se Q w é uma subvariedade de Q , então a
inclusão Q w Ä Q é própria se, e só se, Q w é fechada em Q .
Ex IV.18 Sejam I e I w dois espaços vectoriais de dimensão finita e 0 À I w Ä I
uma aplicação contínua. Mostrar que a aplicação 0 é própria se, e só se,
m0 ÐBÑm Ä _ quando mBm Ä _, ou seja, mais precisamente, se, para
cada V !, existe < ! tal que, sempre que mBm <, tem-se m0 ÐBÑm V .
Ex IV.19 Sejam Q § I e Q w § I w duas variedades. Se 0 ß 1À Q w Ä Q são duas
aplicações suaves próprias, diz-se que 0 e 1 são suave e propriamente
homotópicas se exisitir uma aplicação suave própria LÀ Ò!ß "Ó ‚ Q w Ä Q tal
que, para cada B − Q w ,
LÐ!ß BÑ œ 0 ÐBÑ,
LÐ"ß BÑ œ 1ÐBÑ.
Diz-se então que L é uma homotopia suave própria de 0 para 1 (comparar
com III.7.5).
Mostrar que, quando 0 ß 1À Q w Ä Q são suave e propriamente homotópicas,
tem-se, para cada :, L-: Ð0 Ñ œ L-: Ð1ÑÀ L-: ÐQ Ñ Ä L-: ÐQ w Ñ.
Sugestão: Começar por verificar que, se : " e = œ Ð=Ð>ßBÑ ÑÐ>ßBÑ−Ò!ß"Ó‚Q w é
uma forma diferencial suave de grau : sobre Ò!ß "Ó ‚ Q w , nula fora dum coms § Ò!ß "Ó ‚ Q w , então a forma diferencial suave de grau : " sobre
pacto O
w
Q T = œ ÐT =B ÑB−Q w , definida em III.7.2, é nula fora do compacto
s § Q w . Verificar então que, nas condições de III.7.6, quando a forma
1# ÐOÑ
diferencial suave, fechada, de grau : " sobre Q , = œ Ð=C ÑC−Q for nula
fora de um certo compacto contido em Q , a forma diferencial suave de grau
: ", 5 œ Ð5B ÑB−Q , sobre Q w , construída na respectiva demonstração, é
nula fora de um certo compacto contido em Q w .
Ex IV.20 Viu-se, nas diferentes alíneas do exercício II.27, que, dado um
diagrama comutativo do tipo
-
.
-w
.w
Ö!× Ä I Ä J Ä K Ä Ö!×
3Æ3
5Æ5
7 Æ7
,
Ö!× Ä I w Ä J w Ä Kw Ä Ö!×
com as duas linhas exactas, se duas das três aplicações lineares 3, 5 e 7
280
Cap. IV. Introdução à cohomologia de de Rham
forem isomorfismos, então o mesmo acontece à terceira. Mostrar que este
resultado pode ser obtido como consequência imediata do lema dos cinco
(IV.5.14).
Ex IV.21 Sejam I um espaço euclidiano e F § I a bola aberta de centro ! e
raio " de I , F œ ÖB − I ± mBm "×. Mostrar que F é difeomorfa a I e,
mais precisamente, que tem lugar um difeomorfismo 0 À F Ä I , definido por
B
0 ÐBÑ œ
,
È" mBm#
cujo inverso 1À I Ä F está definido por
1ÐCÑ œ
C
.
È" mCm#
Ex IV.22 (O grau de uma aplicação própria) Sejam Q § I e Q w § I w
variedades sem bordo, de dimensão 7, suavemente orientadas, e
suponhamos que Q é conexa e não vaziaÞ
a) Seja 0 À Q w Ä Q uma aplicação suave própria. Mostrar que existe um, e
um só, - − ‘ tal que, qualquer que seja = − H7
- ÐQ à ŠÑ (Š œ ‘ ou ‚),
(
Qw
0 ‡ = œ - ( =.
Q
Diz-se então que - é o grau da aplicação suave = e nota-se - œ degÐ0 Ñ.
Sugestão: Lembrar que têm lugar aplicações lineares, definidas a partir do
integral, ë À L-7 ÐQ Ñ Ä Š, ë À L-7 ÐQ w Ñ Ä Š e que, por IV.5.26, a primeira é
um isomorfismo, pelo que, à aplicação linear L-7 Ð0 ÑÀ L-7 ÐQ Ñ Ä L-7 ÐQ w Ñ,
fica associada uma aplicação linear Š Ä Š, pela condição de fazer comutativo o diagrama
L-7 ÐQ Ñ
3Æë
Š
L-7 Ð0 Ñ
Ä
Ä
L-7 ÐQ w Ñ
3Æë .
Š
b) Nas condições anteriores, suponhamos que C! − Q é um valor regular da
aplicação suave 0 (cf. I.5.1). Mostrar que 0 " ÐÖC! ×Ñ é um conjunto finito,
eventualmente vazio, ÖB" ß B# ß á ß B8 × e notar, para cada " Ÿ 3 Ÿ 8, &3 œ "
ou &3 œ ", conforme o isomorfismo H0B3 À XB3 ÐQ w Ñ Ä XC! ÐQ Ñ conserve, ou
inverta as orientações. Mostrar que se pode escolher, para cada " Ÿ 3 Ÿ 8,
s 3 de Q w , com B3 − Y
s 3 , tal que a restrição de 0 seja um
um aberto Y
s
difeomorfismo de Y 3 sobre um aberto Z3 de Q , que conserve, ou inverta, as
s 3 sejam disjuntos dois a dois. Sugestão:
orientações e que os abertos Y
"
Reparar que 0 ÐÖC! ×Ñ é uma variedade compacta de dimensão !.
c) Na continuação de b), mostrar que se pode escolher um aberto Z de Q ,
com C! − Z , e, para cada " Ÿ 3 Ÿ 8, um aberto Y3 de Q w , com
Exercícios
281
s 3 , de modo que se tenha 0 ÐY3 Ñ œ Z e 0 " ÐZ Ñ œ - Y3 .
B3 − Y3 § Y
Sugestão: Lembrando que 0 é uma aplicação fechada, pela alínea a) do
s 3 Ñ é um fechado de Q que não
exercício IV.17, deduzir que 0 ÐQ Ï - Y
contém C! .
d) Nas condições de b), mostrar que se tem
degÐ0 Ñ œ " &3 ,
8
3œ"
em particular degÐ0 Ñ − ™. Sugestão: Nas condições de c), utilizar o teorema
da partição da unidade para garantir a existência de uma aplicação suave
:À Q Ä Ò!ß "Ó, nula fora de uma parte compacta de Z e tal que :ÐC! Ñ œ " e,
'
sendo então = − H7
- ÐQ Ñ, =C œ :ÐCÑ Z 96XC ÐQ Ñ , mostrar que Q = ! e cal‡
'
cular Q w 0 =.
e) Deduzir das alíneas anteriores e do teorema de Sard que, qualquer que seja
a aplicação suave própria 0 À Q w Ä Q , tem-se degÐ0 Ñ − ™ e que, se 0 não é
sobrejectiva, tem-se mesmo degÐ0 Ñ œ !.
f) Mostrar que, se 0 À Q w Ä Q é um difeomorfismo, então degÐ0 Ñ œ „".
Ex IV.23 (Outra vez o teorema fundamental da Álgebra)
a) Sendo 8 ", mostrar que tem lugar uma aplicação suave própria
08 À ‚ Ä ‚, definida por 08 ÐDÑ œ D 8 , para a qual se tem degÐ08 Ñ œ 8.
Sugestão: Verificar que cada D Á ! é um ponto regular de 08 , e com o
isomorfismo H08 D À ‚ Ä ‚ a conservar as orientações.
b) Sejam 8 " e, para cada ! Ÿ 3 Ÿ 8 ", +3 − ‚ e consideremos a correspondente aplicação polinomial 0 À ‚ Ä ‚, definida por
0 ÐDÑ œ D 8 +8" D 8" â +" D +! .
Mostrar que 0 é uma aplicação suave própria e que 0 é suave e propriamente
homotópica à aplicação 08 À ‚ Ä ‚ referida em a) pela homotopia
LÀ Ò!ß "Ó ‚ ‚ Ä ‚ definida por
LÐ>ß DÑ œ D 8 >Ð+8" D 8" â +" D +! Ñ,
e deduzir que se tem degÐ0 Ñ œ 8.
c) Concluir de b) que a aplicação 0 À ‚ Ä ‚ é sobrejectiva e, em particular,
que existe D tal que 0 ÐDÑ œ !.
Ex IV.24 Seja Q § I uma variedade sem bordo, de dimensão 7, suavemente
contráctil e suavemente orientada. Mostrar que se tem L-: ÐQ Ñ œ Ö!×, para
cada : Á !, e que L-7 ÐQ Ñ é um espaço vectorial de dimensão " (generalização de IV.4.11)77. Sugestão: Utilizar o teorema de dualidade de Poincaré,
lembrando IV.1.13.
77Pode-se
provar que, se Q é uma variedade suavemente contráctil, então o fibrado
tangente X ÐQ Ñ é trivial, em particular admite uma orientação suave (cf., por exemplo, o
282
Cap. IV. Introdução à cohomologia de de Rham
Ex IV.25 (Um lema de Álgebra Linear) Sejam I e J espaços vectoriais sobre
Š e Šw ¨ Š. Sejam -À I Ä J
uma aplicação linear e
-‡ À PÐJ à Šw Ñ Ä PÐIà Šw Ñ a respectiva dual. Mostrar que -‡ é injectiva se, e
só se, - é sobrejectiva e que -‡ é sobrejectiva se, e só se, - é injectiva.
Sugestão: Aplicar IV.5.18 às sucessões exactas
-
Ö!× Ä kerÐ-Ñ Ä I Ä J
J
IÄJ Ä
Ä Ö!×
-ÐIÑ
(embora uma demonstração directa seja também possível).
Ex IV.26 Sejam Q § I e Q w § I w variedades sem bordo, suavemente orientadas, com dimensões 7 e :, respectivamente, a segunda das quais suavemente contráctil. Sejam 1" À Q ‚ Q w Ä Q e 1# À Q ‚ Q w Ä Q w as projecções canónicas. Lembrando que, pelo exercício IV.24, L-: ÐQ w Ñ é um espaço
vectorial de dimensão ", e portanto que a aplicação linear sobrejectiva
ë À L-: ÐQ w Ñ Ä Š é um isomorfismo, podemos fixar Ò3Ó − L-: ÐQ w Ñ tal que
ë ÐÒ3ÓÑ œ ". Consideremos sobre Q ‚ Q w a orientação, que se verifica
facilmente ser suave, correspondente a munir cada um dos espaços vectoriais
XÐBßCÑ ÐQ ‚ Q w Ñ œ XB ÐQ Ñ ‚ XC ÐQ w Ñ da orientação produto (cf. II.7.25).
a) Utilizar o teorema de dualidade de Poincaré e a conclusão do exercício
IV.14 para deduzir que se tem L-5 ÐQ ‚ Q w Ñ œ Ö!×, para cada 5 :.
b) Mostrar que, para cada 5 !, tem lugar uma aplicação linear
-5 À L-5 ÐQ Ñ Ä L-:5 ÐQ ‚ Q w Ñ,
definida por
-5 ÐÒ=ÓÑ œ Ò1"‡ = • 1#‡ 3Ó.
c) Mostrar que a aplicação linear -7 À L-7 ÐQ Ñ Ä L-:7 ÐQ ‚ Q w Ñ verifica a
condição de se ter ë Ð-7 ÐÒ=ÓÑÑ œ ë ÐÒ=ÓÑ, para cada Ò=Ó − L-7 ÐQ Ñ.
Sugestão: Dadas as bases ?" ß á ß ?7 de XB ÐQ Ñ e @" ß á ß @: de XC ÐQ w Ñ,
utilizar a caracterização do produto exterior em II.5.12 para mostrar que
Ð1"‡ = • 1#‡ 3ÑÐBßCÑ ÐÐ?" ß !Ñß á ß Ð?7 ß !Ñß Ð!ß @" Ñß á ß Ð!ß @: ÑÑ œ
œ =B Ð?" ß á ß ?7 Ñ 3C Ð@" ß á ß @: Ñ.
d) Mostrar que, para cada ! Ÿ 5 Ÿ 7, a aplicação linear
-5 À L-5 ÐQ Ñ Ä L-:5 ÐQ ‚ Q w Ñ
é um isomorfismo. Sugestão: Considerando o isomorfismo
exercício 5.4 de [10]). A condição de Q estar suavemente orientada poderia portanto não
ser exigida expressamente.
Exercícios
283
L 75 Ð1" ÑÀ L 75 ÐQ Ñ Ä L 75 ÐQ ‚ Q w Ñ
(cf. o exercício IV.14) e as aplicações bilineares de Poincaré
075 À L 75 ÐQ Ñ ‚ L-5 ÐQ Ñ Ä Š
075 À L 75 ÐQ ‚ Q w Ñ ‚ L-:5 ÐQ ‚ Q w Ñ Ä Š,
mostrar que, para cada 5 − L 75 ÐQ Ñ e = − L-5 ÐQ Ñ, tem-se
075 ÐL 75 Ð1" ÑÐÒ5 ÓÑß -5 ÐÒ=ÓÑÑ œ 075 ÐÒ5 Óß Ò=ÓÑ
e deduzir daqui, e do teorema de dualidade de Poincaré que
‡
-5 À PÐL-:5 ÐQ ‚ Q w Ñà ŠÑ Ä PÐL-5 ÐQ Ñà ŠÑ
é um isomorfismo, aplicando, em seguida, o exercício IV.25.
e) Reparar que as alíneas a) e d) implicam que, para todo o 5 − ™, os espaços
vectoriais L-5 ÐQ Ñ e L-:5 ÐQ ‚ Q w Ñ são isomorfos.
Ex IV.27 a) Seja I um espaço euclidiano de dimensão 8 #. Mostrar que
L-: ÐI Ï Ö!×Ñ œ Ö!×, para cada : distinto de " e 8 e que L-" ÐI Ï Ö!×Ñ e
L-8 ÐI Ï Ö!×Ñ são espaços vectoriais de dimensão ". Mais precisamente,
sendo :À Ó!ß _Ò Ä Ò!ß _Ò uma aplicação suave, de suporte compacto, tal
_
que '! :Ð>Ñ .> œ ", mostrar que tem lugar uma forma diferencial fechada
3 − H"- ÐI Ï Ö!×Ñ, definida por
3B ÐAÑ œ :ÐmBmÑ
ØBß AÙ
,
mBm
e que Ò3Ó constitui uma base de L-" ÐI Ï Ö!×Ñ. Sugestão: Considerar o difeomorfismo 0 À I Ï Ö!× Ä W ‚ Ó!ß _Ò, definido por
B
0 ÐBÑ œ Ð
ß mBmÑ,
mBm
e atender ao isomorfismo descrito no exercício IV.24.
b) O que se poderá dizer sobre os espaços de cohomologia com suporte compacto de I Ï Ö!×, no caso em que I é um espaço euclidiano de dimensão "?
Ex IV.28 Seja Q § I uma variedade sem bordo, de dimensão 7, suavemente
orientada e seja E § Q uma variedade fechada, sem bordo, de dimensão :,
também suavemente orientada. Mostrar que existe então um, e um só,
Ò=Ó − L 7: ÐQ Ñ tal que, qualquer que seja Ò3Ó − L-: ÐQ Ñ,
( 3ÎE œ ( = • 3
E
Q
(diz-se então que Ò=Ó é o dual de Poincaré da variedade orientada E).
Sugestão: Utilizar o teorema de dualidade de Poincaré.
284
Cap. IV. Introdução à cohomologia de de Rham
Ex IV.29 Coloquemo-nos nas notações do exercício IV.16, em que verificámos
que, considerando em W " § ‚ a orientação usual, para a variedade
“ œ W " ‚ W " , o espaço de cohomologia L " Ð“Ñ tem dimensão # e admite
como base Ò=" Óß Ò=# Ó, onde =4 œ 14‡ ÐZ 96W " Ñ e 1" ß 1# À “ Ä W " são as
projecções canónicas. Consideremos em “ a orientação produto usual e
consideremos as subvariedades compactas de dimensão ", E" œ W " ‚ Ö"× e
E# œ Ö"× ‚ W " , em ambos os casos com a orientação produto usual (na
variedade Ö"×, de dimensão !, consideramos, naturalmente, a orientação
canónica). Verificar que os duais de Poincaré das variedades compactas E" e
E# , são, respectivamente, os elementos #"1 Ò=# Ó e #"1 Ò=" Ó de L " ГÑ.
Ex IV.30 Seja I um espaço euclidiano orientado de dimensão 8 # e
lembremos que, pelo exercício IV.27, L-" ÐI Ï Ö!×Ñ é um espaço vectorial de
dimensão ", admitindo uma base Ò3Ó, onde 3 − H"- ÐI Ï Ö!×Ñ é uma forma
diferencial fechada verificando
3B ÐAÑ œ :ÐmBmÑ
ØBß AÙ
,
mBm
para uma certa aplicação suave de suporte compacto :À Ó!ß _Ò Ä Ò!ß _Ò,
_
verificando '! :Ð>Ñ .> œ ". Seja H − H8" ÐIÏÖ!×Ñ a forma diferencial
ângulo sólido orientado, isto é, a definida por H œ 0 ‡ ÐZ 96W 8" Ñ, onde
0 À I Ï Ö!× Ä W 8" é a aplicação suave definida por 0 ÐBÑ œ BÎmBm (cf.
III.9.16), a qual, pela alínea b) do exercício III.49, verifica
HB Ð?" ß á ß ?8" Ñ œ
"
Z 96I ÐBß ?" ß á ß ?8" Ñ.
mBm8
a) Verificar que L 8" ÐI Ï Ö!×Ñ é um espaço vectorial de dimensão ", que a
forma diferencial H é fechada e que Ò=Ó é uma base de L 8" ÐI Ï Ö!×Ñ.
Sugestão: Reduzir o resultado a IV.3.13, usando um isomorfismo isométrico
entre ‘8 e I , que conserve as orientações.
b) Mostrar que 3 • H − H8- ÐI Ï Ö!×Ñ verifica
Ð3 • HÑB œ :ÐmBmÑ
"
Z 96I
mBm8"
e deduzir que
(
3 • H œ .ÐW 8" Ñ.
IÏÖ!×
Sugestão: Para cada B − I Ï Ö!×, considerar uma base ortonormada directa
?" ß á ß ?8" de XBÎmBm ÐW 8" Ñ (com a orientação que vem de olhar para W 8"
como o bordo da bola fechada) e utilizar a base ortonormada directa de I ,
B
mBm ß ?" ß á ß ?8" , para calcular a componente de Ð3 • HÑB no elemento de
volume de I .
Exercícios
285
c) Fixado B! − W 8" , mostrar que o conjunto E dos pontos da forma >B! ,
com > − Ó!ß _Ò, é fechado em I Ï Ö!× e é uma variedade de dimensão ",
naturalmente difeomorfa a Ó!ß _Ò. Considerando em E a orientação suave
para a qual o referido difeomorfismo conserva as orientações, mostrar que se
tem
( 3ÎE œ "
E
e deduzir que o dual de Poincaré da variedade E é
Ð"Ñ8"
"
ÒHÓ − L 8" ÐI Ï Ö!×Ñ.
.ÐW 8" Ñ
d) Verificar que o dual de Poincaré da variedade orientada de dimensão
8 ", W 8" § I Ï Ö!×, é !. Sugestão: Reparar que o único caso não trivial
é aquele em que 8 œ #.
Ex IV.31 (Um lema de Álgebra Linear) Seja I um espaço vectorial sobre Š,
de dimensão finita 8, e seja 0À I ‚ I Ä Š uma aplicação bilinear alternada
não degenerada, isto é, tal que, para cada B − I Ï Ö!×, exista C − I tal que
0ÐBß CÑ Á !.
a) Mostrar que 0 define cada um dos espaços como dual do outro.78
b) Diz-se que um subespaço vectorial J § I é não degenerado se a
restrição de 0 a J ‚ J for ainda não degenerada. Mostrar que, se Bß C − I
são tais que 0ÐBß CÑ Á !, então o subespaço vectorial J gerado por B e C tem
dimensão # e é não degenerado.
c) Se J § I é um subespaço vectorial de dimensão 5 , define-se o seu ortogonal (relativamente a 0) como sendo o conjunto J ¼ dos B − I tais que
0ÐBß CÑ œ !, para todo o C − J . Mostrar que J ¼ é um subespaço vectorial de
dimensão 8 5 e que ÐJ ¼ Ѽ œ J . Sugestão: Mostrar que, por composição
do isomorfismo FÀ I Ä PÐIà ŠÑ, associado a 0, com a operação de
restrição, se obtém uma aplicação linear sobrejectiva I Ä PÐJ à ŠÑ, cujo
kernel é J ¼ e reparar que se tem trivialmente J § ÐJ ¼ Ѽ .
d) Mostrar que um subespaço vectorial J é não degenerado se, e só se,
J J ¼ œ Ö!× e deduzir que, se J é não degenerado, então J ¼ é também
não degenerado.
e) Deduzir de b), c) e d) que, se 8 Á !, então 8 # e I admite um
subespaço vectorial não degenerado de dimensão 8 # e concluir que 8 tem
que ser par.
Ex IV.32 Seja Q § I uma variedade compacta, sem bordo, suavemente orientada, com dimensão 8 œ #:, com : ímpar. Mostrar que o espaço vectorial
L : ÐQ Ñ tem dimensão par. Sugestão: Verificar que a aplicação de Poincaré
78É
claro que, reciprocamente, toda a aplicação bilinear alternada que defina um dos
espaços como dual do outro, é não degenerada, no sentido anterior.
286
Cap. IV. Introdução à cohomologia de de Rham
0: À L : ÐQ Ñ ‚ L : ÐQ Ñ Ä Š está nas condições do exercício IV.31, tendo em
conta o teorema de dualidade de Poincaré.
Ex IV.33 É fácil, utilizando IV.1.4 ou IV.2.6, apresentar exemplos de variedades
não conexas com um espaço de cohomologia de de Rham de dimensão
infinita. O objectivo deste exercício é o de dar um exemplo de uma variedade
conexa com um espaço de cohomologia de de Rham de dimensão infinita.
Para cada : − ™, notemos B: œ Ð#:ß !Ñ − ‘# . Seja Q œ ‘# Ï ÖB: ×:−™ .
a) Mostrar que Q é um aberto conexo de ‘# , em particular uma variedade
conexa de dimensão #. Sugestão: Q é a união de dois conjuntos de
intersecção não vazia, que estão contidos na aderência de abertos convexos.
b) Seja W § ‘# , W œ ÖB − ‘# ± mBm œ "×, com a orientação que lhe vem de
ser bordo de F œ ÖB − ‘# ± mBm Ÿ "×. Para cada : − ™, seja 0: À Q Ä W a
aplicação suave definida por
B B:
0: ÐBÑ œ
mB B: m
e seja =: − H" ÐQ Ñ a forma diferencial =: œ 0:‡ Z 96W . Mostrar que se tem
. =: œ !, o que nos permitirá considerar os elementos Ò=: Ó − L " ÐQ Ñ.
c) Para cada : − ™, seja W: œ ÖB − ‘# ± mB B: m œ "×, com a orientação
que lhe vem de ser bordo de F: œ ÖB − ‘# ± mB B: m Ÿ "×. Mostrar que se
tem 'W: =: ÎW: œ #1 e, utilizando o teorema de Stokes, que 'W: =; ÎW; œ !, para
cada ; Á :, e deduzir daqui que os elementos Ò=: Ó − L " ÐQ Ñ são linearmente
independentes, e portanto que L " ÐQ Ñ tem dimensão infinita.
Ex IV.34 (Generalidades sobre a complexificação) Sejam I um espaço
vectorial real, I‚ um espaço vectorial complexo e 0À I ‚ I Ä I‚ um
isomorfismo real. Vamos dizer que 0 define I‚ como complexificado de I ,
ou que I‚ é um complexificado de I definido por 0, se se tem 0Ð!ß BÑ œ 3
0ÐBß !Ñ, para cada B − I .
a) (Existência) Mostrar que, se I é um espaço vectorial real, então existe
sobre I ‚ I uma estrutura de espaço vectorial complexo definida pela
estrutura complexa N À I ‚ I Ä I ‚ I , N ÐBß CÑ œ ÐCß BÑ, (cf. II.1.4) e
que I ‚ I é então um complexificado de I , definido pelo isomorfismo
identidade. Mostrar ainda, utilizando II.1.6, que, se I‚ é um complexificado
de I , definido pelo isomorfismo 0À I ‚ I Ä I‚ , então 0 é mesmo um
isomorfismo complexo, quando se considera em I ‚ I a estrutura de espaço
vectorial complexo atrás referida.
b) Sejam I e J espaços vectoriais reais e -À I Ä J uma aplicação linear.
Sejam I‚ e J‚ complexificados de I e J , definidos pelos isomorfismos
0À I ‚ I Ä I‚ e (À J ‚ J Ä J‚ . Mostrar que tem então lugar uma aplicação linear complexa -‚ À I‚ Ä J‚ (a complexificada de - ) definida pela
condição de tornar comutativo o diagrama
Exercícios
287
I‚I
0 Æ0
I‚
-‚-
Ä
-‚
Ä
J ‚J
( Æ( .
J‚
Verificar e precisar as propriedades de functorialidade que garantem que
ÐM.I Ñ‚ œ M.I‚ e que Ð. ‰ -Ñ‚ œ .‚ ‰ -‚ , deduzindo, em particular, que, se
-À I Ä J é um isomorfismo, então -‚ À I‚ Ä J‚ é também um
isomorfismo e Ð-‚ Ñ" œ Ð-" Ñ‚ .
c) (Unicidade) Demonstrar e precisar a afirmação de que, se I‚ e I‚w são
dois complexificados de I , então existe um isomorfismo complexo, naturalmente definido, de I‚ sobre I‚w .
d) Suponhamos que I‚ é um complexificado de I , definido pelo isomorfismo 0À I ‚ I Ä I‚ . Seja ÐB4 Ñ4−N uma família de vectores de I . Mostrar
que esta família é linearmente independente (resp. geradora, resp. uma base
de I ) se, e só se a família Ð0ÐB4 ß !ÑÑ4−N de vectores de I‚ for linearmente
independente (resp. geradora, resp. uma base de I‚ ). Deduzir, em particular,
que a dimensão, finita ou infinita, de I‚ , enquanto espaço vectorial
complexo, é igual à dimensão de I , enquanto espaço vectorial real.
Sugestão: Mostrar que, para +4 ß ,4 − ‘, tem-se
" Ð+4 3,4 Ñ 0ÐB4 ß !Ñ œ 0ˆ" +4 B4 ß " ,4 B4 ‰.
4
4
4
Ex IV.35 (Complexificação de complexos de cocadeias) Consideremos um
complexo de cocadeias real G ñ , definido pelos espaços vectoriais reais G : e
pelos operadores de cobordo . : À G : Ä G :" . Seja, para cada :, G‚: um complexificado de G : , definido pelo isomorfismo 0: À G : ‚ G : Ä G‚: , e consideremos as aplicações lineares complexificadas .‚: À G‚: Ä G‚:" correspondentes.
a) Mostrar que se tem então um complexo de cocadeias complexo G‚ñ ,
definido pelos G‚: e pelos operadores de cobordo .‚: À G‚: Ä G‚:" .
b) Verificar que, considerando o complexo de cocadeis produto G ñ ‚ G ñ ,
definido pelos G : ‚ G : e pelos operadores de cobordo . : ‚ . : (cf. IV.2.4),
a família 0ñ dos 0: À G : ‚ G : Ä G‚: é um isomorfismo de complexos de cocadeias reais, ao qual fica portanto associado, para cada : , um isomorfismo
L : Ð0ñ ÑÀ L : ÐG ñ ‚ G ñ Ñ Ä L : ÐG‚ñ Ñ.
c) Lembrando que, por IV.2.5, L : ÐG ñ ‚ G ñ Ñ é um produto de L : ÐG ñ Ñ e
L : ÐG ñ Ñ, com as projecções L : ÐG ñ ‚ G ñ Ñ Ä L : ÐG ñ Ñ definidas respectivamente por ÒÐBß CÑÓ È ÒBÓ e ÒÐBß CÑÓ È ÒCÓ, deduzir que tem lugar um isomorfismo real
s0: À L : ÐG ñ Ñ ‚ L : ÐG ñ Ñ Ä L : ÐG‚ñ Ñ,
288
Cap. IV. Introdução à cohomologia de de Rham
que a cada par ÐÒBÓß ÒCÓÑ associa L : Ð0ñ ÑÐÒÐBß CÑÓÑ, e mostrar que este isomorfismo define L : ÐG‚ñ Ñ como complexificado de L : ÐG ñ Ñ.
Ex IV.36 (Mudança de escalares na cohomologia)
a) Seja J um espaço vectorial real. Mostrar que, para cada : !, E: ÐJ à ‚Ñ
é um complexificado de E: ÐJ à ‘Ñ, definido pelo isomorfismo
0: À E: ÐJ à ‘Ñ ‚ E: ÐJ à ‘Ñ Ä E: ÐJ à ‚Ñ,
0 : Ð= ß 3 Ñ œ = 3 3 .
b) Seja Q § I uma variedade. Mostrar que, para cada : − ™, H: ÐQ à ‚Ñ é
um complexificado de H: ÐQ à ‘Ñ, definido pelo isomorfismo
0: À H: ÐQ à ‘Ñ ‚ H: ÐQ à ‘Ñ Ä H: ÐQ à ‚Ñ,
0: Ð=ß 3Ñ œ = 3 3, e H:- ÐQ à ‚Ñ é um complexificado de H-: ÐQ à ‘Ñ, definido
pelo isomorfismo
0: À H-: ÐQ à ‘Ñ ‚ H-: ÐQ à ‘Ñ Ä H-: ÐQ à ‚Ñ,
definido pela mesma fórmula.
c) Deduzir de b) que, se Q § I é uma variedade, então, para cada :,
L : ÐQ à ‚Ñ é um complexificado de L : ÐQ à ‘Ñ e L-: ÐQ à ‚Ñ é um complexificado de L-: ÐQ à ‘Ñ, em particular, a dimensão de L : ÐQ à ‚Ñ, como espaço
vectorial complexo, coincide com a dimensão de L : ÐQ à ‘Ñ, como espaço
vectorial real e a dimensão de L-: ÐQ à ‚Ñ, como espaço vectorial complexo,
coincide com a dimensão de L-: ÐQ à ‘Ñ, como espaço vectorial real.
Ex IV.37 (Número de Lebesgue de uma cobertura) Sejam \ um espaço
métrico compacto e ÐY4 Ñ4−N uma família de abertos de \ , com união \ .
Mostrar que existe então $ ! tal que, qualquer que seja o subconjunto E de
\ com diâmetro menor que $ , exista 4 tal que E § Y4 (a um número $ !
nestas condições dá-se o nome de número de Lebesgue da cobertura aberta
de \ pelos conjunto Y4 ). Sugestão: Supondo que não existia um tal $ ,
mostrar que se pode escolher, para cada natural 8, B8 − \ tal que a bola
aberta F"Î8 ÐB8 Ñ, de centro B8 e raio "Î8, não esteja contida em nenhum dos
Y4 e chegar então a um absurdo, examinando o que sucede com um ponto
B − \ que seja aderente à sucessão ÐB8 Ñ8− .
Ex IV.38 (Dois cubos dentro duma esfera) Sejam 8 " e \ § W 8 um 5 -cubo
topológico e ] § W 8 um <-cubo topológico tais que \ ] œ g. Utilizando
a sucessão exacta de Mayer-Vietoris com suporte compacto, mostrar que:
a) Supondo que 8 #, L-8 ÐW 8 Ï Ð\ ] ÑÑ e L-" ÐW 8 Ï Ð\ ] ÑÑ têm
dimensão " e L-: ÐW 8 Ï Ð\ ] ÑÑ œ Ö!×, para cada : Á "ß 8, em particular
W 8 Ï Ð\ ] Ñ é conexo.
b) Supondo que 8 œ ", L-8 ÐW 8 Ï Ð\ ] ÑÑ é um espaço vectorial de
dimensão # e L-8 ÐW 8 Ï Ð\ ] ÑÑ œ Ö!×, para cada : Á 8, em particular
W 8 Ï Ð\ ] Ñ tem duas componentes conexas.
Exercícios
289
Ex IV.39 (Um cubo dentro de ‘8 ) Sejam 8 " e \ § ‘8 um 5 -cubo topológico. Aplicando a conclusão do exercício anterior, com < œ !, mostrar que:
a) Supondo que 8 #, L-8 Б8 Ï \Ñ e L-" Б8 Ï \Ñ têm dimensão " e
L-: Б8 Ï \Ñ œ Ö!×, para cada : Á "ß 8, em particular ‘8 Ï \ é conexo.
b) Supondo que 8 œ ", L-8 Б8 Ï \Ñ tem dimensão # e L-: Б8 Ï \Ñ œ Ö!×,
para cada : Á 8, em particular ‘8 Ï \ tem duas componentes conexas.
Ex IV.40 (Um cubo e uma esfera dentro duma esfera) Sejam 8 ", \ § W 8
uma esfera topológica de dimensão 8 " e ] § W 8 um <-cubo topológico
tais que \ ] œ g. Utilizando a sucessão exacta de Mayer-Vietoris com
suporte compacto, mostrar que:
a) Supondo que 8 #, L-8 ÐW 8 Ï Ð\ ] ÑÑ e L-" ÐW 8 Ï Ð\ ] ÑÑ têm dimensões # e ", respectivamente, e L-: ÐW 8 Ï Ð\ ] ÑÑ œ Ö!×, para cada : Á "ß 8,
em particular W 8 Ï Ð\ ] Ñ tem duas componentes conexas. Além disso,
sendo Y" e Y# as duas componentes conexas de W 8 Ï \ , o cubo ] está
contido numa delas, por exemplo Y" , e então as componentes conexas de
W 8 Ï Ð\ ] Ñ são Y" Ï ] e Y# .
b) Supondo que 8 œ ", L-8 ÐW 8 Ï Ð\ ] ÑÑ é um espaço vectorial de
dimensão $ e L-: ÐW 8 Ï Ð\ ] ÑÑ œ Ö!×, para cada : Á 8, em particular
W 8 Ï Ð\ ] Ñ tem $ componentes conexas. Além disso, sendo Y" e Y# as
duas componentes conexas de W 8 Ï \ , o cubo ] está contido numa delas,
por exemplo Y" , e então Y" Ï ] tem duas componentes conexas e estas duas
e Y# são as três componentes conexas de W 8 Ï Ð\ ] Ñ.
Ex IV.41 (Uma esfera dentro de ‘8 ) Sejam 8 " e \ § ‘8 uma esfera
topológica de dimensão 8 ". Aplicando a conclusão do exercício anterior,
com < œ !, mostrar que:
a) Supondo que 8 #, L-8 Б8 Ï \Ñ e L-" Б8 Ï \Ñ têm dimensões # e ",
respectivamente, e L-: Б8 Ï \Ñ œ Ö!×, para cada : Á "ß 8, em particular,
‘8 Ï \ tem duas componentes conexas. Além disso, destas duas, uma é
limitada e outra não e a fronteira de ambas é igual a \ (teorema de
Jordan-Brouwer em ‘8 ).
b) Supondo que 8 œ ", L-8 Б8 Ï \Ñ tem dimensão $ e L-: Б8 Ï \Ñ œ Ö!×,
para cada : Á 8, em particular, ‘8 Ï \ tem $ componentes conexas. Além
disso, destas três, uma é limitada e as outras duas não e a fronteira da
componente limitada é igual a \ .79
Ex IV.42 Sejam 8 # e \ § ‘8 uma esfera topológica de dimensão 8 ". O
teorema de Jordan-Brouwer em ‘8 (já obtido na alínea a) do exercício
IV.41), afirma-nos que ‘8 Ï \ tem então duas componentes conexas, uma
limitada e outra ilimitada, ambas com fronteira igual a \ . Apresentar uma
demonstração alternativa deste facto por métodos puramente topológicos a
partir do correspondente resultado em W 8 (cf. IV.6.12). Sugestão:
79As
afirmações sobre as componentes conexas de ‘ Ï \ , quando \ é uma esfera
topológica de dimensão ! são de demonstração directa trivial.
290
Cap. IV. Introdução à cohomologia de de Rham
Considerar
o
homeomorfismo,
projecção
estereográfica,
0 À W 8 Ï Ö/8" × Ä ‘8 , definido em IV.3.8, e mostrar que, se a um aberto
conexo de W 8 (8 #) se retira um dos seus elementos, obtém-se ainda um
aberto conexo.
Ex IV.43 Sejam \ß ] § ‘8 dois subconjuntos arbitrários e 0 À \ Ä ] um
homeomorfismo. Mostrar que se tem então 0 ÐintÐ\ÑÑ œ intÐ] Ñ.
Sugestão: Utilizar o teorema da invariância do domínio de Brouwer.80
Ex IV.44 Verificar que, se 8 " e :À Ò!ß "Ó8 Ä Ò!ß "Ó8 é um homeomorfismo,
então, nas notações de IV.6.3, : aplica `ÐÒ!ß "Ó8 Ñ sobre `ÐÒ!ß "Ó8 Ñ. Deduzir
que é possível definir, para cada 8-cubo topológico \ , com 8 ", o que é o
seu bordo `Ð\Ñ, que este é então uma esfera topológica de dimensão 8 " e
que, se \ e ] são cubos topológicos de dimensão 8 e 0 À \ Ä ] é um
homeomorfismo, então 0 Ð`Ð\ÑÑ œ `Ð] Ñ. Mostrar ainda que, se \ § ‘8 é
um 8-cubo topológico, então `Ð\Ñ coincide com a fronteira topológica de \
em ‘8 .
Ex IV.45 (Um lema topológico) Sejam \ um espaço topológico compacto, ]
um espaço topológico separado e :À \ Ä ] uma aplicação contínua e
sobrejectiva. Mostrar que, se ^ é um espaço topológico, uma aplicação
1À ] Ä ^ é contínua se, e só se, 1 ‰ :À \ Ä ^ é contínua.81
Sugestão: Utilizar a caracterização das aplicações contínuas como aquelas
para as quais a imagem recíproca de qualquer fechado é fechada, mostrando
que um conjunto F § ] é fechado se, e só se, :" ÐFÑ § \ é fechado.
Ex IV.46 Se \ é um espaço topológico, chama-se caminho de Jordan em \ a
uma aplicação contínua :À Ò+ß ,Ó Ä \ , com + , em ‘, tal que 0 Ð+Ñ œ 0 Ð,Ñ
e 0ÎÒ+ß,Ò seja injectiva.82 Mostrar que um espaço topológico \ é uma esfera
topológica de dimensão " se, e só se, for separado e existir um caminho de
Jordan sobrejectivo em \ . Sugestão: Utilizar o exercício anterior,
lembrando a aplicação contínua :À Ò!ß #1Ó Ä W " , definida por
:Ð>Ñ œ ÐcosÐ>Ñß sinÐ>ÑÑ.
Ex IV.47 a) Seja 8 " e consideremos a bola aberta e a bola fechada de ‘8 ,
com a norma euclidiana,
F" œ ÖB − ‘8 ± mBm "×,
F " œ ÖB − ‘8 ± mBm Ÿ "×.
Lembrar que, pelo exercício IV.21, existe um homeomorfismo :À F" Ä ‘8 ,
80Ao
contrário do que possa eventualmente parecer a um leitor mais apressado, este
resultado não é uma trivialidade topológica.
81Este facto costuma ser expresso pela afirmação de que a topologia de ] é a topologia
final determinada pela topologia de \ e pela aplicação :.
82Por vezes também se usa o nome curva de Jordan, mas preferimos aquele porque
estamos a dar outro siginificado à palavra “curva”.
Exercícios
291
definido por
:ÐBÑ œ
B
,
È" mBm#
e que, por IV.3.8, existe um homeomorfismo 0 À W 8 Ï Ö/8" × Ä ‘8 (projecção estereográfica), definido por
B
0 ÐBß >Ñ œ
.
">
Mostrar que existe uma aplicação contínua 0 À F " Ä W 8 , definida por
0 ÐBÑ œ œ
0" Ð:ÐBÑÑ,
/8" ,
se mBm "
.
se mBm œ "
b) Deduzir de a) e do exercício IV.45 que um espaço topológico \ é uma
esfera topológica de dimensão 8 se, e só se, é separado e existe uma
aplicação contínua sobrejectiva F " Ä \ cuja restrição à hipersuperfície
esférica W" œ ÖB − ‘8 ± mBm œ "× seja constante e cuja restrição à bola F"
seja injectiva e não sobrejectiva.
c) Verificar que o que se viu em b) implica trivialmente a caracterização mais
geral que diz que, dado um cubo topológico ] de dimensão 8, com bordo
`Ð] Ñ (cf. o exercício IV.44), um espaço topológico \ é uma esfera
topológica de dimensão 8 se, e só se, é separado e existe uma aplicação
contínua sobrejectiva ] Ä \ cuja restrição a `Ð] Ñ seja constante e cuja
restrição a ] Ï `Ð] Ñ seja injectiva e não sobrejectiva.
Ex IV.48 (O problema das três casas e das três lojas) Neste problema clássico,
são dadas três casas e três lojas e pretendem-se construir estradas que não se
intersectem ligando cada casa a cada loja. Quando se tenta resolver
experimentalmente este problema, constata-se que se conseguem traçar oito
das estradas mas, ao tentar a nona, isso revela-se impossível (na figura 12,
notámos B" ß B# ß B$ as casas e C" ß C# ß C$ as lojas e não conseguimos traçar a
estrada de B$ a C# ). O objectivo deste exercício é a prova de que o problema
é, efectivamente, impossível de resolver. O problema pode ser colocado no
quadro de ‘# ou de W # mas é no quadro de W # que é mais cómodo tratá-lo.83
até faz mais sentido colocar o problema no quadro de W # , na medida em que nós
habitamos na superfície da Terra.
83Aliás,
292
Cap. IV. Introdução à cohomologia de de Rham
Figura 12
Aliás, pensando na projecção estereográfica, é fácil de constatar que a inexistência de solução no quadro de W # arrasta a inexistência de solução no
quadro de ‘# . Podemos então formalizar o enunciado deste exercício do
seguinte modo:
São dados seis pontos distintos B" ß B# ß B$ ß C" ß C# ß C$ em W # . Mostrar que não
existem aplicações contínuas 03ß4 À Ò!ß "Ó Ä W # , onde " Ÿ 3 Ÿ $ e " Ÿ 4 Ÿ $,
com 03ß4 Ð!Ñ œ B3 , 03ß4 Ð"Ñ œ C4 , 03ß4 ÐÓ!ß "ÒÑ § W # Ï ÖB" ß B# ß B$ ß C" ß C# ß C$ × e
com os conjuntos 03ß4 ÐÓ!ß "ÒÑ disjuntos dois a dois.
Sugestão: Supor que existiam aplicações 03ß4 nas condições anteriores e
tentar chegar a um absurdo seguindo os seguintes passos.
a) Notemos E3ß4 œ 03ß4 ÐÒ!ß "ÓÑ e
\ œ E"ß" E"ß# E"ß$ E#ß" E#ß# E#ß$ ,
\" œ E"ß# E#ß# E#ß$ E"ß$ ,
\# œ E"ß" E#ß" E#ß$ E"ß$ ,blablablablab
\$ œ E"ß" E#ß" E#ß# E"ß#
(cf. a figura 13 — reparar não estamos ainda a fazer intervir o ponto B$ ).
Mostrar que \" ß \# e \$ são esferas topológicas de dimensão ".
Sugestão: Utilizar o exercício IV.46.
Exercícios
293
x1
x2
A 2,3
x3
A 1,1
A 1,3
A 2,2
A 2,1
A 1,2
y1
y3
y2
Figura 13
b) Tendo em conta o teorema de Jordan-Brouwer, considerar
A componente conexa, ]" , de W # Ï \" , que não contém C" ,
A componente conexa, ]# , de W # Ï \# , que não contém C# ,
A componente conexa, ]$ , de W # Ï \$ , que não contém C$ .
Verificar que ]" , ]# e ]$ estão contidos em W # Ï \ e deduzir que estes três
abertos são componentes conexas de W # Ï \ .
c) Mostrar que os três abertos ]" , ]# e ]$ são distintos. Sugestão: Lembrar
que o teorema de Jordan-Brouwer garante que frÐ]4 Ñ œ \4 .
d) Utilizar o teorema de Mayer-Vietoris com suporte compacto para mostrar
que L-# ÐW # Ï \Ñ tem dimensão $ e deduzir daqui que W # Ï \ tem $ componentes conexas, e portanto que estas são precisamente ]" , ]# e ]$ .
Sugestão: Reparar que \ a a união da "-esfera topológica \" com um
"-cubo topológico, cuja intersecção com \" é um conjunto com # elementos,
portanto uma !-esfera topológica.
e) Sendo ]4 a componente conexa de W # Ï \ que contém B$ , utilizar a
aplicação contínua 0$ß4 À Ò!ß "Ó Ä W # para chegar ao absurdo procurado.
Ex IV.49 Verificar que, se formos mais cuidadosos na demonstração de IV.7.4,
podemos conseguir que se verifique a condição suplementar [ Q œ Y
(esta condição não se verifica na situação sugerida na figura 11, que ilustra
aquele resultado).
Ex IV.50 Nas condições de IV.7.4, sendo +À Y Ä [ a inclusão, que sabemos
verificar F ‰ + œ M.Y À Y Ä Y , mostrar que a aplicação suave
+ ‰ FÀ [ Ä [ é suavemente homotópica a M.[ , isto é, existe uma aplicação
294
Cap. IV. Introdução à cohomologia de de Rham
suave LÀ Ò!ß "Ó ‚ [ Ä [ tal que LÐ!ß CÑ œ FÐCÑ e LÐ"ß CÑ œ C.
Sugestão: Tomar
LÐ>ß CÑ œ FÐCÑ >ÐC FÐCÑÑ.
Ex IV.51 Deduzir do exercício IV.50 que, se Q § I é uma variedade compacta
e sem bordo, então existe um aberto [ de I , com Q § [ , tal que, sendo
+À Q Ä [ a inclusão, cada L : Ð+ÑÀ L : Ð[ Ñ Ä L : ÐQ Ñ é um isomorfismo.
Ex IV.52 Sejam I um espaço euclidiano de dimensão 8 ", F a bola fechada,
F œ ÖB − I ± mBm Ÿ "×,
e W § F a hipersuperfície esférica,
W œ ÖB − I ± mBm œ "×.
Verificou-se em III.8.7 que não existe nenhuma aplicação contínua
0 À F Ä W tal que 0 ÐBÑ œ B, para cada B − W (uma retracção contínua de F
sobre W ). Redemonstrar este resultado utilizando IV.7.10 e o facto de
L 8" ÐFÑ ter dimensão inferior à de L 8" ÐWÑ.
Ex IV.53 Seja I um espaço euclidiano de dimensão ímpar 8 $ e seja W § I a
hipersuperfície esférica unitária, W œ ÖB − I ± mBm œ "×. Seja 0 À W Ä W a
aplicação suave definida por 0 ÐBÑ œ B.
a) Mostrar que L 8" ÐWÑ é um espaço vectorial de dimensão " e que a
aplicação linear L 8" Ð0 ÑÀ L 8" ÐWÑ Ä L 8" ÐWÑ é a multiplicação por ".
Sugestão: Verificar que, quando se considera em W a orientação usual, 0
inverte as orientações e lembrar o isomorfismo ' À L 8" ÐWÑ Ä Š.
b) Utilizar IV.7.9 para deduzir que a aplicação 0 À W Ä W não é homotópica a
M.W À W Ä W e proceder então como na demonstração de III.8.9 para redemonstrar que, para cada aplicação contínua \À W Ä I , existe B − W tal que
\ÐBÑ − ‘B (teorema da esfera despenteada).84
Ex IV.54 Sejam I um espaço euclidiano e Q § I uma variedade de dimensão
7, compacta, orientável e não vazia. Verificou-se em III.8.3 que não existe
nenhuma retracção suave de Q sobre o bordo `" ÐQ Ñ. Mostrar que não
existe mesmo nenhuma retracção contínua de Q sobre `" ÐQ Ñ.
Sugestão: Supor que existia uma tal retracção contínua 0 À Q Ä `" ÐQ Ñ.
Começar por mostrar que `" ÐQ Ñ é fechado em Q . Considerar então uma
vizinhança tubular da variedade compacta, sem bordo, `" ÐQ Ñ e ter em conta
o teorema de aproximação III.8.6 para construir uma retracção suave de Q
sobre `" ÐQ Ñ.
84As
conclusões desta alínea são também trivialmente válidas para 8 œ ".
Exercícios
295
Ex IV.55 (Fibrados vectoriais de dimensão ") Sejam Q uma variedade conexa
e não vazia85, I um espaço euclidiano e ÐIB ÑB−Q um fibrado vectorial de
dimensão ", com IB § I . Para cada B − Q , seja WB § IB o conjunto dos
A − IB tais que mAm œ ", conjunto que tem portanto dois elementos. Seja
W § Q ‚ I,
W œ ÖÐBß AÑ − Q ‚ I ± A − WB ×.
a) Mostrar que, se o fibrado vectorial ÐIB ÑB−Q é trivial, então W é
difeomorfo a Q ‚ Ö"ß "×, em particular W tem duas componentes conexas,
cada uma das quais intersectando cada ÖB× ‚ WB .
Sugestão: Mostrar que existe uma secção suave Ð[B ÑB−Q do fibrado
vectorial, tal que, para cada B − Q , m[B m œ ".
b) Mostrar que, se o fibrado vectorial ÐIB ÑB−Q não é trivial, então W é
conexo.
Sugestão: Supor que W não é conexo e considerar dois abertos disjuntos não
vazios Y e Z de W , com união W . Mostrar que Q fica união disjunta dos três
abertos Q" , Q# e Q$ constituídos, respectivamente, pelos pontos B tais que
ÖB× ‚ WB § Y , pelos pontos B tais que ÖB× ‚ WB § Z e pelos pontos B tais
que ÖB× ‚ WB tem um ponto em Y e um ponto em Z , e deduzir, do facto de
Q ser conexa, que Q œ Q$ . Para mostrar que estes conjuntos são abertos,
atender a que, tendo em conta a), para cada B! − Q , existe um aberto E de
Q , com B! − E, tal que W ÎE œ ÖÐBß AÑ − W ± B − E× tenha duas
componentes conexas, cada uma das quais intersectando cada ÖB× ‚ WB .
Mostrar que se obtém então uma secção suave Ð[B ÑB−Q do fibrado vectorial,
pela condição de se ter [B − WB e ÐBß [B Ñ − Y .
Ex IV.56 Sejam I um espaço euclidiano de dimensão 8 " e Q § I uma
variedade de dimensão 8 ", compacta, conexa, sem bordo e não vazia. Seja
[ ¨ Q uma vizinhança tubular de Q , correspondente a um certo < ! (cf.
IV.7.5)Þ
a) Considerar o fibrado vectorial de dimensão ", de base Q , que a cada
B − Q associa XB ÐQ Ѽ , lembrando que a variedade Q é orientável se, e só
se, este fibrado vectorial é trivial. Nas notações do exercício IV.55, mostrar
que tem lugar um difeomorfismo de W ‚ Ó!ß <Ò sobre [ Ï Q , definido por
ÐÐBß AÑß >Ñ È B >A,
e deduzir que [ Ï Q tem duas componentes conexas, se a variedade Q é
orientável, e [ Ï Q é conexo, se a variedade Q não é orientável.
b) Verificar que o aberto [ é sempre conexo. Sugestão: Verificar que [ é
união do conexo Q com uma família de conexos intersectando Q , um para
cada B − Q .
c) Utilizar a sucessão exacta de Mayer-Vietoris com suporte compacto,
85ou,
mais geralmente um subconjunto conexo e não vazio de um espaço vectorial de
dimensão finita.
296
Cap. IV. Introdução à cohomologia de de Rham
relativamente à decomposição de I como união dos abertos [ e I Ï Q ,
cuja intersecção é [ Ï Q , lembrando que L-8" ÐIÑ œ Ö!×, para deduzir
que, se Q for orientável, I Ï Q tem duas componentes conexas e, se Q não
for orientável, I Ï Q é conexo. Nota: Usando técnicas diferentes das que
temos vindo a estudar, por exemplo o grau módulo # (cf. o capítulo 2, §5 de
[8]), pode-se provar que, sob as hipóteses deste exercício, I Ï Q tem sempre
pelo menos duas componentes conexas. Na posse desse resultado, este
exercício permitir-nos-ia concluir que toda a subvariedade compacta, conexa,
sem bordo e de dimensão 8 " de um espaço vectorial de dimensão 8 é
orientável.86
86A
hipótese de a subvariedade ser conexa é claramente dispensável, uma vez que
podemos sempre aplicar a conclusão a cada uma das componentes conexas desta.
Índice de Símbolos
.0 ÐEÑ
.8 ÐEÑ
-0
.I ÐEÑ
ØÐBß CÑß ÐBw ß Cw ÑÙ
13ß4
.Q ÐEÑ
W œ ÖB − I ± mBm œ "×
:À Ó!ß _Ò ‚ W Ä I Ï Ö!×
58
W< , F<
+81ÐGÑ
,+<ÐQ Ñ
Š
I
P: ÐIà J Ñ
PÐIà J Ñ
P! ÐIà J Ñ œ J
P:‘ ÐIà J Ñ
P:‚ ÐIà J Ñ
04" ßáß4: À I : Ä Šw
" À I Ä PÐPÐIà ŠÑà ŠÑ
0 Œ (À I :; Ä Šw
-" Œ -# Œ â Œ -5 − P:" :# â:5 ÐIà Šw Ñ
-‡ Ð0Ñ, -‡ À P: ÐJ à Šw Ñ Ä P: ÐIà Šw Ñ
0ÎI
Æ8
invÐ5 Ñ
sgÐ5 Ñ
Ð4 † 5Ñ
sgÐN Ñ
5
s Ð0Ñ, 5
s À P: ÐIà Šw Ñ Ä P: ÐIà Šw Ñ
E: ÐIà J Ñ
W : ÐIà J Ñ
AltÐ0Ñ, AltÀ P: ÐIà J Ñ Ä E: ÐIà J Ñ
SymÐ0Ñ, SymÀ P: ÐIà J Ñ Ä W : ÐIà J Ñ
0•4" ßáß4: − E: ÐIà Šw Ñ
det − E7 Њ7 à ŠÑ
detÐ-Ñ
1
2
2, 3
3
4
5
9
18
18
19
20
28
29
37
38
39
39
40
40
40
41
43
43
44
44
45
45
45, 46
45, 46
45
47
48
49
49
50
51
52
54
55
298
Índice de Símbolos
0 • ( − E:; ÐIà Šw Ñ
0 ( − W :; ÐIà Šw Ñ
0" • â • 08 − E:" â:8 ÐIà Šw Ñ
0" â 08 − W :" â:8 ÐIà Šw Ñ
intB Ð0Ñ, intB À P: ÐIà J Ñ Ä P:" ÐIà J Ñ
74 − Æ:
!ÐB" ß á ß B8 Ñ
sgÐBÑ, sgÀ I Ï Ö!× Ä Ö"ß "×
sgÐ-Ñ
Z 96I − E8 ÐIà ‘Ñ
)À I Ä PÐIà ‘Ñ
‡0, ‡À E: ÐIà ŠÑ Ä E8: ÐIà ŠÑ
)˜À I Ä E8" ÐIà ‘Ñ
B" ‚ â ‚ B8"
det‚ Ð-Ñ
det‘ Ð-Ñ
trÐGÑ
trÐ-Ñ
tr‚ Ð-Ñ − ‚
tr‘ Ð-Ñ − ‘
0 œ Ð0B ÑB−Q
0 ‡ 0 œ ÐH0B‡ Ð00 ÐBÑ ÑÑB−Qs
0ÎQs
)Ð\Ñ, )" Ð=Ñ
H0 œ ÐH0B ÑB−Q
gradÐ0 Ñ œ )" ÐH0 Ñ
Z 96 œ ÐZ 96B ÑB−Q
Ò\ß ] Ó
.=
divÐ\Ñ
?0
rotÐ\Ñ
_\ Ð0Ñ
int\ Ð0Ñ œ Ðint\B Ð0B ÑÑB−Q
' =, ' =
Q
^B
[B
T = œ ÐT =B ÑB−Q
:! ß :" À Q Ä Ò!ß "Ó ‚ Q
F œ ÖB − I ± mBm Ÿ "×
'
' ‡ '
ÐEß0 Ñ = œ E 0 =, 0 =
3À I Ï Ö!× Ä W
HÀ I Ï Ö!× Ä E8" ÐIà ‘Ñ
nÐEß 0 Ñ œ 'ÐEß0 Ñ H, nÐ0 Ñ
57
58
60
61
64
64
68
69
71
79
80
81
86
87
91
91
91
91
91
91
99
102
102
105
106
106
106
107
107
115
116
116
120
128
131
141
142
144
145
150
156
164
164
164
Índice de Símbolos
299
nÐEÑ
164
170
`
`:4
`
`B4
.D œ .B 3 .C, .D œ .B 3 .C
`0 `0
`D , `D
=À H Ä Q
:= À Y= Ä Y=
_\ Ð] Ñ
`0
`8
F > Ð+Ñ, W> Ð+Ñ
# À P++ ÐJ à J Ñ Ä E# ÐJ à ‘Ñ
rotÐ\Ñ
f\B À XB ÐQ Ñ Ä XB ÐQ Ñ
B ‚ C − P++ ÐJ à J Ñ
+.À J Ä P++ ÐJ à J Ñ
nC ÐEß 0 Ñ, nC Ð0 Ñ, nC ÐEÑ
H:Š ÐQ Ñ, H: ÐQ à ŠÑ
. : À H: ÐQ Ñ Ä H:" ÐQ Ñ
G ñ œ ÐG : Ñ:−™
^ : ÐG ñ Ñ, F : ÐG ñ Ñ
^ : ÐG ñ Ñ
L : ÐG ñ Ñ œ F
: ÐG ñ Ñ
ÒBÓ − L : ÐG ñ Ñ
HñŠ ÐQ Ñ
:
^Š: ÐQ Ñ, FŠ
ÐQ Ñ
LŠ: ÐQ Ñ œ
ñ
:
^Š: ÐQ Ñ
:
FŠ
ÐQ Ñ
- œ Ð- Ñ:−™
L : Ð-ñ ÑÀ L : ÐG ñ Ñ Ä L : ÐG w ñ Ñ
` : À L : ÐG ww ñ Ñ Ä L :" ÐG ñ Ñ
Hñ ÐY Ñ ‚ Hñ ÐZ Ñ
-: À H: ÐQ Ñ Ä H: ÐY Ñ ‚ H: ÐZ Ñ
.: À H: ÐY Ñ ‚ H: ÐZ Ñ Ä H: ÐY Z Ñ
0 ß 0 À W 8" Ï Ö/8 × Ä ‘8"
1 ß 1 À ‘8" Ä W 8" Ï Ö/8 ×
ë À L 7 ÐQ Ñ Ä Š
H:- ÐQ Ñ
Hñ- ÐQ Ñ
^-: ÐQ Ñ, F-: ÐQ Ñ, L-: ÐQ Ñ
L-: Ð0 ÑÀ L-: ÐQ Ñ Ä L-: ÐQ w Ñ
=ÏQ
ë À L-7 ÐQ Ñ Ä Š
0: À L : ÐQ Ñ ‚ L-7: ÐQ Ñ Ä Š
.: À H-: ÐY Z Ñ Ä H-: ÐY Ñ ‚ H-: ÐZ Ñ
-: À H-: ÐY Ñ ‚ H-: ÐZ Ñ Ä H-: ÐQ Ñ
171
171
171
175
175
176
179
179
183
183
183
183
184
190, 192
195
195
195
195
196
196
196
196
196
198
198
214
217
217
217
220
220
220
225
225
225
227
227
230
236
241
241
300
Índice de Símbolos
h0
h=
248
248
Índice Remissivo
alternada (aplicação multilinear)
49
ângulo
28
ângulo sólido
28
ângulo sólido (forma diferencial)
164
ângulo sólido orientado 164, 164, 190, 192
anti-holomorfa (aplicação)
172
antilinear (aplicação)
39
anti-simétrica (aplicação multilinear)
49
aplicação fechada
274
aplicação linear de conexão
214
aplicação de Poincaré
236
aplicação própria
226
base associada
42
baricentro
29
base de abertos
247
base directa
68
base negativa
68
base positiva
68
base retrógrada
68
Bézout (teorema de)
46
bidual
43
bordo de cubo topológico
285
boreliano pequeno
8
Brouwer (teorema de)
153, 260
caminho
158
caminho de Jordan
286
campo vectorial
105
campo vectorial de Killing
176
campos vectoriais 0 -relacionados
125
campo tensorial
99
campo tensorial suave
99
Cauchy (fórmula integral de)
181
central (projecção)
31
centro de figura
29
cobordo
195, 195
cociclo
195
coeficiente de dilatação
2, 3
cohomologia de de Rham
196
complexificado
282, 283
complexo de cocadeias
195
complexo de cocadeias produto
204
complexo de cocadeias soma
210
complexo de de Rham
196
conjugado (espaço vectorial)
38
conjunto de revolução
30
conjunto total
7
conserva as orientações
71, 131
contável
247
continuamente homotópica
193
contráctil (suavemente)
147
coordenadas polares generalizadas
19
crítico (ponto)
21, 34
crítico (valor)
21, 34
cubo topológico
251
de Rham (cohomologia)
196, 225
de Rham (complexo)
196, 225
decomponível (tensor)
92
derivada covariante
183
derivada exterior
107
derivada de Lie
120
derivada normal
179
determinante (função)
54
determinante de aplicação linear
55
diagrama comutativo
78, 198
directa (base)
68
divergência
115
divergência (teorema da)
141
dual (espaço)
234, 234
dual (aplicação linear)
44
dual de Poincaré
279
elemento de volume
79, 106
esfera depenteada (teorema)
154
esfera topológica
251
espaço de cohomologia
196
espaço topológico homogéneo
258
espaço vectorial orientado
68
essencialmente finita (família)
205
estereográfica (projecção)
32, 182
estrutura complexa
38
exacta (forma diferencial)
148, 196
extensão trivial
227
fechada (forma diferencial)
148, 196
5-finito
13
fluxo
175
forma diferencial
101
forma diferencial ângulo sólido
164
forma diferencial exacta
148, 196
forma diferencial fechada
148, 196
forma diferencial integrável
131, 156
fórmula integral de Cauchy
181
fórmula de Green
179
função determinante
54
função harmónica
175, 179
gradiente
106
302
gráfico
28
Green (fórmula de)
179
Green (teorema de)
178
grupo de Lie
34
grupo simétrico
45
harmónica (função)
175, 179
holomorfa (aplicação)
172
homogéneo (espaço topológico)
258
homotopia contínua
261
homotopia suave
147
homotopia suave própria
275
homotópica (continuamente)
193, 261
homotópica (suavemente)
147
i-base de abertos
247
identidade de Jacobi
176
imagem recíproca
44, 102
injecções associadas
206
injecções canónicas
228
integral de forma diferencial
131
integrável (forma diferencial)
131, 156
inverte as orientações
71, 131
isometria
16
isomorfismo canónico
80
isomorfismo de compl. de cocadeias 198
isomorfismo negativo
71
isomorfismo positivo
71
Jacobi (identidade de)
176
Jordan (caminho)
286
Jordan-Brouwer (teorema)
255, 258
Killing (campo vectorial)
176
laplaciano
115
Lebesgue (medida de)
3, 10
lema dos cinco
96, 240
lema de Poincaré
148
lema da serpente
214
Lie (derivada de)
120
Lie (grupo de)
34
Lie (parêntesis de)
107
localmente fechado
22
Mayer-Vietoris (sucessão exacta) 218, 242
medida de contagem
11
medida de Lebesgue
3, 10
módulo homotopia suave
268
morfismo de complexos de cocadeias 198
negativa (base)
68
negativamente relacionadas
67
normal unitária exterior
141
normal unitária positiva
140, 142
número de inversões
45, 46
número de Lebesgue
284
operador de cobordo
195
operador prismático
145
orientação
68
orientação associada
69
Índice Remissivo
orientação canónica
69, 94
orientação induzida
77, 134
orientação negativa
69
orientação positiva
69
orientação produto
76
orientação transversa
77
orientação transversa canónica
134
orientações compatíveis
74
Pappus (teorema de)
31
par bola-esfera topológico
185
parêntesis de Lie
107
paridade
45, 47
pequeno (boreliano)
8
Poincaré (lema de)
148
Poincaré (teorema de dualidade)
249
Poincaré (variedade)
237
ponto crítico
21, 34
ponto regular
21, 34
positiva (base)
68
positivamente relacionadas
67
prismático (operador)
145
produto de aplicações lineares
270
produto de espaços vectoriais
202
produto exterior
57
produto externo
87
produto externo alternativo
183
produto interior
64
produto tensorial
43
projecção central
31
projecção estereográfica 32, 182, 218, 220
projecções associadas
207
prolongamento euclidiano
101
prolongamento suave
99
propriedade da média
179
regular (ponto)
21, 34
regular (valor)
21, 34
0 -relacionados (campos vectoriais)
125
restrição de campo tensorial
102
retracção
149
retrógrada (base)
68
rotacional
116
rotacional alternativo
183
Sard (teorema de)
23, 34
semi-espaço
77
semi-espaço negativo
77
semi-espaço positivo
77
simétrica (aplicação multilinear)
49
sinal
45, 46, 47
sinal de isomorfismo
71
sistema compatível de orientações
78
soma de espaços vectoriais
206
soma de aplicações lineares
271
Stokes (teorema de)
138, 142, 158
suave (campo tensorial)
99
Índice Remissivo
suavemente contráctil
147, 201
suavemente homotópica
147, 160
subespaço associado
93
sucessão exacta
72, 72
sucessão exacta de cohomologia
214
sucessão exacta curta
73, 213
suporte compacto
133, 225
tangente unitária positiva
142
tensor
43
tensor covariante
43
tensor decomponível
92
teorema de Bézout
46
teorema de Brouwer
153, 260
teorema da divergência
141
teorema de dualidade de Poincaré
249
teorema da esfera despenteada
154
teorema fundamental da Álgebra 189, 277
teorema de Green
178
teorema de invariância da dimensão
258
teorema de invariância do domínio
260
teorema de Jordan-Brouwer
255, 258
teorema de Pappus
31
303
teorema de Sard
23, 34
teorema de Stokes
138
teorema de Stokes clássico
142
teorema de Stokes singular
158
teorema da variedade esburacada
161
total (conjunto)
7
traço
91, 91
trajectória
158
tranposição
45
transposição consecutiva
45
valor crítico
21, 34
valor regular
21, 34
variedade esburacada (teorema)
161
variedade de Poincaré
237
variedade singular
156
vector directo
69
vector negativo
69
vector positivo
69
vector retrógrado
69
vector unitário positivo
79
vizinhança tubular
263, 265
Bibliografia
[1]
BERGER, GAUDUCHON, MAZET, Le spectre d'une variété Riemannienne, Springer, Lecture Notes, 194, 1971.
[2]
BERGER M., GOSTIAUX B., Géométrie Différentielle, Armand Colin,
Paris, 1982.
[3]
BOTT R., TU L.W., Differential Forms in Algebraic Topology, Springer,
GTM 82, 1982.
[4]
DIEUDONNÉ, J., Eléments d'Analyse, Vol III, Gauthier-Villars, Paris,
1970.
[5]
GODBILLON C., Éléments de Topologie Algébrique, Hermann, Paris,
1971.
[6]
GODBILLON C., Géométrie Différentielle et Mécanique Analytique,
Hermann, Paris, 1969.
[7]
GREUB W., HALPERIN S., VANSTONE R., Connections Curvature and
Cohomology, Vol I, Academic Press, 1972.
[8]
GUILLEMIN V., POLLAK A., Differential Topology, Prentice-Hall,
1974.
[9]
LANG S., Analysis II (Real Analysis numa edição posterior),
Addison-Wesley, Reading, Mass., 1969.
[10] MACHADO A., Geometria Diferencial—Uma Introdução Fundamental,
Cosmos, Lisboa, 1991.
[11] MACHADO A., Medida e Integração, Textos e Notas do CMAF, 3,
Lisboa, 1976
[12] MACHADO A., Tópicos de Álgebra Linear e Multilinear, Textos e Notas
do CMAF, 42, Lisboa, 1990.
[13] MACHADO A., Tópicos de Análise e Geometria, Vol I e II, Textos e
Notas do CMAF, 7 e 14, Lisboa, 1977 e 1978.
[14] MARCO, G., Fibrations of real valued functions, Nonlinear Analysis,
Theory Methods & Applications Vol. 28, No. 10, 1997.
[15] MILNOR, J., Topology from the Differentiable Viewpoint, The University
Press of Virginia, Charlottesville, 1965.
[16] RUDIN, W., Real and Complex Analysis, McGraw Hill, 1974.
[17] SPIVAK, M., Calculus on Manifolds, Benjamin, Menlo Park, 1965.
306
Bibliografia
[18] SPIVAK, M., A Comprehensive Introduction to Differential Geometry, Vol
I e II, Publish or Perish, Berkeley, 1979.
[19] WARNER F. W., Foundations of Differentiable Manifolds and Lie
Groups, Scott and Foresman, 1971.
[20] WHITNEY, A function not constant on a connected set of critical points,
Duke Math. Jour. 1, 1935, pp. 514–517.
Download