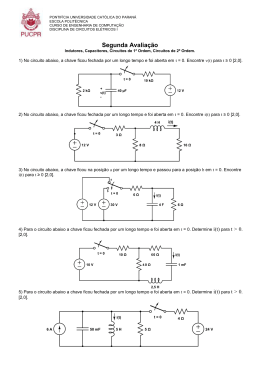
PONTIFÍCIA UNIVERSIDADE CATÓLICA DO PARANÁ
ESCOLA POLITÉCNICA
CURSO DE ENGENHARIA DE COMPUTAÇÃO
DISCIPLINA DE CIRCUITOS ELÉTRICOS II
Segunda Avaliação
Circuitos Trifásicos, Resposta em Frequência.
1) Para o circuito abaixo, encontre a função de transferência H(ω)=Vo(ω)/Vs(ω) e diga qual tipo de filtro passivo o
circuito implementa [1,5].
2) Dada a função de transferência abaixo, coloque-a na forma padrão e trace os diagramas de Bode de magnitude
e de fase no papel semilog em anexo. Indique nos diagramas cada um dos componentes e seus respectivos
valores. [3,5].
𝐇 𝜔 =
𝑗𝜔 + 1
𝑗𝜔(𝑗𝜔 + 10)
3) Um circuito RLC paralelo tem R=5kΩ, L=8mH e C=60µF. Determine: (a) a frequência de ressonância; (b) a
largura de banda; (c) o fator de qualidade [1,0].
4) Para o filtro abaixo, encontre a função de transferência H(ω)=Vo(ω)/Vi(ω), determine a frequência de corte em
Hz e diga qual tipo de filtro passivo o circuito implementa [2,5].
5) Para o circuito trifásico abaixo, calcule as correntes de fase e de linha [1,5].
NOME:_______________________________________________________________________________________________
___________________________________________________________________________________________
𝑠𝑒𝑛 𝜔𝑡 ± 180! = −𝑠𝑒𝑛𝜔𝑡, 𝑐𝑜𝑠 𝜔𝑡 ± 180! = −𝑐𝑜𝑠𝜔𝑡, 𝑠𝑒𝑛 𝜔𝑡 ± 90! = ±𝑐𝑜𝑠𝜔𝑡, 𝑐𝑜𝑠 𝜔𝑡 ± 90! = ∓𝑠𝑒𝑛𝜔𝑡
!
𝑧 = 𝑥 + 𝑗𝑦 = 𝑟∠𝜑 = 𝑟𝑒 !" = 𝑟(𝑐𝑜𝑠𝜑 + 𝑗𝑠𝑒𝑛𝜑), 𝑟 = 𝑥 ! + 𝑦 ! , 𝜑 = 𝑡𝑎𝑛!! , 𝑥 = 𝑟𝑐𝑜𝑠𝜑, 𝑦 = 𝑟𝑠𝑒𝑛𝜑
!
𝑒 ±!" = 𝑐𝑜𝑠𝜑 ± 𝑗𝑠𝑒𝑛𝜑 , 𝑣 𝑡 = 𝑉! 𝑐𝑜𝑠 𝜔𝑡 + 𝜑 ⟺ 𝑽 = 𝑉𝑚∠𝜑 !
𝐙 = 𝑅 + 𝑗𝑋 = 𝐙 ∠𝜃, 𝐙 = 𝑅 ! + 𝑋 ! , 𝜃 = 𝑡𝑎𝑛!! , 𝑅 = 𝐙 𝑐𝑜𝑠𝜃, 𝑋 = 𝐙 𝑠𝑒𝑛𝜃
𝐶=
𝑄!
𝑃(𝑡𝑎𝑛𝜃! − 𝑡𝑎𝑛𝜃! )
=
!
!
𝜔𝑉!"#
𝜔𝑉!"#
!
!
!
!
!
𝑝 𝑡 = 𝑉! 𝐼! 𝑐𝑜𝑠 𝜃! − 𝜃! + 𝑉! 𝐼! 𝑐𝑜𝑠 2𝜔𝑡 + 𝜃! + 𝜃!
!
!
!
!
𝑃 = 𝑉! 𝐼! 𝑐𝑜𝑠 𝜃! − 𝜃! = Re[VI * ]
Z! = Z ∗!! 𝑃!"# =
V!!
!
!!!!
𝑉!"# =
!!
!
Forma Padrão;