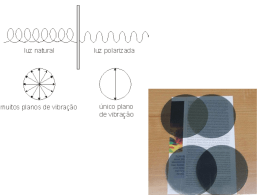
Colégio Ari de Sá
TC 2 – Revisão – ENEM – Física – Prof. João Paulo
Parte 1 – Questões de Ondulatória (Física 3)
1ª. questão
Terras à vista
Vasculhar o universo atrás de planetas com as mesmas características da Terra é um desafio estatístico e também tecnológico.
Mas os cientistas garantem: ainda acharemos um mundo parecido com o nosso.
Por Marco Túlio Pires
“Faz apenas 19 anos que os cientistas descobriram os primeiros planetas fora do Sistema Solar - ou
exoplanetas. Hoje são 685 confirmados e outros 2.000 candidatos. Mas quase nenhum pode abrigar
alguma forma de vida, obsessão maior dos caçadores de novos mundos. Uma rara exceção é o
planeta HD 85512 b, a 36 anos-luz de distância, um dos 50 achados mais recentes do Observatório
Europeu do Sul (ESO, na sigla em inglês). Mas por que é tão difícil encontrar um exoplaneta como a
Terra? Como os astrônomos descobrem mundos fora do Sistema Solar?
Técnicas - De acordo com físico Claudio Melo, da Universidade Federal do Rio Grande do Norte
(UFRN) e astrônomo do ESO, existem dois métodos de maior sucesso para caçar exoplanetas. Um
deles se chama técnica de trânsito e é usada pelo Observatório Espacial Kepler, da NASA, a agência
espacial americana. A outra, batizada de velocidade radial, está presente em um instrumento do ESO
responsável pela confirmação dos 50 exoplanetas mais recentes, chamado HARPS. O método da
velocidade radial é um pouco mais complicado que a técnica de trânsito, apesar de ter o mesmo
princípio: medir uma variação periódica no comportamento dos astros. Esta técnica identifica se o
movimento de uma estrela está sendo influenciado pela gravidade de um eventual planeta em sua
órbita. Quanto maior a influência, maior a massa do planeta. Para medir esta influência, os
telescópios do ESO verificam se a estrela está "bamboleando" em função da presença de planetas. Se
estiver, as ondas de luz emitidas vão se achatar ou se espaçar conforme a estrela se aproxime ou se
afaste da Terra”.
Adaptado de: < http://veja.abril.com.br/noticia/ciencia/terras-a-vista >, com modificações
Acesso em 25/04/2012
Como pudemos observar no artigo anterior, a Física e seus fenômenos são muito importantes nas mais
diversos métodos de observações astronômicas. De acordo com o texto, uma das técnicas utilizadas para a
busca de exoplanetas é a chamada técnica da velocidade radial. Em que fenômeno ondulatório se
fundamenta essa técnica?
a.)
b.)
c.)
d.)
e.)
Difração da luz
Refração da luz
Polarização luminosa
Interferência luminosa
Efeito Doppler da luz
Gabarito: [E]
2ª. questão
Tsunamis
O que são e como se formam?
“O termo "tsunami" vem do japonês significando tsu (porto) e nami (onda). O
termo foi criado por pescadores que,
vindo da pesca, encontraram o porto
desvastado, ainda que não tenham visto
nem observado a onda no alto mar. Um
tsunami pode ser gerado por qualquer
distúrbio que desloque uma massa
grande de água, tal como um sismo
(movimento no interior da terra), um
deslocamento da terra, uma explosão
vulcânica ou um impacto de meteoro.
Os tsunamis podem ser gerados sempre
que o fundo do mar sofre uma
deformação
súbita,
deslocando
verticalmente a massa de água. As
ondas são o resultado da ação da
gravidade sobre a perturbação da
massa de água. Os tsunamis têm um
comportamento muito diferente das típicas ondas de surf; propagam-se a altas velocidades e podem
percorrer distâncias transoceânicas sem grande perda de energia. Tipicamente, cerca de dez minutos
antes de um tsunami, o mar recua da costa, expondo parte do leito marinho. Se a inclinação for rasa,
este recuo pode exceder 800 metros. As pessoas inconscientes do perigo podem permanecer na
costa, devido à curiosidade, mas este pode ser um sinal de advertência da vinda de um tsunami. Pode
haver diversas ondas, com intervalos entre dois e quarenta e cinco minutos. Estas características
ocorrem porque as tsunamis possuem períodos extremamente longos e também grandes
comprimentos de onda. A distinção entre os tsunami e outras ondas sobre a água são seus períodos
de oscilação que variam muito. Sua velocidade de propagação depende da profundidade h do oceano
1/2
e da aceleração local da gravidade: v = (gh) , e seu período permanece constante durante a
propagação”.
Disponível em: < http://www.portalsaofrancisco.com.br/alfa/tsunami/tsunami-9.php >,
Acesso em 30.05.2012
Considere , uma situação hipotética em que um tsunami inicia sua propagação em alto mar com período de
5,0 minutos, a 4.000 m do leito oceânico, e que atinge o litoral propagando-se a 40 metros do fundo. A
amplitude transversal de um tsunami também varia com a profundidade, de tal maneira que para a
profundidade de 4000 m seu valor é de 1,0 m e ao atingir o litoral a 40 metros do solo oceânico terá valor de
2
3,2 m. Adote g = 10 m/s .
Pode-se afirmar que, para o tsunami:
a.) seu comprimento de onda, ao se aproximar do litoral, vale 60 km.
b.) à medida que se aproxima do litoral, sua freqüência diminui.
c.) os prejuízos causados por ele devem-se especialmente ao alto valor da velocidade com que atinge o
litoral.
d.) ao se aproximar da praia, seu comprimento de onda é reduzido por um fator igual ao da redução de sua
velocidade.
e.) o “agigantamento” de sua amplitude ao se aproximar do litoral significa que a energia transportada é
muito maior que aquela em alto mar.
Gabarito: [D]
3ª. questão
Cálculos renais e a Litotripsia ultrassônica
A Física a serviço da Medicina
Nem todos os cálculos urológicos requerem
tratamento. Pedras que são assintomáticas não
obstruem e não causam danos ao trato urinário,
podendo ficar simplesmente sob observação. Cerca
de 80% das pedras vão ser eliminadas
espontaneamente junto com a urina. Entretanto,
estas pedras podem causar dores severas até que
sejam eliminadas. Quando uma pedra é muito
grande para ser eliminada, ela pode ser quebrada
através de um tratamento chamado Litotripsia. A
litotripsia ultrassônica é baseada em um sistema de
ondas mecânicas, produzidas pela expansão e
contração de um cristal piezoelétrico excitado com
corrente alternada, as quais são transmitidas por
contato da sonda para o cálculo. O litotritor
ultrassônico consiste em uma sonda de aço oca
cuja extremidade possui um cristal piezo-cerâmico conectado a um gerador externo. A energia
elétrica estimula o cristal que vibra na frequência de ressonância. A corrente alternada causa rápida
expansão e contração, produzindo vibrações mecânicas de alta frequência que são propagadas
através da sonda, permitindo a fragmentação do cálculo.
Adaptado de < http://www.litotripsia.com.br/litotripsia_invasiva.php >,
Acesso em 13.11.2012
O texto anterior descreve muito bem o importante procedimento urológico da Litotripsia. Acerca dos aspectos
ondulatórios envolvidos na técnica, é correto afirmar que:
a.) as ondas ultrassônicas utilizadas são transversais e transportam consigo os cálculos renais.
b.) o texto sugere que a transferência de energia da onda para o cálculo se dá através do fenômeno da
ressonância, que pode ocorrer para qualquer valor de frequência.
c.) em qualquer parte dos vários e diferentes tecidos urológicos, a velocidade da onda ultrassônica
permanece a mesma, modificando-se apenas a frequência nas transições da onda de um tipo de tecido
para o outro.
d.) quando a onda com frequência igual (ou muito próxima) à frequência natural de vibração do cálculo
incide sobre ele, produz ressonância, favorecendo muito a transferência de energia para o cálculo, o que
acaba por fragmentá-lo.
e.) as vibrações mecânicas de alta frequência, citadas no texto, são muito úteis porque, além poderem
fragmentar os cálculos renais, ainda são capazes de propagar no vácuo, o que permitiria a elas terem
aplicações, por exemplo, em fragmentações de possíveis asteróides que viessem pelo espaço em
direção à Terra.
Gabarito: [D]
4ª. questão
Como funciona o sensor de estacionamento?
Ultimamente, tem se tornado popular o uso de sensores
de estacionamento, principalmente na parte traseira dos
carros. (...) Em alguns modelos, são incluídos no painel
avisos luminosos ou até mesmo um display onde indica a
distância do objeto. Em casos mais simples, o aviso de
distância do sensor de estacionamento funciona através
do som, onde um bip vai se repetindo de forma mais
rápida quando o objeto fica mais próximo e se torna
contínuo quando chegou ao seu limite. O funcionamento
é simples e a tecnologia já é conhecida há um bom
tempo: o chamado ultrassom. (...) Funciona da seguinte forma: uma alta frequência sonora é emitida
pelo sensor e esse sinal reflete no objeto a ser medido voltando para o sensor. (...) Se o sinal não
retorna em um determinado tempo, quer dizer que o objeto está muito distante ou que simplesmente
a onda sonora não conseguiu refletir, o que acarreta na limitação do sistema, que não reconhece
objetos muito pequenos ou fora do raio de ação dos sensores.
Adaptado (com modificações) de < http://como-funcionam.blogspot.com.br/2009/02/comofunciona-o-sensor-de.html >, Acesso em 27.11.2012
O texto descreve fisicamente o funcionamento de um sensor de estacionamento através do uso de ondas
sonoras. Nesse funcionamento, o aspecto determinante para o cálculo da distância ao objeto é que
a.)
b.)
c.)
d.)
e.)
o ultrassom utilizado é uma onda inaudível, pois somente ondas sonoras com essa característica
poderiam refletir no objeto e retornar para o sensor.
o ultrassom utilizado é uma onda longitudinal, único tipo de onda capaz de sofrer difração em torno do
objeto e retornar para o sensor.
o sensor calcula o tempo que o ultrassom demora para ir até o objeto e voltar, obtendo assim a
distância, independentemente da velocidade do som no ambiente considerado.
o comprimento de onda do ultrassom utilizado é muito grande comparado ao de outras ondas sonoras,
facilitando assim a reflexão.
conhecendo a velocidade média do som no ambiente considerado e o tempo que o ultrassom demora
para ir até o objeto e voltar para o sensor, pode-se determinar a distância desejada.
Gabarito: [E]
5ª. questão
Uma corda de densidade e elasticidade uniformes, está pendurada no alto de um teto, no ponto B, e
inicialmente encontra-se em equilíbrio. Em seguida, uma criança produz uma seqüência de pulsos periódicos
e transversais à direção vertical, na extremidade inferior da corda, no ponto A, e observa o movimento de
propagação dos pulsos que sobem pela corda. Com fundamentos na teoria ondulatória para ondas
mecânicas, é correto afirmar que
a.) o módulo da força tensora, a que a corda está submetida, é tanto menor quanto mais próxima do teto.
b.) a velocidade de propagação dos pulsos vai diminuindo enquanto eles sobem, porque o campo
gravitacional é contrário ao sentido de propagação dos pulsos.
c.) a velocidade de propagação dos pulsos, na corda, é constante.
d.) a distância entre os pulsos, na corda, vai diminuindo, à medida que os pulsos vão subindo.
e.) um determinado pulso da onda sobe acelerado.
Gabarito: [E]
6ª. questão
O Sr. Rubinato, um músico aposentado, gosta de ouvir seus velhos discos sentado em uma poltrona. Está
ouvindo um conhecido solo de violino quando sua esposa Matilde afasta a caixa acústica da direita (C d) de
uma distância l, como visto na figura abaixo.
Em seguida, Sr. Rubinato reclama: - Não consigo mais ouvir o Lá do violino, que antes soava bastante forte!
Dentre as alternativas abaixo para a distância l, a única compatível com a reclamação do Sr. Rubinato é
Note e adote:
O mesmo sinal elétrico do amplificador é ligado aos dois alto-falantes, cujos cones se movimentam em fase.
A frequência da nota Lá é 440 Hz.
A velocidade do som no ar é 330 m/s.
A distância entre as orelhas do Sr. Rubinato deve ser ignorada.
a.)
b.)
c.)
d.)
e.)
38 cm
44 cm
60 cm
75 cm
150 cm
Gabarito: [A]
7ª. questão
Um órgão é um instrumento musical composto por diversos tubos sonoros, abertos ou fechados nas
extremidades, com diferentes comprimentos. Num certo órgão, um tubo A é aberto em ambas as
extremidades e possui uma frequência fundamental de 200 Hz. Nesse mesmo órgão, um tubo B tem uma das
extremidades aberta e a outra fechada, e a sua frequência fundamental é igual à frequência do segundo
harmônico do tubo A. Considere a velocidade do som no ar igual a 340 m/s. Os comprimentos dos tubos A e
B são, respectivamente:
a.)
b.)
c.)
d.)
e.)
42,5 cm e 31,9 cm.
42,5 cm e 63,8 cm.
85,0 cm e 21,3 cm.
85,0 cm e 42,5 cm.
85,0 cm e 127,0 cm.
Gabarito: [C]
8a. questão
Uma das extremidades de um fio de comprimento 3,0 m é presa a um diapasão elétrico; a outra passa por
uma roldana e sustenta um peso de 3,6 N que mantém o fio esticado. Fazendo o diapasão vibrar com uma
frequência constante de 300 Hz, o fio apresenta uma configuração com três ventres, como pode ser
observado na figura a seguir:
A ordem de grandeza da densidade linear desse fio, em kg/m, vale
a.)
b.)
c.)
d.)
e.)
–4
10 .
3
10 .
–5
10 .
–2
10 .
–1
10 .
Gabarito: [C]
Parte 2 – Questões de Hidrostática e Gravitação (Física 1)
9a. questão
Os precursores no estudo da Hidrostática propuseram princípios que têm uma diversidade de aplicações em
inúmeros “aparelhos” que simplificam as atividades extenuantes e penosas das pessoas, diminuindo muito o
esforço físico, como também encontraram situações que evidenciam os efeitos da pressão atmosférica. A
seguir, são apresentadas as situações-problema que ilustram aplicações de alguns dos princípios da
Hidrostática.
Situação I – Um sistema
hidráulico de freios de alguns
carros, em condições adequadas,
quando um motorista aciona o
freio de um carro, este para após
alguns segundos, como mostra
figura acima.
Situação II – Os pedreiros,
para nivelar dois pontos em
uma obra, costumam usar
uma
mangueira
transparente, cheia de água.
Observe a figura acima, que
mostra como os pedreiros
usam uma mangueira com
água para nivelar os azulejos
nas paredes.
Situação III – Ao sugar na
extremidade e de um canudo,
você provoca uma redução na
pressão do ar em seu interior. A
pressão atmosférica, atuando
na superfície do líquido, faz com
que ele suba no canudinho.
Assinale a alternativa que corresponde, respectivamente, às aplicações dos princípios e do experimento
formulados por:
a.)
b.)
c.)
d.)
e.)
Arquimedes (Situação I), Pascal (Situação II) e Arquimedes (Situação III)
Pascal (Situação I), Arquimedes (Situação II) e Stevin (Situação III)
Stevin (Situação I), Torricelli (Situação II) e Pascal (Situação III)
Pascal (Situação I), Stevin (Situação II) e Torricelli (Situação III)
Stevin (Situação I), Arquimedes (Situação II) e Torricelli (Situação III).
Gabarito: [D]
10a. questão
Para oferecer acessibilidade aos portadores de dificuldade de locomoção, é utilizado, em ônibus e
automóveis, o elevador hidráulico. Nesse dispositivo é usada uma bomba elétrica, para forçar um fluido a
passar de uma tubulação estreita para outra mais larga, e dessa forma acionar um pistão que movimenta a
plataforma. Considere um elevador hidráulico cuja área da cabeça do pistão seja cinco vezes maior do que a
área da tubulação que sai da bomba. Desprezando o atrito e considerando uma aceleração gravitacional de
2
10m/s , deseja-se elevar uma pessoa de 65kg em uma cadeira de rodas de 15kg sobre a plataforma de 20kg.
Qual deve ser a força exercida pelo motor da bomba sobre o fluido, para que o cadeirante seja elevado com
velocidade constante?
a.)
b.)
c.)
d.)
e.)
20N
100N
200N
1000N
5000N
Gabarito: [C]
11a. questão
Um cubo maciço e homogêneo, com 40 cm de aresta, está em equilíbrio estático flutuando em uma piscina,
com parte de seu volume submerso, conforme desenho abaixo.
3
Sabendo-se que a densidade da água é igual a 1 g/cm e a distância entre o fundo do cubo (face totalmente
submersa) e a superfície da água é de 32 cm, então a densidade do cubo:
a.)
b.)
c.)
d.)
e.)
3
0,20 g/cm
3
0,40 g/cm
3
0,60 g/cm
3
0,70 g/cm
3
0,80 g/cm
Gabarito: [E]
12a. questão
Uma esfera maciça de aço está suspensa em um dinamômetro, por meio de um fio de massa desprezível, e
todo este aparato está imerso no ar. A esfera, ainda suspensa ao dinamômetro, é então mergulhada
completamente num líquido de densidade desconhecida. Nesta situação, a leitura do dinamômetro sofre uma
3
diminuição de 30% em relação à situação inicial. Considerando a densidade do aço igual a 8 g/cm , a
3
densidade do líquido, em g/cm , é aproximadamente
a.)
b.)
c.)
d.)
e.)
1,0.
1,1.
2,4.
3,0.
5,6.
Gabarito: [C]
13a. questão
No poema “O que se afasta”, o eu poético de Sísifo desce a montanha afirma, por comparação, que as
coisas perdem seu peso e gravidade, percepção que está relacionada ao envelhecimento do homem:
“De repente você começa a se despedir
das pessoas, paisagens e objetos
como se um trem
— fosse se afastando (...)”.
Aproveitando o ensejo literário, imagine um objeto próximo à superfície da Terra e uma situação hipotética,
porém sem abrir mão de seus importantes conhecimentos de Física.
Supondo a possibilidade de haver alteração no raio e/ou na massa da Terra, assinale a opção que traz uma
hipótese que justificaria a diminuição do peso desse objeto, que se mantém próximo à superfície do Planeta:
a.)
b.)
c.)
d.)
e.)
diminuição do raio da Terra e manutenção de sua massa.
aumento da massa da Terra e manutenção de seu raio.
aumento do raio da Terra e diminuição de sua massa, na mesma proporção.
diminuição do raio da Terra e aumento de sua massa, na mesma proporção.
diminuição do raio da Terra e diminuição de sua massa, na mesma proporção.
Gabarito: [C]
14a. questão
TEXTO PARA A PRÓXIMA QUESTÃO:
Nesta prova, quando necessário, adote os seguintes valores:
2
Aceleração da gravidade: g = 10 m/s .
−11
2
2
Constante da gravitação universal: G = 6 x 10 N m / kg .
Velocidade do som no ar: v = 340 m/s .
24
Massa da Terra: M = 6 x 10 kg.
Constante π = 3.
Os satélites artificiais são uma conquista da tecnologia moderna e os seus propósitos são variados. Existem
satélites com fins militares, de comunicação, de monitoramento etc. e todo satélite tem uma órbita e uma
velocidade orbital bem determinadas. Nesse contexto, considere um satélite de comunicação que descreve
4
uma órbita circular em torno da Terra com um período de revolução de 8 x10 s.
Com base nessas informações e desprezando o movimento da Terra, é correto afirmar que esse satélite gira
em torno da Terra com uma velocidade orbital de:
a.)
b.)
c.)
d.)
e.)
1000 m/s
1500 m/s
2000 m/s
3000 m/s
3500 m/s
Gabarito: [D]
15a. questão
A tabela a seguir resume alguns dados sobre dois satélites de Júpiter.
Nome
Diâmetro
aproximado (km)
Raio médio da órbita em
relação ao centro de Júpiter
(km)
Io
3,64  103
4,20  105
Europa
3,14  103
6,72  105
Sabendo-se que o período orbital de Io é de aproximadamente 1,8 dia terrestre, pode-se afirmar que o
período orbital de Europa expresso em dia(s) terrestre(s), é um valor mais próximo de
a.)
b.)
c.)
d.)
e.)
0,90
1,50
3,60
7,20
9,80
Gabarito: [C]
Resoluções – TC 2 – ENEM – Prof. João Paulo
Parte 1 – Questões de Ondulatória (Física 3)
Resolução da questão 1
A técnica da velocidade radial, de acordo com o texto, fundamenta-se na mudança da frequência medida
para a luz vinda da estrela para a Terra. Devido ao efeito Doppler, a freqüência medida é maior (ondas mais
achatadas) quando há aproximação
e menor (ondas menos achatadas) quando há afastamento entre a Terra e a estrela:
Resposta: [E]
Resolução da questão 2
a.) Falsa, pois se o período da tsunami é, na questão, constante e vale 5 min, ou seja, 300s, sua freqüência
½
será de 1/300 Hz. Como a velocidade ao se aproximar do litoral será dada por v = (10 x 40) = 20 m/s ,
seu comprimento de onda será: 20 =  . 1/300   = 6000 m = 6km.
b.) Falsa, pois a freqüência é constante , visto que o período também é.
c.) Falsa, pois os maiores prejuízos devem-se à grande amplitude.
d.) Verdadeira, pois sendo a freqüência constante, v e  serão grandezas proporcionais.
e.) Falsa, pois o agigantamento se dá devido à redução da velocidade se transformar em aumento da
amplitude. a energia transportada é a mesma.
Resposta: [D]
Resolução da questão 3
A descrição do texto sugere bastante a ocorrência do fenômeno da ressonância. Com certas frequências
muito bem definidas, chamadas frequências naturais de vibração, é possível realizar uma transferência muito
eficiente de energia de uma fonte para um receptor, como foi o caso da onda ultrassônica em ressonância
com o cálculo. Com essa grande absorção energética, os cálculos acabam se fragmentando em partes
menores, podendo ser, eventualmente, eliminados pela urina.
Resposta: [D]
Resolução da questão 4
O fenômeno ondulatório em que é fundamentado o funcionamento do sensor de estacionamento é a
reflexão. O ultrassom emitido pelo sensor vai até o objeto e retorna, gastando um certo tempo t.
Conhecendo esse tempo e a velocidade média v do som no ambiente considerado, é possível então
determinar a distância d do sensor até o objeto, usando-se:
v
Resposta: [E]
2d
v.Δt
d
Δt
2
Resolução da questão 5
a.) falsa, pois o módulo da força tensora se torna maior quanto mais próximo da extremidade superior, pois
teremos uma maior massa pendurada solicitando tracionando o fio.
b.) falsa, pois de acordo com a relação de Taylor, o módulo da velocidade muda com a densidade linear do
fio , que neste casso é constante conforme o enunciado, e com a força de tração, que nesse caso é
variável.
c.) falsa, de acordo com a explicação feita na opção b.
d.) d)falsa, pois de acordo com a relação fundamental da ondulatória, quanto maior a velocidade de
propagação, maior o comprimento de onda.
e.) verdadeira, pois como a tração vai aumentando no sentido ascendente, a velocidade também terá seu
módulo aumentado, o que caracteriza um movimento acelerado.
Resposta: [E]
Resolução da questão 6
Dados: v = 330 m/s; f = 440 Hz.
Se o Sr. Rubinato não está mais ouvindo o Lá é porque está ocorrendo interferência destrutiva. Para que
ocorra tal fenômeno é necessário que a diferença de percurso entre o ouvinte e as duas fontes ( no caso, )
seja um número ímpar (i) de meios comprimentos de onda. O menor valor de
é para i = 1.
v

330


 f 


 0,375 m   38 cm.
2
2
2  400
Resposta: [A]
Resolução da questão 7
Dados: f1A = 200 Hz; f2A = 2 f1A = 400 Hz; v = 340 m/s.
Das expressões das frequências em tubos aberto e fechado, temos:

v
v
340
 LA 

 0,85 m. 
L A  85 cm.
f1A 
2
L
2
f
2
200 

A
1A


v
340
f  v
 LB 

 0,2125 m. 
LB  21,3 cm.
 1B 4 L
4
f
4
400 

B
1B

Resposta: [C]
Resolução da questão 8
Do enunciado temos que : 3

= 3 m   = 2 m. Calculando-se o módulo da velocidade de propagação,
temos: v = 2 x 300 = 600 m/s.
Utilizando-se a relação de Taylor, temos que : 600 =
Resposta: [C]
μ=
μ=
 μ = 10 kg/m.
-5
Parte 2 – Questões de Hidrostática e Gravitação (Física 1)
Resolução da questão 9
- Situação I – aplicação do freio hidráulico, baseado no princípio de Pascal: qualquer acréscimo de pressão
efetuado num ponto de um líquido em repouso é transmitido integralmente aos demais pontos desse
líquido.
- Situação II – aplicação do princípio de Stevin: pontos de um mesmo líquido que estão na mesma horizontal
estão sob mesma pressão.
- Situação III – Princípio de Torricelli: (já explicado no texto)
Resposta: [D]
Resolução da questão 10
O módulo do peso (P) do conjunto a ser elevado é:


P  mpessoa  mcad  mplat g  P   65  15  20 10  1.000 N.
Como a velocidade é constante, aplicando a expressão do Princípio de Pascal:
Fmotor
F
P
1.000

 motor 
 Fmotor  200 N.
A tub
Apistão
A tub
5  A tub
Resposta: [C]
Resolução da questão 11
Se o corpo está em repouso, o peso e o empuxo têm a mesma intensidade:
dcubo vimerso
P  E  dcubo Vcubo g  dágua Vimerso g 


dágua
Vcubo
Abase himersa
d
 cubo 
dágua
Abase Hcubo

dcubo 32

1
40
Resposta: [E]
Resolução da questão 12
As figuras ilustram as situações.
 dcubo  0,8 g /cm3 .
Se a tração sofre uma diminuição de 30%, então T 2 = 70% de T1.
Nas duas situações a esfera está em equilíbrio.
Fig 1: T1  P



Fig 2: T2  E  P  0,7 T1  E  P  0,7 P  E  P  E  P  0,7 P  E  0,3 P.
Como a esfera está totalmente imersa, fazendo a razão entre o peso e o empuxo, temos:

P  dC V g

E  dL V g


 
P dC V g

E dL V g

P
8

0,3 P d L
 d L  0,3  8  dL  2,4 g /cm3 .
Resposta: [C]
Resolução da questão 13
Para diminuir o peso desse objeto, deveríamos diminuir o campo gravitacional terrestre (g). Analisando a
expressão, vejamos o que aconteceria se aumentássemos o raio e diminuíssemos a massa na mesma
proporção. Sendo k esse fator, temos:
GM

g  2
R

G M R2
g'
g

M



 g' 

3 2 G M
G 
g
k3
k R

 k   g'  G M
g' 
k 3 R2

 k R 2
O peso diminuiria, ficando dividido pelo cubo desse fator.
Resposta: [C]
Resolução da questão 14
A força de atração gravitacional é a força centrípeta.
GMm
r2
m
GM  2πr 
GM
v2


 v2 

r
r
r
 T 
2
r3 
GMT2
4π2

6x1011 x6x1024 x64x108
 64x1021
4x9
 r  4x107 m
V
2πr 2x3x4x107

 3000m / s .
T
8x104
Resposta: [D]
Resolução da questão 15
Matematicamente, a terceira lei de Kepler pode ser expressa por:
T2
r3
orbital, r o raio médio orbital e K uma constante de proporcionalidade.
 K , em que T representa o período
Como os satélites Io e Europa giram em torno do mesmo centro, que é Júpiter, devido à força gravitacional
trocada com o planeta, podemos escrever que:
T2Europa
r 3Europa

T2Io
r 3Io

T2Europa
(6,72.105 )3
TEuropa  3,64 dias terrestres.
Resposta: [C]

(1,8)2
(4,20.105 )3
 T2Europa  13,27