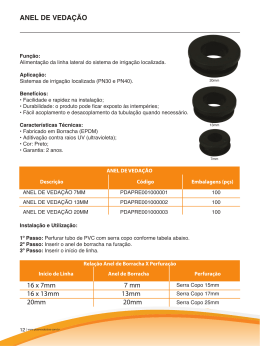
Revista Brasileira de Ensino de Fsica vol. 20, no. 3, Setembro, 1998
307
Vanderlei S. Bagnato
Editor da RBEF
Instituto de Fsica de S~ao Carlos-USP
Caixa Postal 369 13.560-970. S~ao Carlos, SP
Comentario sobre o artigo:
\Determinac~ao da Densidade e da Massa dos Aneis de Saturno"
Wilson Lopes
Universidade Guarulhos1
Universidade de Mogi das Cruzes2
Prezado Editor da RBEF:
Atraves do conhecimento da profundidade ou espessura optica media do anel B de Saturno, da sua densidade media e da densidade das partculas que o constituem, pode-se ampliar os resultados do artigo \Determinacao da Densidade e da Massa dos Aneis de Saturno" (Lopes, 1995): determinando-se o raio medio das
partculas, o numero de partculas por unidade de volume e o numero de partculas que constitui esse anel.
Supondo-se que uma regi~ao do espaco contem um
numero muito pequeno de partculas, por unidade de
volume, um raio de luz que a atravessa o fara sem
muita diculdade, correspondendo a um valor de espessura optica desprezvel, muito proximo de zero. Por
outro lado, admitindo-se que o numero de partculas,
por unidade de volume, seja t~ao grande que o raio luminoso n~ao consegue atravessa-la, diz-se que a regi~ao
tem espessura optica innita.
A espessura optica e denida por:
= ds
= n ds
(1)
onde n e o numero de partculas por unidade de volume, , representa a secc~ao de choque em torno de
cada partcula para a radiac~ao luminosa de frequ^encia
(Rybicki e Lightman, 1979) e ds e a dist^ancia percorrida pela radiac~ao no meio.
Se a radiac~ao luminosa forma um ^angulo com a
normal a superfcie, tem-se:
ds = dy=cos
= secdy:
(2)
Substituindo-se (2) em (1), vem:
d = n secdy:
(3)
d
1
2
Figura 1: A radiac~ao atravessa um comprimento ds, de uma
camada de espessura dy, formando com a reta normal a superf
cie um a^ngulo .
Universidade Guarulhos, Praca Tereza Cristina 1, CEP 07023-070, Guarulhos, SP
Universidade de Mogi das Cruzes, Caixa Postal 411, CEP 08780-911, Mogi das Cruzes, SP.
308
Wilson Lopes
Se = 0 ds = dy e
d = n dy
(4)
ou seja, a profundidade optica depende da dist^ancia
percorrida pela radiac~ao que e a propria espessura da
camada.
O perl de um anel de forma elptica, de espessura 2b = 2 6 103 m (Wilson, 1995), raio interno
R1 = 9 1 107 m e externo R2 = 11 7 107 m, em
relac~ao ao referencial x O y , e dado por:
x2 + y2 =1
(5)
a2 b2
onde a = (R2;R1 )=2 e b representam, respectivamente,
os semi-eixos maior e menor da secc~ao reta do anel (a
espessura do anel e denida por AB = 2b).
0
0
0
0
0
a) A radiac~ao luminosa que atravessa o anel e paralela
ao eixo de rotac~ao de Saturno (o eixo de rotac~ao
do planeta e dos aneis s~ao, praticamente, coincidentes).
b) As partculas que constituem o anel s~ao todas de
forma esferica, de raio medio r e se encontram uniformemente distribudas.
c) A secc~ao de choque de cada partcula, em relac~ao
a radiac~ao luminosa, e dada por: = r2:
Integrando-se a express~ao (4) e levando-se em considerac~ao a hipotese c, obtem-se a profundidade optica
para a dist^ancia y, a saber:
=2 = n
r2y :
(8)
Substituindo-se (7) em (8), obtem-se:
p
= 2n
r2 R 2b
(;x + R2)(x ; R1 )
2 ; R1
Figura 2: Secc~ao reta do anel de Saturno. O anel gira em
torno do eixo de rotac~ao de Saturno, Oy. R, e R2 sao, respectivamente, os raios intemo e externo do anel. O ponto
P, pertencente ao perl el
ptico, apresenta coordenadas (x',
y') em relac~ao ao sistema x'O'y' e coordenadas (x, y) em
relac~ao ao sistema xOy.
Para se escrever a equac~ao, do mesmo perl elptico,
em relac~ao ao sistema referencial xOy, devem-se proceder, na equac~ao (5), as seguintes transformac~oes:
x = x ; (R1 + R2)=2 e y'= y:
0
;
x ; R1 +2 R2 2 y2
+ b2 = 1 :
a2
Resolvendo-se a equac~ao (6) em y, vem:
(6)
p
y = (R 2b
(;x + R2)(x ; R1):
(7)
2 ; R1)
A equac~ao (7) dene o perl elptico do anel, em
relac~ao ao sistema xOy, onde Oy e o eixo de rotac~ao de
Saturno.
Para uma soluc~ao simples do problema, assumem-se
as seguintes hipoteses:
(9)
A equac~ao (9) fornece a profundidade optica do anel,
a uma dist^ancia x do eixo de rotac~ao de Saturno, apos
a radiac~ao ter percorrido a dist^ancia 2y.
O valor maximo da profundidade optica, na equac~ao
(9), ocorre para x = (R1 + R2)=2
max = n
r2 2b
(10)
e o valor medio da profundidade optica e denido por3
1
= R ; R
2
1
Z
anel
dx
Z R2
p
= 2n
r2 (R ;2bR )2
;x + R2)(x ; R1) dx:
2
1
x=R1
= 41 n 2 r2 2b :
(11)
A partir da equac~ao (11), obtem-se:
nr2 = 242b :
(12)
Por outro lado, a densidade media do anel e denida
por:
3 A integral que resulta no valor m
edio da profundidade optica, equac~ao (11), foi resolvida com o auxlio das integrais 146 e 145,
nesta ordem, do Handbook of Chemistry and Physics, 1971.
Revista Brasileira de Ensino de Fsica vol. 20, no. 3, Setembro, 1998
= m n
(13)
= 43 r3 p n onde p e n representam, respectivamente, a densidade
de cada partcula e o numero de partculas por unidade
de volume. Da equac~ao (13), pode-se escrever:
3 (14)
n
4
p :
Com as equac~oes (12) e (14) obt^em-se, respectivamente, o raio medio das partculas, constituintes do
anel, e o numero de partculas por unidade de volume,
a saber:
r3 =
2b
r = 3
16 (15)
n = 4
3 r3 :
(16)
p
e
p
Substituindo-se, na equac~ao (15), = 0 101 103
kg/m3, 2b = 2 60 103 m (Largura sugerida por Lopes,
1995, compatvel com a massa do anel determinada por
McLaughlin e Talbot, 1977), P = 2 50 103kg/m3
(densidade tpica de material rochoso) e = 1 5 (Esposito et al., 1983) t^em-se, para o raio medio das
partculas, r = 41 2 m. Substituindo-se esse valor do
raio medio na equac~ao (16), obtem-se a densidade de
partculas por unidade de volume n = 1 37 10 7
m3. Sendo V = 2 2b (R22 ; R21 )=4 = 3 97 1019
m3 o volume do anel B, pode-se calcular o numero de
partculas que o constitui: N = n V = 4 77 1012.
Desta maneira, a massa do anel B sera dada por:
MB = Nm = N 4
r3 p =3 = 3 50 1021 kg ou, ent~ao,
MB = 6 15 10 6 MS (MS = 5 69 1026 kg representa
a massa de Saturno), que concorda com o valor encontrado por MacLaughlin e Talbot (1977). Por outro
lado, para uma densidade p = 1 00 103 kg/m3 (densidade tpica de gelo) e a mesma profundidade optica,
;
;
309
obtem-se, respectivamente, para o raio medio, numero
de partculas por unidade de volume e para o numero
de partculas: 103 m, 2 20 10 8 m 3 e 7 63 1011
(para estes valores a massa do anel continua a mesma).
;
;
Refer^encias Bibliogracas
1. L. W. Esposito, M. O'Callaghan, E. Simmons, C.
W. Hord, A. West, A. L. Lane, R. B. Pomphrey, D.
L. Co een, M. Sato, \ Voyager Photopolarimeter
Stellar Occultation of Saturn's Rings". Journal of
Geophysical Research: 88(A1), 8643 (1983).
2. Handbook of Chemistry and Physics. Editor:
Robert C. Weast. Cleveland: ed. 51. Chemical
Rubber CO. p. A-172. 1971.
3. W. Lopes, \Determinac~ao da Densidade e da
Massa dos Aneis de Saturno". Revista Brasileira
de Ensino de Fsica. S~ao Paulo, 17(4), 265 (1995).
4. W. I. McLaughlin, e T. D. Talbot, \On the Mass
of Saturn's Rings". Monthly Notices R. Astr. Soc.
London, 179 (3), 619 (1977).
5. G. B. Rybicki e A. P. Lightman, Radioactive Processes in Astrophysics, New York: John Wiley &
Sons, 1979, 382 p.
Sem mais para o momento, subscrevo-me,
Atenciosamente,
Wilson Lopes
Resid^encia:
Wilson Lopes
Rua Jo~ao Marcelo Santoni, 325
Parque Renato Maia
CEP 07114-120,
Guarulhos, SP.