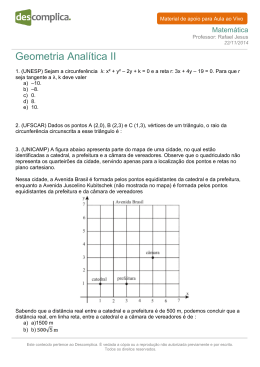
Texto para as questões 28 e 29
A figura abaixo apresenta parte do mapa de uma cidade, no qual estão identificadas a catedral, a prefeitura
e a câmara de vereadores. Observe que o quadriculado não representa os quarteirões da cidade, servindo
apenas para a localização dos pontos e retas no plano cartesiano.
Nessa cidade, a Avenida Brasil é formada pelos pontos equidistantes da catedral e da prefeitura, enquanto a
Avenida Juscelino Kubitschek (não mostrada no mapa) é formada pelos pontos equidistantes da prefeitura e
da câmara de vereadores.
y
7
Avenida Brasil
6
5
4
câmara
3
2
1
prefeitura
catedral
x
▼
1
2
3
4
5
6
7
Questão 29
O ponto de interseção das avenidas Brasil e Juscelino Kubitschek pertence à região definida por
a) (x − 2) 2 + (y − 6) 2  1.
b) (x − 1) 2 + (y − 5) 2  2.
c) x ∈ ]1, 3[, y ∈ ]4, 6[.
d) x = 2, y ∈ [5, 7].
Resolução
Do enunciado temos a figura, em que a Avenida Juscelino Kubitschek está representada pela reta mediatriz j
do segmento BC — afinal, os pontos dessa avenida são equidistantes da prefeitura B e da câmara C. Ainda, o
ponto P é a intersecção das avenidas Brasil e Juscelino Kubitschek.
y
7
6
Avenida Brasil (x = 2)
j
5
P
4
câmara
3
C(5, 3)
2
1
M(4, 2)
prefeitura
catedral
B(3, 1)
A
x
1
2
3
4
5
6
7
M: ponto médio de BC;
3+5 1+3
M
∴ M(4,2)
,
2
2
(
)
↔
O coeficiente angular da reta BC é igual a
↔
3–1
, ou seja, 1.
5–3
Como as retas j e BC são perpendiculares, o coeficiente angular da reta j é igual a –1.
Uma equação da reta j é igual a y – 2 = –1 ⋅ (x – 4), ou seja, y = –x + 6.
Fazendo x = 2, temos y = –2 + 6, ou seja, y = 4 ∴ P(2, 4)
Entre as alternativas, a única que apresenta uma região à qual o ponto P(2, 4) pertence é a alternativa b,
(x – 1)2 + (y – 5)2 < 2, pois (2 – 1)2 + (4 – 5)2 < 2.
Resposta: b