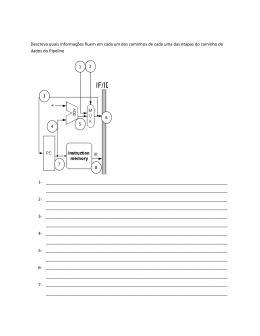
Instituto Superior Técnico
Departamento de Engenharia Electrotécnica e de Computadores
Arquitectura de Computadores
2º sem. 2004/05
2005/06/6
2º Teste
Duração: 1,5 horas
Grupo I – Superpilining [5 valores]
Admita que tem um pipeline com emissão simples, execução em ordem , 1 andar de
fetch, 1 andar de descodificação, múltiplos andares de execução (que incluem o acesso à
memória de dados), e 1 andar de write-back. Admita ainda as seguintes latências:
MUL.D = 5 ciclos, ADD.D = 3 ciclos, DIV.D = 2 ciclos, operações sobre inteiros = 1
ciclo. Admita bypassing total e que necessita de 2 ciclos para acessos à memória de
dados, isto é, os loads e stores precisam de 3 ciclos (incluindo o cálculo dos endereços).
Finalmente, as condições dos branches são calculadas no primeiro andar de execução
(unidade de execução de inteiros).
[2 val] a) Admita que este pipeline é formado por uma sequência linear de andares, em
que andares posteriores servem de nops para instruções mais curtas. Desenhe cada andar
do pipeline como uma caixa (sem pormenores internos), e dê-lhe uma designação
apropriada. Descreva as operações efectuadas em cada um dos andares e mostre todos
os caminhos de bypass (com setas entre andares). O seu objectivo consiste em construir
um pipeline que nunca faz stalls, a menos que um operando não esteja pronto.
Identifique cada uma das setas com o tipo de instruções que fazem o forward dos seus
resultados ao longo do caminho correspondente à seta.
[1 val] b) Quantos “branch delay slots” são necessários com esta arquitectura? Porquê?
[1 val] c) Uma predição dinâmica de saltos poderia melhorar o desempenho do
pipeline? Porquê?
[1 val] d) No pipeline de 5 andares que se conhece da teórica, um LW seguido de um
SW que usa o registo carregado no LW para escrever na memória de dados não produz
stalls. Por exemplo:
LW
SW
R4, 0(R2)
R4, 0(R3)
Isto ainda é verdade com o pipeline da alínea a)? Porquê?
Grupo II –Caches [7 valores]
Para este problema, use a seguinte informação: cache com 96 bytes de capacidade total;
1 palavra = 4 bytes; política de substituição de blocos do tipo LRU; e a cache está
inicialmente vazia.
1 de 5
[3 val] a) Considere a hipótese de desenhar uma cache associativa de 3 vias com blocos
de 2 palavras. Preencha a tabela que se segue, admitindo a sequência de endereços
decimais nela indicada (de cima para baixo). Os endereços são de bytes. No caso de
existir um “miss”, coloque um X na coluna adequada. No caso de haver um “hit”,
indique o tipo de localidade usada para justificar o “hit” (temporal ou espacial). Se
achar preferível, preencha em primeiro lugar a tabela da alínea c) deste problema.
Ender. de leitura (byte)
Decimal
0
4
8
12
0
4
8
36
132
116
16
4
64
112
84
20
64
60
56
36
Binário
0000
0000
0000
0000
0000
0000
0000
0010
1000
0111
0001
0000
0100
0111
0101
0001
0100
0011
0011
0010
Tipo de “miss”
Obrigat. Conflito Capacidade
Localidade no “hit”
Temporal
Espacial
0000
0100
1000
1100
0000
0100
1000
0100
0100
0100
0000
0100
0000
0000
0100
0100
0000
1100
1000
0100
[2 val] b) Qual é o “miss rate” no acesso a esta cache? E qual é o tempo médio de
acesso ao sistema de memória em que a cache se inesere (apenas existe esta cache no
nível 1, e não existem níveis superiores de caches), se o “hit time” no acesso à cache for
de 2 ciclos de relógio e se o acesso à memória levar 60 ciclos de relógio?
[2 val] c) Mostre o estado final da cache, indicando na tabela que se segue os endereços
dos bytes de início de cada palavra em cada bloco da cache.
Índice
Endereço de memória do byte de início das palavras
guardadas am cada bloco
Palavra 0
Palavra 1
0
1
2
2 de 5
3
Grupo III – Escalonamento estático e dinâmico [6 valores]
O código MIPS que se segue calcula a expressão E = A*B + C*D em vírgula flutuante
(FP), tendo os endereços de A, B, C D e E sido previamente guardados nos registos R1,
R2, R3, R4 e R5, respectivamente.
L.D
L.D
MUL.D
L.D
L.D
MUL.D
ADD.D
S.D
F0,
F1,
F0,
F2,
F3,
F2,
F0,
F0,
0(R1)
0(R2)
F0, F1
0(R3)
0(R4)
F2, F3
F0, F2
0(R5)
[2val] a) Calcule o número de ciclos de relógio necessários à execução deste código
(mais exactamente, o número de ciclos entre a emissão da primeira instrução e a
emissão da última, inclusivé) admitindo um pipeline simples com execução em ordem e
sem bypass (forwarding), e com emissão simples.
O caminho de dados (datapath) inclui uma unidade de load/store, um somador FP e um
multiplicador FP. Admita as seguintes latências, em ciclos de relógio: load = 2,
multiplicação FP = 4 e adição FP = 2.
O Write-back (WB) para os registos FP demora 1 ciclo.
Admita que todas as unidades funcionais são completamente pipelined, e que não
existem conflitos no WB.
Admita ainda que todas as instruções antes do primeiro Load já terminaram as suas execuções,
e que existe uma FIFO com capacidade infinita para guardar as instruções no andar de emissão.
Use a tabela que se segue.
Ciclo
0
1
2
3
4
5
6
7
8
9
10
11
Instrução descodificada
(entra no andar de
emissão)
L.D
F0,0(R1)
Instrução emitida
(entra no andar de
execução)
3 de 5
Ciclo de WB para a
instrução emitida
12
13
14
15
16
17
18
19
20
[2val] b) Reordene as instruções dadas (escalonamento estático) por forma a minimizar
o tempo de execução no mesmo pipeline anterior. Mostre a nova sequência e o número
de ciclos de relógio de execução das instruções reordenadas.
Use a tabela que se segue.
Ciclo
Instrução descodificada
(entra no andar de
emissão)
Instrução emitida
(entra no andar de
execução)
Ciclo de WB para a
instrução emitida
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[2val] c) Admita agora que o pipeline anterior foi aumentado com um dispositivo de
escalonamento dinâmico especulativo. A emissão continua a ser simples. Ignore
conflitos estruturais, com excepção da descodificação, que continua a exigir um ciclo
por instrução. Mostre como é agora feita a execução do código original da alínea a), e
quantos ciclos são necessários para a sua execução.
Compare com os resultados obtidos por optimização com o escalonamento estático da
alínea b).
Será que o código optimizado com escalonamento estático executaria mais rapidamente
nesta máquina, que possui escalonamento dinâmico? Porquê?
4 de 5
Use a tabela que se segue.
Ciclo
Instrução descodificada
(entra no andar de
emissão)
Instrução emitida
(entra no andar de
execução)
Ciclo de WB para a
instrução emitida
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Grupo IV – Memória virtual [2 valores]
Admita o seguinte esquema de memória virtual:
(i)
endereços virtuais de 32 bits
(ii)
páginas com 8 kbytes
(iii) memória física com 64 Mbytes
(iv)
TLB com mapeamentro directo e 128 entradas, com uma página física por
entrada
(v)
Cada TLB possui um bit de Validade e um bit “Dirty”.
[2val] Determine o tamanho de cada entrada (PTE) do TLB em número de bits, se
usar o número mínimo de bits de endereço físico. Desenhe esquematicamente a
estrutura do TLB.
5 de 5