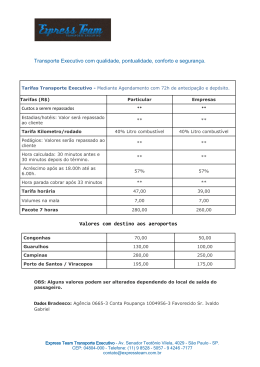
ABORDAGEM PEDAGÓGICA PARA UM SISTEMA DE MEDIDAS
UTILIZADO NO SERTÃO PERNAMBUCANO: LITRO, CUIA E SACA
Jorge Antônio Cavalcante Lima
[email protected]
Zita Maria da Silva Nascimento
[email protected]
Ernani Martins dos Santos
[email protected]
RESUMO
O presente artigo propõe uma abordagem pedagógica para um sistema de medidas
utilizado no sertão de Pernambuco, retomando as discussões dos etnoconhecimentos
propostos originalmente por Lima; Nascimento e Santos (2005). Nessa abordagem
focamos no trabalho com a Matemática Escolar, discutindo a concepção da
Etnomatemática, como campo de conhecimento da Educação Matemática, trabalhando a
visão de “ticas de matema”, descrita por D´Ambrósio (1993), de alguns comerciantes do
município de Tacaratu em Pernambuco. A partir dessa discussão, propomos uma
compreensão do conhecimento matemático a partir do ponto de vista cultural e de como,
a partir dele, podemos agir sobre nossa realidade com intuito de transformá-la ou
preservá-la a partir do trabalho com a Matemática em sala de aula.
Palavras-Chave: Sistema de Medidas; Etnomatemática; Matemática Escolar.
1. INTRODUÇÃO/JUSTIFICATIVA: ESTADO DA ARTE
Neste trabalho retomamos um estudo etnomatemático de um sistema de
quantificar grãos, utilizado no sertão pernambucano. A descoberta do sistema e suas
relações matemáticas foram apresentadas e discutidas originalmente por Lima e
Nascimento sob a orientação de Santos (2005), numa pesquisa maior sobre as
abordagens de etnoconhecimentos utilizados em Tacaratú - Pernambuco e apresentadas
no intuito de discussão científica por Santos (2006a), Santos (2006b) e Santos (2007).
Neste artigo, além do resgate do trabalho inicialmente discutido e apresentado, tratamos
do viés histórico do sistema de medidas, de suas possíveis relações com o sistema
oficial adotado no Brasil e de como é possível trabalhá-lo na sala de aula de
Matemática.
Sabemos que o conhecimento matemático foi desenvolvido seguindo caminhos
diferentes nas diversas culturas, provocado pela experiência própria e a prática em si,
através de movimentos de idas e vindas, com rupturas de paradigmas, frutos da
2
construção de constantes conhecimentos a partir do contexto natural, social e cultural.
Neste sentido temos a Matemática, enquanto ciência, sendo “considerada necessária e
indispensável à humanidade, a matemática é parte integrante de nosso viver e, por
consequência, de qualquer proposta curricular” (MENDES, 2004, p. 15).
Percebemos que é a partir da busca de significados e explicações que o homem
desenvolve saberes e fazeres matemáticos, na tentativa de conviver e compreender sua
realidade e seu ambiente, considerando aspectos sociais, culturais, econômicos e
políticos.
Ao falarmos de conhecimento matemático associado a formas culturais distintas,
é possível se chegar a um conceito a respeito do que se entende por etnomatemática:
Etno é hoje aceito como algo muito amplo, referente ao contexto cultural, e,
portanto, inclui considerações como linguagem, jargão, códigos de
comportamentos e símbolos; matema é uma raiz difícil que vai à direção de
explicar, de conhecer, de entender; a tica vem sem dúvidas de tchne, que é a
mesma raiz da raiz de técnica (D´ AMBRÓSIO 1998, p. 05).
Assim, podemos dizer que a Etnomatemática estuda a matemática culturalmente
produzida, ou seja, que este ramo da Educação Matemática é arte ou técnica de
explicar, de conhecer e de entender os processos matemáticos nos diversos contextos
culturais.
A
Etnomatemática
problematiza
as
diferentes
maneiras
de
se
lidar
matematicamente com o mundo, trazendo os diversos modos de calcular, medir,
estimar, inferir e raciocinar, problematizando o conhecimento que tem sido considerado
como o conhecimento acumulado pela humanidade (KNIJINIK, 2004).
A perspectiva que Knijnik (1996) denominou “Abordagem Etnomatemática”
pode ser vista como uma proposta para o ensino da Matemática, procurando resgatar a
intencionalidade do sujeito através do seu fazer matemático, ao se preocupar com que a
motivação seja gerada por uma situação-problema a ser selecionada por ele, com a
valorização e o encorajamento às manifestações das ideias e opiniões de todos.
Essa abordagem proposta por Knijnik (1996) avança em alguns pontos cruciais,
tais como na discussão do critério de seleção dos conteúdos e, principalmente, no
tratamento que confere aos saberes populares: não se busca usar os saberes populares
unicamente como material intelectual, ponte a partir da qual os saberes acadêmicos
seriam aprendidos. Segundo a pesquisadora, o processo pedagógico é orientado num
duplo sentido: por um lado, o propósito de ensinar Matemática Acadêmica, socialmente
legitimada, cujo domínio os próprios grupos subordinados colocam como condição para
3
que possam participar da vida social, cultural e econômica de modo menos
desvantajoso. Por outro lado, a Matemática Popular não é considerada meramente um
folclore, algo que merece ser resgatado para que o povo se sinta valorizado, embora esta
operação possa produzir tal efeito. As práticas matemáticas populares são “interpretadas
e decodificadas, tendo em vista a apreensão de sua coerência interna e sua estreita
conexão com o mundo prático”, o que as habilita a continuarem sendo utilizadas em
situações que o aluno saberá julgar adequadas (KNIJNIK, 1996, p. 62).
Destacamos, ainda, um ponto principal do processo pedagógico que Knijnik
destaca em seu trabalho: os saberes acadêmicos e populares não devem ser tratados de
modo dicotômico. Suas relações devem ser continuamente examinadas, tendo como
parâmetro de análise as relações de poder envolvidas no uso de cada um desses saberes.
Esta visão não dicotômica é também posta por Meira (1993), que defende a ideia de que
é possível estabelecer relações entre a Matemática Escolar e a Matemática Extraescolar1
de forma a propor uma Educação Matemática mais significativa, sem que seja
necessário buscar uma correspondência ingênua entre os conceitos matemáticos
praticados na escola e os conceitos presentes na vida extraescolar como posto em
Spinillo (2005).
Acreditamos que a produção do conhecimento matemático não pode estar
desvinculada dos movimentos sociais e da cultura de quem produz essa Matemática.
Nesse sentido, podemos afirmar que há um entrelaçamento entre a Matemática
produzida, a sociedade que a produz e a cultura que subsidia essa produção. Tal
entrelaçamento é construído através de um processo cognitivo, mediado pela ação
criativa de diversos operadores mentais, impulsionados pela necessidade de ler,
compreender e explicar a realidade inventada e validada pela sociedade humana.
A Matemática vai se construindo e reconstruindo, sendo ressignificada a cada
momento histórico e de acordo com as exigências da sociedade. Segundo Mendes
(2004) essas exigências se configuram nas atividades socioculturais que vão se
formulando no processo de adaptabilidade cognitiva que é característico da sociedade
humana. Com isso, vamos exigindo de nós mesmos, enquanto sociedade, uma produção
ou reprodução da Matemática, de acordo com as necessidades evidenciadas nas
atividades praticadas nos contextos sociais nos quais estamos inseridos e, para isso,
1
Tratamos a Matemática escolar e extraescolar aqui comungando com a ideia de Spinillo (2005), que diz
que a primeira é considerada de natureza formal, científica, sistematizada, associada a contextos de sala
de aula e a segunda como informal, espontânea, como conhecimento do dia a dia, associada às ruas, a
casa e a contextos sociais.
4
necessitamos produzir ou reproduzir a Matemática existente dos nossos antepassados,
dos povos antigos. Nesse sentido, é necessário procurarmos entender o processo
epistemológico da Matemática, ou seja, o processo gerativo desse conhecimento, o
porquê de sua organização e sistematização.
Um dos caminhos mais pertinentes para se chegar à compreensão do conceito
posto acima e, por consequência, dar melhor significado ao conhecimento matemático
atual é o da própria História da Matemática. Nela vemos que durante muitos anos se
desprezou toda e qualquer visão que não derivasse do modelo matemático europeu.
Todo conjunto de saberes que não se enquadrava no modelo eurocêntrico não foi
admitido pelas elites como conhecimento científico. Desta forma, a própria Matemática
foi produzindo uma linguagem universal, mas seu verdadeiro sentido acabou sendo
encoberto para boa parte das comunidades que não se enquadravam ao modelo imposto,
como evidenciado nos trabalhos de Bicudo e Garnica (2003), e D´Ambrósio (2005,
2002, 1998). Em princípio, isto causou muitos entraves no desenvolvimento da
Matemática enquanto ciência, uma vez que a visão eurocêntrica despreza o fato de que
todas as pessoas, todos os povos, em diferentes culturas, possuem formas de lidar com o
conhecimento matemático que lhes são próprias. Isto pode ser observado em grupos
indígenas brasileiros, em comunidades agrícolas do interior do Brasil, em moradores de
centros urbanos, dentre outros. Todos produzem alguma forma de conhecimento
matemático, como vemos em pesquisas como as de Santos (2011), Rodrigues (2010),
Brito, Lucena e Silva (2006); Pereira (2006); Costa e Silva (2005); Esquincalha (2004);
Bandeira (2004); Bandeira e Morey (2002), dentre muitos outros. É claro que estes
conhecimentos estão fortemente ligados às práticas, vivências e às necessidades de cada
um destes grupos em questão. O cotidiano está impregnado de saberes e fazeres
próprios da cultura. A todo instante os indivíduos estão comparando, classificando,
quantificando, medindo, explicando, generalizando, inferindo e de algum modo
avaliando, usando assim os instrumentos materiais e intelectuais que são próprios à sua
cultura.
As raízes culturais que compõem a sociedade são as mais variadas. A
Matemática é uma forma cultural, do ponto de vista da Etnomatemática, que tem suas
origens num modo de trabalhar quantidades, medidas, formas e operações,
características de um modo de pensar, de raciocinar e de seguir uma lógica localizada
num determinado sistema de pensamento. Esta visão serviu para quebrar muitos
paradigmas acerca da Educação Matemática.
5
Não muito diferente das demais civilizações, o homem sertanejo também
desenvolveu um conhecimento matemático bastante interessante, que pode facilitar a
compreensão de diversos conceitos e subsidiar a prática pedagógica da Matemática,
uma vez que estes saberes são concretos e fazem parte do convívio de alguns adultos,
jovens e crianças sertanejas, ao menos em parte do sertão pernambucano, como ocorre
na cidade de Tacaratu, sertão do São Francisco. A este tipo de conhecimento
matemático, a essas habilidades de um determinado povo, de uma determinada cultura,
damos o nome de “ticas de matema” que seria “a arte ou técnica de explicar, de
conhecer, de entender, de agir numa situação” (D´Ambrósio, 1993, p. 91). Nesse
sentido, os processos de efetuar um cálculo, de realizar contagens, medições,
ordenações e classificações encontradas em grupos culturais seriam também necessários
para o desenvolvimento do conhecimento matemático.
2. AS “TICAS DE MATEMA” DOS COMERCIANTES DE TACARATU2
Um sistema adotado durante muito tempo para medir e quantificar cereais no
sertão é ainda encontrado em Tacaratu. Esta cidade dista 453 quilômetros de Recife,
capital do estado de Pernambuco, e está em um vale ao sul da ribeira do Rio Moxotó, no
alto da serra de mesmo nome. Tacaratu significa na língua Pindaé “serras de muitas
pontas ou cabeças”. O município assinala sua existência desde o século XVII, tendo
como origem uma “maloca” de índios, denominada “Cana Brava”. Ele foi alvo de uma
missão dirigida por padres da Congregação de São Felipe Nery, dando lugar a aldeia
chamada de Brejo dos Padres, que futuramente veio a se tornar a cidade de Tacaratu. O
município atualmente é composto por dois distritos e noventa povoados, sendo o
primeiro distrito a sede do município de Tacaratu e o segundo distrito a Vila de
Caraibeiras. Hoje em dia ainda existem algumas tribos indígenas na região e estas
contribuíram e contribuem para o surgimento e formação da cultura local.
A partir de uma abordagem etnográfica e de convívio na região, identificamos
indícios de atividades etnomatemáticas nesse município. A utilização da cuia no
comércio local de Tacaratu se refere a uma forma de quantificar grãos, comumente
vendidos nas feiras livres do nordeste, tais como feijão, milho, arroz, etc. e também
outros produtos de consumo da alimentação do sertanejo como a farinha de mandioca,
por exemplo. Esses alimentos são comumente vendidos por quilo e grama (unidades de
2
As “ticas de matema” descritas nesse artigo são fruto da pesquisa de Lima; Nascimento; Santos (2005).
6
medidas de massa) nos supermercados, mercadinhos e feiras de todo o Brasil. O
referido sistema de medidas de massa utiliza a cuia, nome utilizado na região, que se
refere a uma caixa cúbica de madeira.
A pesquisa de campo (pesquisa empírica) aconteceu entre os meses de julho e
dezembro de 2005. A mesma foi realizada apenas nos dois distritos da cidade (Centro e
Vila Caraibeiras), uma vez que nessas regiões é que se encontram o comércio e as feiras
da cidade, onde ainda é comum localizar alguns comerciantes que trabalham com a
cuia. Procuramos trabalhar no dia em que ocorre a feira da região, entrevistando e
questionando todos os comerciantes de trabalhavam com a cuia e que aceitavam
participar deste processo da pesquisa. O passo inicial foi identificar e se familiarizar
com os nomes do sistema por eles utilizado e o do instrumento de medidas já citado, a
cuia.
A primeira descoberta interessante foi que ao invés de serem pesados, os
produtos eram medidos em recipientes padronizados e assim eram comercializados por
toda a região. Esta prática foi uma ideia desenvolvida para suprir carência de balanças,
que a mais de um século atrás era um instrumento muito caro e um bem de poucos. Por
outro lado vinha também a desconfiança dos produtores, pois as balanças mais
primitivas não eram tão precisas e muitos “atravessadores” se aproveitavam disto para
levar vantagem em cima dos agricultores. Desta forma, medir seus produtos em
recipientes ao invés de pesá-los tornou-se uma solução segura e viável para o homem do
campo no momento de comercializar seus produtos.
A criação do sistema de medidas nasceu com base numa unidade de volume
do sistema internacional de medidas, o litro. Neste sistema de medida o recipiente
“litro” é uma medida padronizada formada por uma caixa de madeira cúbica, cujo
interior mede 10 centímetros de lado, perfazendo um volume de 1.000 cm3, o que
corresponde a 1dm3, que é exatamente igual a 1 litro.
Figura 01 – Descrição do Litro
7
Quando questionados sobre o conhecimento da unidade litro, os
comerciantes nas feiras da região respondiam que litro correspondia a 01 (uma) cuia
cheia de cereais. Quando perguntamos se o litro serviria apenas para “medir”
quantidades de líquidos, como a água e o leite, por exemplo, eles explicavam que isto
era possível também, mas litro era uma cuia cheia de feijão ou farinha, por exemplo.
Isto nos revela que, de alguma forma, aquelas pessoas sabiam a correlação entre 01dm3
e 01 litro, já que utilizam a nomenclatura litro para a cuia cheia. Porém, a unidade litro
não se refere apenas às medidas de capacidade como comumente utilizamos. Neste
sentido, de alguma forma, em algum tempo atrás, alguém que conhecia o nosso atual
sistema formal de medidas e a nossa Matemática Formal, instituída numa visão
eurocêntrica, sugeriu ou idealizou a utilização do sistema litro, para suprir questões
culturais de necessidade da região, já apontadas acima.
A descoberta seguinte foi a da utilização de múltiplos da unidade “litro”.
Quando questionados sobre como faríamos para comprar uma grande quantidade de
feijão, por exemplo, os comerciantes apresentaram um novo instrumento de medidas.
Essa segunda medida é a “cuia”. Ela é uma expressão indígena que significa
“recipiente onde se cabem muitas unidades”. Fazendo jus ao nome, o recipiente “cuia”,
também conhecido por salamim, é uma caixa em forma de prisma cujo seu interior
mede 16 cm de altura, por 25 cm de comprimento e 25 cm de largura, perfazendo um
volume de 10. 000 cm3, o que corresponde a 10 dm3, ou seja, 10 litros.
Figura 02 – Descrição da Cuia (Salamim)
A terceira medida é a saca, que até hoje ainda é utilizada mundialmente na
comercialização do café e nacionalmente na comercialização de boa parte dos cereais e
dos produtos vendidos em atacados e em grandes produtores. Porém esta “saca” possui
algumas particularidades. Ao contrário da medida em quilogramas, que considera uma
saca de feijão, por exemplo, pesando 50 kg, a saca do sistema “cuia-litro” não é dada
8
pela massa em quilogramas e sim pelo volume em cuias. Sendo assim, neste sistema
uma saca mede 06 cuias de salamim, que correspondem a 60 dm3, ou 60 litros. Vale
salientar que a saca era um grande envelope de tecido, a maioria deles feitos em estopa,
medindo cerca de 1,20 m de comprimento por 0,60 m de largura. Em função do
desconfortável peso que ficava uma saca quando cheia, o que causava bastante danos
físicos aos carregadores, o envelope da saca atualmente utilizado na região tem como
medidas cerca 1 m de comprimento por 0,50 m de largura, comportando apenas 05
cuias, ao invés de 06.
2.1 AS MEDIDAS RENTES E AS MEDIDAS EM COCULOS
As medidas deste sistema, descrito acima, são também chamadas de medidas
rentes. Medida de maneira ao colocar os cereais dentro do interior do litro ou da cuia,
passa-se uma régua rente à base superior para que o volume não ultrapasse a altura do
recipiente. Essa medida chamada de “medida rente” assim como as unidades de
medidas do sistema recebem também este nome, litro rente (ou litro prato) e cuia rente
(ou cuia prato), ou também salamim, como é mais conhecida. Porém, a forma com que
mais se utiliza esse sistema é através das medidas em “coculo”. A palavra “coculo” na
verdade é um desvio de pronúncia da palavra “cálculo”, que neste contexto assume o
significado de “bem medido”, de “capacidade máxima”, de “medida calculada”, como
explicado não só pelos comerciantes da região. No processo de medição em coculo o
conteúdo é colocado na cuia ou no litro de maneira que o volume do recipiente
ultrapassa as bordas do recipiente até formar uma pirâmide com este excesso, o volume
que ultrapassa as bordas do recipiente é que é o chamado “coculo”.
Figura 03 – Descrição da Medida em Coculo
9
2.2 RELAÇÕES EXISTENTES ENTRE AS MEDIDAS RENTES E AS MEDIDAS
DE COCULO
Existem relações matemáticas muito interessantes que podem ser encontradas
entre as medidas de coculo e as medidas rasas. São elas:
●10 litros de coculo constituem, juntas, um volume igual ao de um salamim de coculo
(assim como na medida rasa);
● Uma cuia de coculo aproxima-se bastante, em muitos casos, de 11 litros rasos;
● O coculo de uma cuia, ou seja, o excesso de medida que ultrapassa as bordas da cuia
formando uma pirâmide grande de base quadrada, possui um volume de
aproximadamente 1 litro raso.
2.3 O MEIO LITRO E A MEIA CUIA
Outra técnica muito interessante, que inclui também o campo da geometria,
utilizada dentro deste sistema, é a maneira de medir o meio litro e a meia cuia.
Inteligentemente os comerciantes perceberam que toda vez que mediam cuia de farinha,
ao começar derramá-la no saco formava-se uma área plana de farinha que se estendia
dos ângulos da base até o ângulo opostos superiores do recipiente.
Abertura do Recipiente
Farinha sendo derramada
3. LEVANDO O SISTEMA PARA A SALA DE AULA: PROPOSTA
PEDAGÓGICA
A formação do aluno como cidadão hoje é uma das questões contempladas pelos
Parâmetros Curriculares Nacionais de Matemática (BRASIL, 1998). A preocupação dos
educadores em geral, é a de transformar a sala de aula em um ambiente que contribua
para essa formação.
10
A resistência do sistema educacional em adaptar os conteúdos matemáticos às
condições determinadas pela dinâmica cultural do lugar acaba distanciando o aluno da
escola.
Considerando que o conhecimento construído na escola deve servir como
instrumento de compreensão de questões mais amplas, a Educação Matemática tende a
estar atenta à compreensão de contextos socioculturais diversificados, de modo a incluir
aspectos de educação informal, contribuindo para a construção de uma proposta de
Educação Matemática realmente significativa.
Nesse contexto, a Etnomatemática apresenta-se como uma possibilidade real de
entender o ciclo de geração, organização e difusão do conhecimento, observando o
pensamento da atividade matemática de certo grupo.
O cotidiano está impregnado dos saberes fazeres próprios da cultura. Os
indivíduos trocam, aprendem, ensinam conhecimentos que adquirem de maneira
informal, onde a escola não entra como mediadora desse conhecimento, este é fruto de
sua realidade como diz Ferreira (2003, p.18):
A proposta pedagógica da Etnomatemática é fazer da matemática algo vivo,
lidando com situações reais no tempo (agora) e no espaço(aqui). E, através da
crítica, questionar o aqui e agora. Ao fazer isso, mergulhamos nas raízes
culturais e praticamos dinâmica cultural. Estamos, efetivamente,
reconhecendo na educação a importância das várias culturas e tradições na
formação de uma nova civilização, transcultural e transdisciplinar. (...) Por
tudo isso, eu vejo a Etnomatemática como um caminho para uma educação
renovada, capaz de preparar gerações futuras para uma civilização mais feliz.
Quando ensinamos Matemática nas escolas, geralmente, não permitimos que os
alunos tenham acesso a vivência necessária para chegar à Matemática real, pois
negamos a eles uma série de atitudes e habilidades, para que eles criem um ambiente
adequado para que possam fazer Matemática espontaneamente.
É evidente a necessidade que as escolas têm de acelerar o processo de
construção e aquisição do conhecimento que a humanidade levou milhares de anos
acumulando.
Porém, não podemos oferecê-lo pronto e acabado para os alunos.
Devemos, portanto, dar oportunidade para que eles possam vivenciar um pouco essa
experiência, refletindo sobre suas realidades, para que sejam conduzidos ao
conhecimento. Por isso, devemos dar o enfoque da Etnomatemática para a Matemática,
trazendo a sua contribuição para as escolas, proporcionando aos alunos uma vivência
que somente faça sentido se eles estiverem em seu ambiente natural e cultural. Neste
sentido estamos criando situações variadas que possam despertar e aguçar o interesse e
a curiosidade que os alunos possuem naturalmente, para tornar a Matemática agradável
11
de ser aprendida, tendo como objetivo conectar a Matemática ensinada nas escolas com
a Matemática presente em seu cotidiano. Nesta visão, D´ Ambrósio (1993, p. 327) põe
que:
É necessário modificarmos a imagem que a matemática possui de funcionar
como uma máquina seletora que determina quais alunos irão concluir cada
estágio escolar. Devemos discutir também sobre a importância da matemática
para a construção da cidadania, com ênfase, principalmente, na participação
crítica e autônoma dos alunos, proporcionando-lhes o estabelecimento de
conexões da matemática com outros temas de sua vida cotidiana.
Os professores enquanto mediadores do processo de ensino-aprendizagem da
Matemática devem esclarecer ao aluno a importância desta ciência como instrumento
para melhor compreensão do mundo que está a sua volta e, também, como um
conhecimento que procura estimular o interesse, a curiosidade, a criatividade, a
criticidade, a investigação e a resolução de problemas. Mas, para que estas habilidades
sejam adequadamente desenvolvidas nós, professores e educadores, devemos explorar
os conteúdos matemáticos de maneira inovadora.
O conhecimento matemático construído e a sua utilização não foram feitos
somente por matemáticos e cientistas, mas também, por maneiras diferentes de encarar
as coisas que nos cerca, por todos os grupos sociais que, ao longo da história,
desenvolveram e utilizaram as habilidades necessárias para contar; localizar; medir;
representar e explicar o mundo, de acordo com as suas necessidades e interesses. Assim,
a Matemática surge de acordo com as necessidades do momento histórico e por isso
temos que valorizar o saber matemático culturalmente construído para que possamos
aproximá-lo do saber escolar, no qual os alunos fazem parte, para que eles se tornem
efetivamente o agente ativo desse processo de ensino-aprendizagem. Dessa forma,
estaremos contribuindo para superar o mito que a Matemática é um conhecimento
direcionado somente para uma elite que está presente em determinados grupos culturais
ou em algumas sociedades desenvolvidas.
Ao utilizarmos a Matemática como instrumento social e de cidadania devemos
assegurar uma forte fundamentação conceitual, para evitarmos que os conteúdos sejam
explorados somente sob uma forma instrumentalizada ou folclórica, desenvolvendo o
raciocínio lógico e a capacidade de pensar, para que os alunos possam ir além da
simples memorização, contribuindo dessa maneira para a evolução do espírito crítico e
para mostrar a Matemática como um “saber” ligado à vida e a história dos seres
humanos.
12
É no sentido do que foi discutido acima, nesta parte do artigo, que propomos
uma alternativa de trabalhar o sistema de medidas existente em Tacaratu (que utiliza a
cuia como medida de massa), ao menos nas escolas da região. O sistema Litro, Cuia e
Saca pode ser trabalhado para dar mais significado ao nosso sistema de medidas de
massa e de capacidade, que é baseado no Sistema Internacional de medidas. Antes,
porém, sugerimos um trabalho bem feito entre os conceitos de peso e massa3 que não
abordaremos neste trabalho.
Seria importante que, ao iniciar o trabalho, todos os alunos estivessem
familiarizados com sistema de medidas da cuia, pois podem existir alunos que não
conheçam o sistema apesar de viverem em Tacaratu. Neste caso, o professor pode
realizar visitas às feiras livres da região mostrando aos alunos como o sistema funciona.
Isto serviria não só como informação para os que desconhecem o sistema, mas também,
como campo de pesquisa para os estudantes. Eles poderiam questionar os comerciantes
da região sobre o sistema, que produtos mais vendem, qual dos recipientes é mais
utilizados, etc. Outra alternativa mais voltada para a sala de aula seria trabalhar o
sistema no próprio ambiente da sala, fazendo manipulações e medições com os alunos
utilizando as caixas de medidas.
Após esta fase, o professor trabalharia a unidade fundamental do sistema, o litro,
e os seus múltiplos, o salamim e a saca e o significado da palavra cuia no sistema,
geralmente adotada a partir do recipiente salamim. Dando continuidade ao estudo, o
próximo passo seria trabalhar as medidas rentes e as medidas de coculo, já
mencionadas, bem como a maneira de se medir meia cuia.
Estando bem familiarizados com o sistema, o trabalho seguinte seria com o
Sistema Internacional de medidas adotado pelo Brasil, assim como em outros países
latinos, que utiliza o grama como unidade fundamental. O pontapé inicial seria
apresentar o sistema adotado em nosso país e, em seguida, levantar questionamentos do
tipo: “Trabalhamos este sistema de medidas na nossa cidade? Em que situações?” “Por
que será que nas feiras existem comerciantes que trabalham com a cuia e não com o
quilo?” Conhecido o nosso sistema de medidas de massa e esclarecidas às possíveis
dúvidas e análises com relação ao sistema cuia, é hora de apresentar os múltiplos e
3
Massa é a quantidade de matéria que um corpo possui, sendo, portanto, constante em qualquer lugar da
terra ou fora dela. Peso de um corpo é a força com que esse corpo é atraído (gravidade) para o centro da
terra.
13
submúltiplos do grama. O ideal, neste processo é esclarecer ou apontar pistas que
mostrem o quilograma como a outra unidade mais trabalhada nesse sistema, após o
grama.
Nessa fase das explicações, caso não tenha acontecido, seria interessante
apresentar tópicos históricos da região, com possível auxílio do professor de história da
turma, mostrando, inclusive, a necessidade e o surgimento do sistema cuia em Tacaratu,
já comentado anteriormente. De crucial importância, pegando o viés histórico do
trabalho, o professor deve esclarecer que este sistema de medidas que adotamos no
nosso país foi imposto ao Brasil em 1862 e idealizado pelo governo francês em 1795.
Possivelmente, a idealização do sistema parte da necessidade de trabalhar os sistemas de
medidas atrelados ao sistema de numeração decimal, uma vez que as contagens também
são feitas com múltiplos de dez. Antes, as estimativas de volume eram o “punhado” que
foi substituído pela “cuia de cinco litros”. A imposição foi feita pelo governo português
da época, na tentativa de eliminar as raízes culturais de nosso povo (utilização do
punhado e cuia), como mostrado por Senna, apud Bandeira (2004, p. 49). Em hipótese,
como Tacaratu surgiu no século XVII, o idealizador do sistema na região, que já deveria
conhecer o sistema imposto por Portugal, fez as adaptações necessárias e continuou a
trabalhar com a cuia como unidade de medida, porém com capacidade diferente. Isto
preservou as raízes culturais na região.
Para trabalharmos as medidas de capacidade, o sistema Litro, Cuia e Saca nos
fornece a correlação fundamental entre volume e medidas de capacidade do sistema
adotado no Brasil: 1l (um litro) equivale a 1dcm3 (um decímetro cúbico). O professor
pode trabalhar o conceito de volume, partindo dos recipientes litro, salamim e saca,
inclusive resgatando as correlações existentes: 10 litros equivale a 01 salamim e 01 saca
comporta 05 cuias ou salamins. Esta abordagem sobre volume poderá esclarecer a
questão do por que utilizamos o litro, unidade fundamental, para medidas de capacidade
e não de volume. O aluno deve perceber que há a necessidade de preenchermos todo o
espaço dentro de um recipiente qualquer para termos realmente o volume de um sólido
(o que não acontece quando preenchemos um recipiente com sólidos de qualquer
gênero). Por isso, os líquidos são utilizados nas medidas de capacidade e assim, a razão
de termos leite, óleo, refrigerante, suco, dentre outros, como medidas de capacidade,
utilizando o litro como unidade fundamental. Uma boa experimentação seria utilizar um
recipiente transparente de 01 (um) litro e preenchê-lo com vários sólidos (grãos, pedras,
sólidos menores, etc.) e também com vários líquidos (água, óleo, etc.). Eles perceberão
facilmente que com os líquidos o volume permanece constante, ou seja, o recipiente fica
14
totalmente preenchido. Colocando material sólido no recipiente irão aparecer pequenos
espaços entre os sólidos, não preenchendo todo o volume do recipiente. Quanto maior
for o volume do sólido posto no recipiente menor será a ocupação do espaço do mesmo
(volume do recipiente). A partir deste entendimento, os alunos podem ter contato com a
convenção: 01 kg (um quilograma) equivale a 01 1dcm3 (um decímetro cúbico) que
também equivale a 01 l (um litro). O professor deve esclarecer que isto só é possível
utilizando-se água pura (destilada), com uma temperatura constante de 4º C e que esta
condição foi estabelecida para relacionar as medidas de massa, com as medidas de
capacidade e volume. Importante dar pequenos esclarecimentos sobre água destilada 4e
sobre a medida de temperatura Celsius5. Com isto, pretende-se esclarecer aos alunos que
há uma relação entre as medidas de massa, de capacidade e volume, mas esta difere da
que acontece no sistema Cuia, Litro e Saca. A diferença se dá exatamente porque não se
trabalha apenas com água destilada com litro no sistema de medidas de Tacaratu e sim
com farinha e outros grãos de consumo da população. Então, as pessoas ao comprarem
01 l (um litro) de feijão ou farinha, por exemplo, não estariam levando um quilo deste
alimento, como comumente encontramos estes produtos em mercados e supermercados,
já empacotados, ou quando pedimos para pesá-los em alguma balança. Um litro, a
partir da cuia, tem mais que um quilograma no nosso sistema, uma vez que essa
correlação só é possível com a água destilada. Esse seria mais um momento de
experimentação do professor com os alunos. Sugerimos que eles efetuem o
preenchimento de um litro de vários grãos comprados com a cuia e depois efetuem a
pesagem, em qualquer tipo de balança, com as devidas explicações pertinentes a balança
utilizada, verificando a quantidade de massa, vulgarmente chamada de “peso”, de um
litro de cada tipo de grão. Isso abriria uma boa discussão para o trabalho do conceito de
densidade pelo professor de ciências, o que não será comentado neste trabalho. O
professor a partir de então, deve deixa claro que trabalhar com a cuia não está errado,
que ninguém quer levar vantagem com isto. Comprar um litro de feijão ao invés de um
quilo, por exemplo, seria mais vantajoso em termos de volume, de quantidade do
produto, porém eles devem verificar o que é economicamente melhor. Será que um litro
4
Água destilada é água que foi obtida através da destilação (condensação do vapor de água obtido pela
ebulição) de água normal que contém, em geral, outras substâncias dissolvidas.
5
Celsius (°C) designa a unidade de temperatura, assim denominada em homenagem ao astrônomo sueco
Anders Celsius (1701–1744), que foi o primeiro a propô-la em 1742.
15
com a cuia é mais barato que um quilo? Este seria um trabalho interessante e que não
foi objeto de estudo neste trabalho.
4. CONSIDERAÇÕES FINAIS
Este estudo nos evidenciou que mesmo conhecendo o sistema de medidas de
massas utilizado oficialmente no Brasil e que é exaustivamente estudado e trabalhado
nas escolas, existem pessoas de Tacaratu que ainda utiliza um velho sistema de medidas
da região, que perdura desde o início das atividades comerciais no município. Isso
evidencia que as raízes culturais desses cidadãos influenciam os procedimentos
matemáticos práticos por eles utilizados, independentemente do que é aprendido nas
escolas, trazendo muitas vezes a cultura imposta por outros povos.
O presente abre espaço analisarmos as possíveis correlações entre a cuia e as
unidades de medidas de massa do nosso sistema, principalmente as mais utilizadas
como o quilo e a grama, com indagações do tipo: Quantos quilos e/ou gramas há numa
cuia? Isto nos abre espaço, também, para detalhar melhor as relações de volume e
aprofundar as correlações com o sistema de medidas de massa.
Esses e muitos outros saberes populares podem ser utilizados como instrumentos
pedagógicos pelo professor e pode facilitar muito a compreensão de conceitos
matemáticos pelos estudantes da região, uma vez que os mesmos estão em contato
direto com estes conhecimentos e poderiam ser aproveitados na sala de aula.
A
Etnomatemática
privilegia
o
raciocínio
qualitativo.
Um
enfoque
etnomatemático está ligado a uma questão maior, raramente desvinculado de outras
manifestações culturais tais como religião, arte ou conhecimento popular. A
Etnomatemática traz, assim, uma concepção multicultural e holística da Educação.
A etnomatemática pode ser uma ferramenta impressionantemente simples e
eficaz na tarefa de desmistificar a Matemática e aproximá-la das necessidades locais.
Procuramos neste estudo trabalhar a Etnomatemática como recurso facilitador,
para que o aluno compreenda problemas matemáticos. É preciso, neste sentido, que ele
mergulhe em sua cultura e entenda sua origem. Porém, para que isto ocorra, é
necessário que as escolas respeitem as concepções de mundo que nossos alunos
possuem. Assim, nossos alunos compreenderão que a Matemática existe dentro de uma
cultura e por meio dela nós agimos sobre nossa realidade, com intuito de transformá-la
ou preservá-la.
16
REFERÊNCIAS BIBLIOGRÁFICAS
BANDEIRA, Francisco de Assis. Um caminho para uma pesquisa em Etnomatemática:
o caso dos horticultores da comunidade de Gramorezinho in: Educação (Etno)
Matemática – Pesquisa e Experiências. Natal, Flecha do Tempo, 2004.
BANDEIRA, Francisco de Assis; MOREY, Bernadete Barbosa. A matemática e a
cultura de hortaliças: Uma pesquisa em etnomatemática in: Anais do V EPEM,
Garanhuns, 2002. CD-ROM.
BICUDO, Maria Aparecida Viggiani; GARNICA, Antonio Vicente Marafioti. Etnoargumentações: ultrapassando o panorama eurocêntrico in: Filosofia da Educação
Matemática. Belo Horizonte, Autêntica, 2003.
BRASIL. Parâmetros curriculares nacionais de matemática. Brasília, MEC: SNEF,
1998.
BRITO, Maria A; LUCENA, Isabel; SILVA, Francisco Hermes da. Etnomatemática e a
Cultura Amazônica: Um caminho para fazer Matemática em sala de aula in: Anais do I
SIPEMAT, Recife, 2006. CD-ROM.
COSTA, Wanderleya Nara Gonçalves; SILVA, Evanisio da. Matemática do negro no
Brasil in: Scientific American Brasil. Edição Especial: Etnomatemática. São Paulo,
Duetto, 2005.
D´AMBRÓSIO, Ubiratan. Volta ao mundo em 80 matemáticas in: Scientific American
Brasil. Edição Especial: Etnomatemática. São Paulo, Duetto, 2005.
____________________ Etnomatemática: Elo entre as tradições e a modernidade. Belo
Horizonte, Autêntica, 2002.
____________________ Etnomatemática. São Paulo, Ática, 1998.
____________________ A transdisciplinaridade como acesso a uma história holística
in: Rumo a nova transdisciplinaridade: sistemas abertos de conhecimento. São Paulo,
Summus, 1993.
ESQUINCALHA, Agnaldo C. Etnomatemática: Um estudo da evolução das idéias in:
Anais do VIII ENEM, Recife, 2004. CD-ROM.
FERREIRA, Eduardo Sebastiani. Cidadania e Educação Matemática. Revista da SBEM,
ano 1, número 1, 2º semestre 2003.
KNIJNIK, Gelsa. Exclusão e resistência: educação matemática e legitimidade cultural.
Porto Alegre: Artes Médicas, 1996.
_____________. Itinerários da etnomatemática: questões e desafios sobre o cultural, o
social e o político na educação matemática. In: KNIJNIK, Gelsa; WANDERER,
17
Fernanda; OLIVEIRA, Claúdio José de (Org.). Etnomaremática, currículo e formação
de professores. Santa Cruz do Sul: EDUNISC, 2004.
LIMA, Jorge Antônio; Nascimento, Zita Maria da Silva; SANTOS, Ernani Martins dos.
A etnomatemática e as suas contribuições para o homem sertanejo em Tacaratu.
Monografia de Especialização em Programação do Ensino de Matemática. FFPG, 2005.
MEIRA, Luciano. O “mundo – real” e o dia-a-dia no ensino da matemática in: A
educação matemática em revista. Ano 01, nº. 1, SBEM, p. 19-27, 1993.
MENDES, Iran de Abreu. Matemática: Ciência, Saber e Educação in: Educação (Etno)
Matemática – Pesquisa e Experiências. Natal, Flecha do Tempo, 2004.
PEREIRA, Franz K. A Matemática entre a floresta e o rio: Uma experiência de
Etnomatemática em classes multiseriadas no Marajó – PA in: Anais do I SIPEMAT,
Recife, 2006. CD-ROM.
RODRIGUES, Thiago Donda. A Etnomatemática no contexto do ensino inclusivo.
Curitiba: CRV, 2010.
SANTOS, E. M. A Etnomatemática como aporte às práticas de ensino de jovens e
adultos. São Cristóvão: Anais do V Colóquio Internacional de Educação e
Contemporaneidade, 2011.
_____________. Uma proposta de como abordar na sala de aula o litro, a cuia e a saca –
um sistema de medidas utilizado no sertão de pernambucano. Belo Horizonte: IX
Encontro Nacional de Educação Matemática, 2007.
_____________. Cuia e litro: Um estudo etnomatemático no município de Tacaratu.
Recife: Simpósio Internacional de Pesquisa em Educação Matemática, 2006a.
_____________. Cuia e litro: Um estudo etnomatemático no município de Tacaratu.
Caruaru: VI Encontro Pernambucano de Educação Matemática, 2006b.
SPINILLO, Alina Galvão. Concepções do professor sobre o conhecimento extra-escolar
do aluno e suas implicações para o ensino da matemática in: Boletim GEPEM. Nº. 47 –
Julho/Dezembro, p. 11-30 2005.