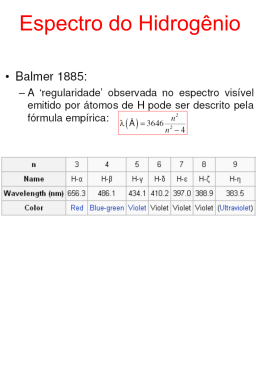
01.
Um átomo de hidrogênio inicialmente em repouso emite
um fóton numa transição do estado de energia n para o
estado fundamental. Em seguida, o átomo atinge um
elétron em repouso que com ele se liga, assim
permanecendo após a colisão. Determine literalmente a
velocidade do sistema átomo + elétron após a colisão.
Dados: a energia do átomo de hidrogênio no estado n é E n
2
= E 0 /n e c a velocidade da luz.
02.
Para explicar as raias espectrais do átomo de hidrogênio,
Niels Bohr formulou a hipótese de que para o elétron de
massa m e carga e, descrevendo uma órbita circular de raio
r e velocidade v em torno do núcleo, a quantidade
mvr
= (h/2π)n era quantizada, onde n = 1,2,3, e h é a
constante de Planck. De acordo com o exposto, determine
a expressão do raio das órbitas do elétron em função
somente de e, h, m, n, π e ε 0 .
03.
Um paralelepípedo de comprimento a 0 , largura b 0 e altura
c 0 viaja a uma velocidade próxima à da luz na direção de a 0
. Mostre que a densidade deste objeto, nesta velocidade,
do ponto de vista de um observador na Terra, é:
d0
, onde d 0 é a densidade própria do corpo em
d=
  v 2 
1 −   
  c  
b)
05.
04.
O tempo de meia vida de estados eletrônicos metaestáveis de alguns átomos é utilizado na construção de
relógios atômicos. Classicamente, pode-se definir o tempo
de vida τ de uma partícula de massa m e carga q ,
movendo-se numa órbita circular de raio r com aceleração
E
a e energia total de módulo Et , como τ = t , sendo PR ,
PR
nessa órbita, a potência irradiada pela carga acelerada,
dada
pela
seguinte
equação:
q2 2 a2
=
4 πε 0 3 c3
permissividade
luz no vácuo.
O modelo de
=
PR
b)
2
 mc2 
9
c 3,0 × 108 m / s , onde e é a
 =
 1,42 × 10 ; =
 E0 
carga do elétron e  é a constante de Planck dividida
por 2π .
www.cursosimbios.com.br
UFG • 2013
Antipartículas, raras na natureza, possuem carga elétrica
oposta à de suas partículas correspondentes. Se
encontrássemos uma fonte de antipartículas, poderíamos
produzir uma grande quantidade de energia, permitindo
que elas se aniquilassem com suas partículas. Dessa forma,
calcule:
a)
a quantidade de energia que seria liberada se 2,0
gramas de antimatéria fossem aniquiladas com 2,0
gramas de sua matéria (considere a velocidade da
8
luz igual a 3,0 × 10 m/s);
b)
por quanto tempo essa energia abasteceria uma
cidade com um milhão de habitantes, considerando
que uma pessoa consome, em média, 100 kWh por
mês.
07.
Segundo a Teoria da Relatividade Restrita de Albert Einstein,
o tempo transcorre de maneira diferente para observadores
com velocidades diferentes. Isso significa que, para um
observador em um referencial fixo, transcorre um intervalo
de tempo ∆t entre dois eventos, enquanto para um
observador em um referencial que viaja com uma velocidade
constante v, em relação ao referencial anterior, o intervalo
de tempo entre os mesmos eventos será ∆t' . Os dois
intervalos de tempo estão relacionados por
∆t'
,
∆t =
2
v
1-  
c
2
hidrogênio, calcule:
a)
a energia perdida pelo elétron, na transição do
primeiro estado excitado par ao estado fundamental;
(2,0 pontos)
4 πε0 2
e2
= 0,53 × 10 −10 m ;
; r0
Dados:=
E0 = 13,6 eV =
me2
8πε0
Calcule a energia E , em elétron – volts, do fóton
emitido.
considerando que a quantidade de movimento do
sistema se conserva, qual é a velocidade v de recuo
do átomo?
06.
16  c  Et 
 
 Et , na qual ε 0 é a
3  r  mc2 
dielétrica do vácuo e c é a velocidade da
Bohr foi bem sucedido ao fornecer as
E
energias do átomo de hidrogênio, expressas por En = − 02 ,
n
2
com raios de órbitas rn = r0n . Para o elétron do átomo de
o tempo de meia vida do primeiro estado excitado,
usando definição básica. (3,0 pontos)
De acordo com o modelo de Bohr, as energias possíveis dos
estados que o elétron pode ocupar no átomo de
E
hidrogênio são, aproximadamente, dadas por En = − 02 ,
n
em que E 0 = 13,6eV e n =1,2,3,4,........ O elétron faz uma
transição do estado excitado n = 2 para o estado
fundamental n =1. Admitindo que a massa do átomo de
–27
hidrogênio é igual à massa do próton m p = 1,6×10 , faça o
que se pede nos itens seguintes.
a)
repouso.
02
MARATONA
Professor • Greg
18/01/2013
Física
1
que representa uma dilatação temporal. Nesta expressão, c
é a velocidade da luz no vácuo. Com esta teoria surge o
paradoxo dos gêmeos: para o piloto de uma espaçonave
que realizou uma viagem espacial, com uma velocidade
constante de 0,8c, transcorreram 18 anos até o seu retorno
à Terra.
Para o gêmeo que ficou na Terra, calcule quanto tempo
durou a viagem do seu irmão, o piloto.
08.
Um gás ideal realiza o ciclo termodinâmico constituído por
duas isotermas, AB e CD, e duas isóbaras, BC e DA,
ilustradas na figura abaixo. As temperaturas
correspondentes às isotermas AB e CD valem 300 K e 500
K, respectivamente.
•
o coeficiente de performance (e) é dado por
Q
e = 2 , sendo W o trabalho fornecido para que o
W
refrigerador funcione.
Com base no exposto, atenda às solicitações abaixo.
a)
Determine a variação de entropia em um ciclo.
b)
Calcule a quantidade de energia (calor) Q 1 liberada
para o ambiente em cada ciclo.
c)
Obtenha o coeficiente de performance (e) desse
refrigerador.
GABARITO:
1) Gab: V =
pressão
B
2) Gab: r =
C D
500K
300K
A
D
volume
a)
b)
09.
Indique se o módulo Q a do calor absorvido na
transformação BC é maior, igual ou menor do que o
módulo Q c do calor cedido na trans-formação DA.
Justifique a sua resposta.
Calcule a variação da energia interna nesse ciclo.
O refrigerador é um dos utensílios eletrodomésticos mais
presentes na vida moderna. Desde sua invenção, hábitos
de consumo vêm se modificando, em grande parte, devido
a sua capacidade de armazenar alimentos por longos
períodos. Sendo uma máquina térmica, um refrigerador
opera em ciclos. Na figura abaixo, está ilustrado, num
diagrama T-S, o ciclo (dcbad) realizado por um refrigerador
de Carnot. Imagine um refrigerador operando nesse ciclo,
com temperatura interna T 2 = –3 ºC (270K) num ambiente
à temperatura T 1 = 27 ºC (300K).
E0  n2 − 1 


c mH  n2 
ε0h2 2
n
πme2
3) Gab: em sala
4) Gab:
a)
∆E =−10,2 eV
b)
τ2 =3,0x10 −9 s
5) Gab:
a)
b)
6) Gab:
a)
b)
E = 10,2 eV
3,4 m/s
14
∆E = 3,6 × 10 J
1,0 mês
7) Gab:
30 anos
8) Gab:
a)
b)
Os processos BC e DA são isobáricos, caracterizados
pelo mesmo calor específico e sofrem a mesma
variação de temperatura. então Q a =Q c
zero
9) Gab:
a)
b)
∆S = 0 ;
Q 1 = 300J ;
270
c) =
e = 9
30
Diagrama T-S para um refrigerador de Carnot operando
entre as temperaturas T 1 e T 2 .
Admita que, em cada ciclo, uma quantidade de energia
(calor) Q 2 = 270 J é retirada do interior desse refrigerador.
Para esse ciclo, considere:
∆Q
•
a variação de entropia (∆S) dada por ∆S = ,
T
sendo ∆Q a energia (calor) e T a temperatura;
www.cursosimbios.com.br
2