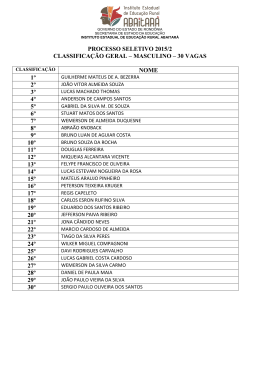
Geometria analítica
Professor Me: Lucas Corrêa de Almeida
Definição
A palavra “geometria” vem do grego “geometrien” onde “geo”
significa terra e “metrien” medida. Geometria foi, em sua origem,
a ciência de medição de terras.

O historiador grego Heródoto (500 a.C.) atribuiu aos
egípcios o início da geometria, mas outras civilizações antigas
(babilônios, hindus, chineses) também possuíam muitas
informações geométricas.

Prof. Me: Lucas Corrêa de Almeida
Definição
 Geometria plana
A geometria plana, também chamada geometria
elementar ou Euclidiana, teve início na Grécia antiga. Esse
estudo analisava as diferentes formas de objetos, e baseia-se
em três conceitos básicos: ponto, reta e plano.
Prof. Me: Lucas Corrêa de Almeida
Definição
 Geometria espacial
Ramo da geometria que estuda a medida do espaço
ocupado por um sólido. Cálculo dos volumes de um cubo, prisma,
pirâmide, cone, cilindro, esfera e de um paralelepípedo.
Prof. Me: Lucas Corrêa de Almeida
Definição
 Axioma
O termo axioma é originado da palavra grega αξιωμα
(axioma), que significa algo que é considerado ajustado ou
adequado, ou que tem um significado evidente. Entre os
filósofos dos gregos antigos, um axioma era uma reivindicação
que podia ser vista para ser verdade sem nenhuma necessidade
de prova.
Exemplos:
1 - Dados quaisquer dois pontos distintos, A e B, existe uma única reta que
os contém
Prof. Me: Lucas Corrêa de Almeida
Definição
2 – Em cada reta existem ao menos dois pontos distintos
3 - Dois segmentos são congruentes (iguais) se eles têm a mesma medida.
4 - Dois ângulos são congruentes (iguais) se eles têm a mesma medida.

Observação. Usamos o termo congruentes, e não iguais, para distinguir
do termo “igual”, que significa, matematicamente, o “mesmo objeto
matemático”.
Prof. Me: Lucas Corrêa de Almeida
Definição
 Alguns símbolos usados em geometria
 A, B, C,....  ponto
 r, s, t,...  reta
 AÔB, DÔE,...  Ô ângulo do vértice O ou medida de ângulo
Prof. Me: Lucas Corrêa de Almeida
Definição
 𝐴𝐵,...  segmento de extremidade A e B, ou reta que passa por
A,B
 𝛥 ABC  triângulo de vértices A,B,C
 AB ≡ CD  segmento AB congruente ao segmento CD
Prof. Me: Lucas Corrêa de Almeida
VETORES
Prof. Me: Lucas Corrêa de Almeida
Grandezas físicas
 Podemos dizer de modo mais usual que grandeza é tudo
aquilo que pode variar quantitativamente.
 Deste modo, grandezas físicas são as que podem ser
medidas.
 São divididas em dois grupos: escalares e vetoriais.
Prof. Me: Lucas Corrêa de Almeida
Vetores e Escalares
 Um vetor possui módulo assim como direção e sentido. Uma
grandeza vetorial possui tanto módulo (valor numérico) quando
direção e sentido, portanto, pode ser representado por um vetor.
Exemplo: deslocamento, velocidade e aceleração.

Nem toda grandeza física envolve uma direção e/ou um
sentido. Essas grandezas são denominadas grandezas escalares.
Que são grandezas que só possuem um valor e uma unidade:
Exemplo: temperatura, massa, tempo.
Prof. Me: Lucas Corrêa de Almeida
Representação de um vetor
 É um ente matemático representado por um segmento de reta
orientado. E tem algumas características básicas.
 Possuí módulo. (Que é o comprimento da reta)
 Tem uma direção (plano em que se analisa)
 E um sentido. (Que é pra onde a “flecha” está apontando).
Sentido
Módulo
Direção da
Reta Suporte
 Exemplo:
Prof. Me: Lucas Corrêa de Almeida
Representação de uma Grandeza Vetorial
 As grandezas vetoriais são representadas da
seguinte forma: a letra que representa a
grandeza, e uma a “flechinha” sobre a letra.
Da seguinte forma...
𝑵
𝑣
𝑩
𝑑
𝑨
𝑴
𝑶
𝐹
𝑷
Prof. Me: Lucas Corrêa de Almeida
Comparação entre vetores
 Vetores iguais
a
r
b
s
 Mesmo Módulo
 Mesma Direção
 Mesmo Sentido
𝑎=𝑏
O vetor 𝑎 é igual ao vetor 𝑏.
Prof. Me: Lucas Corrêa de Almeida
Comparação entre vetores
 Vetores Opostos
a
r
b
s
c
t
 Sobre os vetores 𝑏 e 𝑐 podemos afirmar:
 Tem o mesmo módulo, mesma direção mas sentidos
opostos.
𝑎 = 𝑏 = −𝑐
 O vetor 𝑐 é oposto aos vetores 𝑎 e 𝑏 .
Prof. Me: Lucas Corrêa de Almeida
Vetores
 Observações
a)
Quando escrevemos: 𝑣 = 𝐴𝐵, estamos dizendo que um vetor 𝑣 é
determinado pelo segmento orientado AB.
Exemplo:
𝑣 = 𝐴𝐵
b) Quando dois vetores são paralelos, indicamos por 𝑢//𝑣.
Exemplo:
𝑎//𝑏
Prof. Me: Lucas Corrêa de Almeida
Vetores
c)
Dois vetores 𝑢 e 𝑣 são iguais, e indica-se por 𝑢 = 𝑣, se tiverem
iguais o módulo, a direção e o sentido; Observe:
𝒖≠𝒗
Sentidos opostos
𝒖≠𝒗
Módulos diferentes
𝒖≠𝒗
Direções e sentidos
diferentes
𝒖=𝒗
Módulo, direção e
sentido iguais.
d) Qualquer ponto do espaço é representante do vetor
zero (ou
vetor nulo), que é indicado por 0 ou 𝐴𝐴 (a origem coincide com a
extremidade). Por não possuir direção e sentidos definidos,
considera-se paralelo a qualquer vetor
𝐴
𝑉𝑒𝑡𝑜𝑟: 0 𝑜𝑢 𝐴𝐴
Prof. Me: Lucas Corrêa de Almeida
Vetores
e)
A cada vetor não-nulo 𝑣 corresponde um vetor oposto −𝑣, de
mesmo módulo e mesma direção de 𝑣 , porém, de sentido
contrário. Se 𝑣 = 𝐴𝐵, o vetor 𝐵𝐴é o oposto de 𝐴𝐵, isto é, 𝐴𝐵 =
− 𝐴𝐵 = 𝐵𝐴.
𝑣 = 𝐴𝐵=−𝐵𝐴
Prof. Me: Lucas Corrêa de Almeida
Vetores
f)
- O vetor 𝑢 é unitário se 𝑢 = 1.
- A cada vetor 𝑣, com 𝑣 ≠ 0, é possível associar dois vetores
unitários de mesma direção de 𝑣  𝑢 e −𝑢 . Na figura,
vemos 𝑣 = 6 e 𝑢 = −𝑢 = 1
- O vetor 𝑢 unitário que tem o mesmo sentido de 𝑣 é chamado
versor de 𝑣.
Prof. Me: Lucas Corrêa de Almeida
Vetores
g)
Quando dois vetores 𝑢 e 𝑣 são ortogonais, e indica-se por 𝑢 ⊥
𝑣.
𝑢⊥𝑣
i)
Dois vetores são coplanares se existir algum plano onde estes
vetores estão representados
Prof.:
Prof.
Me: Lucas Corrêa
Corrêa de Almeida
Exercícios
1) A figura abaixo é constituída de nove quadrados congruentes.
Decidir se é verdadeira ou falsa cada uma das seguintes afirmações.
A
L
K
J
B
C
M
N
P
O
I
H
D
E
F
G
Prof. Me: Lucas Corrêa de Almeida
Exercícios
2) A figura abaixo representa um paralelepípedo retângulo. Decidir se é
verdadeira ou falsa cada uma das afirmações
H
E
G
F
D
A
C
B
Prof. Me: Lucas Corrêa de Almeida
Soma vetorial
 Há duas regras para realização da soma vetorial:
 Regra do paralelogramo;
 Regra do polígono.
Prof. Me: Lucas Corrêa de Almeida
Soma vetorial  regra do paralelogramo
𝑎
+
𝑏
=
𝑎
𝑆
𝑏
Assim:
𝑆 =𝑎+𝑏
Neste caso os vetores são transpostos de forma a
fecharem um paralelogramo, esta regra é eficaz somente com
dois vetores.
OBS: Paralelogramo porque traça-se uma reta paralela saindo da
origem do outro seguimento.
Prof. Me: Lucas Corrêa de Almeida
Exemplos
Dado os vetores ....
Prof. Me: Lucas Corrêa de Almeida
Soma vetorial  regra do polígono
𝑌
𝑎
+
𝑋
W
𝑏
𝑎
𝑍
=
𝑋
W
𝑌
𝑏
𝑍
𝑆
Assim: 𝑆 = 𝑎 + 𝑏 ou 𝑆 = 𝑋𝑌 + 𝑊𝑍
Nesta regra o vetor posterior “sai” da extremidade do primeiro.
Prof. Me: Lucas Corrêa de Almeida
Soma vetorial
 Propriedades
 Sendo 𝑢, 𝑣 e 𝑤 vetores quaisquer, a adição admite as seguintes
propriedades:
Comutativa: 𝑢 + 𝑣 = 𝑣 + 𝑢
ii. Associativa: 𝑢 + 𝑣 + 𝑤 = 𝑢 + (𝑣 + 𝑤)
iii. Elemento neutro: 𝑢 + 0 = 𝑢
i.
iv.
Elemento oposto: 𝑢 + (−𝑢) = 0
Prof. Me: Lucas Corrêa de Almeida
Exercícios
3) Dado dois vetores 𝑢 e 𝑣 não paralelos, construir no mesmo gráfico
os vetores 𝑢 + 𝑣, 𝑢 − 𝑣, 𝑣 − 𝑢 e −𝑢 − 𝑣, todos com origem em um
mesmo ponto.
𝑣
−𝑢
𝑢
−𝑣
Prof. Me: Lucas Corrêa de Almeida
Exercícios
4) Com base na Figura abaixo, expressando-os com origem no ponto
A:
A
L
K
J
B
C
M
N
P
O
I
H
D
E
F
G
Prof. Me: Lucas Corrêa de Almeida
Exercícios
5) Com base na figura abaixo, determinar os vetores abaixo,
expressando-os com origem no ponto A:
H
E
G
F
D
A
C
B
Prof. Me: Lucas Corrêa de Almeida
Componentes de vetores
 Uma técnica mais organizada para somar vetores envolve
álgebra, mas exigem que vetores sejam colocados em sistema de
coordenadas. Um componente de um vetor é a projeção do
mesmo sobre o eixo.
𝑦
𝑎𝑦
𝑎
𝜃
𝑎𝑥
𝑥
ax=componente de 𝑎 na coordenada x
ay=componente de 𝑎 na coordenada y
Este processo é chamado de decomposição de vetores.
Portanto:
𝑎𝑦
𝑎𝑦
𝑎𝑥
sin 𝜃 =
cos 𝜃 =
tan 𝜃 =
𝑎
𝑎
𝑎𝑥
Prof. Me: Lucas Corrêa de Almeida
Módulo de um vetor
Considere o vetor no plano cartesiano:
𝑦(𝑚)
𝑣
4
onde 𝑣𝑥 = 3 𝑚 e 𝑣𝑦 = 4 𝑚
3
𝑥(𝑚)
O módulo do vetor 𝑣, pode ser encontrado através de uma
simples relação trigonométrica, conhecida como teorema de
Pitágoras. Fazendo:
𝑎² = 𝑏² + 𝑐² →
𝑣
2
= 3² + 4² →
𝑣 = 9 + 16 → 𝑣 = 5𝑚
Prof. Me: Lucas Corrêa de Almeida
Módulo de um vetor
Podemos então dizer que, para encontrarmos o módulo de um vetor
basta elevarmos seus componentes ao quadrado, soma-los e logo
tirar a raiz:
𝑣 =
𝑣²𝑥 + 𝑣²𝑦
No caso da soma de mais vetores, o módulo pode ser
encontrado, fazendo a relação:
𝑣 =
𝑣²𝑥 + 𝑣²𝑦 + 𝑣²𝑧 + ∙∙∙ +𝑣²𝑛
Prof. Me: Lucas Corrêa de Almeida
Observações
a.
Se todos os vetores são paralelos e não-nulos, proporcionais a 𝑣
podemos ordena-los na mesma reta
Por outro lado, supondo 𝑢//𝑣, com 𝑣 ≠ 0, sempre existe um número
real ∝ tal que 𝑢 =∝ 𝑣
Por exemplo, na figura abaixo, onde DC está dividido em cinco
segmentos congruentes (de mesmo comprimento), em relação ao
vetor 𝐴𝐵 ( 𝐴𝐵 = 2), tem-se
𝐵𝐷 = −2 𝐴𝐵
3
𝐴𝐵 = 𝐴𝐵
2
𝐶𝐷 =
−5
𝐴𝐵
2
Prof. Me: Lucas Corrêa de Almeida
Observações
b.
Sabemos que cada vetor 𝑣, 𝑣 ≠ 0, é possível associar dois vetores
unitários paralelos a 𝑣.
𝑣
𝑢
−𝑢
O vetor unitário
𝑎
𝑣
𝑣 ou
𝑣
𝑣
de mesmo sentido de 𝑣 é versor de 𝑣.
Exemplo:
𝑣
5
-
Se 𝑣 = 5, o versor de 𝑣 é ;
-
Se 𝑣 = , o versor de 𝑣 é 3𝑣 ;
-
Se 𝑣 = 10, o versor de 𝑣 é
1
3
𝑣
.
10
Prof. Me: Lucas Corrêa de Almeida
Exemplo
Exemplo:
Prof. Me: Lucas Corrêa de Almeida
Problemas pospostos
Livro: Paulo Winterle
Página: 14 – n°s: 1 e 2
Página: 15 – n°s: 4, 5 e 6
Pàgina: 16 – n°s: 8 e 12
Prof. Me: Lucas Corrêa de Almeida
VETORES UNITÁRIOS ou
BASE CANÔNICA
Prof. Me: Lucas Corrêa de Almeida
Vetores Unitários
 Um vetor unitário é um vetor que possui módulo igual a 1. Sua
única função é especificar uma direção e um sentido, ou seja, ele
não possui dimensão e nem unidade.
 São representados da seguinte maneira:
𝑎 = 𝑎𝑥 𝑖 + 𝑎𝑦 𝑗 + 𝑎𝑧 𝑘
Prof. Me: Lucas Corrêa de Almeida
Vetores Unitários

Podemos expressar qualquer vetor deste sistema de coordenadas. Por
exemplo 𝑎 𝑒 𝑏 abaixo:
𝑎 = 𝑎𝑥 𝑖 + 𝑎𝑦 𝑗
𝑏 = 𝑏𝑥 𝑖 + 𝑏𝑦 𝑗 + 𝑏𝑧 𝑘

Este sistema é chamado de sistema de coordenadas dextrogiro;

𝑎𝑥 e 𝑎𝑦 são chamados de componentes escalares (ou como dito antes,
simplesmente componentes);

𝑎𝑥 𝑖 𝑒 𝑎𝑦 𝑗 são vetores, chamados componentes vetoriais de 𝑎.

Exemplo:
𝑎𝑥 𝑖
𝑎
𝑎𝑦 𝑗
𝑎 = 𝑎𝑥 𝑖 + 𝑎𝑦 𝑗
Prof. Me: Lucas Corrêa de Almeida
Somando os vetores componente a componente
 Dado os vetores 𝑎 𝑒 𝑏, calcule soma: 𝑅 = 𝑎 + 𝑏
𝑎 = 𝑎𝑥 𝑖 + 𝑎𝑦 𝑗 + 𝑎𝑧 𝑘
𝑏 = 𝑏𝑥 𝑖 + 𝑏𝑦 𝑗 + 𝑏𝑧 𝑘
𝑅 = 𝑅𝑥 𝑖 + 𝑅𝑦 𝑗 + 𝑅𝑧 𝑘
 Sendo:
𝑅𝑥 = 𝑎𝑥 𝑖 + 𝑏𝑥 𝑖
𝑅𝑦 = 𝑎𝑦 𝑗 + 𝑏𝑦 𝑗
𝑅𝑧 = 𝑎𝑧 𝑘 + 𝑏𝑧 𝑘
 Se calcularmos a diferença, teremos:
𝑅 =𝑎−𝑏
𝑅 = 𝑎𝑥 − 𝑏𝑥 𝑖 + 𝑎𝑦 − 𝑏𝑦 𝑗 + 𝑎𝑧 − 𝑏𝑧 𝑘
Prof. Me: Lucas Corrêa de Almeida
Exercício
 Dado os vetores realize a soma e faça um gráfico contendo cada
um e a resultante:
𝑎 = 4,2 𝑖 − 1,5 𝑗
𝑏 = − 1,6 𝑖 + 2,9 𝑗
𝑐 = − 3,7 𝑖
 Exercícios do livro: 1/2/3/4/5/6/7/8/9/11/12/13
Prof. Me: Lucas Corrêa de Almeida
Multiplicação de Vetores
Multiplicação de um vetor por um escalar (número)
 Se multiplicarmos um vetor (𝑎) por um escalar (S), obteremos um
novo vetor S𝑎. Seu módulo é o produto de 𝑎 pelo valor absoluto de
S. Sua direção e sentido são os mesmo se S > 0 e contrário se S <
0.
 Exemplo:
Se 𝑆 = 4 e 𝑎 = 2𝑖 + 3𝑗 − 6𝑘, então:
𝑆𝑎 = 4(2𝑖 + 3𝑗 − 6𝑘) 𝑆𝑎 = 8𝑖 + 12𝑗 − 24𝑘
Prof. Me: Lucas Corrêa de Almeida
Multiplicação de Vetores
Multiplicação de vetor por vetor
 Existem duas formas de multiplicar vetor por vetor
 1 ª PRODUTO ESCALAR (produz um escalar):
O produto escalar de 𝑎 𝑒 𝑏 é definido como:
OBS:
𝑎 . 𝑏 = 𝑎 . 𝑏 . cos 𝜃
 Se 𝜃=0° cos 0° = 1 𝑎 . 𝑏 = 𝑎𝑏 (vetores paralelos)
 Se 𝜃=90° cos 90° = 0 𝑎 . 𝑏 = 0 (vetores ortogonais)
O produto escalar obedece a lei comutativa
𝑎 .𝑏 = 𝑏 .𝑎
Prof. Me: Lucas Corrêa de Almeida
Multiplicação de Vetores – Produto escalar
 Quando dois vetores estão escritos em notação de vetores
unitários:
𝑎 = 𝑎𝑥 𝑖 + 𝑎𝑦 𝑗 + 𝑎𝑧 𝑘
𝑏 = 𝑏𝑥 𝑖 + 𝑏𝑦 𝑗 + 𝑏𝑧 𝑘
 podemos escrever seu produto escalar como:
𝑎 . 𝑏 = 𝑎𝑥 𝑖 + 𝑎𝑦 𝑗 + 𝑎𝑧 𝑘 . 𝑏𝑥 𝑖 + 𝑏𝑦 𝑗 + 𝑏𝑧 𝑘
𝑎 . 𝑏 = 𝑎𝑥 𝑏𝑥 𝑖. 𝑖 + 𝑎𝑥 𝑏𝑦 𝑖. 𝑗 + 𝑎𝑥 𝑏𝑧 𝑖. 𝑘
𝑎𝑦 𝑏𝑥 𝑗. 𝑖 + 𝑎𝑦 𝑏𝑦 𝑗. 𝑗 + 𝑎𝑦 𝑏𝑧 𝑗. 𝑘
𝑎𝑧 𝑏𝑥 𝑘. 𝑖 + 𝑎𝑧 𝑏𝑦 𝑘. 𝑗 + 𝑎𝑧 𝑏𝑧 𝑘. 𝑘
𝑎 . 𝑏 = 𝑎𝑥 𝑏𝑥 + 𝑎𝑦 𝑏𝑦 + 𝑎𝑧 𝑏𝑧
Prof. Me: Lucas Corrêa de Almeida
Multiplicação de Vetores
 2º PRODUTO VETORIAL (produz outro vetor)
O produto vetorial de 𝑎 𝑒 𝑏, (lê-se a vetorial b), produz um terceiro
vetor 𝑐 cujo módulo é dado por:
𝑐 = 𝑎𝑥𝑏
Onde o módulo pode ser calculado como: 𝑎𝑥𝑏 = 𝑎𝑏 𝑠𝑒𝑛 𝜃
OBS:
 Se 𝜃 = 0°ou 180°sin 𝜃 = 0 𝑐 = 𝑎𝑥𝑏 = 0
 Se 𝜃 = 90° sin 𝜃 = 1 𝑐 = 𝑎𝑥𝑏 = 𝑎𝑏
 Se 𝜃 = 270°sin 𝜃 = -1 𝑐 = 𝑎𝑥𝑏 = −𝑎𝑏
Prof. Me: Lucas Corrêa de Almeida
Multiplicação de Vetores – Produto vetorial
 Para determinarmos a orientação (direção e sentido) do vetor
resultante, devemos usar a regra da mão direita. O sistema de
coordenadas que obedecem esta regra são chamadas de
dextrogiro.
Regra da mão direita (onde o primeiro
vetor do produto vetorial é o dedo
indicador, e o segundo o dedo médio)
Dextrogiro
Prof. Me: Lucas Corrêa de Almeida
Multiplicação de Vetores – Produto vetorial
 Na notação de vetores unitários, podemos escrever:
𝑎 𝑥 𝑏 = 𝑎𝑥 𝑖 + 𝑎𝑦 𝑗 + 𝑎𝑧 𝑘 𝑥 𝑏𝑥 𝑖 + 𝑏𝑦 𝑗 + 𝑏𝑧 𝑘
𝑎 𝑥 𝑏 = 𝑎𝑥 𝑏𝑥 𝑖. 𝑖 + 𝑎𝑥 𝑏𝑦 𝑖. 𝑗 + 𝑎𝑥 𝑏𝑧 𝑖. 𝑘
𝑎𝑦 𝑏𝑥 𝑗. 𝑖 + 𝑎𝑦 𝑏𝑦 𝑗. 𝑗 + 𝑎𝑦 𝑏𝑧 𝑗. 𝑘
𝑎𝑧 𝑏𝑥 𝑘. 𝑖 + 𝑎𝑧 𝑏𝑦 𝑘. 𝑗 + 𝑎𝑧 𝑏𝑧 𝑘. 𝑘
𝑎 𝑥 𝑏 = 𝑎𝑥 𝑏𝑦 𝑘 + 𝑎𝑥 𝑏𝑧 −𝑗
+𝑎𝑦 𝑏𝑥 −𝑘 +𝑎𝑦 𝑏𝑧 𝑖
𝑎𝑧 𝑏𝑥 𝑗 + 𝑎𝑧 𝑏𝑦 −𝑖
𝑎 𝑥 𝑏 = 𝑎𝑥 𝑏𝑦 𝑘 − 𝑎𝑥 𝑏𝑧 𝑗 − 𝑎𝑦 𝑏𝑥 𝑘
𝑎𝑦 𝑏𝑧 𝑖 + 𝑎𝑧 𝑏𝑥 𝑗 − 𝑎𝑧 𝑏𝑦 −𝑖
 Organizando teremos:
𝑎 𝑥 𝑏 = (𝑎𝑦 𝑏𝑧 − 𝑎𝑧 𝑏𝑦 )𝑖 + (𝑎𝑧 𝑏𝑥 − 𝑎𝑥 𝑏𝑧 )𝑗 + (𝑎𝑥 𝑏𝑦 − 𝑎𝑦 𝑏𝑥 )𝑘

Exercícios do livro: 10/14/15/16/17/18
Prof. Me: Lucas Corrêa de Almeida
Multiplicação de Vetores – Produto vetorial
Outro modo importante para determinação do produto vetorial é
através da determinante, observe:
𝑖
𝑎 𝑥𝑏 = 𝑑𝑒𝑡 𝑎𝑥
𝑏𝑥
𝑗
𝑎𝑦
𝑏𝑦
𝑘
𝑎𝑧
𝑏𝑧
𝑖
= 𝑎𝑥
𝑏𝑥
𝑗
𝑎𝑦
𝑏𝑦
𝑘 𝑖
𝑎𝑧 𝑎𝑥
𝑏𝑧 𝑏𝑥
𝑗
𝑎𝑦 =
𝑏𝑦
𝑎𝑦 𝑏𝑧 𝑖 + 𝑎𝑧 𝑏𝑥 𝑗 + 𝑎𝑥 𝑏𝑦 𝑘 − 𝑎𝑥 𝑏𝑧 𝑗 + 𝑎𝑧 𝑏𝑦 𝑖 + 𝑎𝑦 𝑏𝑥 𝑘 =
𝑎 𝑥 𝑏 = 𝑎𝑦 𝑏𝑧 − 𝑎𝑧 𝑏𝑦 𝑖 + 𝑎𝑧 𝑏𝑥 − 𝑎𝑥 𝑏𝑧 𝑗 + (𝑎𝑥 𝑏𝑦 − 𝑎𝑦 𝑏𝑥 )𝑘
Podemos observar que o resultado obtido é idêntico ao resultado
anterior:
Resultado anterior
𝑎 𝑥 𝑏 = (𝑎𝑦 𝑏𝑧 − 𝑎𝑧 𝑏𝑦 )𝑖 + (𝑎𝑧 𝑏𝑥 − 𝑎𝑥 𝑏𝑧 )𝑗 + (𝑎𝑥 𝑏𝑦 − 𝑎𝑦 𝑏𝑥 )𝑘
Prof. Me: Lucas Corrêa de Almeida
Exercício
1)
Dado os vetores:
𝑎 = 3𝑖 + 2𝑗 − 3 𝑘
𝑒
𝑏 = 2 𝑖 − 2𝑗 + 𝑘
Faça:
a) 𝑎 . 𝑏
b) 𝑏 . 𝑎
c) 𝑎 𝑥 𝑏
d) 𝑏 𝑥 𝑎
Prof. Me: Lucas Corrêa de Almeida
Vetores na Geometria analítica
Veremos agora como representar os vetores no plano
cartesiano.
Considere o vetor 𝑢, representado no plano cartesiano XOY,
conforme figura ao lado:
𝑦
Podemos observar que:
𝑢 = 𝑂𝑃
𝑢 = 𝑃 −O
𝑦
𝑢 = 𝑥, 𝑦 − (0,0)
𝑃
𝑢
Portanto:
𝑢 = 𝑥, 𝑦
O
𝑥
𝑥
Logo, o vetor 𝒖, fica expresso através de um par ordenado,
referido à origem do sistema de coordenadas cartesianas.
As coordenadas (x,y) do ponto final de u são chamadas de
componentes de u.
Prof. Me: Lucas Corrêa de Almeida
Exemplo
Dado os vetores 𝑎 = (4,3, −2) e 𝑏 = (−1,2,3), calcule para eles:
a) A soma.
b) Multiplicar o resultado da soma pelo escalar 5.
c) O produto escalar.
d) O produto vetorial.
Prof. Me: Lucas Corrêa de Almeida
Problemas propostos
Livro: Paulo Winterle
Página:
Página:
Página:
Página:
40 – n°s: 1, 2, 3 e 5.
41 – n°s: 7 e 16
66 – n°s: 1, 2 e 3
87 – n°s: 1, 2 e 3
Prof. Me: Lucas Corrêa de Almeida
Produto misto
Sejam três vetores 𝑢, 𝑣 e 𝑤:
𝑢 = (𝑥1 , 𝑦1 , 𝑧1 )
𝑣 = (𝑥2 , 𝑦2 , 𝑧2 )
𝑤 = (x3 , y3 , z3 )
O produto misto de 𝑢, 𝑣 e 𝑤 é indicado por (𝑢, 𝑣, 𝑤) e é dado pelo
número real:
𝑥1
𝑢 . 𝑣 x 𝑤 = 𝑢, 𝑣, 𝑤 = [u, v, w] = 𝑥2
𝑥3
𝑦1
𝑦2
𝑦3
𝑧1
𝑧2
𝑧3
 Se o produto misto for nulo, significa que os vetores são
coplanares.
 Observe que a ordem dos vetores é importante. A cada troca de
posição o produto misto muda de sinal.
Prof. Me: Lucas Corrêa de Almeida
Produto misto
 Propriedades:
i.
ii.
iii.
iv.
𝑢 , 𝑣 , 𝑤 = 0, se um deles é o vetor nulo ou se forem coplanares.
𝑢 ,𝑣 ,𝑤 = − 𝑣 ,𝑢 ,𝑤 = 𝑣 ,𝑤 ,𝑢 = …
𝑚𝑢 , 𝑣 , 𝑤 = 𝑚 𝑢 , 𝑣 , 𝑤
𝑢 + 𝑎, 𝑣 , 𝑤 = 𝑢 , 𝑣 , 𝑤 + 𝑎 , 𝑣 , 𝑤
Sobre a condição de coplanaridade entre 3 vetores:

𝑢 , 𝑣 , 𝑤 = 0 Vetores coplanares  Lineram. dependente (LD)

𝑢 , 𝑣 , 𝑤 ≠ 0  Vetores não coplanares  Linearm. Independente (LI)
Prof. Me: Lucas Corrêa de Almeida
Produto misto – interpretação geométrica
Geometricamente, o módulo do produto misto é igual ao
volume do paralelepípedo de arestas determinadas pelos vetores
não-coplanares 𝑢, 𝑣 e 𝑤.
𝑢
𝑤
𝑣
𝑉𝑃 = 𝑢 , 𝑣 , 𝑤
Prof. Me: Lucas Corrêa de Almeida
Produto misto – interpretação geométrica
Exemplo:
Sejam os vetores 𝑢 = (3, 𝑚, −2) , 𝑣 = (1, −1,0) e 𝑤 = (2, −1,2) .
Calcular o valor de 𝑚 para que o volume do paralelepípedo
determinado por 𝑢, 𝑣 e 𝑤 seja 16 𝑢. 𝑣. (unidades de volume)
Prof. Me: Lucas Corrêa de Almeida
Produto misto – interpretação geométrica
Outra forma geométrica que podemos encontrar com o
produto misto é o volume do tetraedro.
𝑢
𝑤
Dado pela equação:
𝑣
𝑉𝑇 =
𝑢 ,𝑣 ,𝑤
6
Prof. Me: Lucas Corrêa de Almeida
Produto misto – interpretação geométrica
Exemplo:
Sejam os pontos 𝐴(1,2, −1), 𝐵(5,0,1), 𝐶(2, −1,1) e 𝐷(6,1, −3), vértices
de um tetraedro. Calcular o volume do tetraedro, sabendo que 𝑢 =
𝐴𝐵, 𝑣 = 𝐴𝐶 e 𝑤 = 𝐴𝐷.
Prof. Me: Lucas Corrêa de Almeida
Exercícios
Livro: Paulo Winterle
Página: 99 – n°s: 1, 2, 3, 4 e 5.
Página: 100 – n°s: 6, 8 e 9.
Prof. Me: Lucas Corrêa de Almeida
A RETA
Prof. Me: Lucas Corrêa de Almeida
A Reta – equação vetorial da reta
Consideremos um ponto 𝐴(𝑥1 , 𝑦1 , 𝑧1 ) e um vetor não nulo 𝑣
= 𝑎, 𝑏, 𝑐 . Só existe uma reta 𝑟 que passa por 𝐴 e tem direção de 𝑣.
Um ponto 𝑃(𝑥, 𝑦, 𝑧) pertence a 𝑟 se e somente se, o vetor 𝐴𝑃 é
paralelo a 𝑣, isto é:
𝐴𝑃 = 𝑡. 𝑣
Para algum real 𝑡, temos:
𝑃 − 𝐴 = 𝑡. 𝑣
ou
P = A + 𝑡𝑣
(1)
(2)
ou em coordenadas:
𝑥, 𝑦, 𝑧 = 𝑥1 , 𝑦1 , 𝑧1 + 𝑡 𝑎, 𝑏, 𝑐
(𝟑)
Qualquer uma dessas equações é denominada equação
vetorial de r. O vetor 𝑣 é chamado vetor diretor da reta 𝑟 e 𝑡 é
denominado parâmetro.
Prof. Me: Lucas Corrêa de Almeida
A Reta – equação vetorial da reta
Exemplo:
A reta r que passa por A(1,-1,4) e tem direção de 𝑣 = (2,3,2),
tem equação vetorial, de acordo com (3):
𝑥, 𝑦, 𝑧 = 𝑥1 , y1 , z1 + t a, b, c
(3)
Desta igualdade vem:
𝑟: 𝑥, 𝑦, 𝑧 = 1, −1,4 + 𝑡 2,3,2
(4)
onde (𝑥, 𝑦, 𝑧) representa um ponto qualquer de r.
Se desejarmos obter pontos de r, basta atribuir valores
para t, Por exemplo, para 𝑡 = 1, obtêm-se:
𝑥, 𝑦, 𝑧 = 1, −1,4 + 1 2,3,2
𝑥, 𝑦, 𝑧 = (3,2,6)
E, portanto, 𝑃1 = (3,2,6) ∈ 𝑟
Prof. Me: Lucas Corrêa de Almeida
A Reta – equação vetorial da reta
De forma análoga.
para 𝑡 = 2, obtém-se 𝑥, 𝑦, 𝑧 = 1, −1,4 + 2 2,3,2 = 5,5,8
e, portanto, 𝑃2 5,5,8 ∈ 𝑟;
para 𝑡 = 3, obtém-se o ponto 𝑃3 7,8,10 ;
para 𝑡 = 0, obtém-se o próprio ponto 𝐴 1, −1,4 ;
para 𝑡 = −1, obtém-se o ponto 𝑃4 −1, −4,2 ;
E assim por diante. Se t assumir todos os valores reais, teremos todos os
infinitos pontos da reta.
O gráfico mostra os pontos obtidos com seus correspondentes parâmetros.
Prof. Me: Lucas Corrêa de Almeida
A Reta - equação vetorial da reta
 Observações:
a) Vimos que cada real 𝑡 corresponde um ponto 𝑃 ∈ 𝑟 . A recíproca também é
verdadeira, isso é, a cada 𝑃 ∈ 𝑟 corresponde um número real 𝑡, Por exemplo, sabe-se
que o ponto 𝑃(5,5,8) pertence à reta.
𝑟: 𝑥, 𝑦, 𝑧 = 1, −1,4 + 𝑡 2,3,2
Logo, o ponto (5,5,8) é particular (𝑥, 𝑦, 𝑧) na equação (4) e, portanto, é
verdadeira a afirmação:
(5,5,8) = 1, −1,4 + 𝑡 2,3,2 , para algum real 𝑡.
Desta igualdade, vem
(5,5,8) = 1, −1,4 + 𝑡 2,3,2 ou (4,6,4) = +𝑡 2,3,2 , e portanto 𝑡 = 2.
b) A equação (4) não é única equação vetorial de 𝑟. Existem, na verdade, infinitas,
pois basta tomar outro ponto 𝑟 (em vez de 𝐴) ou outro qualquer não-nulo que seja
múltiplo de 𝑣. Por exemplo, a equação:
𝑥, 𝑦, 𝑧 = 1, −1,4 + 𝑡 4,6,4
É outra equação vetorial de 𝑟 onde se utilizou o vetor 2𝑣 = (4,6,4) como vetor
diretor em vez de 𝑣 2,3,2 .
Prof. Me: Lucas Corrêa de Almeida
Equações Paramétricas da Reta
Da equação vetorial da reta
𝑥, 𝑦, 𝑧 = 𝑥1 , 𝑦1 , 𝑧1 + 𝑡 𝑎, 𝑏, 𝑐
ou ainda
𝑥, 𝑦, 𝑧 = 𝑥1 + at, 𝑦1 + 𝑏𝑡, 𝑧1 + 𝑐𝑡
pela condição de igualdade, obtém-se:
𝑥 = 𝑥1 + 𝑎𝑡
𝑦 = 𝑦1 + 𝑏𝑡
𝑧 = 𝑧1 + 𝑐𝑡
Esta equação é chamada equação paramétrica da reta.
Prof. Me: Lucas Corrêa de Almeida
Equações Paramétricas da Reta
Exemplos
Prof.:
Prof.
Me: Lucas Corrêa
Corrêa de Almeida
Equações Paramétricas da Reta
Prof.:
Prof.
Me: Lucas Corrêa
Corrêa de Almeida
Equações Paramétricas da Reta
Prof. Me: Lucas Corrêa de Almeida
Equações Paramétricas da Reta
Prof. Me: Lucas Corrêa de Almeida
Equações Paramétricas da Reta
Prof. Me: Lucas Corrêa de Almeida
Equações Paramétricas da Reta
3) Escrever a equações paramétricas da reta r que passa por
𝐴(3, −1, −2) e 𝐵 1,2,4 sabendo que 𝑣 = 𝐴𝐵.
Prof. Me: Lucas Corrêa de Almeida
Equações paramétricas de um segmento de Reta
Consideremos a reta r do exemplo anterior e nela o segmento AB.
As equações paramétricas do segmento AB são as mesmas da reta r, porém,
com o 𝟎 ≤ 𝒕 ≤ 𝟏.
Considere 𝐴(3, −1, −2) e 𝐵 1,2,4 a equação paramétrica do segmento de
rate AB será:
𝑥 = 3 − 2𝑡
AB: 𝑦 = −1 + 3𝑡
𝑧 = −2 + 6𝑡
Podemos observar que:
para 𝑡 = 0, obtém-se o ponto A.
para 𝑡 = 1, obtém-se o ponto B.
e para 𝑡 entre 0 e 1, obtém-se os pontos entre A e B.
Observação:

A equação 𝑃 = 𝐴 + 𝑡(𝐵 − 𝐴) também pode ser expressa de modo equivalente por:
𝑃 = 𝑡𝐵 + 1 − 𝑡 𝐴
Prof. Me: Lucas Corrêa de Almeida
Equações Simétricas da Reta
Equações simétricas da reta.
Das equações paramétricas
𝑥 = 𝑥1 + 𝑎𝑡
𝑦 = 𝑦1 + 𝑏𝑡
𝑧 = 𝑧1 + 𝑏𝑡
com 𝑎, 𝑏 e 𝑐 ≠ 0, temos:
𝑡=
𝑥 − 𝑥1
𝑎
𝑡=
𝑦 − 𝑦1
𝑏
𝑡=
𝑧 −𝑧1
𝑐
Como para cada ponto da reta corresponde um só valor para 𝒕,
obtemos as igualdades:
𝑥 − 𝑥1 𝑦 − 𝑦1 𝑧 − 𝑧1
=
=
𝑎
𝑏
𝑐
Sendo estas equações conhecidas como equações simétricas da reta.
Prof. Me: Lucas Corrêa de Almeida
Equações Simétricas da Reta
Exemplo:
Prof. Me: Lucas Corrêa de Almeida
Equações reduzidas da Reta
Equações reduzidas da reta.
São equações formadas quando associamos uma coordenada geométrica em
função de outra.
Exemplo:
Seja a reta r definida pelo ponto 𝐴(2, −4, −3) e pelo vetor diretor 𝑣 =
(1,2,3) e expressa pelas equações simétricas:
𝑥−2 𝑦+4 𝑧+3
𝑟:
=
=
1
2
−3
Expressando duas variáveis em função da terceira, teremos:
𝑥−2 𝑦+4
=
1
2
𝑥−2 𝑧+3
=
1
−3
1 𝑦+4 =2 𝑥−2
𝑦 + 4 = 2𝑥 − 4
𝑦 = 2𝑥 − 8
1 𝑧 + 3 = −3 𝑥 − 2
𝑧 + 3 = −3𝑥 + 6
𝑧 = −3𝑥 + 3
Sendo estas duas ultimas chamadas de equações reduzidas da reta r.
Prof. Me: Lucas Corrêa de Almeida
Ângulo de duas retas
Ângulo de duas retas.
Sejam as retas 𝑟1 e 𝑟2 com as direções
𝑣1 e 𝑣2 , respectivamente.
Chama-se ângulo de duas retas 𝑟1 e 𝑟2
o menor Ângulo de um vetor diretor de 𝑟1 e de
um vetor diretor de 𝑟2 . Logo, sendo 𝜃 este
ângulo, tem-se:
cos 𝜃 =
𝑣1 .𝑣2
𝑣1 𝑣2
, com 0 ≤ 𝜃 ≤
𝜋
2
Observações:
 Quando o ângulo entre as retas forem de 90° (𝑟1 ⊥ 𝑟2 ) o produto escalar
entre elas é zero  𝑣1 . 𝑣2 = 0
Prof. Me: Lucas Corrêa de Almeida
Ângulo de duas retas
Exemplo:
Prof. Me: Lucas Corrêa de Almeida
Reta ortogonal a duas retas
Reta ortogonal a duas retas.
Podemos também determinar uma terceira reta 𝑟3 e direção 𝑣3 ,
tomando como referências duas retas 𝑟1 e 𝑟2 não-paralelas com direções 𝑣1
e 𝑣2 .
Se 𝑣3 é ortogonal aos vetores 𝑣1 e 𝑣2 , temos:
𝑣3 . 𝑣1 = 0
𝑣3 . 𝑣2 = 0
Quando temos esta condição de ortogonalidade entre o vetor 𝑣3 com os
vetores 𝑣1 e 𝑣2 , podemos dizer que 𝑣3 é resultado do produto vetorial entre
𝑣1 e 𝑣2 .
𝑣3 = 𝑣1 𝑥 𝑣2
Prof. Me: Lucas Corrêa de Almeida
Reta ortogonal a duas retas
Exemplo:
OBS: veja o tópico “INTERCESÃO ENTRE DUAS RETAS” na página
118.
Prof. Me: Lucas Corrêa de Almeida
Exercícios
Livro: Paulo Winterle
Página: 118 – n°s: 1, 4, 5, e 6.
Página: 119 – n°s: 8, 12 e 13.
Página: 120- – n°: 20
Prof. Me: Lucas Corrêa de Almeida
O PLANO
Prof. Me: Lucas Corrêa de Almeida
Equação geral do plano.
Observe o plano 𝜋 abaixo, contendo dois vetores 𝑛 e 𝐴𝑃:
Vemos que 𝑛 e 𝐴𝑃 são ortogonais, e sabemos que pelo produto
escalar entre eles o resulta é zero:
𝑛 ∙ 𝐴𝑃 = 0
Prof. Me: Lucas Corrêa de Almeida
Equação geral do plano.
Sabendo que 𝐴𝑃 = 𝑃 − 𝐴, temos:
𝑛 ∙ (𝑃 − 𝐴) = 0
Se 𝑛 = 𝑎, 𝑏, 𝑐 , 𝑃(𝑥, 𝑦, 𝑥) e 𝐴(𝑥1 , 𝑦1 , 𝑧1 ), teremos:
𝑎, 𝑏, 𝑐 ∙ 𝑥, 𝑦, 𝑧 − 𝑥1 , 𝑦1 , 𝑧1
=0 →
𝑎, 𝑏, 𝑐 ∙ 𝑥 − 𝑥1 , 𝑦 − 𝑦1 , 𝑧 − 𝑧2 = 0 →
𝑎 𝑥 − 𝑥1 ) + 𝑏(𝑦 − 𝑦1 ) + 𝑐(𝑧 − 𝑧2 = 0 →
𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 − 𝑎𝑥1 − 𝑏𝑦1 − 𝑐𝑦3 = 0
Se fizermos −𝑎𝑥1 − 𝑏𝑦1 − 𝑐𝑦3 = d , teremos a equação geral do
plano:
𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 + 𝑑 = 0
Prof. Me: Lucas Corrêa de Almeida
Equação geral do plano.
Observações
a) Assim como 𝑛 = (𝑎, 𝑏, 𝑐) é um vetor normal a 𝜋, qualquer vetor
múltiplo de 𝑛 é ortogonal (normal) ao plano.
b) Para obtermos os pontos de um plano, basta atribuir valores a
duas variáveis e calcular o valor da outra equação dada.
Exemplo: considere a equação: 𝜋: 3𝑥 + 2𝑦 − 𝑧 + 1 = 0 , se
atribuirmos valores para 𝑥 e 𝑦 como sendo 4 e 2 respectivamente,
encontraremos valores para 𝑧. Neste caso 𝑧 será 9, e assim, o ponto
encontrado será: (4, −2,9).
Prof. Me: Lucas Corrêa de Almeida
Exemplo
Exemplo 1: Obter uma equação geral do plano π que passa pelo ponto
A(2, −1,3) e tem 𝑛 = (3,2,4) como um vetor normal.
Prof. Me: Lucas Corrêa de Almeida
Exemplo
Exemplo 2: Escreva uma equação geral do plano 𝜋 que passa pelo
ponto 𝐴(2,1,3) e é paralelo ao plano
𝜋1 : 3𝑥 − 4𝑦 − 2𝑧 + 5 = 0
Prof. Me: Lucas Corrêa de Almeida
Exemplo
Exemplo 3: A reta
𝑥 = 5 + 3𝑡
𝑟: 𝑦 = −3 + 2𝑡
𝑧 =𝑡+𝑡
é ortogonal ao plano 𝜋, que passa pelo ponto 𝐴(2,1, −2). Determine
uma equação geral de 𝜋.
Solução
Como 𝑟 ⊥ 𝜋, qualquer vetor diretor de 𝑟 é um vetor normal ao plano. Sendo 𝑛 =
(3,2,1) um destes vetores, uma equação de 𝜋 é da forma:
3𝑥 + 2𝑦 + 𝑧 + 𝑑 = 0
Como 𝐴 𝜖 𝜋, deve-se ter: 3 2 + 2 1 + −2 + 𝑑 = 0, assim 𝑑 = −6, portanto, uma
equação de 𝜋 é
3𝑥 + 2𝑦 + 𝑧 − 6 = 0
Prof. Me: Lucas Corrêa de Almeida
Equação vetorial e paramétrica do plano
Observe o plano 𝜋 abaixo, que possui um ponto 𝐴(𝑥0 , 𝑦0 , 𝑧0 ) e dois
vetores 𝑢 = 𝑎1 , 𝑏1 , 𝑐1 e 𝑣 = (𝑎2 , 𝑏2 , 𝑐2 ) paralelos ao plano 𝜋, sendo 𝑢 e
𝑣 não-paralelos.
Para todo ponto 𝑝(𝑥, 𝑦, 𝑧) no plano, os vetores 𝐴𝑃 , 𝑢 e 𝑣 são
coplanares. Mas para que 𝑃 pertença ao plano, deve existir dois
números reais ℎ e 𝑡 tais que:
𝑃 − 𝐴 = ℎ𝑢 + 𝑡𝑣
Prof. Me: Lucas Corrêa de Almeida
Equação vetorial e paramétrica do plano
ou
𝑃 = 𝐴 + ℎ𝑢 + 𝑡𝑣
Se substituirmos as coordenadas de cada pontos e vetor, teremos:
𝑥, 𝑦, 𝑧 = 𝑥0 , 𝑦0 , 𝑧0 + ℎ 𝑎1 , 𝑏1 , 𝑐1 + 𝑡 𝑎2 , 𝑏2 , 𝑐2
Está equação é denominada equação vetorial do plano 𝜋. Com 𝑢 e 𝑣 os
vetores diretores.
Prof. Me: Lucas Corrêa de Almeida
Equação vetorial e paramétrica do plano
Da equação da reta, podemos construir a paramétrica
𝑥 = 𝑥0 + 𝑎1 ℎ + 𝑎2 𝑡
𝑦 = 𝑦0 + 𝑏1 ℎ + 𝑏2 𝑡
𝑧 = 𝑧0 + 𝑐1 ℎ + 𝑐2 𝑡
Estas equação são chamadas de equações paramétricas de 𝜋,
sendo ℎ e 𝑡 variáveis auxiliares denominadas parâmetros.
Prof. Me: Lucas Corrêa de Almeida
Exemplo
Exemplo 4: Seja o plano π que passa pelo ponto 𝐴(2,2, −1) e é
paralelo aos vetores 𝑢 = (2, −3,1) e 𝑣 = (−1,5, −3). Obter:
Uma equação vetorial.
b) Um sistema de equações paramétricas.
c) Uma equação geral de 𝜋.
a)
Solução
a) 𝑥, 𝑦, 𝑧 = 𝑥0 , 𝑦0 , 𝑧0 + ℎ 𝑎1 , 𝑏1 , 𝑐1 + 𝑡 𝑎2 , 𝑏2 , 𝑐2 →
𝑥, 𝑦, 𝑧 = 2,2, −1 + ℎ 2, −3,1 + 𝑡 −1,5, −3
Prof. Me: Lucas Corrêa de Almeida
Exemplo
𝑥 = 𝑥0 + 𝑎1 ℎ + 𝑎2 𝑡
b) 𝑦 = 𝑦0 + 𝑏1 ℎ + 𝑏2 𝑡
𝑧 = 𝑧0 + 𝑐1 ℎ + 𝑐2 𝑡
→
𝑥 = 2 + 2ℎ − 𝑡
𝑦 = 2 − 3ℎ + 5𝑡
𝑧 = −1 + ℎ − 3𝑡
c) 𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 + 𝑑 = 0
Com na equação geral temos que encontrar o vetor ortogonal aos
vetores 𝑢 e 𝑣.
Prof. Me: Lucas Corrêa de Almeida
Exemplo
Para encontrar o vetor 𝑛, basta fazer o produto vetorial entre 𝑢 e 𝑣,
pois como sabemos o produto vetorial entre dois vetores, resulta
num vetor ortogonal aos dois. Assim:
𝑢𝑥𝑣=𝑛
𝑖
𝑗
𝑘
𝑢 𝑥 𝑣 = 2 −3 1 = (4,5,7)
−1 5 −3
Assim: 4𝑥 + 5𝑦 + 7𝑧 + 𝑑 = 0. Utilizando o ponto 𝐴, temos:
4 2 + 5 2 + 7 −1 + 𝑑 = 0
Portanto, a equação geral de reta será:
→
𝑑 = −11
4𝑥 + 5𝑦 + 7𝑧 − 11 = 0
Prof. Me: Lucas Corrêa de Almeida
Ângulo de dois planos
Considere os planos 𝜋1 e 𝜋2 com vetores normais 𝑛1 e 𝑛2 ,
respectivamente.
Chama-se ângulo de dois planos, o menor ângulo que um vetor
normal de um plano forma o vetor normal o outro plano.
𝑛1 ∙ 𝑛2
cos 𝜃 =
𝑛1 𝑛2
Prof. Me: Lucas Corrêa de Almeida
Exemplo
Exemplo 5: Determine o ângulo entre os planos:
𝜋1 : 2𝑥 + 𝑦 − 𝑧 + 3 = 0
e
𝜋2 : 𝑥 + 𝑦 − 4 = 0
Prof. Me: Lucas Corrêa de Almeida