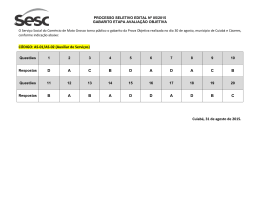
Simulado OBM – Nível 1
Gabarito Comentado
Questão 1. Renata digitou um número em sua calculadora, multiplicou-o por 3, somou 12, dividiu o
resultado por 7 e obteve o número 15. O número digitado foi:
a)
b)
c)
d)
e)
31
7
39
279
27
Resolução.
Esta questão pode ser resolvida de duas maneiras: por equação algébrica (conteúdo que será estudado
no 8º ano) ou por operações inversas. A resolução que apresentaremos aqui será a segunda.
Ao final das operações Renata obteve o número 15.
Para encontrar o 15, ela dividiu algum número por 7. Então, multipliquemos 15 por 7:
Para encontrar o 105, ela somou algum número por 12. Então, Subtrairemos 12 de 105:
Para encontrar o 93, ela multiplicou algum número por 3. Então, dividamos 93 por 3:
Portanto, o número digitado por Renata é 31.
Gabarito: a
Questão 2. Numa competição de ciclismo, Carlinhos dá uma volta completa na pista em 30 segundos, enquanto que Paulinho leva 32 segundos para completar uma volta. Quando Carlinhos completar a
volta número 80, Paulinho estará completando a volta número:
a) 79
b) 78
c) 76
d) 77
e) 75
Resolução.
Gabarito: e
Teste 1ª Unidade 8º ano
Para completar 80 voltas Carlinhos leva
.
Se dividirmos o tempo que Carlinhos leva para completar as 80 voltas pelo tempo que Paulinho leva
para completar 1 volta, teremos o número de voltas que Paulinho dará em 2400 segundos. Logo,
MATEMÁTICA
2
Questão 3. Elevei um número positivo ao quadrado, subtrai do resultado o mesmo número e o que
restou dividi ainda pelo mesmo número. O resultado que achei foi igual:
a)
b)
c)
d)
e)
Ao próprio número
Ao dobro do número
Ao número mais 1
À raiz quadrada do número
Ao número menos 1
Resolução.
Esta questão pode ser resolvida de duas maneiras: por equação algébrica (conteúdo que será estudado
no 8º ano) ou por atribuição de valores. A resolução que apresentaremos aqui será a segunda.
Consideremos o número positivo igual a 2.
Assim, faremos o que pede a questão:
 Elevei um número positivo ao quadrado
 Subtrai do resultado o mesmo número
 O que restou dividi ainda pelo mesmo número
Resultado
Consideremos o número positivo igual a 5.
Assim, faremos o que pede a questão:
 Elevei um número positivo ao quadrado
 Subtrai do resultado o mesmo número
 O que restou dividi ainda pelo mesmo número
Resultado
Portanto, o resultado que achei foi igual ao número menos 1
Gabarito: e
Questão 4. Escreva um número em cada círculo da fila abaixo, de modo que a soma de três números
quaisquer vizinhos (consecutivos) seja 12.
3
5
a)
b)
c)
d)
e)
3
2
1
4
7
Teste 1ª Unidade 8º ano
No último círculo à direita deve estar escrito o número:
MATEMÁTICA
3
Resolução.
Gabarito: a
Obs.: Existem outros números possíveis, mas o último sempre é o 3.
Questão 5. Joãozinho brinca de formar quadrados com palitos de fósforo como na figura a seguir.
A quantidade de palitos necessária para fazer 100 quadrados é:
a)
b)
c)
d)
e)
296
293
297
301
28
Resolução.
Os quatro quadrados da figura acima são formados por 13 palitos de fósforo: 4 palitos do primeiro
quadrado, mais 3 palitos para cada quadrado que irá ser formado. Desta forma, temos
. Como temos quatro quadrados formados, a quantidade de palitos é dada por: 4 palitos para o primeiro
quadrado mais 3 palitos para o restante de quadrados, que é o total de quadrados menos o primeiro.
Logo,
.
Assim, para fazer 100 quadrados precisamos de
palitos.
Gabarito: d
a)
b)
c)
d)
e)
Quarenta e oito.
Quarenta e nove.
Cinqüenta.
Cinqüenta e um.
Cinqüenta e quatro.
Teste 1ª Unidade 8º ano
Questão 6. Qual é a quantidade total de letras de todas as respostas incorretas desta questão?
MATEMÁTICA
4
Resolução.
O total de letras nas cinco respostas é 63, sendo 13 nas respostas das alternativas A e B, 9 na resposta
da alternativa C, 12 na resposta da alternativa D e 16 na resposta da alternativa E. Como 63 – 13 =
50, 63 – 9 = 54, 63 – 12 = 51 e 63 – 16 = 47, a única alternativa correta é a D.
Gabarito: d
Questão 7. As figuras a seguir são construídas com palitos pretos e brancos. Para construir as figuras,
os palitos pretos foram colocados apenas nas bordas e os brancos apenas no interior. A figura de número
n corresponde a um retângulo 3 por n. Continuando esse procedimento, quantos palitos brancos teremos
na figura 2002?
1
a)
b)
c)
d)
e)
2
3
2001
4004
12006
10007
10010
Resolução.
 Na figura 1 temos 2 palitos brancos.
 Na figura 2 temos 7 palitos brancos.
 Na figura 3 temos 12 palitos brancos, etc.
Isso mostra que a seqüência de figuras é formada acrescentando-se sempre 5 palitos brancos a quantidade anterior.
Assim, na figura de número 2002, teremos 2 + (2001)  5 = 10007 palitos brancos.
Gabarito: d
Questão 8. Escrevendo todos os números inteiros de 100 a 999, quantas vezes escrevemos o algarismo 5?
a)
b)
c)
d)
e)
250
270
271
280
292



Nas unidades, do 105 ao 995, o algarismo 5 aparece 90 vezes.
Nas dezenas, do 150 ao 259, do 250 ao 259, …, do 950 ao 959, o algarismo 5 aparece 90 vezes.
Nas centenas, do 500 ao 599, o algarismo 5 aparece 100 vezes.
Teste 1ª Unidade 8º ano
Resolução.
MATEMÁTICA
5
Desta forma totalizamos: 90 + 90 + 100 = 280 vezes.
Gabarito: d
Questão 9. Joana escreve a seqüência de números naturais
onde cada número, com exceção do primeiro, é igual ao anterior mais cinco. Joana pára quando encontra o primeiro número de três
algarismos. Esse número é:
a) 100
b) 104
c) 101
d) 103
e) 102
Resolução.
Os números da seqüência, quando divididos por 5, deixam resto igual a 1. O menor número de três algarismos nessas condições é o 101.
Gabarito: c
Questão 10. Escrevem-se os números naturais numa faixa decorativa, da seguinte maneira:
1
2
3
5
6
4
7
8
Assinale a figura correta:
a)A)
2001
B)
b)
2000
2000
d)
D)
2000
2001
2001
e)
2000
C)c)
2001
2001
E)
2000
Resolução.
Teste 1ª Unidade 8º ano
Observando como os números aparecem nos cantos, percebemos que aparecem
MATEMÁTICA
6
d
lo
ltip
ú
m is 1
ma
lo d
ltip
ú
m is 2
ma
lo
ltip
m ú is 3
ma
e4
4
de
lo
ltip
mú
e4
e4
lo d
p
i
lt
m ú is 1
ma
4
de
Como 2000 é múltiplo de 4, a resposta correta é:
2001
2000
Gabarito: d
Questão 11. 2 melancias custam o mesmo que 9 laranjas mais 6 bananas; além disso, meia dúzia de
bananas custa a metade de uma melancia. Portanto, o preço pago por uma dúzia de laranjas e uma dúzia
de bananas é igual ao preço de:
a) 3 melancias
b) 4 melancias
c) 6 melancias
d) 5 melancias
e) 2 melancias
Resolução.
Se 6 bananas custam o mesmo que metade de uma melancia, então 12 bananas custam o mesmo que
uma melancia. E, 24 bananas custam o mesmo que 2 melancias, que custam o mesmo que 9 laranjas
mais 6 bananas. Assim, 9 laranjas custam o mesmo que 18 bananas, ou seja, 2 bananas custam o mesmo que 1 laranja. E, 12 laranjas custam o mesmo que 24 bananas.
Logo, 12 laranjas mais 12 bananas custam o mesmo que 24 bananas e 12 bananas, ou seja, custam o
mesmo que 36 bananas. Como 12 bananas custam o mesmo que 1 melancia, então, 36 bananas custam
o mesmo que 3 melancias.
Gabarito: a
1. Sabendo-se que 15 alunos são meninas e que nesta classe o número de meninas é maior que o número
de meninos, o número de meninos nesta classe é:
a) 7
b) 8
c) 9
d) 10
e) 11
Teste 1ª Unidade 8º ano
Questão 12. Contando-se os alunos de uma classe de 4 em 4 sobram 2, e contando-se de 5 em 5 sobra
MATEMÁTICA
7
Resolução.
O número total de alunos da turma é menor que 30, é par, é maior que 15 e deixa resto 1 quando dividido por 5. Logo, é 26. Temos 11 meninos.
Gabarito: e
Questão 13. Observe as multiplicações a seguir:
Para obter
a) 29
b) 99
c) 72
d) 41
e) 81
devemos multiplicar
por:
Resolução.
Os exemplos dados mostram que 12 345 679
mos
multiplicar 12 345 679 por 9 9 = 81.
9k = kkk kkk kkk. Assim, para obter 999 999 999 deve-
Gabarito: e
Questão 14. Outro dia ganhei 250 reais, incluindo o pagamento de horas extras. O salário (sem horas
extras) excede em 200 reais o que recebi pelas horas extras. Qual é o meu salário sem horas extras?
a) 200 reais
b) 150 reais
c) 225 reais
d) 175 reais
e) 180 reais
Resolução.
 Salário + horas extras = 250
 Salário – horas extras = 200.
Logo, o dobro do salário é igual a 450, portanto o salário é
reais.
Questão 15. A prefeitura de uma certa cidade fez uma campanha que permite trocar 4 garrafas de 1 litro vazias por uma garrafa de 1 litro cheia de leite. Até quantos litros de leite pode obter uma pessoa que
possua 43 dessas garrafas vazias?
a) 11
b) 12
Teste 1ª Unidade 8º ano
Gabarito: c
MATEMÁTICA
8
c) 13
d) 14
e) 15
Resolução.
Ele separa 40 garrafas vazias e as troca por 10 garrafas de 1 litro cheias de leite.
Esvaziadas as 10 garrafas, ele pode juntá-las com as 3 vazias que restaram e trocá-las por 3 garrafas
cheias, sobrando ainda 1 garrafa vazia.
Esvaziando as 3 cheias e juntando com a garrafa vazia ele ainda pode obter em troca mais uma garrafa
cheia.
Ao todo ele pode obter, por sucessivas trocas, 10 + 3 + 1 = 14 garrafas cheias de leite, todas elas a
partir das 43 vazias que ele possuía.
Gabarito: d
Questão 16. 1 litro de álcool custa R$0,75. O carro de Henrique percorre 25 km com 3 litros de álcool.
Quantos reais serão gastos em álcool para percorrer 600 km?
a) 54
b) 72
c) 50
d) 52
e) 45
Resolução.
Para saber quantos reais de álcool Henrique gastará para percorrer 600km, devemos dividir 600 por
25. Desta forma, saberemos quantos 3 litros de álcool precisaremos.
Assim, precisaremos de
de álcool. Como cada litro de álcool custa R$ 0,75, multiplicamos a quantidade de litros necessária pelo valor do litro. Logo,
Serão gastos R$
54,00.
Gabarito: a
Questão 17. Escrevem-se, em ordem crescente, os números inteiros e positivos que sejam múltiplos de
7 ou de 8 (ou de ambos), obtendo-se
a) 406
b) 376
c) 392
d) 384
e) 400
.O
número escrito é:
O mínimo múltiplo comum de 7 e 8 é 56.
Entre dois múltiplos consecutivos de 56 há sete múltiplos de 7 e seis múltiplos de 8. Assim, os múltiplos
de 56 são os elementos de ordem 14, 28, 42, … da seqüência. Portanto, o 98  elemento da seqüência é
igual a 56 7 = 392 e o 100 é 392 + 8 = 400
Gabarito: e
Teste 1ª Unidade 8º ano
Resolução.
MATEMÁTICA
9
Questão 18. Quatro amigos vão visitar um museu e um deles resolve entrar sem pagar. Aparece um
fiscal que quer saber qual deles entrou sem pagar.




Eu não fui, diz o Benjamim.
Foi o Carlos, diz o Mário.
Foi o Pedro, diz o Carlos.
O Mário não tem razão, diz o Pedro.
Só um deles mentiu. Quem não pagou a entrada do museu?
a)
b)
c)
d)
e)
Mário
Pedro
Benjamim
Carlos
não é possível saber, pois faltam dados
Resolução.
Mário e Carlos não podem ter ambos dito a verdade, pois somente um entrou sem pagar.
Se Mário não falou a verdade, então o que Carlos disse é verdadeiro, o que Pedro disse é verdadeiro e
o que Benjamim disse é verdadeiro. Disso se conclui que Pedro entrou sem pagar (Se Mário disse a
verdade, Carlos não disse e Pedro disse, o que é contraditório).
Gabarito: b
Questão 19. A figura abaixo foi desenhada em cartolina e dobrada de modo a formar um cubo.
Qual das alternativas mostra o cubo assim formado?
A)
B)
D)
E)
C)
Resolução.
Gabarito: b
Teste 1ª Unidade 8º ano
Se montarmos o cubo vemos que a única resposta possível é a letra b.
MATEMÁTICA
10
Questão 20. O retângulo da figura a seguir está dividido em 7 quadrados. Se a área do menor quadrado é igual a 1, a área do retângulo é igual a:
a)
b)
c)
d)
e)
42
44
45
48
49
Resolução.
Completando a figura com quadradinhos de lado 1, vemos 3 quadrados de área 1, 1 quadrado de área
9, 2 quadrados de área 4 e 1 quadrado de área 25. Logo a área do retângulo é 3 + 9 + 2 4 + 25 = 45.
Gabarito: c
Questão 21. A calculadora de Juliana é bem diferente. Ela tem uma tecla D, que duplica o número escrito no visor e a tecla T, que apaga o algarismo das unidades do número escrito no visor. Assim, por
exemplo, se estiver escrito 123 no visor e apertarmos D, teremos 246; depois, apertando T, teremos 24.
Suponha que esteja escrito 1999. Se apertamos D depois T, em seguida D, depois T, teremos o número:
a)
b)
c)
d)
e)
96
98
123
79
99
Resolução.
Gabarito: d
Teste 1ª Unidade 8º ano
Ao apertarmos o D, temos
Ao apertarmos o T, temos o algarismo das unidades apagado
Ao apertarmos o D, temos
Ao apertarmos o T, temos o algarismo das unidades apagado
MATEMÁTICA
11
Questão 22. Marcos quer pesar três maças numa balança de dois pratos, mas ele dispõe de apenas um
bloco de 200 gramas. Observando o equilíbrio na balança, ele observa que a maçã maior tem o mesmo
peso que as outras duas maçãs juntas; o bloco e a maçã menor pesam tanto quanto as outras duas maçãs
juntas; a maçã maior junto com a menor pesam tanto quanto bloco. O peso total das três maçãs é:
a)
b)
c)
d)
e)
250 g
300 g
350 g
400 g
450 g
Resolução.
Se a maça grande é igual a maça média mais a maça pequena e a maça pequena mais 200 é igual a
maça grande mais a maça média, então a maça pequena mais 200 é igual a duas maças médias mais a
maça pequena, ou seja, a maça média pesa 100 g.
Se a maça grande mais a maça pequena pesa 200 e a maça grande é igual a 100 mais a maça pequena,
então o dobro da maça pequena é 100, ou seja, a maça pequena pesa 50 g. Então a maça grande pesa
150 g e a soma é 300 g.
Gabarito: b
Questão 23. Esmeralda compra cinco latas de azeite a quatro reais e setenta centavos a lata, cinco latas
de leite em pó a três reais e doze centavos cada e três caixas de iogurte com seis iogurtes cada caixa ao
preço de oitenta centavos por iogurte. Paga com uma nota de cinqüenta reais e quer saber quanto irá
receber de troco. Qual das expressões aritméticas a seguir representa a solução para este problema?
a)
b)
c)
d)
e)
Resolução.
Ela compra:
 5 latas de azeite a R$ 4,70 a lata,
 5 latas de leite a R$ 3,12 cada
 3 caixas de iogurte com 6 iogurtes em cada caixa a R$ 0,80 por iogurte.
O total gasto com esses itens é
.
Como ela paga com uma nota de R$ 50,00, ela irá receber de troco
Gabarito: c
Teste 1ª Unidade 8º ano
.
MATEMÁTICA
12
Questão 24. O quociente e o resto na divisão de 26097 por 25 são, respectivamente:
a)
b)
c)
d)
e)
1043 e 22
1044 e 3
143 e 22
1044 e 22
144 e 3
Resolução.
Como
, o quociente procurado é 1043 e o respectivo resto é 22.
Gabarito: a
Questão 25. Uma pesquisa foi feita entre pessoas de ambos os sexos, em igual número, com a seguinte pergunta: Entre as cores azul, vermelho e amarelo, qual é a cor que você prefere? Cada pessoa apresentou a sua preferência por uma, e só uma, dessas cores. E o resultado da pesquisa aparece nos gráficos
abaixo:
Podemos concluir que, em relação ao total de pessoas pesquisadas, a ordem de preferência das cores é:
a) I, II, III
b) I, III, II
c) II, I, III
d) II, III, I
e) III, II, I
Resolução.
Seja 2n o número de pessoas entrevistadas. A quantidade de pessoas cuja preferência é pela cor I é de
19% das mulheres e 50% dos homens, ou seja,
; pela cor II é de
e pela cor III é
. Nesse caso, a ordem
de preferência das cores é II, III, I.
Observação: nessas situações, quando se fala em ordem, é usual colocarmos em ordem crescente. Porém, serão consideradas corretas as duas maneiras: crescente ou decrescente.
Teste 1ª Unidade 8º ano
Gabarito: b ou d ambas devem ser consideradas como resposta correta