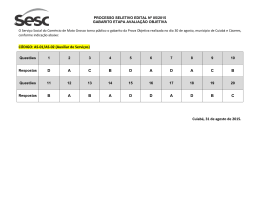
2ª Série – 2014
MATEMÁTICA – FILOSOFIA
MATEMÁTICA – Questões de 01 a 20
1)
(ENEM) Uma pessoa decidiu depositar moedas de 1, 5, 10, 25 e 50 centavos
em um cofre durante certo tempo. Todo dia da semana ela depositava uma
única moeda, sempre nesta ordem: 1, 5, 10, 25, 50, e, novamente, 1, 5, 10, 25,
50, assim sucessivamente.
Se a primeira moeda foi depositada em uma segunda-feira, então essa pessoa
conseguiu a quantia exata de RS 95,05 após depositar a moeda de
a)
b)
c)
d)
2)
1 centavo no 679º dia, que caiu numa segunda-feira.
5 centavos no 186º dia, que caiu numa quinta-feira.
10 centavos no 188º dia, que caiu numa quinta-feira.
25 centavos no 524º dia, que caiu num sábado.
(UFU) Dois ciclistas estão em fases distintas de preparação. O técnico desses
atletas elabora um planejamento de treinamento para ambos, estabelecendo o
seguinte esquema:


ciclista 1: iniciar o treinamento com 4 km de percurso e aumentar, a cada
dia, 3 km a mais para serem percorridos;
ciclista 2: iniciar o treinamento com 25 km de percurso e aumentar, a cada
dia, 2 km a mais para serem percorridos.
Sabendo-se que esses ciclistas iniciam o treinamento no mesmo dia e que o
término desse treinamento se dá quando os atletas percorrem a mesma
distância em um mesmo dia, pode-se afirmar que ao final do treinamento o
ciclista 1 percorre uma distância total, em km, de
a)
b)
c)
d)
3)
781
714
848
915
(UFAM) Dada a progressão aritmética, (13, 20, ...). Então a soma desde o 30°
até o 42° termo é:
a)
b)
c)
d)
3096
4012
3354
3543
SISTEMA EQUIPE DE ENSINO
GABARITO 1
1
MATEMÁTICA – FILOSOFIA
4)
(ESPM-2007) Uma competição esportiva é realizada de n em n anos (n inteiro
e maior que 1). Sabe-se que houve competição nos anos de 1931, 1959 e
1994. Assinale a alternativa que apresenta a próxima data dessa competição a
partir deste ano.
a)
b)
c)
d)
5)
2010.
2012.
2011.
2008.
(MACK) Os múltiplos de 7, existentes entre 20 e 508, são em número de:
a)
b)
c)
d)
6)
2ª Série – 2014
72
70
68
67
Os números inteiros positivos são dispostos em "quadrados" da seguinte
maneira:
123
456
789
10 11 12
13 14 15
16 17 18
19 __ __
__ __ __
__ __ __
O número 500 se encontra em um desses "quadrados". A "linha" e a "coluna"
em que o número 500 se encontra são, respectivamente:
a)
b)
c)
d)
7)
Em janeiro de certo ano, João estava ganhando R$700,00 por mês. Seu
patrão prometeu aumentar seu salário em R$40,00 todos os meses. Quanto
João estará ganhando em dezembro do ano seguinte?
a)
b)
c)
d)
2
2e2
3 e 3.
2e3
3e2
R$ 1700,00.
R$ 1720,00.
R$ 1600,00.
R$ 1620,00.
GABARITO 1
SISTEMA EQUIPE DE ENSINO
2ª Série – 2014
8)
1
9
2
8
O valor positivo de x que torna a sucessão ( , 𝑥, ) uma PG é
a)
b)
c)
d)
9)
MATEMÁTICA – FILOSOFIA
1/2
1/4
3/2
3/4
(UFRGS) Numa PG de razão positiva, o primeiro termo é igual ao dobro da
razão, e a soma dos dois primeiros é 24. Nessa progressão a razão é
a)
b)
c)
d)
1
2
3
4
10) A soma dos termos de uma PG é expressa por 𝑆𝑛 = −3 + 3𝑛+1 . A razão da
progressão é
a)
b)
c)
d)
2
3
6
√2
11) (UA-AM) Se
a)
1
b)
1
2
c)
d)
2
4
1
1

4 1 0 1 2
, então o valor de 2x é:
.

2 0 x  1 1 
SISTEMA EQUIPE DE ENSINO
GABARITO 1
3
MATEMÁTICA – FILOSOFIA
2ª Série – 2014
12) (UA-AM) Sendo as matrizes
 1 0
A  
 2 6
1
 2A  B 
2
a)
b)
c)
d)
 4
  8 2  1

 , B  
1
 0 4 10 
3
C é igual a:
2
 6  8 7
 , a matriz
C  
 4  2 6 
  11 13  3 


 2 17  6 
  17 18 19 


 0 17  12 
  11 13 19 


  12 11  6 
  17 18  3 


  12 11  6 
13) (PUC-MG) Se 𝐴 = [
a)
b)
c)
d)
e
1
𝑎
2
9 −4
] e 𝐴2 = [
], o valor do produto ab é:
𝑏
−8 17
–4
–6
–8
– 12
14) (UNIRIO) Considere as matrizes
3 5 
 4
A  2 1 , B    e C  2 1 3 .
3 
0  1
A adição da transposta de A com o produto de B por C é:
a)
b)
c)
d)
4
impossível de se efetuar, pois as matrizes são todas de tipos diferentes.
impossível de se efetuar, pois não existe a soma da transposta de A com
o produto de B por C.
possível de se efetuar e o seu resultado é do tipo 2 x 3.
possível de se efetuar e o seu resultado é do tipo 3 x 2.
GABARITO 1
SISTEMA EQUIPE DE ENSINO
2ª Série – 2014
MATEMÁTICA – FILOSOFIA
15) (UFV) Considere A, B e I matrizes quadradas, de mesma ordem e com
elementos arbitrários. Se I é a matriz identidade e B é a inversa de A, então
(2A + 3B) · (A – B) é igual a:
a)
b)
c)
d)
2 A2  2I  3B 2
2 A2  I  3B 2
2 A2  I  3B 2
2 A2  2I  3B 2
16) (UE-CE)
Sejam
M . Mt  P,
as
sendo
matrizes
Mt
 3 q

M 
 n 3


e
 6 6
 .
P  
 6 6
a matriz transposta de M, então
n2  n . q
Se
é
igual a:
a)
b)
c)
d)
6
9
12
18
17) Se a matriz
a)
b)
c)
d)
2 y
 1
 x
1 0 

 x  1 0 1 
é simétrica, então
xy
é igual a:
1
9
1
8
1
8
SISTEMA EQUIPE DE ENSINO
GABARITO 1
5
MATEMÁTICA – FILOSOFIA
2ª Série – 2014
18) (FUNREI) Uma matriz n x n é chamada de quadrado mágico quando a soma
dos elementos de cada linha, de cada coluna, da diagonal principal e da outra
diagonal é igual.
Se a matriz 4 x 4 dada por
ct d u
abr s
a)
b)
c)
d)
1
4

7

r
2 3 a
5 6 b 
8 c d

s t u
é um quadrado mágico, então
é igual a:
3
8
7

32
2
3
5

16

19) O dono de uma rede de lojas representou, numa matriz, o número de discos
vendidos em cada loja, nos primeiros dias do mês passado. Na matriz A, cada
elemento
aij
indica o número de discos vendidos pela loja i no dia j.
23 11 16 4 0
A  18 24 13 26 4
 8 2 9 16 1 
Todas afirmativas estão corretas, EXCETO:
a)
b)
c)
d)
6
A loja 3 vendeu mais discos no dia 4.
No dia 4, a loja 1 foi a loja que vendeu menos discos.
A rede vendeu menos discos no dia 1.
A loja 2 a campeã de vendas no período.
GABARITO 1
SISTEMA EQUIPE DE ENSINO
2ª Série – 2014
MATEMÁTICA – FILOSOFIA
20) São dadas as matrizes A e B, quadradas, de ordem n e invertíveis. A solução
da equação
A . X 1 . B1  I n , onde I n é a matriz identidade de ordem n, é
a matriz X tal que
a)
X  A1 . B
c)
X  B . A1
X  B 1 . A
d)
X  A . B 1
b)
SISTEMA EQUIPE DE ENSINO
GABARITO 1
7
MATEMÁTICA – FILOSOFIA
2ª Série – 2014
FILOSOFIA – Questões de 21 a 30
21) (Paes/UNIMONTES) Philosophía é uma palavra grega composta de duas
outras: Philo, aquele ou aquela que tem um sentimento amigável”, e Sophía,
“sabedoria”. Daí filosofia significar “amizade pela sabedoria” ou “amor e
respeito pelo saber”. A invenção dessa palavra é atribuída a
a)
b)
c)
d)
Tomás de Aquino.
Cirilo de Alexandria.
Machado de Assis.
Pitágoras de Samos.
22) (UNICENTRO) Assinale a alternativa CORRETA. A Filosofia tem como
principal característica a
a)
b)
c)
d)
tendência a oferecer respostas reticentes para os problemas, isto é,
colocado um problema, sua solução nunca é conclusiva, sendo sempre
submetida à discussão, nunca sendo aceita como uma verdade absoluta.
tendência à racionalidade, isto é, a razão e somente a razão, com seus
princípios e regras, é o critério da explicação de alguma coisa.
exigência de que o pensamento seja sempre dialético, isto é, o filósofo é
aquele que justifica suas ideias provando que segue uma lei universal do
pensamento: que a contradição não indica erro ou falsidade, mas sim
devir e transformação.
recusa de explicações imanentes do problema em questão e, portanto,
exigência de que, para cada problema, seja buscada uma explicação
preestabelecida, já que o pensamento filosófico é um fato histórico
enraizado no passado.
23) (UFSJ-PAS) A construção de uma cosmologia que desse uma explicação
racional e sistemática das características do universo, em substituição à
cosmogonia, que tentava explicar a origem do universo baseada nos mitos, foi
uma preocupação da Filosofia
a)
b)
c)
d)
8
medieval.
antiga.
iluminista.
contemporânea.
GABARITO 1
SISTEMA EQUIPE DE ENSINO
2ª Série – 2014
MATEMÁTICA – FILOSOFIA
Leia o texto para responder as questões 24 e 25.
(UNIMONTES) O primeiro filósofo de que temos notícias é Tales, da colônia
grega de Mileto, na Ásia Menor. Tales foi um homem que viajou muito. Entre
outras coisas, dizem que, certa vez, no Egito, ele calculou a altura de uma
pirâmide medindo a sombra da mesma no exato momento em que sua própria
sombra tinha a mesma medida de sua altura. Dizem ainda que, em 585 a.C.,
ele previu um eclipse solar.
(GAARDER, J. O Mundo de Sofia.
São Paulo: Companhia das Letras, 1995).
24) Aos primeiros filósofos que se debruçaram sobre os problemas do cosmo,
podemos chamá-los, além de pré-socráticos, de
a)
b)
c)
d)
naturalistas ou fisicistas.
existencialistas.
empiristas.
espiritualistas.
25) Tales, entre outros filósofos pré-socráticos, defendia que a natureza possuía
um elemento formador de toda a realidade. Para ele, este elemento chamdo
de arque (ou arché) era o (a)
a)
b)
c)
d)
terra
fogo
água
ar
26) (UNIMONTES) Lembremos a figura de Sócrates. Dizem que era um homem
feio, mas, quando falava, exercia estranho fascínio. Podemos atribuir a
Sócrates duas maneiras de se chegar ao conhecimento. Essas duas maneiras
são denominadas de
a)
b)
c)
d)
doxa e ironia.
ironia e maiêutica.
maiêutica e doxa.
maiêutica e episteme.
SISTEMA EQUIPE DE ENSINO
GABARITO 1
9
MATEMÁTICA – FILOSOFIA
2ª Série – 2014
27) (UNIMONTES/Mod) Sócrates (470-399 a.C) nasceu e viveu em Atenas,
Grécia. Filho de um escultor e de uma parteira, conhecia a doutrina dos
filósofos que o antecederam e a de seus contemporâneos. Discutia em praça
pública sem nada cobrar. Não deixou livros. Conhecemos muitas de suas
ideias por meio de seus discípulos. As melhores ideias de Sócrates podem ser
conhecidas por um de seus discípulos, que é
a)
b)
c)
d)
Platão.
Alexandre.
Parmênides.
Homero.
28) (UFU-2009) Platão (428 – 347 a.C.), discípulo de Sócrates e mestre de
Aristóteles, fundador da Academia, é até hoje um dos filósofos mais
importantes da história da filosofia. Círculos culturais e intelectuais no mundo
inteiro dedicam-se a estudar sua obra.
Sobre o modo como Platão expressou seu pensamento, assinale a alternativa
CORRETA.
a)
b)
c)
d)
Platão jamais escreveu textos filosóficos.
Platão escreveu textos filosóficos na forma de romances.
Platão escreveu textos filosóficos na forma de poesias.
Platão escreveu textos filosóficos na forma de diálogos.
29) (UFSJ) Considerando o pensamento de Platão na “Alegoria da Caverna”, é
CORRETO afirmar que
a)
b)
c)
d)
10
os prisioneiros entendem como única realidade o conhecimento que se
afasta dos sentidos.
os prisioneiros fundamentam o seu conhecimento na reflexão sobre o
mundo da caverna.
a opinião é certa de si mesma quanto mais afastada se encontra da
verdade.
a verdadeira realidade, para os prisioneiros, é aquela que vai além dos
sentidos.
GABARITO 1
SISTEMA EQUIPE DE ENSINO
2ª Série – 2014
MATEMÁTICA – FILOSOFIA
30) Observe a HQ abaixo e responda à questão.
O diálogo da história em quadrinho, nos permite concluir
a)
b)
c)
d)
se tratar da Alegoria da caverna de Platão.
se tratar dos discursos em praça pública proferidos por Sócrates.
se tratar das experiências de reflexão da luz feitas por Aristóteles.
se tratar das lutas entre os mitólogos e os filósofos.
SISTEMA EQUIPE DE ENSINO
GABARITO 1
11
MATEMÁTICA – FILOSOFIA
12
GABARITO 1
2ª Série – 2014
SISTEMA EQUIPE DE ENSINO