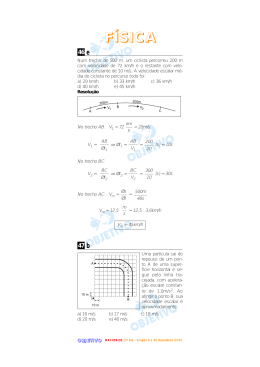
Questão 46
Num trecho de 500 m, um ciclista percorreu
200 m com velocidade constante de 72 km/h e
o restante com velocidade constante de 10 m/s.
A velocidade escalar média do ciclista no percurso todo foi:
a) 29 km/h
b) 33 km/h
c) 36 km/h
d) 40 km/h
e) 45 km/h
a) 16 m/s
d) 20 m/s
b) 17 m/s
e) 40 m/s
c) 18 m/s
alternativa B
Vamos considerar o trecho CD como um quarto
de uma circunferência de raio 30 m.
alternativa E
Na primeira parte do percurso, a velocidade (v1 )
do ciclista é v1 = 72 km/h = 20 m/s. Assim, o intervalo de tempo (∆t1 ) da primeira parte é
∆S1
200
∆t1 =
=
= 10 s.
v1
20
Na segunda parte do percurso, o intervalo de
∆S 2
300
tempo (∆t 2 ) é ∆t 2 =
=
= 30 s.
v2
10
A velocidade escalar média (v m ) do ciclista no
percurso todo é dada por:
∆S
500
m
vm =
=
= 12,5
⇒
∆t1 + ∆t 2
10 + 30
s
⇒
v m = 45 km/h
Assim, da figura, o deslocamento escalar (∆S) entre os pontos A e B é dado por:
2 π ⋅ 30
∆S = ∆S AC + ∆SCD + ∆SDB = 50 +
+ 50 ⇒
4
⇒ ∆S = 147,1 m.
Como temos um MUV, da Equação de Torricelli,
temos:
v 2 = v 02 + 2a ⋅ ∆S = 0 2 + 2 ⋅ 1,0 ⋅ (147,1) ⇒
Questão 47
⇒ v = 17 m/s
Uma partícula sai do repouso de um ponto A
de uma superfície horizontal e segue pela linha tracejada, com aceleração escalar constante de 1,0 m/s2 . Ao atingir o ponto B, sua
velocidade escalar é aproximadamente:
Questão 48
No sistema a seguir, o atrito é desprezível, o
fio e a polia são ideais e a mola M, de massa
desprezível, tem constante elástica 200 N/m.
Quando o corpo B é seguro, a fim de se manter o conjunto em equilíbrio, a mola está deformada de ..... e, depois do corpo B ter sido
abandonado, a deformação da mola será de
..... .
física 2
As medidas que preenchem correta e respectivamente as lacunas, na ordem de leitura,
são:
a) 2,5 cm e 3,0 cm.
b) 5,0 cm e 5,0 cm.
c) 5,0 cm e 6,0 cm.
d) 10,0 cm e 10,0 cm.
e) 10,0 cm e 12,0 cm.
alternativa C
Quando o corpo B é seguro, as forças que atuam
sobre o corpo A são dadas por:
Como o conjunto encontra-se em equilíbrio, temos que:
R A = 0 ⇒ k ⋅ x = m A ⋅ g ⇒ 200 ⋅ x =
= 1,0 ⋅ 10 ⇒ x = 0,050 m ⇒
x = 5,0 cm
Ao abandonarmos o corpo B, as forças que atuam
sobre os corpos A e B são dadas por:
Do Princípio Fundamental da Dinâmica, temos:
(A) k ⋅ x’ − m A ⋅ g = m A ⋅ γ
(B) mB ⋅ g sen 30 o − k ⋅ x’ = mB ⋅ γ
Somando as equações, vem:
mB ⋅ g sen 30 o − m A ⋅ g = (m A + mB ) γ ⇒
⇒ 4,0 ⋅ 10 ⋅
1
− 1,0 ⋅ 10 = (1,0 + 4,0) γ ⇒
2
⇒ γ = 2,0 m/s 2 .
De (A) vem:
200 ⋅ x’ −1,0 ⋅ 10 = 1,0 ⋅ 2,0 ⇒ x’ = 0,060 m ⇒
⇒ x’ = 6,0 cm
Questão 49
Uma pequena esfera E1 , de massa 100 g, é
abandonada do repouso no ponto A de um trilho altamente polido, deslizando até se chocar frontalmente com uma esfera E2 , de
massa 300 g, inicialmente em repouso no
ponto B. O choque ocorre com coeficiente de
restituição 1. Após o choque:
a) a esfera E1 retorna pelo trilho e atingirá a
altura máxima de 20,00 cm em relação à parte horizontal, enquanto a esfera E2 se deslocará no sentido de B para C, com velocidade
de 2,0 m/s.
b) a esfera E1 retorna pelo trilho e atingirá a
altura máxima de 40,00 cm em relação à parte horizontal, enquanto a esfera E2 se deslocará no sentido de B para C, com velocidade
de 2,0 m/s.
c) ambas as esferas se deslocarão sobre o trilho no sentido de B para C, cada qual com velocidade de 2,0 m/s.
d) as esferas E1 e E2 se deslocarão sobre o trilho no sentido de B para C, com velocidades
respectivamente iguais a 1,0 m/s e 3,0 m/s.
e) a esfera E1 permanecerá parada em B e a
esfera E2 se deslocará sobre o trilho no sentido de B para C, com velocidade de 4,0 m/s.
alternativa A
Sendo o atrito desprezível, a esfera E1 atinge a
esfera E 2 com uma velocidade v1 = 2gh =
= 2 ⋅ 10 ⋅ 0,8 = 4 m/s.
Para o choque, temos:
Qantes = Qdepois ⇒ m1v1 = m1v1’ + m 2v 2 ’ ⇒
⇒ 100 ⋅ 4 = 100 ⋅ v1’ + 300 ⋅ v 2 ’ ⇒
(I)
⇒ v1’ + 3v 2 ’ = 4
Sendo o coeficiente de restituição (e) igual a 1,
vem:
v ’ − v 1’
v ’ − v 1’
e = 2
⇒1 = 2
⇒
v1 − v 2
4 −0
física 3
(II)
⇒ v 2 ’ − v 1’ = 4
Somando (I) e (II), temos:
4 v 2 ’ = 8 ⇒ v 2 ’ = 2 m/s
De (I), vem:
v1’ + 3 ⋅ 2 = 4 ⇒ v1’ = −2 m/s
Assim, após o choque, a esfera E1 retorna pelo
trilho e atingirá a altura máxima (h’) dada por:
v’ 2
( −2) 2
⇒ h’ = 0,2 m ⇒ h’ = 20 cm
h’ = 1 =
2g
2 ⋅ 10
Já a esfera E 2 se deslocará no sentido de B para
C, com velocidade v 2 ’ = 2 m/s .
Do Princípio Fundamental da Dinâmica, vem:
Questão 50
Questão 51
Um veículo necessita deslocar-se num trecho
circunferencial de um autódromo, com velocidade escalar constante de 180 km/h. O raio
de curvatura da trajetória é 820 m. Para que
esse movimento seja possível, independentemente do atrito entre os pneus e a pista, a estrada deverá apresentar uma sobrelevação,
em relação à horizontal, correspondente a um
ângulo α mínimo, aproximadamente igual a:
a) 2o
b) 7o
c) 13o
d) 17o
e) 20o
A figura mostra um móbile constituído por
duas barras de massas desprezíveis que sustentam os corpos A, B e C por fios ideais.
Sendo a massa do corpo A 45 g, a massa do
corpo C, que mantém o conjunto em equilíbrio na posição indicada, deve ser igual a:
2o
7o
13 o
17o
20 o
Rcp = N senα
mg = N cosα
⇒
mv 2
= N senα
R
mg = N cosα
Dividindo as equações e adotando g = 10 m/s 2 ,
temos:
(180/3,6) 2
v2
= tgα ⇒
= tgα ⇒ tgα = 0,305
Rg
820 ⋅ 10
Da tabela fornecida, o ângulo α mínimo é aproximadamente igual a17 o .
a) 10 g
b) 20 g
c) 30 g
d) 40 g
e) 50 g
sen 0,035 0,122 0,225 0,292 0,342
alternativa D
cos 0,999 0,992 0,974 0,956 0,940
Para a barra no nível mais baixo, no equilíbrio, temos:
tan 0,035 0,123 0,231 0,306 0,364
alternativa D
Desprezando o atrito entre os pneus e a pista, as
forças que atuam sobre o carro são dadas por:
M R (O) = 0 ⇒ m A ⋅ g ⋅ 10 = mB ⋅ g ⋅ 30 ⇒
⇒ 45 ⋅ 10 = mB ⋅ 30 ⇒ mB = 15 g
R = 0 ⇒ T = m A ⋅ g + mB ⋅ g ⇒ T = 45 ⋅ g +
+ 15 ⋅ g ⇒ T = 60 ⋅ g
Para a barra no nível mais alto, no equilíbrio, temos:
física 4
M R (O’) = 0 ⇒ 60 ⋅ g ⋅ 20 = mC ⋅ g ⋅ 30 ⇒
⇒
mC = 40 g
Sendo ∆L = L0 α∆θ, temos:
∆L
= L0 α ⇒ 2,0 ⋅ 10 −4 = 4,00 α ⇒
∆θ
⇒ α = 5,0 ⋅ 10 −5 oC −1
Questão 52
A constante universal dos gases perfeitos é
R = 8,2 ⋅ 10−2 (atmosfera ⋅ litro)/(mol ⋅ kelvin).
Questão 54
O produto (atmosfera ⋅ litro) tem a mesma dimensão de:
a) pressão.
b) volume.
c) temperatura.
d) força.
e) energia.
Em uma experiência, tomamos um corpo sólido
a 0o C e o aquecemos por meio de uma fonte térmica de potência constante. O gráfico a seguir
mostra a temperatura desse corpo em função
do tempo de aquecimento. A substância que
constitui o corpo tem, no estado sólido, calor
específico igual a 0,6 cal/(g.o C). O calor latente de fusão da substância desse corpo é:
alternativa E
Sendo atmosfera e litro as unidades, respectivamente, de pressão e volume, temos:
[força]
[pressão] ⋅ [volume] =
⋅ [área] ⋅ [distância] =
[área]
=
[energia]
Questão 53
O gráfico abaixo nos permite acompanhar o
comprimento de uma haste metálica em função de sua temperatura. O coeficiente de dilatação linear do material que constitui essa
haste vale:
a) 40 cal/g
d) 70 cal/g
b) 4.10−5 oC−1
c) 5.10−5 oC−1
d) 6.10−5 oC−1
Analisando a substância no estado sólido, a potência (P) da fonte térmica é dada por:
mc ∆θ
m ⋅ 0,6 ⋅ (60 − 0)
Q
P =
=
=
=
∆t
∆t
3 −0
= 12m cal/min
Durante a fusão, temos:
mLf
mLf
Q’
P =
=
⇒ 12m =
⇒
8 −3
∆t’
∆t’
Lf = 60 cal/g
Questão 55
−5 o −1
e) 7.10
C
alternativa C
Do gráfico, vem:
∆L
4,02 − 4,00
m
=
= 2,0 ⋅ 10 −4 o
∆θ
120 − 20
C
c) 60 cal/g
alternativa C
⇒
a) 2.10−5 oC−1
b) 50 cal/g
e) 80 cal/g
Na ilustração, o corpo de
pequena espessura, constituído de acrílico transparente (índice de refração =
= 1,4), tem a forma de um
semi-círculo de centro O.
física 5
Quando imerso no ar (índice de refração = 1,0),
é atingido por um raio luminoso monocromático no ponto P. A alternativa que melhor representa a trajetória do raio luminoso após
atingir P é:
a)
b)
c)
d)
a) v
b) v
c) v
d) v
e) v
−2π sen (10π t + π )
+2π cos (10π t + π )
− π sen (10π t + π /2)
+ π cos (10π t + π /2)
−2π sen (10π t + 2π/3)
alternativa A
Como o corpo é abandonado da posição que
mostra a figura, a fase inicial (ϕ0 ) é π rad e a amplitude é A = 20 cm = 0,2 m.
A pulsação é ω = 2 πf = 2 π ⋅ 5 = 10 π rad/s.
Assim, a velocidade (v) adquirida pelo corpo, no
SI, varia com o tempo (t) obedecendo a função:
v = −A ⋅ ω ⋅ sen ( ωt + ϕ0 ) ⇒
⇒ v = −0,2 ⋅ 10 π ⋅ sen (10 π ⋅ t + π ) ⇒
⇒
e)
=
=
=
=
=
v = −2 π ⋅ sen (10 π ⋅ t + π )
Questão 57
alternativa C
Como o raio de luz incidente em P tem sua direção passando pelo centro O, por geometria ele é
normal à superfície semi-circular sofrendo refração para dentro do corpo sem desviar-se.
Já no interior do corpo, irá incidir em O e passar
para o ar (meio menos refringente) afastando-se
da reta normal que passa pelo ponto.
Obs.: é necessário admitir que não ocorre reflexão total em O.
Questão 56
Um corpo apoiado sobre uma superfície horizontal lisa e preso a uma mola ideal, comprimida de 20 cm, é abandonado como mostra a
figura. Esse corpo realiza um m.h.s. de freqüência 5 Hz, sendo O o seu ponto de equilíbrio. A velocidade (v) adquirida pelo corpo, no
SI, varia com o tempo (t) obedecendo à função:
Durante o século XX, o desenvolvimento da
Física no campo nuclear foi notório, e a descoberta de partículas elementares acabou sendo uma das responsáveis por esse fato. Foram construídos diversos aceleradores de
partículas para pesquisa e com eles muitas
teorias foram não só comprovadas, como também aprimoradas. Considere duas dessas
partículas: um próton, que pode ser identificado como sendo o núcleo do átomo de Hidrogênio (11 H), e uma partícula alfa, que pode ser
identificada como sendo o núcleo do átomo de
Hélio (42 He).
Quando, no vácuo, um próton e uma partícula alfa se dirigem um contra o outro, no instante em que a distância entre eles é d, a força de interação eletrostática tem intensidade:
k0 ... constante eletrostática do vácuo
e ... carga elétrica elementar
a) F = k0
2e
d2
e2
d2
4e
e) F = k0 2
d
c) F = k0
b) F = k0
2 e2
d2
d) F = k0
4 e2
d2
física 6
alternativa B
Sendo a carga do próton q = e e da partícula alfa
Q = 2e, da Lei de Coulomb, temos:
k ⋅|Q|⋅|q|
k ⋅2e ⋅e
Fel. = 0 2
= 0
⇒
d
d2
⇒
Fel. = k 0
2 e2
d2
A resistência equivalente é dada por:
R ⋅ R2
72 ⋅ 36
+ 24 ⇒
+ R3 =
Req. = 1
72 + 36
R1 + R 2
⇒ Req. = 48 Ω
Assim a corrente (i) em L3 é obtida de:
U
12
i = 2,5 ⋅ 10 −1 A
i =
=
⇒
Req.
48
Questão 59
Questão 58
Três lâmpadas, L1 , L2 e L3 , identificadas,
respectivamente, pelas inscrições (2 W − 12 V),
(4 W − 12 V) e (6 W − 12 V), foram associadas
conforme mostra o trecho de circuito a seguir.
Entre os terminais A e B aplica-se a d.d.p. de
12 V. A intensidade de corrente elétrica que
passa pela lâmpada L3 é:
a) 2,5 ⋅10−1 A
c) 1,0 A
e) 2,0 A
Deseja-se alimentar a rede elétrica de uma
casa localizada no sítio ilustrado a seguir.
Em A tem-se o ponto de entrada do sítio, que
“recebe” a energia da rede pública e, em B, o
ponto de entrada da casa. Devido a irregularidades no terreno, as possibilidades de linhas de transmissão de A até B apresentadas
pelo eletricista foram a 1 (linha pontilhada) e
a 2 (linha cheia); porém, somente uma será
instalada. Com uma mesma demanda de
energia, independentemente da opção escolhida e utilizando-se fios de mesmo material,
deseja-se que no ponto B chegue a mesma intensidade de corrente elétrica. Para que isso
ocorra, o diâmetro do fio a ser utilizado na linha 1 deverá ser igual:
b) 3,3 ⋅10−1 A
d) 1,6 A
alternativa A
As resistências elétricas R1 , R 2 e R3 das lâmpadas L1 , L2 e L3 , respectivamente, são dadas
por:
R1 =
P =
12 2
2
12 2
U2
U2
⇒R =
⇒ R2 =
⇒
4
R
P
R3 =
R1 = 72 Ω
⇒ R 2 = 36 Ω
R3 = 24 Ω
12 2
6
a) ao diâmetro do fio utilizado na linha 2.
b) a 0,6 vezes o diâmetro do fio utilizado
linha 2.
c) a 0,72 vezes o diâmetro do fio utilizado
linha 2.
d) a 1,2 vezes o diâmetro do fio utilizado
linha 2.
e) a 1,44 vezes o diâmetro do fio utilizado
linha 2.
na
na
na
na
física 7
alternativa D
Considerando os fios homogêneos e de secção
circular constante, para as condições pedidas, devemos ter:
R1 = R 2
l
l
⇒ ρ 12 = ρ 22
l
d
d2
π
π
1
R =ρ
πd 2
4
4
4
72 + 72
100
⇒
= 2 ⇒ d1 = 1,2 d 2
d12
d2
Questão 60
Numa das etapas de uma experiência para a
determinação de massas atômicas, um íon
monovalente positivo tem de passar entre as
placas de um capacitor plano sem ser desviado. A d.d.p. entre as placas do condensador é
U e, para se atingir o objetivo, existe também
um campo magnético uniforme de vetor indução B, com a intensidade convenientemente
ajustada. Desprezando a ação gravitacional,
quanto ao sentido de B e a polaridade das
placas do condensador, a figura que melhor
representa essa etapa da experiência é:
a)
b)
c)
d)
e)
alternativa B
O íon estará sujeito somente à ação de uma força
elétrica Fel . , de mesma orientação do campo elétrico E e de uma força magnética Fmag . , que obedece à regra da mão esquerda.
Para não sofrer desvio, deve ocorrer o equilíbrio
entre estas forças, cuja possibilidade apresenta-se somente na situação da alternativa B, por
possuírem sentidos opostos, como indicado a seguir: