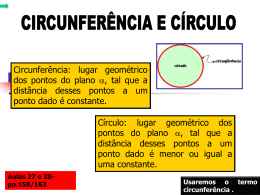
Matemática e suas
Tecnologias - Matemática
Ensino Fundamental, 6º Ano
Circunferência – raio, diâmetro e
comprimento – conceitos iniciais
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Você já viu essa placa de trânsito?
Sabe o que ela significa?
Imagem: Юкатан / Creative Commons Attribution-Share Alike 3.0 Unported.
Ela indica o Trânsito de Ciclistas.
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Você sabia?
A bicicleta é um meio de transporte muito
antigo. Apesar dos automóveis terem se
tornado o meio mais comum de locomoção
nas grandes cidades, a bicicleta ainda possui
adeptos.
Geralmente os ciclistas escolhem utilizar a
bicicleta, porque ela não polui o meio
ambiente e porque, ao pedalar, praticam uma
atividade física.
Você usa bicicleta em seu dia a dia?
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Mas, o que é Bicicleta?
A bicicleta é um veículo com duas rodas
presas a um quadro, movido pelo
esforço do próprio usuário (ciclista)
através de pedais.
Informações retiradas do site http://pt.wikipedia.org/wiki/Bicicleta
(acessado em 29/0/2012,9horas)
Você gosta de pedalar?
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Observe a bicicleta.
1- Quais os elementos
que você conhece da
bicicleta?
2 – Tente explicar o
significado de alguns
deles.
Você deve ter pensado
nas rodas.
Imagem: imoni / public domain.
Ela é mesmo muito
importante.
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Curiosidade sobre a Roda
A roda foi uma das maiores
invenções da humanidade.
O antigo povo egípcio já fazia
uso de toras de madeira para
transportar grandes pesos.
Imagem: Autor desconhecido / Public Domain.
Veículos com rodas puxadas por animais já eram usados
na antiga Mesopotâmia. Um dos vestígios deixados por
essa civilização é uma pedra de argila, datada de 3500
a.C., com o desenho de uma carroça que usava discos de
madeiras como rodas.
Texto retirado do livro Tudo é Matemática.(2005, p.200)
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Imagem: Autor desconhecido / Public
Domain.
A evolução da roda
Com o tempo, para que a roda se tornasse mais leve e
veloz, foram-se fazendo aberturas, o que deu origem à roda
com raios. Por volta de 2000 a.C., sumérios e persas
usavam rodas feitas de madeira com aros protegidos por
uma circunferência de metal para evitar o desgaste.
Texto retirado do livro Tudo é Matemática.(2005, p.200)
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Roda de Bicicleta
Aro
Disco
central
Raios
Pneu
Os raios ligam o aro
ao disco central
Imagem: Herr Kriss / GNU Free Documentation License.
Lembrou de alguma coisa?
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Vamos Comparar.
Aro
Disco
central
raio
Raios
centro
Pneu
Os raios ligam o
aro ao disco
central
Imagem: Herr Kriss / GNU Free
Documentation License.
Percebeu algo semelhante?
circunferência
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Conhecendo a circunferência
A partir de um ponto num plano (o centro), uma
circunferência é a linha formada por todos os
pontos desse plano, que estão a uma mesma
distância do centro.
Pode-se usar um compasso para desenhar
circunferências.
Todo segmento de reta que une o centro a um ponto
da circunferência é um raio da circunferência.
Texto retirado do volume 2 da coleção Viver, Aprender – PNLD EJA
2011 (p.147, grifos nossos)
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Alguns dos significados da palavra Raio
1 – Luz intensa e viva.
2 – Descarga elétrica entre uma nuvem e o solo,
com relâmpagos e trovões.
3 – Segmento de reta que vai duma circunferência,
ou duma superfície esférica, até o seu centro.
Texto retirado do dicionário Aurélio Buarque de Holanda, 2001 (pág. 617).
Qual deles é o significado matemático?
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Você sabia?
O diâmetro corresponde ao dobro da distância do raio
da circunferência.
diâmetro
d= 2r
Você já ouviu falar do diâmetro em outras situações?
Quais?
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Atividade 1 - Conceitos
Vamos responder com nossas palavras:
1 – O que é circunferência?
2 – O que é o raio da circunferência?
3 – Qual a relação entre o raio e o diâmetro de uma
circunferência?
4 – O que o raio da bicicleta tem em comum com o
raio da circunferência, além do nome?
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Um situação do dia-a-dia
A história de Dionísio
Ele trabalha para uma empresa de entregas, a Leva e Traz.
A empresa paga valores fixos aos seus motobóis para
percursos compreendidos num raio de 50km de sua sede. Para
serviços que ultrapassem essa distância, há um acréscimo por
quilômetro percorrido.
A região onde não há acréscimo é determinada, portanto, por
uma circunferência, tendo como centro a empresa e um raio
de 50 km.
Texto retirado do volume 2 da coleção Viver, Aprender – PNLD EJA 2011 (p.147,
grifos nossos)
Reconheceu os termos em destaque?
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Observando a história de Dionísio
Você percebeu que há uma região limitada para as
entregas da empresa, sem acréscimos de valores para os
motobóis?
Essa região, limitada pela circunferência, chama-se círculo.
Círculo
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Atividades 2 – Uso de Compasso
Observe as imagens. Elas mostram o uso do compasso:
Imagem: Original uploader was Mcgill at en.wikibooks (Original text : Mcgill Mcgill) /
public domain.
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
1- Agora, utilizando um compasso, desenhe o que se pede:
a) Duas circunferências com raios diferentes, mas com
o mesmo centro.
b) Duas circunferências com raios iguais, mas com
centros diferentes.
c) Duas circunferências com centros diferentes, mas
com pelo menos um ponto em comum.
Atividades retiradas do volume 2 da coleção Viver, Aprender – PNLD EJA
2011 (p.149)
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
2 - Trace uma circunferência com 3cm de raio e, em seguida:
-Marque uma ponto qualquer nessa circunferência.
-Mantendo a mesma abertura do compasso, coloque a
ponta-seca nesse ponto e marque um novo ponto na
circunferência. A partir desse novo ponto, faça o mesmo
para marcar outro ponto sobre a circunferência. Repita
esse procedimento até marcar 6 pontos.
-Trace seis circunferências tendo como centros os pontos
marcados e mantendo a mesma abertura do compasso
(mesmo raio).
-Use cores para finalizar seu desenho.
Atividades retiradas do volume 2 da coleção Viver, Aprender – PNLD EJA 2011 (p.149)
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Como você faria para medir o comprimento do aro da roda
de uma bicicleta?
http://www.youtube.com/watch?v=XBmPhL
rUMYE
Você faria o mesmo?
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Você concorda?
Como o aro de uma bicicleta lembra uma circunferência, a
medida assim obtida pode ser chamada comprimento da
circunferência, e ser representada por C.
Texto adaptado do livro A conquista da Matemática – 4ª etapa EJA (2001, p.196)
Você sabia que há um valor
comum
a
todas
as
circunferências. Mesmo as de
comprimentos diferentes?
Imagem: Nova / GNU Free Documentation License.
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Observe isso.
Se dividirmos o comprimento C da circunferência pelo
comprimento do seu diâmetro (2r) encontraremos um
número irracional chamado π(pi) e que vale
aproximadamente 3,14. Esse valor é encontrado para
qualquer tamanho de circunferência.
Você sabia que π(pi) é uma letra do alfabeto grego?
Você pode testar isso em casa. Mas, lembre-se que
precisa conhecer o diâmetro da circunferência ou o seu
raio.
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Comprimento da Circunferência
A partir do que já vimos, é possível percebermos que há
outra forma de descobrir o comprimento da
circunferência.
Você é capaz de deduzir como?
Veja como podemos fazer isso matematicamente,
Se C =π, então C= 2r. π ou C=2πr
2r
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
Atividade 3 - Problemas
1- Use π=3,1, calcule e responda em seu caderno:
a) Qual é o comprimento de uma circunferência com
raio 3,5cm?
b) Qual é o comprimento de uma circunferência que tem
diâmetro de 12cm?
a) O comprimento de uma circunferência é de 43,4cm.
Qual é a medida do raio? E do diâmetro
Questão retirada do livro Tudo é Matemática.(2005, p.201)
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
2 - Determine o comprimento de uma circunferência que
tem 9 cm de raio.
3 - Qual é o comprimento r do raio de uma circunferência
que tem 18,84 cm de comprimento?
4 - Uma circunferência tem 10,5 cm de diâmetro. Nessas
condições, qual é o comprimento dessa circunferência?
Questões retiradas do livro A conquista da Matemática
4ª etapa EJA (2001, p.196 e 197)
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
5 - Uma pista circular tem 25 m de raio. Quantos metros
percorre uma pessoa que dá 20 voltas em torno dessa
pista?
6 - Ao percorrer uma distância de 6280m, uma roda dá
2000 voltas completas. Qual é o raio dessa roda?
7 - Se uma pessoa der 10 voltas completas em torno de um
jardim circular, ela percorrerá 2198 m. Qual é o diâmetro
desse jardim?
Questões retiradas do livro A conquista da Matemática – 4ª etapa EJA (2001, p.197)
Matemática, 6º Ano
Circunferência – raio, diâmetro, comprimento – conceitos
iniciais
8 – O quadrado ABCD da figura tem 80cm de lado. Qual é o
comprimento da circunferência inscrita nesse quadrado?
D
C
r
A
B
9 – Qual é a medida de uma correia acoplada a duas rodas
iguais de 10cm de raio e cujos centros estão a 5 cm de
distância um do outro?
Questões retiradas do livro A conquista da Matemática – 4ª etapa EJA (2001, p.197)
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
Referências Bibliográficas
DANTE, L. R. Tudo é Matemática. 7ª série. São
Paulo: Ed. Ática, 2005.
GIOVANNI, J. R. et al. A Conquista da Matemática.
4ª etapa da EJA São Paulo : Ed. FDT, 2001.
Vários autores. Coleção Viver, Aprender. Vol. 4 EJA. São Paulo: Ed. Global, 2009.
FERREIRA, Aurélio B. de H. Miniaurélio Século XXI:
O minidicionário da língua portuguesa. Rio de
Janeiro: Nova Fronteira, 2001.
Tabela de Imagens
n° do
slide
2
direito da imagem como está ao lado da
foto
Юкатан / Creative Commons AttributionShare Alike 3.0 Unported.
imoni / public domain.
link do site onde se consegiu a informação
http://commons.wikimedia.org/wiki/File:1.24_road
_sign.svg
5
http://commons.wikimedia.org/wiki/File:Japanese_
CityCycle_LadiesType.jpg
6 Autor desconhecido / Public Domain.
http://commons.wikimedia.org/wiki/File:Ur_chariot
.jpg
7 Autor desconhecido / Public Domain.
http://commons.wikimedia.org/wiki/File:1885Benz.j
pg
8 e 9 Herr Kriss / GNU Free Documentation
http://commons.wikimedia.org/wiki/File:Sport_bicy
License.
cle_wheel.jpg
16 Original uploader was Mcgill at en.wikibooks http://commons.wikimedia.org/wiki/File:Geom_dra
(Original text : Mcgill Mcgill) / public
w_circle_sequence.png
domain.
20 Nova / GNU Free Documentation License. http://commons.wikimedia.org/wiki/File:Ordinary_
bicycle01.jpg?uselang=pt
Data do
Acesso
19/09/2012
19/09/2012
19/09/2012
19/09/2012
19/09/2012
20/09/2012
20/09/2012