Lista de exercícios de funções,
logaritmos e trigonometria.
Questões UFPR 2003 a 2012 1˚ e 2˚
fase
Professor Carlos (KIKO)
1) (UFPR-2003)Um grupo de estudantes
decidiu viajar de ônibus para participar de
um encontro nacional. Ao fazerem uma
pesquisa de preços, os estudantes receberam
de uma empresa a seguinte proposta, na qual
o preço de cada passagem depende do total
de passageiros: cada passageiro pagará R$
90,00 mais o valor de R$ 5,00 por lugar que
eventualmente ficar vago no ônibus. Sabendo
que o ônibus tem 52 lugares, é correto
afirmar:
01) Se viajarem 30 passageiros, cada um deles
pagará R$ 110,00.
02) Se o total de passageiros for x, o preço (em
reais) de cada passagem será calculado pela
expressão 90 + 5(52 – x).
04) Se viajarem 40 pessoas, a empresa deverá
receber um total de R$ 6.000,00, referente ao
pagamento das passagens.
08) Se viajarem x pessoas, o valor total (em
reais) que a empresa deverá receber, referente
ao pagamento das passagens, é calculado pela
04) Um som de 40 decibéis tem intensidade
igual a 10000 × I0.
08) Se um som tem nível sonoro de 10 decibéis,
então outro som que é dez vezes mais intenso
que aquele tem nível sonoro igual a 100
decibéis.
16) Se três sons têm níveis sonoros de 50, 60 e
70 decibéis, e suas intensidades são,
respectivamente, I1, I2, e I3, então esses números
formam, nessa
geométrica.
ordem,
uma
progressão
3)(UFPR-2004)Em determinado país, o
imposto de renda a ser pago por cada pessoa
é calculado da seguinte forma:
a) o rendimento bruto é decomposto em
faixas de valores;
b) ao valor compreendido em cada uma
dessas faixas é aplicado um percentual;
c) os valores que resultam da aplicação dos
percentuais às diversas faixas de valores são
somados;
d) o resultado dessa soma corresponde ao
imposto total a ser descontado. As faixas de
valores são:
1ª) até $1.000,00;
2ª) acima de $1.000,00, até $2.000,00;
3ª) acima de $2.000,00, até $3.000,00;
4ª) acima de $3.000,00.
O gráfico abaixo representa a relação entre o
rendimento bruto, x, e o rendimento líquido,
y, após o desconto doimposto de renda.
2
expressão 300x – 5x .
16) O valor total máximo que a empresa poderá
receber pelo pagamento das passagens ocorrerá
quando o total de passageiros for igual a 35.
2) (UFPR-2003 ) O nível sonoro de um som
de intensidade I, medido em decibéis, é
calculado pela fórmula 10 × log0II, onde log
representa logaritmo na base 10, e I0 é um
valor de referência que corresponde
aproximadamente à menor intensidade de
som audível ao ouvido humano. Com base
nessas informações, é correto afirmar:
01) Se um som tem intensidade I0, então o seu
nível sonoro é igual a zero.
02) Um som de 1 decibel tem intensidade igual
a 10 × I0.
Com base nessas informações, é correto
afirmar:
01) Não há desconto para rendimentos brutos
inferiores a $1.000,00.
02) O percentual aplicado à segunda faixa é de
5%.
04) Para um rendimento bruto de $1.050,00, o
rendimento líquido
após o desconto do imposto de renda é $997,50.
08) Se 2000 < x ≤ 3000, então y = 0,85(x -2000)
+ 1900.
16) Para um rendimento bruto de $3.500,00, o
desconto do imposto de renda é igual a 10%
desse rendimento.
4)(UFPR-2004) Uma pessoa de 2 m de altura,
passeando pela cidade, caminha em linha
reta em uma rua horizontal, na direção da
portaria de um edifício. A pessoa pára para
ver o topo desse edifício, o que a obriga a
olhar para cima num ângulo de 30 graus com
a horizontal. Após caminhar 49 m, pára uma
segunda vez para ver o topo do edifício e tem
que olhar para cima num ângulo de 45 graus
com a horizontal. Suponha que cada andar
do edifício tenha 3 m de altura. Utilize 3 1,7.
Nessa situação, é correto afirmar:
01) O edifício tem menos de 30 andares.
02) No momento em que a pessoa pára pela
primeira vez, ela está a 160 m da portaria do
edíficio.
04) Quando a pessoa pára pela segunda vez, a
distância em que ela se encontra da portaria é
igual à altura do edifício.
08) Se, depois da segunda vez em que pára, a
pessoa caminhar mais 35 m em direção à
portaria, para ver o topo do edifício será
necessário erguer os olhos num ângulo maior do
que 60 graus com a horizontal.
5)(UFPR-2005 1˚ fase)Calcule o seno do
maior ângulo de um triângulo cujos lados
medem 4, 6 e 8 metros.
a)
d) 2π
e) 8
8)(UFPR-2006 1˚fase) Dadas as funções f :R
→R e g :R →R definidas por f(x) = ax + b e
g(x) = x² , considere as seguintes afirmativas:
I. (g o f)(1) = (a + b)² .
II. (f o g)(−x) = (f o g)(x) , para qualquer x R.
III. (g o f)(x) = (f o g)(x) , para qualquer x R.
Assinale a alternativa correta.
a) Somente as afirmativas I e II são verdadeiras.
b) Somente a afirmativa I é verdadeira.
c) Somente as afirmativas II e III são
verdadeiras.
d) Somente as afirmativas I e III são
verdadeiras.
e) As afirmativas I, II e III são verdadeiras.
9)(UFPR-2006 1˚ fase) Na figura ao lado está
representado um período completo do gráfico
da função:
`
( )
√
b)
c)
√
d)
√
e)
6)(UFPR-2005 1˚fase) Considere as seguintes
afirmativas a respeito da função f: D → R
definida por ( )
I . O ponto x=1 não pertence ao conjunto D.
II.
( )
III.
( )
IV.
A função inversa de
.
( )
.
Assinale a alternativa correta.
a) Somente as afirmativas I, II e III são
verdadeiras.
b) Somente as afirmativas I e IV são
verdadeiras.
c) Somente as afirmativas II e III são
verdadeiras.
d) Somente as afirmativas I, III e IV são
verdadeiras.
e) Todas as afirmativas são verdadeiras.
7)(UFPR 2006 1˚fase) O período da função f:
R → R, definida por f(x)= sen(2x ), é:
a) π
b)π/2
c)π/4
Para cada ponto B sobre o gráfico de f, fica
determinado um triângulo de vértices O, A e
B, como na figura ao lado. Qual é a maior
área que um triângulo obtido dessa forma
pode ter?
a)3
b)12
c)6
d)8
e)9
10)(UFPR-2006 1˚fase) Uma determinada
substância radioativa desintegra-se com o
tempo, segundo a função ( )
sendo
a massa inicial, k uma constante
característica da substância e t o tempo dado
em anos. Sabendo que a quantidade inicial de
100 g dessa substância radioativa diminui
para 50 g em 28 anos, calcule quanto tempo
será necessário para que 100 g dessa
substância se reduzam a 25 g. (Considere
2 = 0,7 )
a) 64 anos
b) 48 anos
c) 72 anos
d) 42 anos
e) 56 anos
11)(UFPR-2006 1˚ fase)O tanque de
combustível de um posto de gasolina possui o
formato de um cilindro circular reto e está
instalado de modo que as bases estão na
vertical. Para saber o volume de combustível
presente no tanque, o funcionário utiliza uma
régua graduada e só necessita observar a
altura alcançada pelo combustível dentro do
tanque. Essa régua foi confeccionada com
base no estudo da função que relaciona o
volume v com a altura h, desde zero até a
altura total T. Qual dos gráficos abaixo mais
se aproxima do gráfico dessa função?
a)
b)
c)
d)
e)
12)(UFPR-2006 2˚fase) Uma empresa possui
uma máquina que fabrica discos de metal a
partir da especificação do raio r. O controle
de qualidade dessa empresa detectou que
essa máquina está produzindo discos de raio
maior que o especificado, ocasionando um
desperdício de material acima do esperado.
Para quantificar o erro E cometido na
fabricação de um disco de raio r+x, o
controle de qualidade utiliza a seguinte
expressão:
E = A (r+x ) − A (r)
sendo A (r) a área do disco de raio r e
A(r+x) a área do disco de raio r + x , com x >
0
Fixando r = 10 cm, resolva os itens abaixo.
a) Qual é o erro E cometido na fabricação de
um disco de raio 10,5 cm?
b) O controle de qualidade dessa empresa
estipulou que o erro máximo aceitável na
fabricação desses discos é de 1% do valor da
área A(r). Para atender essa exigência, qual é
o valor máximo permitido para x?
A
13)(UFPR-2006 1˚fase) O lucro diário L é a
receita gerada R menos o custo de produção
C. Suponha que, em certa fábrica, a receita
gerada e o custo de produção sejam dados,
em reais, pelas funções R(x) = 60x–x² e
C(x) = 10(x+40), sendo x o número de itens
produzidos no dia. Sabendo que a fábrica
tem capacidade de produzir até 50 itens por
dia, considere as seguintes afirmativas:
I. O número mínimo de itens x que devem ser
produzidos por dia, para que a fábrica não
tenha prejuízo, é 10.
II. A função lucro L(x) é crescente no
intervalo [0, 25].
III. Para que a fábrica tenha o maior lucro
possível, deve produzir 30 itens por dia.
IV. Se a fábrica produzir 50 itens num único
dia, terá prejuízo.
Assinale a alternativa correta.
a) Somente as afirmativas II e IV são
verdadeiras.
b) Somente as afirmativas I e II são verdadeiras.
c) Somente as afirmativas I, II e IV são
verdadeiras.
d) Somente as afirmativas II e III são
verdadeiras.
e) Somente as afirmativas I, III e IV são
verdadeiras.
14)(UFPR-2007 1˚ fase) Abaixo
estão
representados os gráficos das funções f e g.
Sobre esses gráficos, considere as seguintes
afirmativas:
1. A equação f(x).g(x) = 0 possui quatro
soluções no intervalo fechado [-10, 10] .
2. A função y = f(x).g(x) assume apenas
valores positivos no intervalo aberto (0, 3) .
3. f(g(0)) = g(f(0)).
4. No intervalo fechado [3, 10], a função f é
decrescente e a função g é crescente.
Assinale a alternativa correta.
a) Somente as afirmativas 1, 2 e 4 são
verdadeiras.
b) Somente as afirmativas 3 e 4 são verdadeiras.
c) Somente as afirmativas 1, 3 e 4 são
verdadeiras.
d) Somente as afirmativas 2 e 3 são verdadeiras.
e) Somente as afirmativas 1 e 2 são verdadeiras.
15)(UFPR-2007 1˚fase) Considere a função f
definida no conjunto dos números naturais
pela expressão f(n + 2) = f(n) + 3, com n IN, e
pelos dados f(0) = 10 e f(1) = 5. É correto
afirmar que os valores de f(20) e f(41) são,
respectivamente:
a) 21 e 65.
b) 40 e 56.
c) 40 e 65.
d) 21 e 42.
e) 23 e 44.
16)(UFPR-2007 1˚fase) Um medicamento é
administrado continuamente a um paciente, e
a concentração desse medicamento em mg/ml
de sangue aumenta progressivamente,
aproximando-se de um número fixo S,
chamado nível de saturação. A quantidade
desse medicamento na corrente sangüínea é
dada pela fórmula q(t) = S.[1- 0,2t], sendo t
dado em horas.
Com base nessas informações, considere as
afirmativas a seguir:
1. Se q(t0 ) = S / 2 , então t0 = log2
2. Se t > 4 , então q(t) > 0,99.S
3. q(1) = 8.S/10
Assinale a alternativa correta.
a) As afirmativas 1, 2 e 3 são verdadeiras.
b) Somente as afirmativas 2 e 3 são verdadeiras
c) Somente a afirmativa 2 é verdadeira.
d) Somente a afirmativa 3 é verdadeira.
e) Somente as afirmativas 1 e 2 são verdadeiras.
17)(UFPR-2007 2˚fase) Um determinado tipo
de canhão para artilharia antiaérea dispara
projéteis que descrevem uma trajetória
parabólica. Após vários disparos, um grupo
de engenheiros militares constatou que,
desprezando-se a resistência do ar, os
projéteis lançados a partir do solo descrevem
uma parábola de equação
sendo x e y dados em metros e k um fator
positivo relacionado à inclinação que pode
ser ajustado diretamente no canhão.
a) Que valor se deve atribuir a k para que um
projétil lançado por esse canhão atinja o solo a
exatamente 400 m do ponto de disparo?
b) Qual é o menor valor que se deve atribuir a k
para que um projétil lançado por esse canhão
atinja a altura de 1000 m?
18)(UFPR-2007 2˚fase)Em um experimento
feito em laboratório, um pesquisador colocou
numa mesma lâmina dois tipos de bactérias,
sabendo que as bactérias do tipo I são
predadoras das bactérias do tipo II. Após
acompanhar o experimento por alguns
minutos, o pesquisador concluiu que o
número de bactérias tipo I era dado pela
função f(t)= 2.3t+1 e que o número de
bactérias do tipo II era dado pela função ,
g(t) 3.24-2t ambas em função do número t de
horas.
a) Qual era o número de bactérias, de cada um
dos tipos, no instante inicial do experimento?
b) Esboce, no plano cartesiano ao lado, o
gráfico das funções f e g apresentadas acima.
c) Após quantos minutos a lâmina terá o mesmo
número de bactérias do tipo I e II?
(Use log2 = 0,30 e log3 = 0,47 )
19)(UFPR-2007 2˚fase) O retângulo ao lado
está inscrito em uma circunferência de raio
r=1, com os lados paralelos aos eixos
coordenados.
e) Somente a afirmativa 2 é verdadeira.
21) (UFPR-2008 1˚fase) Na figura ao abaixo,
os pontos A e P pertencem à circunferência
de centro na origem e raio 1, o ponto R
pertence ao eixo das abscissas e o ângulo t,
em radianos, pode variar no intervalo (0, ) ,
dependendo da posição ocupada por P.
a) Encontre a área e o perímetro do retângulo
em função do ângulo α (0≤ α ≤ ).
b) Determine α para que a área do retângulo seja
máxima.
c) Determine α para que o perímetro do
retângulo seja máximo.
20)(UFPR-2008 1˚fase) Alguns processos de
produção permitem obter mais de um
produto a partir dos mesmos recursos, por
exemplo, a variação da quantidade de níquel
no processo de produção do aço fornece ligas
com diferentes graus de resistência. Uma
companhia siderúrgica pode produzir, por
dia, x toneladas do aço tipo Xis e y toneladas
do aço tipo Ypsilon utilizando o mesmo
processo de produção. A equação
,chamada de curva de
transformação de produto, estabelece a
relação de dependência entre essas duas
quantidades. Obviamente deve-se supor x ≥ 0
e y ≥ 0 . Com base nessas informações,
considere as seguintes afirmativas:
1. É possível produzir até 20 toneladas do aço
tipo Xis por dia.
2. A produção máxima de aço tipo Ypsilon,
por dia, é de apenas 2 toneladas.
3. Num único dia é possível produzir 500 kg
de aço tipo Ypsilon e ainda restam recursos
para produzir mais de 12
toneladas do aço tipo Xis.
Assinale a alternativa correta.
a) Somente as afirmativas 1 e 3 são verdadeiras.
b) Somente as afirmativas 1 e 2 são verdadeiras.
c) Somente as afirmativas 2 e 3 são verdadeiras.
d) Somente a afirmativa 1 é verdadeira.
Com base nessas informações, considere as
afirmativas a seguir:
1. O comprimento do segmento AP é 2cos t.
2. A área do triângulo OAP, em função do
ângulo t, é dado por f(t) = ½ sen t.
3. A área do triângulo ORP, em função do
ângulo t, é dado por g(t) = ¼ sen(2t).
Assinale a alternativa correta.
a) Somente a afirmativa 3 é verdadeira.
b) Somente a afirmativa 2 é verdadeira.
c) Somente as afirmativas 2 e 3 são verdadeiras.
d) Somente as afirmativas 1 e 3 são verdadeiras.
e)Somente as afirmativas 1 e 2 são verdadeiras.
22)(UFPR-2008 1˚fase) Um método para se
estimar a ordem de grandeza de um número
positivo N é usar uma pequena variação do
conceitode notação científica. O método
consiste em determinar o valor x que satisfaz
a equação
= N e usar
propriedades dos logaritmos para saber o
número de casas decimais desse número.
Dados log2 = 0,30 e log3 = 0,47, use esse
método para decidir qual dos números
abaixo mais se aproxima de N =
.
a)
b)
c)
d)
e)
23)(UFPR-2008 2˚fase) O teste de alcoolemia
informa a quantidade de álcool no sangue
levando em conta fatores como a quantidade
e o tipo de bebida ingerida. O Código de
Trânsito Brasileiro determina que o limite
tolerável de álcool no sangue, para uma
pessoa dirigir um automóvel, é de até 0,6 g/L.
Suponha que um teste de alcoolemia acusou a
presença de 1,8 g/L de álcool no sangue de
um indivíduo. A partir do momento em que
ele pára de beber, a quantidade, em g/L, de
álcool no seu sangue decresce segundo a
função ( )
sendo o tempo t
medidos em horas.
a) Quando t = 2, qual é a quantidade de álcool
no sangue desse indivíduo?
b) Quantas horas após esse indivíduo parar de
beber a quantidade de álcool no seu sangue
atingirá o limite tolerável para ele poder dirigir?
(Use log2 = 0,30 e log3 = 0,47 )
a) Se o retângulo tiver a medida da altura igual a
um terço da medida da base, qual é a sua área?
b) Se a medida da base do retângulo inscrito for
x, obtenha uma expressão da área do retângulo
em função de x.
24)Considere x,y
[
] tais que
e
.
a) Calcule os valores de cos x e cos y.
c) Calcule a maior área possível desses
retângulos inscritos.
b) Calcule os valores de sen(x + y) e cos(x − y) .
25)(UFPR-2008 2˚fase) Considere as funções
reais
f(x) = 2 + √ e g(x) = (x² − x + 6).(2x – x²):
a) Calcule (f o g)(0) e (g o f )(1) .
27)(UFPR-2009 1˚fase) A estrutura de um
telhado tem a forma de um prisma triangular
reto, conforme o esquema ao lado. Sabendo
que são necessárias 20 telhas por metro
quadrado para cobrir esse telhado, assinale a
alternativa que mais se aproxima da
quantidade de telhas necessárias para
construí-lo. Considere √
b) Encontre o domínio da função (f o g)(x) .
26)(UFPR-2008 2˚fase) Num triângulo ABC
com 18 cm de base e 12 cm de altura, é
inscrito um retângulo com a sua base sobre o
lado AB, conforme a figura ao lado.
a) 4080
b) 5712
c) 4896
d) 3670
e) 2856
28)(UFPR-2009 1˚fase)Em estudos realizados
numa área de proteção ambiental, biólogos
constataram que o número N de indivíduos
de certa espécie primata está crescendo em
função do tempo t (dado em anos), segundo a
expressão N(t)=
Supondo que o
instante t = 0 corresponda ao início desse
estudo e que essa expressão continue sendo
válida com o passar dos anos, considere as
seguintes afirmativas:
1. O número de primatas dessa espécie
presentes na reserva no início do estudo era
de 75 indivíduos.
2. Vinte anos após o início desse estudo, o
número de primatas dessa espécie será
superior a 110 indivíduos.
3. A população dessa espécie nunca
ultrapassará 120 indivíduos.
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente as afirmativas 1 e 2 são verdadeiras.
c) Somente as afirmativas 1 e 3 são verdadeiras.
d) Somente as afirmativas 2 e 3 são verdadeiras.
e) As afirmativas 1, 2 e 3 são verdadeiras.
29)(UFPR-2009 2˚fase) Para atrair novos
clientes, um supermercado decidiu fazer uma
promoção reduzindo o preço do leite. O
gerente desse estabelecimento estima que,
para cada R$ 0,01 de desconto no preço do
litro, será possível vender 25 litros de leite a
mais que em um dia sem promoção. Sabendo
que, em um dia sem promoção, esse
supermercado vende 2600 litros de leite ao
preço de R$ 1,60 por litro:
a) qual é o valor arrecadado por esse
supermercado com a venda de leite em um dia
sem promoção?
b) qual será o valor arrecadado por esse
supermercado com a venda de leite em um dia,
se cada litro for vendido por R$ 1,40?
c) qual é o preço do litro de leite que fornece a
esse supermercado o maior valor arrecadado
possível? De quanto é esse valor arrecadado?
30)(UFPR-2009 2˚fase)Uma fábrica de
produtos químicos possui um sistema de
filtragem do ar que é ligado automaticamente
toda vez que a quantidade de poluentes no ar
atinge certo nível previamente estabelecido.
Sabe-se que a quantidade Q(t) de poluentes
no ar dessa fábrica, depois de ligado o
sistema de filtragem, é dada em função do
tempo pela expressão:
( )
sendo a quantidade
Q(t) medida e partícula por litro de ar e o
tempo t eminutos.
a) Qual a quantidade de poluentes existente no
ar no instante inicial t=0 em que o sistema de
filtragem foi acionado? E quinze minutos depois
da filtragem ter sido iniciada?
b)Esse sistema de filtragem está programado
para desligar automaticamente no momento em
que a quantidade de poluentes no ar atingir 12
partículas por litro de ar. Quantas horas esse
sistema de filtragem precisa funcionar até
atingir o ponto de desligamento automático?
c) Encontre constantes a, b e c tais que
( )
, examinando essa expressão, justifique
a seguinte afirmação: “o sistema de filtragem
dessa fábrica não é capaz de reduzir a
quantidade de poluentes no ar para valores
abaixo de 10 partículas por litro de ar.
31)(UFPR-2009 2˚fase) O gráfico ao lado
corresponde a uma função exponencial da
forma ( )
, sendo a e b constantes e
a)Calcule os valores a e b da expressãode f(x)
que correspondem a este gráfico
b) Calcule o valor de x para o qual se tem f(x) =
1.
c) Dado k> 0qualquer, mostre que o ponto
(
) satisfaz a equação f(x)=k.
32)(UFPR-2010 1˚fase) Suponha que o
horário do pôr do sol na cidade de Curitiba,
durante o ano de 2009, possa ser descrito pela
função f(t) = 18,8 − 1,3 sem(
)
sendo t o tempo dado em dias e t = 0 o dia 1o
de janeiro. Com base nessas informações,
considere as seguintes afirmativas:
1. O período da função acima é 2π .
2. Foi no mês de abril o dia em que o pôr do
sol ocorreu mais cedo.
3. O horário em que o pôr do sol ocorreu
mais cedo foi 17h30.
Assinale a alternativa correta.
a) Somente a afirmativa 3 é verdadeira.
b) Somente as afirmativas 1 e 2 são verdadeiras.
c) Somente as afirmativas 1 e 3 são verdadeiras.
d) Somente as afirmativas 2 e 3 são verdadeiras.
e) As afirmativas 1, 2 e 3 são verdadeiras.
33)(UFPR-2010 2˚fase) Sabe-se que a
velocidade do som no ar depende da
temperatura. Uma equação que relaciona
essa velocidade v (em
metros por segundo) com a temperatura t
(em graus Celsius) de maneira aproximada é
v = 20 √
. Com base
nessas informações, responda às seguintes
perguntas:
a) Qual é a velocidade do som à temperatura de
27 ˚ C? (Sugestão: use √ = 1,73)
b) Costuma-se assumir que a velocidade do som
é de 340 m/s (metros por segundo). Isso ocorre
a que temperatura?
34)(UFPR-2010 2˚fase)Suponha que o tempo
t (em minutos) necessário para ferver água
em um forno de micro-ondas seja dado pela
função t(n) = a.
sendo a e b constantes e n o número de copos
de água que se deseja aquecer.
a) Com base nos dados da tabela ao lado,
determine os valores de a e b.
Sugestão: use log2 = 0,30 e log3 = 0, 45.
b) Qual é o tempo necessário para se ferverem 4
copos de água nesse forno de micro-ondas?
35)(UFPR-2010 2 ˚fase) Uma calha será
construída a partir de folhas metálicas em
formato retangular, cada uma medindo 1 m
por 40 cm. Fazendo-se duas dobras de
largura x, paralelas ao lado maior de uma
dessas folhas, obtém-se três faces de um bloco
retangular, como mostra a figura da direita.
a) Obtenha uma expressão para o volume desse
bloco retangular em termos de x.
b) Para qual valor de x o volume desse bloco
retangular será máximo?
36)(UFPR-2010 2˚fase) Considere a função f
definida pela expressão
38)(UFPR-2011 1˚fase) Um importante
estudo a respeito de como se processa o
esquecimento foi desenvolvido pelo alemão
Hermann Ebbinghaus no final do século XIX.
Utilizando
métodos
experimentais,
Ebbinghaus determinou que, dentro de
certas condições, o percentual P do
conhecimento adquirido que uma pessoa
retém após t semanas pode ser aproximado
pela fórmula
(
)
, sendo
que a e b variam de uma pessoa para outra.
Se essa fórmula é válida para um certo
estudante, com a = 20 e b = 0,5 , o tempo
necessário para que o percentual se reduza a
28% será:
a) entre uma e duas semanas.
b) entre duas e três semanas.
c) entre três e quatro semanas.
d) entre quatro e cinco semanas.
e) entre cinco e seis semanas.
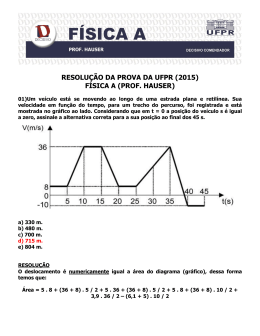
39)(UFPR-2011 1˚fase) O gráfico ao lado
representa a velocidade de um veículo
durante um passeio de três horas, iniciado
às 13h00. De acordo com o gráfico, o
percentual de tempo nesse passeio em que o
veículo esteve a uma velocidade igual ou
superior a 50 quilômetros por hora foi de:
a)Calcule f(0) e f(π/4) .
b) Para quais valores de x se tem f(x) = 0?
37) (UFPR-2010 2˚fase)Uma parábola é o
gráfico de uma função da forma y = ax²+ bx
+ c, com a ≠ 0.
a) Encontre a função cujo gráfico é a parábola
que contém os pontos P = (–1,2), Q = (1,2) e
R = (2,5).
Sugestão: utilize os pontos dados para construir
um sistema linear.
a) 20%.
b) 25%.
c) 30%.
d) 45%.
e) 50%.
40)(UFPR-2011 2 ˚fase) 100 litros de uma
solução contêm inicialmente 75% de álcool e
25% de água. Indiquemos por f(x) a
concentração de água nessa solução após x
litros da água serem removidos, isto é,
( )
b) Existe uma parábola que contém os pontos
P = (–1, –1), Q = (1,3) e R = (2,5)? Justifique.
á
çã
çã
a)Qual o valor de f(0)?
á
á
b) Obtenha a expressão de f(x) em termos de x.
41)(UFPR-2011 2˚fase) Suponha que a
expressão P = 100 + 20 sen(2 t) descreve de
maneira aproximada a pressão sanguínea P,
em milímetros de mercúrio, de uma certa
pessoa durante um teste. Nessa expressão, t
representa o tempo em segundos. A pressão
oscila entre 20 milímetros de mercúrio acima
e abaixo dos 100 milímetros de mercúrio,
indicando que a pressão sanguínea da pessoa
é 120 por 80. Como essa função tem um
período de 1 segundo, o coração da pessoa
bate 60 vezes por minuto durante o teste.
Sendo assim, calcule o ponto em que os raios
de luz verticais refletidos em (1,1) e (2,4) se
encontrarão.
a) Dê o valor da pressão sanguínea dessa
pessoa em t = 0 s; t = 0,75 s.
b) Em que momento, durante o primeiro
segundo, a pressão sanguínea atingiu seu
mínimo?
42)(UFPR-2011 2˚fase) Alguns telescópios
usam espelhos parabólicos, pois essa forma
geométrica reflete a luz que entra para um
único ponto, chamado foco. O gráfico de y =
x², por exemplo, tem a forma de uma
parábola. A luz que vem verticalmente, de
cima para baixo (paralelamente ao eixo y),
encontra a parábola e é refletida segundo a
lei de que o ângulo de incidência é igual ao
ângulo de reflexão. Essa lei implica que os
raios de luz verticais, encontrando a parábola
no ponto (a,a2), serão refletidos na direção da
reta
43)(UFPR-2012 1˚fase) Para se calcular a
intensidade luminosa L, medida em lumens, a
uma profundidade de x centímetros num
determinado lago, utiliza-se a lei de BeerLambert, dada pela seguinte fórmula:
log( )= -0,08x
Qual a intensidade luminosa L a uma
profundidade de 12,5 cm?
a) 150 lumens.
b) 15 lumens.
c) 10 lumens.
d) 1,5 lumens.
e) 1 lúmen.
Gabarito
(
)
1-22
2-21
3-25
4-09
5-b
6-a
7-a
8-a
9-b
10-e
11-a
12-a)10,25
b) O valor máximo é x = √
– 10 ou x ≅
0,05 cm
13-c
14-e
15-c
16-b
17-a)O projétil deve atingir o solo (ordenada
y=0) a 400 metros do ponto de lançamento
(abscissa x = 400), portanto, deve-se
determinar k de modo que 400 seja raiz da
equação 16k²x-kx²=0. Assim, 400k(16k 400)= 0
0 =16k (400) k(400)
Como 0 k > 0, o produto acima é nulo apenas
quando 16k - 400 = 0, o que fornece
K=25
b) Como o projétil descreve um movimento
parabólico, a altura máxima H será atingida
no vértice da parábola, o qual possui
ordenada
t ≅ 0,84 horas , ou seja, após 50,4 minutos
19-a) Como o retângulo está em um círculo
de raio 1 e seus lados são paralelos aos eixos
coordenados, segue das definições de seno e
cosseno do ângulo α que a base b do
retângulo é 2 cosα e a altura h 2 senα é .
Logo:
A área A é dada por:
A = b.h = (2 cos α).( 2 sen α) = 4.(cosα).(sen α)
= 2.sen (2α).
O perímetro P é dado por:
P = 2 b + 2 h = 4 (cos α + sen α).
b) No intervalo [0,π/ 2] a função sen(2α)
atinge seu máximo quando sen(2α) = 1, ou
seja, quando α = π /4. Logo o máximo da
função
A = 2sen(2α) ocorre em α = π /4.
c)
, então
18-a) O instante inicial ocorre quando t = 0,
assim o número de bactérias é:
Tipo I: ( )
= 6.
Tipo II ( )
= 48.
b)
c)
20-c
21-c
22-b
23-a) Basta substituir t = 2 na função dada
obtendo o valor de 0,9 g/L de álcool no
sangue.
( )
b) Basta determinar o valor t1 para o qual
Q(t1) = 0,6; pois Q é uma função exponencial
com expoente negativo e tempos maiores que
t1 implicarão uma quantidade menor de
álcool no sangue do indivíduo. Sendo assim
( )
(
E portanto a lâmina terá o mesmo número de
bactérias de ambos os tipo após t =
)
( )
24) a) Como x e y correspondem a ângulos
agudos, uma forma válida de resolver a
questão é construir um triângulo retângulo
de lados 3, 4 e 5 e usar as expressões do seno
e cosseno como quociente entre catetos e
hipotenusa para
obter os valores.
Outra forma de resolver esta questão é
utilizar a relação trigonométrica sen²a + cos²
a = 1 para obter os valores
cos x = ±
e.
cos y = ± Como ,
(
x, y
[ 0, ,
∈ deve-se concluir que os cossenos
procurados são os valores
positivos.
(
)
)
Logo h=4, e a área do retângulo A= 12.4=
48cm².
b) Denotando por h a altura do triângulo
CDE segue por semelhança de triângulos,
que
b) Aqui basta utilizar as fórmulas da soma e
diferença de arcos e os valores calculados
anteriormente para obter:
Logo a altura do retângulo será
12 −
e a área do retângulo, em função
de x, será A(x) = base × altura, ou seja,
25)a) Como g(0) = 0, f(1) = 3 e g(3) = −36
então
c)Basta encontrar o ponto de máximo da
função quadrática A(x), o qual ocorre no
vértice, com x = 9, e
b) Para que seja possível calcular o valor da
função
em um ponto x, é necessário garantir que o
valor dentro da raiz quadrada seja um
número maior ou igual a zero, ou seja,
Logo o domínio da função pertence ao
intervalo fechado [0,2]
26) a) Usando semelhança de triângulos
27 – a
28 - c
29-a)Multiplicar a quantidade de litros de
leite vendida pelo preço de cada litro, ou seja,
2600 × R$ 1,60 = R$ 4160,00.
b) Observar que quando é dado um desconto de R$
0,20, será possível vender 20 × 25 = 500 litros de
leite a mais que em um dia sem promoção. Neste
caso, será possível vender 2600 + 500 = 3100 litros a
R$ 1,40, e o valor arrecadado será de 3100 × R$ 1,40
= R$ 4340,00
c) O valor arrecadado V(x) é função do
desconto x dado por sendo o valor do
desconto
dado em reais e
V(x)=(1,60-x).(2600+25.100x)
=
2500x²+1400x+4160.
Como V é uma função quadrática com
coeficiente negativo no termo de ordem 2,
então o valor máximo de V(x) é atingido no
vértice da parábola correspondente, ou seja,
t = 289 − 273 = 16˚C.
em
34-a)
fazendo
Logo ( )
V(0,28)= 4356,00
t(1,5)
teremos
a=1,
30)a)No instante t=0 tem –se Q(0)=50
partículas por litro de e após 15 minutos tem
se Q(15)=30 partículas por litro de ar.
Também se sabe que
t(2) = 2, de onde se conclui que 2 = 1,5⋅
Aplicando logaritmos obtemos b=0,5
por isso t(n)=1,5.
b) O objetivo é encontrar o valor t para o
qual se tem Q(t) = 12, ou seja, resolver a
equação
b) Quando n = 4 temos t(4) = 1,5⋅
.
= 1,5⋅ 2
= 3 min
35-a) O volume V do bloco retangular, em
metros cúbicos, é dado por V = 1⋅ (0, 4 − 2x)⋅
Obtendo t = 285 minutos, que corresponde a
4,75 horas , ou 4 horas e 45 minutos.
c)Como
x = −2x² + 0, 4x
b) O volume V será máximo quando o valor
de x corresponder ao vértice da parábola
dada pela função quadrática
V = −2x² + 0, 4x , isto é, quando
(
E procuramos as constantes a, b,c tais que
)
36-a) Calculando diretamente o determinante
Comparando as duas expressões para Q(t),
concluímos que c=15 e a=10 e ac+b=750 é igual
b=600.
Analisando a expressão ( )
pode-se
concluir que à medida que o valor de t aumenta, o
quociente
diminui, ficando cada vez mais
próximo de zero, porém será sempre positiva.
Assim o valor ( )
ficará cada vez
mais próximo de 10, porém sempre maior que 10.
temos
f(x) = 2⋅ ⋅ cos(2x) − 2⋅ cosx⋅ senx = cos(2x) −
sen(2x). Logo,
f(0) = cos(2⋅ 0) − sen(2⋅ 0) = 1
f(( )
b) Para que f(x) = 0 devemos ter cos(2x) =
sen(2x), ou seja,
37-a) Substituindo os pontos P, Q e R na
função y = ax² + bx + c obtemos o sistema
{
31) a)Substituir os valores f(0)=1/2 e f(4)=2
na expressão ( )
obtendo duas
equações exponencias.De f(0)=1/2, obtém – se
b= - 1, e de f(4)=2, e b= -1 obtém – se a =1/2.
Subtraindo a segunda equação da primeira
temos b = 0, de modo que nosso sistema se
torna:
b) Resolver a equação exponencial
obtendo x=2.
fornecendo a = 1 e c = 1. Portanto, a função
procurada é y = x² + 1.
((
c)Calcular
(
b) Procedendo como antes, substituindo os
pontos P, Q e R na função y = ax² + bx + c,
obtemos o sistema
))
=K
{
32-d
33-a)substituindo t=27˚C, temos
= 20 √
= 20 √
= 20.10 √
200. 1,73 = 346 m/s.
Para v = 340m/s temos 340 = 20. √
de onde se obtém que t + 273 = 17² , ou seja,
{
=
Resolvendo de forma análoga ao item
anterior, encontramos a = 0, b = 2 e c = 1, ou
seja, y = 2x + 1, cujo gráfico não é
uma parábola segundo a definição
apresentada.
38-c
39-e
40-a)Pelos dados temos f(0)=
b) ( )
41-a) P(0) 100 20sen(20) 100 mmHg e
P(0,75) 100 20sen(20,75) 80 mmHg
b) O mínimo ocorrerá quando
2t 32ou seja, quandot 3/4 0,75 s .
42-Em (1,1) a reta será: 4× 1× y + (1- 4× 1)x =
1, ou 4y - 3x = 1.
Em (2,4) a reta será: 4× 2× y + (1- 4× 4)x = 2 ,
ou 8y -15x = 2.
Resolvendo o sistema{
temos 9×
x = 0. Assim, x = 0 e
y = 1/4
, e portanto os raios de luz se encontrarão
em[ ]
43-d