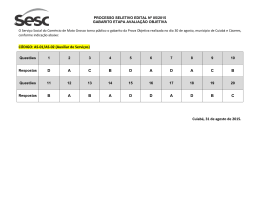
EXERCITANDO - GABARITOS E COMENTÁRIOS
COMPLETO
MATEMÁTICA E SUAS TECNOLOGIAS
MATEMÁTICA I
QUESTÃO 3
QUESTÃO 1
GABARITO: D
COMENTÁRIO:
GABARITO B
COMENTÁRIO: No horário mostrado, 1 hora e 54 minutos, o
ponteiro das horas e dos minutos formam um ângulo central
agudo de 93°, pois:
Ponteiro dos minutos
Ponteiro das horas
 x 
  1 .

3
2
Assim: Nmáx = 320 + 180  1 = 500
60 minutos ____________ 30
 x  27

54 minutos ____________ x
Assim: Nmin = 320 + 180  (-1) = 140
A produção
é máxima
quando
sen
x 
   1 .
 3
2
A produção é máxima quando sen 
QUESTÃO 4
GABARITO: A
COMENTÁRIO: O tempo de uma oscilação, em segundos, é o
2
3
 s. Assim, em 6
 8  4
 3 
6
 8 oscilações
segundos, o atleta faz com o braço
3
4
período da função f(t), que é
completas.
QUESTÃO 5
Logo, o arco externo do relógio, com 20 cm de raio vale,
aproximadamente:
93
93
2R 
2 320  31cm
360
360
GABARITO: B
COMENTÁRIO:
Depois de uma hora de viagem o navio 1 (N 1) terá percorrido
16 km e o navio 2 (N2) terá percorrido 6 km.
Temos, então, a seguinte figura:
QUESTÃO 2
GABARITO: E
COMENTÁRIO:
tg 30° =
h
3

h  10 3
Então: h = 5 5 3 + 5
Logo: H = 5 3 + 6 m
Sendo d a distância entre os navios, temos:
d2  162  62  2  16  6  cos 60
 1
d2  256  36  192   
 2
d2  196
d  14km
www.contatomaceio.com.br
1
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 6
Portanto, a família Pardal deverá pagar
k
15000

 R$ 1.250,00.
12
12
GABARITO: B
COMENTÁRIO:
QUESTÃO 10
GABARITO: A
COMENTÁRIO:
α= 180o  75o  45o  60o
Aplicando o teorema dos senos, temos:
AC
sen60
o

8
sen45
6 100 5
6 1

    x  12
x 125 8
x 2
QUESTÃO 11
o
GABARITO: C
COMENTÁRIO:
25
20
5
 45 
 45 
 45  2,25 L.
100
100
100
2
3
AC.
 8.
2
2
AC  4 6
QUESTÃO 7
QUESTÃO 12
GABARITO: E
COMENTÁRIO:
65cm . 200 000 = 13 000 000 cm = 130km
Logo, a distância real será de 130km.
GABARITO:
COMENTÁRIO:
O tempo necessário para que um capital C triplique,
aplicado a uma taxa de 12%, capitalizado mensalmente, é
QUESTÃO 8
dado por
3C  C(1  0,12)n  1,12n  3
GABARITO: A
COMENTÁRIO:
 log1,12n  log3
x
y
z
19200



36000 45000 63000 36000  45000  63000
 x  4800
x
y
z
2




  y  6000
36000 45000 63000 15
 z  8400

 n  log1,12  log3
 0,05  n  0,47
 n  9,4,
isto é, 9 meses e 0,4  30  12 dias.
QUESTÃO 13
QUESTÃO 9
GABARITO: D
COMENTÁRIO:
Sejam x, y e z, respectivamente, as despesas das famílias
Tatu, Pinguim e Pardal.
Como a despesa é inversamente proporcional ao consumo,
vem
k
x
20
x
y
z
k


k y
.
1
1
1
15
k
20 15 12
z
12
Daí, como a despesa total foi de 3.000 reais, temos
k
k
k
x  y  z  3000 


 3000
20 15 12
 3k  4k  5k  3000  60
GABARITO: C
COMENTÁRIO: Indicando por A a área da figura 1, temos a
seguinte sequência de áreas:
A 
 A A A
 A, , , ,..., ,...
2 3 4
n
Logo, a área da figura 100 é:
A
202

4
100 100
QUESTÃO 14
GABARITO: D
COMENTÁRIO:
Do enunciado, obtemos a sequência (3; 7; 11; ...),
Que é uma PA de razão 4.
Queremos obter S15:
 k  15000.
2
www.contatomaceio.com.br
MATEMÁTICA E SUAS TECNOLOGIAS
S15 =
a1  a15  15
Como 2 funcionários desistiram de participar, a cota de cada
participante passou a ser 2700 .
2
n2
Primeiramente, vamos encontrar a15:
a15 = a1 + 14r  a15 = 3 + 14  4 
 a15 = 3 + 56  a15 = 59
S15 =
Assim:
2700   n  2   8  n  n  2 
2700 2700
2700n

8


n2
n
n  n  2 
n  n  2 
 3  59  15  465
2700n  2700n  5 400  8n2  16n 
2
8n2  16n  5 400  0  n2  2n  675  0 
Serão plantadas 465 mudas.
n  27 ou n  25 (não serve)
QUESTÃO 15
Resposta: 27 funcionários.
GABARITO: B
COMENTÁRIO: Temos que os valores pagos nessas
parcelas formam uma P.G. de razão q =
1 = 256.
Sendo Sn =

1 1  qn
1q

1
de 10 termos e
2
a soma dos n primeiros termos da
P.G., termos, para n = 10:
1

256  1  10 
 2 
1.023
S10 =
= 511,50
 512 
1
1.024
1
2
Portanto, Hélio pagou o total de R$ 511,50 pela máquina
de lavar.
MATEMÁTICA II
QUESTÃO 16
GABARITO: A
COMENTÁRIO:
Sejam a e c, respectivamente, as quantidades de ingressos
vendidos de arquibancada e cadeira.
Sabemos que o número de pagantes de meia-entrada foi
40% de 5 715, ou seja, 0,4 ∙ 5 715 = 2 286.
Assim, temos o seguinte sistema:
QUESTÃO 18
GABARITO: E
COMENTÁRIO:
Sabemos que:
V  90
km 90000m
m

 25
h
3600s
s
Assim, em 1 segundo (tempo de reação do condutor), o
carro percorreu 25 m.
Do momento da frenagem até parar completamente, temos
que:
D
902
8100

 40,5m
250  0,8 200
Portanto, a distância procurada é:
25 + 40,5 = 65,5
QUESTÃO 19
GABARITO: B
COMENTÁRIO:
Temos que:

C(300) = 45 → a  300 + b = 45

C(396) = 37 → a  396 + b = 37
Assim, obtemos o sistema:
300a  b  45 300a  b   45


396a  b  37 396a  b  37
a  b  5715
a  c  5715


 a  2667 e c  3048
2
c
a   2286 4a  c  13716

3
6

96a = -8 → a = 
8
1
→a=
96
12
 1
300ª + b = 45 → 300     x = -70
Portanto, o valor total arrecadado foi:
 12 
2
1
1
5
Portanto,
C(x)
=
0,
devemos
ter:
 2667  10   2667  20   3048  15   3048  30
3
3
6
6
1
1
 x  70  0   x  70  x  840
 17780  17780  7620  76200 
12
12
119380
Logo, o automóvel chegará, no máximo, até o quilômetro
Resposta: R$ 119 380,00.
840.
Resposta: Alternativa B
QUESTÃO 17
GABARITO: C
COMENTÁRIO:
Seja n o número de funcionários da empresa. Assim, se
todos os funcionários participassem do bolão, cada um
pagaria 2700 .
n
www.contatomaceio.com.br
QUESTÃO 20
GABARITO: D
COMENTÁRIO:
Como 10  t  14, temos que o menor e o maior tempo de
viagem possíveis são, respectivamente, t =10 horas e t =14
horas.
Resposta: 10 horas e 14 horas.
3
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 21
QUESTÃO 24
GABARITO: B
COMENTÁRIO:
Temos, em 2 horas:
k2
x0
1
 x0  e 2  ek
2
2
Assim, em 5 horas, teremos:
GABARITO: B
COMENTÁRIO:
x  x0  e
 x0 
k5
2
1
P

2
5
1
 1 2
 x0  (e )  x  x 0     x 0 

2
25
k
 x0 
5
2
1 2
4 2 2
 x0  0,177 17,7%de x0
4 2
Sabemos que
 x0 
2
1,41
 x0 

8
8
QUESTÃO 22
GABARITO: A
COMENTÁRIO:
C
C
1
C (5 600) = 0  C0  10k  5600  0  10k 5 600 
2
2
2
C0
Determinamos t, para que C(t) =
.
32
Assim:
C0 10kt 
C0
1
 1
10kt   10kt   
32
32
2

10kt  10k5600

5
Resposta: 28 000 anos.
QUESTÃO 23
GABARITO: A
COMENTÁRIO:
m
m
m(10)  0  m0  2k 10  0  210k  21 
2
2
1
10k  1  k 
10
t
Assim, a função é dada por m(t)  4  106 1010 .
6
10
.
2048
Então:
4  10  10
6
t
10
t
10
t
106
1

 1010 

2048
4  2048
1
1
t
 13  213 
 13  t  130
11
2 2
2
10
Portanto, o tempo procurado é 130 minutos, ou seja, 2
horas e 10 minutos.
10

2
P
3
P

1
9
Determine t, para que
90
9
P 
P.
100
10
Assim :
f(t) 

 P  t 
P
9

 P  9 1  9  2 3    10 
P
   10

 

1 9  2 3 


t


 P  
 1 
9 1  9  2 3    10  9 1  9     10 

 9  


 
t
2 t
9  9  9  9  10  9  0  t  2
t
Portanto, em 2 horas 90% da população tem acesso à
notícia.
Resposta: 2 horas.
QUESTÃO 25
10k 28000  k  t  k  28000  t  28000
Determinemos t, para que m(t) 

P


P
P
1
P

 
 1 9  2 3  2  9 2 3  1 
P

2
  P31 
 P3 
3
1 9 2
1 9  2  1 9  2 




5
1
10k  5 600 , obtemos :
2
Como
2
50
P
P ,
100
2 então:
f(1) 
GABARITO: D
COMENTÁRIO:
Tempo
Início
Após 1 ano
Após 2 anos
2
Área (km )
8
8 ∙ 1,5
2
(8 ∙ 1,5) 1,5 = 8 ∙ 1,5
Após n anos
8 ∙ 1,5
n
128  8 1,5n  27  23 1,5n  1,5n  24 
log2
log2
 4

log1,5
3
log  
2
log2
0,30
0,30
4
 4
 4

log3  log2
0,48  0,30
0,18
n  log1,5 24  4 
4
5 20

3
3
6,6
Resposta: aproximadamente 6,6 anos.
QUESTÃO 26
GABARITO: E
COMENTÁRIO:
12
12
Sabemos que 20% de 10 = 0,2 ∙ 10 .
Assim, o tempo procurado é dado por:


 1012 
1012
t  50In  12
 50In 

12 
12 
 10  0,2 10 
 0,8 10 
50In

1
10
5
 50In
 50In  50  In5  In4  
0,8
8
4

50  In5  In22  50  In5  2In2   50  1,6  2  0,7  
50  1,6  1,4   50  0,2  10
4
www.contatomaceio.com.br
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 27
Pf = Pi (1 i ) t
80.000 = 150 000 (1- 01) t
GABARITO: E
COMENTÁRIO:
 1,110
P(0)  40  40  A 10
0,04  0
  40  A 1011  A  40  A  40 101,1
1,1
10
Assim, o tempo aproximado para o animal atingir 250 kg é
dado por:
 1,110   250  101,1 1 10  
40 101,1 10
0,04 t
0,04 t
250 25
25
1,1 1 10 0,04 t 

 log10
 log

40
4
4




1,1 1  10 0,04t  log25  log4  1,1 1  10 0,04t 
8  9 

15  10 
t
Log  8  = log
 15 
 9 
 10 
 
t
Log 8 – log 15 = t  (log 9 – log 10)
3 log 2 – (log 3+ log 5) = t (2 log 3 – log 10)
3x 0,3 – (0,48 + 0,7) = t(2x 0,48 -1)
-0,28 = -0,04t -> t= 0,28 = 7 meses.
log5  log4  2  log5  2  log2 
2
0,04
10


2   log  log2 


2
QUESTÃO 31
2   log10  log2  log2  2  1  0,3  0,3  
2  0,4  0,8  1  10
80000
 (0,9)t
150000
0,04t
GABARITO: A
COMENTÁRIO: Todos os cidadãos do conjunto B têm
registro, e alguns têm mais de um registro diferente, logo a
função é sobrejetora mas não injetora.
0,8 8
3



 10 0,04t 
1,1 11 11
3
 log10 0,04t  log3  log11 
11
0,04t  0,48  1,04  0,04t  0,56 
log
QUESTÃO 32
0,04t  t  14
Resposta: aproximadamente 14 meses.
QUESTÃO 28
GABARITO: A
COMENTÁRIO:
Seja x o valor que a primeira pessoa pagou pelo automóvel.
Assim, temos que:
x  1,1  1,1  0,9  13068  1,089x  13068 
13068
 x  12000
1,089
Portanto, a primeira adquiriu o automóvel por R$ 12 000,00.
x
QUESTÃO 29
GABARITO: D
COMENTÁRIO:
Seja C o capital inicialmente emprestado.
Temos que o montante M ao fim de t anos é dado por:
M = C ∙ (1 + 0,08)t = C ∙ (1,08)t
Determinemos t, para que M = 1,8 ∙ C.
Então:
t
t
t
C ∙ (1,08) = 1,8 ∙ C → (1,08) = 1,8 → log (1,08) = log1,8 → t ∙
log1,8
log 1,08 = log1,8 → t =
log1,08
GABARITO: D
COMENTÁRIO: Ele separa 40 garrafas vazias e as troca por
10 garrafas de 1 litro cheias de leite. Esvaziadas as 10
garrafas, ele pode juntá-las com as 3 vazias que restaram e
trocá-las por 3 garrafas cheias, sobrando ainda 1 garrafa
vazia. Esvaziando as 3 cheias e juntando com a garrafa vazia,
ele ainda pode obter em troca mais uma garrafa cheia. Ao
todo, ele pode obter, por sucessivas trocas, 10 + 3 + 1 = 14
garrafas cheias de leite, todas elas a partir das 43 vazias que
ele possuía.
QUESTÃO 33
GABARITO: E
COMENTÁRIO:
L(x) = 12x + 15(120 – x) – [6x + 6(120 – x)]
L(x) = –3x + 1080
QUESTÃO 34
GABARITO: C
COMENTÁRIO:
Sejam a, b, c e d, respectivamente, os números de
QUESTÃO 30
conceitos A, B, C e D.
De acordo com as informações, obtemos
50a  10b  5c  d  400

c  a  10
d  5b

Então,
50a  10b  5(a  10)  5b  350  55a  15b  350
GABARITO: D
COMENTÁRIO:
Dado: log 2 = 0,30
log 3 = 0,48
Sabendo que a é par, isto é, a  2k, k  , vem
3b  70  22k.
Utilizando as aproximações dadas, temos: t  0,255
0,35
Resposta: aproximadamente 7,3 anos.
www.contatomaceio.com.br
7,3 .
 3b  70  11a.
5
MATEMÁTICA E SUAS TECNOLOGIAS
Portanto, por inspeção, k só pode ser 3 e, assim,
2
b  4  2 , que é um quadrado perfeito.
QUESTÃO 35
GABARITO: A
COMENTÁRIO: Sejam x e y, respectivamente, o preço de
um suco e o preço de um sanduíche.
De acordo com o consumo e a despesa de cada mesa, temos
que
2x  3y  14
.

4x  5y  25
Subtraindo a primeira equação da segunda, obtemos
2x  2y  11  x  y  5,50, ou seja, o valor da despesa
da mesa 3 é
R$ 5,50.
Considerando o sistema cartesiano na figura acima, temos a
função do segundo grau fatorada:
h(x) = a(x + 32).(x + 32) e o ponto (-28,2)
1

80
3 = a.(28 – 32).(-28 + 32) ↔ a =
1
Portanto h(x) = 80 .(x – 32).(x + 32)
A altura máxima será quando x for zero.
1

80
Portanto h(0) =
.(0 – 32). (0 + 32) = 12,8m

QUESTÃO 40
GABARITO: C
COMENTÁRIO:
QUESTÃO 36
GABARITO: C
COMENTÁRIO: Admitindo que o número de celulares
vendidos por mês (y) possa ser expresso como função
polinomial do primeiro grau do seu preço (x). Portanto,
y  a  x  b.
Resolvendo o sistema com as equações 1400 = 250 . a + b e
1700 = 200 . a + b temos: a  6 e b  2900.
Logo, y = –6x + 2900; se o preço for 265 reais, serão
vendidos y = –6  265 + 2900 = 1310 unidades.
A + A + 40 = x.(60 – 3x)
2
2A = -3x + 60x – 40
3
 x2  30x  20
A= 2
Xv  
30
 10m
 3
2  
 2
QUESTÃO 37
GABARITO: C
2
COMENTÁRIO: yv = – [(–4) – 4 . 0,1 . 90]/4 .0,1 = 50
QUESTÃO 38
GABARITO: D
COMENTÁRIO: De acordo com as informações do problema,
podemos escrever:
61=0,5 p + 1  p = 120 mil habitantes.
Fazendo p(t) = 120 na segunda função, temos:
2
2
120 = 2t – t + 110  2t – t – 10 = 0  t = 2,5 ou t = - 2
(não convém).
Logo, t é, no mínimo, 2 anos e 6 meses.
QUESTÃO 39
2
Amax = 30 x 40 → 300 m , logo
A + A + 40 = 300
2A = 260
A = 130 → 10 . d = 130
d = 13 e 30 – d = 17
QUESTÃO 41
GABARITO: C
COMENTÁRIO: [C]
I. Para L(x) = 0, temos x1 = 0 ou x2 = 200 (raízes da
função). Assim, a forma fatorada do lucro será:
L(x) = a.(x-0).(x-200)
II. L(15) = 10 200 → a.(15-0)(15-200) = 10 200 → a = - 8.
Daí, L(x) = -8 . x(x – 200) → L(100) = -8 . (100) . (-100) →
L(100) = 80 000
GABARITO: A
COMENTÁRIO:
6
www.contatomaceio.com.br
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 45
MATEMÁTICA III
QUESTÃO 42
GABARITO: B
COMENTÁRIO:
meninos
LB
LE
Total
10%T=20
10%T
40%T
T=200
meninas
50%T
10%T=20
60%T=120
Total
80%T
20%T
100%
QUESTÃO 43
GABARITO: E
COMENTÁRIO: Se 40 alunos se inscreverão SOMENTE em
universidades particulares, então 280-40=240 alunos irão se
inscrever em universidades federais e/ou estaduais.
O total de inscrições para universidades federais e/ou
estaduais é igual a 220+200 = 420, porém, há apenas 240
alunos. Isso quer dizer que 420-240=180 alunos farão suas
inscrições em ambos os tipos de faculdade.
Assim, 220-180 = 40 alunos farão a inscrição para o
vestibular somente em universidades estaduais.
Diagrama de Venn
QUESTÃO 44
GABARITO: C
COMENTÁRIO:
Sendo x o número total de entrevistados e y o número de
homens analfabetos temos que:
do total de entrevistados 70% são homens (homens
alfabetizados + homens analfabetos)
0,7x = 33 + y
y = 0,7x - 33 ---> Equação 1
do total de entrevistados 80% são analfabetos (homens
analfabetos + mulheres analfabetas)
0,8x = y + 58
y = 0,8x - 58 ---> Equação 2
Igualando a equação 1 com a equação 2:
0,7x - 33 = 0,8x - 58
0,1x = 25
x = 25/0,1
x = 250
www.contatomaceio.com.br
GABARITO: C
COMENTÁRIO:
Se (r,n) denota o palpite correto sobre o resultado do jogo
do time n, segue que
(r, n)  {(d, 1), (d, 2), (v, 3), (d, 4), (v,5)}.
Desse modo, NA  NB  4 e NC  3.
Portanto, NA  NB  NC.
QUESTÃO 46
GABARITO: c
COMENTÁRIO:
80% adm emp.
70% sexo masculino
50% adm pub. sexo masculino
500 mulheres adm pub
nesses enunciados podemos analisar que 50% dos
candidatos de adm pub. eram do sexo masculino logo os
outros 50% seriam do sexo feminino e como afirma que 500
mulheres é o numero de candidatas de adm pub. logo o
total de candidatos e de 1000 para adm pub. , como 80% do
total de candidatos escolheram adm. emp.
20% 1000
80% X
20X = 80000
X = 4000 candidatos para adm de emp.
sabemos que temos um total de 5000 candidatos, e que so
70%Sãoo do sexo masculino, logo isso vale 5000 * 0,7 = 3500
candidatos do sexo masculino nos dois cursos. mais como
500 já estão no curso de adm pub. restam 3000 para adm de
empresa.
Então o numero de candidatos do sexo masculino para
administração de empresas e de 3000 pessoas.
QUESTÃO 47
GABARITO: E
COMENTÁRIO:
Se “A”, “B” e “C” forem os tres casais, existem 6 ordens
diferentes de se sentarem:
ABC, ACB, BAC, BCA, CAB, CBA.
II. Cada casal pode sentar-se de duas maneiras diferentes:
homem-mulher/ mulher-homem.
III.O numero total pedido e 2 . 2. 2 . 6 = 48
QUESTÃO 48
GABARITO: B
COMENTÁRIO: Temos as posições inicial e final definidas
com uma possibilidade e 4 possibilidades para cada posição
intermediária (preta fina, preta grossa, branca fina, branca
7
grossa), ou seja 4 maneiras de se completar as posições
restantes.
Logo, deste total, devemos retirar as situações em que todas
7
as barras intermediárias são brancas ou pretas, restando 4
14
– 2 = 2 – 2 possibilidades.
7
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 49
QUESTÃO 52
GABARITO: E
COMENTÁRIO: As regiões a serem coloridas são as
seguintes:
GABARITO: A
COMENTÁRIO:
Pelo diagrama de vem temos:
250
100
250
400
550
200
700
Daí temos 81,7% do total pois 2450/3000=81,7%
QUESTÃO 53
Logo, temos 4 opções para RS, 3 para SC, 3 para PR, 3 para
SP, 3 para MG, 2 para RJ (pois RJ tem fronteira com SP e MG)
e 2 para ES.
4
2
Portanto, 4  3  3  3  3  2  2 = 4  3  2
QUESTÃO 50
GABARITO: D
COMENTÁRIO:
FORRO –a
Mpb--b
Os setores a e b representam 180º, que equivale a 50%. Se a
representa 35%, b representa o que falta para 50%, ou seja
15%.
Os setores c e d representam, também 180º, ou 50% e como
são iguais, 25% cada um.
se 15% são 270 respostas
100% são x respostas, fazendo uma regra de tres simples.
Vem
que:
x = 1800 respostas no total.
25 % de 1800 é 450
QUESTÃO 51
GABARITO: B
COMENTÁRIO: Número de pessoas que consomem ambas
frutas:
L e B = 25
L e M = 20
L e M e B = 100
B e M = 30
Número de pessoas que consomem somente uma fruta:
L = 40
B = 90
M = 95
Então, "O número de pessoas que consomem maçã e não
consomem laranja é de:"
M + (B e M) = 95 + 30 = 125
GABARITO: C
COMENTÁRIO: 10 placas
QUESTÃO 54
GABARITO: B
COMENTÁRIO: Temos que escolher 3 cardiologistas de um
total de 5,1 anestesista de um total de 2 e 4 instrumentores
de um total de 6. Como a ordem da escolha não determina
uma equipe diferente, aplicamos combinação simples, ou
seja:
n!
Cn,p 
(n  p)! p!
Vamos verificar os grupos de 3 cardiologistas, entre 5
disponíveis:
5!
5!
C5,3 

 10
(5  3)!3! 2!3!
Agora vamos qualificar os grupos de anestesistas. Se são 2 e
temos que escolher 1, temos apenas 2 possibilidades, ou
seja, C2,1 = 2.
Por fim, vamos ver quantas possibilidades temos de escolher
4 instrumentores de um total de 6:
6!
6!
C6,4 

 15
(6  4)!4! 2!4!
Com a equipe é formado por cardiologistas e anestesista e
instrumentores, multiplicamos as combinações. Assim:
C5,3 x C2,1 x C6,4 = 10.2.15 = 300.
QUESTÃO 55
GABARITO: A
COMENTÁRIO:
4
5
4
4
4
4
4
4
5  4 = 81.920
7
QUESTÃO 56
GABARITO: B
COMENTÁRIO: Primeiro escolhemos 4 barras para serem
iluminadas entre as disponíveis.
8
www.contatomaceio.com.br
MATEMÁTICA E SUAS TECNOLOGIAS
Depois, desprezamos a ordem de escolha das 4 barras, pois
uma vez formado o símbolo, a ordem da escolha não é
importante.
X
876 5 2 8 7 6  5

¨ 70
4!
4  3  2 1
Ma 
QUESTÃO 57
-125000 X-200000 125000
DAÍ: 750000 X-200000 325000
MATEMÁTICA IV
QUESTÃO 58
GABARITO: E
COMENTÁRIO:
0.1  1.3  2.6  3.8  4.10  5.7  6.5
 3,6
40
QUESTÃO 59
xi
fi
xi  fi
fac
0
1
2
3
25
30
55
90
0
30
110
270
25
55
110
200
Total
200
4
 xi  fi  410
i1
A média aritmética é dada por
4
x
i1
n

410
 2,05.
200
Da tabela, temos que o número de filmes alugados
mais frequente é 3. Logo, Mo  3.
O elemento mediano é
EMd 
n 200

 100, ou seja, os termos centrais são o
2
2
100º e o 101º. Como a mediana é a média aritmética
dos termos centrais, quando o número de observações
(n) é par, segue que Md 
GABARICO: B
COMENTÁRIO:
I. Falsa.
Morrem,
por
ano,
mais
de
0,26  13000  3.380 pedestres em acidentes de
trânsito.
II. Falsa. Não foi informado o número total de jovens
entre 10 e 14 anos.
0,77  76%  58,52%
III. Verdadeira.
dos
atropelamentos aconteceram em lugares onde não
havia facilidades para pedestres.
IV. Verdadeira. 0,18  26%  4,68% das vítimas fatais
de trânsito são pedestres atropelados em
interseções.
QUESTÃO 62
GABARITO: A
COMENTÁRIO: [A]
Considere a tabela abaixo.
 xi  fi
212952  246875
 229 913,5.
2
QUESTÃO 61
GABARITO: C
COMENTÁRIO:
Média =
181419, 181796, 204804, 209425, 212952, 246875,
255415, 290415, 298041, 305088.
A mediana (Ma) é a média aritmética dos dois termos
centrais da sequência acima.
22
 2.
2
QUESTÃO 60
GABARITO: B
COMENTÁRIO: Colocando os dados em ordem
crescente, temos:
www.contatomaceio.com.br
GABARITO: D
COMENTÁRIO:
Supondo que a média percentual pedida refere-se
apenas aos estudantes das capitais onde o abuso é
mais frequente, vem
35,6  35,3  35,2  33,3  32,6  32,2  31,6  31,4  31,2  30,8  30,8
11
360

 32,73.
11
Portanto, a alternativa que apresenta o valor mais
próximo da média é a [D].
Observação: Considerando apenas 10 capitais no
cálculo da média, teríamos
35,6  35,3  35,2  33,3  32,6  32,2  31,6  31,4  31,2  30,8
10
329,2

 32,92.
10
Aparentemente, essa foi a interpretação do
examinador. Porém, o gráfico apresenta exatamente
11 capitais.
QUESTÃO 63
GABARITO: C
COMENTÁRIO: O número de usuários da banda larga
em 2007 era de 0,3  7,7  8 milhões. Logo, como
0,3
 100%  3,75%  4%, segue que menos de 4%
8
dos usuários da banda larga usavam a banda larga
móvel em 2007.
9
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 64
QUESTÃO 68
GABARITO: A
COMENTÁRIO:
GABARITO: D
COMENTÁRIO:
17  8  30  21  7  x 83  x

(média aritmética)
6
6
x  17
(mediana)
2
83  x x  17

 1  x  13
6
2
83  13
Logo, a média será:
 16
6
QUESTÃO 65
GABARITO: C
COMENTÁRIO:
QUESTÃO 69
GABARITO: C
COMENTÁRIO:
Considerando o ponto médio de cada intervalo salarial e
ponderando-se pelos respectivos pesos, temos que o salário médio
dos empregados, em reais, é:
QUESTÃO 70
GABARITO: E
COMENTÁRIO:
QUESTÃO 66
QUESTÃO 71
GABARITO: D
COMENTÁRIO:
A moda é o termo que mais aparece na sequência, que
nesse caso vale R$ 49,00, representada pelos meses
janeiro, fevereiro e abril de 2012. Para determinar a
mediana, temos que colocar a sequência em ordem
crescente; sendo assim, temos: set/11; mai/11;
ago/11; abr/11; jul/11; out/11; nov/11; dez/11; jan/12;
fev/12; abr/12; mar/12; jun/11.
A mediana de uma sequência de termos ímpares é
representada pelo termo central da sequência que
nesse caso é o mês de nov/11.
GABARITO: E
COMENTÁRIO:
8.0 + 3.50 + 7.100 + 14.150 + 5.200 + 20.250 + 3.300
0 + 150 + 700 + 2100 + 1000 + 5000 + 900
9850 pessoas
QUESTÃO 67
GABARITO: C
COMENTÁRIO:
QUESTÃO 72
GABARITO: B
COMENTÁRIO:
Quantidade de alunos com idade menor ou igual a 18
anos = 12
Quantidade total de alunos = 20
Número de elementos do evento 12
P

 60%
Espaço amostral
20
QUESTÃO 73
GABARITO: C
COMENTÁRIO: Queremos calcular a probabilidade
condicional de que a peça defeituosa tenha sido da
máquina M, ou seja, P(M | defeituosa) 
10
60
1
 .
120  60 3
www.contatomaceio.com.br
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 74
P(E | I ) 
GABARITO: A
COMENTÁRIO: O número total de assentos é igual a
(9  12  13)  6  2  8  220. Além disso, o número de
assentos em que o passageiro sente-se desconfortável
é (9  12  13)  2  68.
Portanto, a probabilidade do passageiro ser sorteado
com uma poltrona entre duas pessoas é mais
aproximada de
68
 100%  31%.
220
n(E  I )
n( I )

n(E  I)
n(E  I)  n(I  E)
300

300  300
1

2.
QUESTÃO 77
QUESTÃO 75
GABARITO: A
COMENTÁRIO:
Sejam U, I e E, respectivamente, o conjunto universo,
o conjunto dos alunos que falam inglês e o conjunto
dos alunos que falam espanhol.
Queremos calcular P(E | I ).
Sabendo que n(U)  1200, n(I)  600, n(E)  500 e
GABARITO: D
COMENTÁRIO:
Considere a figura.
n(I  E)  300, temos
n(I E)  n(U)  n(I  E)  1200  300  900.
Além disso, pelo Princípio da Inclusão-Exclusão,
obtemos
n(I E)  n(I)  n(E)  n(I E)  900  600  500  n(I E)
 n(I E)  200.
Portanto,
300 1

600 2
A região indicada é a que João tem a menor
probabilidade de acertar. Nessa região ele ganha 4
prêmios.
QUESTÃO 78
QUESTÃO 76
GABARITO: B
COMENTÁRIO:
A probabilidade de um parafuso escolhido ao acaso ser
defeituoso é dada por
P  P(A e defeituoso)  P(B e defeituoso)
54
25
54  38


 1 

100 1000  100  1000
3,098

.
100

Daí, como
2
3,098
4


,
100
100
100
segue-se que o
desempenho conjunto dessas máquinas pode ser
classificado como Bom.
www.contatomaceio.com.br
GABARITO: E
COMENTÁRIO:
P = 100 – 0,09 = 0,91 = 91%.
QUESTÃO 79
GABARITO: D
COMENTÁRIO:
Resultados que darão a vitória a José: {(1,6), (2,5),
(3,4), (4,3), (5,2), (6,1)}.
Resultados que darão a vitória a Paulo: {(1.3), (2,2),
(3,1)}.
Resultados que darão a vitória a Antônio: {(2,6), (3,5),
(4,4), (5,3), (6,2)}.
Resposta: José, já que há 6 possibilidades para formar
sua soma, 5 possibilidades para formar a soma de
Antônio e apenas 3 possibilidades para formar a soma
de Paulo.
11
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 80
QUESTÃO 83
GABARITO: D
COMENTÁRIO:
GABARITO: C
COMENTÁRIO:
Considere o diagrama abaixo.
P=
10 5

14 7
QUESTÃO 81
GABARITO: D
COMENTÁRIO:
Probabilidade de congestionamento =
probabilidade de não haver congestionamento
1
–
Queremos calcular a probabilidade condicional:
P(saudável | negativo) 
n(saudável  negativo)
.
n(negativo)
Portanto, de acordo com o diagrama, temos que
380
380  40
19

21.
P(saudável | negativo) 
E1E3 =1-0,2.0,5 = 0,9
E1E4 = 1 -0,2.0,7 = 0,86
E2E5 = 1 – 0,3.0,6 = 0,82 (menor probabilidade)
E2E5 = 1 – 0,3.0,4 = 0,88
O trajeto E2E4 não existe.
QUESTÃO 82
GABARITO: D
COMENTÁRIO:
De acordo com os dados da tabela, obtemos o seguinte
diagrama.
QUESTÃO 84
GABARITO: C
COMENTÁRIO:
Urna 1 e bola branca ou urna 2 e bola vermelha =
1 2 1 1 1 1
9
     
2 5 2 2 5 4 20
QUESTÃO 85
GABARITO: B
COMENTÁRIO:
Probabilidade de uma unidade defeituosa não
apresentar defeito: 1 – 0,8 = 0,2.
Probabilidade de uma unidade defeituosa não ser
detectada por nenhum inspetor.
0,2  0,2  0,2 = 0,008.
Probabilidade de uma unidade defeituosa ser
detectada por pelo menos um inspetor.
1 – 0,008 = 0,992.
Portanto, a probabilidade de um estudante
selecionado ao acaso preferir apenas MPB é dada por
110
 100%  11%.
1000
12
www.contatomaceio.com.br
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 86
Logo,
a
variância
pedida
será
dada
por:
2
 1

 2 saca 
1
2

   saca / hect  .
4
 hectare 


GABARITO: D
COMENTÁRIO:
QUESTÃO 90
A probabilidade de se escolher uma pessoa que fala
Português é:
P
GABARITO: E
COMENTÁRIO:
O
resultado
0,14x  0,03x  0,6x
 0,77  77% .
x
é
dado
por
MATEMÁTICA V
QUESTÃO 91
QUESTÃO 87
GABARITO: B
COMENTÁRIO:
Número de escolhas para os dois passageiros faltosos:
C22,2 
pedido
(0,7  0,15)  400000  340.000.
22!
 231.
2!.20!
Probabilidade de comparecerem exatamente 20
passageiros: P = 231  (0,9)20  (0,1)2 (20 compareçam e
2 faltaram).
Portanto, a resposta correta é a alternativa [B].
GABARITO: C
COMENTÁRIO:
2
3
C  2C
28C 1 28
3
5

 
3C
15 3C 45
QUESTÃO 92
GABARITO: D
COMENTÁRIO:
7
2 4
3 12
. 1210 +   1210   . 1210 + x = 1210
5 11
8 55
11
x = 165 km
QUESTÃO 88
GABARITO: D
COMENTÁRIO:
Considere a tabela abaixo, em que e j é o índice de
eficiência descrito no enunciado.
GABARITO: C
COMENTÁRIO:
1
1
1


t t  9 20
2
Tj  Pj
Vj
Tj
Pj
Ij
ej 
Malhada
Mamona
Maravilha
Mateira
Mimosa
360
310
260
310
270
12,0
11,0
14,0
13,0
12,0
15
12
12
13
11
288,0
284,2
303,3
310,0
294,5
t – 49t + 180 = 0
t = 45 h
Ij
Por conseguinte, a vaca que apresentou o melhor
índice de eficiência foi a Mateira.
QUESTÃO 94
GABARITO: E
COMENTÁRIO:
8
1
1


34  105 4,25 425000
QUESTÃO 95
GABARITO: A
5
1760  F1
7
8
COMENTÁRIO: 
2 440  3 F
8 1
QUESTÃO 89
RESPOSTA: E
Desvio padrão =
QUESTÃO 93
F1 = 320 litros
90 kg
30000 m 2
1
saca
30 kg

 2
.
10000 m2 hectare
www.contatomaceio.com.br
13
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 96
GABARITO: A
COMENTÁRIO:
x: valor inicial de cada uma das n parcelas.
x . n = (x + 60)(n – 3)
20n – x = 60 *
x . n = (x + 125)(n – 5)
25n – x = 125 **
Resolvendo o sistema entre as equações * e **, temos n = 13
Das 24 latas, 8 são não recicladas e 16 recicladas
1 = 0,05 . y
y = 20 (unidades de energia necessárias para a produção de
cada lata não reciclada)
Logo, 8 . 20 + 16 . 1 = 176 unidades de energia
QUESTÃO 102
GABARITO: D
COMENTÁRIO: 0,475x = 20 + 0,36(x – 30)
x = 80
QUESTÃO 97
GABARITO: E
COMENTÁRIO:
Gasolina:
= 11 km/L
11 km – R$ 2,20
1 km
– x
x = R$ 0,20
Álcool:
= 7 km/L
7 km – y
1 km – R$ 0,20
y = R$ 1,40
QUESTÃO 98
GABARITO: B
COMENTÁRIO:
15  12000
 10
12000  x
QUESTÃO 103
GABARITO: A
COMENTÁRIO: 0,1 . x = 0,5
x = 5 kg
QUESTÃO 104
GABARITO: B
COMENTÁRIO:
x: renda per capta (R$)
y: PIB (R$)
z: população
x = y/z
z = y/x
z = 1,564y/1,36x
z = 1,15y/x (aumento de 15% na população)
x = 6000 L
QUESTÃO 105
QUESTÃO 99
GABARITO: C
COMENTÁRIO:
Sendo C o capital empregado, temos:
0,7 ⋅ C + 0,2 ⋅ 0,3 ⋅ C = 3 800,00 ∴ C = 5 000,00
GABARITO: D
COMENTÁRIO:
8000  7200
= R$ 3200,00
18000
6000  7200
y=
= R$ 2400,00
18000
4000  7200
z=
= R$ 1600,00
18000
x=
QUESTÃO 100
GABARITO: D
COMENTÁRIO: O valor comercial, em reais, de álcool
produzido diariamente por um corta-cana é: 8 . 100 . 1,20 =
960.
O valor diário, em reais, que um corta-cana recebe, em
média, é: 2,50 . 8 = 20. Assim, um corta-cana precisaria
trabalhar 960/20 = 48 dias, para comprar todo o álcool
produzido por ele diariamente.
QUESTÃO 101
GABARITO: E
COMENTÁRIO:
o
x: n de latas não recicladas
1/3 = x/24
x=8
14
QUESTÃO 106
GABARITO: D
COMENTÁRIO:
Valor a ser aplicado: R$ 500,00
• poupança → 500 ⋅ (1,0056) = 502,80. O imposto é zero.
• Rendimento total: R$ 502,80
• CDB → 500 ⋅ (1,00876) = 504,38. O imposto é igual a
4,38 ⋅ 0,04 = 0,17.
Rendimento total: 504,38 – 0,17 = 504,21
Assim, a aplicação mais vantajosa é o CDB.
QUESTÃO 107
GABARITO: C
COMENTÁRIO:
12
A: M = C(1 + 0,03) = 1,426C (maior rentabilidade)
B: M = C(1 + 0,36) = 1,36C
2
C: M = C(1 + 0,18) = 1,3924
www.contatomaceio.com.br
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 108
QUESTÃO 112
GABARITO: C
COMENTÁRIO:
Montante em 3 meses:
3
M = 20000(1 + 0,02) = R$ 21224,16
GABARITO: B
COMENTÁRIO:
QUESTÃO 109
2
2
2
AC = 200 + 320 – 2 . 200 . 320.cos 60° 
2
1
AC = 40.000 + 102.400 – 2. 64000 . 
2
2
GABARITO: B
COMENTÁRIO:
1,2x (preço de venda da calça)
2
2
AC = 142.400 – 64000  AC = 78400  AC = 784 x
100
AC = 280m
x
(preço de venda da camisa)
3
x
1,3 . (preço de venda da saia)
2
x
x
2(1,2x + 1,4 . + 1,3 . ) 0,9 = 4,17x
3
2
1,4 .
B
Angulo alterno interno
60°
60°
QUESTÃO 110
320m
GABARITO: C
COMENTÁRIO:
x = (44000 – x)1,2
x = R$ 24000,00
A
MATEMÁTICA VI
C
QUESTÃO 111
GABARITO: D
COMENTÁRIO: Dados:
- Lados paralelos e simétricos
- Ângulo central – Giros curtos
Ângulo interno – pequeno.
a)
Não possui lados paralelos.
b)
Lados paralelos
- Ângulo central = 90°
- Ângulo interno = 90°
c)
Não possui lados paralelos.
d)
Lados paralelos
- Ângulo central = 60°
- Ângulo interno = 120°
e)
Lados paralelos – Ângulo central = 45°
Ângulo interno = 135°
Observamos que o hexágono regular possui melhores
características para o problema, pois o octógono regular é
mais redondo que o hexágono
www.contatomaceio.com.br
QUESTÃO 113
GABARITO: C
COMENTÁRIO:
DADOS:
Triângulo de lados 3, 4, 5. (Triângulo retângulo)
RESOLUÇÃO: Devemos verificar se o triângulo formado é
semelhante ao triângulo retângulo (3, 4 e 5)
a) 23,20 e 15  Não são proporcionais a 5, 4 e 3.
b) 60cm; 40cm e 30cm  Não são proporcionais a 5, 4, e
3.
c) 1m; 0,8m e 0,6m é proporcional a 5, 4 e 3, verificamos
melhor colocando-os em cm: 100cm; 80cm e 60cm.
d) 5m; 4m e 2m  Não são proporcionais a 5, 4 e 3
e) 3,5m; 3m e 1m  Não são proporcionais a 5, 4 e 3
QUESTÃO 114
GABARITO: B
COMENTÁRIO:
2
DADOS: A = 19.000.000 km
2
2
6
2
RESOLUÇÃO: R = 19000000  3,14R = 19.10  R =
6
19
. 10 
3,14
3
R=
3
6,05 . 10  R = 2,45 x 10  R = 2450km
15
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 115
Figura
GABARITO: A
COMENTÁRIO:
1m
4m
1m
3m
10km
A
B
10km
1m
1m
10km
C
6m
A
10km
3
1m - 200
B
2
18m - x
x = R$ 3600,00
10km
A
10km
C
B
V1 
Vprima  Vcilindro
2

6  4  3    22  3 72  3  12 72  36


 18
2
2
2
10km
QUESTÃO 118
D
A
10km
C
GABARITO: A
COMENTÁRIO:
B
10km
A
IMPERMEABILIZAR
D
I
B
I
base
2
2
I
A = 6 +   A = 7  A = 7.3,14  A = 21,98 m
QUESTÃO 116
I
I
I
2
I
2
GABARITO: D
COMENTÁRIO:
1 rolo  10m
Quantidade de rolos:
B
DADOS:
L
2
.h + R
A = 2Rh + R  A = 2.1.3 + .1 
A
10km
= A + A  A = (2P)
M
n rolos  21,98m2
Custo: 2,198 x 20 = R$ 43,96
N
40
120
A
e
75
50
 n = 2,198 rolos
QUESTÃO 119
30
C
p
BCD
D
Q
85
P
50  120  130
 150 (p = semiperímetro)
2
=A
+A

=
A
ABC
ABCD
A
130
ABCD
A
ABCD
BCD
40  30
 150(150  50)(150  130)(150  120)
2
= 600 + 150  100  20  30 = 600 + 10  10  150 x 6
GABARITO: D
COMENTÁRIO:
DADOS:
V
caixa
3
3
= 512 L = 512 dm = 512.000 cm
Resolução:
=
128 L
= 600 + 100  30 = 3600
A
= 85 x 75 = 6.375
80 cm
MNPQ
A=A
MNPQ
–A
ABCD
80 cm
= 6.375 – 3600 = 2.775
3
V
QUESTÃO 117
GABARITO: C
COMENTÁRIO: Na figura temos a metade do volume da
diferença entre um prisma e um cilindro.
16
caixa
V
= 512.000  a = 512.000  a = 80 cm
retirado
2
3
= 128 L = 128.000 cm 
80 .h = 128.000  h = 20 cm
www.contatomaceio.com.br
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 120
GABARITO: E
COMENTÁRIO:
Caixa 1: Q = 4.12 + 2.4 + 2.3 = 48 + 8 + 6  Q
fita
Caixa 2: Q
Caixa 3: Q
fita
fita
fita
= 2.12 + 4.4 + 2.3 = 24 + 16 + 6  Q
= 2.12 + 2.4 + 4.3 = 24 + 8 + 12  Q
= 62 cm
fita
fita
= 46 cm
= 44 cm
Resolução:
V =V –V 
A
QUESTÃO 121
GABARITO: D
COMENTÁRIO:
TEOREMA 1: Toda seção paralela à base de um cone forma
um outro cone semelhante ao primeiro.
TEOREMA 2: A razão entre o volume de sólidos semelhantes
é igual ao cubo da razão de semelhança.
2
1
V =V–V –V 
A
1
1
V = V – 2V
A
1
1
1
15
VA   122  15  2   62   VA  144.5  36.5  VA  540cm3
3
3
2
QUESTÃO 124
GABARITO: E
COMENTÁRIO:
A (0;0), B (50;0), C (60;30) e D (30;60)
E (x;y)  estação transmissora
d =d ;d =d
EA
EB
EC
ED
V = Volume do cone menor
(I) dEA  dEB  (x  0)2  (y  0)2  (x  50)2  (y  0)2 
V = Volume do tronco
x2  y2  x2  100y  2500  y2  x  25
V = Volume do cone
(II)dEC  dED  (x  60)2  (y  30)2  (x  30)2  (y  60)2 
1
2
3
V1
V1
1 V 1
V
 10 
  
  1   V1 
V1  V2  20 
V1  V2 8
V 8
8
QUESTÃO 122
GABARITO: A
COMENTÁRIO:
Vesfera
Vcone 
 2Vcone  Vesfera
2
1
4 R3
h
2    R2  h 
 h  2R   2
3
3
R
QUESTÃO 123
GABARITO: C
COMENTÁRIO:
(25  60)2  (y  30)2  (25  30)2  (y  60)2 
1225  y2  60y  900  25  y2  120y  3600 
60y  1500  y  25
Logo: E (25; 25)
QUESTÃO 125
GABARITO: A
COMENTÁRIO:
Pela condição dada, temos:
Equação da reta que passa por “A” e “B” é paralela a reta do
rio (r):
r: 4x – 3y – 13 = 0
Logo, a distância entre duas retas paralelas distintas é dada
tomando-se um ponto da primeira reta ( ) e aplicando a
distância deste à outra reta (r)
A(1; 2)  AB , então dAr = dABr , com isso teremos:
A(1; 2) e (r): 4x – 3y – 13 = 0
| 4.1  3.2  13 | | 2  13 | | 15 | 15
dAr 



3
5
16  9
25
42  (3)2
QUESTÃO 126
12
V = Volume da pirâmide menor
1
V = Volume do Tronco
GABARITO: D
COMENTÁRIO:
Pela condição dada, temos:
Sendo P(1, 5) e Q(3, 1) pontos da circunferência é
diametralmente opostos, temos:
2
V = Volume do artefato
A
V= Volume da pirâmide maior
www.contatomaceio.com.br
17
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 129
GABARITO: C
COMENTÁRIO:
2
A  6m  tomada  1
Cálculo do raio
2
R  dCQ  (3  2)2  (1  3)2  12   2  5
2
Equação reduzida:
(x – a) + (y – b) = R  (x – 2) + (y – 3) =
2
2
2
2
2
 5
2

Equação geral:
2
2
2
2
x – 4x + 4 + y – 6y + 9 = 5  x + y – 4x – 6y + 8 = 0
QUESTÕES COMPLEMENTARES
QUESTÃO 127
GABARITO: D
COMENTÁRIO:
Dados:
1m de linha  10 cm de contorno
1 agasalho  R$ 0, 05x (10 cm de linha) + 2, 50
A > 6m  1 tomada por 5m em fração de perímetro
espaçados uniformemente.
RESOLUÇÃO:
2
AD = 3x 2, 8 = 8, 4m
(2P)D = 3 + 2, 8 + 3 + 2, 8 = 11, 6m
Logo, precisaremos de 3 tomadas.
QUESTÃO 130
GABARITO: C
COMENTÁRIO:
Dados: Escala  1:10 (cada comprimento da casa de boneca
é 1/10 do real)
RESOLUÇÃO:
1  l1  1cm  (2P)1  3cm  3.(2p)1  9cmde bordado
2  l2  2cm  (2P)2  6cm  3.(2p)2  18cmde bordado
Total bordado por agasalho = 27 cm
1m de linha --- 10 cm de bordado
x
--- 27 cm de bordado
RESOLUÇÃO:
1
X  .14  X  1, 4m
10
 x = 2,7m de linha
A
y
2
1
.25  y  2, 5m
10
= 1, 5 x 2, 5 = 3, 5m
terreo
R$ 0, 05 --- 10 com de linha
x --- 270 com de linha
QUESTÃO 131
 y = R$ 1,35
Valor por agasalho  R$ 1,35 + R$ 2, 50  R$ 3, 85
Serão 50 agasalhos, logo 50 x 3, 85  R$ 192, 50
GABARITO: B
COMENTÁRIO:
2
Custo = R$ 0, 10/100cm
Valor da venda é proporcional ao volume.
QUESTÃO 128
GABARITO: B
COMENTÁRIO:
Sejam n e n , respectivamente, o número de voltas da
A
B
engrenagem maior e o número de voltas da engrenagem
menor. Desse modo, se r e r são os raios dessas
A
B
engrenagens, então
nA  2π  rA  nB  2π  rB  375  rA  1000  rB
8
 rA   rB .
3
Portanto,
8
 r  r  11
3 B B
 rB  3cm.
rA  rB  11 
18
RESOLUÇÃO:
Embalagem 1:
2
Área: 2Ab + AL = 2 . 7 . 7 + 4 . 7 . 10  Área = 378cm
3
Volume= Ab. h = 7 . 7 . 10 = 490cm
Embalagem 2:
2
Área: 2Ab + AL = 2 .  . 4 + 2 .  . 4 . 10  Área = 100, 48 +
2
251, 2 = 351, 68cm
2
3
Volume= Ab. h =  . 4 . 10 = 160 x 3, 14 = 502, 4cm
www.contatomaceio.com.br
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 132
GABARITO: A
COMENTÁRIO
acubo = 3 dm = 30 cm
Rvela = 3 cm, hvela = 7,4 cm e  = 3
RESOLUÇÃO:
3
3
3
Vparafina = a = 30 = 27.000cm
2
2
3
Vvela = .R .h  Vvela = 3.3 .7,4  Vvela = 27x7,4 cm .
Vparafina 27.000 1.000
Número de velas =


 135
Vvela
27x7,4
7,4
QUESTÃO 133
QUESTÃO 137
GABARITO: D
COMENTÁRIO:
3
R = 4 cm, h = 10 cm, mpeixe = 90%mrecheio, dsalmão = 0,35 g/cm
e=3
RESOLUÇÃO:
1
Vrecheio   π  42  10  160cm3
3
Considerando que o peixe representa 90% do volume do
3
recheio, temos: 0,9.160 = 144cm (volume do salmão).
Portanto, a massa do salmão será dada por 0,35.144 = 50,4g.
GABARITO: E
COMENTÁRIO:
QUESTÃO 134
GABARITO: A
COMENTÁRIO:
Rsemiesfera = 4 cm, Rcone = hcone = 4 cm e Vareia = 25%Vampulheta
RESOLUÇÃO:
Vareia = 25%Vampulheta  Vareia = 0,25(Vsemiesfera + Vcone) 
V
areia
= 0,25   1  4π  43  1  π  42  4  1  64π  16π cm3 .
2
3
3

4
QUESTÃO 135
GABARITO: A
COMENTÁRIO:
 com uma rolha na forma de cilindro, é possível vedar
garrafas com aberturas do tipo1 e do tipo 2.
 com uma rolha na forma de cone, é possível vedar
garrafas com abertura do tipo 1.
 dos formatos de rolha sugeridos existe, pelo menos, um
que não consegue vedar garrafas com abertura do tipo
2.

somente a rolha na forma de esfera pode vedar
garrafas do tipo 2.
 com uma rolha na forma de cone, é possível vedar
apenas garrafas com abertura do tipo 3.
QUESTÃO 136
GABARITO: D
COMENTÁRIO:
2
2
2
2
x = 10 + 30  x = 100 + 900  x = 10 10
www.contatomaceio.com.br
Aplicando o teorema de Pitágoras:
2
2
2
AB = 3 + 4  AB = 5
Observamos, no gráfico, que na ordenada y = –5 o agente
secreto não chega ao chão e, para x = 3, ele alcança C, o
topo do prédio.
QUESTÃO 138
GABARITO: E
COMENTÁRIO:
P(4,3) e r: 3x + 4y + 6 = 0
RESOLUÇÃO:
Para que o morador percorra a menor distância possível
deveremos calcular a distância do ponto P(4,3) à reta r: 3x +
4y + 6 = 0.
Com isso, basta lembrarmos que:
Ax0  By0  C
dPr 
a 2  b2
Substituindo, temos:
3.4  4.3  6 12  12  6
30
dpr 


 6km
9  16
25
32  42
19
MATEMÁTICA E SUAS TECNOLOGIAS
QUESTÃO 139
GABARITO: D
COMENTÁRIO:
2
2
Circunferência: x + y + 6x – 4y – 12 = 0.
Bancas de revista: A (1, 6); B (1, 1) e C (1, 5).
RESOLUÇÃO:
Para verificarmos a posição relativa de um ponto em relação
a uma circunferência, basta substituirmos o ponto na
equação da circunferência e observamos o resultado obtido,
classificando-o de acordo com a seguinte situação:
 0 (P está fora da circunferência)

xo2  yo2  Axo  Byo  C  0 (P pertence a circunferência)
,log o :
 0 (P está no interior da circunferência)

A(1, 6)  1 + 6 + 6.1 – 4.6 – 12 = 7 (A banca A está no
exterior da praça)
2
2
B(1, 1)  1 + 1 + 6.1 – 4.1 – 12 = -8 (A banca B está no
interior da praça)
2
2
C(1, 5)  1 + 5 + 6.1 – 4.5 – 12 = 0 (A banca C está no
limite da praça)
2
2
QUESTÃO 140
GABARITO: C
COMENTÁRIO:
6
1 UA = 150 x 10 km.
e = c/a  0,96 = c/a  c = 0,96a
distância mínima desse cometa ao Sol é igual a 0,58 UA, ou
seja, a – c = 0,58.
RESOLUÇÃO:
a – c = 0,58  a – 0,96a = 0,58  0,04a = 0,58 
a = 14,5 UA
a + c = a + 0,96a = 1,96a = 1,96x14,5 UA =1,96 x 14,5 x 150 x
6
6
10 = 4.263 x 10 km.
20
www.contatomaceio.com.br