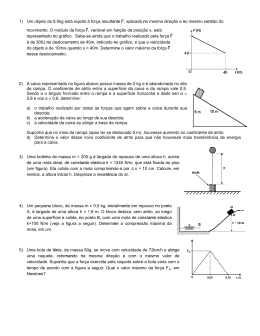
4- Movimento relativo
1– Um carro dirige-se de sul para norte numa estrada retilínea, com velocidade constante de
90 km h−1. Um camião aproxima-se em sentido contrário com velocidade constante de
100 km h−1. Determine:
1.1 – a velocidade do camião em relação ao carro;
−190 km h−1
1.2 – a velocidade do carro em relação ao camião.
190 km h−1
1.3 – De que forma variam as velocidades relativas após o camião e o carro se terem
cruzado?
não variam
2– A bússola de um avião indica que este desloca-se de sul para norte, e o seu indicador
de velocidade do ar regista uma velocidade de voo constante de valor 240 km h−1. A
velocidade do vento em relação ao solo é de 100 km h−1 no sentido de oeste para este.
Determine:
2.1 – o módulo da velocidade do avião em relação ao solo;
260 km h−1
2.2 – o ângulo que esta velocidade faz com a direção sul-norte;
23° NE
2.3 – em que direção deve o avião voar, de modo a que quando visto do solo siga na
direção sul-norte;
25° NO
2.4 – qual o novo valor da velocidade do avião em relação ao solo.
218 km h−1
3– O tapete rolante do terminal de um aeroporto mede 35 m de comprimento e move-se com
velocidade constante de 1.0 km h−1. Suponha uma pessoa numa das extremidades do tapete
rolante, e deslocando-se com velocidade constante de 1.5 km h−1 em relação ao tapete.
Determine quanto tempo leva à pessoa para alcançar a outra extremidade do tapete se esta
se move:
3.1 – no mesmo sentido do tapete;
50.4 s
3.2 – no sentido oposto ao tapete.
252 s
4– Duas pontes (A e B) sobre um rio distam 1500 m entre si, estando a ponte B a jusante da
ponte A. Dois amigos devem fazer um percurso desde a ponte A até à ponte B e regressar
à ponte A. Um deles vai de barco com velocidade constante de 4.0 km h−1 em relação à
água. O outro caminha pela margem do rio com velocidade constante de 4.0 km h−1. A
velocidade da água é igual a 2.8 km h−1 no sentido da ponte A para a B. Determine o tempo
que cada amigo demora a fazer o percurso de ida e volta.
5– Uma canoa navega com velocidade de 0.40 m s−1 em relação à Terra, no sentido NE. A
canoa desloca-se num rio que se escoa com velocidade de 0.50 m s−1 em relação à Terra,
no sentido E. Determine o módulo, a direção e o sentido da velocidade da canoa em relação
ao rio.
17
45 min
1 h 28 min
0.36 m s−1
38°. 2 ONO
5- Centro de massa
1– Três partículas, A, B e C, de massa 2.0 kg, 3.0 kg e 1.0 kg, respectivamente, ocupam inicialmente as posições indicadas na figura.
Num dado instante t, passam a mover-se em relação ao referencial Oxy com velocidades
~vA = 2.0êx + 4.0êy (m s−1 ), ~vB = −2.0êx (m s−1 )
e ~vC = 6.0êx − 2.0êy (m s−1 ). Determine:
1.1 – a posição inicial do centro de massa do sistema;
~rCM =(2.0 , 2.3) m
1.2 – para o instante t:
1.2.1 – a velocidade do centro de massa;
1.2.2 – o momento linear do sistema
~vCM =(0.67 , 1.0) m s−1
~psist =(4.0 , 6.0) kg m s−1
2– O bloco representado na figura é constituído por duas
porções, A e B, de materiais diferentes. Sabendo que
mA = mB , localize , relativamente ao sistema de eixos
representado na figura, o centro de massa do bloco.
~rCM =(3 , 8 , 1.5) cm
3– O João, de massa 50 kg, está sentado num barco, de massa 200 kg, que se encontra inicialmente em repouso. Num dado instante, desloca-se para a popa do barco, que dista 2.0 m da
posição em que se encontrava inicialmente. Desprezando a resistência da água e o efeito
do vento, calcule o afastamento do barco relativamente à margem.
d=0.4 m
4– Uma granada de massa m, lançada para cima com a velocidade de 100 m s−1, fazendo 60°
com a horizontal, explode quando atinge o ponto mais alto da trajectória, dividindo-se em
dois fragmentos de massas iguais. Um destes cai segundo a vertical (ver figura).
4.1 – A que distância do ponto de lançamento cai o segundo fragmento?
x2 =1305 m
4.2 – Que energia se liberta na explosão, expressa em percentagem da energia cinética
inicial?
25%
18
5– Um carro de massa 120 kg desloca-se sobre um carril, com velocidade constante, de valor
e sentido 3 êx (m s−1). Sobre ele e na sua parte traseira encontra-se um homem de massa
80 kg. Em determinado instante, o homem salta do carro, afastando-se dele com velocidade −0.5 êx (m s−1).
Determine a velocidade do carro após a saída de homem.
3.2 êx (m s−1 )
6– Um corpo de massa m = 0.20 kg, desloca-se num plano horizontal, sem atrito, com velocidade v = 10 m s−1. Pretende-se fazer para o corpo em 2.0 s, exercendo para o efeito uma
força horizontal.
6.1 – Represente o sistema de forças a que o corpo está sujeito.
6.2 – Indique onde estão aplicadas as forças, que constituem com cada uma das forças
referidas na alínea anterior, pares acção-reacção.
6.3 – Determine:
6.3.1 – a intensidade da força referida no texto;
6.3.2 – o espaço percorrido pelo corpo até parar.
7– Nas extremidades de uma jangada com 8 m de comprimento e 10 kg de massa, encontramse dois rapazes de massas 70 kg e 80 kg. Eles dirigem-se um para o outro, encontrando-se
a meio da jangada. Admitindo a inexistência de forças exteriores, determine quanto se
deslocou a jangada.
~
F=−1.0
êx N
∆x=10.0 m
0.25 m
8– Dois corpos de massas m1 = 3.0 kg e m2 = 1.0 kg deslocam-se no plano XOY com velocidades respectivamente iguais a ~v1 = 4 t êx e ~v2 = 3 t êx + 2 êy (SI). Calcule:
~vCM =(3.8 t , 0.5)
8.1 – a velocidade e a aceleração do centro de massa do sistema;
8.2 – as velocidades de cada um dos corpos em relação ao centro de massa;
8.3 – o momento linear do sistema em relação ao centro de massa.
~aCM =(3.8 , 0)
~v1,CM =(0.25 t , −0.50)
~v2,CM =(−0.75 t , 1.50)
9– Um rapaz de massa 40 kg encontra-se na extremidade de um barco de massa 120 kg e
comprimento 8 m, que flutua num lago.
Determine a distância percorrida pelo barco quando o rapaz se desloca até à outra extremidade.
19
2m
6- Leis de Newton e atrito
1– Um carro foi abandonado numa rampa com as rodas bloqueadas (isto é, estão impedidas
de rodar). O coeficiente de atrito estático entre a borracha dos pneus e o piso da rampa é
de 0.9.
Entre que valores pode variar a inclinação da rampa para que o carro não deslize?
0°≤ θ ≤ 42°
2– Os antigos egípcios moviam grandes blocos de pedra, arrastando-os, pelo deserto, sobre
tábuas. Admitir que o coeficiente de atrito cinético entre a areia e as tábuas é 0.3 e que
cada homem é capaz de exercer uma força de 500 N, numa direcção que faz 30° com a
horizontal.
Qual o número mínimo de homens que são necessários para arrastar um bloco de 700 t
numa superfície horizontal?
4134
3– Um bloco de massa m = 1.0 kg está apoiado numa superficíe horizontal, estando sujeito a
duas forças horizontais, F~ 1 e F~ 2 , de módulo respectivamente 6.0 N e 8.0 N. Caracterize a
aceleração do bloco nos seguintes casos:
3.1 – As forças têm a mesma linha de acção e o mesmo sentido;
~a=(14 , 0) m s−2
3.2 – As forças têm a mesma linha de acção e sentidos opostos;
~a=(2 , 0) m s−2
3.3 – As forças são perpendiculares entre si.
~a=(8 , 6) m s−2
4– Um automóvel de massa 900 kg puxa um atrelado de massa 100 kg. O motor do automóvel
desenvolve uma força de intensidade 2000 N. Determine:
4.1 – a intensidade da força de tensão do cabo que liga o atrelado ao automóvel;
200 N
4.2 – o módulo da aceleração do automóvel quando se move com o atrelado;
2 m s−2
4.3 – o módulo da aceleração do automóvel quando se move sem o atrelado;
2.2 m s−2
5– Um elevador vazio de massa 5000 kg está a mover-se verticalmente para baixo, com aceleração constante. Partindo do repouso, desloca-se 30 m em 10 s. Determine o módulo da
tensão no cabo que sustenta o elevalor.
47 000 N
6– Considere três corpos de massas mA = 10 kg, mB = 15 kg e mC = 20 kg, colocados sobre
uma superfície horizontal e ligados entre si por cabos. É aplicada sobre o corpo C uma
força F~ horizontal de intensidade 50 N. Supondo desprezável o atrito, determine:
6.1 – o módulo da aceleração do sistema;
A
6.2 – o módulo da tensão em cada cabo.
20
B
C
F~
a=1.1 m s−2
11 N ; 27.5 N
7– Sendo os esforços musculares forças interiores que não afectam o movimento do centro
de massa, explique porquê e como conseguimos caminhar numa superfície horizontal.
8– Um vagão, com velocidade de 72 km h−1, transporta três caixotes de pesos iguais a 5 kgf,
10 kgf e 15 kgf, afastados uns dos outros e assentes no plano horizontal. Se o vagão
for travado até parar numa distância de 100 m, qual ou quais dos caixotes irão deslizar,
sendoµe = 0.6?
nenhum
9– O rotor, existente em alguns parques de diversões, consiste
num cilindro com 4.0 m de diâmetro que roda em torno do
eixo, colocado verticalmente. Os passageiros encostam-se
às paredes laterais de lona e o cilindro roda. Sendo 0.40 o
coeficiente de atrito estático entre as roupas e a lona, qual a
velocidade angular mínima do cilindro para que os passageiros não caiam, mesmo que se retire a base?
ωmin =3.5 rad s−1
10– Com forças de igual intensidade (40 N) tenta-se arrastar, sobre uma superfície horizontal,
os blocos A e B.
Dados; µe = 0.10; µc = 0.05; sin θ = 0.80; cos θ = 0.60; mA = mB = 10 kg.
F~ θ
10.1 – Verifique se os blocos se movem ou não.
A
B
10.2 – Determine a aceleração de cada um dos blocos.
θ
F~
movem-se
aA =2.1 m s−2
aB =1.7 m s−2
11– Para que o movimento se torne iminente, quanto deverá valer
~ O coeficiente de atrito estático entre os blocos e os planos
F?
em que assentam é 0.25; mB = 2mA ; mB = 40 kg.
F=43 N
12– A força que acelera um automóvel numa estrada horizontal é o atrito (estático) entre o
asfalto e os pneus. Se o asfalto estiver seco, o coeficiente de atrito estático é 0.75; se
estiver molhado, é 0.50; se estiver coberto de gelo, é 0.25. Calcule a velocidade máxima
com que um automóvel pade fazer uma curva com segurança, em cada uma das condições
mencionadas, se a curva tiver 200 m de raio.
13– Num lanço defeituoso de uma estrada, o lado exterior da curva, de raio 200 m, é mais
baixo que o interior. Calcule a velocidade máxima com que um automóvel pode fazer a
curva com segurança. Dados: θ = 15°, µe = 0.60.
14– Uma caixa de 1.5 kgf, encostada a uma parede vertical, está em repouso sob a
~ Que força mínima F~ impedirá a caixa de cair?
acção de uma força F.
Dados: µe = 0.50 e µc = 0.30
vseco =139 km h−1
vmolhado =114 km h−1
vgelo =81 km h−1
36 km h−1
F~
30 N
21
15– Entre os livros A e B (mA = 2.0 kg; mB = 4.0 kg) há atrito (µe = 0.30 e µc = 0.20); entre B
e a mesa horizontal não há atrito.
15.1 – Que força máxima F~ se pode aplicar a B, sem que haja
deslizamento de A sobre B? Qual a aceleração do conjunto
nestas condições?
15.2 – Descreva o movimento dos livros no caso de F = 12 N e
no caso de F = 24 N.
F=18 N ; a=3 m s−2
A e B solidários
A desliza sobre B
16– Um bloco A de 3.0 kg assenta num bloco B de 5.0 kg e este, por sua vez, assenta num
plano horizontal. Os coeficientes de atrito, tanto estático como cinético, entre A e B e
entre B e o plano horizontal são iguais a 0.20. Aplica-se em B uma força F~ horizontal, de
tal modo que A fica na iminência de deslizar sobre B.
~ Que aceleração têm os blocos?
16.1 – Que valor tem F?
F=32 N ; a=2 m s−2
16.2 – Descreva o movimento dos blocos caso não houvesse atrito.
A em repouso
B em m.u.a.
17– Considere o sistema constituído pelos dois blocos A e B representado na figura. Dados: mB = 3mA ; mB = 40 kg; µe = 0.20;
µc = 0.10; sin θ = 0.60; cos θ = 0.80.
17.1 – Mostre que o sistema entra em movimento.
17.2 – Calcule a aceleração do sistema.
a=1.4 m s−2 ; A sobe
22
7- Conservação da energia
1– Um carrinho de 400 g move-se na calha, situada no plano vertical, representada na figura.
A parte circular tem 20 cm de raio.
E
1.1 – Que velocidade mínima deve ter o carrinho em A, para percorrer toda a calha?
vA =3.2 m s−1
F
1.2 – Nas condições de 1.1, qual a resultante em D? E qual a reacção
~vA
da calha em C?
1.3 – Que velocidade deve ter o carrinho em A para que no ponto E
a reacção da calha tenha a mesma intensidade que o peso?
A
D
60° C
B
Fres,D =13 N ; RC =18 N
G
v=3.5 m s−1
2– A parte circular da pista, que se situa num plano vertical, tem raio igual a 10 cm.
2.1 – De que altura mínima se deve deixar cair um carrinho
para que ele passe no ponto B? Um carrinho mais pesado
necessitaria de mais ou de menos altura?
h=0.25 m
2.2 – Nas condições de 2.1, que força exerce sobre a pista um
carrinho de 100 g, quando passa no ponto A?
F=1.5 N
3– Liga-se uma pedra a um fio de comprimento l e fixa-se a outra extremidade deste a um
ponto O.
3.1 – Calcule a velocidade mínima ~v0 que se deve imprimir à pedra para que:
3.1.1 – o fio atinja a posição horizontal;
3.1.2 – o conjunto realize uma volta completa.
v0 =
√
v0 =
√
2gl
5gl
3.2 – Descreva o movimento no caso de ~v0 estar compreendido entre os valores encontrados em 3.1.
3.3 – Se v0 for mais do que suficiente para dar a volta completa, mostre que a diferença
entre os módulos da tensão no ponto mais alto e no ponto mais baixo é 6 P, sendo P
o peso da pedra.
4– Do ponto A de uma calha AB, existente no plano vertical, deixa-se cair, sem velocidade
inicial, um corpo P. Este, ao chegar a B, passa a mover-se livremente sob a acção do
peso. As alturas de A e de B, medidas em relação ao ponto mais baixo da trajectória, são
hA = 1 m e hB = 0.2 m.
4.1 – Calcule hC .
hC =0.8 m
4.2 – Mostre que hC é sempre inferior a hA .
23
α
1.8 m
t voo
=2
h
s
5– Um operário, a trabalhar no telhado de uma casa, deixa cair
um martelo de massa igual a 750 g. Este escorrega sobre o
telhado de inclinação α com a horizontal e com um desnível
de 1.8 m. Dois segundos depois de perder o contacto com
o telhado alcança o solo, a uma distância de 6 m da vertical
de lançamento (da vertical que passa pela extremidade do
telhado). Determine, considerando g = 10 m s−2 e desprezando todas as forças dissipativas:
5.1 – o módulo da velocidade com que o martelo atinge a
base do telhado;
v=6 m s−1
5.2 – o valor do ângulo α;
α=60°
5.3 – a altura da extremidade do telhado relativamente ao
solo, sendo este horizontal.
6m
h=30.4 m
6– Uma força de 160 N estica 0.050 m uma certa mola a partir do seu estado de repouso.
Determine:
6.1 – a força necessária para esticar essa mola 0.015 m a partir do seu estado de repouso;
48 N
6.2 – a força necessária para comprimir essa mola 0.020 m a partir do seu estado de repouso;
64 N
6.3 – o trabalho necessário para esticar essa mola 0.015 m a partir do seu estado de repouso;
0.36 J
6.4 – o trabalho necessário para comprimir essa mola 0.020 m a partir do seu estado de
repouso.
0.64 J
7– Uma menina aplica uma força F~ paralela ao eixo Ox sobre um trenó de 10.0 kg que está
a deslocar-se sobre a superfície congelada de um lago. À medida que ela controla a velocidade do trenó, a componente F x da força que ela aplica varia com a coordenada x como
indica a figura ao lado. Determine o trabalho realizado pela força F~ quando o trenó se
desloca:
7.1 – de x = 0 a x = 8 m;
40 J
F x (N)
7.2 – de x = 8 a x = 12 m;
20 J
10
7.3 – de x = 0 a x = 12 m.
60 J
7.4 – Suponha que o trenó esteja inicialmente em repouso para x = 0 m. Despreze o atrito entre o
trenó e a superfície do lago. Use o teorema do
trabalho-energia para determinar a velocidade do
trenó em:
7.4.1 – x = 8 m;
7.4.2 – x = 12 m.
24
5
4
8
12 x(m)
√
8 m s−1
√
12 m s−1
8– Observe a figura: o fio OA, de comprimento 1.0 m, é colocado horizontalmente e a esfera,
de massa 2.0 kg, é largada sem velocidade inicial. Calcule:
√
8.1 – as velocidades em B e em C;
√
8.2 – os módulos das tensões em A, em B e em C;
0 N ; 30 N ; 60 N
8.3 – o módulo da resultante nos mesmos três pontos.
20 N ; 26 N ; 40 N
9– É necessário realizar um trabalho de 12.0 J para esticar 3.00 cm uma mola a partir do seu
comprimento de repouso (sem deformação). Determine o trabalho necessário para esticar
4.00 cm essa mola a partir do seu comprimento sem deformação.
10 m s−1 ;
21.3 J
10– Como parte de um exercício de treino, um atleta deita-se de costas e empurra com os pés
uma plataforma ligada a duas molas duras dispostas de modo a ficarem paralelas. Quando
o atleta empurra a plataforma comprime ambas as molas de igual forma. Sabendo que o
atleta realiza 80.0 J de trabalho para comprimir as molas 0.200 m a partir do seu estado de
repouso, determine:
10.1 – o módulo da força necessária para manter a plataforma nessa posição;
800 N
10.2 – a quantidade de trabalho adicional que o atleta precisa de realizar para comprimir
a plataforma mais 0.200 m;
240 J
10.3 – qual a força máxima que o atleta deve aplicar nessa situação.
1600 N
11– Suponha duas molas elásticas, A e B, de constantes de elasticidade KA e KB respectivamente, arranjadas em série (ver figura) e submetidas a uma força F. Determine:
11.1 – o alongamento da mola A;
KA
11.2 – o alongamento da mola B;
KB
F~
F/KA
F/KB
11.3 – o alongamento total;
∆xA +∆xB
11.4 – a constante de elasticidade de uma nova mola equivalente a este arranjo das molas
A e B.
Keq = K A+KB
K K
A
B
11.5 – Relacione este resultado com o funcionamento do complexo músculo-tendinoso.
12– Suponha duas molas elásticas, A e B, de constantes de elasticidade KA e KB respectivamente, arranjadas em paralelo (ver figura) submetidas a uma força F, de tal modo que o
deslocamento de ambas as molas seja o mesmo, i.e., ∆xA = ∆xB = ∆x. Determine:
KA
12.1 – a força a que está sujeita a mola A;
F~
12.2 – a força a que está sujeita a mola B;
12.3 – a força total a que estão sujeitas ambas as molas;
KB
12.4 – a constante de elasticidade de uma nova mola equivalente a este arranjo das molas
A e B.
12.5 – Relacione este resultado com o funcionamento do complexo músculo-tendinoso.
25
KA ∆x
KB ∆x
F=FA +FB
Keq =KA +KB
20 m s−1