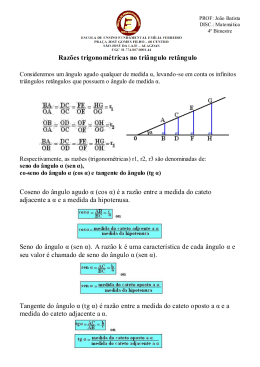
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
Caro aluno,
Esse material foi elaborado com o objetivo de ajudá-lo a selecionar argumentos
apresentados em solução de situação-problema do cotidiano, usando alguns conceitos
geométricos (Habilidade 13 de CNI/EM da Matriz de Referência para Avaliação).
Dessa forma é de extrema importância que você faça uma leitura atenta do material e
sempre que surgir uma pergunta tente respondê-la.
Você poderá fazê-la em casa ou aqui no Polo, mas é muito importante que você:
1. procure o Monitor sempre que tiver alguma dúvida;
2. faça toda a atividade com muito atenção, consultando os livros do Novo Telecurso e os
materiais disponíveis na sala de plantão ou indicados por seu Monitor (como a Biblioteca do
Polo e o Portal EJA – www.educacao.org.br/eja);
3. apresente a Atividade pronta ao Monitor até o dia ____/____/____
Bons estudos!
Página 1
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
O que é trigonometria?
Em princípio, Trigonometria é o estudo da relações entre as medidas de
ângulos e lados nos triângulos retângulos (trigono = triângulo e metria
= medida). A comprovada importância do triângulo – figura básica em
qualquer estudo de Geometria – justifica o grande interesse pelo assunto.
Existem, ainda, inúmeras situações em que a Trigonometria é de grande utilidade para
outros ramos da ciência, como a Engenharia, a Física, a Astronomia, etc.
Historicamente, a Trigonometria liga-se à Astronomia, tendo em vista a dificuldade natural
que esta apresenta com relação ao cálculo dessas distâncias impossíveis.
Antes de iniciarmos nosso estudo sobre Trigonometria, convém relembrarmos alguns
conceitos importantes. Todo triângulo retângulo, além do ângulo reto, possui dois ângulos
agudos cuja soma é 90º, completando, assim os 180º da soma dos ângulos internos.
Razões Trigonométricas
Catetos e Hipotenusa
Em um triângulo chamamos o lado oposto ao ângulo reto de hipotenusa e os lados
adjacentes de catetos.
Observe a figura:
Hipotenusa:
Catetos:
e
Página 2
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
Seno, Cosseno e Tangente
Considere um triângulo retângulo BAC:
Hipotenusa:
Catetos:
Ângulos:
,
e
.
Tomando por base os elementos desse triângulo, podemos definir as seguintes razões
trigonométricas:
Seno de um ângulo agudo é a razão entre a medida do cateto oposto a esse ângulo e
a medida da hipotenusa.
Assim:
Página 3
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
Cosseno de um ângulo agudo é a razão entre a medida do cateto adjacente a esse
ângulo e a medida da hipotenusa.
Assim:
Tangente de um ângulo agudo é a razão entre a medida do cateto oposto e a medida
do cateto adjacente a esse ângulo.
Assim:
Lembre-se: Na linguagem comum, cateto oposto, é o cateto que está de frente para o
ângulo, e cateto adjacente, é o cateto que fica ao lado do ângulo.
Página 4
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
Exemplo:
1) Uma escada apoiada em uma parede, num ponto distante 4 m do solo, forma com
essa parede um ângulo de 60°. Qual é o comprimento da escada em metros?
(cos 60º = )
Solução:
Cos 60º = Cateto Adjacente
Hipotenusa
Página 5
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
Agora vamos pensar:
1) Para calcular a altura de um prédio, o topógrafo colocou seu teodolito na praça em
frente. Ele mediu a distância do prédio ao teodolito com uma trena e encontrou 27m.
Mirando o alto do prédio, ele verificou, na escala do teodolito, que o ângulo formado
por essa linha visual com a horizontal é de 58º. Se a luneta do teodolito está a 1,7m
do chão, qual é a altura do prédio? (Considere tg 58º = 1,6).
2) Dado o triângulo retângulo ARE , reto em R.
Sabe-se que o ângulo RÂE mede 60º, se AR = 5cm, então a hipotenusa mede, em cm:
(Considere cos 60º = 0,5)
a)
b)
c)
d)
e)
2,5
5
10
15
1
Página 6
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
3) Para determinar a altura de uma torre, um topógrafo coloca um teodolito a 100m de
sua base e obtém um ângulo de 30º, conforme ilustra a figura. Sabendo que a luneta
do teodolito está a 1,70m do chão, qual é a altura aproximada da torre? (tg 30º =
0,58)
4) Um avião levanta vôo e sobe fazendo um ângulo de 15º com a horizontal. A que
altura ele estará e qual a distância percorrida quanto sobrevoar uma torre a 2 Km do
ponto de partida? (tg 15º = 0,268 e cos 15º = 0966
5) (AAP) Um arame de 18 metros de comprimento é esticado do nível do solo (suposto
horizontal) ao topo de um poste vertical. Sabendo que o ângulo formado pelo arame
com o solo é de 30º, calcule a altura do poste. (Adote sen 30º = 0,5)
a) 18m.
b) 36m.
c) 9m.
d) 4,5m.
e) Nenhuma.
Página 7
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
6) Um topógrafo foi chamado para obter a altura de um edifício. Para fazer isto, ele colocou
um teodolito (instrumento ótico para medir ângulos) a 200 metros do edifício e mediu
um ângulo de 30°, como indicado na figura a seguir. Sabendo que a luneta do teodolito
está a 1,5 metros do solo, pode-se concluir que, dentre os valores adiante, o que
MELHOR aproxima a altura do edifício, em metros, é: Use os valores: sen 30° = 0,5 , cos
30° = 0,866 e t g 30° = 0,577
a)
b)
c)
d)
e)
112
115
117
120
124
7) Um alpinista deseja calcular a altura de uma encosta que vai escalar. Para isso, afasta-se,
horizontalmente, 80 m do pé da encosta e visualiza o topo sob um ângulo de 55º com o
plano horizontal. Calcule a altura da encosta. (Dados: sen 55º = 0,81, cos 55º = 0,57 e tg
55º = 1,42)
Página 8
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
BIBLIOGRAFIA:
Gelson Iezzi, Osvaldo Dolce, David Mauro Degenszajn, Roberto Périgo.
Matemática Volume Único – Atual Editora
http://www.somatematica.com.br/fundam/raztrig/razoes.php
http://www.profcardy.com/exercicios/area.php?area=TRIGONOMETRIA
http://www.cnsd.g12.br/download/1anoem_mat1.pdf?rnd=7416
http://www.mundovestibular.com.br/articles/5923/1/Exercicios-deTrigonometria/Paacutegina1.html
Página 9
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
Gabarito Comentado
1. O que se pede para ser calculado é a altura do prédio para isso usaremos tg =
1,6 =
1,6 . 27 = x
43,2 = x
43,2 + 1,7 = 44,9m
2. Resposta C
Cos =
0,5 =
0,5x = 5
X=
X = 10
3. Resposta C
Página 10
E.E.F.M.E.P.J.A.EMBAIXADOR ASSIS CHATEAUBRIAND
Polo Bradesco – Educação a Distância
DESENVOLVENDO HABILIDADES – CIÊNCIAS DA NATUREZA I - EM
4.
5. Resposta C
Sen 30º =
0,5 =
0,5 . 18 = x
x=9m
6. tg =
0,577 =
5,577 . 200 = x
115,4 = x
115,4 + 1,5 = 116,9m – alternativa C
7. tg =
1,42 =
1,42 . 80 = x
x = 113,6m
Página 11