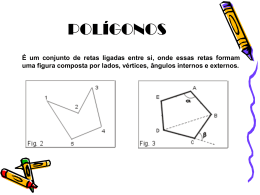
Unidade didáctica:
circunferência e
polígonos
Matemática – 9º ano
POLÍGONOS. Ângulos de um polígono
DEFINIÇÃO:
Um polígono é uma superfície plana limitada por uma
linha poligonal fechada.
Em qualquer polígono podemos considerar ângulos
internos e ângulos externos.
POLÍGONOS. Ângulos de um polígono
CLASSIFICAÇÃO QUANTO AOS ÂNGULOS
POLÍGONO CONVEXO
POLÍGONO CÔNCAVO
Unindo dois quaisquer dos
Existem sempre, pelo
seus pontos, o segmento
menos, dois dos seus
de recta obtido está
pontos que unidos, formam
sempre contido no
um segmento que não está
polígono.
contido no polígono.
POLÍGONOS. Ângulos de um polígono
CLASSIFICAÇÃO QUANTO AOS ÂNGULOS/ LADOS
POLÍGONO REGULAR
Todos os lados e ângulos
são geometricamente
iguais.
POLÍGONO NÃO REGULAR
Nem todos os lados e
ângulos são
geometricamente iguais.
POLÍGONOS. Ângulos de um polígono
SOMA DAS MEDIDAS DAS AMPLITUDES DOS
ÂNGULOS INTERNOS
DE UM POLÍGONO CONVEXO
Sabemos que:
 a soma das medidas das amplitudes dos ângulos
internos de um triângulo é igual a 180º….
 um polígono pode ser dividido em triângulos,
traçando as suas diagonais (segmentos de recta
que unem vértices não consecutivos)…
Então, preenchendo a seguinte tabela, traçado
todas as diagonais possíveis que partem de um
só vértice, podemos dividi-los em triângulos…
POLÍGONOS. Ângulos de um polígono
SOMA DAS MEDIDAS DAS AMPLITUDES DOS
ÂNGULOS INTERNOS
DE UM POLÍGONO CONVEXO
Quadrilátero
Pentágono
Hexágono
Heptágono
…
n lados
…
Nº de lados
4
5
6
7
...
Nº de
triângulos
que ficou
dividido
2
3
4
5
…
Soma dos
ângulos
internos de
um polígono
2x180º
3x180º
4x180º
5x180º
n
n-2
… (n - 2)x180º
POLÍGONOS. Ângulos de um polígono
SOMA DAS MEDIDAS DAS AMPLITUDES DOS
ÂNGULOS INTERNOS
DE UM POLÍGONO CONVEXO
CONCLUSÃO
A soma Si das medidas das amplitudes dos ângulos internos
de um polígono (convexo) com n lados é dada pela expressão:
Si = (n - 2) x 180º
Se polígono for regular com n lados, qual a medida da amplitude
de um ângulo interno?
POLÍGONOS. Ângulos de um polígono
Se polígono for regular, todos os ângulos são
geometricamente iguais.
Então:
A amplitude de um ângulo interno de um polígono (convexo)
regular com n lados é dada pela expressão:
Si (n  2) 180º

n
n
POLÍGONOS. Ângulos de um polígono
SOMA DAS MEDIDAS DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS
DE UM POLÍGONO CONVEXO
Consideremos, por exemplo, um pentágono:
Repare:
 A, B, C, D, E são vértices.
 a, b, c, d, e são ângulos internos.
 a’, b’, c’, d’, e’ são ângulos externos
POLÍGONOS. Ângulos de um polígono
SOMA DAS MEDIDAS DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS
DE UM POLÍGONO CONVEXO
Repare:
 a + a’ = 180º
 b + b’ = 180º
 c + c’ = 180º
 d + d’ = 180º
 e + e’ = 180º
POLÍGONOS. Ângulos de um polígono
SOMA DAS MEDIDAS DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS
DE UM POLÍGONO CONVEXO
Assim, a soma das medidas das
amplitudes de todos os ângulos,
quer externos, quer internos, é
então:
5 x 180º = 900º
Sendo o pentágono com 5 lados,
a soma das medidas das
amplitudes dos ângulos internos
é igual a:
(5-2) x 180º = 3 x 180º = 540º
POLÍGONOS. Ângulos de um polígono
SOMA DAS MEDIDAS DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS
DE UM POLÍGONO CONVEXO
Então, a soma das medidas das
amplitudes dos ângulos
externos do pentágono será:
900º - 540º = 360º
Ou seja:
a’ + b’ + c’ + d’ + e’ = 360º
O que se passará com os outros
polígonos?
POLÍGONOS. Ângulos de um polígono
SOMA DAS MEDIDAS DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS
DE UM POLÍGONO CONVEXO
CONCLUSÃO
A soma das medidas das amplitudes dos ângulos externos
não depende do número de lados do polígono convexo.
Então:
A soma Se das medidas das amplitudes dos ângulos
externos de qualquer polígono (convexo) é igual a 360º
POLÍGONOS inscritos numa circunferência
Cada uma das seguintes figuras representa
uma circunferência e um polígono:
O polígono está
inscrito na
circunferência
O polígono não
está inscrito na
circunferência
POLÍGONOS inscritos numa circunferência
Cada uma das seguintes figuras representa
uma circunferência e um polígono:
Todos os seus
vértices são pontos
da circunferência
Nem todos os seus
vértices são pontos
da circunferência
POLÍGONOS inscritos numa circunferência
Cada uma das seguintes figuras representa
uma circunferência e um polígono:
Nenhum destes polígonos é regular
POLÍGONOS inscritos numa circunferência
Um polígono é regular se tiver todos os lados e todos os
ângulos geometricamente iguais entre si.
Dada uma circunferência é SEMPRE possível
inscrever nela um plígono regular
Se um polígono não for regular, NEM SEMPRE é
possível fazê-lo
POLÍGONOS inscritos numa circunferência
RECORDA
Numa circunferência,
a arcos iguais correspondem cordas
iguais e vice–versa.
e
a ângulos ao centro iguais
correspondem arcos iguais e cordas
iguais e vice–versa.
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
Vamos construir os seguintes
polígonos regulares:
Triângulo regular (equilátero)
Quadrado
Pentágono regular
Hexágono regular
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
O triângulo regular:
TRIÂNGULO
EQUILÁTERO
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
TRIÂNGULO EQUILÁTERO
Como inscrever um triângulo
equilátero numa circunferência ?
Começamos, então, por construir
uma circunferência.
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
TRIÂNGULO EQUILÁTERO
Repara que:
 A amplitude de uma
circunferência é de 360º.
 Se conseguirmos medir 3
ângulos ao centro com a
mesma
amplitude,
vamos
obter 3 arcos iguais e,
consequentemente, 3 cordas
com a mesma medida.
360º : 3 = 120º
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
TRIÂNGULO EQUILÁTERO
?
?
B
?
120º
A
120º
120º
C
?
?
?
?
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
O quadrado
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
QUADRADO
Para construir o quadrado
vamos repetir o procedimento
anterior.
360º : 4 = 90º
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
QUADRADO
?
?
B
?
A
C
o06
D
?
?
?
?
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
O pentágono
regular
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
PENTÁGONO REGULAR
O processo é sempre o mesmo:
•Neste caso dividimos a
circunferência em 5 arcos
iguais.
•Para isso, traçamos 5 ângulos
ao centro com amplitude 72º , já
que 360º : 5 = 72º.
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
PENTÁGONO REGULAR
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
O hexágono
regular
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
HEXÁGONO REGULAR
Não tem nada que saber:
•Agora é só dividir a
circunferência em 6 arcos
iguais.
•Como 360º : 6 = 60º, traçam-se
ângulos ao centro com 60º de
amplitude.
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
HEXÁGONO REGULAR
60º
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
REPARA NO SEGUINTE:
Em todas as construções, tal como em
todas as de outros polígonos regulares
Basta traçar um ângulo ao centro com o
transferidor
Uma vez determinado um arco, obtemos
dois vértices do polígono que queremos
construir
Com o compasso obténs os
restantes
( Porque se sabe que os comprimentos dos arcos são iguais )
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
CONCLUSÃO
Para construir qualquer polígono regular
de n lados segue-se sempre o mesmo
procedimento, dividindo a circunferência
em n arcos geometricamente iguais.
Faz-se
360
n
0
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
ACTIVIDADE
O caso do Hexágono Regular
A
Justifica que:
 OA  OB
60º
B
 OÂB  OB̂A
 o OAB
é equilátero.
Se o é equilátero, então tem os
lados todos iguais e, portanto, o
lado do hexágono é igual ao
raio da circunferência .
POLÍGONOS inscritos numa circunferência
Construção de POLÍGONOS REGULARES
O caso do Hexágono
Regular
PROPRIEDADE
A
60º
B
O lado de um hexágono regular
inscrito numa circunferência é
igual ao raio dessa
circunferência.
Cuidado!!!
Esta propriedade só é
válida para os
hexágonos!
Áreas de POLÍGONOS regulares
Em cada um dos polígonos regulares, traçou-se o segmento
de recta [OT], que une o centro da circunferência ao ponto
médio T do lado, sendo-lhe perpendicular.
Chama-se apótema de um polígono regular
ao segmento de recta que une o centro do
polígono com o ponto médio de qualquer um
dos lados.
A apótema é perpendicular a esse lado.
Áreas de POLÍGONOS regulares
Como determinar a área de um pentágono regular?
Consideremos um pentágono
inscrito numa circunferência...
 Dividimos o pentágono em
5 triângulos
geometricamente iguais.
 Quando decompomos o
pentágono em triângulos
verificamos que a apótema
coincide com a altura do
triângulo.
A área do pentágono é igual a 5 vezes a área de um dos
triângulos.
A ABCDE   5  A AOB 
Áreas de POLÍGONOS regulares
Como determinar a área de um pentágono regular?
Designando por L a medida do
lado do pentágono, temos:
L  ap
A AOB  
2
Logo:
P  5L
A ABCDE   5  A AOB 
L  ap
A ABCDE   5 
2
ap
A ABCDE   5 L 
2
ap
A ABCDE   P 
2
P
A ABCDE    ap
2
Áreas de POLÍGONOS regulares
Como determinar a área de um pentágono regular?
Então, a área de um pentágono
regular pode-se determinar
usando a seguinte fórmula:
P
A ABCDE    ap
2
Se experimentares com outros polígonos regulares,
verifica-se a mesma fórmula.
Áreas de POLÍGONOS regulares
SÍNTESE
 Para calcular a área A de um polígono regular pode-se
recorrer à seguinte fórmula:
P
A   ap
2
ap  apótema
 Em alternativa à fórmula, é sempre possível dividir o
polígono regular de n lados em n triângulos
geometricamente iguais.
A área A do polígono será a soma das áreas dos
triângulos em que foi dividido:
A  n  A
(altura do triângulo = apótema do polígono)