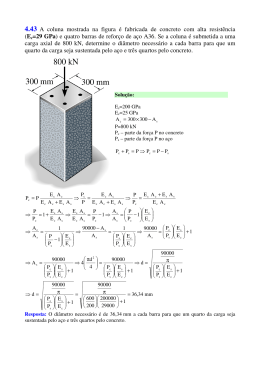
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
Ex. 4-5 A barra de aço mostrada na figura ao lado tem um diâmetro de 5 mm. Ela é
rigidamente fixada à parede A e, antes de ser carregada, há uma folga de 1 mm entre
a parede B’ e a extremidade da barra. Determine as reações em A e B’ para uma força
axial P=20 kN aplicada à barras conforme indicado. Despreze as dimensões do colar.
Faça Eaço = 200 GPa.
Solução:
Por equilíbrio: FA + FB = 20 kN
(1)
n
Pela restrição de deslocamento total de A até C:  AC  
i 1
N i Li
 1 mm (2)
Ei Ai
Dados:
Eaço = 200 GPa = 200 kN/mm2
d = 1,5 mm
LAC = 400 mm
LCB = 800 mm
Esforços normais:
NAC = FA
NCB = FA – 20
Áreas das seções transversais:
d 2 (5 mm ) 2
A

 19,63495 mm 2
4
4
N AC L AC N CB L CB
F  20  800
FA  400
 AC 

 1 mm   AC 
 A
1
E aço A
E aço A
200  19,63495 200  19,63495
 FA  400  FA  800  20  800  200  19,63495
 FA  400  800  200  19,63495  20  800
 FA 
200  19,63495  16000
 16,60583 kN
1200
De (1) vem que:
 FB  20  16,60583  3,394174 kN
Resposta: As reações em A e B são 16,6 kN e 3,39 kN, respectivamente.
www.profwillian.com
página 1
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
4.42 A coluna de concreto é reforçada com quatro barras de aço, cada uma com
diâmetro de 18 mm. Determinar a tensão média do concreto e do aço se a coluna é
submetida a uma carga axial de 800 kN. Eaço = 200 GPa e Ec = 25 GPa.
Solução:
Es=200 GPa
Ec=25 GPa
  18 2 
  1017,88 mm 2
A s  4
4


A c  300  300  A s  88982,1 mm 2
P=800 kN
Pc – parte da força P no concreto
Ps – parte da força P no aço
Pc  Ps  P  Pc  P  Ps
c  s 
Pc L
P L
 s
 Ps E c A c   Pc E s A s   Ps E c A c   P  Ps E s A s 
Ec Ac Es As
 Ps E c A c   PE s A s   Ps E s A s   Ps E c A c   Ps E s A s   PE s A s 
 Ps E c A c  E s A s   P E s A s   Ps  P
Es As
Ec Ac  Es As
200000  1017,88
 67072,3 N
25000  88982,1  200000  1017,88
 Pc  800000  67072,3  732927,7 N
 Ps  800000 
 s 
Ps
67072,3

 65,9 M Pa
A s 1017,88
 c 
Pc
732927,7

 8,24 M Pa
Ac
88982,1
Resposta: A tensão normal média do concreto é de 8,24 MPa e a tensão normal média do aço é de
65,9 MPa.
www.profwillian.com
página 2
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
4.43 A coluna mostrada na figura é fabricada de concreto com alta resistência (Ec=29
GPa) e quatro barras de reforço de aço A36. Se a coluna é submetida a uma carga
axial de 800 kN, determine o diâmetro necessário a cada barra para que um quarto da
carga seja sustentada pelo aço e três quartos pelo concreto.
Solução:
Es=200 GPa
Ec=25 GPa
A c  300  300  A s
P=800 kN
Pc – parte da força P no concreto
Ps – parte da força P no aço
Pc  Ps  P  Pc  P  Ps
Pc  P


Ec Ac
P
Ec Ac
P Ec Ac  Es As
 c 


Ec Ac  Es As
P Ec Ac  Es As
Pc
Ec Ac
P
 E
E A
E A
A
P
P
 1 s s  s s 
 1  s    1 c
Pc
Ec Ac
E c A c Pc
A c  Pc
 E s



Ac
90000  A s
1
1
90000  Pc  E s




  
As  P
As
As
 E c 
 Ps  E c 
 Ps  E c
  1 
  
 Pc
 E s 
 Pc  E s 

  1

90000
 d 
90000
90000

 
 As 
 4
d
4
 Pc  E s 







P
E
P
Es 

  c  s 
c
    1




1
 P  E 
 P  E   1
P
E
 s  c 
 s  c 
 s  c 
2
90000
90000


d

 36,34 mm
600
200000
 Pc  E s 



    1


 1
200
29000




P
E
 s  c 
Resposta: O diâmetro necessário é de 36,3 mm a cada barra para que um quarto da carga seja
sustentado pelo aço e três quartos pelo concreto.
www.profwillian.com
página 3
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
4.45 Os dois tubos são feitos do mesmo material e estão acoplados como mostrado
abaixo. Supondo que a área da seção transversal de BC seja A e a de CD seja 2A,
determinar as reações em B e D quando a força P for aplicada na junção C.
Solução:
FB
Por equilíbrio: FB + FD = P
FD
(1)
n
Pela restrição de deslocamento total de B até D:  BD  
i 1
N i Li
 0 (2)
Ei Ai
Esforços normais:
NBC = FB
NCD = FB – P
L
FB  P  L
FB 
N BCL BC N CDL CD
2
2 0
 BD 

0
EA
E2A 
EA
E2A 
F  P   0
 FB  B
2
2F  FB  P 
 B
 0  3FB  P  0
2
P
 FB 
3
De (1) vem que:
 FD  P  FB  P 
P 2P

3 3
Resposta: As reações em B e D são P/3 e 2P/3, respectivamente.
www.profwillian.com
página 4
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
4.53 A coluna central B da estrutura mostrada na figura tem um comprimento
original de 124,7 mm, enquanto as colunas A e C têm comprimentos de 125 mm. Se
as vigas do topo e da base forem consideradas rígidas, determine a tensão normal
média atuante em cada coluna. As colunas são feitas de alumínio e tem área de seção
transversal média de 400 mm². Considere Eal=70 GPa.
Solução:
Equações de equilíbrio estático:
 Fy  0  FA  FB  FC  P  0
 FA  FB  FC  P
M
B
(1)
 0  FA  0,2  FC  0,2  0
 FA  FC
(2)
FA
FB
FC
Equação de compatibilidade de deslocamentos:
 A   C   B  0,3 mm
FA 125 FB 124,7

 0,3 mm
EA
EA
FA 125 mm
FB 124,7 mm

 0,3 mm
kN
kN
2
2
P = 800 kN/m × 0,2 m
70
 400 mm
70
 400 mm
mm 2
mm 2
kN


FA 125 mm  FB 124,7 mm  0,3 mm   70
 400 mm 2 
2
 mm

 125 FA  124,7 FB  8400
(3)
 A   B  0,3 
Resolvendo as equações (1), (2) e (3):
FA  FC  75,726 kN
FB  8,5470 kN
Assim:
 A  C 
FC 75,726 kN
kN

 0,1893
2
A
400 mm
mm 2
FB 8,5470 kN
kN

 0,02137
2
A
400 mm
mm 2
Resposta: As tensões normais médias atuantes nas colunas A, B e C são 189 MPa, 21,4 MPa e
189 MPa, respectivamente.
B 
www.profwillian.com
página 5
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
4.115 O conjunto consiste em duas barras AB e CD do mesmo material, com módulo
de elasticidade E1 e coeficiente de expansão térmica 1, e uma barra EF com módulo
de elasticidade E2 e coeficiente de expansão térmica 2. Todas as barras têm o mesmo
comprimento L e área da seção transversal A. Se a viga rígida estiver inicialmente
horizontal na temperatura T1, determinar o ângulo que ela faz com a horizontal
quando a temperatura aumenta para T2.
Solução:
F  0  F  F  F  0  F  F  F
 M  0   F (d )  F ( d )  0  F  F
y
A
C
A

FA
C
FC
E
FE
C
A
E
A
C
E
E
A
E
 A   AB T   AB F  1 LT2  T1  
FA L
E1A
 C   CD T   CD F  1 LT2  T1  
FC L
E1A
 E   EF T   EF F   2 LT2  T1  
FE L
E2A
0
(1)
(2)
Compatibilidade geométrica:
 E   A  E  C
  A
  A

 E
  E  C   E   A  2 E  2C  C  E
2d
d
2
2
FL
FL
 2 LT2  T1   E  1LT2  T1   A
FL
E2A
E1A
1LT2  T1   C 
(3)
E1A
2
Resolvendo as equações 1, 2 e 3 simultaneamente, temos:
E E AT2  T1  2  1 
FA  FE  1 2
5E 2  E1
FC  2 
E1 E 2 AT2  T1  2  1 
5E 2  E1
Assim:
tg()   
E  A
2d
 
3E 2 LT2  T1  2  1 
d5E 2  E1 
Resposta: O ângulo que a viga rígida faz com a horizontal é:
www.profwillian.com
(
)(
(
)
)
página 6
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
7) Uma barra tem seção reduzida como se vê na figura ao lado, está engastada entre
suportes rígidos (indeslocáveis), e suporta uma força axial, P. Calcular as reações de
apoio em A e B, supondo A1= área da seção transversal na parte esquerda e A2 = área
da seção transversal direita. (Usar os seguintes valores numéricos: P= 76 kN; A1=500
mm2; A2=750 mm2; a=140 mm; b=420 mm; E=140GPa).
P
A
B
a
b
Solução:
Tornando a barra isostática, tirando o apoio B, podemos calcular o deslocamento total que é a soma
dos deslocamentos de cada trecho (tomando as seções à direita).
N  L1 N 2  L 2
 1

A
P
B
E1  A1 E 2  A 2

 R B  b  R B  P   a

E  A2
E  A1
RA
 b
a  Pa
 
   R B 

E

A
E

A
E  A1
2
1 

RB
a
b
No entanto, para que o apoio exista, esse deslocamento total deve ser nulo:
 b
 b
a  Pa
a  Pa
 
 
 0  R B 

 R B 


A1
 E  A 2 E  A1  E  A1
 A 2 A1 
 420 140  76000  140
RB


500
 750 500 
 R B  25333,33 N
Através da equação da isostática podemos encontrar o valor de RA
F  0  RA  RB  P  0 
R A  25333,33  76000  0
 R A  50666,67 N
Resposta: As reações em A e B são 50,7 kN e 25,3 kN, respectivamente.
www.profwillian.com
página 7
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
8) Uma barra de aço A36, de 5 cm de diâmetro, se encaixa entre dois suportes
rígidos, à temperatura ambiente. Calcular as reações de apoio, quando a temperatura
aumenta 20°C. Admitir o coeficiente de dilatação térmica do aço  = 12 × 10-6 °C-1 e
o módulo de elasticidade longitudinal do aço E = 200 GPa.
A
B
50 cm
Solução:
RA
B
A
RB
50 cm
F
 0  RA  RB  0  RA  RB  R
(1)
Caso não existisse o apoio B, teríamos o encurtamento devido à força R:
 AB R  R L
EA
y
Caso não existisse o apoio B, teríamos o alongamento devido à variação de temperatura T:
 AB T   L T
Como o apoio existe, não temos alongamento nem encurtamento da barra, daí a equação de
compatibilidade de deslocamentos:
 AB R   AB T  R L   L T
EA
 R  E A  T
Assim:
kN 5 cm 

 12  10 6 o C1  20o C
2
cm
4
 R  94,2477796 kN
2
R  20000
Resposta: As reações em A e B são de compressão iguais a 94,2 kN.
www.profwillian.com
página 8
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
9) O tubo de aço de 500 mm de comprimento é preenchido com concreto e sujeito a
uma força compressiva de 80 kN. Determine as tensões no concreto e no aço devidas
a este carregamento. O tubo de aço tem diâmetro externo de 80 mm e um diâmetro
interno de 70 mm. Considere Eaço=200 GPa e Econc=24 GPa
80kN
Solução:
P=força no tubo
Pc=parte da força P no concreto
Ps=parte da força P no aço
P  Pc  Ps
Compatibilidade de deslocamentos
PL
PL
Pc
P
P  Ps
P
P
P
P
c  s  c  s 
 s 
 s  s  s 
EcAc EsAs
EcAc EsAs
EcAc EsAs
EsAs EcAc EcAc
 Ps
E A  EsAs
E A  EsAs
1
1
P
P


 Ps c c

 Ps c c
P
EsAs EcAc EcAc
EsAsEcAc
EcAc
EsAs
 Ps  P
EsAs
EcAc  EsAs
Como:
E s  200 kN / mm 2
As 
e
E c  24 kN / mm 2
 2
80  70 2  1178,097 mm 2
4

Assim:

e
Ac 
 2
70  3848,451 mm 2
4
200  1178,097
 57,471 kN
24  3848,451  200  1178,097
Pc  P  Ps  80  57,471  22,529 kN
Ps  80 
Então as tensões no aço e no concreto são:
P
57471 N
s  s 
 48,8 M Pa
A s 1178,097 mm 2
c 
Pc
22529 N

 5,85 M Pa
A c 3848,451 mm 2
Resposta: A tensão normal média do concreto é de 5,85 MPa e a tensão normal média do aço é de
48,8 MPa.
www.profwillian.com
página 9
Resistência dos Materiais
Exercícios de Barras Estaticamente Indeterminadas
10) Qual seria a reação, R, da barra engastada da figura abaixo, se ao invés de uma
variação de temperatura T, a barra tivesse um comprimento inicial a L+L em lugar
de L. (Admitir a distância entre os suportes igual a L.)
R
R
L
L
R
Solução:
Retirando o apoio superior e aplicando a reação R como uma carga, podemos calcular o
deslocamento  na extremidade da barra:
R. L
(1)

E. A
mas sabemos que este deslocamento é L, ou melhor:
=L (2)
R. L
combinando (1) e (2), temos que: L 
E. A
L
portanto a reação é: R  E. A.
L
Resposta: As reações de apoio são compressivas iguais a
www.profwillian.com

página 10