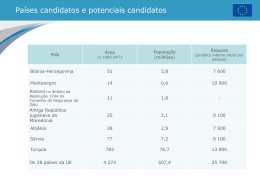
MATEMÁTICA
FORMULÁRIO
sen
cos
tg
30o
45o
60o
1
2
2
2
3
2
3
3
2
2
3
2
1
2
1
3
n!
p! (n − p)!
1) an = a1+ (n-1) r
9) Cnp =
a +a 
2) Sn =  1 n  n
 2 
2
10) Vcilindro = π r h
3) an = a1 qn –1
11) Vcubo = a 3
(
)
a1 q n − 1
4) S n =
q−1
a
5) S = 1
1− q
n!
6) Anp =
(n − p)!
13) dA,B=
7) Pn = n!
15) α =
n!
α ,β
8) P n =
α! β!
16)
12) (x – a)2 + (y – b)2 = r2
( xB − x A )2 + ( y B − y A )2
14) C = 2π r
l
r
a = b = c
sen senB̂ senĈ
Questão 21
Assinale a(s) proposição(ões) CORRETA(S).
01. Na implantação do novo plano diretor de uma cidade, um cidadão teve parte de seu
terreno de esquina desapropriado pela prefeitura para alargamento das duas avenidas
laterais. Do terreno, em forma de quadrado, foi perdida uma faixa de 3 m de largura ao
sul e uma faixa de 4 m de largura a leste. Se a área do terreno ficou reduzida à metade,
então a medida do perímetro do terreno antes da desapropriação era de 48 m.
02. Se na planta de um edifício em construção, cuja escala é 1:50, a área de uma sala
2
2
retangular é de 80 cm , então a área real da sala projetada é de 40 m .
04. Se um corpo com peso de 80 N é abandonado em um plano inclinado, cujo ângulo de
elevação é de 30°, sendo desprezível o atrito entre o corpo e o plano, então a
intensidade da reação normal de apoio é de 40 N.
08. Se x, y, z e w são os menores valores numéricos inteiros para que a equação
química xAu(OH)3 + yH4P2O7 → zAu4(P2O7)3 + wH2O fique balanceada, então
x + y + z + w = 20.
Questão 21
Gabarito: 09 (01+08)
Número de acertos: 898 (13,11%)
Grau de dificuldade previsto: fácil
Grau de dificuldade obtido: médio
Proposições
01
Percentual de
45,0
incidência (%)
02
04
08
16
32
64
42,0
38,0
52,0
0,07
0
0
A questão envolve a aplicação de conhecimentos matemáticos como equação do 2°
grau, área e perímetro de figuras planas, razões e proporções, relações trigonométricas no
triângulo retângulo e sistemas lineares a situações-problema e a outras áreas de
conhecimento como Física e Química. Além da resposta correta 09 (01+08), outras
respostas predominaram no quadro de freqüência, que são, em ordem decrescente de
preferência: 08 – 11,03%; 02 – 10,08%; 10 (02+08) – 9,20%; 04 – 8,16%; 01 – 8,06%; 06
(02+04) – 6,88%; 12 (04+08) – 6,57%; 03 (01+02) – 6,13%; 05 (01+04) – 5,72%; 13
(01+04+08) – 4,50%. Como se pode verificar através dos índices das respostas 01 e 08, na
dúvida, os candidatos optam pelo acerto parcial. A proposição correta 01 obteve 45% da
preferência dos candidatos e foi responsável também pelos índices alcançados por outras
respostas das quais fazia parte, como se pode observar acima. É provável que a dificuldade
dos candidatos nesta proposição tenha sido a leitura, compreensão, interpretação e
transcrição da situação-problema para a linguagem matemática, já que os tópicos envolvidos
são: equação do 2° grau, área e perímetro de figuras planas. A grande responsável pelo erro
e pelo espalhamento nesta questão foi a consideração das proposições 02 e 04 como
corretas, com 42% e 38% da preferência dos candidatos, respectivamente. A proposição 02,
incorreta, foi a com o maior índice de preferência dos candidatos. É surpreendente o fato de
que um percentual tão significativo dos candidatos tenha considerado esta proposição como
correta, pois ela envolve o conceito de escala, um dos mais básicos e fundamentais temas
explorado no Ensino Fundamental, não somente na disciplina de Matemática, mas também
em outras disciplinas, como Geografia, na confecção de mapas, plantas e maquetes; Artes,
na ampliação e redução de desenhos; além de aparecer em anúncios imobiliários de alguns
jornais e revistas. Para intuir a veracidade ou não da proposição, o candidato poderia tomar
um retângulo qualquer de 80 cm2 de área, por exemplo, 10 cm de comprimento por 8 cm de
largura, aplicar o conceito de escala e verificar que as medidas reais do retângulo seriam
500 cm (5m) por 400 cm (4m), o que daria uma área de 20 m2 e não de 40 m2 conforme
afirmava a proposição. Talvez a maioria dos candidatos que assinalou a proposição 02 como
correta tenha feito simplesmente 80 cm2 x 50 = 400 cm2, sem dar a devida atenção às
transformações de unidades e ao fato de que se trata de medidas de área. Portanto, deveria
fazer 80 cm2 x 50 x 50 = 200.000 cm2 (20 m2). Os candidatos que assinalaram a proposição
04 como verdadeira, provavelmente tiveram dificuldades em aplicar seus conhecimentos de
Matemática e/ou Física do Ensino Médio, em especial aqueles relativos às relações
trigonométricas no triângulo retângulo e às leis de Newton, ou simplesmente combinaram os
dados do enunciado com os do formulário, fazendo o seguinte cálculo:
1
80 N ⋅ sen30º = 80 N ⋅ = 40 N . A proposição correta 08 obteve 52% da preferência dos
2
candidatos e foi responsável também pelos índices alcançados por outras respostas das
quais fazia parte, como se pode observar acima. Talvez o bom índice obtido por esta
proposição se deva ao fato de que ela poderia ser resolvida tanto pela aplicação dos
conhecimentos matemáticos de sistemas lineares como dos conhecimentos químicos de
balanceamento de uma equação química. Isso vem corroborar no sentido de que a
interdisciplinaridade proposta pela Banca tem boa aceitação e é perfeitamente
compreendida pelos candidatos.
Questão 22
Assinale a(s) proposição(ões) CORRETA(S).
01. João e Pedro são dois meninos que recolhem latinhas de cerveja e refrigerante para
ajudar no orçamento familiar. Enquanto João trabalha 4 horas por dia, Pedro trabalha
5 horas por dia. Ao final do dia recolhem 180 latinhas. Se a divisão das latinhas for feita
proporcionalmente às horas trabalhadas, então João fica com 100 latinhas e Pedro fica
com 80 latinhas.
02. Um retângulo tem 10 cm de comprimento e x cm de largura. A equação que corresponde
à área A em função do perímetro P do retângulo, em centímetros quadrados, é
A = 5P − 100 .
04. O plano de saúde A, que cobra R$ 140,00 de mensalidade e R$ 50,00 por consulta, é
mais econômico para o cliente do que o plano B, que cobra R$ 200,00 de mensalidade
e R$ 44,00 por consulta, independentemente do número de consultas.
08. Se três moedas perfeitas distinguíveis forem lançadas ao ar simultaneamente, então o
número de resultados possíveis é 6.
16. Uma circunferência é dividida em 17 arcos iguais de 2 cm de comprimento cada um. O
diâmetro dessa circunferência é de 10,82 cm, considerando a aproximação de duas
casas decimais e π = 3,14 .
Questão 22
Gabarito: 18 (02+16)
Número de acertos: 1020 (14,87%)
Grau de dificuldade previsto: fácil
Grau de dificuldade obtido: médio
Proposições
01
Percentual de
26,0
incidência (%)
02
04
08
16
32
64
43,2
36,3
32,0
46,0
0
0
A questão compreende cinco proposições, envolvendo a aplicação de conhecimentos
básicos e fundamentais de alguns dos principais tópicos do Ensino Fundamental e Médio:
proporcionalidade, área e perímetro de figuras planas, composição de funções, função afim
e probabilidade. Nesta questão, as outras respostas que predominaram no quadro de
freqüência, foram: 02 – 9,08%; 16 – 8,48%; 04 – 7,65%; 08 – 6,91%; 12 (04+08) – 5,55%; 20
(04+16) – 5,00%; 01 – 4,29%; 05 (01+04) – 3,78% e 10 (02+08) – 3,24%. Mais uma vez fica
evidente no quadro de freqüência de respostas da prova a preferência dos candidatos em
não arriscar e tirar proveito do acerto parcial, como se pode observar através dos índices
das respostas 02 – 9,08% e 16 – 8,48%. As grandes responsáveis pelo erro e pelo
espalhamento nesta questão foram as indicações das proposições 01, 04 e 08 como
corretas, com 26%, 36,3% e 32% da preferência dos candidatos, respectivamente. Em
ambos os casos, é surpreendente o fato de os candidatos tomarem estas proposições como
corretas. No caso da proposição 01, não havia sequer a necessidade de o candidato efetuar
algum cálculo para verificar a veracidade ou não da afirmação, bastava prestar atenção ao
fato de que, se a divisão das latinhas é proporcional às horas trabalhadas, então Pedro, que
trabalhou mais horas do que João, não poderia ficar com menos latinhas do que este. Da
mesma forma, não eram necessários cálculos para saber que a proposição 04 é falsa, pois o
custo dos dois planos de saúde A e B são compostos de uma parte fixa e uma parte variável
que corresponde ao número de consultas, e não independente deste número, conforme
afirma o enunciado. A opção de 7,65% dos candidatos pela resposta 04 pode ser um
indicativo de que os mesmos têm sérios problemas na aplicação de seu pensamento
algébrico e com mais razão ainda de seu pensamento geométrico. No caso da proposição
08, é surpreendente o fato de que 32% dos candidatos a consideraram como correta, já que
a sua veracidade ou não podia ser facilmente verificada a partir do espaço amostral do
experimento: {(C, C , C ), (C , C , K ), (C , K , C ), (C , K , K ), ( K , C , C ), ( K , K , C ), ( K , K , K )} , onde (C : cara; K : coroa) .
Esperava-se um índice superior aos 43,20% obtidos pela proposição 02, já que ela envolve
alguns dos mais básicos e fundamentais temas do Ensino Fundamental e Médio, ou seja,
área e perímetro de figuras planas associados à composição de funções. Para resolver a
proposição, isto é, determinar corretamente a equação que corresponde à área A em função
do perímetro P do retângulo de 10 cm de comprimento por x cm de largura, bastava ao
candidato fazer: A = b ⋅ h ⇒ A = 10 ⋅ x e P = 2b + 2h ⇒ P = 2b + 2 x , isolar x na segunda
equação e substituir na primeira, ficando com A = 5 P − 100 . Para a proposição 16 também se
esperava um índice superior aos 46% obtido pela proposição, por tratar-se da aplicação da
fórmula do comprimento de uma circunferência, tópico este muito explorado no Ensino
Fundamental e Médio. Para resolver a proposição bastava que o candidato, com o auxílio do
formulário, fizesse: C = 2 ⋅ 17cm ⇒ C = 34cm , mas C = 2 ⋅ π ⋅ r ⇒ 34 = (2 ⋅ r ) ⋅ 3,14 ⇒ ∅ = 10,82cm .
Ambas as proposições referem-se a conteúdos de geometria plana do Ensino Fundamental,
o que leva a crer que este assunto não é bem assimilado pelos candidatos, pois para
resolvê-los há necessidade de entendimento e aplicação dos conceitos básicos a respeito
destes temas. Isso sugere uma reflexão a todos aqueles envolvidos e preocupados com a
melhoria do ensino da Matemática em todos os níveis, em particular a respeito do
desenvolvimento do pensamento geométrico dos estudantes. Será que o ensino de
geometria continua sendo colocado em segundo plano, apesar de todo o movimento das
pesquisas na área de Educação Matemática e dos PCN (1998) destacarem a importância de
se resgatar o trabalho com Geometria no Ensino Fundamental?
Questão 23
Assinale a(s) proposição(ões) CORRETA(S).
01. As telas dos televisores costumam ser medidas em polegadas. Quando se diz que um
televisor tem 29 polegadas, isto significa que a diagonal da tela mede 29 polegadas, isto
é, aproximadamente 73,66 cm. Então, um televisor cuja diagonal da tela meça 30,48 cm
terá 12 polegadas.
02. Se, inicialmente, um relógio marcava exatamente 15h, então, após o ponteiro menor (das
horas) percorrer um ângulo de 142º, o relógio estará marcando 19h44min.
04. Se um bolo de chocolate, em forma de cilindro, tem por base um círculo de 20 cm de
diâmetro, mede 8 cm de altura e custa R$ 15,00, então um outro bolo feito da mesma
massa e tendo a mesma forma cilíndrica, só que medindo 40 cm de diâmetro e 16 cm de
altura, custará R$ 30,00.
08. A soma dos números ímpares de 27 a 75 é 1173.
16. Se o lucro de uma empresa é dado por L(x) = 4(3 – x)(x – 2), onde x é a quantidade
vendida, então o lucro da empresa é máximo quando x = 2,2.
Questão 23
Gabarito: 03 (01 + 02)
Número de acertos: 1187 (17,31%)
Grau de dificuldade previsto: médio
Grau de dificuldade obtido: médio
Proposições
01
Percentual de
65,0
incidência (%)
02
04
08
16
32
64
47,0
42,0
17,1
19,0
0,01
0
A questão envolve a aplicação de conhecimentos básicos e fundamentais de alguns
dos principais tópicos do Ensino Fundamental e Médio, regra de três simples, unidades de
medidas de arcos e ângulos, semelhança, progressão aritmética e função quadrática.
17,31% dos candidatos inscritos acertaram esta questão. Um dos fatores que pode ter
contribuído para o índice alcançado é o fato de que as proposições corretas 01 e 02 eram as
mais fáceis da questão, o que deve ter feito com que a maioria dos candidatos nem tentasse
resolver as outras opções. Embora esta tenha sido a questão mais fácil de toda a prova,
obtendo o maior índice de acerto entre as respostas corretas, é necessário destacar que
este índice foi muito baixo, principalmente, levando em conta o nível de dificuldade das
proposições e os tópicos elementares a que elas se referem. Como se pode observar, mais
de 80% dos candidatos teve dificuldades em trabalhar com estes temas que são bastante
explorados na Educação Básica dos candidatos. As proposições corretas 01 e 02 obtiveram
65% e 47% da preferência dos candidatos, respectivamente, e foram responsáveis pelos
índices das respostas 01 – 15,43% e 02 – 5,92%, reforçando a tese de que, na dúvida, os
candidatos optam pelo acerto parcial. Para resolver as proposições 01 e 02 bastava ao
candidato aplicar seus conhecimentos de grandezas proporcionais, em particular da regra de
três simples. No caso da proposição 01, se 29 polegadas correspondem a 73,66 cm, então
30,48cm corresponderá a 12 polegadas, conforme afirma o enunciado. Da mesma forma, na
proposição 02, se o ponteiro menor (das horas) leva 60 minutos para percorrer 30º, então
para percorrer 142º levará 284 minutos (4horas e 44 minutos). Portanto, o relógio estará
marcando 19h4min (15h+4h44min). A proposição incorreta 04 obteve 42% da preferência
dos candidatos e foi responsável pelos índices obtidos pelas respostas: 05 (01+04) –
10,03%; 04 – 8,21%; 07 (01+02+04) – 5,22% e 06 (02+04) – 4,78%. É surpreendente o fato
de um índice tão elevado dos candidatos tomarem esta proposição como correta, pois
quando se constrói um objeto semelhante a outro, dobrando as medidas dos segmentos
correspondentes, todas as linhas são ampliadas na mesma proporção, resultando um objeto
com todos os comprimentos duplicados. Mas isso vale apenas para os comprimentos. Não é
verdade que as áreas de regiões correspondentes nos dois objetos também resultem
duplicadas, assim como também não é verdade que o volume do objeto grande passe a ser
o dobro do volume do pequeno. As proposições incorretas 04 e 08 obtiveram 42% e 17,1%
da preferência dos candidatos, respectivamente. Ainda assim considera-se um índice
relativamente alto para estas proposições, já que as mesmas poderiam facilmente ser
resolvidas aplicando conhecimentos básicos de progressão aritmética e função quadrática.
No caso da proposição 04, bastaria ao candidato com o auxílio do formulário fazer:
 27 + 75 
75 = 27 + (n − 1).2 ⇒ n = 25 . A seguir faz-se S n = 
 ⋅ 25 ⇒ S n = 1275. Para a proposição
 2 
08 faz-se: L( x) = 4(3 − x)( x − 2) ⇒ L( x) = −4 x 2 + 20 x − 24 . Logo o lucro da empresa é máximo em
b
20
xv = −
⇒ xv = −
⇒ xv = 2,5 .
2a
2(−4)
Questão 24
Assinale a(s) proposição(ões) CORRETA(S).
01. A figura a seguir representa uma trilha com as 28 peças do jogo de dominó. No jogo de
dominó uma trilha é uma linha formada por peças que se “casam”: nas ligações, as
duas partes sempre devem ter o mesmo número de pontos. Se a trilha representada na
figura começa com o número três, então ela também termina com o número três.
•
••
•
••
02.
125 3 2
m é a área da figura resultante das instruções a seguir: 1a) Ande 10 m; 2a) Gire
3
90º para a esquerda; 3a) Ande 10 m; 4a) Gire 30º para a esquerda; 5a) Ande 10 m; 6a)
Gire 120º para a esquerda; 7a) Ande 10 m; 8a) Gire 30º para a esquerda; 9a) Ande 10 m.
04. A figura a seguir representa a tesoura do telhado de uma casa. A telha que vai ser
usada é a telha francesa, que exige uma inclinação de pelo menos 40% para que a
água das chuvas escoe. Essa inclinação de 40% é obtida da seguinte maneira: partindo
da extremidade para o topo do telhado, para cada metro na horizontal, sobe-se 40% de
metro na vertical. Portanto, o comprimento da viga AC é 29 m .
C
A
B
M
10 m
08. Os 100 quartos de um hotel serão numerados de 1 a 100 utilizando placas do tipo:
1 ,
2 , 3 , 4 , 5 , 6 , 7 , 8 ,
9 e
0 . Para efetuar esta numeração
serão necessárias ao todo 190 placas.
Questão 24
Gabarito: 05 (01 + 04)
Número de acertos: 956 (13,97%)
Grau de dificuldade previsto: médio
Grau de dificuldade obtido: médio
Proposições
01
Percentual de
48,2
incidência (%)
02
04
08
16
32
64
28,4
56,0
34,3
0,04
0,01
0
O percentual de candidatos que obtiveram acerto total nesta questão ficou muito
aquém do esperado, frente ao fato de que os temas envolvidos nas proposições são,
realmente, básicos do Ensino Fundamental, como números pares e ímpares, sistema de
numeração decimal e geometria plana. Apenas 13,97% responderam corretamente, com um
correlato espalhamento, distribuído entre várias respostas. Listando por ordem decrescente
das preferências as respostas, têm-se: 04 – 17,09%; 01 – 12,53%; 08 – 9,20%; 06 (02+04) –
8,71%; 09 (01+08) – 7,66%; 12 (04+08) – 5,90%; 02 – 4,97%; 03 (01+02) – 3,84%; 07
(01+02+04) – 3,52% e 10 (02+08) – 3,11%. Como se pode verificar através dos índices das
respostas 01 e 04, na dúvida, os candidatos optam pelo acerto parcial. A proposição correta
01 obteve 48,2% da preferência dos candidatos, ela tratava de números pares e ímpares
aplicados ao jogo de dominó. Portanto, um tema que desde muito cedo está constantemente
presente na vida dos candidatos assim como o jogo de dominó, que em geral está presente
em praticamente todas as faixas etárias, desde a infância até a terceira idade. Para resolver
a proposição 01 o candidato deveria levar em conta que o número três, como os outros,
aparece oito vezes numa trilha completa. Como ele começa a trilha, sobram sete números
três. No miolo da trilha, por causa dos “casamentos”, ele aparece um número par de vezes,
ou seja, seis vezes. Logo, sobra o número três para o fim da trilha. O fato tanto da resposta
01 como da proposição 01 terem alcançado os índices acima levanta uma questão para
reflexão: Será que os candidatos aplicaram seus conhecimentos matemáticos? Aqui surge
outra questão interessante para reflexão: Os candidatos utilizaram seus conhecimentos
acadêmicos (par ou ímpar) ou do senso comum (jogar dominó), ou ainda ambos para
resolver a proposição? No caso da proposição correta 04, esperava-se um índice superior
aos 55% obtidos, tendo em vista que porcentagem e Teorema de Pitágoras são temas muito
explorados ao longo de toda Educação Básica dos candidatos. Para resolver a proposição
faz-se: med (CM ) = 40 ⋅ 5 ⇒ med (CM ) = 2m .
100
A
seguir
tem-se:
(
( )) + (med (CM ))
(med ( AC )) 2 = med AM
2
2
⇒ med ( AC ) =
(5)2 + (2 )2
⇒ med ( AC ) = 29 m .
As
grandes
responsáveis pelo erro e pelo espalhamento nesta questão foram as indicações das
proposições 02 e 08 como corretas, que obtiveram 28,4% e 34,3% da preferência dos
candidatos, respectivamente. Provavelmente, a maior dificuldade dos candidatos na
proposição 02 foi seguir as instruções dadas no enunciado e orientar-se geometricamente,
isto é, fazer a passagem da linguagem materna para a linguagem matemática. Seguindo as
instruções do enunciado, o candidato chegaria à figura 2, composta por um triangulo
eqüilátero (I) junto a um quadrado (II). A seguir o candidato poderia determinar a área A
125 3 2
dada por A = AI + AII e compará-la a
m , ou simplesmente, verificar que a proposição
3
125 ⋅ ( 3 ≈ 1,7)
era falsa, pois AII = 100m 2 >
.
3
É surpreendente o fato de que quase 35% dos candidatos tenham considerado esta
proposição como correta, tendo em vista o nível elementar do tema envolvido e a
~
simplicidade da situação-problema proposta, que era calcular o número de placas do tipo: 1,
~
~
~
~
~
~
~
~
~
~
2 , 3, 4 , 5 , 6 , 7 ,8 , 9 e 0
~
~
~
~
~
~
~
~
para numerar os 100 quartos de um hotel. Ora, para numerar os
~
nove primeiros quartos, de 1 a 9, serão necessárias 9 placas. Do 10 ao 99, são noventa
quartos, sendo que em cada um serão utilizadas 2 placas. Portanto, para esses 90 quartos
serão necessários 180 placas. Para o quarto de número 100, serão necessárias mais 3
placas. Logo, ao todo, têm-se 9 + 180 + 3 = 192 placas e não 190 conforme afirma a
proposição.
Questão 25
Na figura a seguir determine a medida do segmento AB, em cm, sabendo que sen a = 0,6.
B
a
C
.
a
100 cm
Assinale o resultado encontrado no cartão-resposta.
A
Questão 25
Gabarito: 96 (questão aberta)
Número de acertos: 556 (8,26%)
Grau de dificuldade previsto: médio
Grau de dificuldade obtido: difícil
A questão envolve alguns dos principais objetivos do estudo da trigonometria no
Ensino Fundamental e Médio como: resolver problemas aplicando as relações fundamentais
entre as razões trigonométricas. O grau de dificuldade obtido vem confirmar um fato, já
apontado em relatórios de anos anteriores, de que a Trigonometria é um dos tópicos que os
candidatos têm mais dificuldades de resolver, seja nos vestibulares ou nas Escolas, ainda
mais quando a questão envolve vários aspectos sobre o tema. O que chama atenção na
análise dos resultados obtidos nesta questão é o fato de que mais de 90% dos candidatos
tiveram dificuldades de trabalhar com esses conceitos básicos de trigonometria. Além da
resposta correta 96 com 8,26%, outras três respostas predominaram no quadro de
freqüência, que são: 60 – 13,91%; 80 – 10,89% e 50 – 4,07%. Como se pode observar, as
respostas 60 e 80 superaram inclusive o índice da resposta correta da questão. Por tratar-se
de uma questão aberta, a probabilidade de acerto casual é reduzida, assim como a
possibilidade de se fazer uma inferência a respeito dos possíveis raciocínios desenvolvidos
pelos candidatos. É provável que os candidatos que responderam 60, tenham feito
x
⇒ 0,6 ⋅ 100 = x ⇒ x = 60cm , sem dar a devida atenção ao fato de
simplesmente: senα =
100
que o ângulo considerado era de 2α . No caso da resposta 80, é possível que os candidatos
2
tenham feito: sen 2α + cos 2 α = 1 ⇒ (0,6 ) + cos 2 α = 1 ⇒ cos α = 0,8 . A seguir, calcularam
y
equivocadamente y em vez de x , fazendo: cos α =
⇒ y = 0,8 ⋅ 100 ⇒ y = 80 conforme a
100
figura abaixo. Finalmente, o motivo que levou os candidatos a darem 50 como resposta não
aparece de forma clara. A hipótese mais plausível é de que eles tenham se baseado no
desenho fornecido e sido impulsionados pela sua intuição visual, considerando o lado
AB como a metade de 100 cm. Outra possibilidade é que os candidatos talvez tenham
construído uma escala a partir das medidas dadas no desenho e depois a compararam com
o lado desconhecido. A seguir são apresentadas duas maneiras pelas quais os candidatos
poderiam resolver corretamente a questão. A partir da
figura ao lado tem-se:
1ª Maneira
2
a) sen 2α + cos 2 α = 1 ⇒ (0,6 ) + cos 2 α = 1 ⇒ cos α = 0,8
y
b) cos α =
⇒ y = 0,8 ⋅ 100 ⇒ y = 80cm
100
x
c) senα =
⇒ x = 0,6 ⋅ 160 ⇒ x = 96cm
160
2ª Maneira
2
2
2
2
a) sen α + cos α = 1 ⇒ (0,6 ) + cos α = 1 ⇒ cos α = 0,8
x
x
b) sen2α =
⇒ 2 ⋅ senα ⋅ cos α =
⇒ x = 2 ⋅ (0,6 ) ⋅ (0,8) ⋅ 100 ⇒ x = 96cm .
100
100
Questão 26
Assinale a(s) proposição(ões) CORRETA(S).
01. Considere duas caixas-d’água de mesma altura: uma em forma de cubo e a outra, em
2
forma de paralelepípedo retângulo com área da base de 6 m . Se o volume da
3
caixa cúbica tem 4 m a menos que o volume da outra caixa, então a única
medida possível da aresta da caixa cúbica é 2 m .
02. É possível construir um poliedro regular, utilizando-se seis triângulos eqüiláteros.
04. Na figura 1, estão representados três sólidos e, na figura 2, estão representadas três
planificações. Fazendo corresponder cada sólido com sua planificação, tem-se a
relação A→1, B →3 e C→2.
figura 2
figura 1
A
B
3
C
2
1
08. Um retângulo, quando girado em torno de seu lado maior, descreve um cilindro cujo
volume tem 432π cm3. Se o lado maior do retângulo mede o dobro da medida do lado
menor, então a área desse retângulo é de 72 cm2.
Questão 26
ANULADA
Questão 27
Assinale a(s) proposição(ões) CORRETA(S).
01. O gráfico que representa a função trigonométrica f ( t ) = 2 sen( 3t +
f(t)
2
1
-2
-1
0
-1
-2
1
2
t
π
3
) , t , é:
02. Um estudo do impacto ambiental provocado pelo desmatamento de uma região prevê
que a quantidade de pássaros de certa espécie irá diminuir segundo a lei: n( t ) = n0 .4
−
t
5
em que n0 (n0 > 0) é a quantidade estimada de pássaros antes do início do
desmatamento e n(t) é a quantidade existente t anos depois. Então o tempo necessário
para que a população de pássaros dessa espécie se reduza à oitava parte da população
no início do desmatamento é de 7,5 anos.
04. Um produto que custa hoje R$ 100,00 terá seu preço reajustado em 3% a cada mês.
Fazendo-se uma tabela do preço deste produto, mês a mês, obtém-se uma progressão
geométrica de razão 1,03.
08. São dados dois arcos de 60º. Um está sobre uma circunferência de 4 cm de diâmetro e o
outro, sobre uma circunferência de 6 cm de diâmetro. Comparando os comprimentos
desses arcos, pode-se afirmar que o primeiro é o maior.
16. Uma das aplicações dos logaritmos é na medida da intensidade de terremotos. Na
escala Richter, a intensidade I de um terremoto é definida por: I =
2
E
log , em
3
E0
que E é a energia liberada pelo terremoto, em kWh, e E0 = 10 −3 kWh . Assim,
aumentando em uma unidade a intensidade do terremoto, a energia liberada fica
multiplicada por 100.
Questão 27
Gabarito: 06 (02+04)
Número de acertos: 760 (11,10%)
Grau de dificuldade previsto: difícil
Grau de dificuldade obtido: médio
Proposições
01
Percentual de
25,0
incidência (%)
02
04
08
16
32
64
42,1
60,1
21,3
44,0
0,01
0
A questão envolve a aplicação de conhecimentos básicos e fundamentais de alguns
dos principais tópicos do Ensino Médio, gráficos de funções trigonométricas, equações
exponenciais, progressões geométricas, medida do comprimento de arcos e equações
logarítmicas. Nesta questão, o grau de dificuldade previsto pela banca se confirmou como
pode ser observado a partir das freqüências das diversas respostas dos candidatos: 04 –
17,36%; 20 (04+16) – 8,78%; 16 – 6,42%; 18 (02+16) – 5,91%; 22 (02+04+16) – 5,15%; e 02
– 4,96%. Novamente, percebe-se que, na dúvida, os candidatos optam pelo acerto parcial,
assinalando apenas aquela(s) proposição(ões) que têm certeza, neste caso 02 e 04. A
veracidade da proposição 02 era facilmente obtida, bastando ao candidato fazer:
t
2t
−
−
1
1
n(t ) = n0 ⇒ n0 = n0 ⋅ 4 5 ⇒ 2− 3 = 2 5 ⇒ t = 7,5anos . Da mesma forma, para a proposição 04,
8
8
bastava ao candidato montar a seqüência (100; (1,03) ⋅ 100; (1,03) 2 ⋅ 100;...; (1,03) n .100;...) para
verificar que se tratava de uma progressão geométrica conforme afirmava a proposição.
Como se pode observar, a grande responsável pelo erro e pelo espalhamento nesta questão
foi a consideração da proposição 16 como correta, que obteve o alto índice de 43,97% da
preferência dos candidatos. Para verificar que a proposição era falsa, bastava ao candidato
2
E

subtraindo
a
segunda
equação
da
primeira,
tem-se
fazer:
 I = 3 log E

0

 I + 1 = 2 log E1

3
E0
3
.
2
E
E
3
E
1 =  log 1 − log  ⇒ = log 1 ⇒ E1 = E ⋅ 10 2
3
E0
E0 
2
E
Portanto,
a
proposição
é
falsa,
pois
3
2
E1 = E ⋅ 10 ⇒ E1 = 10 10 E é diferente de E1 = 100 E conforme afirma a proposição. É
surpreendente o fato de que 25% e 21,3% dos candidatos tenham considerado as
proposições 01 e 08 como corretas, tendo em vista o nível elementar de dificuldade
envolvido nas duas situações. No caso da proposição 01, bastaria ao candidato calcular
f (0) = 2 sen(3 ⋅ 0 +
π
) ⇒ f (0) = 3 para verificar que o gráfico apresentado não representava a
3
função trigonométrica dada, pois f (0) = −2 . Para verificar a veracidade ou não da
proposição 08, não havia sequer a necessidade do candidato efetuar algum cálculo, bastava
prestar atenção ao fato de que, se os dois arcos dados são de 60º, então o de maior
comprimento está sobre a circunferência de maior raio e não ao contrário, como afirma a
proposição.
Questão 28
Assinale a(s) proposição(ões) CORRETA(S).
01. Em uma clínica médica trabalham cinco médicos e dez enfermeiros. Com esse número
de profissionais é possível formar 200 equipes distintas, constituídas cada uma de um
médico e quatro enfermeiros.
02. Entre os anagramas da palavra ÁGUA, 6 começam por consoante.
04. A partir de 12 pontos distintos marcados numa circunferência podem ser feitos 440
triângulos unindo-se três desses pontos.
08. Um dado (cubo de seis faces congruentes) perfeito, cujas faces estão numeradas de
1 a 6, é lançado duas vezes sucessivamente. A probabilidade de que o produto dos
pontos obtidos seja maior que 12 é de 13/36.
16. O total de números pares que se obtém permutando os algarismos 1, 2, 2, 5, 5, 5 e 6
é 180.
Questão 28
Gabarito: 24 (08+16)
Número de acertos: 245 (3,58%)
Grau de dificuldade previsto: difícil
Grau de dificuldade obtido: difícil
Proposições
01
Percentual de
28,2
incidência (%)
02
04
08
16
32
64
49,0
32,2
42,0
35,2
0,02
0
A questão compreende cinco proposições típicas do Ensino Médio, envolvendo os
conteúdos de Análise Combinatória e Probabilidade. O objetivo da questão era avaliar a
capacidade dos candidatos de aplicar, na resolução de situações-problema, os conceitos de
combinação simples, permutação com repetição e de probabilidade. Segundo os resultados
obtidos, essa foi a questão da prova a ter o menor índice de acerto e, portanto a mais difícil.
As expectativas da Banca a respeito do grau de dificuldade da questão se confirmaram, ou
seja, os candidatos têm dificuldades em aplicar o seu raciocínio combinatório e probabilístico
a situações-problema. No entanto, é surpreendente o fato de que mais de 96% dos
candidatos tivessem dificuldades de trabalhar com estes temas que, além de serem muito
explorados no Ensino Médio e nos vestibulares, são bastante aplicados em situaçõesproblema não só de Matemática como de outras disciplinas, como por exemplo o estudo de
probabilidades na Biologia. Ao analisar o quadro de freqüência de respostas observa-se,
além da resposta correta, um correlato espalhamento, distribuído entre várias respostas, que
são em ordem decrescente de preferência: 02 – 16,39%; 10 (02+08) – 9,41%; 08 – 9,01%;
16 – 5,29%; 04 – 4,73%; 20 (04+16) – 3,99%; 01 – 3,40% e 12 (04+08) – 3,39%.
Novamente, percebe-se que, na dúvida, os candidatos optam pelo acerto parcial,
assinalando apenas aquelas proposições que têm certeza, neste caso 08 e 16, as quais
obtiveram 42% e 35,2% da preferência dos candidatos, respectivamente. A grande
responsável pelo erro e pelo espalhamento nesta questão foi a consideração das
proposições 02 e 04 como corretas, que obtiveram índices de 49% e 32,2%,
respectivamente. A proposição 02 foi a proposição incorreta da prova a ter o maior índice de
preferência dos candidatos. Talvez os candidatos que consideraram a proposição 02 como
P3 = 3!= 6 , sem darem a devida atenção
3!
ao fato de que se trata de uma permutação com repetição e o resultado correto é P32 = = 3 .
2!
No caso da proposição 04, é provável que os candidatos tenham cometido algum erro ao
12!
12!
fazer o cálculo C12,3 =
⇒ C12,3 = 220 , como por exemplo C12,3 =
⇒ C12,3 = 440 . A
9!3!
9!3
proposição incorreta 01 obteve 28,2% da preferência dos candidatos. Uma hipótese para
que os mesmos tenham considerado esta proposição como correta é que tenham feito uso
meramente manipulativo dos dados presentes no enunciado, aliando a isso um raciocínio
equivocado e simplista da situação. Consideraram que uma equipe é formada de um médico
e quatro enfermeiros, como são cinco médicos, fizeram 5 x 4 = 20, mas como são 10
enfermeiros, então colocaram 20 x 10 = 200. A respeito da proposição 08, bastaria ao
candidato determinar o espaço amostral através da tabela abaixo:
correta tenham feito simplesmente
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
13
e confirmando a veracidade da
36
proposição. No caso da proposição 16, as expectativas da banca se confirmaram, ela foi a
proposição correta da prova com maior grau de dificuldade, obtendo o menor índice da
A seguir, calcular a probabilidade do evento, fazendo
preferência dos candidatos, 35,2%.
6! 6!
P63 + P62,3 = +
= 120 + 60 = 180 .
3! 2!3!
Para
resolvê-la,
o
candidato
deveria
fazer:
Questão 29
Assinale a(s) proposição(ões) CORRETA(S).
01. O efeito estufa é a retenção de calor na Terra causada pela concentração de diversos
tipos de gases na atmosfera. Segundo os cientistas, o resultado mais direto do efeito
estufa será o aumento da temperatura do planeta em até 5,8 ºC ao final de 100 anos.
Supondo que nos próximos 100 anos a temperatura do planeta aumente linearmente em
função do tempo, então daqui a aproximadamente 34,4 anos haverá um acréscimo de
2 ºC nessa temperatura.
02. A figura a seguir representa parte do mapa de um país, em que o ponto C(6,0) foi o
epicentro de um terremoto cujos efeitos foram sentidos, no máximo, até um raio de 5 km.
(Considere 1 unidade linear do plano cartesiano correspondendo a 1 km.) Com base na
figura, pode-se afirmar que a região afetada pelo terremoto é representada, nesse
sistema de eixos, pela inequação x 2 + y 2 + 12 x + 11 ≤ 0 .
y
0
(6,0)
x
04. Um projétil desloca-se no plano cartesiano e seus deslocamentos, em metros, na
 x = t +5
horizontal e na vertical, são descritos, respectivamente, pelas equações: 
 y = 3t + 6
em que t ( t ≥ 0 ) representa o tempo em minutos. A distância percorrida pelo projétil
entre o ponto A, para t = 0, e o ponto B, para t = 5 minutos, é de 20 metros.
08. Se, a partir de cada vértice de um cubo de madeira com x (x >2) cm de aresta retirou-se
um cubinho com 1 cm de aresta, então o volume do bloco remanescente, em cm3, após
a retirada dos pequenos cubos, é V = ( x 2 + 2 x + 4 )( x − 2 ) .
Questão 29
Gabarito: 09 (01+08)
Número de acertos: 984 (14,40%)
Grau de dificuldade previsto: difícil
Grau de dificuldade obtido: médio
Proposições
01
Percentual de
67,0
incidência (%)
02
04
08
16
32
64
34,0
33,0
45,0
0,06
0
0
Nesta questão, esperava-se que o candidato aplicasse seus conhecimentos sobre
geometria analítica, geometria espacial, polinômios e equações algébricas. Além da
resposta correta 09 (01+08), outras respostas predominaram no quadro de freqüência, que
são, em ordem decrescente de preferência: 01 – 24,18%; 05 (01+04) – 7,57%; 08 – 6,03%;
10 (02+08) – 5,81%; 03 (01+02) – 5,50%; 02 – 5,24%; 11 (01+02+08) – 5,15%; 13
(01+04+08) – 4,80%; 04 – 4,58%; 06 (02+04) – 4,07% e 12 (04+08) – 3,91%. O fato do
índice da resposta 01 ser superior ao da resposta correta vem, novamente, reforçar a tese
de que os candidatos preferem não arriscar e, na dúvida, optam pelo acerto parcial. A
proposição 01 foi a proposição correta da prova a ter o maior índice de preferência dos
candidatos (67%), pois tratava-se de uma situação que tanto poderia ser resolvida usando
os conhecimentos de funções, em particular de função linear, como de geometria analítica,
equação da reta que passa por dois pontos. A grande responsável pelo erro e pelo
espalhamento nesta questão foi a consideração das proposições 02 e 04 como corretas. Em
relação à proposição 02, causa estranheza o fato de que 34% dos candidatos a tenham
considerado como correta, já que bastava ao candidato utilizar a ajuda do formulário e
desenvolver
a
inequação
a
seguir
para
verificar
que:
2
2
2
2
2
2
2
No caso da proposição
(x − 6) + ( y − 0) ≤ (5) ⇒ x + y − 12x + 11 ≤ 0 ≠ x + y + 12 x + 11 ≤ 0 .
incorreta 04, também causa estranheza o índice que ela alcançou (33%), pois envolvia dois
tópicos elementares de geometria analítica, que são a aplicação da equação paramétrica de
uma reta e o cálculo da distância entre dois pontos. O que mais surpreende em relação ao
índice obtido é que, para verificar a veracidade ou não da proposição, bastava ao candidato
aplicar os valores de t nas equações dadas para a obtenção dos pontos A(5,6) e B(10,21) , e
a seguir aplicar a fórmula da distância entre dois pontos que estava no formulário para o
cálculo da mesma. Uma possibilidade a ser considerada para que os candidatos tenham
indicado esta proposição como correta é o uso meramente manipulativo dos dados
presentes no enunciado aliado a algum erro grosseiro de cálculo, como por exemplo:
d AB = (10 − 5) + (21 − 6 ) = 20 ou d AB = (10 + 21) − (5 + 6) = 20 . No caso da proposição 08,
esperava-se um índice superior aos 45%, já que para verificar sua veracidade bastava ao
candidato utilizar-se do auxílio do formulário para determinar o volume de um cubo de aresta
x cm. Como um cubo tem oito vértices e de cada um retirou-se um cubo de aresta 1 cm,
fica-se com: Vbloco = x 3 − 8 cm3. A seguir, o candidato deveria aplicar a propriedade distributiva
(
)
ao produto V = x 2 + 2 x + 4 ( x − 2) para verificar que Vbloco e V eram iguais, isto é, eram duas
representações analíticas distintas do mesmo objeto matemático.
Questão 30
Assinale a(s) proposição(ões) CORRETA(S).
01. O elemento a 64 da matriz A = (a i j ) de ordem 8, onde a i j = (− 1)i + j ⋅
2i
, é 3.
j
02. O triângulo ABC, cujas coordenadas dos vértices são A(0,0), B(0,2) e C(10,20), tem 20
unidades de área.
t
t t
04. Para duas matrizes A e B de mesma ordem, vale sempre: (AB) = A B .
08. A matriz inversa da matriz A =
1
2
−5 1
é a matriz A − 1 =
1
−
1
5
1
2 .
1
16. O elemento b23 da matriz B = At, onde A = (ai j)3x 2, e ai j = 2i + j, é 8.
Questão 30
Gabarito: 17 (01+16)
Número de acertos: 1068 (15,62%)
Grau de dificuldade previsto: fácil
Grau de dificuldade obtido: médio
Proposições
01
Percentual de
57,0
incidência (%)
02
04
08
16
32
64
26,0
47,0
28,0
52,0
0,01
0
A questão compreende cinco proposições, envolvendo alguns dos principais objetivos
do estudo de matizes e determinantes como: identificar os elementos de uma matriz e os
tipos mais freqüentes de matrizes; reconhecer e aplicar as propriedades das operações com
matrizes; determinar as matrizes transposta e inversa de uma matriz dada; calcular
analiticamente a área de um triângulo utilizando o cálculo de determinante. A Banca
considerou a questão fácil, mas acabou tendo grau médio de dificuldade. Essa foi a segunda
questão mais fácil de toda a prova, demonstrando que o tema matrizes e determinantes é
bem explorado no Ensino Médio. Embora considerado pelos estudantes como muito fácil,
esperava-se um índice superior ao obtido pela questão. Por outro lado, fica a dúvida se o
resultado seria o mesmo caso a Banca exigisse nas proposições uma aplicabilidade destes
tópicos como ocorreu em outras questões da prova. Ainda que somente 15,62% dos
candidatos tenham apontado como corretas apenas as proposições 01 e 16, estas
proposições obtiveram um bom índice da preferência dos candidatos, 57% e 52%,
respectivamente. Cabe destacar a facilidade com que ambas as proposições podiam ser
resolvidas. No caso da proposição 01, o candidato deveria substituir os valores de i = 6 e
2i
6 + 4 2(6)
j = 4 em aij = (−1)i + j . ⇒ a64 = (− 1) .
obtendo a64 = 3 conforme afirmado no enunciado.
j
4
Da mesma forma, na proposição 16, tem-se b23 = a32 , como a32 = 2(3) + 2 = 8 , então b23 = 8 . A
proposição 02 obteve índice de 25,72%, ou seja, mais de um quarto do total dos candidatos
teve dificuldades de calcular a área do triângulo ABC , seja através do cálculo analítico com
aplicação do uso de determinante ou através da geometria plana utilizando o cálculo de
áreas de figuras planas. Nesta questão, as outras respostas que predominaram no quadro
de freqüência, foram: 01 e 21 – 7,97%; 04 – 7,03%; 05 (01+04) – 5,66%; 20 (04+16) –
5,28%; 12 (04+08) – 4,45%; 16 – 4,12% e 08 – 3,95%. Mais uma vez, fica evidente no
quadro de freqüência de respostas da prova a preferência dos candidatos de não arriscar e
tirar proveito do acerto parcial, como se pode observar através dos índices das respostas 01
e 16. A grande responsável pelo erro e pelo espalhamento nesta questão foi a consideração
das proposições 04 e 08 como corretas, com 47% e 28% da preferência dos candidatos,
respectivamente. A proposição 04 foi a proposição incorreta da prova com o segundo maior
índice de preferência dos candidatos. Talvez a maioria dos candidatos que assinalou tal
proposição como correta tenha aplicado de forma equivocada as propriedades das potências
numéricas às matrizes, sem levar em conta as propriedades do produto de matrizes. No
caso da proposição 08, bastava ao candidato fazer o produto da matriz A dada pela sua
suposta inversa também dada A−1 para verificar que o resultado é diferente da matriz
identidade I 2 e, portanto, a proposição era falsa.