CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA DE MINAS GERAIS
DIRETORIA DE PESQUISA E PÓS – GRADUAÇÃO
PROGRAMA DE PÓS – GRADUAÇÃO EM MODELAGEM MATEMÁTICA E
COMPUTACIONAL
UMA ABORDAGEM NUMÉRICA PARA
DETERMINAÇÃO DE TENSÕES E
DEFORMAÇÕES EM CILINDROS DE
LAMINADORES QUÁDRUOS
André Luiz Martins Pires Horta
CEFET - MG
Belo Horizonte
2009
1
André Luiz Martins Pires Horta
UMA ABORDAGEM NÚMERICA PARA
DETERMINAÇÃO DE TENSÕES E
DEFORMAÇÕES EM CILINDROS DE
LAMINADORES QUÁDRUOS
Dissertação apresentada ao Programa
de
Pós-Graduação
em
Modelagem
Matemática e Computacional do Centro
Federal de Educação Tecnológica de
Minas Gerais, como
requisito parcial
para obtenção do título de Mestre em
Modelagem Matemática e Computacional
Orientador: Prof. Dr.Yukio Shigaki
Co-Orientador:Prof.Dr.Felício Bruzzi Barros
Belo Horizonte
2009
2
SERVIÇO PÚBLICO FEDERAL
CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA DE MINAS GERAIS
COORDENAÇÃO DO CURSO DE MESTRADO EM MODELAGEM MATEMÁTICA E
COMPUTACIONAL
UMA ABORDAGEM NÚMERICA PARA DETERMINAÇÃO DE TENSÕES E
DEFORMAÇÕES EM CILINDROS DE LAMINADORES QUÁDRUOS
Dissertação de Mestrado apresentada por André Luiz Martins Pires Horta,
em 31 de março de 2009, ao curso de Mestrado em Modelagem
Matemática e
Computacional do CEFET-MG, e aprovada pela banca examinadora constituída
pelos professores:
Prof. Dr.Yukio Shigaki (orientador)
Centro Federal de Educação Tecnológica de Minas Gerais
Prof. Dr.Felício Bruzzi Barros ( co-orientador)
Universidade Federal de Minas Gerais
Prof. Dr. Gray Farias Moita
Centro Federal de Educação Tecnológica de Minas Gerais
Prof. Dr. José Maria Ramón Caccioppoli
Universidade Federal de Minas Gerais
Visto e permitida a impressão.
Belo Horizonte,
Prof. Dr. Sérgio Ricardo de Sousa
Coordenador do Curso de Mestrado em Modelagem Matemática e Computacional
3
DEDICATÓRIA
Dedico este trabalho
A minha esposa e ao meu filho , pela
compreensão durante minha ausência
nos vários momentos de pesquisa e
dedicação no trabalho a esse projeto
A
minha
mãe
pelo
incentivo e
tolerância para com minha ausência,
permitindo que eu dedicasse tempo ao
estudo.
4
AGRADECIMENTOS
Em primeiro momento agradeço a Deus, pela saúde e proteção nas longas
estradas que enfrentei para conclusão desse trabalho.
Ao meu orientador, professor DR. YUKIO SHIGAKI, por sua atenção,
orientação, paciência, incentivo e sabedoria durante todas as reuniões que tivemos.
Ao meu Co-Orientador, professor DR. FELÍCIO BRUZZI BARROS, que
mesmo mudando de instituição continuou me dando todo apoio e atenção
no
desenvolvimento desse trabalho.
Ao Coordenador do Mestrado em Modelagem Matemática e Computacional,
professor DR SÉRGIO RICARDO DE SOUSA, que tem buscado sempre incentivar a
pesquisa aplicada aos alunos do curso.
Ao SENAI, empresa onde trabalho e que tenho tanto orgulho de fazer parte, e
a pessoa do Sr. Alexandre Magno Leão, Diretor Regional do SENAI-MG, pelo apoio
e incêntivo.
À Solidminas pelo empréstimo do software SolidWorks.
E a todos que de alguma forma contribuíram para esta construção.
5
RESUMO
Este trabalho consiste em desenvolver uma abordagem numérica para
determinar
as tensões e deformações em cilindros de
laminadores quádruos.
Foram utilizados para esta abordagem dois métodos, a saber: O Método dos
Coeficientes de Influência (MCI), que tem como propósito
fornecer a carga de
laminação atuante nos cilindros, e o Método de Elementos Finitos (MEF), que tem
como objetivo
determinar as tensões e deformações sofridas nos cilindros de
trabalho e encosto, quando solicitados pela carga de laminação anteriormente
determinada pelo MCI.
Nestas simulações foi considerado, também, o carregamento do torque nos
cilindros. Os resultados demonstraram concordância entre os perfis obtidos por
ambos os métodos, mas as tensões de contato resultaram discrepantes. Com este
modelo foi possível identificar antecipadamente regiões dos cilindros que possam
sofrer maior concentração de tensão e deformação, de forma a evitar possíveis
danos tais como:
fadiga, desgaste e até a
quebra dos cilindros nas regiões
identificadas.
Palavras-Chaves: Laminação de produtos planos, Cilindros, Elementos Finitos.
6
ABSTRACT
This study aims to calculate the stress and deformations in roll rolling of 4-hi
rolling mills. It was employed two methods for this analysis, namely: The Method of
Coefficients of Influence (MCI), which provides the rolling load acting on the cylinders
and the Finite Element Method (FEM), which aims to determine the stress and
deformations in the rolls and back to work when requested by the rolling load of
previously determined by the ICM method. In these simulations was also considered
loading due to the torque on the roll. The results showed a good agreement with the
practical situations, and it was possible to identify in advance regions of rolls that
may have higher stress concentration and deformation, in order to avoid possible
damage such as fatigue, wear and even the breaking of cylinders in the regions
identified.
Key Words: Flat Rolling; Rolls; Finite Elements.
7
LISTA DE FIGURAS
FIGURA 1
Resfriamento dos cilindros de laminação... ..........................................25
FIGURA 2
Resfriamento do cilindro de trabalho em uma cadeira quádruo ..........26
FIGURA 3 Conjunto de cilindros de trabalho e encosto............. .............................28
FIGURA 4 Montagem em forma de cadeira........................ ....................................28
FIGURA 5 Camisa para cilindro................................................................................29
FIGURA 6 Problemas devido à flexão dos cilindros de laminação................ ..........33
FIGURA 7 Laminador quádruo....... ..........................................................................33
FIGURA 8 Flexão dos cilindros........... .....................................................................34
FIGURA 9 Representação esquemática da força de laminação................................34
FIGURA 10 Curvas típicas ligando o ângulo de ataque.......... .................................35
FIGURA11 Representação do ângulo de ataque......................................................36
FIGURA12 Relação do coeficiente de atrito com a temperatura......... .....................36
FIGURA13 Relação entre a carga e o diâmetro do cilindro.......................................38
FIGURA14 Descrição das variáveis que definem as coroas ....................................39
FIGURA 15 Braço de alavanca na laminação..................... ......................................40
FIGURA 16 Bloco para análise de tensões ...........................................................................45
FIGURA 17 Tensões agindo nos blocos................................... ................................46
FIGURA 18 Representação esquemática da região de deformação na laminação..46
FIGURA 19 Discretização de um laminador quádruo para o MCI.............................49
FIGURA 20 Desenho esquemático do processo de laminação.................................53
FIGURA 21Subdivisão do cilindro e da tira................................................................54
FIGURA 22 Exemplo de aplicação do Método dos Elementos Finitos......................58
FIGURA 23 Sólido tridimensional, vetor de deslocamento de um ponto...................59
FIGURA 24 Elemento representativo do estado de tensão.......................................60
FIGURA 25 Elemento tetraédrico de 10 nós............................... ..............................64
FIGURA 26 Elemento tetraédrico de 10 nós..............................................................65
FIGURA 27 Fotomicrografia (100x) de trincas na superfície e na subsuperfície em
um cilindro cementado e encruado.......................................................72
8
FIGURA 28 Concentração geométrica de tensão.................. ...................................74
FIGURA 29 Lascamento em cilindros de laminação..................................................75
FIGURA 30 Fraturas em cilindros de laminação .................................. ...................75
FIGURA31 Representaçãoesquemática de uma cadeira de quádruo................ ......79
FIGURA 32 Pressão de contato laminador 1........................................... .................80
FIGURA 33 Representação da reta passando por 2 pontos P1 e P2........................81
FIGURA 34 Representação em cada passe do Perfil do Laminador 1.......... ...........87
FIGURA 35 Representação das cargas passe do Perfil do Laminador 1.................87
FIGURA 36 Pressão WR do laminador 2............................. .....................................88
FIGURA 37 Representação em cada passe do Perfil do Laminador 2.................... .91
FIGURA 38 Representação das cargas passe do Perfil do Laminador 2............. ....92
FIGURA 39 Cilindros de Trabalho................. ...........................................................................93
FIGURA 40 Cilindro de Encosto................ ................................................................93
FIGURA 41 Aplicação da Simetria no modelo................ ......................................................94
FIGURA 42 Aplicação da restrição do Tipo Fixo ao modelo........... ..........................94
FIGURA 43Aplicação da restrição utilizando um plano de referência ao modelo......95
FIGURA 44 Componentes de contato....................................................................... 96
FIGURA 45 Componentes de contato dos cilindros............................... ...................96
FIGURA 46 Cargas de laminação e torque aplicados................... ............................97
FIGURA 47 Modelo com geração de malha.............................. ................................98
FIGURA 48 Resultados do Laminador1, sem torção e com refinamento da malha.100
FIGURA 49 Malha gerada no Laminador1 com refinamento.... .............................101
FIGURA 50 Resultado do deslocamento máximo em Y sem o toque com a malha
refinada........... ......................................................................................101
FIGURA 51 Resultado da deformação máximo em Y sem o torque com a malha
refinada............................. ....................................................................102
FIGURA 52 Resultado da tensão de von Mises com o torque na malha refinada..103
FIGURA 53 Malha gerada no laminador I com malha refinada com torque............103
FIGURA 54 Resultado do deslocamento máximo com o toque e a malha refina .104
FIGURA 55 Pressão de Contato entre os cilindros, sem o torque...........................105
FIGURA 56 Representação dos pontos da PC do COSMOS, s/ torque..................106
FIGURA 57 Carga entre os cilindros de trabalho e encosto do laminador 1 s/ tor..107
FIGURA 58 Pressão de contato entre os cilindros, sem considerar a torção e com
9
malha refinada........................................ ............................................107
FIGURA 59 Resultado da tensão de von Mises com o torque e com refinamento da
malha.....................................................................................................108
FIGURA 60 Resultado da PC com o torque e com refinamento...................... .......109
FIGURA 61 Malha gerada no laminador 2 com a malha refinada e o torque.........109
FIGURA 62 Resultado do deslocamento máximo em Y com o torque e a malha
refinada...................... ..........................................................................109
FIGURA 63 Resultado da tensão de von Mises sem o torque e com refinamento
da Malha.............................................. ................................................110
FIGURA 64 Resultado da PC sem o torque e com refinamento da malha..............110
FIGURA 65 Malha refinada sem o torque........................ .......................................111
FIGURA 66 Resultado do deslocamento máximo em Y sem o toque e com a
malha refinada.............................. .....................................................111
FIGURA 67 Resultados via MEF e MCI/Berger........................... ...........................113
FIGURA 68 Resultados dos perfis, via MEF e MCI/Berger............... .....................114
FIGURA 69 Carga distribuída de laminação no contato entre os cilindros............116
FIGURA 70 Cargas de contato entre cilindros, obtidas por MCI/Berger (linha
contínua)e MEF sem o torque..............................................................116
FIGURA 71 Cargas de contato entre cilindros....................................................................117
FIGURA 72 Representação da PC no modelo de elementos finitos................ ......118
FIGURA 73 Diferenças nas pressões de contato cilindro de trabalho e encosto....119
FIGURA 74 Perfis finais da chapa laminada......................................... ..................121
FIGURA 75 Carga de laminação distribuída no contato entre o cilindro.................121
FIGURA 76 Perfis finais da chapa , obtidas pelo MCI/Berger e
MEF com o torque................................... ................................................................122
FIGURA 77 Perfis finais da chapa laminada, obtidas por MCI/Berger e MEF. sem o
torque....................................................................................................123
FIGURA 78 Cargas de contato entre cilindros, obtidas por MCI/Berger
(linha contínua) e MEF com o torque.................................................124
FIGURA 79 Cargas de contato entre cilindros, obtidas por MCI/Berger (linha
contínua) e MEF sem o torque.............................................................125
FIGURA 80 Representação da pressão de contato em uma seção transversal
do cilindro............................................................................................127
10
LISTA DE TABELAS
TABELA 1 Modos de falhas na superfície e suas causas....................................73
TABELA 2 Resultados da pressão Wr obtido do programa MCI/Berger a cada
100 mm do semi – comprimento............................................................81
TABELA 3 Resultado da constante k correspondente a cada 100 mm......... ......83
TABELA 4 Resultado do torque a cada 100 mm ao longo do cilindro de
trabalho do laminador 1.........................................................................86
TABELA 5 Resultados da pressão Wr obtido do programa MCI/Berger
a cada 25 mm do semi-comprimento do laminador 2......................89
TABELA 6 Resultado da constante k correspondente a cada 100mm
Laminador 2........................................................................................89
TABELA 7 Torque do laminador 2.........................................................................90
TABELA 8 Parâmetros da malha do laminador 2.................................................98
TABELA 9 Parâmetros da malha do laminador 1..................................................99
TABELA 10 Análise da Tensão, deformação e deslocamento do Laminador 1,
sem o Torque.....................................................................................102
TABELA 11 Análise da Tensão, deformação do Laminador 1, com torque..........104
TABELA 12 Análise da Tensão, deformação do Laminador 1 e 2........................111
TABELA 13 Carga distribuída obtida pelo MCI/Berger Laminador 1......................120
TABELA 14 Análise dos resultados dos perfis dos lamadores...............................126
11
LISTA DE ABREVIATURAS
ABM – Associação Brasileira de Metais
CJ- Coroa Absoluta
Cr – Coroa Relativa
CAD - Desenho Através do Computador
MEF – Método dos Elementos Finitos
MCI – Método dos Coeficientes de Influência
PC- Pressa de Contato
Wr - Cilindro de Trabalho
12
LISTA DE SIGLAS
µ - Coefiente de Atrito
K – Coeficiente para determinação da pressão final de cada segmento
13
SUMÁRIO
1
INTRODUÇÃO.................................................................................................17
1.1 Caracterização do Problema.....................................................................17
1.2 Motivações................................................................................................18
1.3 Objetivos. .................................................................................................19
1.4 Estruturação deste Trabalho.....................................................................20
2
O PROCESSO DA LAMINAÇÃO DE PRODUTOS PLANOS..........................21
2.1 Processo de resfriamento dos cilindros.....................................................24
2.2 Cilindros de laminação...............................................................................27
2.2.1 Cilindros de trabalho.........................................................................29
2.2.2 Cilindro de Encosto ( Back-Up Rolls)................................................29
2.2.3 Retificação de cilindros.....................................................................30
2.3.4 Cálculo da profundidade de retificação dos cilindros........................31
2.2.5 Tratamento Térmico Diferencial nos cilindros de laminação.............32
2.2.6 Perfil dos cilindros de laminação.......................................................32
2.2.7 Determinação do diâmetro dos cilindros...........................................35
2.2.8 Coroa absoluta e coroa relativa da chapa.........................................38
3 TORQUE E CARGA DE LAMINAÇÃO..............................................................39
3.1 Torque na Laminação de Chapas..............................................................39
3.2 Cálculo da carga de laminação de chapas a frio........................................43
3.2.1 Deformação Homogênea..................................................................43
3.2.2 Cálculo da Carga de Laminação Através das Tensões Locais..... ..44
4 SOBRE O MÉTODO DOS COEFICIENTES DE INFLUÊNCIA.........................49
4.1 Introdução....................................................................................................49
4.2 O Desenvolvimento do método................................................................... 50
4.2.1 Características principiais do método MCI/Berger..............................51
4.3 Modelo de cálculo de carga de laminação....................................................51
4.4 MCI/Berger....................................................................................................54
14
4.4.1Compatibilidade no contato cilindro-cilindro..........................................56
5 SOBRE O MÉTODO ELEMENTOS FINITOS.....................................................58
5.1 Introdução ao Método dos Elementos Finitos.............................................58
5.2 Elemento Tetraédrico Quadrático de 10 Nós..............................................59
5.3 Campo de Deslocamentos, (OÑATE, 1995)............................................... 59
5.4 Campo de Tensões e Deformações, (OÑATE, 1995).................................60
5.5 Princípio da Energia Potencial Estacionária, (ASSAN, 1996).....................61
5.6 Discretização do Campo de Deslocamento, (OÑATE, 1995)......................62
5.7 Elemento Isoparamétrico.............................................................................64
5.8 Equilíbrio do Elemento, (OÑATE, 1995)......................................................67
6 DANOS NA LAMINAÇÃO...................................................................................70
6.1 Introdução.....................................................................................................70
6.2 Modelos e Falha por Fadiga Superficial Contato Dinâmico
(NORTON,2000)...........................................................................................70
6.3 Modos de Falhas na Superfície e suas Causas...........................................72
7 MODELO DE LAMINADORES QUÁDRUOS EM ELEMENTOS FINITOS.........76
7.1 Introdução.....................................................................................................76
7.1.1 Características do primeiro modelo..................................................... 76
7.2 Estrutura Geometria dos Laminadores Modelados em Elementos Finitos.....80
7.2.1 Determinação da Pressão Wr do laminador 1 no MCI/Berger............80
7.2.2 Torque aplicado ao modelo..................................................................83
7.3 Resultados do laminador 1 no MCI/Berger....................................................87
7.3.1 Determinação da Pressão Wr do laminador 2 no MCI/Berger..............88
7.3.2 Determinação do torque do laminador 2 no MCI/Berger......................90
7.4 Resultados do laminador 2 no MCI/Berger....................................................91
7.4.1 Representação da distribuição de carga em cada passe do laminador
2 no programa MCI/Berger..................................................................91
7.5 Aplicação das Condições de Contorno............................................................92
7.5.1 Restrições aplicadas ao modelo no progama COSMOS Works..........93
7.5.2 Restrições de Simetria aplicado ao modelo........................................93
7.5.3 Aplicação da restrição ao cilindro de encosto....................................... 94
7.5.4 Aplicação da restrição ao cilindro de trabalho.......................................95
7.5.5 Condições de Contato entre os Cilindros..............................................95
7.5.6 Aplicação das cargas.............................................................................97
15
7.5.7 Geração da malha..................................................................................97
8 RESULTADOS FINAIS.....................................................................................100
8.1 Resultados do laminador 1, utilizando o programa COSMOS Works........100
8.1.1 Resultados do Laminador 1, sem Torção e c/ malha refinada..........100
8.1.2 Resultados do Laminador 1, com Torção e..c/ malha refinada.........103
8.1.3 Resultado do Laminador 1, da Pressão de Contato (PC) sem
torção e com a malha refinada.........................................................104
8.2 Resultados do laminador 2, utilizando o programa COSMOS Works.......108
8.2.1 Resultados do Laminador 2, com torção e com a malha a refinada.108
8.2.2Resultados do Laminador II, sem o Torque e com a malha refinada110
8.3 Análise dos Resultados.............................................................................112
8.3.1 Análise dos Resultados da Tensão de von Mises, Deslocamento
em Y e deformação dos laminadores I e II ( Tabela 12)...................112
8.3.2 Análise da Comparação do Perfil Gerado pelo Programa
MCI/Berger e Elementos Finitos do laminador 1.............................120
8.3.3 Análise da Comparação da Pressão de Contato Gerada
pelo Programa MCI//Berger e Elementos Finitos...........................115
8.3.4 Análise da Comparação do Perfil Gerado pelo Programa
MCI/Berger e Elementos Finitos do laminado 2..............................120
8.3.5 Resultado do Perfil de Contato entre os cilindros do laminador 2
com o torque......................................................................................122
8.3.6 Resultado do Perfil de Contato entre os cilindros do laminador 2
sem o torque......................................................................................123
8.3.7 Análise Resultado Final da Pressão de Contato entre os cilindros
do laminador 2.....................................................................................124
9 CONCLUSÕES..............................................................................................126
8.6 Proposta para Trabalhos Futuros................................................................129
APÊNDICE A – Problemas de contato (NICHOLSON,2003)............................130
APÊNDICE B – Comandos MCI/Berger............................................................133
APÊNDICE C – Exemplos de Danos em cilindros de laminação......................171
REFEÊNCIAS....................................................................................................175
16
1- INTRODUÇÃO
1.1- Caracterização do Problema
O problema constitui em uma abordagem numérica nas análises de tensões
e deformações, ocasionadas pela pressão de contato entre os cilindros e a chapa.
Para esta abordagem foram utilizados dois métodos o Método de Coeficiente
de Influência (MCI) ), o qual fornece a carga de laminação, considerando a deflexão
dos cilindros, (PAWELSKI et al., 1985)
e o Método de Elementos Finitos (MEF),
que fornece a tensão e a deformação, além do torque que foi considerado nos
resultados obtidos. Com estes simuladores numéricos foi possível identificar as
regiões onde ocorrem maior concentração de tensão e deformação nos cilindros
durante a deformação plástica da chapa.
O
uso
destes
simuladores
contribui
significativamente
para
o
dimensionamento correto dos cilindros, possibilitando a sua otimização. Tanto a
simulação quanto a otimização têm evoluído ao longo de cada ano, e o seu
desempenho tem demonstrado considerável melhoria
à medida que cresce
a
capacidade dos computadores (KOPP, 1996).
O laminador adotado na simulação deste trabalho é o do tipo quádruo, por
sua ampla utilização nas indústrias. Este tipo de laminador é composto por 4
cilindros, sendo dois de trabalho e dois de encosto. A disposição desses cilindros é
de forma que os cilindros de trabalho operem em contato com a chapa, e
os
cilindros de encosto em contato com os cilindros de trabalho.
Quando estes cilindros estão em operação, surgem grandes cargas de
laminação, que os deformam elasticamente por flexão, por esforço cortante e
achatamento localizado. Estas cargas aparecem durante a deformação plástica da
tira ou chapa.
Durante este processo, os cilindros sofrem desgastes, fadiga, trincas,
lascamento e até rupturas, ocasionadas por elevadas tensões, provocadas pela
ação das cargas de laminação.
17
1.2 - Motivações
A motivação em desenvolver este projeto tem como premissa contribuir para
o campo da ciência metalúrgica, mais especificamente a laminação de produtos
planos em laminadores quádruos. Esse tipo de laminadores são muito utilizados no
setor siderúrgico que busca produzir de forma eficiente produtos cada vez mais
planos.
Esta preocupação por parte desse setor em produzir produtos planos com
alta qualidade, tem haver em grande parte com o aumento da vida útil dos cilindros
de laminação, que durante seu processo sofrem grandes esforços, ocasionando o
aparecimento de tensões e deformações no conjunto cilindro de trabalho e encosto.
Esses esforços causam danos nos cilindros que se manifestam em forma de
trincas, encruamento, lascamento e fadiga. Como resultado estes danos ocasionam
imperfeição no perfil das chapas.
Sabe-se que a maioria dos danos causados em cilindros de laminação, estão
relacionados diretamente à magnitude das tensões e deformações que surgem
durante o processo de laminação.
Por outro lado, existe uma dificuldade grande em se considerar a carga de
laminação distribuída ao longo da largura da tira. Os modelos mais completos
consideram a modelagem da tira em elementos finitos e os cilindros como rígidos
(SHIGAKI, 2001), o que impossibilita a análise de tensões que surgem nesses
mesmos cilindros. Além disso, nenhum dos modelos considerou o efeito do torque
sobre a distribuição de tensões sobre os cilindros.
Dessa forma a motivação em desenvolver este trabalho esta ligado a
abordagem numérica obtido pelos métodos MCI e MEF, utilizando
modelos de
cilindros de laminadores quádruos, para análise de tensão e deformação
considerando a carga do torque e sem considerá-la.
18
1.3-Objetivos
O objetivo geral desse trabalho consiste em uma abordagem númerica para
determinar as tensões e deformações em cilindros de laminadores quádruos. Para
esse fim foram utilizados dois métodos o Método dos Coeficientes de Influência
(MCI), que fornece a carga de laminação, e o Método de Elementos Finitos que
determina as tensões e deformações nos cilindros de laminação.
Dessa forma, esse trabalho propõe os seguintes objetivos específicos:

Conhecer o funcionamento do MCI/Berger;

Determinar as cargas de laminação, através do MCI/Berger;

Aplicar o Método de Elementos Finitos para identificar as regiões de
tensão e deformação nos cilindros;

Comparar os resultados de perfis e pressão de contato gerados pelo
MCI/Berger e Método de Elementos Finitos.
19
1.4 Estruturação deste Trabalho
A apresentação deste trabalho não está na ordem cronológica do
desenvolvimento realizado mas, por uma questão de clareza, serão apresentadas,
no Capítulo 2 a contextualização teórica do trabalho, em relação aos processos de
laminação, resfriamento dos cilindros, tipos, emprego dos materiais empregados na
construção dos cilindros e seus tratamentos.
O Capítulo 3 apresenta de forma objetiva os principais elementos do torque e
carga de laminação, formulação do método de Bland e Ford.
O Capítulo 4, um dos mais importantes desse trabalho, trata-se do método
dos coeficientes de influência que foi amplamente utilizado no desenvolvimento do
modelo. Este capítulo traz informações das características e desenvolvimento do
cálculo da carga de laminação ao longo do comprimento do cilindro.
O Capítulo 5 trata sobre o Método dos Elementos Finitos, apresenta o
desenvolvimento das equações empregadas no modelo e suas principais
formulações.
O Capítulo 6 apresenta de forma resumida informações sobre os danos
causados na laminação, os modelos e as falhas ocasionadas por fadiga superficial
de contato dinâmico.
O Capítulo 7 trata sobre o modelo de laminadores quádruos em elementos
finitos. Os resultados desse modelo em MEF, foram obtidos pelo programa do
COSMOS Works, que é um sub-programa do Solidworks 2008.
O Capítulo 8 apresenta os resultados finais com e sem o torque de
laminação, a comparação dos resultados do MCI/Berger com o método de
elementos finitos, e os perfis da pressão de contato dos modelos estudados.
O Capítulo 9, finalmente, traz as conclusões finais desse trabalho e
proprostas de trabalhos futuros.
20
2- O PROCESSO DE LAMINAÇÃO DE PRODUTOS PLANOS
Segundo Edwards (1973) em 1904 construiu-se o primeiro laminador a frio
com motores CC independentemente controlados. Dez anos mais tarde surge outro
laminador a frio com tração entre as cadeiras e uma bobinadeira. O primeiro
laminador a frio de 4 cilindros e quatro cadeiras foi instalado nos Estados Unidos no
ano de 1926.
Hoje, existem os mais variados tipos de equipamentos de laminação, com 4, 6
e até de 20 cilindros de laminação, utilizando sistemas sofisticados de controle de
perfis.
De uma maneira sintética, a laminação consiste basicamente na passagem de
uma material por dois cilindros de trabalho, instalados em cascata (tandem) e girando
em sincronismo, de modo a reduzir a espessura da tira a um valor desejado. Este
processo pode ser feito a quente ou a frio, conforme apresenta a Figura 2.1.
Figura 2.1 – Processo de Laminação de chapa
(RIZZO, 2001)
O par de cilindros de trabalho motorizado sempre estará em contato com o
material processado. A função dos cilindros é diminuir o curvamento ou flexão de todo
o conjunto. Esta flexão tem origem na reação da chapa à deformação e será
minimizada utilizando cilindros de encosto com medidas de diâmetros próximos à
largura da mesa dos cilindros.
21
Segundo Rizzo (2001), inicialmente, a tira é deformada elasticamente até que
o nível de tensão seja suficiente para provocar deformação plástica permanente. Na
região de entrada,
a velocidade da chapa é inferior à velocidade periférica dos
cilindros. À medida que a espessura diminui, a velocidade da chapa aumenta em
função da necessidade de manter constante a vazão do material, admitindo-se que a
densidade não é modificada pela redução. Finalmente, conforme a chapa avança pela
região de deformação, sua velocidade torna-se igual à velocidade dos cilindros de
trabalho. Este ponto é identificado como ponto neutro. Forças horizontais de atrito
puxam a chapa em direção aos rolos. Este processo é chamado de mordida da chapa
As variáveis principais controladas na laminação a frio são a espessura de
saída e a forma (ou planicidade). O perfil e a forma não devem ser confundidos.
Beal (1991), define o perfil como a distribuição de espessura ao longo da
largura da tira. A forma por sua vez, é definida por Bryant et. al. (2008), como o grau
de empeno transversal da tira. Esse empenamento deve-se a uma distribuição não
uniforme de esforços transversais durante a compressão nas cadeiras, o que causa
alongamentos diferentes em fatias adjacentes da tira.
Segundo Pawelski (1985), a distribuição de carga na redução da espessura
na direção do comprimento da tira de um cilindro quádruo pode ser obtida por um
modelo matemático e numérico. Esse modelo utiliza conhecimentos clássicos de
soluções analíticas desenvolvidos para laminação, gerando informações numéricas
aproximadas na direção da largura da tira. No propósito desse trabalho utilizou-se o
método de coeficiente de influência MCI/Berger.
Esse modelo fornece as seguintes informações:

perfil da tira

distribuição da força de laminação

distribuição das cargas entre cilindro de trabalho e o de encosto

distribuição de tensões a ré e à frente
22
2.1- Cilindros de Laminação
Segundo Gomi (1981), os cilindros são componentes de destaque na
laminação, visto que mantêm contato direto com o produto acabado, sendo
responsável pela forma e aspecto da tira. Por isso devem possuir todo um crítico de
qualidade e acabamento de forma a obter um produto laminado plano. Outro fator
que os colocam nesta posição é o elevado preço, chegando a ser o terceiro custo de
uma usina siderúrgica.
O material usado na fabricação dos cilindros é uma liga de ferro-carbono, com
o carbono variando de 0,50% a 3,80%, composta dos elementos Fe, C, Mn, Si, P; e
para melhorar suas propriedades físicas e mecânicas são adicionados elementos de
liga tais como Cr, Ni, W, Ti, Mo, e V.
Ainda segundo Gomi (1981), os cilindros podem ser:

Cilindros de trabalho: Mantem contato direto com o material laminado e
efetuam o processo de laminação.

Cilindros de encosto ou apoio: Mantem contato com os cilindros de
trabalho impedindo-os de fletir durante os esforços de laminação.
Na Figura 3 pode-se ver um conjunto de cilindros de trabalho e encosto.
Figura 3: Conjunto de cilindros de trabalho e encosto.
(Fonte: ABM - Associação Brasileira de Metais,1981)
23
Os cilindros são montados em forma de cadeira, conforme mostra a Figura 4.
Figura 4: Montagem em forma de cadeira.
(RIZZO, 2007)
2.1.1 – Cilindros de trabalho ( Work Rolls )
De acordo com a Gomi (1981), os cilindros de trabalho são em sua maioria
construídos de compostos de ferro fundido cinzento altamente ligado. Isso devido à
estrutura da matriz desses cilindros apresentarem boas propriedades em relação a
trincas e ao desgaste.
Atualmente segundo Rizzo (2007), são fabricados cilindros de aço rápido, que
têm apresentado bons resultados durante o processo de laminação.
2.1.2-Cilindro de Encosto ( Back-Up Rolls)
São na maior parte cilindros de aço fundido ou aço forjado de alta dureza
apresentam boas propriedades ao desgaste, ao lascamento e a quebra.
Existem também conforme ilustra a Figura 1.5, os cilindros de encosto
encamisados que apresentam resistência ao desgaste ao lascamento bem
superiores aos demais.
24
Figura 5: Camisa para cilindro
(Fonte: ABM - Associação Brasileira de Metais,1981)
2.2- Processo de Resfriamento dos cilindros (RIZZO, 2007)
No processo de laminação a quente, parte do calor da chapa é transmitida
aos cilindros e, dessa forma, esse aquecimento gera uma dilatação do cilindro de
laminação. Como este aquecimento não é regular ao longo da mesa do cilindro e ao
longo do tempo, a variação dimensional resultante não é uniforme ao longo da
largura do cilindro, provocando assim tensões térmicas que podem provocar a
formação de trincas que danificam os cilindros, podendo causar a ruptura do cilindro
(Figura 1.2),
Figura 1.2:Resfriamento dos cilindros de laminação
(RIZZO, 2007).
25
Outro problema relacionado ao aquecimento e dilatação irregular dos cilindros
de laminação é a variação da espessura do produto laminado ao longo de sua
largura, o que resulta em alongamentos desiguais e conseguentemente, formação
de ondulações (falta de planicidade) nos produtos laminados. Neste caso é comum a
utilização do termo “coroa térmica” para se referir a esta variação dimensional dos
cilindros. Observa-se ainda que o aquecimento dos cilindros é progressivo após o
início da laminação, ou seja, a temperatura dos cilindros varia ao longo do tempo, o
que também gera uma variação da coroa térmica ao longo do tempo, dificultando o
controle da planificação dos produtos laminados.
A formação de trincas nos cilindros pode ser evitada por um resfriamento
adequado dos cilindros. Este resfriamento é realizado jateando-se água sobre a
mesa dos cilindros. A quantidade de água a ser utilizada e a sua distribuição
depende dos seguintes fatores:

Comprimento do esboço a ser laminado - quanto mais longo for o
esboço mais intenso deverá ser o resfriamento;

Velocidade de laminação – quanto maior a velocidade, maior deverá
ser a quantidade de água a ser utlizada no resfriamento;

Desgaste do cilindro – à medida que o cilindro é desgastado a
distância ou ângulo de abertura do bico de refrigeração deve ser
ajustada;

Material de construção dos cilindros – quanto mais duros forem os
cilindros, mais eficiente deverá ser o resfriamento, de forma a evitar
a formação de trincas;

Tipo de cadeira – cadeiras reversíveis necessitam de refrigeração
nos dois sentidos;
Para um resfriamento eficiente, não basta apenas lançar água em abundância
sobre os cilindros. É preciso também que os bocais sejam distribuídos
convenientemente ao longo da periferia dos cilindros e que o resfriamento seja
uniforme ao londo do corpo. O ideal é que a refrigeração dos cilindros seja
posicionada o mais próximo possível da saída do material laminado, (Figura 2.3).
26
Figura 2.3: Resfriamento do cilindro de trabalho em uma cadeira quádruo
( RIZZO, 2007)
Para um bom resfriamento é também de grande importância a limpeza da
água. Se a água contiver detritos (carepa, pó) os bicos poderão entupir e o
resfriamento não será uniforme. Outro fator importante na refrigeração é a pressão
da água. Quando a pressão é baixa forma-se uma camada de vapor entre o cilindro
e a água, impedindo que haja retirada de calor do cilindro (RIZZO,2007).
2.3 – Perfil dos cilindros da Laminação
Segundo Helman (1983), os cilindros de laminação comportam-se como vigas
bi-apoiadas em suas extremidades com uma carga em sua região central, adotando,
durante a passagem da chapa, a geometria conforme Figura 6a.
Esta situação acarreta uma espessura não-uniforme no sentido perpendicular
à direção de laminação. Em consegüência, a chapa sofre um alongamento maior
nas bordas que na região central, implicando numa ondulação na chapa, conforme
Figura 6b.
A tendência da chapa em apresentar um alongamento maior nas bordas e a
restrição a esta geometria de deformação exercida pela zona central farão com que
restrição a esta geometria de deformação exercida pela zona central se produzam
na chapa tensões de tração no centro e de compressão nas bordas, conforme
27
Figura 6c. Como resultado deste estado de tensões, podem aparecer, na região
central, fendas perpendiculares à direção de laminação, conforme Figura 6d.
Figura 6: Problemas devido à flexão dos cilindros de laminação
(SHIGAKI, 2001)
Ainda segundo Helman (1983) os defeitos são mais acentuados quando se
laminam chapas finas, devido às elevadas cargas envolvidas e à necessidade de
utilizar cilindros de raio pequeno (relativamente flexíveis).
Devido a problemas de flexão constróem-se cilindros com a geometria em
foma de barril, de forma a minimizar a flexão causada pela deformação exercida na
zona central. Este recurso obrigatório é mais generalizado com uma coroa
corretamente dimensionada, de forma que a parte inferior do cilindro superior e a
parte superior do cilindro inferior devam fletir de modo a resultarem duas faces
paralelas, conforme as Figura 8a e 8b.
Figura 8: Flexão dos cilindros
(Fonte: ABM - Associação Brasileira de Metais,1981)
28
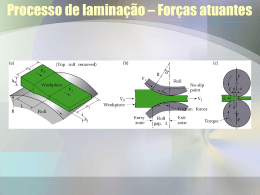
De acordo com Rizzo, (2007), Figura 9, podem-se observar as forças
atuantes durante o processo de laminação. A fim de se corrigir a flexão dos cilindros,
pode-se também aplicar uma carga de contra-flexão nos pescoços.
Figura 9: Representação esquemática da força de laminação.
(RIZZO,2007)
Como ordem de grandeza, flecha máxima, ou melhor a metade da diferença
dos diâmetros no centro e nos extremos deve ser da ordem de 0,02 a 0,15 mm.
2.3.1 – Coroa absoluta e coroa relativa da chapa (YUKIO, 2001)
A “coroa absoluta” (Cj) é definida como a diferença entre a espessura no
centro da tira e a espessura média correspondente a uma certa distância j das
bordas (usualmente de 25 a 40 mm), como pode ser observado na Figura 14
Figura 14: Descrição das variáveis que definem as coroas.
29
C J  hc
h

'
J
 hJ"
2

(2.2)
A coroa é um parâmetro que caracteriza de uma forma simples o perfil da tira,
ao longo da largura da tira. Valores usuais de coroas absolutas variam de 0 a 40 μm,
para tiras [GINZBURG et AZZAM, 1997].
À relação entre coroa absoluta e a espessura no centro da tira chama-se
“coroa relativa” (Crj).
C rJ 
CJ
x 100%
hc
30
(2.3)
3-TORQUE E CARGA DE LAMINAÇÃO
3.1- Torque na Laminação de Chapas
Segundo Helman (1983), o torque necessário para laminação de chapas no
estado estacionário é o produto da força circunferencial líquida pela distância do eixo
do cilindro à circunferência na zona de deformação.
Como as tensões de atrito atuam em sentido oposto em ambos os lados do
ângulo neutro, a força líquida circunferencial por unidade de largura para um cilindro,
Fc, é dada pela expressão:
Fc 
Ainda segundo Helman (1983),
M
R
(3.1)
o torque é afetado pela deformação dos
cilindros, já que o contato do arco de contato não está sobre a linha que une os
centros dos cilindros.
Uma forma simplificada para o cálculo do torque de laminação consiste em
calcular o momento da componente vertical da resultante das forças atuantes na
área de contato, segundo a Figura 15.
Figura 15: Braço de alavanca na laminação
( HELMAN,1983)
A distânica da força P ao centro de rotação do rolo é uma fração do arco de
contato deformado L‟.
31
Desta forma, Helman (1983), defini as equações:
d  .L'
(3.2)
L'  R' h
(3.3)
onde:
De acordo com Helman (1983), os valores de λ são λ = 0,5 para laminação a
quente e λ = 0,45 para laminação a frio. Em conseqüência o torque é dado por:

M  Pd  .L'.R'  pd
(3.4)
0
onde:
M = Torque por unidade de largura da chapa Fc
= Força líquida circunferêncial por unidade de largura
R = Raio Original
P = Força
d = distância do centro de rotação do rolo
L‟ = Arco de contato deformado
λ = constante de laminação
R‟ = Raio deformado
∆h= Variação da espessura da chapa
De acordo com Helman (1983), pode-se calcular o raio R‟ do arco deformado
pela expressão:
32
Equação de Ritchcok;


c
P / W 
R'  R 1 
 h i h f

(3.5)
onde:
hi = espessura inicial
hf = espessura final
P = carga de laminação
W = largura do material
Segundo Hitchcock (1935), o valor de “c” pode ser determinado pela
expressão:
c
16(1  v ²)
E
( 3.6)
onde:
E = módulo de Young [kgf/mm²]
 = o módulo de poisson do material empregado na construção dos cilindros
c ≈ 2,2 x 10 -4 mm² / Kg (para aço)
3.2- O Surgimento do Cálculo da Carga de Laminação de Chapas a Frio
A primeira grande contribuição à teoria de laminação surgiu com a publicação
dos trabalhos de von Kárman (1925). Posteriormente, Orowan (1943),
e as
contribuições de Bland e Ford (1951) a esta teoria, tornaram práticas as suas
aplicações através de simplificações, sem perda significativa de precisão, e fizeram
com que as contribuíções de Bland e Ford, passassem a ser amplamente adotadas
em aplicações reais.
33
3.2.1 - Deformação Homogênea
Segundo Helman (1983), uma estimativa para a carga de laminação de
chapas a frio pode ser obtida considerando o processo de laminação como um
processo de compressão homogênea entre placas bem lubrificadas. As placas são
de comprimento L, igual ao comprimento do arco de contato projetado na dreção de
laminação. Na direção transversal, o comprimento de contato é representado por
“W “ que significa largura da chapa. Dessa forma a área de contato é:
A  LW  W R..h
( 3.7)
Admitindo-se que não ocorra deformação lateral ( hi << W ), a carga de laminação
será
_
_
P  A S  S W R..h
(3.8)
Sendo S a tensão média de escoamento para o estado plano de deformação e Y o
módulo de Yong, Helman defini que:
(S = 1,15 Y)
( 3.9)
P _
 S R.h
W
(3.10)
A força por unidade de largura é:
34
Esta expressão fornece um limite inferior para a carga de laminação, pois ela
não considera o efeito do atrito. Orowan sugeriu um acréscimo de aproximadamente
20% no valor da carga, para incluir tal efeito. Assim finalmente, a carga por unidade
de largura resulta em
_
P*
 1,2 S Rh
W
(3.11)
Ainda que esta equação não seja de aplicação exata a qualquer caso, é útil
para estimativas rápidas da carga. É freqüentemente empregada para obter o
primeiro valor da carga, para calcular o raio deformado dos cilindros de laminação
( R‟), através da equação de Hitchcock.
3.2.2- Cálculo da Carga de Laminação pelo método dos blocos
Segundo Helman (1983), o cálculo das tensões desenvolvidas durante o
processo de laminação através do método de equilíbrio (“slab method “), são
admitidas as seguintes condições:
a) deformação plana
b) deformação homogênea em cada plano
c) coeficiente de atrito constante
d) arco de contato circular ( de raio deformado R‟ )
e) ponto neutro dentro do arco de contato
f) deformação elástica desprezível
35
A análise do processo será feita com referência à Figura 16, onde C separa
duas zonas, as forças de atrito são contrárias. Foi assinalado um ponto genérico a
cada lado do ponto neutro: A, situado na região de saída, e B, na região de entrada.
Figura 16: Bloco para análise de tensões
(HELMAN, 1983)
Figura 17:Tensões agindo nos blocos
(HELMAN, 1983)
36
Figura 18: Representação esquemática da região geométrica de deformação na laminação
( RIZZO, 2007)
Para deduzir a equação de equilíbrio no ponto B, isola-se um bloco de lados
perpendiculares ao plano de laminação, de espessura infinitesimal, caracterizado
como ângulo neutro “ø” ( Figura 17) e melhor representado pela Figura 18.
De forma a simplificar a demosntração da equação de equilíbrio no ponto B
foi apresentado somente a equação final (3.12) do livro do Helman (1983):
hS 
d 
p 
p  d (hS )
 2 R' p( sen   cos  )
1    1  
d  S   S  d
(3.12)
A equação 3.12, de autoria de Von Kárman, é de difícil integração, ainda que
seja fácil obter uma solução numérica, através de um computador. Uma
simplificação por Bland e Ford (1951) permitiu obter uma solução analítica da
equação. Na maioria dos processos de laminação, a variação de pressão de
laminação com a posição sobre o arco de contato é muito maior que a variação da
tensão de escoamento. Por outro lado, a variação do produto hS é ainda menor já
que, ao se elevar S, o valor de h diminiu. Assim, pode-se aceitar que
37
p d
d 
p

(hS )  hS
1  
1  
d  S 
 S  d
(3.13)
Esta suposição não é válida quando o material a ser deformado se endurece
muito rapidamente, ou quando se aplica uma tração à ré elevada. Este último fator
reduz sensivelmente a variação de p/S sobre o arco de contato, Helman (1983).
Entretetando com a capacidade de encruamento dos metais diminui
sensivelmente após uma certa deformação, torna-se pequeno o erro resultante da
suposição anterior, quando utilizada no processo de cálculo dos esforços
correspondentes ao segundo passe e nos passes subsegüentes.
Com a hipótese ( 3.13), a expressão (3.12) se transforma:
hS
d  p
   2 R' psen   cos  
d  S 
(3.14)
As suposições feitas inicialmente por Bland e Ford foram:

O arco de contato é circular mesmo quando ocorre achatamento dos
cilindros

O coeficiente de atrito é constante ao longo de todo arco de contato;

Não existe deformação lateral do material de modo que a laminação
pode ser considerada como um problema de deformação plana;

A deformação é completamente homogênea, isto é, um plano
representado por uma linha vertical na estrada do arco de contato
permanente vertical durante sua passagem pela região;

O critério de escoamento de Von Misses é válido. No Estado plano
de Deformações, este critério estabelece que:
 1   3  2k 
2Y
3
onde:
σ1 ,σ3 = Tensões Principais
Y é a Tensão de escoamento do material em Tração Pura
k é a Tensão de escoamento em compressão plana.
38
( 3.15)
4- SOBRE O MÉTODO DOS COEFICIENTES DE INFLUÊNCIA
4.1-Coeficiente de Influência
Este método surgiu no final da década de 60, para se determinar o perfil da
tira emergente. Chamado de Método dos Coeficientes de Influência ou
simplesmente MCI, (SHOHET e TOWNSEND
et al.1968), desenvolveram este
método que calcula a deflexão elástica dos cilindros devido à flexão e ao
cisalhamento através dos coeficientes de influência, discretizando tira e cilindros em
fatias longitudinais, conforme a Figura 19
Figura 19: Discretização de um laminador quádruo para o método dos
coeficientes de influência
(SHOHET e TOWNSEND et al., 1976)
Uma vez determinados tais coeficientes, montam-se as equações de cálculo
da deflexão para cada cilindro, superpondo os deslocamentos por flexão,
cisalhamento e achatamento localizado (os autores assumem linearidade no
achatamento em função da carga, para a faixa de operação normal). Através das
equações de equilíbrio de cada cilindro e de compatibilidade nas interfaces
cilindro/cilindro e cilindro/tira, determinam-se às cargas distribuídas e o perfil
deformado da tira, iterativamente.
39
O MCI tem demonstrado ser um método de comprovada precisão, sendo
bastante poderoso na solução de problemas de distribuição transversal da
espessura de chapas (GUO, 1990). Deve-se, porém, citar alguns pontos discutíveis
a respeito do modelo (GINZBURG, 1989):

Calcula os coeficientes de influência baseado nas equações de
deflexão de uma viga simples. Contudo, a validade destas equações
é questionável para cilindros curtos (ou seja, cilindros com razão
comprimento/diâmetro reduzido);

Simplifica um problema tridimensional em um bidimensional;

Está baseado na hipótese de contato total do cilindro de trabalho com
o cilindro de apoio.
O modelo apresentado por Pawelski e seus colegas foram implementados
com algumas modificações, e programado em linguagem do MATLAB. O programa
denominado MCI/Berger, em reconhecimento a Bernd Berger (BERGER,1976),
autor do modelo de achatamento de cilindros em contato utilizado no programa, foi
testado e validado (SHIGAKI, 2001).
4.2-Caracteristicas principais do método MCI/Berger
 Calcula-se a deflexão elástica dos cilindros devido à flexão e ao
cisalhamento através dos coeficientes de influência, discretizando a
chapa em fatias longitudinais e cilindros em cortes transversais,
conforme a Figura 19;
 Aplica o modelo de cálculo de carga de Bland-Ford para cada fatia e
Hitchcock para o raio deformado (supõe estado plano de
deformação para cada tira);
 Os achatamentos são calculados através do modelo de Berger;
 O programa é constituído de dois ciclos iterativos principais, sendo
que um deles converge para haver compatibilidade nas interfaces
40
de contato cilindro-cilindro, e o outro converge com o equilíbrio
global de forças;
 Assume-se contato completo ao longo dos cilindros de trabalho e
encosto.
4.3 - Método de cálculo de carga de laminação
O simulador desenvolvido por (SHIGAKI, 2001) neste trabalho, assume como
hipótese o Estado Plano de Deformações (EPD) para a deformação plástica da
chapa. Tal hipótese de EPD justifica-se quando é satisfeita a relação (largura da
tira/arco de contato >10), segundo Watts e Ford (1955), conservativamente. Tal
relação é satisfeita na maioria das situações correntes industriais. Nessa situação, a
deformação transversal da chapa laminada a frio é praticamente nula, confinada a
uma pequena faixa junto às bordas (GUILLERAULT et al., 1987).
Entretanto um dos métodos de cálculos utilizados foi a equação 4.1 de autoria
de Von Kárman representada por:





d
hS
d
p

p



hS
1


1

2́
R
p
sen

cos



 
d
d
S

S



onde,
h: espessura da tira;
S: tensão de escoamento;
: ângulo dentro do arco de contato;
R´: raio deformado;
: coeficiente de atrito;
p: pressão sobre o bloco infinitesimal.
41
(4.1)
Figura 20: Desenho esquemático do processo de laminação.
Bland e Ford sugeriram que o produto hxS é razoavelmente constante,
permitindo, assim, a obtenção de uma solução analítica para a equação (4.1).
 
p
d




hS

2
R
´
p
sen
cos

d
S



(4.2)
assim, a solução analítica final será:
para a saída:
para a entrada:

p
h

C
exp(


H
)
1
S
R
´

p
h

C
exp(


H
)
2
S
R
´
(4.3)
(4.4)
onde,
R

R
´
 ´

H

2 arctg


h
h
f
 f 
(4.5)
Onde:
hf : espessura final;
C1 e C2: constantes que dependem das condições de contorno, mais concretamente
da aplicação de tensão à ré e à frente da tira.
42
4.4- MCI/Berger
O presente programa MCI/Berger, utiliza o modelo de Bland-Ford-Ellis na
direção de laminação e o método numérico dos coeficientes de influência na direção
transversal.
Para tanto dividem-se a chapa e os cilindros em faixas de 2 a 5 mm de
largura. Aqui considerou-se a simetria da laminação. Assumiu-se também, como
hipótese, a possibilidade da superposição dos efeitos de flexão e força cortante pelo
fato do cilindro se deformar elasticamente. Levou-se em consideração também o seu
achatamento,
por
ter
influência
crucial
na
distribuição
de
espessuras,
particularmente nas bordas.
Na Figura 21 é apresentada a forma como cilindro e tira são subdivididos,
para a aplicação do modelo de Bland-Ford e o Método dos Coeficientes de
Influência.
Figura 21: Subdivisão do cilindro e da tira.
O Método dos Coeficientes de Influência calcula a deflexão do cilindro segundo a
equação (as variáveis em negrito representam grandezas vetoriais):
u=ap+bF+cM
43
(4.6)
sendo:
u : vetor de deflexões do cilindro;
a : matriz dos coeficientes de influência (equações 4.7a e 4.7b);
b : vetor de coeficientes para as cargas concentradas (equação 4.8);
c : vetor de coeficientes para os momentos externos (equação 4.9);
p: vetor força por unidade de largura;
F: carga concentrada (do mancal e dos contrafletores);
M: momento fletor externo dos contrafletores.
a ij 


y  1
3 
3y 2i y j  y 3i  y i 

E  6I
A 
(4.7 a)
a ji  a ij
bi 
13
Z
1

y i  y 2i  y 2i 3L  y i 

E A
2I
6I

ci 

(4.7 b)
(4.8)
1 2
y
2 EI i
(4.9)
A seguir são explicitadas as equações que determinam o achatamento dos
cilindros, baseado no método desenvolvido por Berger (BERGER et al.,
1975).

A expressão que calcula o achatamento do cilindro é dada pelas equações
abaixo:
(4.10)
v = [f(2(j-i), s)+f(2(j+I)-2, s)]p


d
(
1

k
)
d
(
1

k
)
2
E
f
(
k
,
s
)

d
(
1

k
)
l
n

d
(
1

k
)
l
n

1
/
2
1
/
2
2
2 2
2 2
1

d
(
1

k
)

4

2 d
(
1

k
)

4

2




d
()
141

k


d
()

k
4
c

()
1

k

()
1

k




2
l
n

2
l
n

d
()
141

k


d
()

k
4
c

()
1

k

()
1

k



2
/
2
21
2
1
/
2
2
2
/
2
21
2
1
/
2
2
(
1

k
)
(
1

k
)

2

2

1
/
2
1
/
2
2
2
2
2
41
c

(

k
)
41
c

(

k
)
(4.11)



 

(
1

2
)
1

k
()
1

k
 ()
2
44 2

2 c



2
3
/
2 2
2
3
/
2


1

(
4
c

()
1

k
)(
4
c

()
1

k
)
c = D/y
(4.12)
d = y/s
(4.13)
s = (R‟h )1/2
(4.14)
onde,
v: vetor de achatamento ao longo da largura (equação 4.10);
vj,i: achatamento da rodela i do cilindro causada por uma força unitária vinda da faixa
j da tira;
s: vetor comprimento do arco de contato (equação 4.14);
E: módulo de elasticidade do material do cilindro;
: coeficiente de Poisson do material do cilindro;
y: largura da faixa;
R‟: raio deformado segundo Hitchcock (HITCHCOCK, 1935), equação (3.5);
h: espessura de entrada menos a espessura de saída (redução);
z: braço de alavanca para a força contrafletora;
y: posição ao longo da largura.
4.5- Compatibilidade no Contato Cilindro-Cilindro
Define-se o contorno da superfície superior do cilindro de trabalho como:
cw = uw – Cmw – vw + vw1
(4.15)
E o contorno da superfície inferior do cilindro de apoio:
cb = ub + Cmb + vb – vb1
(4.16)
sendo,
uw e ub : deflexão elástica dos cilindros de trabalho e de apoio respectivamente;
45
Cmw e Cmb : coroas impostas aos cilindros de trabalho e de apoio
respectivamente;
vw e vb : achatamento dos cilindros de trabalho e de apoio respectivamente;
vw1 e vb1 : achatamento no meio dos cilindros de trabalho e de apoio
respectivamente;
(os termos em negrito representam variáveis vetoriais)
Deve-se notar que uw, ub, Cmw, Cmb, vw e vb são todos vetoriais ao longo
de meia largura do cilindro para u e Cm, e para meia largura da tira para v.
O problema resume-se, então, em calcular as cargas distribuídas nos cilindros
de modo a satisfazer a equação de compatibilidade cb = cw e respeitando o
equilíbrio de forças. O cálculo da carga distribuída de laminação já é conhecido. A
parte mais difícil do problema reside na determinação das cargas de contato. O
problema pode ser resolvido, após manipulação das equações acima, através de
uma equação iterativa envolvendo as cargas distribuídas de contato entre cilindros e
a carga distribuída de laminação na interface cilindro de trabalho/chapa
46
6- DANOS NA LAMINAÇÃO
6.1 Introdução
Segundo Gorni (1981), existem apenas três maneiras segundo as quais
peças ou sistemas podem “falhar” : obsolescência, quebra e desgaste acentuado. A
falha por obsolescência de maneira arbitrária e a falha por quebra são
frequentemente repentinas e podem ser permanentes, já a falha por desgaste
geralmente é um processo gradual e, em alguns casos, reparável.
Ainda segundo Gorni (1981), existem cinco categorias de desgastes:

Desgaste adesivo;

Desgaste abrasivo;

Desgaste por erosão;

Desgaste por corrosão;

Desgaste por fadiga superficial.
6.2- Modelos e Falha por Fadiga Superficial Contato Dinâmico (NORTON, 2000)
De acordo com Norton (2000), existe discordância entre especialistas com
relação ao mecanismo de falha real que resulta em crateração e lascamento nas
superfícies. A possibilidade de se ter uma tensão de cisalhamento máxima na
subsuperfície (rolamento puro) levou alguns a concluírem que a crateação se inicia
na superfície.
A Figura 27 apresenta as trincas tanto superficiais quanto na subsuperfície
em um cilindro de aço cementado sujeito a esforços pesados de rolamento.
Uma extensa pesquisa experimental sobre crateração em contatos de
rolamento foi realizada por Way (1935). Foram feitos mais de 80 ensaios com
cilindros de eixos paralelos em contato sob rolamento puro de diferentes materiais,
lubrificantes e carregamentos, girando até 18 milhões de ciclos, apesar de que a
maioria das amostras falharam entre 500 mil e 1,5 milhão de ciclos. As amostras
47
foram monitoradas para se detectar o aparecimento de trincas superficiais mínimas,
que inevitavelmente antecedem as falhas por crateração, em até 100 mil ciclos
adicionais na presença de um lubrificante.
Superfícies mais duras e mais lisas têm maior resistência a falhas por
crateração. Amostras extremamente polidas não falharam antes de 12x106 ciclos.
Cilindros nitretados com superfícies bastantes duras e núcleos dúcteis e tenazes
foram os materiais que mais tempo resistiram entre os ensaios. Não ocorreu
crateração nas amostras na ausência de óleo, apesar de o rolamento a seco ter
produzido trincas na superfície. As peças com trincas continuaram rolando a seco
sem falhas por mais 5x106 ciclos até que algum lubrificante fosse adicionado. Então
a trinca superficial crescia rapidamente, tornando-se crateras com o formato
característico de cabeça de seta, dentro dos próximos 100 mil ciclos adicionais.
A explicação sugerida para o efeito nocivo do lubrificante foi que, após a
formação de trincas superficiais, orientadas de maneira favorável, elas são
preenchidas com óleo
quando o cilindro se aproxima e fechadas por ele,
pressurizando o fluído aprisionado na trinca. A pressão do fluído gera tensões de
tração na ponta da trinca, causando seu rápido crescimento da trinca
e o
conseqüente surgimento de uma cratera. Lufricantes de alta viscosidade não
eliminam o contato metal-metal, mas retardaram a falha por crateração, indicando
que o fluído tem que conseguir entrar na trinca rapidamente para causar os danos.
Juvinall e Marschek (2008), chegaram a várias conclusões a respeito de como
se projetam cilindros em contato de rolamento de maneira a se retardar falhas por
fadiga de superfície:
1 Não usar óleo (apesar de não ser uma solução prática, já que promove outros
tipos de desgaste discutidos em sessões anteriores )
2 Aumentar a viscosidade do lubrificante
3 Polir as superfícies (entretanto isso é dispendioso de se fazer)
4 Aumentar a dureza da superfície (preferivelmente com um núcleo dúctil e tenaz)
48
Figura 27: Fotomicrografia (100x) de trincas na superfície e na subsuperfície em um cilindro
cementado e encruado
(NORTON, 2000)
Ainda de acordo com Norton (2000), a concentração geométrica de tensão
(CGT) pode atuar na superfície quando, por exemplo, uma peça do contato é menor
axialmente que a outra (comum em juntas de camo-seguidores e mancais de
rolamento). As bordas do cilindro menor geram uma concentração de tensão na
linha de contato com o outro cilindro, como é mostrado na Figura 28a, e a crateração
e o lascamento ocorrerão, preferencialmente, nessa região. Esse é um motivo para
se usar cilindros abaulados, que tenham um grande raio de abaulamento no plano
yz em relação ao raio do rolo, no plano xz. Se o carregamento de contato puder ser
previsto, o raio de abaulamento pode ser dimensionado para propiciar uma
distribuição de tensão uniforme axialmente na região de contato devido às
deformações dos rolos, como pode ser visto na Figura 28.b. No entanto, para
carregamentos
mais
leves,
haverá
uma
região
de
contato
reduzida
e,
consequentemente, maiores tensões no centro, e , para tensões maiores que as de
projeto, a concentração de tensão nas bordas retornará. Pode-se usar um rolo
parcialmente, como na Figura. 28c, mas que pode causar uma certa concentração
de tensão na transição da parte plana para a abaulada. Pode-se mostrar que uma
49
curva logarítmica, como na Figura. 28d, gerará uma distribuição mais uniforme das
tensões para variados níveis de carregamento.
Figuras 28: Concentração geométrica de tensão
(NORTON, 2000)
Rizzo (2007), exemplifica através das Figuras 28 a 30 o lascamento e fraturas
ocorridos em cilindros.
Figura 29: lascamento em cilindros de laminação
(RIZZO, 2007)
50
Figura 30: Fraturas em cilindros de laminação
(RIZZO, 2007)
No apêndice C, da dissertação encontra-se de forma complementar ao
conteúdo de Danos nos cilindros de laminação, outras figuras.
6.3 – TIPOS DE DANOS EM CILINDROS DE LAMINAÇÃO (RIZZO, 2007)
C.1- Os defeitos mais comuns em cilindros de laminação:
C.1.1 - “Banding” –
As superfícies dos cilindros apresentam-se queimadas ( partes
escuras) e certas áreas muito rugosas ocasionado por deficiência de
refrigeração , excesso de campanha ou seleção incorreta do material do
cilindro.
Figura C1:“Banding”
C.1.2-“Peeling‟-
51
Remoção parcial da camada de óxido formada na superfície do cilindro
devido à refrigeração inadequada do cilindro e/ou temperatura de laminação em uma
faixa que facilita o crescimento de óxido no cilindro.
Figura C2:“Peeling”
C.1.3-Colamento( “Strip Welding”)
Devido ao excesso de força de laminação ( elevada redução ou
material frio) ocorre a ruptura e adesão do material laminado na mesa do cilindro ,
ocasionando trincas e esfoliação.
Figura C3:Colamento.
C.1.4-Desgaste Na Borda De Chapas ( “Strip Edge Wear”)
Desgaste superficial na forma de ondas localizadas nas regiões
correspondentes as bordas de chapas laminadas, principalmente nas cadeiras
acabadoras .Este defeito é causado pelo aumento da resistência à deformação na
borda de chapas combinado com elevada taxa de redução ou presença de carepa
dura nas bordas.
52
Figura C4: Desgaste na borde de Chapas
C.1.5-Endurecimento Ou Amolecimento Localizado(„Hard And Soft Spots‟)-
São regiões de alta dureza ou de baixa dureza formadas durante o
processo de fundição de cilindros centrifugados devido à segregaçao de excesso de
carbonetos ( pontos duros) ou falta de carbonetos e presença de grafita ( pontos
macios).
Figura C5:Endurecimento.
C.1.6-Trincas-
São riscos perpendiculares, longitudinais ou inclinados que aparecem na
superfície da mesa do cilindro, formando mosaicos. São provocadas devido a ciclos
de elevado aquecimento ( causada por parada do cilindro, pro exemplo) seguido de
resfriamento brusco.
FiguraC6:Trincas.
C.1.7-Quebra-
53
Ocorre devido a defeitos de fundição ou problemas operacionais.
Figura C7:Quebra
C.1.8-Lascamento-
É originado no interior do cilindro logo abaixo da interface
casca/centro.O lascamento é causado por elevados ciclos de carregamento durante
a aplicação de grandes reduções na laminação de materiais finos e de alta
resistência.
Figura C8:Lascamento.
C.1.9-Fratura-
Fratura devido à carga excessiva de laminação associada ou não com
corrosão sob tensão.
Figura C9: Fratura.
54
7- MODELO DE LAMINADORES QUÁDRUOS EM ELEMENTOS FINITOS
7.1-Introdução:
Este capítulo apresenta as características dos laminadores utilizados nos dois
métodos: o método MCI/Berger, de Shigaki (2001), e
o Método dos Elementos
Finitos.
Os modelos de laminadores foram submetidos a cargas de laminação como
se estivessem em operação real de fábrica. Com aplicação das cargas nos métodos,
foi possível identificar as rergiões de maior concentração de pressão e deformação.
É importante enfatizar que foi analisado resultados levando em consideração
o Torque e sem o Torque.
7.1.1 – Características dos dois laminadores
DADOS DO LAMINADOR I:
Diâmetro do cilindro de trabalho:
450 mm
Coroa usinada do cilindro de trabalho:
0 mm
Módulo de Young do cilindro de trabalho:
21000 kgf/mm²
Diâmetro do cilindro de apoio:
1300 mm
Coroa usinada do cilindro de apoio:
0 mm
Módulo de Poisson dos cilindros:
0.3
Comprimento da face dos cilindros:
1900 mm
Comprimento do braço de contraflexão:
100 mm
DADOS OPERACIONAIS:
Coeficiente de atrito (seco):
0,1
Largura da tira:
1600 mm
55
Módulo de Young da tira:
21000 kgf/mm²
Módulo de Poisson da tira:
0.3
Curva de fluxo (EPD), via Ludwik:
(0,1+78.8 εp0.249) kgf/mm²
Espessura inicial:
4,5 mm
Coroa absoluta inicial:
0 micrometros
Coroa relativa inicial:
-1,9737.10-14 %
Coroa medida da borda da tira (1º cadeira)
25 mm
Tensão à entrada da tira:
0 kgf/mm²
Total na bobinadeira, a ré:
0 tf
Tensão à saída da tira:
0 kgf/mm²
Total na bobinadeira, a frente:
0 tf
Número de fatias do semi-cilindro:
80
Tolerância para o perfil:
0,001 mm
RESULTADOS: do MCI/Berger
Espessuras
Carga de
finais (mm)
laminação (kgf)
Coroa relativa
(%)
Força de
Tempo de
Roll Bending (kgf) processamento (s)
3,89
974433,71
4,89
0
2,23
3,07
1559873,43
10,38
0
2,73
2,48
1529912,84
13,27
0
3,30
2,06
1412035,82
15,14
0
3,44
1,76
1264219,46
16,30
0
4,25
Tempo total de processamento: 15,95 segundos
DADOS DO LAMINADOR 2:
Diâmetro do cilindro de trabalho:
125 mm
Coroa usinada do cilindro de trabalho:
0 mm
Módulo de Young do cilindro de trabalho:
21000 kgf/mm²
Diâmetro do cilindro de apoio:
300 mm
Coroa usinada do cilindro de apoio:
0 mm
Módulo de Poisson dos cilindros:
0,3
56
Comprimento da face dos cilindros:
400 mm
Comprimento do braço de contraflexão:
100 mm
DADOS OPERACIONAIS:
Coeficiente de atrito (seco):
0,1
Largura da tira:
350 mm
Módulo de Young da tira:
21000 kgf/mm²
Módulo de Poisson da tira:
0,3
Curva de fluxo (EPD), via Ludwik:
(0,1+78.8 εp0.249) kgf/mm²
Espessura inicial:
4,5 mm
Coroa absoluta inicial:
0 micrometros
Coroa relativa inicial:
-1,9737.10-14 %
Coroa medida da borda da tira (1º passe)
25 mm
Tensão à entrada da tira:
0 kgf/mm²
Total na bobinadeira, a ré:
0 tf
Tensão à saída da tira:
0 kgf/mm²
Total na bobinadeira, a frente:
0 tf
Número de fatias do semi-cilindro:
45
Tolerância para o perfil:
0,001 mm
Coeficiente para a tolerância da carga q:
0,001
Espessuras
Carga de
Coroa relativa
Força de
finais (mm)
laminação (kgf)
(%)
3,89
99210,05
1,38
0
0,64
3,07
154911,50
2,83
0
0,59
2,48
153402,00
3,55
0
0,58
2,06
142477,64
4,01
0
0,61
1,76
128731,56
4,27
0
0,64
Roll Bending (kgf)
Tempo total de processamento: 3,06 s
57
Tempo de
processamento (s)
7.2 Estrutura Geometria dos Laminadores Modelados em Elementos Finitos
Foram modelados dois laminadores, um de porte pequeno e outro de
porte grande. O desenho de ambos foi feito através do programa Solidworks 2008.
Para a imposição do tipo de material, restrição, contato, geração de malha e simetria
utilizou-se o programa de elementos finitos COSMOS Works.
7.2.1 – Determinação da Pressão WR do laminador 1 no MCI/Berger
O programa MCI/Berger, após processamento dos dados de entrada do
laminador 1, fornece a pressão WR ( pressão entre cilindro de trrabalho e a chapa)
conforme a Figura 32. Esta pressão corresponde à carga de laminação atuante na
operação de laminação de uma chapa de espessura incial de 4,5mm com largura de
1600mm, reduzida para 3,89mm.
O Apêndice B apresenta de forma detalhada todos os comandos utilizados.
Figura 32: Pressão de contato do laminador 1
A pressão obtida foi, posteriormente, lançada no laminador 1, no programa
COSMOS Works. A Tabela 2 apresenta a discretização da pressão a cada 100 mm.
58
Tabela 2- Resultados da pressão Wr obtido do programa MCI/Berger a cada 100 mm do semi comprimento
Pw
Pw
W/2
(kgf/mm²)
(Pa)
(mm)
70,87
694,526
0
71,07
696,486
100
71,73
702,954
200
72,83
713,734
300
74,5
730,1
400
76,7
751,66
500
79,6
780,08
600
83,5
818,3
700
91,5
896,7
800
Um segundo valor necessário para
obter os resultados da pressão no
programa COSMOS, refere-se a uma constante de inclinação da reta “k”. Como a
pressão obtida se trata de uma curva, optou-se por subdividi-la em partes lineares
para aplicá-la ao modelo.
Dessa forma tornou-se necessário o emprego de uma constante k, uma vez
que, o programa COSMOS apresenta a equação da reta inclinada em seu diretório,
para inserção dos dados das cargas obtidas no MCI/Berger.
A Tabela 3 mostra os resultados da constante k, a cada 100 mm do ponto de
origem do cilindro com os resultados tabulados da Pressão WR (pressão entre o
cilindro de trabalho e a chapa).
De forma a facilitar a compreensão, tomou-se como base a Figura 33, onde
obteve-se a constante k, para cada pressão WR correspondente.
59
Figura 33 – Representação da reta passando por 2 pontos P1 e P2.
Através da expressão da equação da reta tem-se:
y2  y1  a( x2  x1 )  a 
y2  y1
x2  x1
(7.1)
Comparando a Equação (7.1) com dois pontos quaisquer da Figura 33, tem-se:
Pi 1  Pi  k W f  Wi   k 
Pi 1  Pi
W f  Wi
(7.2)
onde:
 => P2
P = Pressão Wr inical x10 .N  => P1
m


Pi 1 = Pressão Wr final x106 . N
m2
6
i
2
W  W f  W f (m) => x2  x1
Trabalhando melhor a equação (7.2) tem-se k igual a:
k
60
1
W
 Pi 1


 1
 Pi

(7.3)
Com os valores obtidos no MCI/Berger montou-se construíu-se a Tabela 3
que representa os valores de k (constante de inclinação da reta), para cada pressão
WR, aplicada a cada 100 mm da semi-largura da chapa.
Tabela 3 - Resultado da constante k correspondente a cada 100 mm.


A  Pi x106 . N

m
2


B  Pi 1 x106 . N
m2

W m
k
1
W
 Pi 1


 1
 Pi

694,526
696,486
0,1
0,0282
696,486
702,954
0,1
0,0929
702,954
713,734
0,1
0,1534
713,734
730,1
0,1
0,2293
730,1
751,66
0,1
0,2953
751,66
780,08
0,1
0,3781
780,08
818,3
0,1
0,4899
818,3
896,7
0,1
0,9581
7.2.2 Torque aplicado ao modelo
Com base no desenvolvimento do cálculo do torque apresentado no Capítulo
3, calculou-se inicialmente o torque correspondente ao laminador 1.
Através do MCI/Berger foi possível obter os termos da equação 7.11 e em
seguida calcular o torque de laminação, representado pela força circunferencial
líquida (Fc).
No apêndice sobre (Comandos do MCI/Berger) desse projeto foi apresentado
de forma detalhada todo processo de obtenção dos valores necessários para
calcular Fc, através do uso do MCI/Berger.
Dessa forma os valores necessários para o desenvolvimento do cálculo do
torque do laminador 1, obtidos pelo MCI/Berger foram:

R‟ (raio deformado) = 234,50 mm;
61

q ( carga de laminação) = 974433,71 Kgf , valor referente ao 1º passe
Utilizando-se a Equação (7.5), para determinar o arco deformado tem-se:
Para o primeiro passe:
h  hi  h f => 4,5-3,89=0,61
L'  234,50 x0,61 => L'  11,96 mm
(7.4)
(7.5)
L‟ =arco de contato deformado
Conforme já mencionado:
d  L'
  0,45 (para laminação a frio)
d  L' = 0,45 x 11,96= 5,382 mm = 0,005382m
(7.6)
Onde
d  Distância da força P ao centro de rotação do rolo
Como P é representado pela carga de laminação q, tem-se:
P= 974433,71 Kgf x 9,8 = 9.549.450,358 N
(7.7)
Uma vez que o estudo está sendo feito utilizando a metade dos cilindros de
forma a reduzir o tempo de processamento em elementos finitos, faz-se necessário
reduzir pela metade o valor da carga de laminação, dessa forma:
62
P/2 = 4.774.725,18 N
(7.8)
Portanto, o torque é dado por.

M  P.d  L' P  L' R'  pd ,
0
(7.9)
Logo:
M 
P
d  4.774.725,18 (N) x 0,005382 (m) = 25.697,571 N.m
2
Segundo ( Helman, 1983), M  Fc.R
Logo Fc 
(7.10)
(7.11)
M
25.697,571
=> Fc 
 Fc  114.211,5N
R
225 x10 3
(7.12)
Após calcular Fc, construiu-se a Tabela 4 de forma a obter o valor referente
ao torque a cada 100 mm, para ser aplicado ao modelo em elementos finitos.
Fazendo a distribuição de Fc ao longo da área de contato, foi necessário
obter o comprimento do arco de contato entre a chapa e o cilindro de trabalho,
representado por L. O valor de “L” foi possível obter utilizando o MCI/Berger. Optouse por utilizar a média desse valor, conforme se pode observar na Tabela 4.
63
Tabela 4- Resultado do torque a cada 100 mm ao
longo do cilindro de trabalho do laminador 1.
Semi-
Variação da
Área ao longo de
Fc (N) em cada
comprimento da
posição
cada intervalo da
intervalo
chapa (W/2) mm
(intervalo)
subdivisão
∆V (mm)
A=L*.∆V,
L=8,317mm
A em (mm²)
0
100
100
831,7
14.276,44
100
100
831,7
14.276,44
100
831,7
14.276,44
100
831,7
14.276,44
100
831,7
14.276,44
100
831,7
14.276,44
100
831,7
14.276,44
100
831,7
14.276,44
800 mm
6.653,6 mm²
114.211,5 N
200
200
300
300
400
400
500
500
600
600
700
700
800
total
64
7.3 – Resultados do laminador 1 no MCI/Berger
A Figura 34 representa o perfil da chapa laminada do Laminador 1, obtido
pelo programa MCI/Berger para 5 passes. Neste trabalho foi considerado somente o
primeiro passe.
Figura 34: Representação do Perfil da chapa em cada passe do Laminador 1
A Figura 35, mostra a distribuição de cargas em cada passe do Laminador 1.
A linha tracejada representa a carga “q” entre os cilindros de trabalho e os de
encosto, e a carga “p” entre o cilindro de trabalho e a chapa.
65
Distribuição de cargas
1200
1100
p(-) e q(.) [kgf/mm]
1000
900
800
700
600
500
400
300
0
100
200
300
400
500
600
Semi-largura [mm]
700
800
900
1000
Figura 35: Representação das cargas passe do Perfil do Laminador 1
7.3.1 Determinação da Pressão Wr do laminador 2 no MCI/Berger
Seguindo o mesmo raciocínio na determinação da Pressão Wr, do Laminador
1, a Figura 36 representa graficamente os resultados da Pressão Wr, fornecido pelo
programa MCI/Berger, após processamento dos dados de entrada do laminador 2.
Dessa forma os resultados obtidos no programa MCI/Berger encontram-se
no Apêndice B de forma detalhada, com os comandos executados.
66
70
69
pressão WR [kgf/mm²]
68
67
66
65
64
63
0
5
10
15
20
25
30
semi comprimento da chapa [mm]
35
40
A Figura 36: Pressão WR do laminador II
Também de forma semelhante as Tabelas 5 e 6, fornecem os valores da
Pressão Wr e da constante k, respectivamente.
Tabela 5 - Resultados da pressão Wr obtido do programa MCI/Berger a cada 25 mm do semi comprimento do laminador 2
Pw
Pw
W/2
W/2
(kgf/mm²)
(N/m²) x 106
(mm)
(m)
1
63,3
620,34
0
0
2
63,41
621,42
25
0,025
3
63,75
624,75
50
0,050
4
64,3
630,14
75
0,075
5
65,1
637,98
100
0,100
6
66,1
647,78
125
0,125
7
67,5
661,5
150
0,150
8
69,4
680,12
170
0,170
9
70
686
175
0,175
67
Tabela 6 - Resultado da constante k correspondente a cada 100 mm do laminador 2


A  Pi x106 . N
m2



B  Pi 1 x106 . N
m2

k
W m
1
W
 Pi 1


 1
 Pi

620,34
621,42
0,025
0,0722
621,42
624,75
0,025
0,2143
624,75
630,14
0,025
0,3451
630,14
637,98
0,025
0,4977
637,98
647,78
0,025
0,6144
647,78
661,5
0,025
0,8472
661,5
680,12
0,02
1,4074
680,12
686
0,005
1,7291
7.3.2 Determinação do torque do laminador 2 no MCI/Berger
No apêndice apresenta detalhes, da obtenção do Torque no Laminador II, que
segue também o mesmo raciocínio, desenvolvido no laminador I, conforme mostra a
Tabela 7.
Tabela 7- Torque do laminador 2
Semi-
Variação
Área ao longo de
Fc em cada intervalo
comprimento da
da
cada
Por regra de três
chapa (W/2) mm
posição
intervalo de
(N)
(intervalo)
subdivisão
∆V (mm
A=L.∆V, L=4,18 mm
A em (mm²)
0
25
104,5
3166,79
25
104,5
3166,79
25
104,5
3166,79
25
25
50
50
75
68
75
25
104,5
3166,79
25
104,5
3166,79
25
104,5
3166,79
20
83,6
2.533,43
20,9
633,36
731,5
22.167,52
100
100
125
125
150
150
170
170
175
5
total
7.4 Resultados do laminador 2 no MCI/Berger
A Figura 37, mostra os gráficos obtidos pelo programa MCI/Berger do perfil
em cada passe do Laminador II
69
Perfis
4.5
4
Perfil [mm]
3.5
3
2.5
2
1.5
0
20
40
60
80
100
120
Semi-largura [mm]
140
160
180
Figura 37: Representação em cada passe do Perfil do Laminador 2
7.4.1 Representação da distribuição de carga em cada passe do laminador 2
no programa MCI/Berger
A Figura 38 fornece graficamente pelo programa MCI/Berger a distribuição de
cargas em cada passe do Laminador 2. A linha tracejada representa a carga “q” de
contato entre os cilindros de trabalho e o de encosto e a linha contínua a carga „p”
entre o cilindro de trabalho e a chapa. Utilizou-se apenas o primeiro passe.
70
Distribuição de cargas
700
650
600
p(-) e q(.) [kgf/mm]
550
500
450
400
350
300
250
200
0
20
40
60
80
100
120
Semi-largura [mm]
140
160
180
200
Figura 38: Representação das cargas passe do Perfil do Laminador 2
Importante frisar que na Figura 38 as cargas “p” e “q” representam;
p: carga distribuída de laminação;
q: carga distribuída de contato entre cilindros;
7.5 Aplicação das Condições de Contorno
O primeiro passo foi desenhar os cilindros de laminação em um programa de
computador específico, no caso o SolidWorks 2008. A seguir foram aplicadas as
restrições.
71
Figura 39:Cilindros de Trabalho
Figura 40: Cilindro de Encosto
7.5.1 Restrições aplicadas ao modelo no progama COSMOS Works.
Nesse trabalho aplicou-se no modelo restrições em três regiões, a saber, no
pescoço do cilindro de trabalho, na simetria dos cilindros e no pescoço do cilindro de
encosto. Cada restrição é explicada em seguida.
Como já foi mencionado anteriormente, uma das restrições aplicadas foi a de
dupla simetria. A aplicação da simetria têm como objetivo neste trabalho reduzir o
tamanho do problema, permitindo assim uma economia de tempo de processamento
e a obtenção de resultados mais precisos através de um refinamento que se faz
possível na malha do modelo. Restringiu-se também uma pequena área na face
cilíndrica do pescoço do cilindro, onde se encaixam os mancais, não permitindo o
seu deslocamento radial.
7.5.2 Restrições de Simetria aplicado ao modelo
Aplicou-se a simetria no modelo, nas faces dos dois cilindros por serem
simétricos, de forma a modelar uma parte em vez do modelo completo. Os
resultados nas partes não modladas são deduzidas
da parte modelada pelo
programa. Dessa forma pode-se reduzir o tamanho do problema e obter resultados
mais precisos.
72
A Figura 41, mostra a localização exata onde foi aplicado a simetria no
modelo utilizado.
Figura 41: Aplicação da Simetria no modelo
7.5.3 Aplicação da restrição ao cilindro de encosto
Este tipo de restrição define todos graus translacionais de liberdade como
zero. Ao usar esta restrição não é necessário fazer referência à geometria.
No modelo foi aplicada a restrição do tipo fixo na altura do pescoço do cilindro
de trabalho.
A Figura 42 mostra a aplicação da restrição do tipo “fixo” aplicado ao modelo
Figura 42: Aplicação da restrição do Tipo Fixo ao modelo
73
7.5.4 Aplicação da restrição ao cilindro de trabalho
A Figura 43 mostra a aplicação da restrição utilizando um plano de referência,
de forma a impedir a translação na direção horizontal, no pescoço do cilindro de
trabalho.
Figura 43: Aplicação da restrição utilizando um plano de referência ao modelo
7.5.5 Condições de Contato entre os Cilindros
Foi definido o contato sem penetração ente os cilindros de trabalho e encosto.
Este tipo de contato evita a interferência entre as entidades de origem e de alvo,
mas permite a formação de espaçamentos.
Nas opções de contato foi marcada ainda a opção nó para superfície, que tem
as seguintes características:

Não exige que as faces estejam inicialmente em contato.

Não requer malha compatível entre as faces de origem e de alvo.

Permite que vértices, arestas e faces sejam entidades de origem.

Esta formulação de contato é compatível com o tipo de contato Sem
penetração para estudos estáticos, não-lineares e térmicos. Para estudos
estáticos e não lineares, este tipo de contato impede a interferência entre as
74
faces de origem e de alvo, mas também permite que elas se distanciem entre
si, formando espaçamentos.

Para cada nó da origem, o software atribui uma ou mais faces de elemento no
alvo.
O contato de superficie: previne a interferência, mas permite a separação, (
Figura 44).
Figura 44 : Componentes de contato.
Figura 45: Componentes de contato dos cilindros.
75
7.5.6 Aplicação das cargas
As cargas obtidas nos itens anteriores foram aplicadas ao modelo. A carga de
laminação foi aplicada como sendo uma pressão vertical na área de contato cilindro
de trabalho/chapa. E o torque foi aplicado segundo cargas horizontais na mesma
área de contato da carga de laminação. A Figura 46 mostra as cargas aplicadas.
Figura 46: Cargas de laminação e torque aplicados.
7.5.7 Geração da malha
A geração das malhas é uma etapa crucial da análise do projeto e, por esse
motivo, deu-se especial atenção a esta questão.
Para a geração da malha escolheu-se em “Parâmetros da malha” as
seguintes opções: Para o laminador 1 tipo de malha sólida, refinada, com tamanho
global do elemento de 50 mm, número de nós 363.643 e tamanho do elemento
253.575; já o laminador 2 (menor) também com malha sólida e refinada, número de
elemento 110.550, número de nós 159.098 e tamanho do elemento 13,50 mm.
76
Com o intuíto de especificar um tamanho de malha diferente do empregado
no restante do modelo, foi aplicado um controle de malha nas regiões de contato
entre os cilindros e na região em que será aplicado o carregamento no cilindro de
trabalho. Com isso foi possível especificar tamanhos menores de elementos e,
conseqüentemente, foram obtidos resultados mais precisos nessas regiões
A Figura 47 apresenta um dos laminadores com a malha gerada.
Figura 47: Modelo com geração de malha
Nesse trabalho foram observados os parâmetros da malha refinada e não
refinada, do laminador 1, e 2 conforme mostram as Tabelas 8. e 9.
Tabela 8 - Parâmetros da malha do laminador 2.
Tipo de malha
Sem refinar
Parametros da malha
Resultados
Nº de nós
56.505
Nº de elementos
37.410
Tamanho do elemento
20.2569
Nº de nós
159.098
77
Refinada
Nº de elementos
110.550
Tamanho do elemento
13.50 mm
Tabela 9 - Parâmetros da malha do laminador 1.
Tipo de malha
grossa
fina
Parametros da malha
Resultados
Nº de nós
306.808
Nº de elementos
211.857
Tamanho do elemento
76,25mm
Nº de nós
363.643
Nº de elementos
253.575
Tamanho do elemento
50mm
78
8 - RESULTADOS
São apresentados, a seguir, os resultados da simulação dos dois modelos de
elementos finitos. Foram feitas quatro simulações ao todo, pois para cada um dos
laminadores aplicaram-se as cargas com e sem o torque.
8.1 - Resultados do laminador 1, utilizando o programa COSMOS Works.
Nesta seção sãoapresentados os resultados das análises de tensão e
deformação do laminador 1, através do Método de Coeficientes de Influência
MCI/Berger e o Método de Elementos Finitos do programa COSMOS Works.
8.1.1 Resultados do Laminador 1, sem torção e com a malha refinada
A Figura 48 mostra os resultados da tensão de von Mises, após sofrer um
refinamento da malha. Como pode-se observar a tensão máxima é de 8.009e+008
N/m² e localiza-se na a extremidade na região central de contato entre os cilindros.
Figura 48: Resultados do Laminador 1, sem torção e com a malha refinada
79
Com o refinamento da malha, conforme mostrado na Figura 49, o número
total de nós passou para 265.787 nós, o número total de elementos para 182.648 e
o tamanho médio do elemento para 50 mm.
Figura 49: Malha gerada no Laminador 1 com a malha refinada
O valor do deslocamento máximo em Y (direção vertical) no laminador 1 com
a malha refinada e sem o torque é 3.804e-001 mm, conforme mostra a Figura 50.
Este deslocamento ocorre próximo da extremidade do pescoço do cilindro de
trabalho.
Figura 50: Resultado do deslocamento máximo em Y sem o toque com a malha refinada
80
Figura 51: Resultado do deformação máxima em Y sem o torque, com a malha refinada
Para melhor visualização e comparação dos resultados sem o torque e com
as malhas, a Tabela 10, ilustra de forma resumida os valores fornecidos pelo
COSMOS Works, da tensão de von Mises, deformação e deslocamento
Tabela 10 – Análise da Tensão, deformação e deslocamento do Laminador 1, sem o Torque.
Análise
Malha sem
Tensão de von
Deslocamento UY
Deformação
Mises
(direção vertical)
máxima em Y
(N/m²)
(mm)
(EPSY)
8,015e+008
3,801e-001
3.385e-004
8.009e+008
3.804e-001
3.383e-004
refinar
Malha
refinada
Pode-se concluir de forma parcial nesta seção, que após o refino da malha,
como se pode perceber na Tabela 10, a tensão máxima de von Mises manteve-se
praticamente a mesma, da mesma forma o deslocamento em Y.
81
8.1.2 Resultados do Laminador 1, com torção e com a malha refinada.
A Figura 52, mostra os resultados da tensão de von Mises, considerando a
torção, após sofrer um refinamento da malha. Como pode-se observar a tensão
máxima passou para 8.008e+008 N/m² .
Figura 52: Resultado da tensão de von Mises com o torque na malha refinada
Com o refinamento da malha considerando o torque, conforme apresenta a
Figura 53, o número total de nós mudou para 363.643 nós, e o número total de
elementos também mudou, passando para 253.575,
o tamanho do elemento
diminuiu passando para 50 mm.
Figura 53: Malha gerada no laminador 1 com refinamento da malha e considerando o torque
82
O deslocamento máximo em Y no laminador 1 com a malha refinada e
considerando o torque passou para 3.804e-001 mm, conforme mostra a Figura 54
Figura 54: Resultado do deslocamento máximo com o toque e a malha refinada
Para melhor visualização e comparação dos resultados considerando agora o
torque com e sem a malha refinada, a Tabela 11 ilustra de forma resumida os
valores fornecidos pelo COSMOS Works, da Tensão de von Mises, deformação e
deslocamento.
Tabela 11 – Análise da Tensão, deformação e deslocamento do Laminador 1, com o Torque.
Análise
Tensão de von
Deslocamento UY
Deformação máxima
Mises
(mm)
equivalente
(N/m²)
Malha sem
(ESTRN)
8,015e+008
3,801e-001
3,716e-003
8,009e+008
3,804e-001
2,331e-004
refinar
Malha
refinada
83
Pode-se concluir de forma parcial nesta seção, que após o refino da malha e
considerando o torque, conforme mostra a Tabela 11, que a tensão máxima de von
Mises e o deslocamento, praticamente mantiveram os mesmo valores.
8.1.3 Resultado do Laminador 1, da Pressão de Contato (PC) sem torção e com
a malha refinada.
A Figura 55, apresenta o resultado da pressão de contato (PC) entre os
cilindros de trabalho e encosto do COSMOS Works, sem levar em conta a torção.
Dessa forma é possível observar a distribuição e a magnitude da pressão de
contato.
Figura 55: Pressão de Contato entre os cilindros, sem o torque.
A Figura 56 apresenta graficamente os resultados da pressão de contato
entre os cilindros, representando todos os pontos da PC ao longo do semicomprimento.
84
Figura 56: Representação de todos os pontos da PC do programa COSMOS, sem o torque.
Para se fazer a comparação dos resultados da pressão de contato,
representada na Figura 55 do programa COSMOS Works, com os resultados do
programa MCI/Berger, utilizou-se a expressão 8.1, pois é necessário transformar a
carga distribuída linear do MCI/Berger em pressão. Para se determinar a carga de
laminação entre o cilindro de trabalho e encosto pelo programa MCI/Berger, faz-se:
Pr essc
scc
q
(8.1)
Onde:
q= carga de contato entre os cilindros (kgf/mm²)
pressc = pressão de contato entre os cilindros ( kgf/mm), do MCI/Berger
scc= arco de contato (mm) formado entre o cilindro de trabalho e o de encosto
O apêndice ao final desse trabalho explicita detalhes da expressão 8.1.
Como os valores da carga “q”, são expressos em kgf/mm², no programa
MCI/Berger, houve a necessidade de fazer a transformação para N/m², uma vez que
o programa COSMOS Works, utiliza
pressão e não uma carga distribuída
linearmente como o MCI/Berger.
85
Dessa forma o resultado da carga “q” já transformada é representado pela
Figura 57.
9
8
x 10
7.8
carga entre os cilindros [N/m²]
7.6
7.4
7.2
7
6.8
6.6
6.4
6.2
0
100
200
300
400
500
600
700
semi-comprimento [mm]
800
900
1000
Figura 57: Carga entre os cilindros de trabalho e encosto do laminador 1, sem torque.
A Figura 58 foi obtida fazendo a comparação dos resultados da PC, através
do programa MCI/Berger (-) e o COSMOS Works (*), sem levar em conta a torção e
com a malha refinada.
8
carga entre os cilindros [N/m²]
15
x 10
10
5
0
0
100
200
300
400
500
600
700
semi-comprimento [mm]
800
900
1000
Figura 58: Pressão de contato entre os cilindros, sem considerar a torção e com malha
refinada
86
8.2 Resultados do laminador 2, utilizando o programa COSMOS Works.
Nesta seção apresenta os resultados das análises de tensão e deformação do
laminador 2, de forma análoga ao que foi realizado sobre o laminador 1.
8.2.1 Resultados do Laminador 2, com Torção e com a malha a refinada.
A Figura 59 mostra os resultados da tensão de von Mises, considerando a
torção, após sofrer um refinamento da malha. Como pode-se observar a tensão
máxima passou para 7,987e+008 N/m² .
Figura 59: Resultado da tensão de von Mises com o torque e com refinamento da malha
Figura 60: Resultado da PC com o torque e com refinamento.
87
Com o refinamento da malha considerando o torque, conforme mostra a
Figura 61, o número total de nós mudou para 159.098 nós, e o número total de
elementos também mudou, passando para 110.550, e o tamanho médio do
elemento, mudou para 13,5046 mm
Figura 61: Malha gerada no laminador 2 com refinamento da malha e considerando o torque
O deslocamento máximo em Y no laminador 2 com a malha refinada e
considerando o torque passou para 1.435e-001 mm, conforme mostra a Figura 61.
Figura 62: Resultado do deslocamento máximo em Y com o torque e a malha refinada.
88
8.2.2 Resultados do laminador 2, sem o torque e com a malha refinada
A Figura 63 mostra os resultados da tensão de von Mises do caso sem a
aplicação do torque, após sofrer um refinamento da malha. Como pode-se observar
a tensão máxima mudou para 7,987e+008.
Figura 63: Resultado da tensão de von Mises sem o torque e com refinamento da malha
Figura 64: Resultado da PC sem o torque e com refinamento da malha.
Com o refinamento da malha e sem considerar o torque, o número total de
nós manteve os mesmos valores, ou seja, 159.098 nós, o número total de elementos
110.550 e o tamanho médio do elemento, 13,5046 mm.
89
Figura 65: Malha refinada sem o torque.
O deslocamento máximo em Y no laminador 2 com a malha refinada e sem
considerar o Torque manteve o mesmo valor 1.435e-001 mm, conforme mostra a
Figura 66. Este deslocamento ocorre próximo da extremidade do cilindro de encosto.
Figura 66: Resultado do deslocamento máximo em Y sem o toque e com a malha refinada
Da análise da deformação equivalente, sem o torque na malha refinada,
percebe-se conforme a Figura 65 que também não houve mudança em seu valor de
2.710e-004 ocorrendo na posição próximo da extremidade do cilindro de trabalho
90
8.3 Análise dos Resultados
Neste sub-ítem serão realizadas as análises dos resultados consolidados dos
modelos dos laminadores 1 e 2.
8.3.1 Análise dos Resultados da Tensão de von Mises, Deslocamento em Y e
deformação dos laminadores 1 e 2( Tabela 12).
Tabela 12–Análise da Tensão, deformação e deslocamento do Laminador 1 e 2
Tensão de von
Deslocamento
Deformação
Mises
UY
máxima
(N/m²)
(mm)
em Y
Malha sem
8.015e+008
3.801e-001
5.042e-004
refinar
9.472e+008
1.180e-001
2.889e-003
Malha sem ser
8.015e+008
3.801e-001
5.044e-004
refinada
9.464e+008
1.166e-001
2.889e-003
Malha
7.685e+008
3.807e-001
2.993e-004
refinada
7.987e+008
1.435e-001
2.710e-004
Sem o torque
7.621e+008
3.816e-001
2.909e-004
e malha
7.987e+008
1.435e-001
2.710e-004
Análise
Considerando
o torque
sem o torque
considerando
o torque
refinada
91
Tomar como referência a cor de cada laminador:

Laminador 1

Laminador 2
Pela tabela 12 é possível identificar as variações com e sem o torque, na
malha refinada ou não, para analise da Tensão de von Mises e deslocamento em Y.
Observa-se que as tensões se elevam e os deslocamentos diminuem, como se
esperaria ao elevar o número de elementos finitos empregados.
8.3.2 Análise da Comparação do Perfil Gerado pelo Programa MCI/Berger e
Elementos Finitos do laminador 1.
Foram comparados os resultados de deflexão e de achatamento obtidos pelo
programa MCI/Berger de um modelo de cilindro de trabalho e encosto tridimensional,
modelado com elementos finitos.
A Figura 67 apresenta o perfil de espessuras da chapa, sem o torque.
Observa-se pouca variação no perfil obtido pelo MCI/Berger (linha continua) e o
método de elementos finitos. Pode-se perceber grande semelhança entre as duas
curvas.
3.95
3.9
perfil [mm]
3.85
3.8
3.75
3.7
3.65
3.6
0
100
200
300
400
500
semi-largura [mm]
600
700
Figura 67: Resultados via MEF e MCI/Berger
92
800
A Figura 67 representa o perfil do primeiro passe, onde a chapa sofreu uma
redução de 4,5 mm para 3,89 mm. De posse dos resultados calcularam-se as coroas
absoluta e relativa, o parâmetro de medição foi a espessura da chapa a 25 mm da
borda da chapa.
MCI/Berger:Cr25 =(3,89 – 3,72)/3,89=0,17/3,89 = 0,043, ou 4,3%
( Cj=0,17mm)
MEF 3D: Cr25 =(3,89 – 3,76)/3,89 = 0,13/3,89 =0,033, ou 3,3%
(Cj=0,13mm)
O erro relativo (espessuras) = (3,72 – 3,76)/ 3,72= -0,04 = erro máximo relativo =
-4,0%
Uma das possibilidades dessa diferença entre os resultados da coroa
fornecido por cada método, pode estar relacionada, com o contato do MCI/Berger
em aproximar o cilindro tridimensional por um unidimensional. Outro motivo que
justifique essa diferença pode ser o fato pelo qual o método dos elementos finitos
detalha o pescoço do cilindro de encosto, resultando numa deflexão mais precisa.
Apesar de existir um pequeno erro, pode-se concluir que a forma de ambos
os perfis são muito semelhantes.
Para este mesmo laminador, considerando o torque, podem-se observar os
perfis resultante na Figura 68.
3.9
perfil [mm]
3.85
3.8
3.75
3.7
3.65
0
100
200
300
400
500
semi-largura [mm]
600
700
800
Figura 68: Resultados dos perfis, via MEF e MCI/Berger,
93
De forma semelhante á primeira análise do perfil do modelo, medindo-se as
espessuras a 25 mm das bordas, conforme mesmo procedimento anterior.
Obtiveram-se os seguintes resultados.
MCI/Berger:Cr25 = (3,89 – 3,725)/3,89=0,165/3,89 = 0,042, ou 4,2%
( Cj=0,17mm)
MEF 3D: Cr25 =(3,89 – 3,730)/3,89 = 0,16/3,89 =0,041, ou 4,1%
(Cj=0,16 mm)
O erro relativo(espessura) = (3,725 – 3,730) /3,725 =- 0,005 = -0,5%
A diferença da coroa representado por cada método, pode ser explicado da
mesma forma anterior, ou seja, pode estar relacionada com o refino da malha do
modelo de elementos finitos, ou pela deflexão do pescoço do cilindro. Apesar de
existir um pequeno erro pode-se concluir que a forma de ambos os perfis são
também muito semelhantes, não havendo influência do torque sobre o mesmo.
8.3.3 Análise da Comparação da Pressão de Contato gerada pelo Programa
MCI//Berger e Elementos Finitos
A carga de laminação, mostrada na Figura 69 (linha contínua), será aplicada
ao modelo em elementos finitos. Para essa finalidade foi calculada a pressão de
laminação, dada simplesmente pelo quociente entre a carga distribuída linear e o
arco-de-contato. Deve-se observar que o arco-de-contato é variável ao longo do
comprimento do cilindro devido à variação da carga.
94
Distribuição de cargas
1200
1100
p(-) e q(.) [kgf/mm]
1000
900
800
700
600
500
400
300
0
100
200
300
400
500
600
Semi-largura [mm]
700
800
900
1000
Figura 69: Carga distribuída de laminação linearmente no contato entre os cilindros.
Importante frisar que na Figura 69 as cargas “p” e “q” representam;
p: carga distribuída de laminação;
q: carga distribuída de contato entre cilindros;
A Figura 70, mostra o resultado da pressão de contato do laminador 1,
considerando o torque.
8
16
x 10
pressão de contato [N/m²]
14
12
10
8
6
4
2
0
100
200
300
400
500
600
700
semi-comprimento [mm]
800
900
1000
Figura 70: Cargas de contato entre cilindros, obtidas
por MCI/Berger (linha contínua) e MEF –com o torque
95
A Figura 71, mostra o resultado da pressão de contato do laminador 1, sem
considerar o torque
8
16
x 10
pressão de contato [N/m²]
14
12
10
8
6
4
2
0
100
200
300
400
500
600
700
semi-comprimento [mm]
800
900
1000
Figura 71: Cargas de contato entre cilindros, obtidas
por MCI/Berger (linha contínua) e MEF – sem o torque
96
Figura 72: Representação da PC no modelo de elementos finitos
Observa-se pela Figura 72 que a PC diminui à medida que se afasta da linha
central. Nitidamente percebe-se a distribuição da pressão ao longo do semicomprimento do cilindro de encosto, na região de contato.
Outro fato importante refere-se à distribuição de pressão do cilindro de
trabalho, pois verifica-se que o mesmo não se comporta de forma semelhante ao
cilindro de encosto, conforme mostra a Figura 73. É possível identificar as PC ao
longo da linha central, com pouquíssimas tensões localizadas fora dessa linha no
cilindro de trabalho.
Deve-se observar que as as tensões deveriam ser as mesmas, pois a força
(ação/reação) e as áreas de contato são iguais.
97
Figura 73: Diferenças nas pressões de contato no cilindro de trabalho
e no de encosto.
A Figura 73, representa a PC ao longo da linha central do semi-cilindro,
mostrando as diferenças nas pressões de contato no cilindro de trabalho e no de
encosto
Observa-se a boa concordância entre os resultados do MCI/Berger e MEF em
relação ao perfil gerado. O mesmo não se pode dizer a respeito da carga de contato
entre os cilindros.
Uma vez que o perfil é parecido mas, existem diferenças visíveis dos
resultados em MCI/Berger e elementos finitos.
Dessa forma uma das possibilidades da Pressão de Contato do MCI/Berger
não coincidir com o MEF, pode estar ligado com geração de questão do malha ou
até mesmo, pelo fato do programa MCI/Berger não levar em consideração a carga
aplicada no pescoço do cilindro.
98
8.3.4 Análise da Comparação do Perfil Gerado pelo Programa MCI/Berger e
Elementos Finitos do laminado 2.
Este modelo após geração da malha apresentou os seguintes resultados:

Número de nós:
159.098

Número de elementos:
110.550

Tamanho do elemento:
13.5046 mm
Tabela 13- Carga distribuída obtida pelo MCI/Berger
Laminador II
Pw
(kgf/mm²)
Pw
(N/m²) x 106
W/2
(mm)
70,87
71,07
71,73
72,83
74,5
76,7
79,6
83,5
91,5
694,526
696,486
702,954
713,734
730,1
751,66
780,08
818,3
896,7
0
100
200
300
400
500
600
700
800
99
Com base nos dados da Tabela 13, observa-se na Figura 73 o perfil final da Chapa
Laminada obtidas por MCI/Berger (linha contínua), gerando como resultados o perfil
da chapa laminada a cada passe.
E a distribuição de carga de laminação e de contato entre os cilindros,
conforme mostra a Figura 74, respectivamente. Entende-se como perfil da chapa a
espessura da mesma ao longo da largura. As distribuições da carga de laminação
necessárias para deformar a chapa e representado conforme figura
Metade da chapa foi discretizada em 45 faixas. A carga de laminação para
cada faixa foi calculada pelo método de (Bland-Ford 1948)
Perfis
4.5
4
Perfil [mm]
3.5
3
2.5
2
1.5
0
20
40
60
80
100
120
Semi-largura [mm]
140
160
180
Figura 74: Perfis finais da chapa laminada
Distribuição de cargas
700
650
600
p(-) e q(.) [kgf/mm]
550
500
450
400
350
300
250
200
.
0
20
40
60
80
100
120
Semi-largura [mm]
140
160
180
200
Figura 75: Carga de laminação distribuída linearmente no contato entre os cilindros.
100
8.3.5 Resultado do Perfil de Contato entre os cilindros do laminador 2 – com o
torque
Na Figura 76 observa-se as cargas de contato na interface cilindro de
trabalho/cilindro de encosto.
3.89
3.88
3.87
perfil [mm]
3.86
3.85
3.84
3.83
3.82
3.81
3.8
0
20
40
60
80
100
120
semi-largura [mm]
140
160
180
Figura 76: Perfis finais da chapa laminada, obtidas
por MCI/Berger e MEF- com o torque
A Figura 76- representa o perfil do primeiro passe, onde a chapa sofreu uma
redução de 4,5 mm para 3,89 mm. De posse dos resultados calcularam-se as coroas
absoluta e relativa, o parâmetro de medição foi a 25 mm da espessuras da borda da
chapa da mesma forma como se fez no laminador 1:
MCI/Berger:Cr25 =(3,89 – 3,835)/3,89=0,055/3,89 = 0,014 =1,4%
( Cj=0,055mm)
MEF 3D: Cr25 =(3,89 – 3,85)/3,89 = 0,04/3,89 =0,0102, ou 1,02%
101
(Cj=0,04mm)
O erro relativo(espessura) = 3,835 – 3,85/ 3,835= -0,015 = erro máximo relativo =
-1,5%
Uma das possibilidades dessa diferença entre os resultados da coroa
fornecido por cada método pode estar relacionada ao fato do contato do MCI/Berger
em aproximar o cilindro tridimensional por um unidimensional. Outro motivo que
justifique essa diferença pode ser o fato pelo qual o método dos elementos finitos
detalhar o pescoço do cilindro de encosto, resultando numa deflexão mais precisa.
Apesar de existir um pequeno erro, pode-se concluir que a forma de ambos
os perfis são muito semelhantes.
8.3.6 Resultado do Perfil de Contato entre os cilindros do laminador 2 – sem o
torque
3.92
3.9
perfil [mm]
3.88
3.86
3.84
3.82
3.8
0
20
40
60
80
100
120
semi-largura [mm]
140
160
Figura 77: Perfis finais da chapa laminada, obtidas
por MCI/Berger e MEF - sem o torque
102
180
De forma semelhante á primeira análise do perfil do modelo, medindo-se as
espessuras a 25 mm das bordas, conforme mesmo procedimento anterior.
Obtiveram-se os seguintes resultados.
MCI/Berger:Cr25 = (3,89 – 3,835)/3,89=0,055/3,89 = 0,014, ou 1,4%
( Cj=0,055mm)
MEF 3D: Cr25 =(3,89 – 3,848)/3,89 = 0,042/3,89 =0,0107, ou 1,07%
(Cj=0,042mm)
O erro relativo (espessura) = (3,835 – 3,848)/ 3,835 = -0,013/3,835 = -0,0033mm =
erro máximo relativo á -0,33%
Dessa forma percebeu-se pelos resultado que para um modelo menor
são mais confiáveis.
8.3.7 Análise Resultado Final da Pressão de Contato entre os cilindros do
laminador 2
A Figura 78 mostra o resultado da pressão de contato do laminador 2,
considerando o torque.
Figura 78: Cargas de contato entre cilindros, obtidas
por MCI/Berger (linha contínua) e MEF – com o torque
103
A Figura 79, mostra o resultado da pressão de contato do laminador 2, sem
considerar o torque
Figura 79: Cargas de contato entre cilindros, obtidas
por MCI/Berger (linha contínua) e MEF –sem o torque
Observa-se nesse modelo em elementos finitos a PC com o torque foi
praticamente idêntica à do sem o torque.
Dessa forma o comportamento desse segundo modelo em se tratando da PC
terá as mesmas explicações referentes ao seu resultado do primeiro modelo.
104
9 - CONCLUSÕES
A Tabela 14 condensa os resultados referentes aos perfis de contato dos
laminadores 1 e 2.
Pode-se concluir com base nos resultados que o erro máximo relativo da
espessura da chapa no laminador 1 sem o torque foi maior que o erro relativo
máximo sem o torque. Isto nos permite concluir que sem o torque o perfil obtido pelo
MCI/Berger é bem mais próximo do perfil obtido via elementos finitos.
No laminador 2 (laminador de pequeno porte) a situação foi inversa, ou seja,
com o torque o erro relativo máximo foi maior que o resultado do erro sem o torque.
Tabela 14–Análise dos resultados dos perfis dos laminadores
laminadores
Cr25
CJ
Erro máximo
(%)
(mm)
relativo
(%)
Laminador 1
MCI
4,3
0,17
sem torque
MEF
3,3
0,13
Laminador 1
MCI
4,2
0,17
com torque
MEF
4,1
0,16
Laminador 2
MCI
1,4
0,05
sem torque
MEF
1,1
0,042
Laminador 2
MCI
1,4
0,055
com torque
MEF
1,02
0,04
-4,0
-0,5
-0,3
-1,5
Em referência a tabela 12, que trata dos resultados de tensão, deformação e
deslocamentos obtidos via MEF, podem-se tirar as seguintes conclusões. Observouse no laminador 1 que a tensão obtida com o torque foi 0,8% maior que o caso
sem considerar o torque. Já com relação ao deslocamento sem considerar o torque,
observou-se um erro percentual menor nos resultados, ou seja, 0,02% maior que
com o torque.
105
No caso do laminador 2, não se notou nenhuma diferença nos resultados.
Dessa forma o erro percentual nos dois modelos de laminadores, de um
modo geral, foi muito baixo, praticamente imperceptível.
Pode-se concluir que a adição do torque no modelo não modifica os
resultados de tensão máxima e deflexão máxima.
Com relação à pressão de contato o que se pode concluir conforme os
resultados apresentados através da Figuras 70, 71, 78 e 79 que os resultados do
método de elementos finitos foram maiores que no MCI/ Berger pelo fato do mesmo
levar e conta o valor médio das pressões de contato, representando o resultado
médio em uma única linha. Já no MEF os resultados foram maiores por levar em
conta toda a pressão ao longo da linha central selecionada conforme apresenta a
Figura 80.
Figura 80: Representação da pressão de contato, em uma seção transversal do cilindro
Observa-se ainda que os modelos em elementos finitos praticamente
apresentam os mesmos resultados com poucas diferenças quando se considera ou
não o torque.
Por outro lado
observa-se que em ambos os resultados os valores do
MCI/Berger ficaram abaixo do resultado em elementos finitos.
Uma das possíveis razões para essa diferença entre os resultados da coroa
fornecido por cada método, pode estar relacionada, com o contato do MCI/Berger
em aproximar o cilindro tridimensional por um unidimensional. Outro motivo que
106
justifique essa diferença pode ser pelo fato do método dos elementos finitos detalhar
o pescoço do cilindro de encosto, resultando numa deflexão mais precisa.
Apesar de existir um pequeno erro, pode-se concluir que a forma de ambos
os perfis são muito semelhantes.
Pode-se concluir dessa forma, através das análises anteriores, que o modelo
pode ser aplicado para analise de tensão e deformação em cilindros de laminadores
quádruos com relativa precisão.
107
10- PROPOSTA PARA TRABALHOS FUTUROS
Como tópicos para trabalhos futuros, podem-se sugerir:

Analisar com maior profundade o efeito do pescoço do cilindro de encosto

Investigar a diferença entre os resultados de pressão de contato

Elaborar um programa de computador em que se acoplem o MCI/Berger e o
modelo MEF
108
APÊNDICE A - SOBRE O MÉTODO ELEMENTOS
FINITOS
5.1- Introdução ao Método dos Elementos Finitos
O Método dos Elementos Finitos tem sido aplicado na modelagem da
laminação, com vistas à determinação do perfil transversal da tira. Sua utilização
permite com razoável facilidade a modelagem de laminadores mais complexos. A
título de exemplo, Ginzburg et al. (1987) desenvolveram um programa em que os
cilindros são discretizados em elementos finitos e a rigidez nas interfaces de contato
é aproximada através de coeficientes de resistência à deformação. A Figura 22 é um
exemplo da modelagem de um laminador quádruo.
Figura 22: Exemplo de aplicação do Método dos Elementos Finitos
(GINZBURG,1987)
5.2- Elemento Tetraédrico Quadrático de 10 Nós
O problema estrutural, objeto de estudo deste trabalho, foi analisado pelo
programa COSMOS Works que trabalha de forma integral com o SOLIDWORKS
109
2008. Foi empregado o “Elemento Tetraédrico Quadrático de 10 nós” de formulação
isoparamétrica. O modelo de cálculo desse elemento será a seguir apresentado de
forma resumida com base nos trabalhos de Oñate (1995), Assan (1996) e Cook
(2001).
5.3- Campo de Deslocamentos, (OÑATE, 1995).
A Figura 23 mostra um sólido tridimensional, e um ponto no espaço, cujo
movimento pode ser perfeitamente definido pelas três componentes do vetor
deslocamento u:
u  u, v, w
T
(5.1)
onde u, v, w são as componentes de deslocamentos do ponto segundo as
coordenadas cartesianas x, y, z, respectivamente.
Figura 23: Sólido tridimensional, vetor de deslocamento de um ponto
(OÑATE, 1995)
5.4- Campo de Tensões e Deformações, (OÑATE, 1995)
110
O vetor de tensão (representação compacta do tensor de tensões) quando é
simetria em um ponto contém seis componentes de tensão, conjugadas por seis
respectivas componentes de deformação.

σ  σ x , σ y , σ z , τ xy , τ xz , τ yz

T
(5.2)
onde  x ,  y ,  z são as componentes normais de tensão e  xy , xz , yz são as
componentes tangenciais de tensão. A Figura 24, mostra as componentes de
tensão, segundo três planos no espaço tridimensional.
Figura 24: Elemento representativo do estado de tensão
Para um material de comportamento isotrópico e elástico-linear, a lei
constitutiva dependerá apenas de dois parâmetros, o módulo de elasticidade “E” e o
coeficiente de Poisson”  ”, resultando na seguinte lei constitutiva:


σ  D ε  ε0  σ0
(5.3)
onde ε 0 e σ 0 são os vetores iniciais de deformação e tensão, e D representa a matriz
constitutiva de propriedades elásticas:
111



1
1 
1 

v

1
1 

1

E 1    
D
1   1  2  

 simétrica




0
0
0
0
0
1  2
21   
0



0 

0 

0 

0 

1  2 

21   
0
0
1  2
21   
No caso da deformação inicial de origem térmica, o vetor ε 0 tem
(5.4)
a
seguinte
representação:
ε 0   T 1,1,1,0,0,0
T
(5.5)
Onde  é o coeficiente de dilatação térmica e T é a variação de temperatura.
5.5 - Princípio da Energia Potencial Estacionária, (ASSAN, 1996)
Segundo Assan (1996), a energia de defomação U de um sólido deformável
de volume V pode ser calculada como:
U
1
 x x   y  y   z  z   xy  xy   xz  xz   yz  yz dV  1  σ T εdV

2V
2V
(5.6)
O trabalho externo Ω a ser realizado pelas forças volumétricas b e por ações
externas t, de forma que a estrutura retorne à configuração indeformável pode ser
representado por:
    u T bdV   u T tdS
V
112
S
(5.7)
Sendo S a região onde as ações
vetoriais b e t por meio de suas
componentes cartesianas:
bx 
b  by 
bz 
t x 
t  t y 
t z 
e
(5.8)
A energia potencial total do elemento é descrita pela expressão:
 U  
1 T
ε σ.dV   u T b.dV   u T tdS

2V
V
S
(5.9)
Para problemas em que a energia é quadrática, como no caso da
elasticidade, a minimização desse funcional equivale à nulidade da primeira variação
de  .
    ε T  .dV   u T b.dV   u T tdS  0
V
ou
 ε
V
V
T
(5.10)
S
 .dV   u T b.dV   u T tdS
V
S
Os campos de tensão e deformação (5.2) e (5.3), são o campo de tensão.
5.6-Discretização do Campo de Deslocamento, (OÑATE, 1995).
O elemento utilizado neste trabalho nas análises pelo programa COSMOS
Works e representado na Figura 25 trata-se do elemento tetraédrico de 10 nós. Em
cada nó i são definidos parâmetros de deslocamentos ui, vi, wi, alinhados aos eixos
cartesianos. O campo de deslocamento no interior de um elemento pode, então, ser
descrito da seguinte forma:
113
 u   N1u1  N 2 u 2  ........................  N10u10  10

  


u   v    N1v1  N 2 v 2  .......................  N10v10  =  N i ai( e )  Na ( e )
w 
 i 1
  
N
w

N
w
..........
..........
.....

N
w
2 2
10 10 
 1 1

N  N1 , N 2 , N 3 , N 4 , N 5 , N 6 , N 7 , N 8 , N 9 , Ν10 
(5.11)
(5.12)
onde:
Ni

Ni   0
0

0
Ni
0
0

0
N 
a (e)
a1( e ) 
 (e) 
a 2 
a 3( e ) 
 (e) 
a 4 
ui 
a ( e ) 
 
(e)
5
  ( e )  ; a i   vi 
w 
a 6 
 i
a 7( e ) 
 (e) 
a 8 
a ( e ) 
 9( e ) 
a10 
Figura 25: elemento tetraédrico de 10 nós
(Fonte; COSMOS Works)
114
(5.13)
As funções de forma N i são encontradas em Oñate (1995), descritas
segundo as coordenadas naturais r, s e t, e representadas como:
N1  1  r  s  t 1  2r  2s  2t 
N 2  r 2r  1
N 3  s2s  1
N 4 t 2t  1
N 5  4r 1  r  s  t 
(5.14)
N 6  4rs
N 7  4s1  r  s  t 
N 8  4tr
N 9  4st
N10  4t 1  r  s  t 
5.7 Elemento Isoparamétrico
A Figura 26 representa o elemento tetraédrico isoparamétrico, de 10 nós,
representando nas coordenadas naturais (r, s, e t).
Figura 26: Elemento tetraédrico de 10 nós
(COOK, 2001)
115
Segundo Cook (2001), um elemento é isoparamétrico se sua geometria e o
campo a ser interpolado (no caso o campo de deslocamentos u) utilizar o mesmo
conjunto de funções para a sua descrição (5.12), ou seja:
x   N i xi
i
x   N i xi
i
z   N i zi
(5.15)
i
onde xi , yi e zi são as componentes nodais segundo os eixos cartesianos x,
y e z.
O campo de deformações (derivadas primeiras de u) pode ser então definido
pelas expressões abaixo:
N i


ui


x


N i


vi
y




N i
wi
n 
 n

    N z N    Bi ai( e )  Ba ( e )
i
i 1 
ui  i vi  i 1

y
x 

 N i
N i 
 z ui  x wi 
 N

 i vi  N i wi 
 z
y 
(5.16)
onde B é denominada matriz de deformação do elemento, sendo dada por;
B  B1 , B 2 , B 3 , B 4 , B 5 , B 6 , B 7 , B8 , B 9 , B10 
Sendo Bi a matriz de deformação anunciada ao nó i,
116
(5.17)
 N i
 x

 0


 0
B i   N
 i
 y
 N
 i
 z

 0

0
N i
y
0
N i
x
0
N i
z

0 

0 

N 

z 
0 

N i 

x 
N 
y 
(5.18)
Para o cálculo das derivadas cartesianas das funções de forma deve-se
recorrer à derivação pela regra da cadeia, conforme se ilustra a seguir:
 N i   x
 r   r
 N   x
i



s

  s
 N i   x
 t   t
y
r
y
s
y
t
z  N i. 


r  x 

z  N 
( e ) N i

J
s  y 
x
z  N i 
t  z 
(5.19)
Onde J (e ) é a matriz Jacobiano, definida como:
J ( e)
 N
 r x
 
N
    x
   s
 N
 t x
N
y
r
N
y
s
N
y
t
N 
z
r 
N 
z 
s 
N 
z
t 
(5.20)
Invertendo-se a equação ( 5.19), tem-se a expressão da derivada cartesiana de
N :
117
 N 


 Nx 
 
( e)

 J
 y 
 N 
 z 
 N 
 r 


1  N 


 s 
 N 
 t 
 
(5.21)
O diferencial de volume pode ser expresso como
dx.dy.dz  J ( e) dr.ds.dt
(5.22)
5.8 - Equilíbrio do Elemento, (OÑATE, 1995).
Substituindo na equação (5.10), as expressões da discretização em um
elemento tetraédrico de 10 nós, (5.11 a 5.21), obtêm-se a seguinte equação:
K (e) a (e)  f (e)  q (e)
(5.23)
Onde K (e ) é a matriz de rigidez do elemento, f (e ) é o vetor de forças equivalentes
nodais e q (e ) o vetor de forças nodais de equilíbrio.
A matriz de rigidez é expressa por:
K ( e)  
V (e)
B T DBdV
(5.23)
e sua sub-matriz relacionada com os nós i e j do elemento
Κ ij
(e)
 
V (e)
B Ti D.B j .dV
(5.24)
O cálculo da matriz de rigidez de um elemento tetraédrico isoparamétrico é da forma:
118
K ij( e )  
V
1 1 1
B Ti DB j dxdydz 
(e)
  B
T
i
DB J J ( e ) drdsdt
(5.25)
1 1 1
E a expressão desenvolvida f (e ) :
f (e)  
V (e)
N T bd V  
A( e )
N T tdA  
V (e)
BT Dε 0 dV  
V (e)
BT σ 0 dV  f b(e)  f t(e)  f ( e)  f(e)
(5.26)
Onde a primeira integral representa o vetor de forças do volume, a segunda
as forças de superfície, a terceira e a quarta os vetores de forças devido às
deformações e tensões iniciais, respectivamente.
Os cálculos dos vetores de forças nodais equivalentes, que implicam na
integração sobre o volume do elemento, são representados por:
fb( e)  
V
(e)
NiT bdxdydz  
!
ft ( e)  
V
f( e)  
V
f( e)  
V
1 1 1
(e)
 
!
NiT tdxdydz  
(e)
(e)
!
1 1 1
 
!
NiT  .dxdydz  
!
!
1 1 1
!
NiT .dxdydz  
NiT b J ( e) drdsdt
 
!
!
1 1 1
!
 
!
!
NiT t J ( e) drdsdt
(5.28)
NiT  J (e) drdsdt
(5.29)
NiT J (e) drdsdt
O Apêndice A contém detalhes sobre a formulação do contato no
Método dos Elementos Finitos.
119
(5.27)
( 5.30)
APÊNDICE A - PROBLEMAS DE CONTATO
(NICHOLSON, 2003)
A.1 Introdução
Segundo Nicholson (2003), em muitos problemas práticos, a informação
necessária para a discretização de um problema por Elementos Finitos, por
exemplo, a geometria de um membro e as propriedades dos seus materiais
constitutivos, pode ser determinada com considerável precisão. Por outro lado,
existem casos em que o carregamento absorvido por algum membro não é descrito
de forma tão clara. Isto é especialmente verdadeiro para as cargas transmitidas aos
membros, ao longo de uma interface com um segundo membro. Essa classe de
problemas é chamada de problemas de contato, sendo provavelmente a mais
comum entre as denominadas condições de fronteira encontradas em problemas
práticos.
A Figura A.1, ilustra um exemplo típico de contato, onde as molas são de
rigidez K e as extremidades A, B e C. Na parte superior tem-se o contador o qual
sofre uma solicitação P e na parte inferior o alvo de contato, nesta parte a mola B é
inicialmente representada pelo ponto remoto de alvo g. A solução exata de rigidez é
representada por:
120
2 K   g
Kc  
3K   g
(A.1)
Do ponto de vista do método de elementos finitos, coloca-se a seguinte
dificuldade. Se um nó é fixado no ponto mais baixo B, conforme figura A.1.
Figura A.1
(Nicholson, 2003)
Figura A.2
(Nicholson, 2003)
121
A Figura A.2 é possível, identificar os nós inicialmente ligados, representando
um problema físico. Sendo necessário obedecer a uma penetração constante, de
forma a não mover a região do contato inferior.
Se os nós são considerados estranhos no modelo de Elemento Finito, não
existirá nenhuma força de penetração constante. Existindo uma conecção entre os
nós a rigidez é artificialmente elevada.
Esta dificuldade é superada em um sentido aproximado, por um elemento de
contato bi linear. Em particular, introduzimos uma nova mola, K g como mostrado na
figura A.2.
A rigidez da mola média (na série B em contato com a mola) é agora
denominada K m .
1
1 
Km   

 K K g 
1
(A.2)
A mola média deslocará suavemente, quando o sistema for aberto ( g   ) e
deslocará de forma rígida, quando for fechada g    .
K / 100 g  
Kg  
 100 K g  
(A.3)
Na forma de álgebra elementar, tem-se:
2 K  0,01K
Kc  
2 K  0,99 K
g 
g 
(A.4)
Conseqüentemente, o modelo com o contato será rígido, em 0,5% se o
sistema for aberto, e suave em 0,33%, quando o sistema for fechado (contato). Uma
conclusão que se pode extrair deste exemplo é que a rigidez do elemento do
sistema relacione com a rigidez do contador e do alvo na proximidade do ponto de
contacto.
122
APÊNDICE B– COMANDOS DO MCI/BERGER
B.1- Procedimento para obtenção da Pressão WR do Laminador 1
Inicialmente inseri os dados referentes ao laminador I, no programa MCI/Berger,
esta entrada se da pelo arquivo “quadruov.m”, do programa.
Como o MCI/Berger utiliza o Matlab, para rodar os arquivos, ao digitar o nome do
laminador, automaticamente são fornecidos os dados, conforme se apresenta
abaixo.
B.1.1 - Dados do Laminador 1:
Diâmetro do cilindro de trabalho:
450 mm
Coroa usinada do cilindro de trabalho: 0 mm
Módulo de Young do cilindro de trabalho: 21000 kgf/mm2
Diâmetro do cilindro de apoio:
1300 mm
Coroa usinada do cilindro de apoio:
0 mm
Módulo de Young do cilindro de trabalho: 21000 kgf/mm2
Módulo de Poisson dos cilindros:
0.3
Comprimento da face dos cilindros:
1900 mm
Comprimento do braço de contraflexão:
100 mm
B.1.2- Dados Operacionais:
Coeficiente de atrito (seco):
Largura da tira:
Módulo de Young da tira:
0.1
1600 mm
21000 kgf/mm2
123
Módulo de Poisson da tira:
0.3
Curva de fluxo (EPD), via Ludwik:
Espessura inicial:
0.1+78.8eps^0.249 kgf/mm2
4.5 mm
Coroa absoluta inicial:
0 micrometros
Coroa medida a 25 mm da borda da tira
B.1.3 – Resultados do MCI/Berger referente ao laminador I:
Espessuras
finais (mm)
Carga de
Coroa relativa
laminação (kgf)
(%)
Força de
Tempo
Roll Bending (kgf)
(s)
3.89
974433.71
4.8923
0
2.05
3.07
1559873.43
10.3809
0
2.42
2.48
1529912.84
13.2769
0
3.08
2.06
1412035.82
15.1443
0
3.16
1.76
1264219.46
16.3036
0
3.86
Tempo total de processamento: 14.562 s
B.2- Procedimento para obtenção da Pressão WR do Laminador 1
A título de economia de tempo, fez-se um estudo de análise apenas no
primeiro passe do processo de laminação da tira, para obter a pressão WR entre o
cilindro de trabalho e a chapa.
124
B.2.1- Comandos utilizados no programa MCI/Berger, para obter a
Pressão WR. do Laminador 1
Comando:

pressaoWr=carga(1,1:m)./comprimentoarco;
Resultados Formecidos, após comando:
Columns 1 through 7
70.8721 70.8777 70.8891 70.9066 70.9300 70.9594 70.9949
Columns 8 through 14
71.0365 71.0842 71.1381 71.1982 71.2645 71.3371 71.4161
Columns 15 through 21
71.5015 71.5933 71.6917 71.7966 71.9081 72.0264 72.1514
Columns 22 through 28
72.2833 72.4221 72.5679 72.7208 72.8809 73.0483 73.2230
Columns 29 through 35
73.4051 73.5948 73.7922 73.9973 74.2103 74.4313 74.6604
Columns 36 through 42
74.8978 75.1436 75.3979 75.6610 75.9329 76.2139 76.5042
Columns 43 through 49
76.8042 77.1136 77.4328 77.7864 78.1259 78.4767 78.8392
Columns 50 through 56
79.2137 79.6009 80.0015 80.4164 80.8466 81.2935 81.7585
Columns 57 through 63
82.2437 82.7518 83.2862 83.8517 84.4551 85.1067 85.8227
125
Columns 64 through 67
86.6316 87.5898 88.8340 90.8429
Após obter os valores da pressão WR entre os cilindros, pelo programa
MCI/Berger em cada fragmento. Construiu-se o gráfico pressão WR x semicomprimento. Onde a coordenada y, representa os valores da pressão WR e a
coordenada x, o semi-comprimento do cilindro.
Comandos utilizados:





figure;
plot(ex,(1:67),pressaoWR(1:67));
grid;
xlabel(„semi-comprimentp [mm]‟)
ylabel(„ pressão de contato [ kgf/mm²]‟)
O programa MCI/Berger, após processamento dos comandos de entrada
acima, Constrói-se o gráfico da Figura B.1, conforme se pode observar a curva da
pressão WR, representa uma semi - parábola de concavidade voltada para cima.
Verifica-se que na extremidade da semi-parábola a pressão Wr é máxima.
pressão de contato entre Cw e a chapa[kgf/mm²]
95
90
85
80
75
70
0
100
200
300
400
500
600
semi-comprimento do cilindro de trabalho [mm]
700
Figura B.1 – Pressão Wr do Laminador 1
126
800
De forma a melhorar os resultados, a Figura B.1 foi subdividida em outras
seis figuras. Dessa forma tornou-se mais preciso a obtenção dos resultados da
pressão Wr.
Comandos utilizados, para a construção de cada figura.
:




plot(ex(1:10),pressaoWR(1:10))
grid;
xlabel(„semi-comprimentp [mm]‟)
ylabel(„ pressão de contato [ kgf/mm²]‟)
71.15
pressão WR [kgf/mm²]
71.1
71.05
71
70.95
70.9
70.85
0
20
40
60
80
semi-comprimento [mm]
100
120
Figura B.1a – Pressão WR entre o cilindro de trabalho e a chapa
Conforme pode-se observar a Figura B.2a, a pressão Wr entre o cilindro de
trabalho e a chapa na posição a 100 mm do semi-comprimento equivale à
aproximadamente 70,07 kgf/mm². Um detalhe importante, com a subdivisão da
Figura B.2, foi possível uma visualização maior desse valor.
Como
no
programa do COSMOS Works esta pressão Wr é dada em N/m², a mesma equivale
após transformação a 6,94526 x 108 N/m².
Na següência as demais figuras são apresentadas, com intervalos de
aproximadamente 100 mm, permitindo assim da mesma forma anterior maior
precisão dos resultados da pressão WR.
127
72.1
72
pressão WR [kgf/mm²]
71.9
71.8
71.7
71.6
71.5
71.4
71.3
71.2
71.1
100
120
140
160
180
semi comprimento[mm]
200
220
240
Figura B.1b – Pressão Wr entre o cilindro de trabalho e a chapa, no intervalo de 100 a 240 mm.
73.6
73.4
pressão WR [kgf/mm²]
73.2
73
72.8
72.6
72.4
72.2
72
220
240
260
280
300
semi comprimento[mm]
320
340
360
Figura B.1c – Pressão WR entre o cilindro de trabalho e a chapa, no intervalo de 220 a 360 mm.
128
76
pressão WR [kgf/mm²]
75.5
75
74.5
74
73.5
340
360
380
400
420
semi comprimento[mm]
440
460
480
Figura B.1d – Pressão WR entre o cilindro de trabalho e a chapa, no intervalo de 340 a 480 mm.
79.5
79
pressão WR [kgf/mm²]
78.5
78
77.5
77
76.5
76
75.5
460
480
500
520
540
semi comprimento[mm]
560
580
600
Figura B1e – Pressão WR entre o cilindro de trabalho e a chapa, no intervalo de 460 a 600 mm.
129
84
83.5
pressão WR [kgf/mm²]
83
82.5
82
81.5
81
80.5
80
79.5
79
580
600
620
640
660
semi comprimento[mm]
680
700
720
Figura B.1f – Pressão WR entre o cilindro de trabalho e a chapa, no intervalo de 580 a 720 mm.
91
90
pressão WR [kgf/mm²]
89
88
87
86
85
84
83
700
710
720
730
740
750
760
semi comprimento[mm]
770
780
790
Figura B.1g – Pressão WR entre o cilindro de trabalho e a chapa, no intervalo de 700 a 790 mm.
Após a subdivisão da Figura B.1, foi possível tabular de forma mais preciso, a
pressão WR , conforme mostra a Tabela B.1.
Tabela B.1 - Resultados da pressão Wr obtido através do programa MCI/Berger a cada 100 mm
do semi-comprimento
130
1
2
3
4
5
6
7
8
9
Pw
(kgf/mm²)
Pw
(N/m²) x 106
W/2
(mm)
W/2
(m)
70,87
71,07
71,73
72,83
74,5
76,7
79,6
83,5
91,5
694,526
696,486
702,954
713,734
730,1
751,66
780,08
818,3
896,7
0
100
200
300
400
500
600
700
800
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
B.3- Procedimentos para obtenção da Pressão WR do Laminador 2
Os comandos usados no laminador 2 foram os mesmos utilizados no
laminador 1.
Dessa forma ao inserir os dados do laminador 2, no programa MCI/Berger,
salvá-los e na seqüência digitar o nome do laminador salvo, o programa
imediatamente nos fornece os dados abaixo desse laminador.
B.3.1 Dados do laminador 2:
Diâmetro do cilindro de trabalho:
125 mm
Coroa usinadas do cilindro de trabalho: 0 mm
Módulo de Young do cilindro de trabalho: 21000 kgf/mm2
Diâmetro do cilindro de apoio:
300 mm
Coroa usinada do cilindro de apoio:
0 mm
Módulo de Young do cilindro de trabalho: 21000 kgf/mm2
Módulo de Poisson dos cilindros:
0.3
Comprimento da face dos cilindros:
Comprimento do braço de contraflexão:
400 mm
100 mm
B.3.2 Dados Operacionais do laminador 2:
Coeficiente de atrito (seco):
Largura da tira:
0.1
350 mm
131
Módulo de Young da tira:
21000 kgf/mm2
Módulo de Poisson da tira:
0.3
Curva de fluxo (EPD), via Ludwik:
Espessura inicial:
0.1+78.8eps^0.249 kgf/mm2
4.5 mm
Coroa absoluta inicial:
0 micrometros
Coroa relativa inicial:
1.9737e-014 %
Coroa medida a 25 mm da borda da tira
Só para a primeira cadeira:
Tensão à entrada da tira:
0 kgf/mm2
Total na bobinadeira, a ré: 0 tf
Tensão à saída da tira:
0 kgf/mm2
Total na bobinadeira, a frente: 0 tf
Número de fatias do semi-cilindro:
Tolerância para o perfil:
45
0.001 mm
Coeficiente para a tolerância da carga q:0.001
0.001
0.001
0.001
B.3.3 – Resultados do MCI/Berger referente ao laminador 2
Espessuras
Carga de
Coroa relativa
Força de
finais (mm)
laminação (kgf)
(%)
3.89
99210.05
1.3879
0
0.66
3.07
154911.50
2.8359
0
0.55
2.48
153402.00
3.5526
0
0.52
2.06
142477.64
4.0091
0
0.53
1.76
128731.56
4.2677
0
0.58
Roll Bending (kgf)
Tempo total de processamento: 2.829 s
132
Tempo
(s)
0.001
B.3.4- Resultados da Pressão WR do Laminador 2
Da mesma forma anterior para obter a pressão WR do laminador 2, utiliza o
mesmo procedimento do laminador 1. Inicialmente inseri os dados referentes ao
laminador 2, em seguida entra com os comandos necessários:


pressaoWr=carga(1,1:m)./comprimentoarco;
pressaoWR.*9.8.*1e6
pressaoWR =
Columns 1 through 7
63.3023 63.3094 63.3235 63.3446 63.3727 63.4078 63.4594
Columns 8 through 14
63.5084 63.5644 63.6274 63.6974 63.7744 63.8583 63.9492
Columns 15 through 21
64.0471 64.1519 64.2637 64.3825 64.5083 64.6412 64.7813
Columns 22 through 28
64.9286 65.0833 65.2454 65.4152 65.5930 65.7792 65.9741
Columns 29 through 35
66.1784 66.3929 66.6188 66.8577 67.1119 67.3850 67.6825
Columns 36 through 39
68.0142 68.3990 68.8802 69.5957
É importante observar que os valores da pressão sofreram transformações de
Kgf/mm² para N/m²
Média geral da pressão WR = 65.1644 kgf/mm²
133
B.3.5- Construção dos gráficos da Pressão WR do Laminador 2.
A Figura B.2, mostra graficamente a pressão WR do laminador 2
70
69
pressão WR [Kgf/mm²]
68
67
66
65
64
63
0
20
40
60
80
100
120
semi-comprimento [mm]
140
160
180
A Figura B.2- pressão WR do laminador 2
Na següência as demais figuras são apresentadas, com intervalos de
aproximadamente 100 mm, permitindo assim visualizar melhor
pressão WR em cada intervalo.
63.46
63.44
pressão WR [Kgf/mm²]
63.42
63.4
63.38
63.36
63.34
63.32
63.3
0
5
10
15
20
semi-comprimento [mm]
25
Figura B.2a- pressão WR do laminador 2
134
30
os valores da
64
63.95
pressão WR [Kgf/mm²]
63.9
63.85
63.8
63.75
63.7
63.65
63.6
63.55
63.5
30
35
40
45
50
semi-comprimento [mm]
55
60
Figura B.2b- pressão WR do laminador 2
66.2
66
pressão WR [Kgf/mm²]
65.8
65.6
65.4
65.2
65
64.8
64.6
95
100
105
110
115
semi-comprimento [mm]
120
125
Figura B.2c- pressão WR do laminador 2
135
130
67.8
67.6
pressão WR [Kgf/mm²]
67.4
67.2
67
66.8
66.6
66.4
66.2
66
125
130
135
140
145
semi-comprimento [mm]
150
155
Figura B.2d- pressão WR do laminador 2
69.6
69.4
pressão WR [Kgf/mm²]
69.2
69
68.8
68.6
68.4
68.2
68
156
158
160
162
164
166
semi-comprimento [mm]
168
170
172
Figura B.2e- pressão WR do laminador 2
Com base no gráfico da Figura B.2, construiu-se a Tabela B.2, referente aos
valores da pressão WR a cada 25 mm.
Os valores da Tabela B.2, serão inseridos no programa COSMOS Works.
136
Tabela B.2- Resultados da pressão WR obtido do programa MCI/Berger a cada 25
mm do semi-comprimento – laminador 2
1
2
3
4
5
6
7
8
9
Pw
(kgf/mm²)
Pw
(N/m²) x 106
W/2
(mm)
W/2
(m)
63,3
63,41
63,75
64,3
65,1
66,1
67,5
69,4
70
620,34
621,42
624,75
630,14
637,98
647,78
661,5
680,12
686
0
25
50
75
100
125
150
170
175
0
0,025
0,050
0,075
0,100
0,125
0,150
0,170
0,175
B.4- Cálculo do torque do Laminador 2
Nesse estudo levou-se em conta também o torque. Para o desenvolvimento
do cálculo considerando o torque, foi necessário utilizar a carga laminação obtida
pelo programa do MCI/Berger.
Por uma questão de tempo, trabalhou-se somente com a carga de laminação
do primeiro passe.
Outro ponto importante que deve ressaltar refere-se ao modelo, este se
considerou somente a metade. De forma a minimizar pela metade o tempo de
processamento.
Dessa forma utilizou a metade da carga de laminação.
Como o desenvolvimento do calculo já foi apresentado no capítulo 3 da
dissertação, será abordado no apêndice apenas a parte complementar, que utilizou
para chegar aos resultados.
Um das equações apresentadas no capítulo 3, refere-se ao raio deformado,
da equação B.1. Foi necessário obter o valor médio dele através do programa
MCI/Berger, para determinar o arco de contato deformado “L‟”.
L'  R' h
137
(B.1)
Para chegar aos valores do raio deformado, o programa MCI/Berger, já o
fornece instantaneamente, basta digitar o comando “ raiodeformado “ e na
seqüência aparecem os resultados.
Comando utilizado;

raiodeformado
raiodeformado =
Columns 1 through 7
66.3294 66.3296 66.3299 66.3304 66.3311 66.3319 66.3329
Columns 8 through 14
66.3341 66.3354 66.3370 66.3387 66.3405 66.3426 66.3448
Columns 15 through 21
66.3473 66.3498 66.3526 66.3556 66.3587 66.3621 66.3656
Columns 22 through 28
66.3694 66.3733 66.3774 66.3818 66.3864 66.3912 66.3962
Columns 29 through 35
66.4015 66.4072 66.4131 66.4194 66.4262 66.4335 66.4414
Columns 36 through 42
66.4504 66.4607 66.4736 66.4918 62.5000 62.5000 62.5000
Columns 43 through 45
62.5000 62.5000 62.5000
Através do comando “mean”, chegou-se a média geral do raio deformado igual a
65.8594mm
138
Dessa forma, para determinar L‟, tem-se
Para o primeiro passe h  hi  h f => 4,5-3,89=0,61
L'  R' h => L'  65,86 x0,61 => L'  6,34mm (arco de contato deformado)
A equação 13.2, determina a distância da força P (ao centro de rotação do rolo)
d  L'
(B.2)
  0,45 (para laminação a frio)
d  L' = 0,45x6,34= 2,85 mm = 0,00285m
Logo,
d  2,85( Distância da força P (ao centro de rotação do rolo)
P= q ( carga de laminação), para o 1º passe
Para determinar a força circunferencial líquida, utilizou as equações B.3 e B.4
Fc 
M
R
(B.3)

M  P.d  L' P  L' R'  pd
0
(.4)
Conforme já mencionado, a carga de laminação foi dividida ao meio, uma vez,
que utilizou somente a metade do modelo. O vWalor da carga de laminação no
primeiro passe é 99210.05 Kgf.
Dessa forma: P= 99210.05 Kgf x 9,8 = 972.258,49 N
Onde
P= Força (N)
139
Como o trabalho esta sendo desenvolvido com metade do cilindro de
laminação, logo P/2 = 486.129,25 N
Portanto, através da equação 13.4, obteve-se o semi-momento ou semi-torque.
M 
P
d  486.129,25 (N)x (0,00285m) = 1.385,47 N.m
2
Em seguida, determinou-se a força Fc, força líquida circunferencial, através da
equação 13.3. (Helman, 1983)
Fc 
M
R
=> Fc 
1.385,47
 Fc  22.167,52 N
62,5 x10 3
Onde
R= Raio Original do cilindro de trabalho (mm)
B.4.1- Procedimento adotado para obter a subdivisão da força Fc.
Através do MCI/Berger obteve-se os valores do arco deformado no cilindro de
trabalho em contato com a chapa.
Comando utilizado

arcodecontato.*raiodeformado(1,45),
140
Columns 1 through 7
4.2063
4.2063
4.2061
4.2059
4.2056
4.2052
4.2048
4.2022
4.2013
4.2003
4.1993
4.1942
4.1927
4.1911
4.1894
4.1816
4.1794
4.1771
4.1746
4.1632
4.1598
4.1562
4.1522
Columns 8 through 14
4.2043
4.2036
4.2029
Columns 15 through 21
4.1981
4.1969
4.1956
Columns 22 through 28
4.1876
4.1857
4.1837
Columns 29 through 35
4.1720
4.1693
4.1663
Columns 36 through 39
4.1477
4.1424
4.1360
4.1281
Através do comando „mean‟, obteve-se a média geral do arco deformado
igual a 4.1840 mm.
Em seguida a Tabela B.3, mostra de forma detalhada a distribuição da força
circunferencial liquida a cada 25 mm do semi-cilindro.
141
Tabela B.3- Distribuição da força circunferencial líquida a cada 25mm do cilindro.
Semi-
Variação
Área ao longo de
Fc em cada intervalo
comprimento da
da
cada
Por regra de três
chapa (W/2) mm
posição
intervalo de
(N)
(intervalo)
subdivisão
∆V (mm
A=L.∆V, L=4,18 mm
A em (mm²)
0
25
104,5
3166,79
25
104,5
3166,79
25
104,5
3166,79
25
104,5
3166,79
25
104,5
3166,79
25
104,5
3166,79
20
83,6
2.533,43
20,9
633,36
731,5
22.167,52
25
25
50
50
75
75
100
100
125
125
150
150
170
170
175
total
5
O mesmo procedimento é feito para o laminador 1 (laminador grande), para
determinar a Fc.
142
B.5- Procedimento Adotado para Determinar Graficamente a Pressão de
Contato x Semi-Comprimento do Laminador 1
Após executar a primeira fase já explicada nesse capítulo do apêndice, o
próximo passo foi construir o modelo no programa do Solidworks.
Em seguida utilizou-se o programa do COSMOSWorks, para implementar as
cargas calculadas no itens B.1 e B.4, ou seja, a pressãoWR e o torque. Para que o
modelo operasse de forma real foram submetidas também às condições e contato,
restrição, geração de malha e tipo de material.
Após rodar o programa foi analisado os resultados através das ferramentas:

COSMOSWorks;

Ferramentas de resultados;

Força de reação;

Seleção da área de restrição do pescoço do cilindro de encosto;

Verificação do resultado em “ soma Y”;
Por último comparou os resultados da semi-carga fornecida pelo MCI/Berger
com o resultado do programa COSMOS.
Resumidamente a Tabela B.4, mostra os resultados obtidos.
Tabela B.4- Resultado da carga de laminação
Laminadores
Resultado do COSMOS
Resultado do MCI/Berger
Laminador 1
4.71e+005 N
4.86e+005 N
Laminador 2
4.70e+006 N
5.00e+006 N
Após comparar os resultados dos dois programas, foi possível havendo uma
disparidade pequena construir os gráficos da pressão de contato entre os cilindros e
o perfil final do cilindro e da chapa.
Através do programa COSMOS, selecionaram-se alguns pontos da pressão de
contato (PC), conforme ilustra a Figura B.3.
143
Figura B.3- Resultado da Pressão de Contato entre os cilindros.
Com base nos valores fornecidos pelo programa COSMOS, escolheu-se
aleatoriamente alguns pontos, que foram utilizados na plotagem dos gráficos.
No caso acima escolheram-se
os pontos abaixo e os respectivos
deslocamentos.
Vale ressaltar que esses pontos selecionados do laminador 1, considerou o
torque, na malha refinada.
T=[ 8.715e8
1.102e9 1.031e9 9.57e8
9.454e8 9.436e8 1.063e9
1.125e9
1.192e9
1.008e9
1.039e9
7.334e8
8.232e8
6.898e8
7.758e8
1.042e9
7.281e8]
U=[ 169.23 204.23
239.23 279.23
319.23
519.23 559.23 599.23 669.23 679.23
919.23
9.258e8
359.23
9.446e8
399.23
719.23 760 799.23
439.3
1.19e9
1.023e9
479.3
839.23 879.23
939.23]
No caso acima os pontos selecionados foram colocados na linguagem matlab,
de forma a facilitar a inserção dos mesmos no MCI/Berger, uma vez que utiliza esta
linguagem.
144
B.5.1- Comandos Utilizados para Plotagem do Gráfico da carga de laminação
referente ao 1º passe do Laminador 1.
Na Figura B.4, mostra o resultado da construção do gráfico da carga de
laminação.
Comandos:

figure

plot[U(1:21),T(1:21)]

grid

xlabel(„semi-comprimento [mm]‟)

ylabel(„pressão de contato [N/m²]‟)
9
1.5
x 10
1.4
pressão de contato [N/m²]
1.3
1.2
1.1
1
0.9
0.8
0.7
100
200
300
400
500
600
700
semi-comprimento [mm]
800
900
1000
Figura B.4- Gráfico da pressão de contato do laminador 1, considerando o torque
A Figura B.5- mostra o gráfico da pressão de contato referente ao primeiro
passe do laminador 1.
Os comandos utilizados foram

ex;

pressc(1:80);

scc;

q=(pressc(1,1:80)./scc(1:80));
145

q.*9.8.*1.e6

figure;

plot(ex(1:80),q(1:80))

xlabel(„semi-comprimento [mm]‟)

ylabel(„pressão de contato [N/m²]‟)
Na seqüência têm-se os resultados
ex =
Columns 1 through 7
5.9375 17.8125 29.6875 41.5625 53.4375 65.3125 77.1875
Columns 8 through 14
89.0625 100.9375 112.8125 124.6875 136.5625 148.4375 160.3125
Columns 15 through 21
172.1875 184.0625 195.9375 207.8125 219.6875 231.5625 243.4375
Columns 22 through 28
255.3125 267.1875 279.0625 290.9375 302.8125 314.6875 326.5625
Columns 29 through 35
338.4375 350.3125 362.1875 374.0625 385.9375 397.8125 409.6875
Columns 36 through 42
421.5625 433.4375 445.3125 457.1875 469.0625 480.9375 492.8125
Columns 43 through 49
504.6875 516.5625 528.4375 540.3125 552.1875 564.0625 575.9375
146
Columns 50 through 56
587.8125 599.6875 611.5625 623.4375 635.3125 647.1875 659.0625
Columns 57 through 63
670.9375 682.8125 694.6875 706.5625 718.4375 730.3125 742.1875
Columns 64 through 70
754.0625 765.9375 777.8125 789.6875 801.5625 813.4375 825.3125
Columns 71 through 77
837.1875 849.0625 860.9375 872.8125 884.6875 896.5625 908.4375
Columns 78 through 80
pressc(1:80)
ans =
Columns 1 through 7
592.5329 962.1659 955.6796 887.8217 798.1192 592.5095 962.0643
Columns 8 through 14
955.5909 887.7557 797.9689 592.4169 961.8720 955.3738 887.5345
Columns 15 through 21
797.7350 592.2709 961.5836 955.0467 887.2047 797.3902 592.0711
Columns 22 through 28
961.2005 954.6058 886.7582 796.9448 591.8176 960.7200 954.0526
Columns 29 through 35
147
886.1994 796.3972 591.5102 960.1412 953.3862 885.5272 795.7470
Columns 36 through 42
591.1485 959.4627 952.6055 884.7411 794.9935 590.7317 958.6829
Columns 43 through 49
951.7095 883.8401 794.1358 590.2592 957.8003 950.6966 882.8230
Columns 50 through 56
793.1728 589.7299 956.8131 949.5654 881.6885 792.1033 589.1428
Columns 57 through 63
955.7194 948.3142 880.4352 790.9260 588.4966 954.5171 946.9410
Columns 64 through 70
879.0614 789.6394 587.7901 953.2041 945.4438 877.5655 788.2418
Columns 71 through 77
587.0218 951.7777 943.8204 875.9456 786.7315 586.1900 950.2356
Columns 78 through 80
942.0686 874.1998 785.1067
EDU» scc
scc =
Columns 1 through 7
148
7.6858
7.6850
7.6841
7.6826
7.6807
7.6782
7.6752
7.6581
7.6524
7.6462
7.6394
7.6065
7.5967
7.5864
7.5753
7.5246
7.5102
7.4950
7.4791
7.4076
7.3877
7.3669
7.3452
7.2492
7.2227
7.1953
7.1668
7.0418
7.0077
6.9724
6.9359
6.7771
6.7341
6.6898
6.6441
6.4473
6.3945
6.3402
6.2845
6.0465
5.9792
5.9196
5.8638
Columns 8 through 14
7.6718
7.6677
7.6632
Columns 15 through 21
7.6321
7.6241
7.6156
Columns 22 through 28
7.5637
7.5513
7.5383
Columns 29 through 35
7.4624
7.4450
7.4267
Columns 36 through 42
7.3226
7.2991
7.2746
Columns 43 through 49
7.1372
7.1065
7.0747
Columns 50 through 56
6.8981
6.8591
6.8187
Columns 57 through 63
6.5970
6.5485
6.4986
Columns 64 through 70
6.2273
6.1686
6.1083
Columns 71 through 77
149
5.8126
5.7665
5.7263
5.6938
5.6714
5.6636
5.6755
Columns 78 through 80
5.7482
5.7230
7.2819
q=
Columns 1 through 7
77.0950 77.0995 77.0967 77.0922 77.0857 77.0774 77.0672
Columns 8 through 14
77.0552 77.0414 77.0256 77.0078 76.9880 76.9660 76.9418
Columns 15 through 21
76.9152 76.8862 76.8545 76.8200 76.7826 76.7422 76.6985
Columns 22 through 28
76.6513 76.6005 76.5458 76.4871 76.4242 76.3567 76.2844
Columns 29 through 35
76.2072 76.1247 76.0366 75.9428 75.8428 75.7365 75.6234
Columns 36 through 42
75.5034 75.3760 75.2409 75.0979 74.9465 74.7864 74.6172
Columns 43 through 49
74.4387 74.2503 74.0518 73.8428 73.6228 73.3914 73.1484
Columns 50 through 56
150
72.8932 72.6256 72.3450 72.0512 71.7437 71.4222 71.0863
Columns 57 through 63
70.7358 70.3701 69.9891 69.5924 69.1798 68.7509 68.3055
Columns 64 through 70
67.8431 67.3631 66.8639 66.3448 65.7643 65.2662 64.8161
Columns 71 through 77
64.4193 64.0826 63.8175 63.6418 63.5837 63.6916 64.0467
Columns 78 through 80
64.9536 65.6398 80.8956
EDU» q.*9.8.*1.e6
ans =
1.0e+008 *
Columns 1 through 7
7.5553
7.5557
7.5555
7.5550
7.5544
7.5536
7.5526
7.5468
7.5448
7.5427
7.5403
7.5284
7.5247
7.5207
7.5164
Columns 8 through 14
7.5514
7.5501
7.5485
Columns 15 through 21
7.5377
7.5348
7.5317
Columns 22 through 28
151
7.5118
7.5068
7.5015
7.4957
7.4896
7.4830
7.4759
7.4424
7.4326
7.4222
7.4111
7.3596
7.3448
7.3291
7.3125
7.2366
7.2150
7.1924
7.1685
7.0610
7.0309
6.9994
6.9665
6.8201
6.7796
6.7376
6.6939
6.5018
6.4449
6.3961
6.3520
6.2369
6.2312
6.2418
6.2766
Columns 29 through 35
7.4683
7.4602
7.4516
Columns 36 through 42
7.3993
7.3868
7.3736
Columns 43 through 49
7.2950
7.2765
7.2571
Columns 50 through 56
7.1435
7.1173
7.0898
Columns 57 through 63
6.9321
6.8963
6.8589
Columns 64 through 70
6.6486
6.6016
6.5527
Columns 71 through 77
6.3131
6.2801
6.2541
Columns 78 through 80
6.3655
6.4327
7.9278
Após obter os resultados no programa MCI/Berger, foi possível construir a Figura
B.5, referente à carga de laminação do 1º passe.
152
8
8
x 10
7.8
pressão de contato [N/m²]
7.6
7.4
7.2
7
6.8
6.6
6.4
6.2
0
100
200
300
400
500
600
700
semi-comprimento [mm]
800
900
1000
Figura B.5-carga de laminação do 1º passe, obtido pelo MCI/Berger
A Figura B.6, mostra o resultado da carga de laminação em cada passe.
Distribuição de cargas
1200
1100
p(-) e q(.) [kgf/mm]
1000
900
800
700
600
500
400
300
0
100
200
300
400
500
600
Semi-largura [mm]
700
800
900
1000
Figura B.6-carga de laminação dos cinco passes do laminador 1 obtido pelo MCI/Berger
B.5.2- Comandos Utilizados para Plotagem do perfil da tira do Laminador 1.
153
De forma semelhante à obtenção da carga de laminação, seleciona alguns
pontos ao longo do contato entre o cilindro de trabalho e a chapa.
Comandos utilizados pelo através do programa COSMOSWorks.

deslocamento em UY;

Sonda

Seleciona o perfil

Atualizar
A Figura B.7, mostra os resultados obtidos pelo programa COSMOSWorks, do perfil
da chapa e do cilindro de trabalho
Figura B.7- Obtenção do perfil, através do programa COSMOSWorks
(Figura obtida do programa COSMOS)
Selecionou em seguida alguns pontos referentes ao perfil do cilindro de
trabalho.
154
Onde “ M “ representa o deslocamento em Y e “N” a posição referente a esse
deslocamento.
M=[3.774e-1
3.771e-1
3.784e-1
3.804e-1 3.745e-1 3.765e-1
3.689e-1
3.723e-1
3.739e-1 3.603e-1 3.641e-1
3.551e-1
3.581e-1 3.361e-1 3.422e-1
3.361e-1 2.493e-1 2.869e-1
N=[ 119.23 84.23
429.27
394.19
719.23 684.23
3.66e-1 3.691e-1
3.469e-1 3.186e-1
3.763e-1
3.501e-1
3.262e-1 3.318e-1
2.985e-1]
44.23 19.23 221.72
359.21 324.23
189.11 156.5 319.23 285.1 306.02
519.23
649.23 619.23 780.77
485
449.18
619.23 585 549.23
784.23 749.23]
Comandos utilizados para plotar o gráfico do perfil referente ao primeiro passe

figure;

plot(N(1:27),M(1:27));

grid;

xlabel(„semi-comprimento [mm]‟);

ylabel(„perfil [mm]‟);
A Figura B.8, mostra os resultados do perfil gerado com os pontos obtidos do
primeiro passe do laminador 1, considerando o torque.
155
0.4
0.38
perfil [mm]
0.36
0.34
0.32
0.3
0.28
0
100
200
300
400
500
semi-largura [mm]
600
700
800
. Figura B.8- Perfil referente ao primeiro passe do laminador1, através do programa
MCI/Berger
(Figura obtida do programa MCI/Berger)
Na seqüência, obtém-se os valores necessários no programa MCI/Berger
para plotagem do perfil.
Comandos utilizados;

defac(2,1:67);

u=0.3774-M(1:27);

k=3.8902-2.*u

figure;

plot(N(1:27),k(1:27),'b*');

grid;

hold on;

plot(ex(1:67),defac(2,1:67));

xlabel('semi-largura [mm]');

ylabel('perfil [mm]')
156
resultados dos comandos.
defac(2,1:67)
ans =
Columns 1 through 7
3.8902
3.8902
3.8900
3.8898
3.8896
3.8893
3.8889
3.8867
3.8860
3.8852
3.8843
3.8803
3.8791
3.8778
3.8765
3.8704
3.8687
3.8669
3.8651
3.8568
3.8546
3.8522
3.8498
3.8391
3.8362
3.8332
3.8301
3.8166
3.8129
3.8091
3.8052
3.7882
3.7835
3.7786
3.7736
3.7507
3.7441
3.7370
3.7291
Columns 8 through 14
3.8884
3.8879
3.8873
Columns 15 through 21
3.8834
3.8824
3.8814
Columns 22 through 28
3.8751
3.8736
3.8720
Columns 29 through 35
3.8631
3.8611
3.8590
Columns 36 through 42
3.8472
3.8446
3.8419
Columns 43 through 49
3.8268
3.8235
3.8201
Columns 50 through 56
3.8012
3.7970
3.7927
Columns 57 through 63
3.7683
3.7628
3.7569
Columns 64 through 67
3.7202
3.7096
3.6959
3.6736
157
M=
Columns 1 through 7
0.3774
0.3771
0.3784
0.3804
0.3745
0.3765
0.3763
0.3603
0.3641
0.3660
0.3691
0.3361
0.3422
0.3469
0.3186
0.2493
0.2869
0.2985
Columns 8 through 14
0.3689
0.3723
0.3739
Columns 15 through 21
0.3501
0.3551
0.3581
Columns 22 through 27
0.3262
0.3318
0.3361
EDU» u=0.3774-M(1:27)
u=
Columns 1 through 7
0
0.0003 -0.0010 -0.0030
0.0029
0.0009
0.0011
Columns 8 through 14
0.0085
0.0051
0.0035
0.0171
0.0133
0.0114
0.0083
0.0413
0.0352
0.0305
0.0588
0.1281
0.0905
0.0789
3.8962
3.8844
3.8884
3.8880
3.8560
3.8636
3.8674
3.8736
Columns 15 through 21
0.0273
0.0223
0.0193
Columns 22 through 27
0.0512
0.0456
0.0413
EDU» k=3.8902-2.*u
k=
Columns 1 through 7
3.8902 3.8896
3.8922
Columns 8 through 14
3.8732
3.8800
3.8832
158
Columns 15 through 21
3.8356
3.8456
3.8516
3.8076
3.8198
3.8292
3.6340
3.7092
3.7324
3.7726
Columns 22 through 27
3.7878
3.7990
3.8076
A Figura B.9, mostra o resultado do perfil referente ao primeiro passe pelo programa
MCI/Berger.
3.9
perfil [mm]
3.85
3.8
3.75
3.7
3.65
0
100
200
300
400
500
semi-largura [mm]
600
700
800
Figura B.9- perfil gerado pelo programa MCI/Berger referente ao primeiro passe
A Figura B.10, mostra o perfil gerado por cada passe do laminador 1 no programa
MCI/Berger
159
Perfis
4.5
4
Perfil [mm]
3.5
3
2.5
2
1.5
1
0
100
200
300
400
500
Semi-largura [mm]
600
700
800
Figura B.10- perfil gerado pelo programa MCI/Berger referente ao cinco passes
Da mesma forma obteve os resultados para o laminador 2, seguindo o mesmo
raciocínio. Os resultados com torque e sem torque são obtidos também seguindo os
mesmos procedimentos.
160
REFERÊNCIAS
BERGER, B.; NEUCHÜTZ, E.; MÜCKE, G. Experiences with a flatness control
system including axial roll shifting, 4th International Steel Rolling Conference, pp.
E.13.1-E.13.6, junho 1987.
FORD, H.; ALEXANDER, J. M. Rolling hard materials in thin gauges – basic
considerations, Journal of the Institute of Metals, pp. 193-199, 1959.
GINZBURG, V. B. Basic principles of customized computer models for cold and
hot strip mills, Iron and Steel Engineer, pp. 21-35, September 1985.
GINZBURG, B. V.; AZZAM, M. Selection of optimum strip profile and flatness
technology for rolling mills, Iron and Steel Engineer, pp. 30-38, julho 1997.
GINZBURG, V. B. Steel-rolling technology: theory and practice, Marcel Dekker
Inc.,New York and Basel, 1989.
GINZBURG, VLADIMIR B. Strip profile control with flexible edge backup rolls,
International Rolling Mill Consultants, Inc., Pittsburgh, Pa., 1987.
GUO, R.-M. and SCHUNK, J. H. Determination of optimal work roll crown for a
hot strip mill, Iron and Steel Engineer, pp. 52-60,1989.
GUO, R.-M. Computer model simulation of strip crown and shape control, Iron
and Steel Engineer, pp. 35-42, 1986.
GUO, R.-M. Development of a mathematical model for strip thickness profile,
Iron and Steel Engineer, pp. 32-39, 1990.
GUO, R.-M. Optimal profile and shape control of flat sheet metal using multiple
161
control devices, IEEE Transactions on Industry Applications, pp. 449-457, 1996.
GUO, R.-M. Prediction of strip profile in rolling process using influence
coefficients and Boussinesq’s equations, Transactions of the ASME, Journal of
Manufacturing Science and Engineering, pp. 220-226, 1997
GUO, R-M. Development of a mathematical model for strip thickness profile,
Iron and Steel Engineer, pp. 32-39, setembro 1990.
HELMAN, H. coord. Fundamentos da laminação: produtos planos, ABM, São
Paulo, 1988.
KAJIWARA, T.; FUJINO, N.; NISHI, H. and SHIDA, S. The Hitachi HC-mill - a
breakthrough in strip rolling, Iron and Steel Engineer, pp. 247-255,1976.
LENARD, J. G.; WANG, F.; NADKARNI, G. The role of constitutive formulation in
the analysis of hot rolling, Journal of Engineering Materials and Technology,
Transactions of the ASME, pp. 343-349, 1987.
OROWAN, E. The calculation of roll pressure in hot and cold flat rolling, pp. 1037, agosto 1943.
PAWELSKI, O.; RASP, W.; RIECKMAN, J. Application of a mathematical model
for the cold rolling process on six-high mills, Modelling of Metal forming
Processes, J. L. Chenot and E. Oñate editors, Kluwer Academic Publishers, pp.
304-312, 1988
PAWELSKI, O. and TEUTSCH, H. A mathematical model for computing the
distribution of loads and thickness in the width direction of a strip rolled in
four-high cold-rolling mills, Engineering Fracture Mechanics, 21, nº.4, pp. 853-859,
1985.
162
SINGER, A. R. E. and O'BRIEN, J. J. Control of the shape of metal strip on an
experimental variable camber rolling mill, Journal of the Iron and Steel Institute,
pp. 1003-1010, 1962
TIMOSHENKO, S. P. e GOODIER, J. N. Teoria da Elasticidade, 3a ed., Guanabara
, 1980
ZHENGLIAN, J.; GOUDONG, W.; QIANG, Z. DONGQING, M.; CHONGMING, T.;
GUOLIANG, W. Shifting-roll profile and control characteristics, Journal of
Materials Processing Technology, 37, pp. 53-60, 1993.
F.J. Belzunce, A. Ziadi, C. Rodriguez - Authors: Ziadi, A.; Belzunce, F.J.;
Rodriguez, C.; Riba, J. Source: Materials Science and Technology, Volume 21, ,
pp. 1181-1186, 2005
BERGER, B.; PAWELSKI, O.; FUNKE, P. Die beeinflussung des dickenprofils
von bändern und Blechen durch walzenbiegeeinrichtungen, Stahl und Eisen, 96,
No. 8, pp. 377-381, 1976 a.
GINZBURG, VLADIMIR B. Strip profile control with flexible edge backup rolls,
International Rolling Mill Consultants., Pittsburgh, 1987.
HERTZ, H. Über die berührung fester elastischer körper (On the contact of
elastic solids), J. reine und angewandte Mathematik, 92, pp. 156-171, 1882.
HITCHCOCK, J. H. Roll neck bearings, Report of ASME Res. Committee, 1935.
SHOHET, K. N.; TOWNSEND, N. A. Flatness control in plate rolling, Journal of
the Iron and Steel Institute, pp. 769-775, 1971.
Von KÁRMÁN, T. On the theory of rolling, Z. Angew. Math. Mech., 5, pp. 130-141,
1925.
163
ALEXANDER, J. M. On the theory of rolling, Proc. R. Soc. Lond. A. 326, pp. 535563,1972.
BERGER, B.; PAWELSKI, O.; FUNKE, P. Die beeinflussung des dickenprofils
von bändern und Blechen durch walzenbiegeeinrichtungen, Stahl und Eisen, 96,
No. 8, pp. 377-381, 1976.
FINSTERMANN, G.; ZEMAN, K. Profile and flatness in hot strip mills, VAI Rolling
Mill Info, Technical Report, Version 2, Ver. 1.2, 1996.
FORD, H.; ELLIS, F.; BLAND, D. R. Cold rolling with strip tensions, Journal of the
Iron and Steel Institute, 1951.
D. R. Bland and H. Ford, The calculation of roll force and torque in cold strip
rolling with tensions, Proc. Inst. Mech. Engrs 1948; ( 159 ):144-153.
J. H. Hitchcock, Elastic deformation of rolls during cold rolling, ASME Research
Publication Roll Neck Bearings: 1935.
H. Han. Determination of mean flow stress and friction coefficient by the
modified two-specimen method in cold rolling, Journal of Materials Processing
Technology 2005;( 159): 401-408.
E. N. Dvorkin, M. A. Cavaliere, M. B. Goldschmit, Finite element models in the
steel industry Part I: Simulation of flat product manufacturing processes,
Computers ans Structures 2003;( 81): 559-573.
Y. Shigaki, A study on strip and plate rolling through a mathematical-numerical
model for a 4-high mill, D. Sc. Thesis, Universidade Federal de Minas Gerais:
2001.
N. V. Reddy, G. Suryanarayana, A set-up model for tandem cold rolling mills,
Journal of Materials Processing Technology 2001; ( 116 ): 269-277.
164
B. Berger, O. Pawelski and P. Funke, Die beeinflussung des dickenprofils von
bändern und Blechen durch walzenbiegeeinrichtungen, Stahl und Eisen
1976;96( 8 ): 377-381.
B. Berger, O. Pawelski and P. Funke, Die elastische verformung der walzen von
vierwalzengerüsten, Arch. Eisenhüttenwes 1976; 47( 6 ): 351-356.
F. Hollander and A. G. Reinen, Automatic shape control – Hoogoven‟s 88-in hot
strip mill, AISE Yearly Proceedings:1976. p. 135-143.
YAMADA, K.; OGAWA, S. and ATAKA, M. Three-dimensional analysis of flat
rolling using rigid-plastic finite element method coupled with roll deformation
analysis, NUMIFORM: 1992
YANAGIMOTO, J. and KIUCHI, M. Three-dimensional simulation system for
coupled elastic/rigid-plastic deformations of rolls and workpieces in strip
rolling processes, NUMIFORM: 1992
MITAI, Y. and IRIBE, H. Analysis of strip rolling by three-dimensional rigidplastic FEM, Nippon Steel Technical Report 1992;(January, 52 ).
RIZZO,E.M.S. Processos de laminação dos aços,,ABM,2007
165