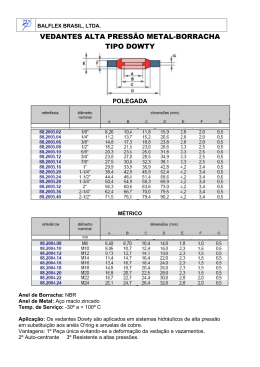
CAMPO ELÉTRICO PRODUZIDO POR UMA LINHA DE CARGA
Considere um anel carregado conforme ao lado. A carga dq
contida em um elemento de comprimento infinitesimal ds é
dada por:
q

s
q  s
Como o sistema é
infinitesimal, então
pode-se escrever:
dq  ds
Essa carga diferencial pode ser tratada como uma carga pontual
que gera um campo elétrico infinitesimal dE:
dq
ds
dE 

2
2
4 0 r
4 0 r
O campo elétrico total é dado somando (integrando) a contribuição de todos os
elementos infinitesimais. Por simetria, o campo deve apontar na direção z, pois
contribuições na direção radial se cancelam em pares simetricamente opostos.
Temos então:
E
 dE cos 
anel
ds z
z
anel 4 0 r 2 r  4 0 r 3
Finalmente, quando usamos
q   2R

2R
0
e
z (2R)
ds 
4 0 r 3
r  z2  R2
temos:
qz
E
3
2 2
4 0 ( z 2  R )
(anel carregado)
No caso em que z>>R o termo z 2  R 2 se aproxima de z 2 e a equação toma a forma:
E
q
4 0 z
2
(anel carregado a grandes distâncias)
CAMPO ELÉTRICO PRODUZIDO POR UM DISCO DE CARGA
Considere agora um disco carregado conforme a Fig. Neste
caso podemos considerar um anel de raio (variável) r e
espessura dr como um elemento infinitesimal do disco. Como
acabamos de descobrir o campo gerado por um anel, é:
E
qz
3
2 2
4 0 ( z  R )
2
A carga dq contida em um elemento de área infinitesimal
e dada por:
Como o sistema é
q
q  A infinitesimal, então dq  dA

pode-se escrever:
A

Onde nesse caso

dA  (2r )dr , assim:
dq   (2r )dr
Portanto, o campo total é dado por:
dE



E
disco
disco
Fazendo a substituição
z du
3

4 0 0 2
u
R
Ou seja,

E
2 0
z (2r )dr
3
2 2

4 0 ( z  r )
2

disco
zdq
3
2 2
4 0 ( z  r )
2
z


4 0
R

0
2rdr
3
2 2
(z2  r )
u  z 2  r 2 e du  2r dr
R


z  2 
z

 1

4 0  2 
4

0
 u 0


z
1  2

2
z R 

R


z
2
 2 2  
z  r  0 4 0

(disco carregado)
2

2
  2

2
z R 
z
Note que quando R → ∞, temos que o campo de uma placa infinita é constante:

E
2 0
(placa infinita carregada)