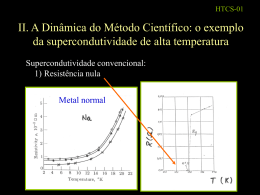
Correlações Eletrônicas
em Nano-superredes
Raimundo R dos Santos
[email protected]
Colaboradores:
• Thereza Paiva (UFRJ)
• Mohammed El-Massalami (UFRJ)
• André L Malvezzi (UNESP/Bauru)
• Eduardo Miranda (UNICAMP)
• Jereson Silva-Valencia (UNICAMP)
Apoio:
Esta apresentação pode ser obtida do site
http://www.if.ufrj.br/~rrds/rrds.html
seguindo o link em “Seminários, Mini-cursos, etc.”
Esquema do seminário
•
•
•
•
Introdução
Nano-superredes de Hubbard
Metodologia
Nano-superredes com interações repulsivas:
Magnetismo, MIT, e distribuição de carga
• Nano-superredes com interações atrativas:
Supercondutividade
• Conclusões
Introdução
Nanosuperredes:
• Heteroestruturas cujas unidades de
repetição têm seções retas com
dimensões nanoscópicas
Nanosuperredes:
• Exemplos já realizados experimentalmente:
 Nanofios de multicamadas magnéticas (GMR)
[Piraux et al.,
(1994)]
 Super-redes
(fotônica)
O  Au
A  GaAs
B  GaP
de
nanofios
semicondutores
[Gudiksen et
al., 2002]
Nanosuperredes:
• Exemplos possíveis (?):
 Super-redes de nanotubos de Carbono
dobras com
pentágonos
e
heptágonos
[Yao et al., 1999]
Super-redes usuais:
 Multicamadas metálicas magnéticas
– p.ex., Fe/Cr/Fe, Fe/Mn/Fe,...
FM
AFM
O acoplamento de exchange entre as camadas magnéticas oscila
com o tamanho do espaçador
E  2 A12
M1  M 2
,
| M1 || M 2 |
M i é magnetização de saturação
da camada i
+ GMR [Baibich et al., 1988]
Teoria de poço quântico [Edwards et al. (1991)] explica qualitativamente aspectos da oscilação do exchange:
• considera a magnetização de cada camada
• períodos de oscilação determinados pelos pontos
extremos da superfície de Fermi do material espaçador
• períodos longos e curtos (teoria e exp); p.ex., Fe/Cr/Fe,
10 a 12 ML + 2 ML
Mas, como entender o papel de fortes correlações eletrônicas,
principalmente no material magnético?
 necessidade de teoria microscópica
 como caracterizar oscilação?
 Multicamadas supercondutor/isolante – p.ex., Nb/Ge
Ge
Nb
Ge
Nb
Ge
DNb
• Tc decresce quando DNb decresce em filmes espessos de Ge
 OK: semelhante ao filme de Nb isolado
• Tc cresce quando DGe  0, para DNb fixo
 efeito de proximidade via Ge passivo?
[Ruggiero et al., (1982)]
 Multicamadas supercondutor/ferromagneto
Fe/Nb/Fe
[Mühge et al., (1996)]
Nb/Gd
[Jiang et al., (1995)]
• Tc oscila quando dFM cresce
 mecanismo ainda não compreendido
• Tc decresce rapidamente para dGd < 7 Å,
quando cessa FM do Gd
 não explicado por teoria (semiclássica): necessidade de teoria microscópica + baixa dimensionalidade
 Multicamadas supercondutoras/vidro de spin – Nb/CuMn
[Mercaldo et al., (1996)]
• Tc oscila com dSG, apesar do material ser vidro de spin
 ordenamento magnético “mais fraco”
 efeito de quebra de pares não deve ser determinante
Mono e Bi-planos:
os carbetos de Boro
R = Sc, Y; Terras raras
RT2B2C
RTBC
T = Ni, Co, Pd, Pt
Coexistência entre ordens (antiferro) magnética (4f)
e supercondutora em alguns
compostos de uma
camada...
[Canfield et al., (1998)]
...mas não se consegue uma sistematização dos dados:
• RT2B2C  1 camada RC T=Ni
R=Sc, Y, Ce, Dy, Ho, Er, Tm, Lu, U, Th  SUC
coexistência SUC e MAG (exceto Lu)
R= Yb  Heavy fermion
• RTBC  2 camadas RC T=Ni  sem SUC, sem HF
• T=Co  1 camada
R=Lu, Tm, Er, Ho Dy, Gd, Ce  sem SUC
• R=La  1 camada
T=Ni  sem SUC; sem MAG
T=Pd, Pt  SUC
Necessário uma teoria simples – int e-fonon + BCS
OK! – que incorpore efeitos de camadas
Características comuns dos diversos sistemas físicos
ilustrados:
• elétrons fortemente correlacionados
• modelos devem incorporar estrutura de camadas
de modo fundamental
• pelo menos uma dimensão reduzida (micro- ou
nanoscópica)
• tratamento por teorias de campo médio desejável,
mas deve-se ter cautela com previsões
Modelo emblemático para spins itinerantes em rede
homogênea: Modelo de Hubbard repulsivo
H  t
c

i c j
 n
 c j ci  U
i , j ,
Favorece o salto dos férmions
entre sítios (termo de banda)
Competição entre graus de
liberdade de carga e de spin
i  ni 
i
Repulsão Coulombiana: a
energia total aumenta se 2
e’s ocuparem o mesmo
orbital
 termo de correlação†
Hubbard  Heisenberg AFM para um e por sítio (banda
semi-cheia) quando U  t
†
para uma apresentação .ppt de revisão sobre aspectos de sistemas fermiônicos fortemente correlacionados, veja
http://www.if.ufrj.br/~rrds/rrds.html e siga os links em “Seminários, Mini-cursos, etc.”
Previsões para o modelo homogêneo em 2 dimensões (T = 0)
Teoria de Campo Médio
(teoria de 1 partícula)
Fortes fluts. AFM’s
Simulações de Monte Carlo
[Hirsch (1985)]
Em 1 dimensão (T = 0) : Ondas de densidade de carga e ondas de
densidade de spin
[Brown and
Grüner (1994);
Grüner
(1988,1994)]
• Banda semi-cheia (=1): só SDW; isolante de Mott
• Dopado: SDW e CDW
N.B.: Em 1-D não há ordem magnética de longo alcance; a SDW é um estado quaseordenado
Se período da CDW incomensurável com a rede
[i.e.,   r a; r racional e a
parâmetro de rede]
 transporte de corrente é
não-ômico
ômico
não-ômico
Explicação: analogia
mecânica
[Brown and
Grüner (1994);
Grüner
(1988,1994)]
O Modelo de Hubbard Atrativo
H  t
 c

i
i , j ,σ

c j  H.c.  U  ni  ni 
i
Características: [Micnas et al. (90)]
• Emparelhamento no espaço real, ao contrário de BCS.
• Equivale a BCS para |U| << t
• Apresenta gap (para excitações) de spin
 SUC’s de alta T
• Mais amigável para cálculos numéricos
 pode ser usado como modelo efetivo para
entender diversas propriedades de supercondutores
(p.ex., inomogeneidades: desordem, super-redes)
QMC: Tc como função de
<n>, para |U| fixo...
[Moreo and Scalapino (1991)]
...e, varrendo-se |U|, obtém-se o
diagrama completo (esquemático)
[Scalettar et al. (1989)]
?
Super-redes de Hubbard
• Caso Repulsivo
 Fe, Ni, Co
 Cu, Ag, Cr
Em uma dimensão:
U0
LU
H  t
L0
 c
i , j ,

i
U=0

c j  c jci  U i ni  ni 
i
[Paiva and dS (1996)]
• Caso Atrativo
Por enquanto:
• papel das camadas nos carbetos de Boro
• desconsideramos momentos localizados (4f)
U<0
U=0
U<0 U=0
U<0
U=0
           RT2B2C
            RTBC

U<0

T2B2
U=0 U=0
U<0
U=0
U=0

RC  sem elétrons f
H  t  (ci ci 1  HC)  U i ni ni   i ni
i
i
i

sítios atrativos
Métodos de Cálculo
Diagonalização de Lanczos:
H 
1
H 1

2
[Malvezzi (2002)]
A matriz de H é gerada sob a forma tri-diagonal
 a0

 b1
H  0

0

 
b1
0
0
a1
b2
0
b2
a2
b3
0
b3
a3











mais econômica em termos de memória
incorporação de simetrias
rápida convergência para obter estado fundamental
Density Matrix Renormalization Group:
Idéia básica: construção da rede “bottom up”, preservando o
tamanho do espaço de Hilbert
blocos
superbloco
• diagonaliza a Hamiltoniana do superbloco via Lanczos
• usa a matriz densidade para selecionar contribuições mais
importantes ao estado fundamental (truncagem)
[Malvezzi (2002)]
Formulação como Líquido de Luttinger:
k
Linearizando a dispersão
perto de kF (processos de
baixas energias)
-kF
kF
Espalhamento para a frente, apenas
(i.e. momento transferido q << 2kF):
 kF
g2
kF
q
kF
g4
q
kF
 excitações sem gap
[Voit (1994); Miranda (2002)]
• A conjectura do Líquido de Luttinger:
o LL descreve, de modo universal, toda a Física de
baixas energias (excitações sem gap) para os
metais 1D
• Parametrização da teoria:
(u, K) e (u, K) dependem das constantes de acoplamento g2 e g4
• Função de correlaçao de carga
K
cos(2kF x)
cos(4kF x)
n(0)n( x) 


A1 1 K  3/ 2
A2
4K
2
p
x
( )
x
ln x
x
 2kF  p n, onde n é a densidade eletrônica
 K é um expoente não-universal (depende da interação)
2kF domina se 1K 4K  K  1/3
• Conexão com LL [Schulz(90)]:
1  E0 ( n )
p u

2
L n
2 K
2
tamanho
do sistema
Calculado pela solução via Bethe ansatz
 K (n,U)
K  1/2  modulação de carga 2kF predomina a 4kF
c.f. previsões antigas via Grupo de Renormalização [Sólyom(‘79)]
• Outras grandezas mensuráveis
– Calor específico: C =  T
onde 2 = 0 vF [u-1 + u -1], com 0 = 2 p kB2 /3vF
– Susceptibilidade magnética:  = 2 K / p u
– Compressibilidade:  = 2 K / p u
– Peso de Drude (condutividade DC): D = 2 u K
Para os Nanotubos de Carbono:
“constante de acoplamento”


8e
g  1 
ln( / 2pR )
 pvF

2
constante dielétrica
comprimento
1 / 2
raio
 g ~ 0.2; c.f. g = 1 para o gás de Fermi
(comportamento LL de fato observado em exp’s de tunelamento)
Nanosuperredes com interações repulsivas:
Magnetismo, MIT, e distribuição de carga
Perfil de momento local, Si2, com Si = ni- ni  mede itinerância
Máximos nos sítios repulsivos
n
Máximos nos sítios livres
Estrutura de super-rede
irrelevante
DMRG
[Malvezzi, Paiva e
dS (2002)]
Mobiilidade dos máximos de Si2
Momento local, Si2, como função da ocupação n
Caso homogêneo: máximo na ocupação isolante, n=1
Lanczos
[Paiva e dS (1998)]
Na SR, a posição do máximo depende do “aspect
ratio”, ℓ  LU /L0  possível isolante de Mott em
nI = [2+ ℓ]/[1+ ℓ]
Verificação do isolante de Mott: gap de carga
c = E (Nc , Ne + 1) + E (Nc , Ne  1)  2 E (Nc , Ne)
onde E (Nc , Ne) é a energia do estado fundamental para Nc
células com Ne elétrons
De fato, se n = nI
tem-se   0
quando Nc  
 isolante de
Mott
Lanczos
[Paiva e dS (1998)]
SR’s de Líquidos de Luttinger
U 0
(g  1)
Diagrama de fases
longas
U=0
(g = 1)
longas
Isolante sem gap
isolante de Mott (gap)
Isolante sem gap
metal
LL
[Silva-Valencia, Miranda e dS (2001,2002)]
1  n 
Compressibilidade:   2 


n   T
 = 0  incompressível (Mott)
  0  compressível (metal), mas
uma das sub-redes é isolante
sistema como um todo o é
LL
LL
[Silva-Valencia, Miranda e dS (2001,2002)]
A SR permite a construção de um material isolante sem gap
Ordenamento magnético em nI = [2+ ℓ]/[1+ ℓ] :
S iz S iz r  ni   ni  ni  r   ni  r  
SDW
Lanczos
[Paiva e dS (2000)]
SDW
Em nI uma expansão em acoplamento
forte leva a um modelo de Heisenberg
numa super-rede, com acoplamento
entre spins em diferentes camadas
sendo mediado pelos elétrons na
camada livre
Frustração
Lanczos
Dopando além de nI: exemplo com LU = 3, L0 = 1
4 spins na camada repulsiva: S = 0
frustração
5 spins na camada repulsiva: S  0
SDW recuperada
Lanczos
Frustração quando Srep =0; induzida por dopagem
[Paiva e dS (2000)]
Análise do gap de spin
s = E (Nc , Ne, Sz = 1)  E (Nc , Ne, Sz = 0)
gaps extrapolados para Nc 
Frustração
s  0
SDW
s = 0
Lanczos
Lanczos
Frustração e SDW também se manifestam no
gap de spin
[Paiva e dS (2000)]
Que arranjo magnético domina a SDW?
• Analisemos o fator de estrutura magnético,
No caso homogêneo, S (q) tem pico em qmax = 2kF = p n
DMRG
DMRG
em alguns casos: picos em qmax  p, e em q* = p
cresce com U e com Ns  robusto
Dois picos  períodos longo e curto
[Malvezzi, Paiva e dS (2002)]
Evolução da posição dos picos com a densidade:
n0 
1
LU  L0
n  
2 L0
LU  L0
homogeneo
2 L  LU
nI  0
LU  L0
DMRG
nU  2  n0
DMRG
qmax = p ncell com ncell = Ne / Nc = n (LU + L0) = densidade p/ célula
 ~ homogêneo
NB: qmax = 0 ↔ frustração, e não FM
• n0 < n < n: qmax = p
• n < n < nI: dois picos  qmax = p e qmax = p neff,
com neff = n (LU + L0)  2 L0 = densidade nas camadas repulsivas
 qmax oscila com n
• n > n I:
qmax = p (2  ncell)
• n < n0 :
SDW’s com todos os q geradas num intervalo 2n0, mais
estreito que no caso homogêneo
[Malvezzi, Paiva e dS (2002)]
Regiões num espaço de parâmetros 3D:
As regiões n < n0 e n > nU
só são importantes para
camadas “finas”
[Malvezzi, Paiva e dS (2002)]
ℓ=1
Evolução da posição do 2o. pico com a “espessura” do espaçador:
n = 11/6
L0
Lanczos
• qmax fornece medida do acoplamento de exchange entre as
camadas
• oscila com L0, para uma densidade eletrônica fixa:
• período L0 = pkF (c.f. previsão de Hartree-Fock para
multicamadas magnéticas)
[Paiva e dS (2000); Malvezzi, Paiva e dS (2002)]
Distribuição de Carga: CDW’s
Caso homogêneo: velha pendência LL vs. Hubbard, mas...
modo de carga 4kF de fato predomina sobre o 2kF, ao
menos para valores de U suficientemente grandes.
Acordo com descrição de LL: amplitude A1(n,U) do modo
2kF  0 para U  U  (n)
Esquematicamente:
n
1
2kF
U  (n)
4kF
0
U
[Paiva e dS (2000b)]
Super-redes – examinemos o fator de estrutura de carga:
C (q ) 
1
Nc
e
iq( ri  r j )
ni n j
i, j
Distribuição de carga na camada
repulsiva determina correlações:
•cúspides em q*= 4kF*,
•com 2kF* = p neff
•onde neff = n (LU + L0)  2 L0
Lanczos
Não é efeito de tamanho:
cúspides mais nítidas à
medida em que Ns cresce
[Paiva e dS (2002)]
Lanczos
Evolução da posição da cúspide com a “espessura” do espaçador:
Lanczos
• q* fornece medida do acoplamento de carga entre as
camadas
• oscila com L0, para uma densidade eletrônica fixa
• período L0 = p2kF
[Paiva e dS (2002)]
Condutividade
  , 
LL
Condutividade confirma a natureza isolante do
sistema, quer o gap de carga seja finito (Mott) ou
nulo (“isolante parcial”)
[Silva-Valencia, Miranda e dS (2001,2002)]
Nanosuperredes com interações atrativas:
Supercondutividade
gap de carga
 excitações de uma partícula
C = E (Nc,Ne+1)+E (Nc,Ne - 1) 2E (Nc,Ne)
C
I
0
S 0
M =0
DC
=0
0
0
peso de Drude
 ()=DC()+g()
N S  2 E0
DC 
2  2  
0
fluxo magnético
atravessando
anel
H  t  (ci ci 1  HC)  U i ni ni   i ni
i
i
35
L0=2
L0=1
30
I
25
20

i
I
15
n ==5/3
5/3
c=C=00
DcD=C=00
S
10
M
5
0
0
5
10
15
20 0
M
S
5
|U|
10
15
20
|U|
De fato, a introdução de uma camada livre
adicional diminui a região SUC
[T Paiva, M El-Massalami, & RRdS, em andamento (2002)]
Sistematização
10
SUC
Co Ni
Rh Pd
Ir Pt
5
Y
Nd Pr La
RPt2B2C
Y
Nd Pr La
RPd2B2C
La
RIr2B2C
Lu Yb TmEr Ho Y Dy Tb Gd Eu SmCe Nd Pr La
RNi2B2C
La
RRh2B2C
Lu Yb TmEr Ho Y Dy Tb Gd Eu SmCe Nd Pr La
RCo2B2C

Metal
0
0
| U4 |
8
12
16
Raio atômico
20
•Fixando os dados sobre a série do Ni, determina-se a fronteira SUC-M
•Adiciona-se as outras séries de metais de transição, respeitando o raio
atômico
•Pode-se prever, a partir daí, se determinado composto será, ou não, SUC
Conclusões
 Geral: caráter 1D capta efeitos de interferências
quânticas na direção da SR de dimensões maiores.
• Dois tipos de isolantes:
• Mott, para n = nI (ℓ)
• Compressível (gapless) para n  nI (ℓ)
• Super-redes magnéticas podem apresentar frustração,
dependendo da combinação entre dopagem e aspect ratio
• Caracterização do acoplamento de exchange via S(q):
• densidades efetivas ncell, neff  qmax
• oscilação com L0 ↔ “superfície” de Fermi: per = p/kF
• oscilação com n : período mais curto que no caso
homogêneo
• Distribuição de Carga:
• modo dominante q* = 4kF*, com 2kF* = pneff
• acoplamento de carga entre células oscila com L0:
período = p/2kF
• SR’s Supercondutoras
• critério (gap de carga e peso de Drude) OK
• modelo explica qualitativamente desfavorecimento
de SUC quando L0 aumenta de 1 para 2
• permite sistematização de dados
Próximos passos
• Nanosuperredes:
• Estudo mais detalhado das CDW’s (DMRG)
• “Escadas” e “tubos”
• Campo magnético  Peso de Drude  GMR
• Tunelamento; biestabilidade na corrente (LLSL)
• Inclusão de momentos localizados (elétrons-f ) e
interação com elétrons de condução: Kondo
[no caso desordenado: implicações para
semicondutores magnéticos diluídos (DMS)]
• 2D e 3D [QMC]:
• Magnetismo
• MIT, Transporte
• Efeitos de estrutura de bandas
 estabilização de estado FM
• Supercondutividade (com momentos localizados)
Referências
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
M N Baibich et al., Phys Rev Lett 61, 2472 (1988)
S Brown and G Grüner, Sci Am 270 (4), 28 (1994)
P C Canfield et al., Phys Today 51 (10), 40 (1998)
D M Edwards et al., Phys Rev Lett 67, 493 (1991)
P Grünberg et al., J Appl Phys 69, 4789 (1991)
G Grüner, Rev.Mod.Phys. 60, 1129 (1988)
G Grüner, Rev.Mod.Phys. 66, 1 (1994)
M S Gudiksen et al., Nature 415, 617 (2002)
J E Hirsch, Phys Rev B 31, 4403 (1985)
J Jiang et al., Phys Rev Lett 74, 314 (1995)
A L Malvezzi, Escola Bras Mec Est - Braz J Phys (2002) ?
A L Malvezzi, T Paiva and R R dos Santos, Phys Rev B 66, 064430
(2002).
L V Mercaldo et al., Phys Rev B 53, 14040 (1996)
R Micnas et al., Rev Mod Phys 62, 113 (1990)
E Miranda, Escola Bras Mec Est - Braz J Phys (2002) ?
A Moreo and D J Scalapino, Phys Rev Lett 66, 946 (1991)
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Th. Mühge et al., Phys Rev Lett 77, 1857 (1996)
T Paiva and R R dos Santos, Phys.Rev.Lett. 76, 1126 (1996)
T Paiva and R R dos Santos, Phys.Rev.B 58, 9607 (1998)
T Paiva and R R dos Santos, Phys.Rev.B 61, 13480 (2000) [b]
T Paiva and R R dos Santos, Phys.Rev.B 62, 7004 (2000)
T Paiva and R R dos Santos, Phys.Rev.B 65, 153101 (2002)
S T Ruggiero et al., Phys Rev B 26, 4894 (1982)
R T Scalettar et al., Phys Rev Lett 62, 1407 (1989)
H J Schulz, Phys.Rev.Lett. 64, 2831 (1990)
T Siegrist et al., Nature 367, 254 (1994)
J Silva-Valencia, E Miranda, and R R dos Santos, J Phys Condens Matt
13, L619 (2001)
J Silva-Valencia, E Miranda, and R R dos Santos, Phys Rev B 65,
115115 (2002)
J Sólyom, Adv.Phys. 28, 209 (1979)
J Voit, Rep.Prog.Phys. 57, 977 (1994)
Z Yao et al., Nature 402, 273 (1999)