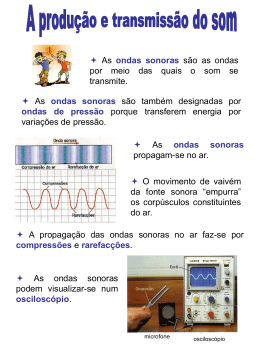
ONDAS SONORAS
O som é uma onda (perturbação) longitudinal, de
fraco (pequena amplitude), estando relacionado com a
pressão, e tridimensional, que se propagam no ar ou em
energia transportada pela onda sonora. Divide-se em:
outros meios materiais, produzida por um corpo vibrante,
☞ Intensidade Física (I): relação entre a energia (E)
sendo de cunho mecânico.
que atravessa uma superfície perpendicular à direção de
AS ONDAS SONORAS NÃO SE PROPAGAM NO
propagação pela área “A” da superfície atravessada, na
VÁCUO; SEU ESTUDO DENOMINA-SE ACÚSTICA.
unidade de tempo (ou potência transportada por área):
Compressã
o
Pressã
o do Ar
Rarefaçã
o
I
Alta
E
A.t
I
ou
P
A
P = E/ t
Unidade SI de I: J/m2.s ou W/m2
Normal
Posição
Baixa
As variações de pressão fazem com que nossos ouvidos
vibrem com a freqüência da onda, o que produz a sensação
fisiológica do SOM. Um ouvido humano normal é
excitado por ondas de freqüências entre aproximadamente
20 Hz e 20.000 Hz (Sons Audíveis)
INFRA - SOM
SOM AUDÍVEL
ULTRA-SOM
Ser Humano
Cachorros,
morcegos ouvem.
Abalos Sísmicos
20 000 Hz
20 Hz
Infra–sons (ou ondas infra-sônicas): são ondas sonoras
de freqüência menor que 20 Hz.
Ultra–sons (ou ondas ultra-sônicas): são ondas sonoras
de freqüência maior que 20.000 Hz.
Velocidade do som
A velocidade do som depende das características do meio
onde se propagam. As ondas sonoras propagam-se em
meios sólidos, líquidos e gasosos. Sua velocidade é maior
nos meios mais rígidos.
V som (sólido) > V som (líquido) > V som ( gases)
Exemplos:
V som/ar = 340 m/s (a 15 °C) V som/ar = 346 m/s (a 25 °C)
V ferrro = 5200 m/s (a 25 °C) V água = 1498 m/s (a 25 °C)
QUALIDADES FISIOLÓGICAS DO SOM:
ALTURA
INTENSIDADE
TIMBRE
A) ALTURA (ou TOM) qualidade que permite
diferenciar um grave (baixo) de um som agudo (alto). A
altura depende apenas de sua freqüência.
Sons GRAVES: freqüência menor homem: 100 ↔ 200 Hz
Sons AGUDOS: freqüência maior  mulher: 200 ↔ 400 Hz
i
f2
f1
Intervalos sonoros (i): define-se por: Sendo f1 e f2 a
freqüência de dois sons, f2  f1
Se f2 = f1  i = 1: diz-se que os sons estão em
UNÍSSONO
Se f2 = 2f1  i = 2, o intervalo é denominado OITAVA.
B) INTENSIDADE (ou SONORIDADE)
Associada à amplitude da onda - é a qualidade que permite
diferenciar um som forte (grande amplitude) de um som
☞ Mínima
Audibilidade)
Intensidade
Audível
(Limiar
da
Io = 10 – 12 W/m2
☞ Máxima Intensidade Física (Limiar da dor–máxima
suportável)
I = 10 0 =1 W/m2
☞ Intensidade Auditiva do som (ou Nível sonoro):
Utilizando-se escala logarítmica (logaritmo decimal),
o Nível Sonoro  de um som é dado por:
 I 
  log 
 I0 
ou
10 
I
I0
I = intensidade física do som;
I0 = menor intensidade física (audível) (10 – 12 W/m2)
Unidade SI de : o bel (símbolo B)
Usualmente, utiliza-se a unidade menor: o decibel (dB)
1 dB = 10 - 1 B
Em ambiente:
Calmo
até 40 dB
Barulhento
60 dB
Com poluição sonora
acima de 80 dB
C) TIMBRE (determinado pela forma da onda):
qualidade que permite diferenciar dois sons de mesma
altura e mesma intensidade, emitidos por fontes distintas.
Exemplo: uma nota musical emitida por um piano e por
um violão diferencia-se por timbre.
FENÔMENOS SONOROS
(propriedades das ondas sonoras)
As ondas sonoras apresentam as propriedades
características dos demais tipos de ondas: Reflexão,
Refração, difração e Interferência. Elas só não podem
ser polarizadas, pois são ondas longitudinais.
Convém destacar alguns fenômenos particulares da
reflexão, que se relacionam com a audição das ondas
sonoras refletidas: Eco, reforço e Reverberação.
Sabe-se que o ouvido humano só consegue distinguir
DOIS SONS que chegam a ele com intervalo de tempo
igual ou superior a 0,1 s, aproximadamente; que é o tempo
de persistência auditiva. Quando duas ondas sonoras
atingem nosso ouvido num intervalo de tempo menor que
0,1 s, não será possível distinguir o segundo som do
primeiro.
Considerando a figura anterior, onde temos uma fonte
sonora em presença de um ouvinte e uma parede que
reflete as ondas sonoras; sendo t1 o tempo do som direto e
t2 o tempo do som refletido. Temos:
REFORÇO: Se t 2  t 1  0
REVERBERAÇÃO: Se t 2  t 1  0,1s
ECO Se t 2  t 1  0,1s
a) ECO: quando o observador ouve separadamente o som
direto e o som refletido após um intervalo de tempo maior
que 0,1s. A menor distância entre o observador e o
obstáculo para provocar o eco deverá ser de 17 m.
marchando, mas sim com passos alternados, para não
haver desabamento.
ALGUMAS FONTES SONORAS
a) Cordas vibrantes
Quando cordas tensas e fixas nas extremidades
vibram, tornam-se fontes sonoras. Originam-se ondas
transversais que se propagam ao longo de seu
comprimento, refletindo-se nas extremidades e, por
interferência, formam-se ondas estacionárias, que transfere
energia ao ar em sua volta, dando origem às ondas sonoras
que se propagam. Os instrumentos musicais de corda,
como piano, violão, violino etc, têm esse mecanismo de
funcionamento. Ou seja, modos de vibração
b) REVERBERAÇÃO: ocorre quando o som refletido
atinge o observador no momento em que o som direto está
se extinguindo, não se distingue um som do outro,
ocasionando o prolongamento da sensação auditiva; isto se
dá num intervalo t < 0,1 s. Obstáculo longe.
c) REFORÇO: quando o observador ouve o som direto
juntamente com o som refletido, ocasionando um aumento
da intensidade sonora (percepção de um som mais forte).
O obstáculo refletor deve estar muito próximo, sendo o
intervalo de tempo praticamente nulo ( t  0 ).
REFRAÇÃO,
SONORA
DIFRAÇÃO
E
INTERFERÊNCIA
Refração do som: ocorre quando uma onda sonora
produzida em um meio passa para outro meio em que sua
velocidade é diferente, mantendo sua freqüência
constante e modificando seu comprimento de onda.
Difração do som: permite-lhe contornar obstáculos com
dimensões de até 20 m. Considerando vsom = 340 m/s, fmin =
20 Hz e fmáx = 20.000 Hz (audível), o comprimento de onda
do som no ar pode variar entre λmin = 1,7 cm e λmáx = 17 m. Na
prática, considera-se essa variação entre 2 cm e 20 m.
Interferência do som: quando um ponto do meio
recebe dois ou mais sons originados por várias fontes ou
por reflexões em obstáculos. O BATIMENTO é um
importante caso de interferência sonora; que ocorre
quando há interferência de ondas sonoras de freqüência
ligeiramente diferentes. A intensidade varia de um som
forte, que se ouve num dado instante, alternando com
silêncio total.
RESSONÂNCIA E FREQÜÊNCIA NATURAL
Ressonância: fenômeno que permite um corpo vibrar,
por influência de outro, na mesma freqüência.
Freqüência natural: é a freqüência própria do
aparelho (fonte), das fontes osciladoras (pêndulos simples,
osciladores harmônicos, etc) ou dos corpos, tais como
prédios, pontes, etc.
O fenômeno da ressonância acontece quando um
sistema vibra forçado por outro sistema, mas com uma
característica; o sistema que provoca a vibração deve estar
perto do outro e vibrar com uma freqüência igual à
freqüência natural desse outro. Por exemplo: o vidro de
uma janela que se quebra ao entrar em ressonância com as
ondas sonoras emitidas por um avião a jato. Tropas
militares que atravessam uma ponte não o fazem
Comprimento de onda e freqüência do enésimo
harmônico (ou enésimo modo de vibrar)
Sendo n o número de fusos (espaço entre nós),
n = 1, 2, 3,
n =1  1° Harmônico ou som fundamental
(modo mais simples)
n = 2  2° Harmônico
n = 3  3° Harmônico,
a) Tubos sonoros
Podem ser abertos nas duas extremidades ou
fechados numa delas. Como nas cordas, a superposição
das ondas incidentes com as refletidas leva à formação de
ondas estacionárias. A coluna de ar do tubo entra em
ressonância com a freqüência emitida pela fonte.
►Tubos abertos nas duas extremidades
Quando soprados, produzem ondas estacionárias com
ventres em ambas as extremidades. Seja;
Sendo n = 1, 2, 3, .., e f1 : freqüência de vibração do som
fundamental ou do 1° harmônico.
Neste caso, obtêm-se freqüências naturais de todos os
harmônicos (pares e ímpares), como nas cordas.
►Tubos fechados numa das extremidades
Quando soprados, pode ocorrer a formação de um
nó na extremidade fechada e um ventre na extremidade
aberta. Apresentam harmônicos de ordens ímpares,
somente.
Sendo i = 1, 3, 5, e f1 a freqüência do som fundamental
ou do 1° harmônico.
EFEITO DOPPLER
(Homenagem ao físico austríaco Christian J. Doppler)
(1803 – 1853)
Fenômeno pelo qual um observador (receptor)
percebe uma freqüência diferente daquela emitida pela
fonte emissora (f F ), devido ao movimento relativo entre
eles. Quando esse movimento é de aproximação, o
observador percebe uma freqüência maior que fF;quando o
movimento é de afastamento, o observador percebe uma
freqüência menor que fF . Supondo-se ambos, observador e
fonte, em movimento relativo sobre a mesma reta; vale a
fórmula geral do EFEITO DOPPLER SONORO:
fF Re al 
VS  VF

fo Aparente
VS  Vo
Sendo:
fF : freqüência da fonte sonora ( freqüência real);
fo : freqüência ouvida pelo observador (f. aparente);
VF : módulo da velocidade da fonte em relação à Terra;
Vo : módulo da velocidade do obs. em relação à Terra;
VS : módulo da velocidade do som em relação à Terra;
Convenções de sinais (+ e ):
Adota-se trajetória positiva (eixo orientado) sempre no
sentido do observador para a fonte, independentemente
dos sentidos dos movimentos destes.
Observação:
O
EFEITO DOPPLER pode ocorrer nos movimentos
ondulatórios em geral. Quando observado em ondas
eletromagnéticas, particularmente ondas luminosas, tal
efeito recebe a denominação EFEITO FIZEAU, em
homenagem ao físico francês Armand H. Louis
Fizeau(1819-1896), por ter explicado o fenômeno nessas
ondas em 1848. Na luz, a variação aparente na
freqüência, causa mudança na cor do corpo O efeito
fizeau tem aplicação importante na determinação da
velocidade das galáxias distantes (astronomia), a partir da
freqüência com que um observador na Terra percebe as
ondas eletromagnéticas que tais galáxias emitem. A luz
emitida por uma galáxia é percebida, por um observador
na Terra, com freqüência menor, indicando afastamento
da galáxia (desvio para o vermelho - cor visível de
menor
freqüência).
Observações
astronômicas
comprovam que as galáxias mais afastadas de nós têm uma
maior velocidade de afastamento; fato este, que constitui a
idéia central da teoria de expansão do universo a partir
do BIG BANG.