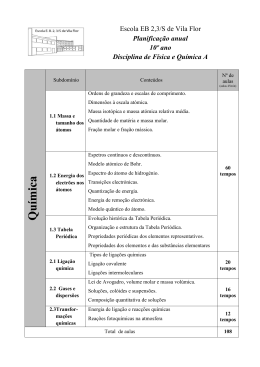
Capítulo 3
CONCENTRAÇÕES, VELOCIDADES E FLUXOS
Antes de apresentarmos as equações fundamentais da difusão de calor e massa, objetivo central
dos Capítulos 4 e 5, é conveniente introduzirmos conceitos associados ao transporte de massa em
misturas. Tais conceitos facilitarão o entendimento físico de alguns termos a serem derivados nas
equações de transporte.
3.1. Concentrações
Considere uma região do espaço de volume V na qual coexistem N espécies químicas
(componentes) distribuídas de forma homogênea, conforme ilustra a Figura 3.1. A concentração
mássica do i-ésimo componente, onde i = 1, 2, 3, ... N, é definida como:
i 
mi
V
(3.1.1)
onde mi é a massa do componente i existente no volume V.
V
Espécie 1 (Massa molar M1)
Espécie 2 (Massa molar M2)
Espécie 3 (Massa molar M3)
Espécie N (Massa molar MN)
Figura 3.1. Componentes de uma mistura ocupando um volume V.
Analogamente, a concentração molar do componente i é definida por:
ci 
ni
V
(3.1.2)
1
Copyright © 2010. Jader R. Barbosa Jr.
onde ni é o número de moles do componente i no volume V. Da relação entre a massa e o número
de moles, tem-se que:
mi
Mi
ni 
(3.1.3)
A fração mássica do componente i é definida por:
mi
m
Xi 
(3.1.4)
onde a massa total dos componentes do volume é:
N
m  mi
(3.1.5)
i1
Na eq. (3.1.4), é comum utilizar o símbolo Xi para frações mássicas em misturas líquidas e Y i
para misturas de gases ou vapores. Por meio da definição da densidade mássica da mistura:
m
V

(3.1.6)
a fração mássica pode também ser escrita na forma:
Xi 
i

(3.1.7)
Do mesmo modo, definimos a fração molar como:
xi 
ni
n
(3.1.8)
onde o número total de moles dos componentes do volume é dado por:
N
n   ni
(3.1.9)
i1
Note que na equação (3.1.8), o símbolo yi também é usado com frequência no caso de
misturas de gases ou vapores. Por meio da definição da densidade molar da mistura:
c
n
V
(3.1.10)
também é possível escrever a fração molar do componente i na forma:
xi 
ci
c
(3.1.11)
A massa molecular equivalente da mistura é definida por:
M

c
(3.1.12)
2
Copyright © 2010. Jader R. Barbosa Jr.
A partir das definições relativas à concentração dos componentes de uma mistura, uma série
de relações básicas pode ser derivada, conforme resumido abaixo:
N
X  1
N
x
i1
(3.1.13)
i
i1
1
i
(3.1.14)
N
x M  M
i1
N
i
(3.1.15)
i
Xi
1
M  M
i1
(3.1.16)
i
Para ilustrar a diferença entre concentrações definidas na base molar e na base mássica,
imagine que em sua rede de pesca um pescador tenha apanhado uma determinada quantidade
total de peixes, compreendendo quantidades individuais de N espécies. Assuma, por simplicidade,
que os peixes pertencentes a uma dada espécie i sejam do mesmo tamanho e assim tenham
individualmente a mesma massa Mi. Entendemos que o equivalente à fração molar será a razão
entre o número de peixes da espécie i e o número total de peixes e, analogamente, o equivalente à
fração mássica será a razão entre a massa total de peixes da espécie i e a massa total de peixes
(devidamente computadas com o auxílio de uma balança). A diferença entre concentrações
definidas a partir das frações molar e mássica surge quando existe, por exemplo, uma disparidade
entre as massas individuais de cada espécie (ou seja, as massas molares) e/ou entre os números de
indivíduos em cada espécie. Se o pescador arrecadou 20 peixes da espécie A (com 400 g cada um) e
2 peixes da espécie B (com 4 kg cada um), as frações molares de A e B serão, respectivamente, de
0,9 e 0,1. Já as frações mássicas serão de 0,5 para cada espécie.
A adoção da base mássica ou da base molar depende de circunstâncias e condições do
problema físico em questão. Há determinadas classes de problemas que favorecem a utilização da
base mássica e vice-versa. Por exemplo, problemas envolvendo o escoamento de fluidos em que os
campos de velocidades e pressões também são incógnitas do problema são mais adequadamente
formulados na base mássica. Já problemas envolvendo processos a pressão e temperatura
constantes, favorecem o emprego da base molar. Essa diferenciação ficará mais evidente ao longo
do texto.
3.2. Velocidades
Considere o escoamento de uma mistura de N espécies químicas. Permita que as espécies

tenham velocidades v i , com relação a um referencial inercial, diferentes entres si. Definimos a
velocidade média mássica como:
3
Copyright © 2010. Jader R. Barbosa Jr.
N

v

 v
i1
N
i i

i1

N

1 N 

v

Xivi


i i
 i1
i1
(3.2.1)
i
ou seja, como a velocidade média ponderada com relação à concentração mássica.
A taxa com a qual a massa da mistura atravessa uma região de área de seção transversal

unitária perpendicular a v é calculada por (kg/m2.s):
 N 
v   ivi
(3.2.2)
i1
Damos o nome de fluxo a uma taxa por unidade de área. Desta forma, a grandeza definida
na Eq. (3.2.2) como o produto entre a densidade mássica e a velocidade média mássica é conhecida
como o fluxo de massa da mistura.
A velocidade média mássica é a velocidade medida experimentalmente em um escoamento

com, por exemplo, um tubo de Pitot ou um anemômetro de fio-quente. Adicionalmente, v é a
velocidade que aparece nas equações de conservação da massa, energia e quantidade de
movimento.
A velocidade média molar, por sua vez, é definida como a velocidade média ponderada com
relação à concentração molar:
N

v* 

c v
i1
N
i i
c
i1

N

1 N 
c
v

xivi


i i
c i1
i1
(3.2.3)
i
Analogamente, a taxa com a qual moléculas da mistura atravessam uma região de área de

seção transversal unitária perpendicular a v * , isto é, o fluxo molar da mistura, é calculada por
(kmol/m2.s):
N


cv*   ci v i
(3.2.4)
i1
 

Tanto v i quanto v e v * são determinadas com relação a um referencia inercial, sendo,
portanto, velocidades absolutas. Usando o conceito de velocidade relativa, podemos definir as
   
velocidades do componente i com relação à média mássica e à média molar: v i  v e v i  v * . Tais
velocidades originam-se da difusão do componente i na mistura. Para ilustrar o conceito de
velocidade de difusão, Cremasco (2002) também faz uso de uma analogia entre os componentes de
uma mistura e espécies de peixe se deslocando em um rio. Cada espécie tem peixes de tamanho e
massa diferentes das outras espécies e pode ter uma velocidade diferente da velocidade média do
meio (neste caso, o rio) com relação a um referencial fixo. Assim, a velocidade de difusão de uma
dada espécie com relação ao meio pode ser negativa ou positiva, dependendo se os peixes daquele
cardume nadam mais rapidamente ou mais lentamente que a velocidade média do rio. Esta
4
Copyright © 2010. Jader R. Barbosa Jr.
velocidade média, por sua vez, pode ser calculada com base na massa de cada cardume (média
mássica) ou no número de peixes em cada cardume (média molar).
3.3. Fluxos
3.3.1. Fluxos de Massa
Entendemos por fluxo a taxa com que uma dada propriedade extensiva é transportada por
uma superfície por unidade de área. Primeiramente, com o auxílio da Figura 3.2, desejamos calcular
a vazão em massa da mistura através da superfície de área dA. Se a taxa de deslocamento da

superfície de controle dA com relação a um referencial fixo é igual a v I , a taxa com a qual a massa
da mistura atravessa a superfície é:
 
  v  vI  n̂dA
dm
(3.3.1)

vi
z
y
x

v
dA

vI
Figura 3.2. Velocidades absolutas através de uma superfície.
Do mesmo modo, a taxa com a qual as moléculas que compõem a mistura atravessam a área
dA é dada por:
 
dn  cv * vI  n̂dA
(3.3.2)
Por outro lado, a taxa com a qual a massa do componente i atravessa a superfície deve ser calculada
com base na velocidade do componente i com relação ao referencial fixo, ao invés da velocidade da

mistura v :
 
 i  Xi vi  vI  n̂dA
dm
(3.3.3)
Da mesma forma, a taxa com a qual moléculas do componente i atravessam a superfície é
dada por:
 
dn i  cx i vi  vI  n̂dA
5
Copyright © 2010. Jader R. Barbosa Jr.
(3.3.4)
No que diz respeito à velocidade, a diferença entre as definições dos fluxos devido a cada
componente e à mistura apresentadas acima é mais facilmente compreendida se utilizarmos
novamente a analogia com o deslocamento dos peixes em um rio. Para um pescador parado junto à
margem (referencial fixo) ou se deslocando em uma canoa, o fluxo (mássico ou molar) de uma dada
espécie é determinado pela velocidade com que os peixes daquela espécie passam por ele, e não
pela velocidade com que o meio se desloca com relação ao referencial fixo.
A fim de definir os vetores fluxo de massa e fluxo molar, por simplicidade, voltemo-nos para

o caso em que v I é nula com relação ao referencial fixo. O vetor fluxo de massa total do
componente i é dado por:



mi  Xi v i  i v i
(3.3.5)
e pode ser decomposto em termos responsáveis pela advecção (equivalente a “se deixar levar pela
correnteza”) e pela difusão (equivalente a “se deslocar no meio, com relação ao meio”):

 
mi  i v  Ji
(3.3.6)
onde:

 
Ji i v i  v 
(3.3.7)
é o fluxo de massa devido à difusão. A relação constitutiva mais utilizada para o fluxo de massa
difusivo é a Lei de Fick. De natureza empírica e inspirada na Lei de Fourier para a condução do calor
(Cussler, 2003), esta relação é validada experimentalmente para misturas de gases a pressões
moderadas e misturas de líquidos e sólidos com diluição em pequenas proporções. Neste caso, para
uma mistura de N componentes em que o soluto (componente i) encontra-se diluído em pequenas
proporções, a Lei de Fick fornece:

(3.3.8)
Ji  Di,eff X i
onde Di,eff é a difusividade molecular efetiva (m2/s) do componente i na mistura. Note que o sinal
negativo na Lei de Fick serve para adequar esta relação constitutiva à 2ª Lei da Termodinâmica, que
estipula que a massa da espécie em questão flui da região de alta para a de baixa concentração.
Para uma mistura binária de componentes 1 e 2, temos:

(3.3.9)
J1  D12X1
onde D12 é a difusividade molecular (ou mássica) de 1 em 2 (m2/s). Em soluções concentradas (isto
é, aquelas em que as frações molares ou mássicas de soluto e solvente são da mesma ordem de
magnitude), D12 pode depender fortemente da concentração, refletindo a inadequação do
gradiente de frações molares ou mássicas em representar a força motriz da difusão (Bird et al.,
2002; Deen, 1998; Taylor e Krishna, 1993). Na realidade, o verdadeiro mecanismo motriz para a
difusão de massa é o gradiente de potenciais químicos que, somente sob algumas condições
especiais, pode ser adequadamente aproximado pelo gradiente de concentrações. Essa descrição
mais generalizada, entretanto, foge do escopo deste texto.
6
Copyright © 2010. Jader R. Barbosa Jr.
Analogamente, o vetor fluxo molar total do componente i é calculado por:



ni  cx i v i  c i v i
 
 c i v *  ji 
(3.3.10)
onde o vetor fluxo molar devido à difusão dado por:

 
ji  ci v i  v *
(3.3.11)
é definido, com base na Lei de Fick, por:

ji  cDi,eff x i
(3.3.12)
Para uma mistura binária, analogamente:

j1  cD12x1
(3.3.13)
Uma explicação mais detalhada acerca da natureza e do comportamento das propriedades
termofísicas de diversas classes de materiais (sólidos, líquidos e gases), incluindo a difusividade
molecular, será apresentada no Capítulo 12, onde também podem ser encontrados valores
tabelados desta propriedade para diversas misturas sob condições específicas.
3.3.2. Relações entre os Fluxos de Massa
Substituindo a equação (3.3.8) na equação (3.3.6), temos:

 
mi  i v  Ji

 i v  Di,eff X i

 X i v  Di,eff X i
(3.3.14)
Introduzindo a velocidade média mássica dada pela equação (3.2.1), temos que a equação
(3.3.14) pode ser escrita na forma:
N


mi  Di,eff Xi  Xi mi
(3.3.15)
i1
Para uma mistura binária, as equações (3.3.14) e (3.3.15) se reduzem a:


m1  X1v  D12X1



m1  D12X1  X1 m1  m2 
(3.3.16)
(3.3.17)
Efetuando a mesma manipulação algébrica para o componente 2, é possível deduzir dois
resultados interessantes. A equação análoga à (3.3.17) para o componente 2 é:



m2  D21X2  X2 m1  m2 
(3.3.18)
Somando as duas equações, temos:
7
Copyright © 2010. Jader R. Barbosa Jr.
D12X1  D21X2
(3.3.19)


J1   J2
(3.3.20)
ou seja:
Como X1  X2 , temos que:
D12  D21
(3.3.21)
isto é, o par 1-2 possui apenas uma difusividade mássica que pode, entretanto, ser função da
composição da mistura, da pressão, da temperatura e da concentração.
Expressões análogas às equações (3.3.16) e (3.3.17) podem ser obtidas para a base molar,
resultando em:


n1  cx1v * cD12x1
(3.3.22)

 
n1  cD12x1  x1 n1  n2 
(3.3.23)


Além disso, é possível mostrar também que j1   j2 .
Taylor and Krishna (1993) discutem uma forma generalizada da Lei de Fick para misturas
multicomponentes, alternativa e mais abrangente do que aquela definida a partir de uma
difusividade molecular efetiva. No caso de um sistema ternário de componentes 1, 2 e 3, por


exemplo, existem dois fluxos de massa difusivos independentes ( j1 e j2 ) e duas forças motrizes

independentes ( x1 e x 2 ), já que  x i  1 e  ji  0 . Através da mesma relação linear entre
i
i
fluxos e gradientes assumida no caso binário, é possível escrever:

~ x  c
~ x
j1 c
11
1
12
2

~
~
j  c x  c x
2
21
1
22
2
(3.3.24)
(3.3.25)
Note que as relações acima sugerem uma dependência cruzada dos fluxos com relação aos
gradientes, nas quais são necessários quatro coeficientes para caracterizar o sistema ternário. Em
uma forma geral para um sistema multicomponente, os vetores fluxo de massa por difusão podem
ser descritos através da relação:
N1

~ x
ji  c
ik
k
(3.3.26)
k 1
que pode ser escrita em notação matricial de dimensão (N-1):
 j   c~ x 

(3.3.27)
i
ou:
8
Copyright © 2010. Jader R. Barbosa Jr.

~
~
~

 
 j1 

11
12
1N   x 1 
  

 ~

~
~
21

 
 j2 
22
2N   x 2 

   c  

   
  

~


 j  
~
~

x




 N1 
N1 ,2
N1 ,N1 
 N1,1
 N1 
(3.3.28)
~ não devem ser confundidos com os coeficientes
Convém salientar que os coeficientes 
ik
Dik associados aos sistemas binários ou pseudo-binários (efetivos), visto que eles não representam
~ podem assumir valores negativos e, de
as interações i-k existentes nestes sistemas. Assim, 
ik
~
~
forma geral não são simétricos, isto é,   . Taylor e Krishna (1993) apresentam de forma
ik
ki
detalhada as metodologias para determinação destes coeficientes.
Naturalmente, as relações para a Lei de Fick Generalizada podem ser estendidas para a base
mássica. Neste caso, é possível escrever relações equivalentes às equações (3.3.26) e (3.3.27) na
forma:
N1

Ji ikXk
(3.3.29)
k 1
e:
J  X

(3.3.30)
i
No entanto, ao contrário das difusividades mássicas de misturas binárias, D12, que
independem da base (molar, mássica ou volumétrica), não existe uma universalidade com relação
~  . Novamente, detalhes específicos
aos coeficientes na forma matricial e, de forma geral, 
ik
ik
podem ser obtidos em Taylor e Krishna (1993). Quando abordados problemas de difusão de massa
de misturas multicomponentes, o presente texto se limitará a situações passíveis de descrição a
partir da lei de Fick baseada na difusividade efetiva.
3.3.3. Fluxos de energia
A taxa com a qual energia interna atravessa uma superfície que se desloca com velocidade

v I em um meio isotérmico é dada por:
 
uv  v I   n̂dA
(3.3.31)
Da mesma forma, a taxa para a entalpia, h  u  p  , pode ser escrita como:
 
hv  v I   n̂dA
(3.3.32)
Na presença de um gradiente de temperatura, energia é transferida através da superfície
por difusão de calor (condução). Assim, de uma forma geral, a taxa total de transferência de energia
através da superfície é dada por:

 
e total  hv  vI  n̂dA  q  n̂dA
(3.3.33)
9
Copyright © 2010. Jader R. Barbosa Jr.

onde q é o fluxo de calor devido à condução. Na ausência de um campo de velocidades (como num
meio sólido ou em um fluido estacionário) e de radiação de calor, o fluxo de calor devido a um
gradiente de temperaturas é o único modo de transferência de energia possível através de qualquer
superfície (curva ou plana) no interior de um meio. A relação constitutiva para o fluxo de calor mais
comum e amplamente utilizada é dada em função do gradiente de temperaturas por meio da Lei de
Fourier. Para um meio isotrópico, ou seja, aquele em que as propriedades não são dependentes da
direção, temos que (Poulikakos, 1994):

q  k T
(3.3.34)
onde k é a condutividade térmica (W/m.K), que é sempre positiva e é função de propriedades
moleculares do meio material e da temperatura. Novamente, o sinal negativo na Lei de Fourier
serve para adequar esta relação constitutiva à 2ª Lei da Termodinâmica, que estipula que o calor
flui da região de alta para a de baixa temperatura.
Compilações extensas de valores de condutividade térmica para diversas classes de
materiais encontram-se disponíveis em livros-texto sobre transferência de calor (Incropera et al.,
2008; Lienhard e Lienhard, 2005). Uma apresentação sintética sobre o comportamento da
condutividade térmica de substâncias puras e misturas será apresentada no Capítulo 12.
A lei de Fourier é empírica e nela está embutida a hipótese de que o fluxo de calor responde
imediatamente ao gradiente de temperatura, fazendo com que perturbações no campo térmico
sejam, a rigor, sentidas instantaneamente em pontos infinitamente distantes da respectiva fonte.
Wang et al. (2008) discutem o fato de que, apesar da lei de Fourier ser aplicável a uma enormidade
de meios materiais e faixas de valores de fluxo de calor e gradientes de temperatura, para
aplicações envolvendo escalas características de comprimento e de tempo bastante pequenas,
novas leis constitutivas precisam ser utilizadas de forma a contemplar a diferença de fase entre o
fluxo de calor e o gradiente de temperaturas. No presente texto, entretanto, tais aplicações não
serão abordadas.
As expressões (3.3.31) a (3.3.33) são válidas tanto para uma substância pura quanto para
uma mistura. Entretanto, neste último caso, é possível lançar mão do conceito de propriedade
parcial para escrever as taxas relacionadas à mistura em função de propriedades dos componentes.
Tomando, por simplicidade, uma mistura binária de massa total m  m1  m2 , a relação entre
a entalpia absoluta da mistura e a entalpia da mistura por unidade de massa é dada por (admitindo
que a pressão e a temperatura se mantenham constantes):
Hm1 ,m2   mhX1 
(3.3.35)
uma vez que as frações mássicas estão relacionadas a partir da igualdade 1  X1  X2 , onde X1 
m1
.
m
Assim, por intermédio da regra da cadeia, é possível mostrar que:
H
h

h
m1 X1
(3.3.36)
10
Copyright © 2010. Jader R. Barbosa Jr.
H
h
m2
(3.3.37)
Com isso, combinando as duas equações acima, temos:
h
H
H


X1 p ,T m1 p ,T ,m m2 p ,T ,m
2
(3.3.38)
1
Os termos do lado direito do sinal da equação acima são denominados entalpias
parciais, ĥi (ou entalpias parciais específicas, já que foram definidas na base mássica) Sendo a
propriedade extensiva entalpia H uma função homogênea de 1º grau, é possível demonstrar que
(Bird et al., 2002; Smith et al., 2000):
 H
H  m1 
 m1



  m  H
2

 m2
p ,T ,m2 


  m ĥ  m ĥ
1 1
2 2

p ,T ,m1 
(3.3.39)
Para uma mistura de N componentes, por analogia, vale que:
N
H  miĥi
(3.3.40)
i1
Entalpias parciais na base molar também podem ser definidas a partir de relações análogas
às equações (3.3.39) e (3.3.40):
 H
H  n1 
 n1



  n  H
 2  n2
p ,T ,n2 


 n h n h
 1 1 2 2
p ,T ,n1 
(3.3.41)
N
H   ni hi
(3.3.42)
i1
onde hi é a entalpia molar parcial do componente i.
Desse modo, a taxa com a qual entalpia da mistura atravessa uma superfície que se desloca

com velocidade v I pode ser dada por:

N

 ĥ v  v   n̂dA
i1
i i
i
(3.3.43)
I
ou por:

N

c h v  v   n̂dA
i1
i i
i
(3.3.44)
I

onde v i é a velocidade do componente i com relação a um referencial fixo. Da mesma forma, a taxa
total com que energia é transferida pela superfície pode ser dada por:
11
Copyright © 2010. Jader R. Barbosa Jr.
N

 
de total   iĥi v i  v I  n̂dA  q  n̂dA
(3.3.45)
i1
ou por:
N

 

de total   ci hi v i  vI  n̂dA  q  n̂dA
(3.3.46)
i1

Para o caso especial em que v I é nula, temos:
N



de total   iĥi v i  n̂dA  q  n̂dA
(3.3.47)
N


de total   ci hi v i  n̂dA  q  n̂dA
(3.3.48)
i1
i1
Em função da velocidade média mássica, é possível escrever a equação (3.3.47) na forma:


N

 

de total  q  n̂dA   iĥi v i  v   iĥi v  n̂dA
i1
(3.3.49)
onde a primeira e a segunda parcelas (esta última dentro do somatório) constituem a parcela do
fluxo de calor devida à difusão definido por:
N


 
  q   iĥi v i  v 
qdif
(3.3.50)
i1
e a terceira parcela é o fluxo advectivo (relacionado à velocidade média mássica da mistura):
N


   iĥi v
qadv
(3.3.51)
i1
É instrutivo observar que o fluxo difusivo se reduzirá ao fluxo por condução quando o meio
 
for composto por uma substância pura e quando for estacionário. Neste caso, v i  v  0 , e a difusão
é devida somente ao calor associado ao gradiente de temperatura.
Substituindo na equação (3.3.50) as equações (3.3.7), (3.3.8) e (3.3.34), temos:
N

  kT   ĥiDi,eff X i
qdif
(3.3.52)
i1
E a taxa de transferência de energia através da superfície, em função das Leis de Fick e
Fourier, passa a ser escrita por:
N
N



de total   kT   ĥiDi,eff X i   n̂dA   iĥi v  n̂dA
i1
i1


12
Copyright © 2010. Jader R. Barbosa Jr.
(3.3.53)
Analogamente, em função da velocidade média molar, a equação (3.3.48) pode ser escrita
na forma:
N

 

de total  q  n̂dA   ci hi v i  v *  ci hi v * n̂dA
(3.3.54)
i1
onde as parcelas devido à difusão e à advecção são dadas por:
N


 
  q   c i hi v i  v *
qdif
(3.3.55)
N


   ci hi v *
qadv
(3.3.56)
i1
i1
Analogamente, em função dos fluxos de massa na base molar e das Leis de Fick e Fourier, a
equação (3.3.53) pode ser escrita por:
N
N



de total   kT   c hiDi,eff x i   n̂dA   ci hi v * n̂dA
i1
i1


(3.3.57)
Uma mistura ideal pode ser caracterizada como aquela em que não existem variações de
suas propriedades de estado (volume, energia interna, entalpia, entropia) decorrentes do processo
de mistura propriamente dito. Assim, para uma mistura ideal, a entalpia absoluta da mistura pode
ser escrita como uma combinação linear das entalpias específicas dos componentes, tanto na base
mássica quanto na base molar, ou seja:
N
H  mihi  Hmix
(3.3.58)
i1
N
~  H
H  nih
i
mix
(3.3.59)
i1
onde, para uma mistura ou solução ideal:
Hmix  0
(3.3.60)
~ são as entalpias específicas do componente i nas
Nas equações (3.3.58) e (3.3.59), hi e h
i
bases mássica (em kJ/kg(i)) e na base molar (em kJ/kmol(i)), respectivamente. Assim, para uma
mistura ideal:
N
N
i1
i1
miĥi  mihi
N
N
i1
i1
(3.3.61)
ni h  nih~
(3.3.62)
Desta forma, para uma mistura ideal, a equação (3.3.49) se reduz a:
13
Copyright © 2010. Jader R. Barbosa Jr.
N

 

de total  q  n̂dA  ihi v i  v   ihi v n̂dA
(3.3.63)
i1
ou, em função das Leis de Fick e Fourier:
N
N




de total   kT   hiDi,eff X i   n̂dA   ihi v  n̂dA
i1
i1


(3.3.64)
Analogamente, na base molar, a taxa com a qual a energia total de uma mistura ideal
atravessa uma superfície fixa em relação a um referencial inercial é dada por:


N

~ v  v *  c h
~
de total  q  n̂dA   cih
i
i
i i v *  n̂dA
i1
(3.3.65)
ou, da mesma forma:
N
N

~ D x   n̂dA  c h
~
de total   kT   ch

i i ,eff
i
i i v * n̂dA
i1
i1


(3.3.66)
Finalmente, no contexto de uma mistura binária ideal, temos que as equações (3.3.64) e
(3.3.66) podem ser escritas como:

(3.3.67)
de total  kT  h1  h2 D12X1 n̂dA  1h1  2h2 v n̂dA
e:






~ h
~ D x  n̂dA  c h
~
~ 
de total   kT  c h
1
2
12
1
1 1  c2h2 v * n̂dA
(3.3.68)
Referências
Bird, R.B., Stewart, W.E., Lightfoot, E.N., 2002, Transport Phenomena, 2nd Ed., Wiley, NY.
Cremasco, M.A., 2002, Fundamentos de Transferência de Massa, 2ª Ed., Ed. Unicamp, Campinas.
Cussler, E.L., 2003, Diffusion: Mass Transfer in Fluid Systems, 2nd Ed., Cambridge University Press,
NY.
Deen, W.M., 1998, Analysis of Transport Phenomena, Oxford University Press, NY.
Incropera, F.P., DeWitt, D.P., Bergman, T.L., Lavine, A.S., 2008, Fundamentos de Transferência de
Calor e de Massa, 6ª Ed., LTC, Rio de Janeiro.
Lienhard IV, J.H., Lienhard V, J.H., 2005, A Heat Transfer Textbook, 3rd Ed. Phlogiston Press,
Cambridge, MA.
Poulikakos, D., 1994, Conduction Heat Transfer, Prentice-Hall, NY.
Smith, J.M., Van Ness, H.C., Abbott, M.M., 2000, Introdução à Termodinâmica da Engenharia
Química, 5ª Ed., LTC, Rio de Janeiro.
Taylor, R., Krishna, R., 1993, Multicomponent Mass Transfer, Wiley, NY.
Wang, L., Zhou, X., Wei, X., 2008, Heat Conduction: Mathematical Models and Analytical Solutions,
Springer-Verlag, Heidelberg.
14
Copyright © 2010. Jader R. Barbosa Jr.