CURSO DE CAPACITAÇÃO
O USO DE FERRAMENTAS TECNOLÓGICAS E AS POSSIBILIDADES
PEDAGÓGICAS NA FORMAÇÃO DOS DOCENTES NA REDE
MUNICIPAL DE GURUPI – TO
A UTILIZAÇÃO DO SOFTWARE GEOGEBRA COMO FERRAMENTA DE ENSINO
EDUCACIONAL: APLICAÇÕES AO ENSINO DA MATEMÁTICA.
AULA 02: Construção de
triângulos.
25/05/13
GURUPI – TO
2013
Pág.: 2
ATIVIDADE 01 -
CONSTRUÇÃO DE TRIÂNGULOS
TRIÂNGULOS:
DEFINIÇÃO:
Se ABC é um triângulo, os seus ângulos
,
,
são os
ângulos interno de um triângulo. Somando os ângulos internos
de um triângulo obtemos 180º.
Com base no conceito apresentado, crie um triângulo qualquer
com vértices A, B, C e insira os valores dos ângulos internos.
Como sugestão, crie os vértices do triângulo nas coordenadas
A=(2,2), B=(5,4) e C= (6,0).
Trace os segmentos de reta nos pontos
,
,
.
Utilize a ferramenta ângulos (janela 8) e determine os ângulos
internos formados entre os segmentos construídos.
Após determinar os ângulos
ângulos formados: L_1={
}
internos,
crie
uma
lista
dos
Obtenha a soma dos ângulos internos. Digite: soma[L_1]
Movimente os vértices do triângulo. (Observe a alteração dos
ângulos internos) e a soma obtida.
Outra Sugestão:
Você pode obter o triângulo utilizando o comando na caixa de
entrada.
Marque os pontos referentes aos vértices.
No campo de entrada digite: Polígono[A,B,C]
Selecione a ferramenta ângulo e clique sobre os segmentos.
Caso o ângulo obtido seja o externo, use Ctrl + Z e clique
novamente sobre os segmentos, porém selecione de modo inverso
a utilizada para obter o ângulo externo. Outra sugestão para
obter o ângulo é selecionar a ferramenta ângulo e clicar sobre
os vértices, ou também utilizar a caixa de entrada digitando o
comando correspondente (ângulos[]).
___________________________________________________________________________
|Geogebra na Sala de Aula| # |www.andreluizifto.xpg.com.br|
Maio 2013
Pág.: 3
Obter a soma dos ângulos internos:
Soma=
Modifique os vértices do triângulo deslocando – o em qualquer
posição. Observe o valor de S. Isso confirma a propriedade que
a soma dos ângulos internos de qualquer triângulo na geometria
euclidiana é 180º.
ATIVIDADE 02 - CONSTRUÇÃO DE TRIÂNGULOS DE ACORDO COM OS
LADOS
TRIÂNGULO EQUILÁTERO – Seja
segmentos iguais, ou seja,
apresenta
a
medida
dos
Exemplo1:
a) Construir um triângulo equilátero cuja medida dos lados é
igual a 5 cm.
b) Construir um triângulo equilátero cuja medida dos lados é
igual a 2,5 cm.
TRIÂNGULO ISÓSCELES segmentos iguais, ou
, ou
apresenta a medida de dois dos seus
seja, num triângulo
ABC temos que
,...
Exemplo2:
a) Construir um triângulo isósceles cuja medida dos segmentos
e
b)
Construir um
e
triângulo
isósceles
cuja
medida
TRIÂNGULO ESCALENO - apresenta a medida dos
diferentes, ou seja, num triângulo ABC temos que
Exemplo3:
a) Construir
=9cm.
um
triângulo
ABC,
sendo
b) Construir um triângulo ABC, sendo
=6cm,
=18cm,
segmentos
seus
lados
.
=12cm,
=3cm, e
e
=2cm.
___________________________________________________________________________
|Geogebra na Sala de Aula| # |www.andreluizifto.xpg.com.br|
Maio 2013
Pág.: 4
(Neste item (b) o que você observou? Foi possível construir o
triângulo?)
ATIVIDADE 03 ESCALENO
E
ISÓSCELES)
DESLIZANTE).
CONSTRUÇÃO DE TRIÂNGULOS (EQUILÁTERO,
UTILIZANDO
OS
SELETORES
(CONTROLE
Com o uso dos seletores (CONTROLE DESLIZANTE) você poderá
criar os triângulos, podendo manipular os seus lados, e assim
classificando-o.
Observe
a
rotina
abaixo
para
construção
do
polígono
(Triângulo).
a)crie três seletores a, b, c (valor mínimo:0 valor máximo 10,
incremento 0,1)
b) crie um ponto na origem;
c) crie um segmento de
comprimento a (seletor)
comprimento
fixo
saindo
ponto
A
e
d) crie duas circunferências dado centro e raio. Para isso(Use
a ferramenta circunferência dados centro e raio), clique no
ponto criado na origem, e quando abrir uma caixa, digite b (b
representa o raio da circunferência). Em seguida, com a
ferramenta (circunferência dados centro e raio) selecionada,
clique no extremo do seguimento obtido do ponto localizado na
origem, e ao abrir a caixa, digite c (representa o raio).
e) Movimente os seletores b ou c para que
você obtenha um
ponto
em
comum
nas
circunferências.
Use
a
ferramenta
interseção para obter o ponto.
f)Use a ferramenta polígono para construir o triângulo com os
vértices: na origem, no extremo seguimento, e
no ponto de
interseção das duas circunferências.
g) insira os ângulos internos no triângulo obtido.
Faça as analogias entre os triângulos obtidos (em relação aos
lados) e com os respectivos ângulos internos.
{Em um triângulo equilátero, isósceles e escaleno o que
observa em relação aos ângulos internos?}
___________________________________________________________________________
|Geogebra na Sala de Aula| # |www.andreluizifto.xpg.com.br|
Maio 2013
Pág.: 5
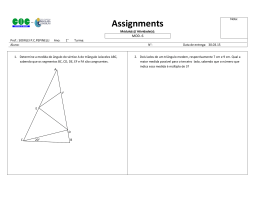
ATIVIDADE 4 - EXERCÍCIOS PROPOSTOS
1) Construir um triângulo
ABC dados os comprimentos dos três
lados, sendo AB=4, BC=5, CA=3
2) Construir um triângulo
CA=4, e o ângulo BÂC=30º.
ABC dados dois lados, sendo AB=6,
3) Mostre geometricamente que em qualquer triângulo o lado
maior é menor que a soma dos outros dois lados.
4) Construa um triângulo retângulo de catetos igual 6 unidades
e 3 unidades. Em seguida determine o perímetro, a medida dos
dois ângulos formados entre os catetos e a hipotenusa, e a
área do triângulo.
5)Esboce um triângulo ABC qualquer, sendo que os seus ângulos
internos
,
,
ATIVIDADE 05 – CONSTRUÇÃO DE TRIÂNGULOS SEMELHANTES
Dizemos que dois triângulos são semelhantes se, e somente se,
os ângulos no mesmo posicionamento forem iguais e os lados
correspondentes, proporcionais. Observe:
Se os lados do triângulo ABC são proporcionais aos ângulos
a’b’c’, as dimensões dos segmentos são obtidos multiplicando
por uma razão “k” de proporcionalidade (K>1, ampliação, ou K<1
redução).
Veja um exemplo:
Utilizando o Geogebra, marque três pontos aleatórios, com a
ferramenta polígono, crie um triângulo ABC.
Em seguida trace uma reta paralela ao lado
,e determine os
ângulos formados no triângulo original e do triângulo obtido
após a reta paralela.
Veja um exemplo
___________________________________________________________________________
|Geogebra na Sala de Aula| # |www.andreluizifto.xpg.com.br|
Maio 2013
Pág.: 6
OBS:Os triângulos
ABC ~
*AB é proporcional a AF
AFG
*AC é proporcional a AG
*BC é proporciona a FG
(Teorema de Tales)
SEMELHANÇA DE TRIÂNGULO UTILIZANDO A FERRAMENTA HOMOTETIA DO
GEOEGEBRA
a) Construa o triângulo
ABC, usando a ferramenta “Polígono”.
b) Marque um ponto W fora do triângulo e logo após, crie retas
que passe por um dos vértices do triângulo e por este ponto W.
c) Na ferramenta (janela 7), clique na opção “Homotetia1 de um
ponto por um fator”. Com esta opção ativada, clique no
interior do triângulo para selecioná-lo e logo em seguida no
ponto W. Observe que a caixa de homotetia se abrirá pedindo o
fator de ampliação (fator maior do que 1) ou redução (fator
menor do que 1). Digite nesta caixa o número 1.5 e mande
aplicar. Um novo triângulo surgirá a partir do triângulo
ABC
e será chamado de A’B’C’.(Você poderá criar um seletor para o
ampliar/reduzir observando os ângulos e a proporção dos lados)
d) Verifique se a razão de semelhança entre os dois triângulos
é igual a 1,5. Para isso, efetue a divisão das medidas dos
lados
do
triângulo
A’B’C’
pelas
medidas
dos
lados
correspondentes do triângulo
ABC. Por exemplo, no campo de
entrada, digite b’/b, que representa o quociente da divisão
das medidas dos lados A’C’ e AC. Depois obtenha os quocientes
a’/a e c’/c.
e)Marque os ângulos dos triângulos, ABC e A’B’C’, e observe
que os ângulos correspondentes são congruentes.
1
Duas figuras homotéticas possuem a mesma forma e seus lados correspondentes (homólogos) são paralelos dois a dois .
Embora as figuras possuam a mesma forma , seus lados não possuem necessariamente a mesma medida , mas, como houve
uma redução ou ampliação numa mesma razão , eles são proporcionais
___________________________________________________________________________
|Geogebra na Sala de Aula| # |www.andreluizifto.xpg.com.br|
Maio 2013
Pág.: 7
Exemplo1: Utilizando o software Geogebra, crie um triângulo
ABC qualquer e em seguida obtenha outro triângulo semelhante
ao ABC, com razão de proporcionalidade igual a K, variando de
-5 até 5. Verifique a razão de proporcionalidade entre os
segmentos correspondentes e também determine os ângulos
internos.
FIGURA ANIMADA
ROSETA
Siga as instruções para construção da figura (“roseta”)
animada, a partir de polígonos.[A sequência apresentada poderá
variar, de acordo com a manipulação dos seus polígonos
conforme interesse].{...as figuras a seguir
representa as
sequências, não contínuas, da roseta obtida por rotação de
polígonos}.
...
Rotina
1) criar o seletor “ n” {min:2
Max:30}
2) Entada alfa: 360/n
3) Criar dois pontos A(0,0) e B(1,0)
4) Criar um circulo de centro A e borda em B
5) Rotação entorno de um ponto B e em A, e caixa digite alfa
6) segmento de A ate B’
7) Bissetriz de B, A, B’
8) Ponto de intersecção de bissetriz com a circunferência
9) fazer dois pontos aleatório em casa segmento AB’, AC, AB
10) Fazer polígono, BED, GBJ, AFHI
11)L_1={pol1,pol2,pol3}
12) L_2=sequência[Girar[L_1,K*alfa],k,1,n]
13) fazer a formatação de seu gosto
___________________________________________________________________________
|Geogebra na Sala de Aula| # |www.andreluizifto.xpg.com.br|
Maio 2013