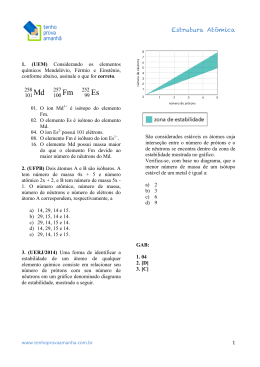
Cálculo das Propriedades Macroscópicas de uma Célula
Combustível
Renata Amaral da Silva e Rubens Souza dos Santos
INSTITUTO DE ENGENHARIA NUCLEAR – IEN
INTRODUÇÃO
OBJETIVO
O núcleo de um reator nuclear é um
arranjo
geométrico
espacial
para
sustentar reações nucleares envolvendo
nêutrons. Um tipo dessas reações seria
a fissão nuclear que ocorre quando um
nêutron, após interagir com um
material, vem a ser absorvido e logo
depois se transformando em dois outros
núcleos menores gerando de dois a três
nêutrons. Outro tipo de reação nuclear
é a transmutação, que pode ocorrer
quando um nêutron, em uma interação
com um núcleo, é absorvido vindo a se
transformar em outro nuclídeo. Um
fator importante a ser determinado é o
fluxo de nêutrons. O fluxo de nêutrons é
influenciado pela iteração dos nêutrons
com materiais no reator com energia
dos nêutrons. No caso dos PWRs, os
chamados reatores térmicos, devemos
considerar dois efeitos importantes,
tanto do ponto de vista da operação
quanto para o transiente. São eles os
efeitos: temperatura no combustível
(Efeito
Doppler),
e
de
densidade/temperatura no moderador.
Um modelo usual para tratar da
distribuição de nêutrons no reator é
baseado
na
Teoria
da
Difusão
Multigrupo, onde a energia total é
discretizada em g grupos de energia.
Em qualquer situação de sua aplicação,
seja para problemas estáticos ou
problemas
transitórios,
devemos
considerar os parâmetros macroscópicos
que dão forma ao conjunto de essas
equações
que
descrevem
o
comportamento dos nêutrons, em
função
das
suas
constantes
macroscópicas (seções de choque de
captura, fissão, coeficiente de difusão,
etc.)
A maioria dos códigos computacionais
de transientes corrige os parâmetros
macroscópicos a partir de uma busca
em
tabelas
previamente
geradas
considerando valores estáticos, i.e.,
para cada estado de densidade e
temperaturas
dos
materiais,
são
calculados esses parâmetros e alocados
em tabelas. O objetivo desse trabalho é
desenvolver uma sub-rotina para ser
incorporada num código computacional
em
desenvolvimento
no
SETER/DIRE/IEN, para cálculos de
transientes em núcleos de reatores, de
maneiras a corrigir as propriedades
durante os transientes.
METODOLOGIA
Conhecendo
os
parâmetros
macroscópicos gerados por um código
considerado exato, por exemplo, o
código HAMMER [1], no estacionário
v
PEg (r ,0) , e calculando esses mesmos
parâmetros por um modelo aproximado
v
v
PAg (r ,0) , definimos parâmetros Fg (r ) ,
espacialmente
distribuídos,
que
preservam as dependências no espectro
de energia dos nêutrons, dados por:
r
PEg (r ,0)
r
Fg (r ) =
r
PAg (r ,0)
(1)
de tal forma que durante o transiente,
os
parâmetros
macroscópicos
são
corrigidos internamente como:
r
r
r
PEg (r , t ) = Fg (r ) PAg (r , t ) .
Uma célula típica de
mostrada na Figura 1,
111
um
(2)
PWR
é
aproveitadas do código HAMMER [1]. A
Tabela 1 mostra alguns resultados. Já a
Tabela 2 mostra os resultados dados
por HAMMER, para um típico PWR de
mesmo enriquecimento.
Vcl
Vf
Vgap
Tabela 1: Cálculo aproximado de constantes, Eq.3.
Figura.1. Célula de PWR
Na figura, V f representa o volume da
região combustível, Vcl revestimento e
Vl o
moderador/refrigerante,
Pg(f )+Pg(cl)⋅(Vcl /Vf )+Pg(l)⋅(Vl /Vf )⋅ζ
1+Vcl /Vf +(Vl /Vf )⋅ζ
νΣ fg (cm −1 )
D g (cm)
1
2
3
4
0.9368E-2
0.2028E-2
0.4957E-2
0.1930E-1
0.2327E-1
0.4892E-4
0.7063E-4
0.1851E-3
1.9570
0.9011
0.6914
0.4655
g
Σ ag (cm −1 )
νΣ fg (cm −1 )
D g (cm)
1
2
3
4
0.4214E-2
0.2353E-2
0.2583E-1
0.8638E-1
0.8383E-2
0.8157E-3
0.1143E-1
0.1433E00
2.3005
1.1619
0.9087
0.3759
Notamos que os valores dos coeficientes
de
difusão
poderia
indicar
uma
aproximação
razoável,
pela
aproximação dada por Eq. 1. No
entanto, há uma brutal divergência nas
seções
de
choques
de
fissão,
principalmente nos grupos de baixa
energia.
CONCLUSÕES
3),
onde, Pg ( f ) , Pg (cl) e Pg (l) representam
os parâmetros nas regiões da célula. No
caso das seções de choques, esse
parâmetro toma a forma:
Pg = Σ g = Nσ g ,
Σ ag (cm −1 )
Tabela 2: Cálculos de constantes com HAMMER.
ζ um
parâmetro que depende da razão dos
fluxos térmicos no moderador e
combustível.
Tendo isto em mente, os parâmetros
macroscópicos da célula, para cada
grupo g de energia é dado por:
)=
Pg(célula
g
(4)
Os resultados preliminares indicam que
o modelo pode funcionar para algumas
constantes,
mas
necessita
um
levantamento
minucioso
das
aproximações aqui propostas, para
implementações num código de cinética
de reatores, para cálculo de transientes.
N
onde N = ρ A representa a densidade
M
isotópica, sendo ρ densidade e M peso
atômico/molecular do material, e N A o
número de Avogadro, 6.02 x10 23 átomos
ou moléculas/mol/cc.
RESULTADOS
REFERÊNCIAS BIBLIOGRÁFICAS
[1]
Barhen, J. et al., 1978. The
HAMMER Code System. Technion, EPRINP-565.
[2]
Yiftah, S. et al., Fast Reactor
Cross Sections, Study Leading to 16
Group Set.
APOIO FINANCEIRO AO PROJETO
Um programa em linguagem FORTRAN
foi desenvolvido para cálculo das
propriedades
dadas
pela
Eq.
3,
programa PRECIN. Tomou-se por base
uma típica célula combustível de um
PWR a 2.68% de enriquecimento. O
fator ς foi assumido como 1. A
colapsação em quatro grupos de energia
foi obtidas a partir de uma tabela de 16
grupos finos da referência [2]. As
constantes
do
hidrogênio
foram
Este projeto tem o apoio financeiro da
Comissão Nacional de Energia Nuclear
(CNEN).
112