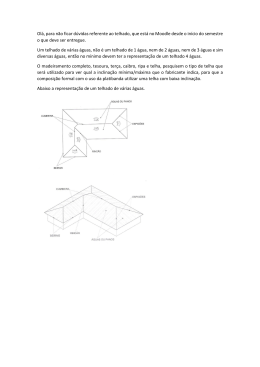
FUNDAÇÃO UNIVERSIDADE FEDERAL DE RONDÔNIA – UNIR
DEPARTAMENTO DE MATEMÁTICA E ESTATÍSTICA – DME
CAMPUS DE JI-PARANÁ
ELIHEBERT SARAIVA
A MATEMÁTICA NA CONSTRUCÃO CIVIL SOB A ÓTICA DOS
CONSTRUTORES
Ji-Paraná
2012
FUNDAÇÃO UNIVERSIDADE FEDERAL DE RONDÔNIA – UNIR
DEPARTAMENTO DE MATEMÁTICA E ESTATÍSTICA – DME
CAMPUS DE JI-PARANÁ
ELIHEBERT SARAIVA
A MATEMÁTICA NA CONSTRUÇÃO CIVIL SOB A ÓTICA DOS
CONSTRUTORES
Trabalho de Conclusão de Curso submetido ao
Departamento de Matemática e Estatística, da
Universidade Federal de Rondônia, Campus de
Ji-Paraná, como parte dos requisitos para
obtenção
do
título
de
Licenciado
em
Matemática, sob a orientação do professor Ms.
Reginaldo Tudeia dos Santos e coorientação da
professora Ms. Ana Lúcia Denardin da Rosa.
Ji-Paraná
2012
2
ELIHEBERT SARAIVA
A MATEMÁTICA NA CONTRUÇÃO CIVIL SOB A ÓTICA DOS CONSTRUTORES
Este Trabalho de Conclusão de Curso foi julgado adequado como parte dos requisitos para a
obtenção do título de Licenciado em Matemática e teve o parecer final como Aprovado no dia
20/12/12 pelo Departamento de Matemática e Estatística, da Universidade Federal de
Rondônia, Campus de Ji-Paraná.
Banca Examinadora
_______________________________________________
Msc. Reginaldo Tudeia dos Santos - Orientador
Universidade Federal de Rondônia – Campus de Ji-Paraná
_______________________________________________
Msc. Ana Lucia Denardin da Rosa- Coorientadora
Universidade Federal de Rondônia – Campus de Ji-Paraná
__________________________________________
Msc. Marlos Gomes de Albuquerque – Universidade Federal de Rondônia
___________________________________________
Msc. Kécio Gonçalves Leite – Universidade Federal de Rondônia
3
AGRADECIMENTOS
Agradeço, primeiramente, a Deus por ter conseguido chegar até aqui;
Em seguida, aos meus pais Arlindo Saraiva Nogueira e Elizabeth Saraiva Rodrigues por
todo o apoio desde os primeiros passos dados em direção ao estudo;
À minha Esposa Franciele Dallabrida pelo apoio e dedicação em todo o curso e,
especialmente, na conclusão deste trabalho, aos meus Irmãos Alasson Saraiva, Alípio
Saraiva e Elawan Saraiva que, a todo tempo, criaram um ambiente de estímulo ao
conhecimento de modo que não o fazíamos em busca de profissão, e, sim, pela busca de
conhecimento;
A todos os professores desta Universidade que contribuíram de algum modo para minha
formação inicial e, em especial, ao Professor Marcos Leandro Ohse, que pôde me mostrar
em pouco tempo de convívio a responsabilidade que temos com a educação do outro, quando
nos é dado o título de professor. Aos professores coordenadores do programa PIBID Marlos
Gomes de Albuquerque e Emerson da Silva Ribeiro, que me proporcionaram uma visão
crítica sobre as práticas e as tendências que norteiam esta honrada profissão;
Aos Professores: orientador Reginaldo Tudeia dos Santos, coorientadora Ana Lúcia
Denardin da Rosa e Luiz Aberto Nogueira pela paciência e perseverança ao me ajudar
nesta difícil tarefa e a todos que contribuíram para esta pesquisa;
A todos os meus amigos que, nestes quatro anos, me aguentaram com toda a chatice que
tenho.
4
SUMÁRIO
página
Resumo .......................................................................................................................................5
Introdução ..................................................................................................................................6
1 Etnomatemática ......................................................................................................................7
1.1 – Considerações sobre Etnomatemática ............................................................8
1.2 – A Etnomatemática como fonte de pesquisa no mundo da construção civil....9
2 Metodologia da pesquisa ....................................................................................................10
3 Pesquisa de campo..............................................................................................................13
3.1 - Ponderações sobre a pesquisa de campo ..................................................................13
3.2 – Técnica de esquadrejar ............................................................................................14
3.3 – Contagem de tijolos na obra ....................................................................................19
3.4 – Cálculo de área para assentar piso e cerâmica .........................................................20
3.5 – Inclinações do telhado .............................................................................................21
3.5.1
Interpretação matemática do problema da inclinação do
telhado..............................................................................................23
3.6 – Colocação de poste ..................................................................................................25
Considerações Finais .............................................................................................................................28
Referências .............................................................................................................................................30
Bibliografias Consultadas ......................................................................................................................31
5
RESUMO
A MATEMÁTICA NA CONTRUÇÃO CIVIL SOB A ÓTICA DOS CONSTRUTORES
Elihebert Saraiva¹
Este trabalho tem por objetivo investigar que tipo de matemática está presente em grupos de
trabalhadores da construção civil. Na pesquisa, foi usado o método de investigação
qualitativo-descritiva e nela constatou-se que a matemática produzida por estes trabalhadores
encontra-se interconectada ao saber/fazer exercido em suas práticas diárias. Constatação esta
observada no âmbito dos estudos embasados pela Etnomatemática, base do referencial teórico
norteador desta pesquisa. A matemática do construtor, não presente em livros didáticos, é
utilizada por ele para tirar o esquadro ou gabarito em uma construção, no cálculo da
quantidade de tijolos, de pisos cerâmicos, na inclinação do telhado e na colocação de um
poste de energia. Este saber matemático é adquirido na prática através de experiências
socioculturais, onde se constrói os conhecimentos matemáticos através de vivências, do seu
modo de compreender o mundo e daquilo que nele acontece.
Palavras-chave: Etnomatemática, Construção Civil, Conhecimento, Grupos Sociais.
¹ SARAIVA, Elihebert. A matemática na construção civi sob a óptica de construtores. 2012. 30f. Monografia
(Licenciatura Plena em Matemática) – Departamento de Matemática e Estatística, Universidade Federal de
Rondônia, Ji-Paraná.
6
INTRODUÇÃO
O presente trabalho tem como objetivo pesquisar e analisar a concepção de
matemática utilizada por profissionais da construção civil, relacionando-a com as fases da
construção de uma obra, bem como o nível de instrução escolar de cada um desses
profissionais em sua prática diária. Destaca-se que o universo humano em estudo restringe-se
a mestres de obra, pedreiros, azulejistas, serventes e encanadores.
Devemos salientar que existem poucos estudos que discutem o tema
Etnomatemática do grupo de profissionais da construção civil. A Etnomatemática é a base
para compreender a matemática nos contextos culturais. Esta ciência, antes considerada de
pouca importância por movimentos que cultuavam a matemática corrente, hoje tem mostrado
sua eficiência em compreender o saber/fazer de grupos sociais que não estão diretamente
ligados à matemática científica.
A escolha desse tema nasceu quando, ao estudar matemática, passei a observar
que vários conceitos de geometria, trigonometria e aritmética estavam presentes na construção
civil, independentemente do grau de complexidade da obra. O interesse em estudar a presença
da matemática empregada na construção foi, ainda, instigado por influência familiar, pois
meus tios são, na sua maioria, trabalhadores da construção civil, onde a matemática
empregada por eles é quase que totalmente desprovida de conceitos estudados em uma sala de
aula. Também tive influência de meu irmão graduando em engenharia sanitária.
Esta pesquisa está estruturada da seguinte forma:
O capítulo I faz uma abordagem sobre Etnomatemática para verificar de que
forma ela está integrada aos conhecimentos matemáticos, em especial na construção civil.
No capítulo II, é relatada a metodologia de pesquisa e apresentados os
procedimentos de coleta e análise de dados.
No capítulo III, fez-se um estudo sobre a matemática utilizada na construção de
uma casa. Fez-se, também, um comparativo entre a matemática formal e a matemática
informal utilizada para resolver os problemas oriundos da construção de alicerces, de paredes,
entre outros.
Por fim, nas considerações finais fez-se uma síntese dos principais aspectos
analisados na pesquisa.
7
1 – ETNOMATEMÁTICA
Etnomatemática é uma palavra formada pela composição das palavras: etno,
matema e tica, que, segundo Duarte (2003, apud D’AMBRÓSIO, 2003, p.15):
Etnomatemática é a arte ou técnica (techné = tica) de explicar, de entender, de se
desempenhar na realidade (matema), dentro de um contexto cultural próprio (etno)”.
Nesta perspectiva, a Etnomatemática procura resgatar, analisar e valorizar o saber e
o fazer matemático produzido em diferentes contextos culturais, os quais não se
referem unicamente a grupos étnicos.
No Brasil, tem-se como propulsor destas ideias o matemático Ubiratan
D’Ambrósio, que considerou duas vertentes de conhecimento matemático: a primeira, a
matemática divulgada no meio acadêmico; e a segunda, a matemática de grupos, para os quais
não se havia uma corrente que a anunciava para o mundo.
Estas duas correntes em estudos etnomatemáticos são de igual teor e importância,
visto que trabalham com o propósito do conhecimento particular de um grupo. Entretanto, a
primeira é enaltecida e respaldada pelo mundo globalizado enquanto a segunda é inferiorizada
e pouco divulgada, como descreve Duarte (2003, p.18):
Neste sentido, ocorre, por parte da Etnomatemática e dos Estudos Culturais, a
rejeição do processo que identifica cultura com “alta cultura”; uma identificação,
obviamente, proposta pelos grupos hegemônicos. As teorizações realizadas por estes
campos procuram não somente “borrar” as fronteiras entre “alta” e “baixa” cultura,
que propiciam a marginalização dos grupos subordinados, mas analisar as relações
de poder que as instituem.
No entanto, a Etnomatemática deve ser interpretada como ferramenta disciplinar e
moderadora para o aprofundamento dos saberes que estão intimamente ligados à cultura e ao
conhecimento, conforme Duarte (2003, apud KNIJNIK, 1999 , p.17) relata:
Portanto esta concepção de Etnomatemática compreende a articulação entre saberes
populares e acadêmicos. Não se trata de glorificar ou exorcizar os saberes populares,
nem tampouco tomá-los como ponto de partida para aquisição dos saberes
acadêmicos, pois isto significaria supor que aqueles são inferiores e que serviriam
somente como origem para aquisição do “verdadeiro” conhecimento matemático, o
acadêmico.
Uma vez que os caminhos da matemática seguem tendências cujo pressuposto
está na universalização, teme-se que aconteça com a cultura matemática aquilo que Duarte
8
(2003, apud SANTOS, 1996, p.20) denominou “epistemicídio”, ou seja, “o extermínio de
formas subordinadas de conhecer” (SILVA, 1998, p. 196). Conclui ainda que a matemática de
hoje marginaliza e silencia as vozes das chamadas “minorias”.
Com as considerações sobre a proposta da Etnomatemática, é possível dizer que o
pensamento matemático feito por diferentes grupos sociais, enquanto fonte de conhecimento,
pode ser estudado pela Etnomatemática.
1.1 – CONSIDERAÇÕES SOBRE ETNOMATEMÁTICA
Na formação matemática do indivíduo, a Etnomatemática foi inicialmente
proposta para atender às necessidades de resgatar e reconhecer o conhecimento de educação
matemática, tomando como base aquilo que ele traz consigo no saber/fazer diário, pois, ao
socializar-nos com outros indivíduos da mesma espécie, estabelecemos relações cognitivas de
aprendizagem que caracteriza e distingue o homem dos demais animais.
Para relatar a dimensão educacional da Etnomatemática, D’Ambrósio (2001, p.43)
explica porque é importante retomar o estudo do saber/fazer do indivíduo: Não se trata de
ignorar nem rejeitar conhecimento e comportamento modernos. Mas, sim, aprimorá-los,
incorporando a ele valores de humanidade, sintetizados numa ética de respeito,
solidariedade e cooperação.
Para o autor, devemos estruturar a ciência concedendo valores humanísticos, pois,
com a modernidade, a matemática tende a ser universalizada e termina por excluir laços
matemáticos relacionados à cultura do indivíduo.
Isto significa que o conhecimento sistematizado, também dito científico, não é o
único meio válido para se produzir o saber. A informação dita científica estará
ininterruptamente ligada ao conhecimento popular de saber/fazer, como enuncia Marconi
(2010, p.58) ao explicar a correlação entre conhecimento popular e conhecimento científico:
O conhecimento vulgar ou popular, às vezes denominado senso comum, não se
distingue do conhecimento científico nem pela veracidade nem pela natureza do
objeto conhecido: o que os diferencia é a forma, o modo ou o método e os
instrumentos do “conhecer”.
A colocação de Marconi retoma preceitos também defendidos por D’Ambrósio
quando nos referimos à intrínseca relação do conhecimento popular às suas práticas
mencionadas neste trabalho como saber/fazer, pois o conhecimento popular tem partido da
prática do ser humano em seus diversos campos de atuação.
9
1.2 – O MUNDO DA CONSTRUÇÃO CIVIL COMO FONTE DE PESQUISA EM
ETNOMATEMÁTICA
A Etnomatemática é um campo de pesquisa com várias vertentes de estudo. Uma
delas é a investigação das práticas da construção civil, onde, até o momento, poucos
pesquisadores se propuseram a investigar seus costumes e suas culturas no que concernem às
práticas matemáticas.
Paulatinamente, pesquisa-se a dimensão histórica e política deste tema por
abranger as práticas que ocorrem em todos os lugares onde existe civilização humana. Em
especial, a matemática de grupos deve ser de interesse da educação matemática, campo que
pode contribuir para o norteamento das dimensões culturais propostas pela matemática.
No contexto da construção civil, a formação da base de seu grupo de profissionais
acontece nos canteiros de obra, ou seja, a maioria destes trabalhadores se qualifica com a
prática, sendo que geralmente passam ao largo por quaisquer cursos específicos de
qualificação. Nesse universo, a aprendizagem é passada de pai para filho, de amigo para
amigo, etc.
Esta pesquisa procurou suportes através da Etnomatemática para compreender a
aplicação dos conceitos matemáticos empregados por tais trabalhadores no âmbito da
construção civil, além de fazer um paralelo entre a matemática formal e a matemática
praticada por esses profissionais.
10
2- METODOLOGIA DA PESQUISA
A abordagem feita nesta pesquisa é do tipo qualitativo-descritiva que, segundo
Marconi (2010, p. 170), consiste em investigações de pesquisas empíricas cuja principal
finalidade é o delineamento ou análise das características de fatos ou fenômenos (...)
utilizando várias técnicas como entrevistas, questionários, formulários, etc. Além de
Marconi, Pena (2012) diz que a abordagem qualitativo-descritiva incide em investigar as
características de fatos ou fenômenos da natureza para a obtenção de dados descritivos,
mediante contato direto e interativo do pesquisador com a situação do objeto de estudo. Além
disso, seu foco de interesse é amplo e não busca enumerar ou medir eventos, bem como não
requer o uso de métodos e técnicas estatísticas.
A presente pesquisa discute a forma matemática utilizada por trabalhadores da
construção civil em sua prática diária. Para isso, os dados foram obtidos por intermédio de
observações no decorrer das atividades desenvolvidas por profissionais da construção civil,
além de entrevista não estruturada. Andrade (1999, apud MARCONI 1990, p. 85) diz que:
Entrevista despadronizada ou não estruturada. Consiste em uma conversação
informal, que pode ser alimentada por perguntas abertas, proporcionando maior
liberdade para o informante. Ainda, no contexto das perguntas não estruturadas
procederemos de forma que a autora descreve como entrevista não dirigida que se
resume em o informante ou entrevistado tem total liberdade para relatar sobre
experiências e opiniões.
Esta opção metodológica foi escolhida por melhor se enquadrar no campo de
pesquisa em Etnomatemática e também por cobrar do pesquisador os menores custos em
recursos financeiros.
Dessa maneira, a fundamentação deste trabalho apoiou-se em autores como:
Andrade (1999), Borges (2009), Salgado (2009), Bicudo (2003), D’Ambrósio (2001), Duarte
(2003) e Marconi (2010). No que concerne ao método de investigação, optou-se pela
abordagem da pesquisa qualitativa, fundamentado em entrevista despadronizada com
trabalhadores da construção civil no município de Ji-Paraná.
Segundo Andrade (1999, p. 134), para a coleta de dados deve-se elaborar um
plano que especifique os pontos de pesquisa e os critérios para a seleção dos possíveis
entrevistados e dos informantes que responderão aos questionários ou formulários. Com
propósitos baseados em Andrade, buscou-se preparar um plano de pesquisa para coleta de
dados, por meio de questionário despadronizado, no qual foi necessário considerar a obra, ou
11
seja, se nela existia construtores que correspondessem aos aspectos abordados nesta
investigação. Em seguida, buscou-se evidenciar a prática do profissional e, por fim, enquadrálo entre uma das classes operárias relatada na pesquisa.
Para entrevistar os construtores, buscou-se, além de evidenciar o perfil dos
trabalhadores, elencar os principais tópicos da matemática empregados na construção civil,
tais como: aritmética, geometria e trigonometria, pois já se antecipava que, na coleta dos
dados, estes tópicos encontrar-se-iam interconectados ao raciocínio e à prática do entrevistado
de modo não sistematizado.
No decorrer da coleta de informações, obtidas por meio de entrevistas
despadronizadas, na pesquisa de campo, fizemos as seguintes análises: observamos, na prática
do construtor, quais dos seus afazeres evidenciavam o envolvimento direto da matemática,
além de analisarmos de que forma seu pensamento matemático interfere em suas atividades
cotidianas.
1ª Etapa – Análise dos afazeres que envolvem o uso da matemática
Para esta etapa, os procedimentos executados na pesquisa buscou-se evidenciar o
uso da matemática de profissionais da construção civil em seu fazer diário. Para a análise das
informações obtidas na pesquisa de campo, procedeu-se da seguinte forma:
 Examinou-se a forma de trabalho efetuado na obra: fundações, alvenaria,
pilares, telhado, etc.;
 Verificou-se a utilização de algumas ferramentas utilizadas e a relação destas
na forma de raciocínio matemático utilizado pelo construtor;
 Analisaram-se quais conteúdos matemáticos eram utilizados pelos construtores
no emprego de seus trabalhos.
2ª Etapa – Análise do saber/fazer dos construtores entrevistados
Para a análise das informações que evidenciasse, por parte dos construtores, o
modo de pensar (matematicamente) na sua prática, procedeu-se da seguinte forma:
 Analisou-se a forma de como é concebida a matemática por esses profissionais;
 Tomou-se, para efeito de estudo, a estrutura de raciocínio usada pelos
construtores;
 Demonstrou-se, além da forma matemática de pensar do construtor, o
desenvolvimento em termos de matemática científica de seus saberes.
12
Com a aplicação desta metodologia, pretendeu-se entender de que forma a
matemática é utilizada neste complexo espaço social. Duarte (2003, p.38) denomina este
espaço de “mundo da construção civil” e explica:
A última dimensão do “mundo da construção civil” que apresento diz respeito às
habilidades desenvolvidas pelos trabalhadores para solucionar situações-problema
que ocorriam nos canteiros-de-obra. Estas habilidades eram estimuladas ora pela
precarização dos instrumentos disponíveis para a execução das tarefas, ora pela
ausência de saberes escolares.
As habilidades mencionadas por Duarte é o tripé deste trabalho, pois, à medida
que os construtores desenvolvem-nas, a matemática é a principal ferramenta na resolução dos
problemas de suas práticas diárias, de modo que algumas formas matemáticas se encontram
fora do conhecimento científico.
13
3- PESQUISA DE CAMPO
3.1– PONDERAÇÕES SOBRE A PESQUISA DE CAMPO
Sabe-se que a matemática surgiu da necessidade humana de contar, de fazer trocas
comerciais, de transformação de seu espaço, etc. Desde a antiguidade até os dias de hoje, a
matemática evolui constantemente e, paralela à evolução, está presente na arte da construção
civil, que também evolui e lança mão de muitos recursos da matemática como ferramenta.
Onde há sociedade, há também construções e relação direta de conceitos
matemáticos estabelecidos entre os trabalhadores e suas obras. Quando se discorre sobre
construções erguidas com o saber/fazer de um profissional pouco embasado em teorias
matemáticas, tem-se a ideia de que se trata de obras com pouco respaldo. Entretanto, ao
contrário do que se julga, este mesmo profissional constrói obras de impecáveis detalhes e
formas matemáticas precisas.
Os profissionais da construção civil trazem consigo uma bagagem de noções
informais sobre numeração, medida, espaço e forma, construída em sua vivência cotidiana.
Essas noções nem sempre estão ligadas diretamente aos conhecimentos adquiridos nas
escolas, mesmo que de forma elementar. O saber matemático utilizado por estes profissionais
é correspondente às suas experiências e acontece nas práticas socioculturais, onde se constrói
os conhecimentos matemáticos através de vivências, do seu modo de compreender o mundo e
daquilo que nele acontece.
É nas situações reais destes profissionais que é possível perceber suas habilidades
ao realizar cálculos matemáticos. Essa pesquisa buscou identificar alguns modelos
matemáticos utilizados na construção civil para resolver situações-problema ali apresentados.
Além disso, procurou-se conhecer o saber/fazer utilizado e desenvolvido por pedreiros e
carpinteiros no seu trabalho nas construções, com seu modo empírico de raciocinar.
Em relação aos conhecimentos matemáticos apresentados pelos profissionais
envolvidos neste trabalho, foi possível identificar o uso de alguns conteúdos, tais como:
geometria, trigonometria e aritmética. É notável como, ainda nos dias de hoje, esses
trabalhadores, em sua maioria, possuem baixa escolaridade, ou sequer frequentaram uma
14
escola formal. Porém, possuem grande aporte e domínio no trabalho devido à experiência
obtida através de longo tempo de serviço.
Quadro 1: Construtores entrevistados que constam na pesquisa
Nome
Profissão
Escolaridade
Idade
Tempo de
Experiências profissionais
Serviço
não ligadas à construção
civil
Construtor Pedreiro
A
33 anos
Nenhuma experiência
27 anos
Nenhuma experiência
19 anos
Nenhuma experiência
Primária
Construtor Pedreiro
B
Quinta Série 41
Primária
Construtor Pedreiro
C
Quinta Série 52
Quinta Série 33
Primária
Na pesquisa, foram entrevistados alguns construtores no que concerne à
escolaridade, idade, tempo de serviço e experiência profissional fora do âmbito da construção
civil, a fim de poder traçar um perfil que indicasse se seu modo de raciocinar teria sofrido
ações relacionadas apenas ao seu meio profissional, ou se teria tido influências de outras áreas
do saber.
3.2 – TÉCNICA DE ESQUADREJAR
Para construir uma casa é preciso, inicialmente, fazer o alicerce. Segundo Borges,
(2009, p.50), “A parte de uma construção que recebe o seu peso e o transfere para o solo
chama-se fundação (alicerce). É a primeira etapa da construção a ser executada e é o pé da
edificação”. De posse da planta da casa, o próximo passo é fazer as medições do terreno,
delimitar o espaço onde que será construída, esquadrejar, tirar o nível, entre outros. Esta
pesquisa buscou entender como é possível fazer alguns tipos de medições tão precisas em
terrenos que, a priori, não estabelece nenhum referencial para que fossem feitas tais medidas.
Ao observar esta prática, foi possível perceber que o carpinteiro usa referências
que lhe servem de parâmetro para, por exemplo, esquadrejar a região a ser construída. O
nome esquadrejar se refere ao uso da ferramenta esquadro, mas que também pode ser
conhecido por outros construtores como gabarito ou marcação da obra.
Ao acompanhar um construtor nas fundações de uma obra feita pelo que o
15
pedreiro denominou de maquete, mostrou-se na prática como realizar o esquadrejamento no
espaço de um terreno a ser construído. Experiência semelhante foi desenvolvida por Duarte
(2003, p.78):
Como sabia que meus informantes, muitas vezes, realizavam algum serviço nos
finais de semana, propus que eles tivessem o número de meu telefone e que, se
fossem “fazer o gabarito”, me avisassem. Foi assim que, em um domingo, recebi o
telefonema de Valmir, convidando-me para observar as marcações de um galpão que
iria construir.
No propósito de obter informações mais detalhadas sobre a prática de esquadrejar,
ao se indagar acerca de quais eram os procedimentos iniciais da obra, o construtor respondeu
o seguinte: “Quando eu vou começar um alicerce, finco uma estaca em um dos pontos onde
será colocada uma das colunas; depois, finco outras duas estacas, formando um triângulo
para fora da área de construção.”. O construtor explicou que, ao final desta etapa, restariam
quatro triângulos, cada um com o vértice de 90º oposto a um dos vértices pertencente ao
quadrilátero formado a partir do esquadrejamento. Ao ser questionado se os triângulos
deveriam ter o mesmo tamanho, ele nos respondeu: “Não, pois o importante é o esquadro.”.
Veja a ilustração dos procedimentos iniciais para a fundação de uma obra na
Figura 1.
Figura 1: Desenho de um esquadrejamento inicial de uma construção
Para esquadrejar uma casa, basta que o ângulo interno, adjacente à parede da
construção do triângulo seja de 90°. Na determinação dessas medidas, a ferramenta utilizada,
16
além de linha e estaca, é um esquadro1, daí o nome esquadrejar.
Para melhor entendimento desse procedimento, foi feito um esboço da figura
geométrica formada pelas marcações do terreno, ao final de todas as marcações e estacas
fincadas.
A Figura 2 ilustra o esquema de um esquadrejamento para uma construção.
60 cm
80 cm
100 cm
Figura 2: Esquema de um esquadrejamento ou gabarito
A terna pitagórica (60 cm, 80 cm, 100 cm), comumente relatada no espaço de
construções civis, que garante ao ângulo a perpendicularidade entre retas, foi encontrada em
uso por este construtor, mas, ao perguntá-lo de onde advém este conhecimento, ele disse: isso
aí é com os engenheiros. Observa-se disto que os conceitos ensinados na escola foram
incorporados à prática deste construtor, mas que, de alguma forma, chega-se a este cotidiano
sem que exista diretamente esta ligação.
Basicamente, parecia ser um processo usado pelo pedreiro para conseguir ângulos
retos, pois estava auxiliado por uma ferramenta que detinha ângulos já estabelecidos pelo
problema. Duarte (2003), em sua dissertação de mestrado, evidenciou a proposição
matemática que, implicitamente, os construtores, de forma geral, usam para garantir que todos
os vértices contenham ângulos retos:
Para garantir que os ângulos do quadrilátero de lados opostos congruentes fossem
efetivamente retos, isto é, que o quadrilátero fosse um retângulo, também observei
um outro procedimento. Este dizia respeito ao fato de ser suficiente produzir
somente um ângulo reto no quadrilátero e assim garantir que os demais ângulos
também tivessem noventa graus.
1
Esquadro: trata-se de uma ferramenta pré-fabricada constituída pela união de duas réguas formando um ângulo
exato de 90°
17
Na observação da entrevista, esta informação - de que não é necessário obter
todos os quatro ângulos retos para garantir que o espaço da obra estava esquadrejado -, foi
repassada e isto confirma as palavras de Duarte (2003), pois, traçadas as linhas que delimitam
o espaço a ser construído, e quando estabelecido um único ângulo reto, temos dois segmentos
de retas que estão fixamente organizados, restando fazer o mesmo processo apenas com o
ângulo oposto a este obtido no quadrilátero, sendo este processo chamado pelo construtor de
“fechar o esquadro”. Dolce e Pompeu (apud Duarte 1990, p 94-95) demonstram,
matematicamente, esta proposição, acerca do qual o pedreiro afirma:
Hipótese: ABCD é paralelogramo
Tese

 
AC


e BD
Demonstração:
D
ABCD é paralelogramo
 
 

 AD // BC  A  B  180º   

A C
 
 

 AB // CD  B C  180º 
Analogamente para
 
BD
D
C

A
C

B
A
B
D

B

C
A
Esta constatação, por meio do teorema, da realidade do construtor é interpretada
da seguinte forma: se, ao formar a região interna da construção, e nela conter um ângulo de
90°, então, isto garante que o ângulo oposto pelo vértice também terá uma abertura angular de
90°. Feito isso, não é necessário que se repita a operação, com o mesmo critério, com os
outros dois ângulos restantes, de modo que economiza tempo para o construtor.
No decorrer da entrevista, o construtor B mostrou que não bastava apenas fazer o
uso da ferramenta, mas que necessitava usá-la corretamente. Segundo ele: “Para uma obra
grande, fica difícil medir, pois um tanto assim de diferença numa obra de 100 metros dá (sic)
2 metros de diferença no final”. Esta diferença “de um tanto assim”, mencionada pelo
pedreiro, refere-se à medida do erro de posicionamento do esquadro em relação às linhas retas
mostradas na figura 3:
18
Figura 3: Demonstração do erro em uma construção
Segundo o pedreiro, esse erro “Dá 2 milímetros num espaço de 1,20 metros,
imagina numa obra de 12 metros daria 20 centímetros” (sic). Em sua fala, é possível
perceber o uso direto de proporcionalidade, pois 0,2 cm está para 1,2 m; então 12 m estará
para 20 cm, que é exatamente correspondente à fala do construtor. A proporcionalidade é um
raciocínio bastante simples usado no cotidiano dos trabalhadores da construção civil. Outra
relação matemática observada, quando se esquadreja, é a ideia de ângulos opostos pelo vértice
e dos ângulos alternos externos. O construtor afirma o seguinte: “O ângulo daqui (de dentro)
é igual o daqui (de fora).”.
O pedreiro explica que o trabalho da maquete se tratava de uma situação
hipotética, pois, no dia-a-dia, deveriam ser levados em consideração outros fatores como
tamanho da obra e nivelamento do terreno.
3.3 – CONTAGEM DE TIJOLOS NA OBRA
Descrevemos uma situação comum em todas as obras de alvenaria visitada. Tratase do cálculo feito pelos pedreiros, de modo geral, para estabelecer, com boa precisão, o
número de tijolos necessários para a construção das paredes de uma casa ou construção
qualquer.
Nas situações onde os profissionais da construção necessitam calcular a
quantidade de tijolos, eles utilizam a relação aprendida com outros pedreiros. Para isso, é
19
preciso conhecer as dimensões do tijolo e a espessura da massa que cada um utiliza entre eles.
Assim, o cálculo é feito efetuando a soma do comprimento das paredes e multiplicando pela
altura, chegando à quantidade de tijolos necessários para construir certo cômodo. Pode-se
perceber que foram trabalhados conceitos matemáticos de aritmética e geometria sem que o
profissional, em muitos casos, jamais tenha frequentado aulas específicas.
Uma das várias maneiras utilizadas pelos pedreiros para calcular a quantidade de
tijolos necessária em uma obra é a seguinte: para cada metro quadrado são necessários, em
média, cinco tijolos de comprimento por sete fileiras – também chamadas de fiadas - de
altura, resultando em um total de 35 tijolos por metro quadrado, conforme ilustra a Figura 4,
com tijolos de dimensões19cm×9cm×14cm.
Figura 4: Contagem dos tijolos na construção civil
Fonte: Trabalho de pós-graduação de Roseli Lima de Oliveira
Importante ressaltar que esta contagem varia conforme as dimensões do tijolo e da
forma que ele será assentado. Entretanto, usualmente, em construções com terrenos planos
onde não requer uma fundação muito elaborada, os tijolos são assentados de forma que a
maior dimensão e a menor formem a área da base do tijolo, restando para a altura do tijolo a
dimensão de medida relativamente proporcional entre as medidas da base.
20
3.4– CÁLCULO DE ÁREA PARA ASSENTAR PISO CERÂMICO
Esta situação retrata a forma utilizada para calcular a quantidade de pisos
cerâmicos que seriam utilizados para cobrir certa superfície. Em todas as construções
visitadas, o procedimento para calcular esta quantidade é o mesmo (ver a Figura 5). Ela ilustra
que os construtores fazem o produto do comprimento pela largura do ambiente, para conhecer
a quantidade de metros quadrados de piso necessários para recobrir tal superfície. No caso em
questão, seriam necessários 36m² de piso.
Figura 5: Demonstração de cálculo de área
Fonte: Trabalho de conclusão de curso de Claydaiane Ferraz Andrade
Nesta figura, têm-se 36 quadrados de um metro cada um, isto é, toda esta região
medindo 6 x 6 foi dividada em quadrados, obtendo no total 36 quadrados.
Com base na ilustração, percebe-se que esta forma de calcular a área de uma
superfície se universaliza à medida que os materiais utilizados são vendidos, utilizando a
forma do metro quadrado como unidade de medida. Apesar de a maioria dos pisos disponíveis
para venda no mercado hoje serem vendidos nas dimensões 40cm por 40cm e 40cm por
21
30cm, eles vêm em caixas, indicando a quantidade de piso em metros quadrados, sendo esse o
motivo da forma de calcular a quantidade de pisos necessários para cobrir determinada
superfície.
3.5– INCLINAÇÕES DO TELHADO
A matemática empregada por pedreiros e carpinteiros na construção de um
telhado utiliza-se de muitos dos conceitos fundamentais da matemática formal, como, por
exemplo, elementos básicos de trigonometria para determinação do seu ângulo de inclinação.
Para resolver um problema desta ordem, o pedreiro faz uso de recursos simples, que, em
linguagem matemática, revelam a mesma proposição usada por um matemático na resolução
do problema de inclinação de uma reta, por exemplo.
Os pedreiros que trabalham em pequenas obras - e neste caso a variação do
tamanho do telhado não é levada em consideração - utilizam aquilo que eles denominam de
desconto. Isto significa que um “desconto de 20%” equivale dizer que, para cada metro de
base do telhado, tomam-se vinte centímetros de altura, resultando no que se chama de caída
do telhado, de modo que, para esta inclinação, se obterá uma tangente de 0,2 e/ou uma
abertura angular de aproximadamente 11º 18’ graus sobre o ângulo do marco zero.
Segundo o construtor, o modo da linguagem é bastante corrente entre os
construtores, e esta inclinação é frequentemente usada para evitar que uma casa molhe por
dentro em tempos de chuva. Talvez esta referência o auxiliasse na construção do telhado. Dos
construtores entrevistados, notou-se que esta prática do desconto predomina porque eles
desconhecem elementos básicos de trigonometria.
Após observação, por vários dias, da construção de um telhado por um senhor que
trabalha em construções há muitos anos, ao ser indagado sobre “qual matemática” ele usava
para fazer a caída (inclinação) do telhado de um apartamento popularmente conhecido como
meia água, o construtor A, iniciou a fala denominando a inclinação do telhado como sendo o
“desconto”. Depois de interrogado de que forma procedia para calcular a inclinação do
telhado, ele respondeu: “Eu faço o seguinte: tiro a medida da base da casa, depois tiro a
altura final do telhado. Então, para saber qual o desconto que tenho no telhado, divido a
altura final pelo tamanho da base e multiplico por 100. Aí tenho o desconto do telhado”.
22
Para mostrar a validade de sua argumentação, ele destacou que este procedimento
vale para qualquer ponto em que se faça essa forma de medição: “O desconto vai ser sempre o
mesmo”. Complementando as informações, ele comentou a respeito do chamado “marco
zero” (Figura 6), certa forma de orientação usada por ele para determinar a inclinação ideal do
telhado.
Figura 6: Modelo do telhado descrito no texto
Observe que, em suas descrições, o construtor, em nenhum momento, mencionou
usar a ideia de triângulos, ângulos ou trigonometria básica. O senhor descrito no trabalho
cursou apenas o ensino fundamental e, segundo seu depoimento, não faz ideia do que se trata
a trigonometria, levando-nos a crer que ele desconhece princípios básicos de trigonometria.
3.5.1– INTERPRETAÇÃO MATEMÁTICA DO PROBLEMA DA INCLINAÇÃO DO
TELHADO
Para melhor compreensão do problema, serão utilizadas incógnitas para as
informações descritas pelo pedreiro. Para a inclinação, ou desconto, como mencionado pelo
pedreiro, será utilizado I, a base será representada por b e a altura por h.
Segundo o pedreiro, o desconto é dado pela equação:
23
(1)
Borges (2010) destaca: os caimentos nos telhados são medidos por porcentagem
de rampa, isto é, a relação entre as distâncias vertical e horizontal expressa em porcentagem.
(P.151). Porém, se observarmos a Figura 6 do triângulo retângulo, percebe-se que a altura (h)
é o cateto oposto e a base (b) é o cateto adjacente do ângulo agudo descrito pelo pedreiro
como sendo o marco zero do telhado.
Em trigonometria, a tangente de um ângulo agudo (tg(α)), no triângulo retângulo,
é dada pela razão entre o cateto oposto (C.O) e o cateto adjacente (C.A) cuja equação é tg(α)=
C.O/C.A. A tangente indica a inclinação do telhado, logo,
( )
que levada na equação (1):
(2)
Traduzindo para a matemática formal, o raciocínio descrito pelo pedreiro quanto à
inclinação do telhado pode ser descrito como sendo o produto entre a tangente do ângulo
obtido no marco zero e 100. Isto instigou a representação na forma das equações (1) e (2),
pois descrever a inclinação de uma reta (telhado) é o mesmo que encontrar a tangente do
ângulo no marco zero do telhado.
Vale destacar que a pouca vivência do pedreiro em relação a cálculos matemáticos
utilizados em sala de aula pode ser a causa da argumentação utilizada em palavras como:
“desconto vezes 100” e “tantos por cento”. Isso pode ser devido às possíveis dificuldades em
trabalhar com frações.
Analisando a linguagem do pedreiro, é possível perceber a carga de influência que
recebeu de outros pedreiros em sua prática diária, o que de certa forma explica sua
argumentação do problema da inclinação do telhado.
Em linguagem matemática, o marco zero pode ser interpretado como sendo o
ângulo compreendido entre o cateto adjacente (base do telhado) e a hipotenusa (parte superior
do telhado). Em sua modelagem, o pedreiro não estabelece nenhuma relação com a noção de
ângulo interno formado com a base e a parte superior do telhado, mas o faz indiretamente,
mesmo que não saiba.
Após demonstrar a funcionalidade de seu método de modelar o problema do
telhado, o pedreiro, na tentativa de explicar que o “desconto” vai ser sempre o mesmo, acaba
24
por usar implicitamente a semelhança de triângulos, de modo que ele argumenta o seguinte:
Depois de pronto o telhado, é só você vê que onde eu medir a base e medir a altura e dividir,
ela (a inclinação) é a mesma em qualquer parte do telhado. Deste modo, ele faz uma medida
na base do telhado e, dali, mede a altura do telhado até sua base. Ao utilizar esse dispositivo,
ele lança mão de semelhança de triângulos, mesmo que não conheça esse assunto.
A Figura 7 é o esboço da estrutura triangular formada. Nela, é possível verificar
que, em qualquer ponto em que o pedreiro utilizar seu procedimento de determinação do
desconto, a inclinação do telhado será a mesma, o que leva à ideia de semelhança de
triângulos.
Figura 7: Esboço da semelhança de triângulo usada pelos pedreiros
Escolhendo na Figura 7, a altura H1 e uma base B1 obtêm, matematicamente, a
relação indicada oralmente pelo construtor A:
(3)
Na semelhança de triângulos, um dos fatores relevantes diz respeito ao fato de
que os ângulos internos dos triângulos são preservados. Na construção do telhado, também
ocorre a preservação do ângulo interno, como pode ser notado na fala do construtor A, que diz
que, onde for medida a base e dividido pela medida da altura do telhado, o resultado é o
mesmo. O problema da inclinação do telhado é resolvido pelo construtor sem o uso explícito
de trigonometria apresentado em livros didáticos, mas de forma implícita.
25
3.6 – COLOCAÇÃO DE POSTE
Na construção de uma casa, exige-se o emprego de instalações elétricas, além da
colocação de postes a fim de instalar o medidor de energia. O construtor C explicou que, ao
instalar um poste em uma residência, é necessário que ele fique aprumado e, para isso, é
importante a utilização de um prumo2. Prumo é uma ferramenta utilizada para determinar a
inclinação de 90° de colunas e paredes em uma construção. No entanto, também é utilizado
para deixar o poste com aproximadamente 90º em relação ao solo. Ele relatou que não é em
todos os casos que o prumo é utilizado, mas, nas situações que necessitam de determinadas
inclinações, é recomendado o seu uso.
Foi-lhe solicitado, então, que desse um exemplo diferente daqueles utilizados para
determinar inclinações de parede. Então ele disse: Você pode pensar na colocação de um
poste: como você vai bater o prumo se ele (o poste) é grosso em baixo e fino em cima?! Sua
indagação retórica mostrou que de fato não era possível estabelecer a inclinação certa, pois o
poste não possuía faces laterais planas.
Seguindo o seu raciocínio, foi possível ouvir sua explicação sobre a forma de
saber se o poste estará na posição correta ou não. Ele disse: Você toma uma distância de uns
trinta metros (distância do poste) e olha na linha do prumo; depois, coloca o prumo no meio
de cima e olha se tá (sic) no meio de baixo. Estes “meio de cima” e “meio de baixo” trata-se
da base superior e da base inferior do poste, respectivamente. Neste momento, foi-lhe
perguntado se isto garantiria a inclinação ideal. O construtor respondeu da seguinte forma: Dá
uma meia volta e repete (o processo), segura na pelota (cabo do prumo) e divide o meio do
fino e o meio do grosso. Os termos “meio do fino” e “meio grosso” retratam as bases superior
e inferior do poste, anteriormente mencionadas.
De fato, este modo de raciocínio resolve satisfatoriamente o problema da
inclinação do poste, já que, fisicamente, o prumo posto na vertical garante a formação de um
ângulo reto com a base do solo. Caso, ao observar o prumo, ele divida igualmente a face
lateral do tronco de pirâmide, que é a figura geométrica à qual o poste se assemelha
matematicamente, e se este processo for repetido em outra face lateral do tronco de pirâmide,
2
Ferramenta formada pela união, dada por uma corda, de um cabo de madeira e um peso em aço,
suficientemente, pesado de modo que mantenha a corda, quando esticada, numa posição perpendicular em
relação ao solo.
26
que não seja a face paralela a da primeira face, é possível concluir que este procedimento
garante uma boa aproximação da perpendicularidade do poste em relação ao solo.
A Figura 8 ilustra o tronco de pirâmide que representa o poste a ser instalado.
Deste modo, é perceptível que não basta tirar o prumo da face do poste para ser possível
estabelecer a relação de inclinação desejada.
Figura 8: Representação do poste
O problema do poste pode ser representado geometricamente como um tronco de
pirâmide, mas a busca aqui é pela forma de pensamento do construtor, de que forma e
recursos ele lança mão para resolver este problema, e, quando possível, estabelecer uma
relação dessa forma de pensamento com a matemática formal. Vale ressaltar que, mesmo em
muitos casos, não tendo conhecimento da matemática formal, o construtor consegue uma
forma matemática indireta para resolver seus problemas. Neste caso, a instalação do poste de
forma que fique perpendicular ao chão.
Ao considerar o método utilizado pelo construtor, buscou-se, então, explorar sua
instintividade. Além disso, aquilo que ele mencionava, com orgulho, acerca da funcionalidade
de seus métodos estava permeado de saberes matemático.
27
CONSIDERAÇÕES FINAIS
Esta pesquisa foi motivada pelo desejo de conhecer melhor a matemática utilizada
pelo grupo de trabalhadores da construção civil, além de produzir um material que servisse de
base de estudo e, possivelmente, utilizada em aulas de matemática para contribuir com uma
aprendizagem significativa. Aprendizagem esta que pode ser alcançada através do
relacionamento dos conteúdos matemáticos aos conhecimentos profissionais dos alunos.
Na construção civil, os trabalhadores utilizam a matemática informal como
ferramenta de apoio a suas práticas para resolver problemas encontrados quando da
construção de uma casa, por exemplo. Desde a preparação para construção dos alicerces ao
esquadrejamento de um poste, eles precisam de algum conhecimento matemático para que
tudo saia dentro dos padrões necessários.
Em muitos casos, mesmo com a ausência de conhecimentos matemáticos formais,
eles utilizam muitos dos conceitos dessa matemática formal, ainda que inconscientemente.
Nesta pesquisa, fez-se um estudo da matemática utilizada por estes trabalhadores, além de se
realizar um paralelo entre esta matemática e alguns conteúdos da matemática formal, entre os
quais se destacam as quatro operações - utilizadas para quantificação de materiais -, o sistema
métrico decimal - utilizado nas medições de comprimentos, largura e alturas, presentes na
construção -, bem como conceitos de área utilizados na determinação da quantidade de
cerâmica necessária e na determinação do espaço a ser ocupado pela casa em determinado
terreno; além desses conteúdos, também foram encontrados conceitos implícitos de perímetro,
relações trigonométricas, noções de escalas, de proporções, entre outros.
Estes saberes obtidos no cotidiano poderiam ser usados como conhecimentos-base
para a construção de conceitos matemáticos a serem ensinados formalmente nas escolas.
Esses conhecimentos poderiam servir de instrumentos motivadores/facilitadores para a
ocorrência da aprendizagem significativa no ensino de matemática.
A matemática é intrínseca à cultura, sendo esta pesquisa apenas uma pequena
parcela de contribuição em relação a este assunto; ressalte-se que esta discussão não encerra
aqui. Ainda existe muito conhecimento matemático a ser pesquisado, uma vez que as
discussões em relação à Etnomatemática presentes nos grupos sociais é fonte inesgotável de
pesquisa. Contudo, é válido destacar que esta pesquisa é apenas uma parcela de contribuição
em relação a este assunto.
28
REFERÊNCIAS
ANDRADE, Claydaine Ferraz de. Matemática aplicada à agrimensura. 2012. 57f.
Monografia (Licenciatura em Matemática) – Departamento de Matemática e Estatística,
Universidade Federal de Rondônia, Ji-Paraná.
ANDRADE, Maria Margarida de, Introdução à Metodologia do Trabalho Científico:
elaboração de trabalhos na graduação. 4. Ed. São Paulo: Atlas, 1999.
BORGES, Alberto de Campos. Práticas das pequenas construções. Volume 1. São Paulo:
Blucher, 2009.
D’AMBRÓSIO, Ubiratan. Etnomatemática: Elo entre as tradições e a modernidade. Belo
Horizonte: Autêntica, 2001.
DUARTE, Claudia Glavam. Etnomatemática e práticas sociais da construção civil. XI
Conferência Interamericana de Educação Matemática, 2003.
D’ AMBROSIO. Ubiratan, Etnomatemática. Belo Horizonte. Editora Ática. 4ª Edição.
MARCONI, Marina Andrade. Fundamentos de metodologia científica. São Paulo, p. 58,
2010.
OLIVEIRA, Roseli Lima. Aplicações Práticas de Conceitos Matemáticos por
Profissionais da Construção Civil. Trabalho de conclusão de Pós Graduação, FIAR, 2009.
PENA, Joab Souza. A história da matemática no Ensino Fundamental: Uma análise dos
livros didáticos de Matemática utilizados nas escolas públicas de Ji-Paraná. 2012. 47f.
Monografia (Licenciatura em Matemática) – Departamento de Matemática e Estatística,
Universidade Federal de Rondônia, Ji-Paraná.
29
BIBLIOGRAFIAS CONSULTADAS
BORGES, Alberto de Campos. Práticas das pequenas construções, volume 1. São Paulo:
Blucher, 2009.
BOYER, Carl B. História da Matemática. Revista por uta C. Merzbach; tradução Elza F.
Gomide- 2 ed. – São Paulo: Edgard Blucher, 1996.
D’AMBRÓSIO, Ubiratan. Etnomatemática: Elo entre as tradições e a modernidade. Belo
Horizonte: Autêntica, 2001.
DUARTE, Claudia Glavam. Etnomatemática e práticas sociais da construção civil.XI
Conferência Interamericana de Educação Matemática, 2003.
D’ AMBROSIO. Ubiratan, Etnomatemática. Editora Ática. 4ª Edição.
RODNEY, Carlos Bassanezi. Ensino – Aprendizagem com modelagem matemática: uma
nova estratégia. São Paulo: Contexto, 2006.
MARCONI, Marina Andrade/LAKATOS, Eva Maria. Fundamentos de metodologia
científica. –7. ED. – São Paulo: Atlas, 2010.
SARAIVA, Elihebert. SANTOS, Reginaldo Tudeia dos. NETO, Sérgio Candido de Gouveia.
ROSA, Ana Lúcia Denardin da Rosa. Matemática na construção civil Seminário educação
2011: Educação e Relações Raciais- 10 anos de estudo e pesquisa na UFMT. ISSN 15184846. Cuiabá-MT.