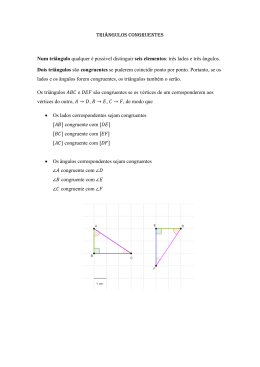
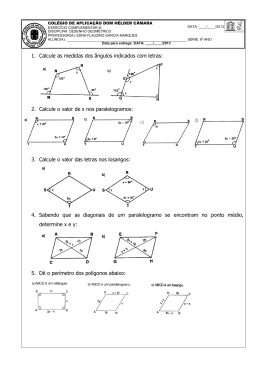
PLANO DE AULA
Dados de identificação
1INSTITUTO FEDERAL CATARINENSE – CAMPUS AVANÇADO SOMBRIO
Município: Sombrio - SC
Disciplina: Matemática
Série : 1ª série
Nível: Ensino Médio
Professora: Elisiane Cardoso de Andrade
Turma:
Tempo previsto: 3 horas
1 Tema: Teoremas da Geometria Plana
1.1 Subtemas:
- Ponto, reta e plano;
- Posições relativas entre retas;
- Ângulos;
- Polígonos (triângulos e quadriláteros).
2 Justificativa
Contemporaneamente os documentos oficiais apontam para a necessidade
de contextualizar os conceitos expostos na sala de aula possibilitando ao aluno a
relação entre seu contexto e os conceitos formais. Também consideram importante
abordar um mesmo tema de diferentes formas em sala de aula.
Estudar os teoremas da Geometria Plana possibilita ao aluno compreender os
conceitos matemáticos que serão abordados posteriormente tais como o teorema de
Pitágoras, semelhança de triângulos, figuras inscritas em uma circunferência,
paralelismo, proporcionalidade, entre outros conceitos.
Além disso, os conceitos básicos da geometria plana podem ser identificados
na diversidade de objetos construídos pelo homem e também nas formas
apresentadas na natureza. São encontrados nos ambientes em que vivemos, por
exemplo: nossas carteiras, janelas, estruturas dos telhados de nossas residências
entre outros. Faz-se necessário seu estudo, visto que estes conceitos da geometria
plana estão inseridos nas diversas áreas profissionais.
4) Objetivos:
a)
Demonstrar geometricamente os teoremas da geometria plana;
b)
Construir triângulos quaisquer, fazer medições de ângulos para mostrar a
soma dos ângulos internos de um triângulo qualquer;
c)
Construir uma porta pantográfica utilizando as ferramentas do GeoGebra, a
partir dos teoremas demonstrados;
d)
Através de material manipulativo, representar paralelogramos;
e)
Resolver problemas aplicados utilizando os teoremas estudados.
5) Conteúdos envolvidos (conteúdos pré-requisitos para o desenvolvimento da
aula).
- Ponto, reta e plano;
- Posições relativas entre retas;
- Ângulos;
- Triângulos;
- Quadriláteros;
6) Estratégias:
6.1- recursos: disponível em sala de aula, televisão ou projetor de slides, folhas de
papel, tesoura, software GeoGebra, animação flash player, quadriláteros
confeccionados com palitos de picolé.
6.2- técnicas: Aula expositiva e dialogada, atividades em sala de aula com materiais
manipulativos e utilização de software.
7) Procedimentos:
A aula será iniciada com a historicização e com uma discussão a respeito de
dois problemas contextualizados envolvendo os teoremas da geometria plana. A
partir da apresentação destes problemas, a história dos conceitos contribuirá para a
justificativa sobre seus estudos.
7.1- Problematização:

Primeira Problematização:
(Paiva, 2004, p.) No projeto de um avião, um engenheiro desenhou três eixos, r, s e
t, que denominou eixo do corpo do avião e eixo das asas, conforme a figura abaixo.
Cada um dos ângulos obtusos que r forma com s ou t mede 30° a mais que a
medida do ângulo AÔB. Sabendo que as asas têm comprimentos iguais, qual a
medida do ângulo 𝑂𝐵 A ?

Segunda Problematização:
Esta problematização tem como intuito trabalhar além do teorema 1, explorarmos os
ângulos (alternos internos, opostos pelo vértice), congruência de lados, retas
paralelas e concorrentes.
Utilizando o Geogebra a partir de retas paralelas, ponto médio, segmentos de retas
e retas perpendiculares o aluno deverá construir uma porta pantográfica, seguindo o
modelo abaixo:
Fonte: ISOLANI, 2002.
7.2- Historicização
Desde os primórdios da humanidade o estudo da Geometria Plana foi posta
em questão, denominada também de Geometria Euclidiana.
Para Bongiovanni (1995), muitos séculos antes de Cristo, desenvolveu-se
uma das mais importântes civilizações na África, os egípicios que tinham suas terras
férteis as margens do rio Nilo. Na região a agricultura era controlada de acordo com
as épocas de cheia e de seca do rio. De junho a setembro ás águas do Nilo
transbordavam e inundavam uma grande quantidade de terras que ficavam a sua
margem. Quando o nível do rio voltava ao normal ficava depositado sob as terras
antes inundadas uma grande quantia de hummus, que fertilizava o solo para a
agricultura.
Após estas inundações era necessária a medição
da extensão das suas
propriedades e redividir as terras, desse modo foram descobrindo diversas
propriedades geométricas. Nesta mesma época os gregos motivados pela
curiosidade científica, começam a usar o raciocinio lógico no estudo da geometria.
O matemático grego Euclides foi quem, pela primeira vez, três séculos antes
de Cristo, reuniu as principais descobertas geométricas de forma lógica e
organizada.
De acordo com Santana (2014), Euclides de Alexandria, escritor, matemático
e frequentador da escola de Platão, realizou seus estudos em Atenas. Também
conhecido como o pai da Geometria Plana, nasceu por volta de 330 a.C. na Síria.
Até hoje não há muitos indícios de como foi a sua trajetória, sabe-se que ele foi
professor de matemática na escola de Alexandria convidado por Ptolomeu I,
governador do Egito em 323 a.C a 283 a.C. Nesta escola Euclides se tornou
conhecido nas disciplinas que lecionava, destacando-se pelo método que utilizava
de ensino que utilizava nas aulas de Geometria e Álgebra.
Atualmente o que se sabe sobre Euclides foi extraído de alguns textos que
foram elaborados séculos após a sua existência no planeta, entre eles os escritos de
Proclo e Pappus de Alexandria.
Proclo se refere a Euclides como o criador da obra “Os Elementos”, a teoria
que foi desenvolvida nesta obra é uma das mais importantes na trajetória e historia
da matemática, levando a muitos educadores adotarem a obra como prioridade nas
aulas de matemática, principalmente nas aulas de Geometria, desde o seu
lançamento até início do século XX. Tornando-se conhecida como Geometria
Euclidiana, onde os seus conceitos foram inseridos como axiomas (proposições que
são consideradas verdades sem a necessidade de provas).
A obra “Os Elementos”, foi dividida em treze volumes, onde cinco abordaram
a geometria plana, três enfocam os números, um fala sobre a teoria das proporções,
outro destaca os incomensuráveis e os três últimos enfocam sobre a geometria no
espaço.
Euclides também foi autor de obras que ressaltam outros temas como por
exemplo: seções cônicas, geometria esférica, teoria dos números, rigor e
perspectivas.
Assim como o seu nascimento a sua morte também está envolvida em
mistérios e as suas datas somente são obtidas através de cálculos aproximados.
Euclides de Alexandria
Fonte: http://www.infoescola.com/biografias/euclides/
7.3- Operacionalização da aula
Inicialmente a professora abordará a turma com a com o historicização do
conteúdo, ressaltando a importância da geometria plana no cotidiano.
Sabe-se que a Geometria Euclidiana pode ser encontra em vários lugares, em
diversos objetos e em várias situações, como por exemplo: o telhado de uma casa
(representando a forma de um triângulo), as mesas da nossa sala de aula (
representando uma figura retangular), quando uma casa está sendo construída o
pedreiro geralmente utiliza um esquadro para certificar-se que os cantos estão
formando um ângulo de noventa graus, a régua que utilizamos representando uma
reta, entre muitas outras funcionalidades.
Após a abordagem acima, a professora iniciará a problematização (problemas
1 e 2). Posteriomente à problematização, a professora irá abordar a demonstração
de onze teoremas da Geometria Euclidiana com o auxílio de material manipulativo e
do software GeoGebra.
Demonstrando os 11 Teoremas da Geometria Euclidiana
Para a demonstração dos teoremas utilizaremos o software GeoGebra, juntamente
com uma animação em flash encontrada no link:
http://www2.mat.ufrgs.br/edumatec/atividades_diversas/teoremas_geometria/Objetos/Geom
etriaPlana.swf
Teorema 1: A soma dos ângulos internos de qualquer triângulo é 180°.
a) Construir os pontos A , B e C;
b) Construir o polígono ABC;
c) Traçar uma reta passando pelos pontos A e B e uma reta passando pelos pontos B e C.
d) Traçar uma reta paralela à reta AB passando por C.
e) Usar a ferramenta ângulo para verificar os ângulos internos do triângulo ABC;
f) Marque o ângulo externo do triângulo ABC em relação ao vértice B;
g) Mover ponto A, B ou C.
Argumentos:
1Do paralelismo das retas temos ângulos
congruentes (alternos internos).
2E também ângulos s congruentes (correspondentes).
3Assim, no triângulo ABC, os ângulos de vértices A, B e C somam um ângulo
raso, ou seja, 180°.
Mostrar teorema demonstrado por meio de material manipulativo. Seguindo as
ações conforme as figuras apresentadas:
1- Recorte um triângulo qualquer;
2- Pinte os três ângulos internos do triângulo;
3- Separe o triângulo em três partes, cada uma contendo um dos ângulos do
triângulo;
4-Junte os três ângulos do triângulo, fazendo coincidir seus vértices. Note que
formou-se um ângulo raso, ou seja, um ângulo de 180°.
Teorema 2: Se um quadrilátero ABCD tem diagonais se bissectando, congruentes e
perpendiculares, então ABCD é quadrado.
a) Inserir pontos A e C;
b) Construir o segmento de reta AC;
c) Construir ponto médio M entre os pontos A e C;
d) Inserir reta perpendicular ao segmento AC, passando por M;
e) Inserir círculo com centro em M, passando pelos pontos A e C;
f) Utilizar a ferramenta interseção de dois objetos, gerando os ponto B e D;
g) Contruir os segmentos AB, BC, CD e AD;
h) Mover ponto A ou C.
Argumentos:
Os segmentos MA, MC, MD e MB são raios do círculo, logo congruentes.
Os ângulos de vértice M são retos.
Aplicando o critério LAL temos a congruência dos triângulos AMB,
BMC, CMD e DMA.
Logo os segmentos AB, BC, CD e DA são congruentes.
E mais, os 4 triângulos são isósceles com ângulos da base de 45°, portanto
os ângulos em A, B, C e D são retos.
Assim mostramos que ABCD é um quadrado.
Teorema 3: Se um quadrilátero ABCD tem os lados consecutivos AB e BC congruentes e os
ângulos de vértices A e B são retos, então ABCD é quadrado.
a) Inseir pontos A e B;
b) Construir o segmento de reta entre os pontos A e B;
c) Construir uma reta perpendicular ao segmento AB passando pelo ponto A;
d) Construir uma reta perpendicular ao segmento AB passando pelo ponto B;
e) Inseir círculo com centro em A, passando por B;
f) Com a ferramenta interseção de dois objetos encontre o ponto D;
g) Trace uma reta paralela a AB passando por D;
h) Com a ferramenta interseção de dois objetos encontre o ponto E;
i) Construir o quadrilátero ABCD
Argumentos:
Observando a figura abaixo temos:
t pararelo à AB logo os ângulos em D e C são retos.
AB e AD são raios do círculo logo o triângulo BAD é isóceles com
ângulos da base de 45°.
Pelo critério LAL os triângulos BAD e BCD são congruentes.
Logo são congruentes os segmentos BA e BC, bem como os segmentos DA e
DC.
Assim mostramos que ABCD é um quadrado.
Teorema 4: Se um quadrilátero ABCD tem um par de lados paralelos e congruentes, o
quadrilátero é um paralelogramo.
a) Inserir pontos A e B e segmento de reta entre AB;
b) Construir retas perpendiculares ao segmento AB passando por A e por B
respectivamente;
c) Interseção de dois objetos, gerando pontos C e D;
d) Inserir segmentos de retas entre os pontos AD, DC, e CB;
e) Esconder as retas;
f) Traçar segmento de reta, formando uma diagonal do ponto B a D;
Argumentos:

Os ângulos ABD e CDB são congruentes pois alternos internos em
retas paralelas.

Como AB e CD congruentes, por LAL os triângulos ABC e
CDB são congruentes.

Assim os ângulos ADB e CBD são congruentes.

Sendo alternos internos, as retas suportes aos segmentos AD e BC são
paralelas.

Portanto ABCD é paralelogramo.
Teorema 5: Em um paralelogramo ABCD os lados opostos são congruentes.
a) Inserir pontos A e B;
b) Traçar uma reta r passando pelos pontos A e B;
c) Construir uma reta paralela s, à reta r;
d) Construir uma reta perpendicular t à reta r passando pelo ponto A;
e) E reta paralela u, a reta t, passando por B;
f) Utilizar a interseção de dois objetos e encontrar os pontos de interseção entre as retas;
g) Construir o polígono formado;
h) Traçar as diagonais.
Argumentos:

Os ângulos ADB e CBD são congruentes pois alternos internos em reta
paralelas.

Da mesma forma são congruentes os ângulos ABD e CDB.

Pelo critério ALA os triângulos DAB e BCD são congruentes.

Logo AD e BC são segmentos congruentes bem como os segmentos AB e
DC.
Teorema 6: Em um paralelogramo ABCD as diagonais se bissectam.

Pelo teorema 5 os lados opostos de ABCD são congruentes.

Os ângulos EDA e EBC são congruentes pois alternos
internos em paralelas.

Os ângulos EAD e ECB também são congruentes pois alternos
Internos em pararelas.

Pelo critério ALA são congruentes os triângulos EAD e ECB.

Portanto os segmentos EA e EC são congruentes bem como os
segmentos EB e ED são congruentes.
Teorema 7: Se um quadrilátero as diagonais se bissectam então o quadrilátero é um
paralelogramo.
a) Inseir os pontos A e C, e o segmento de reta entre os pontos;
b) Inseir o ponto médio O entre o ponto A e C;
c) inseir pontos B e D;
4ª inseir segmenode reta passando pelo ponto O;
5ª temos o quadrilatero ABCD.
Argumentos:

Por construção os segmentos AO e OC são congruentes e também
são congruentes os segmentos OB e OD.

Nos triângulos OAB e OCD os ângulos em O são opostos pelo
vértice, portanto congruentes.

Pelo critério LAL são congruentes os triângulos OAB e OCD.

Logo são congruentes os segmentos AB e DC.

Também são congruentes os ângulos OBC e ODC.

E sendo ângulos alternos internos as retas eAB e OC são paralelas.

Sendo os segmentos AD e DC paralelos e congruentes pelo teorema 4 ABCD
é paralelogramo.
Os teoremas 4, 5, 6 e 7 demonstrados acima, serão trabalhados com material
manipulativo para melhor compreensão dos teoremas.
Fonte: ISOLANI, 2002.
Os alunos devem mover as bases do retangulo, formando diversos quadriláteros.
Observando que os lados opostos são conguentes e paralelos, observando também
que se traçarmos uma diagonais, ambas irão se bisectar.
Teorema 8: Se P é ponto da mediatriz do segmento AB então o segmentos PA e PB são
congruentes.
1ª inserir os pontos A e B;
2ª inserir o segmento de reta entre os pontos A e B;
3ª inserir ponto médio M entre os pontos AB;
4ª reta perpendicular r, passando pelo ponto M;
5ª inserir ponto P na reta r;
6ª inserir segmento de reta entre os pontos PA e PB;
7ª mover ponto A ou B.
Argumentos:
1)
Como M é ponto médio de AB, tem-se MA e MB segmentos congruentes.
2)
Nos triângulos AMP e BMP ao ângulos de vértice M são retos.
3)
Portanto, pelo critéro LAL os triângulos AMP e BMP são congruentes.
4)
Assim PA e PB são segmentos congruentes.
Teorema 9: Dado um triângulo ABC sempre existe um circulo passando pelos três vértices.
1ª inseir os pontos A, B e C;
2ª traçar os segmentos de reta entre os pontos ABC;
3ª traçar a mediatriz r e s, entre os pontos AB e AC;
4ª inserir ponto de interseção O entre as mediatrizes;
5ª inserir cículo sendo o ponto O centro e passando pelos pontos ABC;
6ª mover ponto A.
Argumentos:

Como O pertence a mediatriz r de BC temos OC e OB congruentes.

Como O pertence a mediatriz s de AB temos AO e OB congruentes.

Assim o círculo passando por A também contém os pontos B e C.
Teorema 10: Se um segmento tem extremidades nos pontos médios de dois lados de um
triângulo, então ele é paralelo ao terceiro lado e tem metade do comprimento do terceiro
lado.
1ª inserir os ponto A, B e C;
2ª traçar o segmento de reta entre os pontos;
3ª inserir ponto médio entre AB e AC;
4ª reta paralela à AB, passando por C;
5ª traçar semireta entre os pontos MN;
6ª inserir ponto interseção;
7ª mover ponto A.
Argumentos:

Os ângulos em N são opostos pelo vértice.

AN e NC são congruentes.

Os ângulos em A e C são congruentes pois são alternos internos em
retas paralelas.

Logo os triângulos ANM e CND são congruentes pelo critério ALA.





Assim DC e AM são congruentes.
Portanto CD e BM são congruentes e como são segmentos paralelos.
Pelo teorema 4, BMDC é paralelogramo.
Assim MN é paralelo à BC.
Como N é ponto médio de MD, MN=BC/2.
Teorema 11: Em um triângulo o ponto da interseção de duas medianas divide as
medianas na razão 1:2.
1ª inserir pontos A, B e C;
2ª traçar segmento de reta entre os pontos;
3ª inserir ponto médio entre AB e AC;
4ª segmento de reta entre os pontos MC e NB;
5ª inserir interseção;
6ª inserir ponto médio entre OB e OC.
Argumentos:

Pelo Teorems da Base Média no triângulo BOC, temos QP paralelo à
BC e QP=BC/2.

Pelo Teorema da Base Média no triângulo BAC, temos MN paralelo à
BC e MN=BC/2.

Logo MN e QP são segmentos paralelos e congruentes.

Pelo teorema 4 MNPQ é paralelogramo.

Pelo teorema 6 as diagonais de MNPQ se bissctam.

Como P é pomto médio de CO e Q é ponto médio de BO temos
BQ=QO=ON e CP=PO=OM.

Assim O divide as madianas BN e CM na razão 1:2.
Os teoremas 2, 3, 8, 9, 10 3 11, serão trabalhados com o auxílio do aplicativo
http://www2.mat.ufrgs.br/edumatec/atividades_diversas/teoremas_geometria/Objetos/Geom
etriaPlana.swf
Conclusão da aula:
7.4- Conclusão da aula (atividades e sugestão de atividade).
Resolução dos problemas apresentados inicialmente.
RESOLUÇÃO:
8- Avaliação
Participação e interesse.
8.1 Instrumentos de avaliação:
Será utitizada:
- Uma prova contendo cinco questões, individual e sem consulta;
- Participação dos alunos nas atividades solicitadas.
9- Referências bibliográficas
SANTANA,
Ana
Lucia.
Euclides.
Disponível
<http://www.infoescola.com/biografias/euclides/> Acesso.ago.2014.
em:
ISOLANI, Clélia Maria Martins; et al. Matemática: 7ª série do Ensino Fundamental:
Manual do Professor. 2.ed. Curitiba: Módulo, 2002.
GIOVANNI, José Ruy; et al. A Conquista da Matemática: a+ nova. 1.ed. São Paulo:
FTD, 2002.
PAIVA, Manoel. Matemática. 1.ed. São Paulo: Moderna, 2004.
BONGIOVANNI, Vincenzo; et al. Matemática e Vida: Números, Medidas, Geometria:
Livro do Professor. 7.ed. São Paulo: Ática, 1995. ]