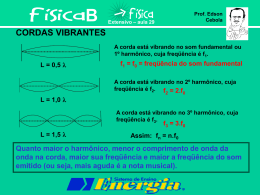
O QUE É SOM?
Onda mecânica longitudinal
(propaga-se
em
meios
materiais).
Velocidade do som
Vsólido > Vlíquido > Vgasoso
VELOCIDADE DO SOM NO
AR
340 m/s a 20º
330 m/s a 0ºC
FREQÜÊNCIA AUDÍVEL
Infra-som
20 Hz
audível
Ultra-som
20.000 Hz
ALTURA: Diferença entre sons
graves (baixo) e sons agudos (alto).
Está relacionado a freqüência
da onda
agudo
grave
INTENSIDADE (VOLUME): Diferença entre sons
fortes e sons fracos.
Está relacionado a Amplitude
da onda
Fraco
Forte
TIMBRE: Diferença entre sons de mesma altura, mesma
intensidade tocados em instrumentos diferentes.
Esta relacionado com a forma
da onda.
NÍVEL SONORO: É a relação entre a intensidade do som
ouvido pela intensidade mínima.
LIMIAR DE AUDIÇÃO: I0 = 10-12 W/m2
I
  10. log10 ( )
I0
unidade: decibel(dB)
EXEMPLO: Um som possui intensidade de 10-7 W/m2. Calcule o nível
sonoro, em dB.
7
10
  10. log( 12 )
10
  10. log(10 )
5
  50dB
ECO: É a reflexão do som
X
No ar a distância mínima para ocorrer
eco é em torno de 17 m, pois:
Como D = 2.X e o tempo mínimo é de 0,1 s.
D  V .t
2 x  340.01
x  17m
EFEITO DOPPLER
Quando uma fonte se aproxima ou se afasta de
um observador a frequência recebida não será
igual a frequência real da fonte.
Observador(VO)
-
+
Fonte(VF)
-
+
v  vo
f  f .(
)
v  vF
´
f` freqüência aparente (percebida pelo ouvinte)
f freqüência real da fonte
v  velocidadedo som
vo  velocidadedo observador
vF  velocidadeda fonte
2. Cordas Vibrantes
 As
cordas vibrantes são fios flexíveis
e tracionados nos seus extremos.
São utilizados nos instrumentos
musicais de corda como a guitarra, o
violino, o violão e o piano.
Velocidade e tração na corda
v
T

Harmônicos nas cordas

Primeiro Harmônico ou Freqüência
Fundamental formam-se, na corda, um fuso com
2 nós.
l
1
2
 1  2  l
v    f  f1 
v
1
 f1 
v
2l
Harmônicos nas cordas

Segundo Harmônico formam-se, na corda, dois
fusos com 3 nós.
2l
l  2  2 
2
v
2v
f2   f2 
 f2 
2l
2
2l
2
v
Harmônicos nas cordas

Terceiro Harmônico forma-se, na corda, três fusos
com 4 nós.
3  3
2l
l
 3 
2
3
v
3 v
f3  
 f3 
3 2  l
2l
3
v
Harmônicos nas cordas

Harmônico n forma-se, na corda, n fusos
com (n+1) nós.
nv
fn 
2l
f n  n. f1
3. Tubos Sonoros
3.1. Tubos Abertos
v  f  f 
v

1 1
2l
l
 1 
2
1
f1 
l
v
1
 f1 
1 v
2l
2  2
2l
 2 
2
2
2v
f2   f2 
2
2l
v
3.1. Tubos Abertos
3  3
2l
l
 3 
2
3
3 v
f3   f3 
3
2l
v
4  4
2l
l
 4 
2
4
4v
f4   f4 
4
2l
v
Tubos Abertos para harmônico n
n  n
2l
l
 n 
2
n
nv
fn 
 fn 
n
2l
v
3.2. Tubos Fechados
PRIMEIRO HARMÔNICO
v  f  f 
v

1 1
4l
l
 1 
4
1
1 v
f1   f1 
1
4l
v
SEGUNDO HARMÔNICO
3  3
4l
l
 3 
4
3
3 v
f3   f3 
3
4l
v
3.2. Tubos Fechados
QUINTO HARMÔNICO
l
5  5
4l
 5 
4
5
5v
f5   f7 
5
4l
v
SÉTIMO HARMÔNICO
7  7
4l
l
 7 
4
7
7v
f7   f7 
7
4l
v
Tubos fechados para harmônico n
4  n
4l
l
 n 
n
n
nv
fn 
 fn 
n
4l
v
Sendo n um número ímpar.