CAPÍTULO 15 – REGRESSÃO CATEGORIAL
15.3. REGRESSÃO ORDINAL
Muitas das variáveis de estudo nas ciências sociais e humanas são ordinais.
Com frequência, a variável dependente toma valores discretos, ou categorias,
ordenáveis mas cujo distância entre elas não é conhecida, nem tão pouco constante. Por exemplo, em estudos de opinião é frequente recorrer a escalas de tipo
Likert, para avaliar o grau de concordância/discordância com determinado tópico
(discordo completamente; discordo; nem concordo nem discordo; concordo; concordo completamente). Em estudos epidemiológicos e de severidade de doença é
usual classificar em graus de severidade uma determinada patologia (severidade
baixa; média; alta). Em aplicações económicas é frequente considerar o grau-de-risco, produtividade, (baixo(a), médio(a), elevado(a)), etc. Adicionalmente, as
escalas ordinais podem resultar da necessidade de operacionalização de variáveis
contínuas que por motivos de mensuração, impacto social, ou outros apenas
podem ser medidas em categorias ordinais. O rendimento económico é um bom
exemplo deste tipo de operacionalização. Se bem que o rendimento possa ser
medido precisamente, até ao último euro, de uma forma geral esta variável é
categorizada em classes ordinais de modo a reduzir a taxa de não respostas (por
exemplo, o nível salarial “baixo – < 500 €”, “médio – 501 a 1000 €” e “alto –
> 1000 €”). Em termos analíticos, as classes das variáveis ordinais são, geralmente, codificadas com valores inteiros de 1 ao número de classes e, por este
motivo, o leitor pode ser levado a usar a regressão linear vulgar. Se bem que para
um número de classes elevados (pelo menos 7) a regressão linear possa ser utilizada, com alguns cuidados, em amostras grandes, na maior parte dos casos, a
utilização da regressão linear com variáveis dependentes ordinais pode produzir
resultados incoerentes ou mesmo incorrectos como demonstraram Winship &
Mare (1984). A recomendação geral, para este tipo de variáveis é a de utilizar a
regressão ordinal ou um outro modelo de regressão que evite a assumpção de
distâncias constantes entre as classes da variável (ver e.g. Long & Freese, 2006).
Por outro lado, se a variável tiver classes ordenáveis, mas uma das suas classes não
o for (por exemplo, a classe “Não sabe/Não tem opinião” que por vezes se encontra nas falsas escalas de tipo Likert), poderá ser preferível recorrer à regressão
multinomial, que não contempla a relação de ordem entre classes. Finalmente, se
a ordenação das classes puder ser feita de forma diferente, em função do contexto
social, experimental, etc. será sensato recorrer à regressão multinomial, já que a
forma de ordenação das classes pode conduzir a diferentes conclusões.
761
ANÁLISE ESTATÍSTICA
15.3.1. O Modelo de Regressão Ordinal
A relação de ordem entre as classes da variável dependente obriga a que a
tarefa de modelar a probabilidade de ocorrência de uma das suas classes, seja feita
em termos de probabilidades acumuladas. Por outro lado, a variável ordinal
medida, pode ser interpretada como a operacionalização de uma outra variável
continua não medida (i.e. latente) como vimos anteriormente a propósito da
regressão binomial. O modelo pode assim ser formalizado de uma forma probabilística cumulativa não-linear ou através da operacionalização de uma variável
latente não medida ou observada directamente.
No MODELO DE PROBABILIDADES CUMULATIVAS, a probabilidade de se observar uma classe inferior ou igual a k do conjunto das K classes da variável dependente, para um determinado vector de observações das variáveis independentes
X, é dada por P (Yj ≤ k|x) = π1 + π2 + ...πk (j = 1, ..., n; k = 1, ..., K) onde
π1 = P (Yj = 1), π2 = P (Yj = 2), ..., πk = P (Yj = k). Naturalmente, porque as
classes são ordenáveis, as probabilidades acumuladas reflectem a ordenação natural P (Yj ≤ 1) ≤ P (Yj ≤ 2) ≤ ... ≤ P (Yj ≤ K – 1). Note que o modelo não engloba a
última classe K uma vez que P (Yj ≤ K) = 1 (i.e. a informação referente à ultima
classe é redundante). Por analogia com a regressão logística, podemos conceptualizar o modelo ordinal como um modelo logístico, com acontecimentos
P (Yj ≤ k) e o seu complementar 1 – P (Yj ≤ k) = P (Yj > k). Para linearizar o
modelo de probabilidade cumulativa não linear, toma-se o Ln do rácio das chances acumuladas P (Yj ≤ k) / P (Yj > k), i.e. o Logit [ P (Yj ≤ k) ], que é:
P(Y j ≤ k | X)
⎛
Logit [ P ( Y j ≤ k | x )] = Ln ⎜
⎜ 1 − P(Y ≤ k | X)
j
⎝
⎞
⎟⎟ =
⎠
⎛ P(Y j ≤ k | X) ⎞
= Ln ⎜
=
⎜ P ( Y > k | X ) ⎟⎟
j
⎝
⎠
= α k + X*β
(k = 1,..., K – 1)
Onde αk representa o parâmetro de localização para as k = 1, ..., K – 1 classes da variável dependente (equivalente à ordenada na origem na regressão
linear), β é o vector dos coeficientes de regressão (declives) e X* é a matriz das
variáveis independentes (sem a coluna de 1’s como na regressão linear, caso con762
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
trário o modelo é indeterminado, pois essa coluna é redundante com os αk). No
caso de uma única variável independente, o modelo simplifica-se a:
⎛ P(Y j ≤ k | x) ⎞
Logit [ P ( Y j ≤ k | x )] = Ln ⎜
⎟⎟ =
⎜
⎝ P(Y j > k | x) ⎠
= α k + β X j ( j = 1, ..., n; k = 1, ..., K – 1)
Note que o coeficiente de regressão (β) não apresenta índice k, obrigando o
modelo a pressupor que o efeito da variável independente sobre o
Logit [ P ( Y j ≤ k | x )] é igual para todas as classes (veremos adiante como testar
este pressuposto conhecido por pressuposto da homogeneidade dos declives).
Os αk são parâmetros de posição de cada uma das classes, reflectindo a característica qualitativa da variável dependente enquanto que o declive único permite
obter um modelo parcimonioso para dados ordinais. Assim, o modelo assume que
o efeito das variáveis independentes sobre o Logit é idêntico para todas as classes
da variável dependente, e que a resposta observada em cada classe apenas se
encontra deslocalizada para a direita ou para a esquerda, em função de αk.
O modelo ordinal atrás definido permite estimar o logaritmo da probabilidade de a variável dependente tomar os valores de classes inferiores ou iguais a k,
comparativamente com a probabilidade de tomar os valores das classes superiores
a k. Se β > 0, quando X aumenta, aumenta a probabilidade de a variável dependente tomar valores de ordem inferiores ou iguais a k, i.e. quando X aumenta, Y
diminui. Se β < 0, então quando X aumenta, Y aumenta. Esta relação entre o
sinal de β e a variação de Y é contrária à interpretação generalizada do sinal de β
em regressão. Assim, sendo β > 0, para que quando X aumenta, aumente a
probabilidade de Y tomar valores de ordem superiores, é necessário re-escrever o
modelo como:
⎛ P(Y j ≤ k | x) ⎞
Logit [ P ( Y j ≤ k | x )] = Ln ⎜
= α k − βX j
⎜ P ( Y > k | x ) ⎟⎟
j
⎝
⎠
E esta é a forma como a regressão ordinal é modelada pela maioria dos softwares de análise estatística (nomeadamente o SPSS, Stata, e o Statistica, entre
outros) pelo que será, também, a forma adoptada neste livro. As duas formas
alternativas do modelo ilustram-se na figura seguinte para uma variável dependente com 3 classes, e uma única variável independente:
763
Logit [ P (Yj £ k | x)] = ak + bXj
Logit [ P (Yj £ k | x)] = ak + bXj
ANÁLISE ESTATÍSTICA
1.0
P (Y £ 1)
0.8
0.6
P (Y £ 2)
0.4
0.2
P (Y £ 3)
0.0
X
1.0
P (Y £ 3)
0.8
0.6
P (Y £ 2)
0.4
0.2
P (Y £ 1)
0.0
X
Note que nas figuras acima, cada uma das curvas é equivalente à curva da
regressão logística em que as classes, dicotómicas, são Yj ≤ k e Yj > k. As curvas
tem exactamente a mesma forma, i.e. a variação da probabilidade em função de
X é igual para todas as classes, estando apenas deslocalizadas horizontalmente
por um factor constante (αk – αk+d ) / β. O rácio das chances acumuladas, igual
para todas as classes, é dado por:
OR k =
P(Y ≤ k | x = x + d ) / P(Y > k | x = x + d )
=
P(Y ≤ k | x = x) / P(Y > k | x = x)
= e − dβ =
1
=
e
764
dβ
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
Neste modelo, o rácio das chances é β-proporcional à distância d entre os dois
pontos da variável independente, para todas as classes da variável dependente e
por isso o modelo é também designado por modelo de chances proporcionais (Agresti,
2002). Em particular, se d = 1, as chances de observar uma classe inferior ou
igual a k, comparativamente com as chances de se observar uma classe superior a
k, variam e – β por cada unidade de X (mantendo constantes as restantes variáveis
independentes).
O ajustamento do modelo ordinal é feito iterativamente com o método da
máxima verosimilhança. Uma vez que o modelo pressupõe que as curvas de
probabilidade das K – 1 classes da variável dependente são iguais para todas as
classes e são calculadas de forma cumulativa, a função de verosimilhança é
(Agresti, 2002):
L =
n
⎡
K
∏ ⎢ ∏ (P(Y
j = 1 ⎣ k =1
⎡
= ∏⎢
⎢
j =1 ⎣
n
≤ k | x j ) − P(Y ≤ k − 1 | x j )
(α −x β)
⎛
e k j
⎜
∏⎜
(αk −x jβ )
k =1 ⎝ 1 + e
K
−
e
( α k −1 − x j β )
1+ e
( α k −1 − x j β )
Y kj
Y kj
⎤
)⎥ =
⎦
⎞
⎟
⎟
⎠
⎤
⎥
⎥
⎦
Onde Ykj regista a classe dicotómica (“≤ k” vs. “> k”) da variável Y para o
sujeito j.
No MODELO DE VARIÁVEL LATENTE, assume-se que existe uma variável
latente continua (η) que não é possível medir directamente, e que a variável
manifesta (Y) resulta do “corte” da variável latente em K-classes, ordinais e
mutuamente exclusivas. O modelo estrutural que relaciona a variável latente com
as variáveis independentes é:
η j = x jβ + ε j
( j = 1, ..., n)
e o modelo de medida que operacionaliza a variável manifesta ordinal Y é:
Yj = k
se
αk–1 ≤ η ≤ αk.
isto é, a variável ordinal toma a classe k, quando a variável latente está entre os
pontos de corte, ou thresholds, αk–1 e αk (–∞ = α0 < α1 < ... < αK = +∞)
765
ANÁLISE ESTATÍSTICA
como ilustra a figura seguinte para uma variável dependente Y com 4 classes e
uma variável independente X:
P (Y = 4 | x3)
classe 4
P (Y = 4 | x2)
P (Y = 4 | x1)
a1
classe 3
a2
classe 2
a3
classe 1
x1
x2
x3
Na representação gráfica acima, o modelo latente é η j = β 0 + β X j + ε j
e basta definir 3 pontos-de-corte, ou thresholds, para delimitar as 4 classes da
variável manifesta Y. Naturalmente, α0 = –∞ e α4 = +∞. As curvas em sino
em torno de cada um dos pontos (xj, ηj) são as curvas de densidade de probabilidade dos erros do modelo tal como na regressão linear (rever cap. 14.1). Assim, a
probabilidade de se observar uma determinada classe para um determinado valor
de X é dada pela área da curva entre dois thresholds, como ilustra a figura para
y = 4 (área a cinzento nas curvas em sino). A probabilidade de se observar uma
determinada classe de Y é então P (Yj = k |xj) = P (αk –1 ≤ η ≤ αk | xj ). Designando por F a função de distribuição dos erros do modelo estrutural, substituindo
ηj por β0 + βX j + ε j e rearranjando os termos, podemos então escrever
P (Yj = k | xj ) = F (αk – β X j ) – F(αk –1 – β X j ) (eliminando a constante β0
que é redundante com α)1 (Long & Freese, 2006). Note que para a classe k = 1,
α0 = –∞ pelo que F (–∞ – β X i ) = 0 e P (Yj = 1|xj) = F (α1 – β X j ). De
(1)
Para além de fixar a ordenada na origem em 0, é também necessário definir a escala de η o que
geralmente se faz fixando a sua variância em 1 (i.e. estandardizando a variável latente).
766
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
modo análogo, para k = 4, α4 = +∞ pelo que F (+∞ – β X i ) = 1 e
P (Yj = 4|xj) = 1 – F (α3 – β X j ). O inverso da função F, i.e. F -1, designa-se
por função de ligação (link function) por fazer a “ligação” linear entre a parte
aleatória do modelo (P [ Y ≤ k ]) e a parte sistemática (X* β). Por exemplo, se F
for a função logística definida anteriormente na regressão logística (rever cap.
15.1.1), F –1 define a função Logit, e o modelo designa-se por modelo logit ordinal; Se F for a distribuição normal, F –1 define a função Probit, e o modelo diz-se
probit ordinal. De uma forma linear generalizada, recorrendo à função Link, o
modelo pode escrever-se como:
Link (P [ Y ≤ k ]) = αk – X*β
No SPSS estão disponíveis 5 funções Link cuja utilização no modelo ordinal, é
recomendável de acordo com o tipo de distribuição de probabilidades que as classes da variável dependente apresentam. As principais recomendações resumem-se
na tabela seguinte (Adaptado de Agresti, 2002; Norušis, 2006; Long & Freese,
2006):
Função Link (F –1)
Usar quando
Logit
⎡ P [Y ≤ k ] ⎤
Ln ⎢
⎣ P [Y > k ] ⎥⎦
As classes de Y apresentam
distribuição uniforme
Log-log
Complementar
Ln ( − Ln (1 − P [Y ≤ k ])
As classes de Y de maior
ordem são as mais frequentes
Log-log
negativo
– Ln (– Ln ( P [Y ≤ k ] )
As classes de Y de menor
ordem são as mais frequentes
Cauchit
Tan (π ( P [Y ≤ k ] – 0.5)
As classes de Y de menores
e maiores ordens
são as mais frequentes
Probit
Φ–1( P [Y ≤ k ] ) onde Φ é a função
de distribuição N (0,1) (ver cap. 15.1.2)
A variável latente
é de tipo normal (assumpção)
A escolha da função Link no ajustamento do modelo, deve pois considerar o
tipo de distribuição das classes da variável dependente. A escolha de uma função
Link inapropriada pode comprometer a significância do modelo e a sua capacidade preditiva.
767
ANÁLISE ESTATÍSTICA
„ O Modelo de “escala”
O SPSS permite ainda definir um modelo ordinal, mais flexível e realista, que
permite controlar diferenças de distribuição de probabilidades das classes da
variável dependente em função das variáveis independentes. Por exemplo, num
estudo sobre opinião acerca da despenalização do aborto, é possível que as respostas apresentem maior variabilidade nas mulheres do que nos homens; num estudo
sobre créditos de risco, é possível que as empresas de novas tecnologias vs. tecnologias tradicionais apresentem maior variabilidade na liquidação dos créditos; a
probabilidade de detectar uma situação anómala é mais variável se o instrumento
de medida apresentar ruído, do que se não apresentar (situação muito frequente
em Biomedicina), etc. Assim, o modelo de “escala” que incorpora o efeito da dispersão das respostas é (Agresti, 2002):
Link ( P [ Y ≤ k ]) =
αk − X * β
e Xγ
Neste modelo, o denominador contem o vector dos parâmetros de escala (γ)
que descreve o padrão de dispersão observado em X. Note que se γ = 0, obtemos
o modelo ordinal original. Quando as frequências das classes extremas são as mais
elevadas, Xγ > 0, e o modelo tende a “aproximar” as probabilidades cumulativas. Por outro lado, se Xγ < 0 as probabilidades cumulativas tendem a afastar-se.
15.3.2. Avaliação da qualidade do modelo
A avaliação da qualidade do ajustamento e do modelo é feita de modo equivalente ao descrito anteriormente para a regressão logística (ver cap. 15.1.4). A
significância do modelo é avaliada pelo teste do rácio de verosimilhanças, ou pelos
testes do Qui-quadrado e da Deviance (se estes puderem ser aplicados) enquanto
que a significância prática do modelo é avaliado pelos pseudo-R2. A avaliação do
tipo de modelo (logit ordinal, probit ordinal, modelo de escala, etc.) pode fazer-se
de uma forma simples, comparando o – 2LL dos dois modelos em causa. O
melhor modelo será aquele que apresentar menor – 2LL. Ainda que não existam,
actualmente, métodos para avaliar a qualidade dos resíduos e observações
influentes específicos para a regressão ordinal, é possível recorrer aos resíduos e
medidas de observações influentes definidos anteriormente para a regressão logística. De acordo com Hosmer & Lemeshow (2000), este processo de análise tem
porém a desvantagem de ser uma aproximação ao modelo estimado, já que os
768
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
coeficientes da regressão ordinal são apenas uma “aproximação” dos coeficientes
da regressão logística. Ainda assim, se o pressuposto da homogeneidade dos declives for válido, a análise de resíduos ordinais com os métodos da regressão logística
produz resultados fiáveis (Long & Freese, 2006). Interessa agora, descrever o
pressuposto da homogeneidade dos declives que é específico da regressão ordinal
15.3.3. Teste à homogeneidade dos declives
O modelo de regressão ordinal apresentado anteriormente assume que a
influência das variáveis independentes sobre a Link (P [ Y ≤ k ]) é igual para todas
as K classes da variável dependente. Isto é, que as linhas da função Link utilizada
sejam paralelas para as K classes (daí este teste também ser designado por teste das
linhas paralelas). Para avaliar este pressuposto é então necessário testar:
H 0 : β1 = β 2 = ... = β K −1
vs.
H1: ∃ k, l : β k ≠ β l
( k ≠ l ; k, l = 1, ..., K − 1)
A estatística de teste é o rácio de verosimilhanças de dois modelos ordinais, o
primeiro assumindo que os declives são iguais (i.e. que H0 é válida) e o segundo
assumindo que os declives possam ser diferentes (i.e. que H1 é válida e que
Link (P [ Yj ≤ k ]) = αk – xj βk). Os – 2LL dos dois modelos são usados para
averiguar se o ganho de – 2LLH1 (com declives livres) relativamente ao – 2LLH0
(com declives homogéneos) é significativo. A estatística de teste é então:
⎡ L H1
2
X LP
= − 2 LL H1 − ( − 2 LL H 0 ) = − 2 Ln ⎢
⎢⎣ L H 0
⎤ a 2
⎥ ∼ χ ( k − 2) p
⎥⎦
Se o p-value = P (χ2 ≥ X2LP) do teste for muito pequeno, rejeita-se H0 e conclui-se que os declives não são homogéneos. Note que se pretende, geralmente,
não rejeitar a H0. É ainda de referir que a escolha da função Link afecta a significância deste teste, e que a rejeição de H0 pode estar simplesmente associada à
escolha de uma função Link inapropriada para a distribuição de probabilidades
observadas nas classes da variável dependente. Por outro lado, se este pressuposto
769
ANÁLISE ESTATÍSTICA
não for validado, poderá ser aconselhável recorrer à regressão multinomial como
alternativa de análise.
15.3.4. Classificação com o modelo
de regressão ordinal
Uma vez ajustado o modelo de regressão ordinal e demonstrada a sua significância estatística, os coeficientes do modelo podem ser usados para predizer a
classificação de novos casos de estudo. Recorrendo, ao inverso da função Link
utilizada no modelo é então possível estimar a probabilidade acumulada de cada
uma das classes da variável ordinal. Por exemplo, no caso da função Link ser a
Logit, tomando o inverso da função Logit é possível definir a função genérica da
probabilidade acumulada (função de distribuição logística) da classe k:
F ( α k − X* β ) = P [ Y ≤ k ] =
1
1 + e−(αk −X
*
β)
De modo equivalente se a função Link for a Log-log complementar, a função
de distribuição é
( αk −X
F ( α k − X* β ) = P [ Y ≤ k ] = 1 − e − e
*β )
Para a Log-log negativa a função de distribuição é
− ( αk −X
F ( α k − X* β ) = P [ Y ≤ k ] = e − e
*β)
Note que estas funções dão as probabilidades acumuladas de se observar uma
classe inferior ou igual a k, e que para determinar a probabilidade de se observar a
classe k, e necessário subtrair a probabilidade de se observar uma classe inferior
ou igual a k – 1. De uma forma generalizada, podemos então escrever, para cada
um dos j = 1, ..., n sujeitos a sua probabilidade de ocorrência para cada uma das
K classes:
P [Yj = 1] = F (α1 – xj β)
P [Yj = 2] = F (α2 – xj β) – F (α1 – xj β)
...
770
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
P [Yj = k] = F (αk – xj β) – F (αk–1 – xj β)
...
P [Yj = K] = 1 – F (αK–1 – xj β)
Finalmente, o sujeito j é classificado na classe k da variável dependente onde
a sua probabilidade de ocorrência for maior. A comparação das classificações
observadas e das classificações previstas pode também ser usada na avaliação da
qualidade do modelo global.
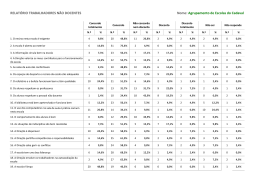
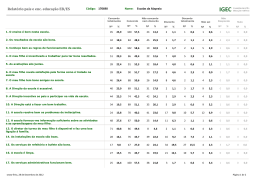
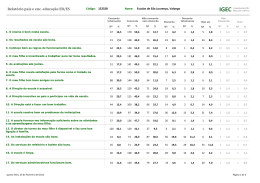
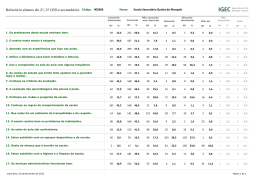
Vejamos agora um exemplo de aplicação da regressão ordinal com o SPSS.
Num estudo sobre a despenalização do aborto, um investigador perguntou a 25
pessoas que passavam na Rua Augusta (amostra de conveniência) qual o seu grau
de concordância com a despenalização do aborto até às 10 semanas, usando para
tal uma escala de tipo Likert com 5 pontos (1 – Discordo completamente; 2 –
Discordo; 3 – Nem concordo nem discordo; 4 – Concordo; e 5 – Concordo completamente). Em simultâneo registou o género dos participantes e a sua idade. A
matriz dos resultados é a seguinte:
Grau de Concordância
Sexo
Idade
5 – Concordo completamente
F
45
1 – Discordo completamente
M
38
3 – Nem concordo nem discordo
F
30
1 – Discordo completamente
F
55
4 – Concordo
F
23
2 – Discordo
F
29
1 – Discordo completamente
M
41
2 – Discordo
F
42
4 – Concordo
M
35
2 – Discordo
F
29
1 – Discordo completamente
M
30
4 – Concordo
F
25
1 – Discordo completamente
F
40
3 – Nem concordo nem discordo
M
35
1 – Discordo completamente
M
47
3 – Nem concordo nem discordo
F
33
1 – Discordo completamente
M
49
5 – Concordo completamente
F
25
2 – Discordo
F
21
771
ANÁLISE ESTATÍSTICA
Grau de Concordância
Sexo
Idade
4 – Concordo
F
28
1 – Discordo completamente
M
25
2 – Discordo
M
21
3 – Nem concordo nem discordo
F
35
2 – Discordo
M
45
4 – Concordo
F
24
Será que a opinião sobre a despenalização do aborto é idêntica entre homens e
mulheres? E qual é o efeito da idade? Depois de codificar a variável género em
“0 – Feminino” e “1 – Masculino”, e de introduzir a base de dados no SPSS, proceda para o menu AnalyzeRegressionOrdinal:
Seleccione a variável Despenalização para a caixa Dependent, a variável Sexo
para a caixa Factor (as variáveis independentes qualitativas são adicionadas como
factores) e a variável Idade para a caixa Covariate(s) (as variáveis independentes
quantitativas são adicionadas como covariáveis):
772
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
para definir o tipo de modelo ordinal a
De seguida clique no botão
ajustar, o número de iterações, etc. As opções do SPSS por default são, de um
modo geral, apropriadas para a maioria das análises, e neste menu, é necessário
apenas seleccionar o tipo de função Link. Seleccione, a opção Logit (ainda que,
como veremos adiante, esta possa não ser a função Link mais apropriada):
Clique no botão
e, de seguida, no botão
para definir as
opções de análise e os resultados a produzir. Na área Display, seleccione a opção
Test of parallel lines e na área Saved variables, seleccione as opções Estimated response
probabilities (para obter a probabilidade de cada sujeito responder a cada uma das
773
ANÁLISE ESTATÍSTICA
classes da variável dependente), e a opção Predicted category (para obter a classe da
variável dependente em que cada sujeito é classificado). Pode ainda seleccionar a
opção Predicted category probability para gravar na base de dados a probabilidade da
classe de resposta onde o sujeito foi classificado:
Clique no botão
, e no botão
pode definir o tipo de modelo a
ajustar: um modelo de efeitos principais (Main effects), um modelo com interacção
(interaction), etc. Seleccione a opção Main effects uma vez que não estamos interessados em testar a interacção entre os factores.
774
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
Clique em
para voltar ao menu da regressão ordinal. O botão
permite definir um modelo de “escala” onde se assume que podem existir
diferenças no padrão de resposta/variabilidade nas classes resultantes dos cruzamentos das variáveis independentes. Por exemplo, poder ser necessário assumir
que as frequências de resposta às 5 classes da variável dependente, são diferentes
entre homens e mulheres. Assim, interessava definir um parâmetro de escala para
a variável Sexo (para as variáveis quantitativas esta assumpção é menos comum, a
menos que a variável seja discreta). Um histograma de frequências permite avaliar a plausibilidade de um modelo de escala para os dados observados. Este tipo
de modelos é pouco frequente nas ciências sociais e humanas pelo que será, por
para obter o output da regresagora, ignorado. Clique finalmente no botão
são ordinal Logit (PoLytomous Universal Model – Ordinal regression):
PLUM – ORDINAL REGRESSION
Warnings
There are 86 (78.2%) cells (i.e., dependent variable levels by combinations of
predictor variable values) with zero frequencies.
Case Processing Summary
Marginal
Percentage
N
Despenalização
Sexo
Valid
Missing
Total
1 - Discordo
completamente
2 - Discordo
3 - Nem concordo
nem discordo
4 - Concordo
5 - Concordo
completamente
F
M
8
32.0%
6
24.0%
4
16.0%
5
20.0%
2
8.0%
15
10
25
0
25
60.0%
40.0%
100.0%
775
ANÁLISE ESTATÍSTICA
Os dois primeiros quadros indicam a percentagem de células, resultantes do
cruzamento das variáveis independentes, que não apresentam qualquer observação. Recorde que a existência de muitas células vazias impede a utilização do teste
do Qui-quadrado do ajustamento. No nosso exemplo, existem 78.2% de células
vazias, pelo que a aplicação deste teste não é aconselhada. Felizmente, esta condição não afecta a distribuição do rácio de verosimilhanças, e a sua aproximação à
distribuição do Qui-quadrado, que é avaliada no quadro seguinte:
Model Fitting Information
Model
Intercept Only
Final
-2 Log
Likelihood
73.442
63.371
Chi-Square
df
10.070
Sig.
2
.007
Link function: Logit.
Goodness-of-Fit
Pearson
Deviance
Chi-Square
86.638
60.599
df
82
82
Sig.
.342
.963
Link function: Logit.
Pseudo R-Square
Cox and Snell
Nagelkerke
McFadden
.332
.348
.132
Link function: Logit.
O quadro do “Model Fiting Information” revela que o modelo ajustado
(Final) é significativamente melhor do que o modelo nulo (intercept only)
(G2 (2) = 10.070; p = 0.007), i.e. que pelo menos uma das variáveis independentes do modelo afecta significativamente as probabilidades de ocorrência das
classes da variável dependente. O quadro do “Goodness-of-fit” apresenta os testes
à qualidade do ajustamento do Qui-quadrado de Pearson e da Deviance. Relembre
que, nestes testes, para que o modelo se ajuste aos dados (H0) é necessário não
rejeitar a hipótese nula. Assim, em ambos os testes o p-value é maior que os níveis
de significância habituais pelo que não se rejeita a H0 de que o modelo se ajusta
aos dados, ainda que a utilização destes testes seja desaconselhada face ao elevado
776
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
número de células com frequências nulas ( X P2 (82) = 86.683; p = 0.342;
D (82) = 60.599; p = 0.963). O quadro dos “Pseudo R-square” apresenta as estimativas dos pseudo-R2 mais comuns na regressão categorial. Todas as estatísticas
calculadas são moderadas a baixas, em particular o pseudo-R2 de McFadden.
O quadro dos “Parameters Estimates” apresenta as estimativas dos Treshold e
dos coeficientes de regressão associados às variáveis independentes, os seus erros-padrão, a estatística de Wald, o p-value do teste, e o respectivo intervalo de confiança:
Parameter Estimates
Threshold
Location
[Despenalização = 1.00]
[Despenalização = 2.00]
[Despenalização = 3.00]
[Despenalização = 4.00]
Idade
[Sexo=.00]
[Sexo=1.00]
Estimate
-2.594
-1.181
-.291
1.410
-.082
1.837
0a
Std.
Error
1.704
1.637
1.620
1.695
.044
.854
.
Wald
2.319
.520
.032
.692
3.427
4.622
.
df
1
1
1
1
1
1
0
Sig.
.128
.471
.858
.405
.064
.032
.
95% Confidence Interval
Lower Bound Upper Bound
-5.933
.745
-4.390
2.028
-3.466
2.885
-1.912
4.733
-.168
.005
.162
3.512
.
.
Link function: Logit.
a. This parameter is set to zero because it is redundant.
Uma vez que a variável dependente apresenta 5 classes, o modelo apresenta 4
thresholds (αk). De um modo geral, estes thresholds são usados apenas para o cálculo de probabilidades, e para além desta utilização, o seu interesse é diminuto.
As estimativas dos declives (coeficientes de regressão) são utilizadas para inferir
da significância das variáveis independentes sobre as probabilidades das classes da
variável dependente (em rigor sobre o Link das probabilidades acumuladas). No
nosso exemplo, porque foi usado a função Logit, o modelo pode escrever-se como:
P [ Y ≤ k] ⎤
Ln ⎡⎢
= α k − ( −0.082 Idade + 1.837 Sexo [0])
P
⎣ [ Y > k ] ⎥⎦
777
ANÁLISE ESTATÍSTICA
ou em Probabilidade não-linear acumulada
P [ Y ≤ k] =
1
1 + e − ( α k − 0.082 Idade +1.837 Sexo [0])
Assim, quando a idade aumenta 1 ano, o Ln da probabilidade de se observar
uma classe de ordem inferior, relativamente a uma classe de ordem superior
aumenta 0.082, i.e. à medida que a idade aumenta, diminui a probabilidade de se
observarem as classes de maior ordem (concordância), relativamente às classes de
menor ordem (discordância). Dito de outra forma podemos afirmar que à medida
que a idade aumenta, diminui a concordância com a despenalização do aborto,
ainda que este efeito seja apenas marginalmente significativo (b = – 0.082;
2
X Wald
(1) = 3.427; p = .064). Uma vez que estamos a usar a função Logit,
podemos calcular o rácio das chances usando a expressão e –β.1 Substituindo β
pela sua estimativa, obtemos e– (– 0.082) = 1.085, ou seja por ano de idade o rácio
da probabilidade de se observarem classes de menor ordem comparativamente à
probabilidade de se observarem classes de maior ordem aumenta 8.5%, revelando
que com o aumento da idade é maior a probabilidade de os inquiridos serem
menos favoráveis à despenalização do aborto. Relativamente à variável Sexo,
podemos afirmar, de acordo com o modelo, que para a classe F relativamente à
classe omitida de referência (M), o Ln da probabilidades de se observar uma classe
de ordem inferior, relativamente a uma classe de ordem superior diminui 1.837.
Na classe F, comparativamente com a classe M, as classes de menor ordem da
variável dependente (discordância) são menos prováveis do que as classes de
maior ordem (concordância) revelando que as mulheres são mais concordantes
com a despenalização do aborto do que os homens. O rácio de chances de se
observar uma classe de menor ordem relativamente a uma classe de maior ordem
pode ser facilmente calculado por e– (1.837) = 0.338. O rácio das chances das
classes de menor ordem (discordância), relativamente às classes de maior ordem
(concordância), diminui 66.2% quando o sexo passa de Masculino (classe de
referência) para Feminino, revelando que as mulheres são mais favoráveis à despenalização do aborto do que os homens. Note que os rácios das chances calculados
para a Idade e para o Sexo, são constantes para todas as classes se os declives do
modelo forem homogéneos. O quadro seguinte “Test of Paralell Lines” permite
testar este pressuposto:
(1)
O cálculo do rácio das chances só é válido se a função Link for a Logit, para as outras funções Link
não faz sentido calcular este rácio.
778
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
Test of Parallel Lines c
Model
Null Hypothesis
General
-2 Log
Likelihood
63.371
52.673a
Chi-Square
10.699b
df
Sig.
6
.098
The null hypothesis states that the location parameters (slope
coefficients) are the same across response categories.
a. The log-likelihood value cannot be further increased after
maximum number of step-halving.
b. The Chi-Square statistic is computed based on the
log-likelihood value of the last iteration of the general model.
Validity of the test is uncertain.
c. Link function: Logit.
O modelo sob H0 (Null Hypothesis) assume que todos os declives são iguais
(i.e. que as linhas das funções Link são paralelas) enquanto que o modelo “General” assume que a H1: Existe pelo menos um declive diferente dos restantes, é
válida. A diferença dos – 2LL permite calcular uma estatística com distribuição
Qui-quadrado, e se esta estatística não for significativa, i.e. se p-value > α, podemos afirmar que o ajustamento do modelo não melhora libertando os coeficientes
de regressão ou que, dito de outra forma, os declives são homogéneos. Contudo,
antes de analisar a significância da diferença entre os dois modelos, é de notar as
notas de rodapé “a” e “b” do quadro. Estas notas indicam que o programa foi
incapaz de alcançar uma solução com o número máximo de passos do algoritmo
(maximum step-halving) previamente definido e que desta forma a validade do teste
não é garantida. Assim, antes de mais, é necessário refazer a análise, e no menu
Options, aumentar o Maximum step-halving para, por exemplo, 50:
779
ANÁLISE ESTATÍSTICA
Eis o novo quadro do teste da homogeneidade dos declives:
Test of Parallel Lines
Model
Null Hypothesis
General
-2 Log
Likelihood
63.371
52.161
Chi-Square
a
df
11.210
Sig.
6
.082
The null hypothesis states that the location parameters (slope
coefficients) are the same across response categories.
a. Link function: Logit.
2
Sendo X LP
(6) = 11.210 e p = 0.082, não rejeitamos a H0 de que os declives são homogéneos, validando assim o pressuposto da homogeneidade dos declives. Não deve, porém, passar despercebido o facto de a significância do teste ser
marginal, i.e. se considerássemos uma probabilidade de erro de tipo I (α) maior,
por exemplo α = 0.10, já não era possível assumir a veracidade do pressuposto
de homogeneidade dos declives. Como referido anteriormente, a não rejeição de
H0 pode dever-se à escolha errada da função Link, e nesta fase da análise o leitor
deveria considerar outros tipos de funções Link atendendo às recomendações feitas atrás (cap. 15.3.1.) (voltaremos adiante a este tópico).
O passo final da regressão ordinal é a avaliação da qualidade de classificação/previsão do modelo. De acordo com as selecções efectuadas no menu Output
foram adicionadas novas variáveis à base de dados que registam a probabilidade
de ocorrência de cada um dos sujeitos em cada uma das 5 classes da variável
dependente (EST1_1; EST2_1; EST3_1; EST4_1; EST5_1); a classe da variável
dependente prevista para cada sujeito (PRE_1) e a probabilidade de classificação
estimada para a classe prevista (PCP_1):
780
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
Uma vez que usamos a função Logit, a probabilidade acumulada de cada uma
das classes é dada por
P [ Y ≤ k | x *] =
1
1+ e
− ( α k − β ' x *)
Assim, para o primeiro sujeito da base de dados no nosso exemplo (Idade = 45;
Sexo = F) a probabilidade da resposta ser na classe 1 da variável dependente é:
P [ Y = 1 | [45 F ] '] = P [ Y ≤ 1 | [45 F ] '] =
=
=
1
1+ e
− ( α k − β ' x *)
=
1
1 + e − [ −2.594 − ( −0.082 × 45 + 1.837 )]
=
= 0.322
781
ANÁLISE ESTATÍSTICA
De modo semelhante as probabilidades da resposta nas outras classes são:
P [ Y = 2 | [45 F ] '] = P [ Y ≤ 2] − P [ Y = 1] =
=
1
1+ e
− [ −1.181 − ( −0.082 × 45 + 1.837 )]
− 0.332 =
= 0.662 − 0.322 = 0.340
P [ Y = 3 | [ 45 F ] '] = P [ Y ≤ 3] − P [ Y ≤ 2] =
=
1
1 + e − [ −0.291 − ( −0.082 × 45 + 1.837 )]
− 0.662 =
= 0.827 − 0.662 = 0.165
P [ Y = 4 | [45 F ] '] = P [ Y ≤ 4] − P [ Y ≤ 3] =
=
1
1+ e
− [ −0.141 − ( −0.082 × 45 + 1.837 )]
− 0.827 =
= 0.963 − 0.827 = 0.136
P [ Y = 5 | [45 F ] '] = P [ Y ≤ 5] − P [ Y ≤ 4] =
= 1 − 0.963 = 0.037
Estes são os valores (arredondados a 2 casas decimais) que se encontram na
base de dados para o primeiro sujeito. Assim, a classe prevista para o primeiro
individuo é a classe “2 – Discordo”, já que é nesta que se observa a maior probabilidade de resposta. De modo semelhante, para o 2º sujeito (Idade = 38;
Sexo = M), as probabilidades de resposta em cada uma das classes são:
P [ Y = 1 | [38 M ] '] = P [ Y ≤ 1 | [38 M ] '] =
=
=
1
1+ e
− [ −2.594 − ( −0.082 ×38 )]
1
= 0.628
782
=
1+ e
− ( α k − β ' x *)
=
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
P [ Y = 2 | [38 M ] '] = P [ Y ≤ 2] − P [ Y ≤ 1] =
=
1
1+ e
− [ −2.594 − ( −0.082 ×38 )]
− 0.628 =
= 0.874 − 0.628 = 0.246
P [ Y = 3 | [38 M ] '] = 0.070
P [ Y = 4 | [38 M ] '] = 0.045
P [ Y = 5 | [38 M ] '] = 0.011
O sujeito 2 é então classificado na classe “1 – Discordo completamente” uma
vez que é nesta que se observa a maior probabilidade de resposta.
Uma outra forma de avaliar a qualidade do modelo é comparando a percentagem de classificações correctas obtidas pelo modelo, com a percentagem de
classificações correctas proporcional por acaso. Relembre que se o modelo não
classificar correctamente pelo menos 25% dos casos mais do que a classificação
correcta proporcional por acaso, a capacidade predictiva do modelo é reduzida
(reveja o cap. 15.1.7). O SPSS (até à v. 15 inclusive) não apresenta estes cálculos,
mas estes são fáceis de realizar cruzando as classes da variável dependente, com as
classes previstas para a variável dependente (usando a nova variável PRE_1 da
base de dados). Recorra então ao menu AnalyzeDescriptive StatisticsCrosstabs:
783
ANÁLISE ESTATÍSTICA
Seleccione agora as variáveis
respectivamente:
Despenalização
e
PRE_1
para as
Rows
e
Columns
De seguida clique no botão
e seleccione a opção Row na área Percentapara obter a percentagem de classificações correctas para cada uma das classes da variável dependente:
ges,
784
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
Clique em
e em
para obter o output. Eis a tabela de contingência que relaciona as classes observadas e as classes previstas na resposta à
questão “Concorda com a despenalização do aborto”:
Despenalização * Predicted Response Category Crosstabulation
Despenalização
Discordo
completamente
Discordo
Nem concordo
nem discordo
Concordo
Concordo
completamente
Total
Count
% within Despenalização
Count
% within Despenalização
Count
% within Despenalização
Count
% within Despenalização
Count
% within Despenalização
Count
% within Despenalização
Predicted Response Category
Discordo
completa
mente
Discordo
Concordo
7
1
0
87.5%
12.5%
.0%
1
2
3
16.7%
33.3%
50.0%
1
2
1
25.0%
50.0%
25.0%
1
0
4
20.0%
.0%
80.0%
0
1
1
.0%
50.0%
50.0%
10
6
9
40.0%
24.0%
36.0%
Total
8
100.0%
6
100.0%
4
100.0%
5
100.0%
2
100.0%
25
100.0%
Note em primeiro lugar, que das 5 classes originais, apenas 3 são previstas
pelo modelo. O modelo prediz correctamente 87.5% da classe “Discordo completamente”. A percentagem de previsões correctas é de 33% para a classe “Discordo”,
80% para a classe “Concordo”, e 0% para as classes “Nem concordo nem discordo”
e “Concordo completamente”. O modelo classifica correctamente 7 + 2 + 4 =
= 13 sujeitos e a percentagem sujeitos classificados correctamente pelo modelo é
13 / 25 × 100 = 52%. Pelo contrário a percentagem de classificação correcta
proporcional por acaso é (0.322 + 0.242 + 0.162 + 0.202 + 0.082) × 100 =
= 23.2%. O modelo classifica assim razoavelmente melhor do que a classificação
por acaso.
O leitor terá já reparado, ao longo da descrição dos resultados do modelo
ordinal Logit, que existem vários problemas com este modelo. Na verdade, o
passo inicial do processo de ajustamento de um modelo ordinal deve ser sempre o
da escolha da função Link apropriada de acordo com a descrição feita anteriormente (reveja a tabela das funções Link no cap. 15.3.1). Fazendo um histograma
de frequências (GraphsHistogram) para a variável “Despenalização”, é possível
observar que as classes de maior frequência são as classes de menor ordem como
se ilustra na figura seguinte:
785
ANÁLISE ESTATÍSTICA
8
Frequencia
6
4
2
0
0
1
2
3
4
5
6
Despenalização
Assim, a função Link mais apropriada será, provavelmente, a função Log-log
negativa. A diferença de qualidade entre os dois modelos pode ser avaliada heuristicamente comparando os – 2LL dos dois modelos. Naturalmente, o melhor
modelo é aquele que apresentar menor – 2LL. Adicionalmente, a significância
dos coeficientes, e do teste de homogeneidade dos declives, bem como a capacidade predictiva dos modelos podem ser também tidos em conta no processo de
decisão da função Link a usar. Refaçamos então o nosso exemplo, mas agora com
a função Link Log-log negativa (mantendo todas as outras opções de análise):
786
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
Eis os novos outputs do SPSS para a regressão ordinal com a função Log-log
negativa:
Warnings
There are 86 (78.2%) cells (i.e., dependent variable levels by combinations of
predictor variable values) with zero frequencies.
Case Processing Summary
8
6
Marginal
Percentage
32.0%
24.0%
4
16.0%
5
20.0%
N
Despenalização
Sexo
Discordo completamente
Discordo
Nem concordo nem
discordo
Concordo
Concordo
completamente
F
M
Valid
Missing
Total
2
8.0%
15
10
25
0
25
60.0%
40.0%
100.0%
Model Fitting Information
Model
Intercept Only
Final
-2 Log
Likelihood
73.442
61.561
Chi-Square
df
11.881
Sig.
2
.003
Link function: Negative Log-log.
Goodness-of-Fit
Pearson
Deviance
Chi-Square
78.884
58.788
df
82
82
Sig.
.577
.975
Link function: Negative Log-log.
Pseudo R-Square
Cox and Snell
Nagelkerke
McFadden
.378
.397
.156
Link function: Negative Log-log.
787
ANÁLISE ESTATÍSTICA
Parameter Estimates
Threshold
Location
[Despenalização = 1.00]
[Despenalização = 2.00]
[Despenalização = 3.00]
[Despenalização = 4.00]
Idade
[Sexo=.00]
[Sexo=1.00]
Estimate Std. Error
-1.498
1.155
-.518
1.124
.139
1.135
1.604
1.276
-.062
.031
1.403
.608
0a
.
Wald
1.682
.212
.015
1.580
4.054
5.328
.
df
1
1
1
1
1
1
0
Sig.
.195
.645
.903
.209
.044
.021
.
95% Confidence Interval
Lower Bound Upper Bound
-3.761
.766
-2.722
1.685
-2.086
2.364
-.898
4.106
-.123
-.002
.212
2.595
.
.
Link function: Negative Log-log.
a. This parameter is set to zero because it is redundant.
Test of Parallel Linesa
Model
Null Hypothesis
General
-2 Log
Likelihood
61.561
51.670
Chi-Square
9.891
df
Sig.
6
.129
The null hypothesis states that the location parameters (slope
coefficients) are the same across response categories.
a. Link function: Negative Log-log.
Comparativamente ao modelo ordinal Logit, o novo modelo Log-log negativo,
apresenta menor – 2LL (61.561 vs. 63.371), sendo o p-value do modelo ordinal
Log-log negativo cerca de 2 × menor do que o p-value do modelo ordinal Logit.
Adicionalmente, a variável idade que no modelo ordinal Logit era apenas marginalmente significativa (p = 0.064) passou a ser estatisticamente significativa no
novo modelo (p = 0.044). Também, no teste da homogeneidade dos declives o p-value do modelo Log-log negativo é maior do que no modelo ordinal Logit (0.129
vs. 0.098), suportando a ideia de que a função Log-log negativa é mais apropriada
para a distribuição de frequências observada nas classes da variável dependente.
Finalmente, a percentagem de classes correctamente classificada é dada na tabela
de contingência seguinte:
788
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
Despenalização * Predicted Response Category Crosstabulation
Despenalização Discordo
completamente
Total
Count
% within Despenalização
Discordo
Count
% within Despenalização
Nem concordo nem Count
discordo
% within Despenalização
Concordo
Count
% within Despenalização
Concordo
Count
completamente
% within Despenalização
Count
% within Despenalização
Predicted Response Category
Discordo
completa
mente
Discordo Concordo
7
1
0
87.5%
12.5%
.0%
1
2
3
16.7%
33.3%
50.0%
1
2
1
25.0%
50.0%
25.0%
1
0
4
20.0%
.0%
80.0%
1
0
1
50.0%
.0%
50.0%
11
5
9
44.0%
20.0%
36.0%
Total
8
100.0%
6
100.0%
4
100.0%
5
100.0%
2
100.0%
25
100.0%
Assim, a taxa de classificações correctas é de 13/25 × 100 = 52% valor que,
contudo, não é melhor do que o obtido com o modelo ordinal Logit.
Interessa agora avaliar a plausibilidade de um modelo ordinal de escala.
Comecemos por fazer o histograma de frequências para as classes da variável
dependente cruzadas com o sexo. Seleccione a opção GraphsHistogram e no menu
do Histogram seleccione a variável Despenalização para a caixa Variable e a variável
Sexo para a caixa Columns:
789
ANÁLISE ESTATÍSTICA
Clique no botão
para obter o gráfico:
Sexo
F
M
Frequencia absoluta
6
5
4
3
2
1
0
1
2
3
4
5
1
2
3
4
5
Despenalização
Como ilustra a figura anterior, a distribuição das frequências de resposta
entre os dois sexos são algo diferentes. Nos homens a classe mais frequente é a
classe “1 – Discordo completamente” enquanto que nas mulheres as classes mais
frequentes são as classes “2 – Discordo” e “4 – Concordo”. Observadas as diferenças das frequências de resposta, entre as classes da variável sexo, podemos agora
averiguar se a introdução de um parâmetro de escala para a variável Sexo, resultará num melhor modelo predictivo. Voltemos ao menu da regressão ordinal no
SPSS: AnalyzeRegressionOrdinal e no menu Scale seleccionemos a variável Sexo
para a caixa Scale model:
790
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
Clique no botão
novo modelo:
e no botão
para obter os outputs para o
PLUM – ORDINAL REGRESSION
Warnings
The TPARALLEL keyword specified in the PRINT subcommand is ignored because
an non-empty SCALE subcommand is specified. The score test for equal slopes
assumption is available only for a model without a scale component, and there are
effects beside the intercept in the location component.
There are 86 (78.2%) cells (i.e., dependent variable levels by combinations of
predictor variable values) with zero frequencies.
Case Processing Summary
8
6
Marginal
Percentage
32.0%
24.0%
4
16.0%
5
20.0%
2
8.0%
15
10
25
0
25
60.0%
40.0%
100.0%
N
Despenalização
Sexo
Discordo completamente
Discordo
Nem concordo nem
discordo
Concordo
Concordo
completamente
F
M
Valid
Missing
Total
Model Fitting Information
Model
Intercept Only
Final
-2 Log
Likelihood
73.442
61.542
Chi-Square
df
11.900
Sig.
3
.008
Link function: Negative Log-log.
Goodness-of-Fit
Pearson
Deviance
Chi-Square
79.892
58.769
df
81
81
Sig.
.514
.970
Link function: Negative Log-log.
791
ANÁLISE ESTATÍSTICA
Pseudo R-Square
Cox and Snell
Nagelkerke
McFadden
.379
.398
.156
Link function: Negative Log-log.
Parameter Estimates
Estimate Std. Error
Threshold [Despenalização = 1.0 -1.419
1.355
[Despenalização = 2.0
-.482
1.162
[Despenalização = 3.0
.136
1.100
[Despenalização = 4.0 1.503
1.316
Location Idade
-.060
.037
[Sexo=.00]
1.363
.659
[Sexo=1.00]
0a
.
Scale
[Sexo=.00]
-.075
.536
[Sexo=1.00]
0a
.
Wald
1.098
.172
.015
1.305
2.718
4.275
.
.020
.
df
1
1
1
1
1
1
0
1
0
95% Confidence Interval
Sig. Lower Bound Upper Bound
.295
-4.074
1.236
.678
-2.759
1.796
.902
-2.020
2.292
.253
-1.076
4.082
.099
-.132
.011
.039
.071
2.656
.
.
.
.889
-1.125
.975
.
.
.
Link function: Negative Log-log.
a. This parameter is set to zero because it is redundant.
Note em primeiro lugar, que no caso dos modelos de escala o SPSS não produz o teste à homogeneidade dos declives. Para comparar o novo modelo de
escala, com o modelo anterior interessa comparar os – 2LL dos dois modelos.
O – 2LL do modelo de escala é 61.542, valor idêntico ao – 2LL do modelo anterior (61.561). Por outro lado, o coeficiente γ associado à variável Sexo é reduzido
2
(1) = 0.020; p = 0.889). O modelo
e não significativo (γ (F ) = – 0.075; X Wald
de escala não apresenta melhores qualidades estatísticas do que o modelo sem
escala. Por questões de parcimónia, o melhor modelo é o modelo mais simples, e
no nosso exemplo, o modelo Log-log negativo é, assim, o mais apropriado para
descrever as probabilidades cumulativas observadas neste estudo.
792
CAPÍTULO 15 – REGRESSÃO CATEGORIAL
„ Exemplo de como reportar resultados
Métodos
(...)
Análise Estatística
(...) Para avaliar se a idade e o sexo apresentavam um efeito estatisticamente
significativo sobre as probabilidades de resposta à variável “Concorda com a
despenalização do aborto até às 9 semanas”, recorreu-se à regressão ordinal
com função Link Log-log negativa. A escolha da função Link foi feita de acordo
com os critérios de distribuição de frequências das classes da variável dependente definidos em Maroco (2007). Consideraram-se também outras funções
Link, nomeadamente a Logit, mas a Log-log negativa foi a que apresentou
melhor significância estatística. O pressuposto do modelo da homogeneidade
2
de declives foi validado ( X LP
(6) = 9.891 e p = 0.129). Todas as análises foram
feitas com o software SPSS (v. 14; SPSS Inc., Chicago) e os outputs do
programa são apresentados em anexo.
Resultados
Os coeficientes e a significância do modelo ordinal ajustado – Ln (– ln (P (Y ≤ k)
= αk – (– 0.062 Idade + 1.403 Sexo [F ]) são apresentados na tabela 1. O modelo
é estatisticamente significativo ( G 2 (2) = 11.881; p = 0.003), ainda que a dimen2
2
são do efeito seja algo reduzida ( RMF
= 0.156; RN2 = 0.397; RCS
= 0.378).
Tabela 1. Estimativas e significância do modelo Log-log negativo ajustado
p-value
Intervalo de
confiança
a 95%
1
.195
]–3.761;0.766[
.212
1
.645
]–2.722; 1.685[
1.135
.015
1
.903
]–2.086; 2.364[
1.604
1.276
1.580
1
.209
]–.898; 4.106[
Idade
–.062
.031
4.054
1
.044
]–.123; –.002[
[Sexo = .00]
1.403
.608
5.328
1
.021
]0.212; 2.595[
Estimativa
Erro-padrão
2
X Wald
[Despenalização
= 1.00]
–1.498
1.155
1.682
[Despenalização
= 2.00]
–.518
1.124
[Despenalização
= 3.00]
.139
[Despenalização
= 4.00]
Localização
Threshold
Parâmetros
g.l.
793
ANÁLISE ESTATÍSTICA
De acordo com o modelo, à medida que a idade aumenta, diminui a probabilidade de se observarem classes de maior ordem (concordância) ( bIdade = –
0.062; p = 0.044). Relativamente ao sexo, observa-se maior probabilidade das
classes de maior ordem (concordância) nas mulheres, comparativamente com
os homens (bF = 1.403; p = 0.021). A evolução das probabilidades de cada
uma das classes em função da Idade e por sexo são ilustradas na figura 1. É
de referir que nos homens a classe mais provável é a classe “1 – Discordo
completamente” e que a probabilidade de observar esta resposta aumenta com
a Idade de forma marcada. Nas mulheres a probabilidade de observar classes
de menor ordem também aumenta com a idade e, a partir dos 45 anos, a
classe 1 é a classe de maior probabilidade. Para as mulheres até aos 30 anos,
a classe de resposta mais provável é a classe “4 – Concordo”, entre os 30 e os
45 anos a classe mais provável é a classe “2 – Discordo” (Fig. 1).
Sexo
F
1,0
0,8
M
Discordo
completamente
Discordo
Nem concordo
nem discordo
Concordo
Concordo
completamente
P[Y=k]
0,6
0,4
0,2
0,0
20
30
40
50
20
30
40
50
Idade
Figura 1. Evolução das probabilidades de resposta em cada uma das 5 classes
da variável “Concorda com a despenalização do aborto” ( · – Discordo completamente; … – Discordo; { – Nem concordo nem discordo; ‘ – Concordo; U –
2
Concordo completamente) ( G 2 (2) = 11.881; p = 0.003; RMF
= 0.156; RN2 = 0.397;
2
RCS = 0.378)
794