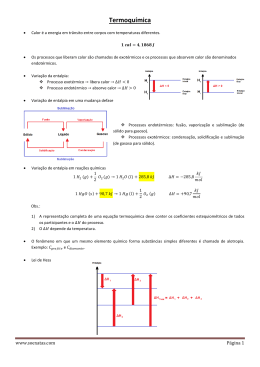
Balanço de Energia em Combustão
O primeira lei da termodinâmica traduzida pelo
balanço de energia permite analisar dois conceitos
importantes na combustão: temperatura adiabática e
poder calorífico que se descrevem de seguida.
Sistema fechado W+Q=∆U=UFinal-UInicial
∆V=0 Æ W=0 e Q=∆U
∆P=0 Æ W=-P ∆V e Q=∆U+ P∆V= ∆H
Sistema aberto (que troca massa com o exterior)
. .
.
DE
v2
= W + Q + ∑ m( h + gz +
)
Dt
2
e −s
Em regime estacionário DE/Dt=0 e desprezando as
variações de energia cinética e potencial:
. .
.
W + Q = m ∆h ou W + Q = ∆H
Num sistema sem variação de volume W=0 e Q=∆H.
h=u+Pv ou H=U+PV pelo que
∆h= ∆u+ ∆(Pv) ou ∆H= ∆U+ ∆(PV).
∆(PV) é muito pequeno para sólidos e líquidos e para
gases pode ser relacionado por ∆(PV)=∆(nR0T)
A diferença entre as variações de entalpia e de
energia interna depende da variação de número de
moles de espécies gasosas na reacção química.
Casos extremos de evoluções na combustão
Isotérmico Æ Entalpia de combustão
Como a reacção de combustão é exotérmica a
entalpia dos produtos é maior que a dos reagentes ou
a variação de entalpia de combustão é negativa
No processo isotérmico ∆H = ∆U+∆(n) R0T
Ou ∆H = ∆U + (nProdutos-nReagentes)Gasosos R0T
Quando se considera a reacção com condições iniciais
e finais com T=25ºC, P=1 atm, definem-se as entalpias
de reacção padrão ∆h 0 , ∆h 0 , ∆H 0 e de modo
equivalente as energias de reacção padrão.
O simetrico das entalpias e energias de reacção
permitem definir o Poder Calorífico, respectivamente
a pressão e a volume constante Æ Calor libertado.
Definem-se ainda dois tipos de valores inferior e
superior dependente de se considerar água no
estado de vapor ou líquido respectivamente:
m
PCS = PCI + w hfg
mf
em base mássica para valores a pressão constante ou
m
PCSv = PCIv + w ufg a volume constante.
mf
Utiliza-se mais a pressão constante por corresponder
a mais aplicações (Excepção nos motores gasolina).
A diferença entre os dois valores é:
PCSv = PCS + R0T0 (nP − nR ) em base molar
Adiabático Æ Temperatura adiabática de combustão
A temperatura final dos produtos é superior à dos
reagentes sendo a entalpia semelhante.
H
Inicial
FAdiabático
FIsotérmico
T
A variação de entalpia de reacção não depende da
quantidade de espécies inertes enquanto a
temperatura adiabática de combustão depende.
Vamos analisar mais este conceito posteriormente.
Entalpias de formação
Como à mesma temperatura reagentes e produtos
têm uma diferença de entalpia, define-se uma base
comum para todas as substâncias, convencionando o
valor nulo para as condições de referência (T=25ºC)
para algumas espécies: C(s), O2, H2, N2, S(s) etc.
Para uma espécie qualquer considera-se a sua
formação a partir das espécies de referência e definese a sua entalpia de formação como a entalpia de
reacção para formar o elemento a partir de outras
espécies às condições de referência para ambos.
Valores normalmente apresentados em base molar.
Exemplos: CO, CO2, H2O(gas), H2O (liq).
o
1


h f CO = ∆h 0  C(s ) + O2 → CO  = −110530 kJ/kmol de CO
2


h f CO2 = ∆h 0 (C(s ) + O2 → CO2 ) = −393520 kJ/kmol de CO2
o
o
1


h f H2O ( g ) = ∆h 0  H 2 + O2 → H 2O( g )  = −241820 kJ/kmol H2O
2


o
1


h f H2O ( l ) = ∆h 0  H 2 + O2 → H 2O(l )  = −285830 kJ/kmol H2O
2


A diferença entre os dois primeiro representa a
entalpia de combustão do monóxido de carbono:
1


∆ h 0  CO + O2 → CO2  = −282990 kJ/kmol
2


A entalpia de formação de água líquida podia ser
obtida do valor de gás - entalpia de vaporização
hfg = hfg MH2O = 2442,3 × 18,02 = 44010 kJ/kmol
C(s), H2, O2, N2
-110530
kJ/kmol
CO
-282990
kJ/kmol
CO2
REFERÊNCIA
-241820
kJ/kmol
-393520
kJ/kmol
H2O (g)
hfg
-285830
kJ/kmol
H2O (l)
A entalpia de formação dos combustíveis podem ser
definidas a partir da entalpia de reacção do
combustível conduzindo à formação dos produtos.
Ex. Metano com poder calorífico inferior 50016 kJ/kg
ou em termos molares 50016x16,04=802256 kJ/kmol
∆ h 0 (CH 4 + 2O2 → CO2 + 2H 2O(g )) = −802256 kJ/kmol
0
∆hCH4 = hf0CO2 + 2 × hf0 H2O − 2 × hf0O2 − hf0CH4 Æ
hf0CH4 = −74850kJ / kmol
A entalpia de formação do combustível no estado
líquido pode ser definido a partir do valor no estado
gasoso, subtraindo a entalpia de vaporização.
0
Ex: hf CH OH ( g ) = −200670 kJ / kmol , hfg = 37900 kJ / kmol
3
hf
0
CH3OH ( l )
= hf0CH3OH ( g ) − hfg CH OH = −238570 kJ / kmol
3
O poder calorífico do combustível no estado líquido
também pode ser obtido a partir do valor
correspodnente no estado gasoso.
A entalpia para qualquer temperatura para uma
espécie é obtida somando à entalpia de formação a
parcela ‘sensível’ (h-h298). Existem tabelas com
valores de entalpia sensível em relação à referência
(298K) ou com valor nulo correspondente a 0K,
quando são obtidos de polinómios (a6i=0)
h/R0= a1iT+ a2iT2/2+ a3iT3/3+ a4iT4/4+ a5iT5/5+ a6i
cp/R0= a1i+ a2iT+ a3iT2+ a4iT3+ a5iT4
Cálculo da temperatura adiabática de combustão
A temperatura adiabática de combustão pode ser
obtida a partir de um balanço de energia, calculando a
entalpia dos produtos como igual à entalpia dos
reagentes.
A partir da aproximação polinomial da entalpia em
função da temperatura pode-se calcular a temperatura.
Ex.
Temperatura
adiabática
estequiometrica de Metano à
referência (298K) com oxigénio:
de
combustão
temperatura de
H Pr od (CO2 + 2H 2O(g )) = H Re ag . (CH 4 + 2O2 ) = −74850 kJ
(
H Pr od (CO2 + 2H 2O(g )) = hf0 + ∆h
)
CO2
(
(
+ 2 × hf0 + ∆h
)
H 2O ( g )
H Pr od (CO2 + 2H 2O(g )) = −877160 + ∆hCO2 + 2 × ∆hH 2O ( g )
)
Função da temperatura
De onde se pode calcular TAdiabático=
Se considerarmos a combustão com ar em vez de
oxigénio o valor da temperatura adiabática vai ser
diferente:
H Pr od (CO2 + 2H 2O(g ) + 7,52N 2 ) = H Re ag . (CH 4 + 2O2 + 7,52N 2 ) = −74850 kJ
(
H Pr od (CO2 + 2H 2O(g ) + 7,52N 2 ) = hf0 + ∆h
)
CO2
(
(
+ 2 × hf0 + ∆h
)
H 2O ( g )
+ 7,52∆hN2
H Pr od (CO2 + 2H 2O(g ) + 7,52N 2 ) = −877160 + ∆hCO2 + 2 × ∆hH 2O ( g ) + 7,52∆hN2
De onde se pode calcular TAdiabático=2226K
)
Balanço de energia em sistemas de combustão
H
Inicial
∆H0
Calor
trocado
Final
T
Num caso geral a temperatura dos reagentes e a dos
produtos são ambas diferenças do estado de referência
Nestes casos para quantificar o calor fornecido
(normalmente<0) Q=∆H tem de se quantificar as
várias parcelas desde a situação inicial à final:
Q = H Pr od − H Re ag =
∑ n& (h
i =Pr od
i
f
0
+ ∆h
)
i
−
∑ n& (h
j =Re ag
j
0
f
+ ∆h
)
j
que também se pode escrever em termos mássicos

&  ∑ x i hf0 + ∆h i − ∑ x j hf0 + ∆h
Q=m
j =Re ag
i =Pr od


&  ∑ x i ∆hi − ∑ x j ∆h j +  ∑ x i hfi0
Q=m

j =Re ag
i =Pr od
 i =Pr od
(
)
(
) 
j

−
∑x h
j =Re ag
j
0
fj




Entalpia de reacção0
= - Poder Calorífico
No caso de combustão completa (Comb. Gasoso)
pode-se obter:
[
]
& Gases c p Re ag (TRe ag − T0 ) − c p Pr od (TPr od − T0 ) + m
& Combustível PC
QTransf = m
Para o caso de combustão incompleta ou quando
ocorre mudança de fase de reagentes e/ou produtos
tem de se quantificar a variação de entalpia
correspondente e incluir na expressão para o calor
transferido.
O rendimento de um equipamento de uma caldeira ou
câmara de combustão é normalmente representado
como a razão entre o calor obtido e a entrada de
energia no sistema. A entrada de energia é
quantificada pelo produto do caudal de combustível
pelo PCS (Poder Calorífico Superior) e a entalpia do ar
de combustão (pode ser pré-aquecido)
Existem dois métodos para determinar o rendimento
de câmaras de combustão: Método directo e indirecto.
Método Directo: Representa a razão entre o calor
obtido na caldeira (do lado da água/vapor) em relação
à entrada total de energia.
Método Indirecto: Representa 1 menos as perdas a
dividir pela entrada total de energia. As parcelas
principais das perdas são:
- Entalpia sensível dos produtos de combustão
- Entalpia latente nos produtos de combustão
(vapor de água nos produtos)
- Perda de vaporização da humidade do ar
- Perda por inqueimados sólidos e gasosos
- Perdas de calor para o ambiente
- Perdas do circuito de água/vapor e outras ...
Existem normas para o cálculo da eficiência de
caldeiras que apresentam esquemáticos (DIN, ASME)