Gisele Nascimento
Patrícia Ferreira de Araújo
Estudo acerca do coeficiente de determinação nos modelos lineares e algumas generalizações.
Trabalho de conclusão de curso apresentado
para a disciplina Laboratório de Estatística II
do curso Bacharelado em Estatística do Setor
de Ciências Exatas, da Universidade Federal
do Paraná.
Orientador: Prof. Fernando L. Pérez
Curitiba – PR
Junho 2009
ESTUDO ACERCA DO COEFICIENTE DE DETERMINAÇÃO NOS
MODELOS LINEARES E ALGUMAS GENERALIZAÇÕES
Alunas: Gisele Nascimento e Patrícia Ferreira de Araújo
Departamento de Estatística
Universidade Federal do Paraná
RESUMO
Nos modelos de regressão uma das medidas da qualidade do ajuste é o chamado coeficiente
de determinação ou R². A definição mais conhecida desta medida é especifica dos modelos de
regressão lineares com resposta Gaussiana. Com o desenvolvimento de novos modelos de
regressão, como os modelos lineares generalizados e outros, faz-se necessário procurar
formas mais gerais de definir o R². Estudaremos duas propostas de generalizar o R² a modelos
de regressão não gaussianos, os chamados R² de Nagelkerke e o R² de Kullback – Liebler.
Mostraremos a utilização destes coeficientes de qualidade do ajuste através de três exemplos.
Palavras-chave: Modelos de regressão, Coeficiente de determinação, Modelos lineares
generalizados, Modelos de regressão família exponencial.
2
Sumário
1.
INTRODUÇÃO .......................................................................................................................................... 4
2.
EXTENSÕES DO R² ................................................................................................................................ 10
2.1 R² DE NAGELKERKE ................................................................................................................................... 10
2.2 R² DE KULLBACK - LEIBLER ....................................................................................................................... 12
2.2.1. Modelos de regressão na família exponencial de densidades .......................................................... 12
2.2.2. Dissimilaridade de Kullback-Liebler ............................................................................................. 13
3.
EXEMPLOS ILUSTRATIVOS................................................................................................................ 17
3.1.
3.2.
3.3.
REGRESSÃO LOGÍSTICA ...................................................................................................................... 17
REGRESSÃO POISSON.......................................................................................................................... 18
REGRESSÃO GAMA ............................................................................................................................. 18
4.
DISCUSSÃO ............................................................................................................................................. 19
5.
BIBLIOGRAFIA ...................................................................................................................................... 21
6.
ANEXOS................................................................................................................................................... 22
6.1 COMANDOS DO R ....................................................................................................................................... 22
1. Introdução
Este trabalho tem por objetivo estudar propriedades importantes do coeficiente de determinação R² no contexto dos modelos lineares assim como algumas das generalizações a outros
modelos de regressão.
Comecemos então pela definição de coeficiente de determinação R² que é uma medida de
bondade do ajuste do modelo selecionado e também uma medida de precisão na predição,
tanto de novas observações quanto da média de novas observações, do modelo de regressão
linear.
Uma medida eficaz de calcular a relação entre duas variáveis aleatórias é o coeficiente de
correlação e o coeficiente de determinação é justamente a correlação ao quadrado entre as
observações y e os valores preditos pelo modelo µ̂ .
Definido como:
R 2 = corr 2 {yi , µˆ } ,
(1)
ou simplesmente
n
∑ (y
R2 = 1−
2
i
− µˆ i )
i=1
n
∑ (y
,
i
− y)
(2)
2
i=1
onde y i são observações independentes, µ̂i os correspondentes valores preditos pelo modelo de regressão linear normal
(3)
yi = β0 + β1 xi1 + ... + β P xip + ε i
e y o correspondente valor predito pelo modelo
y i =β 0 +ε i
(4)
Nestes modelos ε i ,..., ε n ~ N( 0,1 ) , independentes são conhecidos como erros aleatórios.
Lembremos que E(y i ) = µ i = β0 + β1 xi1 + ... + β p x ip e µˆ = βˆ 0 = y , no caso do modelo (4).
4
Podemos afirmar que R² é uma medida de proporção que a soma de quadrados dos desvios de cada yi em relação a y pode ser explicada pelas covariáveis x1 ,......, xn . Então, o R² é
uma medida de bondade do ajuste do modelo (3), incluindo as covariáveis, em relação do modelo (4), no qual nenhuma das covariáveis é considerada. Assim para conjunto de dados com
variável dependente, valor de R² perto de 1 reflete o acréscimo na capacidade de predição do
modelo de regressão, ignorando a perda de informação devido à possível perda de graus de
liberdade.
Por exemplo, os dados mostrados da Figura 1 (a) foram gerados pelo modelo
yi = 2 + 4x i + ε i satisfazendo que var{yi }= 9 e cada ε i ~ N( 0,1 ) , i = 1,......,20 . As estimativas do modelo ajustado são quase perfeitas, como pode ser observado a seguir, assim como o
2
valor do coeficiente de determinação R = 0,9655 . Na outra situação considerada, agora na
Figura 1 (b), em casos onde não faz sentido um modelo de regressão o R² reflete isso, o valor
2
deste coeficiente é R = 0,007684 , indicando independência entre a variável explicativa e a
variável resposta. O modelo estimado para os dados mostrados na Figura 1 (a) é
yˆ = 1.6358+ 4.1386x e para os dados mostrados na Figura 1 (b) é yˆ = 37.3627 + 0,1302x .
O coeficiente de determinação satisfaz algumas propriedades interessantes. Uma delas nos
2
permite melhor interpretar o R², esta propriedade nos diz que 0≤ R ≤ 1 . Podemos perceber
2
que R = 0 somente quando E{y} = y , como é o caso do modelo (4), nesta situação
E{y i }= µ = β 0 , µˆ = βˆ 0 = y , logo
n
∑ (y
n
i
− µˆ )2 = ∑ (yi − y)2 e
i=1
i=1
n
∑ (y
R2 = 1−
i
− y) 2
i=1
n
∑ (y
=0
i
− y)
2
i=1
5
Figura 1: Diferentes modelos de regressão linear simples, (a) ajuste perfeito, (b) modelo errado,
nesta situação não faz sentido um modelo de regressão.
Interpretamos então que R 2 ≈ 0 o modelo não é apropriado para explicar a variável reposta
através das variáveis explicativas selecionadas, significando que R² é uma medida da utilidade
dos outros termos além do β0 no modelo. Para provar que o R² é limitado superiormente por 1
observaremos primeiro que podemos escrever:
n
R2 =
∑ (µˆ
i
− y) 2
i=1
n
∑ (y
.
i
− y)
2
i=1
2
Assim, para provar que R ≤ 1 devemos provar que βˆ
T
X
T
Y ≤ Y
T
Y . Utilizando as
expressões dos estimadores do modelo linear, temos que:
βˆ T X T Y = Y T X(X T X)−1 X T Y = Y T HY,
onde H = X(X T X) −1 X T é uma matriz simétrica e idempotente, ou seja, H T H = HH T = H .
Observemos que
Y T Y − βˆ T X T Y = Y T IY − Y T HY = Y T (I − H)Y,
o objetivo agora é demonstrar que Y T (I − H)Y é uma forma quadrática positiva. Para isso devemos provar que I − H é uma matriz definida positiva. Sabemos que a matriz H é simétrica e
uma condição necessária e suficiente para uma matriz simétrica ser definida positiva é que exista uma matriz não singular P, tal que, I − H = P T P (Rao, 1973).
6
Nesta situação (I − H)(I − H) T = (I − H) T (I − H) = (I − H), logo I − H
além de
idempotente é definida positiva, portanto:
Y T (I − H)Y ≥ 0,
ou seja, Y T (I − H)Y é uma forma quadrática definida positiva, logo Y T Y ≥ βˆ T X T Y , concluindose que R 2 ≤ 1.
n
Um modelo cujo ajuste seja perfeito implicaria que µ̂ i = y i , portanto
∑ (y
i
− µˆ i ) 2 = 0 e
i=1
2
conseqüentemente R = 1 significando que quanto mais próximo de 1 estivasse o valor do coeficiente de determinação melhor o ajuste aos dados do modelo proposto.
É importante notar que altos valores de R² não necessariamente implicam que o modelo de
regressão está bem ajustado. Adicionando variáveis regressoras podemos incrementar o valor
de R² sem importar se as novas variáveis regressoras contribuem de fato para o modelo. Então
é possível que alguns modelos tenham grandes valores de R² e sua qualidade seja ruim para
estimação ou predição de novas observações.
média
variância
correlação
x1
10
8
13
9
11
14
6
4
12
7
5
9
11
y1
8.04
6.95
7.58
8.81
8.33
9.96
7.24
4.26
10.84
4.82
5.68
7.5
4.12
0.82
x2
10
8
13
9
11
14
6
4
12
7
5
9
11
y2
9.14
8.14
8.74
8.77
9.26
8.10
6.13
3.10
9.13
7.26
4.74
7.5
4,12
0.82
x3
10
8
13
9
11
14
6
4
12
7
5
9
11
y3
7.46
6.77
12.74
7.11
7.81
8.84
6.08
5.39
8.15
6.42
5.73
7.5
4,12
0.82
x4
8
8
8
8
8
8
8
19
8
8
8
9
11
y4
6.58
5.76
7.71
8.84
8.47
7.04
5.25
12.50
5.56
7.91
6.89
7.5
4,12
0.82
Tabela 1: Quadro conjunto de dados Anscombe e medidas descritivas assim como correlação
entre x e y em cada caso.
Podemos visualizar isto através dos exemplos em Anscombe (1973). Nesse trabalho o autor
apresentou quatro conjuntos de dados com as mesmas médias, variâncias e correlação entre
as variáveis respostas e explicativa. Estes dados são reproduzidos na Tabela 1.
7
Algumas estatísticas descritivas importantes destes dados, como média, variância e
correlação entre x e y e outras, assumem os mesmos valores e, portanto, as retas de
regressão também coincidem. Outras estatísticas descritivas que não influenciam na estimação
da reta de regressão não coincidem, como é o caso da mediana e os valores extremos.
As estimativas do modelo de regressão y1 = β 0 + β 1 x1 + ε, ε ~ N( 0,1 ) aparecem na Tabela 2
e são comuns a todos os outros modelos, ou seja, as estimativas dos modelos de regressão
relacionados os pares de variáveis (x1 , y1 ),(x 2 , y 2 ),(x3 , y 3 )e(x 4 , y 4 ) coincidem, sendo que o
2
R = 0,665 e o desvio padrão dos resíduos é 1,2370. Também são comuns os resultados da
análise de variância da regressão.
Desvio
Coeficientes Estimativas padrão
Intercepto
3.0001
11.1247
x1
0.5001
0.1179
tobs
(P>|tobs|)
2.6670 0.0257
4.2410 0.0021
Tabela 2: Tabela de análise de regressão
No entanto, observando a Figura 2 fica claro que simplesmente com o valor R² não seria
possível perceber que nos conjuntos de dados N°2 e N°4 um modelo de regressão linear não
faz sentido, no conjunto N°2 devemos transformar a variável explicativa para obtermos um melhor ajuste e no conjunto de dados N° 4 não existe relação alguma entre a variável explicativa e
resposta. No caso do conjunto de dados N°3 existe uma observação muito diferente das outras
que atrapalha completamente e que somente no conjunto de dados N°1 existe uma relação linear entre a covariável e a resposta.
Uma outra propriedade do R² é que ele é crescente conforme aumenta o número de variáveis explicativas, mesmo que as novas variáveis acrescidas nada tenham a ver com a resposta. Devemos lembrar que o procedimento de estimação implica na minimização da função no
espaço de parâmetros da regressão, isto é, em R
n
∑ (y
i
P
.
− xi β) 2
i=1
8
Acontece que se aumentamos em uma dimensão deste espaço, pela inclusão de uma variável explicativa ao modelo, a estimação no espaço de dimensão p seria uma minimização restrita no espaço de dimensão p+1, e sabemos por cálculo que mínimos restritos são maiores do
que mínimos absolutos. Logo o R² obtido no modelo de ordem p é ligeiramente menor do que o
R² obtido no modelo de ordem p+1.
Figura 2: Gráfico de dispersão e reta de regressão estimada para cada um dos conjuntos de
dados apresentados na Tabela 1.
Esta propriedade nos diz que adicionando infinitas covariáveis ao modelo, mesmo que não
tenham nada a ver com o problema em questão, podemos artificialmente melhorar o coeficiente de determinação. Por este motivo o R² serve para medir a qualidade do ajuste, mas não é o
mais apropriado para comparar modelos, com esse objetivo é recomendado o R² ajustado, definido com:
2
Radj
= 1 − (1 − R 2 )
n −1
n − p −1
(6)
e o Critério de Akaike (Akaike, 1974).
9
2. Extensões do R²
2.1 R² DE NAGELKERKE
Este coeficiente de determinação foi estudado em diversos trabalhos durante os anos 80 e
90, mas foi no artigo de Nagelkerke(1991) que estudaram-se suas propriedades e onde foi apresentado de uma maneira mais geral, por esse motivo se atribui o nome Nagelkerke. No artigo referido é discutida uma generalização do coeficiente de determinação R² para modelos de
regressão gerais e uma modificação da definição deste novo R2 permite que se proponha para
modelos discretos.
A utilização do R², o coeficiente de determinação, também chamado de coeficiente de correlação múltipla, está bem estabelecido na análise clássica (Rao, 1973). A sua definição como a
proporção de variância "explicada" pelo modelo de regressão faz com que seja útil como uma
medida de sucesso da predição da variável dependente a partir das variáveis independentes.
É conveniente generalizar a definição de R² para modelos mais gerais, para os quais o conceito da variância residual não pode ser facilmente definido e a máxima verossimilhança é o
critério de ajuste. A seguinte generalização foi proposta por Cox & Snell (1989, pp. 208-9) e,
aparentemente independente, por Magee (1990), mas haviam sido sugeridos anteriormente
para modelos de resposta binária por Maddala (1983),
− log ( 1 − R 2 ) =
2 ˆ
l( β) − l( 0 )
n
{
}
( 1a )
ou
2/ n
 2

R 2 = 1 − exp− l(βˆ) − l( 0 )  = 1 − L( 0 ) / L(βˆ)
 n

{
}
{
}
( 1b )
onde, l( βˆ ) =log L( βˆ ) e l( 0 ) = log L( 0 ) indicam a log da verossimilhança do modelo
ajustado e do modelo nulo, respectivamente. O R² geral definido em (1b) foi estudado por
10
Nalgelkerke (1991), como mencionamos, e por esse motivo chama-se de R2 de Nagelkerke e
escreve-se como R2N.
É possível estabelecer que o R²N , tem as seguintes propriedades:
1. É coerente com o R² clássico, que é a definição geral aplicada, por exemplo, na regressão linear. Isto significa que se a distribuição da variável resposta é normal e o modelo
de regressão linear, então, o R2N coincide com o R2 clássico.
2. É coerente com os estimadores de máxima verossimilhança dos parâmetros do modelo
que maximizam o R², ou seja, o R2N depende das estimativas de máxima verossimilhança dos parâmetros do modelo.
3. É assintóticamente independente do tamanho da amostra n.
4. Interpreta-se como a proporção da “variação” explicada, ou seja, 1-R²N, tem a interpretação da proporção não explicada da “variação”. A variação deve ser entendida como
qualquer medida de distância.
5. É adimensional, ou seja, não depende da unidade de medida utilizada.
Para esclarecer vamos considerar o modelo M1
=
M2 * M3, por exemplo, o modelo M1
contendo apenas a covariável x1, por exemplo, uma constante, enquanto M2 contém x2 e x1 e M3
2
indica o R²N do modelo M2 em relação à M1 etc..., então:
contém x1, x2 e x3. Se R2.1
2
2
2
( 1 − R3.1
) = ( 1 − R3.2
)( 1 − R2.1
)
(2)
Em outras palavras, a proporção de variação não explicada pelo modelo M3 relativamente
ao modelo M1 é o produto da proporção não explicada por M3 em relação a M2 e a proporção
não explicada por M2 em relação a M1.
No entanto, o R²N assim definido atinge um valor máximo teórico de menos de 1 para modelos discretos, ou seja, modelos cuja variável resposta é discreta. É o caso de situações particulares importantes nos modelos lineares generalizados como os modelos de regressão logística e log-linear nos quais as distribuições das variáveis respostas são Bernoulli ou Binomial e
Poisson, respectivamente. Este máximo é igual a:
{
}
max(R 2 ) = 1 − exp 2n −1l( 0 ) = 1 − L( 0 )2 / n
11
Para a regressão logística, com 50% de Y = 1 e 50% de Y = 0 observações, este máximo é
igual a 0.75. Este máximo ocorre quando todas as observações são preditas com probabilidade máxima, isto é P{ Y=1 } = 1 para as observações com Y = 1, e Pr{ Y=1} = 0 para Y = 0 observações.
Isto é claramente inaceitável para um coeficiente R². Foi proposto, portanto, de redefinir como R²N:
R 2 = R 2 /max(R 2 )
As propriedades 1, 2, 3 e 5 são automaticamente satisfeitas, segundo afirma Nagelkerke(1991). Para este mesmo R²N, a propriedade 4 é mais difícil de estabelecer. No entanto, pode afirmar-se que:
{
}
{
}
2
2
2
log 1 − max (R 2.1
) − log 1 − max (R 3.2
) = log ( 1 − R 2.1
)
(4)
e desta forma, o critério na propriedade 4 também pode ser estabelecido para manter o R²N
corrigido pelo seu máximo teórico.
2.2 R² DE KULLBACK - LEIBLER
Como mencionado, para modelos de regressão linear o coeficiente de determinação R² é
amplamente utilizado, pois é uma boa medida do ajuste cujas utilidades e limitações são conhecidas. A aplicação desta medida para modelos não lineares geralmente conduz a uma medida que pode estar fora do intervalo [0,1] e diminui quando regressoras são adicionadas.
Algumas alternativas para R² foram especialmente construídas para modelos não lineares
usando uma variedade de métodos. Aqui estudaremos mais uma proposta de generalização
deste coeficiente, nesta vez utilizará a chamada dissimilaridade Kullback-Liebler e mostraremos as expressões correspondentes quando a variável resposta pertence à família exponencial
de distribuições.
2.2.1. Modelos de regressão na família exponencial de densidades
Suponhamos que a variável dependente Y tem uma distribuição na família exponencial de
densidades da forma:
12
f 0 (y; θ ) = exp[θy − b(θ )]h( y )
onde, θ é o parâmetro canônico, b(θ ) é a função normalizadora e h(y) é uma função conhecida. Diferentes b(θ) correspondem a diferentes distribuições. A média de Y, denotada µ é igual
a derivada b' (θ ) , e pode ser demonstrado que é uma função monótona em θ .
Regressoras são introduzidas pela especificação de µ como uma função do preditor linear
η=x’β, onde x é o vetor de regressoras e β é um desconhecido vetor de parâmetros. Modelos
obtidos por diversas escolhas de b(θ ) e funções de η são chamados modelos lineares generalizados. A função que relaciona a média µ com o preditor linear η=x’β é chamada de função
de ligação e é tal que g(µ)=η.
O vetor de parâmetros β é estimado por máxima verossimilhança, denotando o estimador
como β̂ , baseado na amostra independente {(y i , x i ),i = 1,.... , n}, com f µ (y i ) = f µ (y j )
i
i
para µi = µ j . A estimativa da média para uma observação com regressor x é denotada por
µˆ = µ(x' βˆ ) . Por tudo assumimos que o modelo inclui um termo constante. A estimativa da
média da resposta quando o modelo assume somente um termo constante é denotada por µ̂0 .
2.2.2. Dissimilaridade de Kullback-Liebler
A medida padrão da informação contida nas observações em uma densidade f ( y ) é a
informação esperada ou entropia Shannon’s, definida como E[ log(f(y))] . Esta é a base para
medir o nível de discrepância entre duas densidades ou divergência de Kullback-Lieber, porposta em Kullback e Liebler(1959).
Considere duas densidades, denotada por f µ (y) e f µ (y) , parametrizadas apenas pela mé1
2
dia. Neste caso, a fórmula geral para a dissimilaridade ou divergência de Kullback-Leibler (KL)
é
K( µ 1 , µ 2 ) ≡ 2 E µ log [f
1
µ1
(y) / f µ (y)],
(5)
2
quando um segundo fator é adicionado por conveniência, e E µ
denota expectativa tomada
com relação à densidade
µ1
1
f µ (y).K(µ1 , µ 2 ) é a informação de
1
no que diz respeito a
13
µ2 e é uma medida de quão próximo µ1 está de µ2 . O termo divergência, em vez de distância é usado porque não satisfazem em geral a simetria triangular e propriedades de uma
distância medida. Contudo, K(µ1 , µ2 ) ≥ 0 com igualdade se f µ ≡ f µ .
1
2
Além de f µ (y) e f µ (y) nós também consideramos a densidade f y (y) , para os quais a mé1
2
dia é igual ao conjunto realizado y. Em seguida, o Kullback-Leibler (KL) divergência K(y, µ)
pode ser definido de maneira análoga a (2)
K(y, µ) ≡ 2 E y log [f y (y) / f µ (y)] = 2 ∫ f y (y) log [f y (y) / f µ (y)]dy
(3)
A variável aleatória K(y, µ) é uma medida do desvio da média µ . Para a família exponencial, Hastie (1987) e Vos (1991) mostram que a expectativa em (3) cai fora e:
K(y, µ) ≡ 2log [f y (y) / f µ (y)]
No modelo estimado com n indivíduos o estimador Kullback-Leibler (KL) da divergência
entre n-vetores y e µ̂ é igual ao dobro da diferença entre o valor máximo do log da
verossimilhança possível, isto é, o log da verossimilhança em um modelo completo com o
maior número de parâmetros como observações l(y ' , y),e o log da verossimilhança alcançado
pelo modelo sob investigação em l(µˆ , y) :
n
K(y, µˆ ) = 2∑ [ log f y (y i ) − log f µˆ (y i )] = 2[l(y; y) − l(µˆ ; y)]
i=1
Deixe
µ̂0
i
i
denotar o n-vetor com entradas
(4)
µ̂0 , o ajuste da máxima verossimilhança
estima média da constante do modelo somente. Nós interpretamos K(y, µˆ 0 ) como a estimativa
das informações, de dados sobre a amostra y potencialmente recuperável pela inclusão de regressoras. É a diferença entre a informação contida na amostra de dados sobre y, e os estimados usando informações µ̂0 , a melhor estimativa pontual quando os dados sobre regressoras não são utilizadas, onde a informação é medida pela expectativa tomar no que diz
respeito ao valor observado y. Ao escolher µ̂0 para ser o MLE, K(y, µˆ 0 ) é minimizado. O R²
proposto é a redução proporcional na presente potencialmente recuperável alcançado pelo
modelo de regressão:
2
R KL
= 1 − K(Y, µˆ ) / K(Y, µˆ 0 )
(5)
14
Esta medida pode ser utilizada para ajuste de médias obtidas por qualquer método de estimação.Na seguinte proposição que restringem a atenção para estimativa ML (que minimiza
K ( y, µˆ ) ).
Proposição : Para ML estimativas dos modelos de regressão da família exponencial baseada
2
(5) tem as seguintes propriedades:
na densidade (1), definido em RKL
2
1. R KL não é aumentado quando regressoras são adicionadas.
2
2. 0≤ R KL≤ 1 .
2
3. R KL é um escalar múltiplo da razão da verossimilhança teste para a significância conjunta
da variável explicativa.
2
4. RKL
iguala a razão de verossimilhança índice 1 − l(µˆ ; y) / l(µˆ 0 ; y) se e somente se l(y; y) = 0.
2
5. RKL
medida da redução proporcional na recuperável informação devido à inclusão de regressores, onde a informação é medida pela estimativa Kullback-Leibler divergência (4).
Propriedade 4 é de interesse, tal como o índice da razão de verossimilhança, que mede a
redução proporcional no log da verossimillhança devido à inclusão de regressoras, por vezes é
proposto como uma medida pseudo R² geral. Igualmente ocorre para o modelo Bernoulli, mas
em geral o índice da razão de verossimilhança difere e, para outros modelos discretos a variável dependente, é mais pessimista no que se refere à contribuição de regressores, como
l(y; y) ≤ 0.
No caso contínuo, grandes valores (positivos ou negativos) do índice da razão de
verossimilhança podem ocorrer se l(µˆ 0 ; y) é perto de zero (positivo ou negativo). Em contra2
partida RKL
será sempre limitada por zero e um. A última propriedade define uma informação
2
teórica para RKL
. Um aspecto interessante é que a expressão de K ( y, µˆ ) em (4) equivale a
2
definição deviance. Portanto RKL
pode ser interpretado como sendo baseada na deviance
residual.
2
A tabela a seguir lista as expressões para o RKL
em diversos modelos de regressão gene-
ralizados: normal, Bernoulli, binomial, Poisson, geométrica, exponencial, gama e normal
inversa.
15
16
3. Exemplos Ilustrativos
3.1. REGRESSÃO LOGÍSTICA
Utilizaremos como primeiro exemplo dados de um estudo caso-controle sobre câncer de
esôfago (Gimeno & Souza, 1995). Oitenta e cinco casos de câncer de esôfago foram comparados com 292 controles hospitalares, classificados segundo sexo, idade e os hábitos de beber e
fumar. O hábito de beber foi considerado fator de risco de principal interesse.
Os dados utilizados no estudo de referência foram reproduzidos na Tabela 3.1. Nela observamos que a variável idade foi dividida em dois grupos: “menor”, os menores de 57 anos inclusive e “maior” os maiores de 57 anos de idade.
Tabela 3.1 – Dados de um estudo caso-controle sobre câncer de esôfago (Gimeno & Souza, 1995).
Sexo
Idade
Bebe
Fuma
Caso
Controle
Total
Feminino
menor
N
N
3
30
33
Feminino
menor
N
S
0
15
15
Feminino
menor
S
N
0
14
14
Feminino
menor
S
S
5
13
18
Feminino
maior
N
N
2
41
43
Feminino
maior
N
S
3
8
11
Feminino
maior
S
N
0
6
6
Feminino
maior
S
S
3
2
5
Masculino
menor
N
N
0
9
9
Masculino
menor
N
S
2
12
14
Masculino
menor
S
N
1
8
9
Masculino
menor
S
S
40
58
98
Masculino
maior
N
N
0
6
6
Masculino
maior
N
S
0
19
19
Masculino
maior
S
N
0
4
4
Masculino
maior
S
S
26
47
73
Um primeiro ajuste do modelo de regressão logística foi realizado com todas as variáveis
explicativas: sexo, idade, bebe e fuma. Obteve-se que somente a variável bebe e fuma foram
significativas. Além disso, verificou-se, através do método AIC, que a melhor função de ligação
2
, utilizandoé a complementar log-log. Após achamos o melhor modelo calculamos o RN2 e RKL
se os resultados mostrados a seguir:
2
RN2 = 0,9714 e RKL
= 0,6976 .
17
3.2. REGRESSÃO POISSON
A tabela 3.2 (exemplo 6, pág. 21, livro de Clarice G,B. Demétrio et all.) mostra os dados referentes à contagem de partículas de vírus para 5 diluições diferentes, sendo que foram usadas 4
repetições para as 4 primeiras diluições e 5 repetições para a última diluição. O objetivo do experimento era estimar o número de partículas de vírus por unidade de volume.
Tabela 3.2: Números de partículas de vírus para 5 diluições diferentes.
Diluição
0,3162
0,1778
0,1000
0,0562
0,0316
13
9
4
3
2
14
14
4
2
1
Contagens
17
6
3
1
3
22
14
5
3
2
2
2
RN2 = 0,9861 e RKL
= 0,8682 .
3.3. REGRESSÃO GAMA
Na tabela abaixo são apresentados os resultados de um experimento em que a resistência
(em horas) de um determinado tipo de vidro foi avaliada segundo quatro níveis de voltagem
(em kilovolts) e duas temperaturas (em graus Celsius). Estes dados aparecem no livro Statistical Models and Methods for Uniforme Data, Lawless (1982), pág.338.
Temperatura (°C)
170
180
200
439
904
1092
1105
959
1065
1065
1087
Voltagem (kV)
250
300
572
315
690
315
904
439
1090
628
216
315
455
473
241
315
332
380
350
258
258
347
588
241
241
435
455
2
RN2 = 0,6480 e RKL
= 0,6369 .
18
4. Discussão
Mostramos duas formas de generalizar o R 2 conhecido do modelo de regressão linear,
chamadas RN2 proposto por vários pesquisadores e estudadas suas propriedades por Nalgel2
kerke (1991) e RKL
, o qual é baseado na divergência de Kullback-Leibler, proposto por Ca-
meron e Windmeijer (1996).
Neste trabalho aplicamos as duas generalizações a situações particulares dos modelos lineares generalizados, os quais sabidamente pertencem à família exponencial de densidade:
modelos gama, logístico e Poisson.
Observamos que nos modelos contínuos, isto é, nos modelos de regressão normal e gama
2
os coeficientes RN2 e RKL
coincidem aproximadamente. Nos modelos de regressão discretos:
logístico e Poisson, observamos uma grande divergência entre os valores obtidos dos coefici2
entes RN2 e RKL
.
Para responder à questão em qual coeficiente de determinação confiar, nas situações
discretas, decidimos mostrar comparativamente as observações e estimativas obtidas em cada
situação. Sempre lembrando que os resultados apresentados são referentes ao modelo escolhido como melhor.
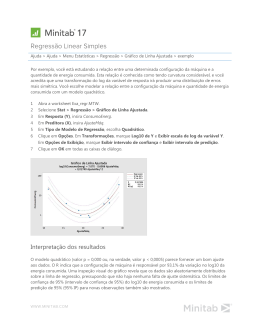
A figura (3a) mostra os valores observados e preditos no exemplo de regressão Poisson.
Observamos que, embora bem ajustado, a variabilidade das observações para cada covariável
não permitiria altos valores de R 2 , logo confiamos no resultado obtido com o coeficiente de
2
determinação R KL , baseado na dissimilaridade de Kullbak-Liebler.
A figura (3b) mostra as proporções observadas e estimadas no exemplo de regressão logística. Neste caso, os pontos vermelhos indicam as estimativas obtidas pelo modelo escolhido,
também observamos que o valor do coeficiente de determinação não deve
Logo confiamos no resultado obtido com o coeficiente de determinação
R2KL
ser muito elevado.
.
19
Regressão Poisson (3a)
Regressão Logística (3b)
Figura 3: Gráfico de valores observados e valores preditos.
2
Como um dos resultados do estudo aqui desenvolvido podemos afirmar que o RKL
subestima o valor do coeficiente de determinação nos modelos discretos. Também podemos
2
são aproximadamente iguais nos modelos
afirmar que o valor dos coeficientes RN2 e RKL
contínuos. Uma afirmação de Nagelkerke (1991) faz toda a diferença nas aplicações práticas, o
valor máximo de RN2 é menor do que 1, logo este coeficiente é utilizado corrigido pelo seu valor
2
máximo. Esta correção mostra que o RKL
subestima o coeficiente de determinação nos
2
modelos discretos, a menos um valor desconhecido por nós, a partir do qual RKL
deve
ser maior do que R N2 . Isto seria um tema de trabalhos futuros de grande interesse.
Baseados nossos conhecimentos atuais, sugerimos dar preferência ao coeficiente de de2
terminação RKL
nos modelos discretos. Nos modelos contínuos é indiferente a utilização de
2
ou R N2 .
RKL
20
5. Bibliografia
Anscombe, F.J. (1973). Graphs in statistical analysis. The American Statistician, 27, 1721.
Cox, D. R. (1972). Regression models and life tables (with discussion). J. R. Ststist. Soc.
B34, 187-220.
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transaction on
Automatic Contrl, AC-19, 715-723.
Cox, D. R. (1975). Partial likelihood. Biometrika 62, 269-76.
Cox, D. R. & SNELL, E. J. (1989). The Analysis of Binary Data, 2nd ed. London: Chapman and Hall.
Maddala, G. S. (1983). Limited-Dependent and Qualitative Variables in Econometrics.
Cambridge University Press.
Magee, L. (1990). R² measures base don Wald and likehood ratio joint significance testes. Am. Statistician 44, 250-3.
Rao, C. R. (1973). Linear Statistical Inference and its Applications, 2nd ed.New York:
Wiley.
Rao, C.R. (1973). Linear Statistical Inference and its Applications. John Wiley and Sons,
second edition.
Gimeno, S.G.A. e Souza, J.M.P. (1995). Utilização de estratificação e modelo de regressão logística na análise de dados de estudos caso-controle. Revista de Saúde Pública, Vol. 29 n°4, pp. 283-289.
Lawless, J.F. (1982). Statistical Models and Methods for Lifetime Data. John Wiley, New
York.
21
6. Anexos
6.1 COMANDOS DO R
Exemplo Regressão Logística
#
# Exemplo de regressão logística
#
# Gimeno & Souza (1995). Utilização de estratificação e modelo de
regressão logítica
# na análise de dados de estudos casos-controle.
#
# Revista de Saúde Pública, Vol.29, No.4, pp.283-289
#
# Dados
#
Sexo=c(rep("Feminino",8),rep("Masculino",8))
Sexo=factor(Sexo)
Idade=c(rep(c(rep("menos",4),rep("mais",4)),2))
Idade=factor(Idade)
Bebe=c(rep(c("N","N","S","S"),4))
Bebe=factor(Bebe)
Fuma=c(rep(c("N","S"),8))
Fuma=factor(Fuma)
Caso=c(3,0,0,5,2,3,0,3,0,2,1,40,0,0,0,26)
Controle=c(30,15,14,13,41,8,6,2,9,12,8,58,6,19,4,47)
#
# Modelo de regressão logística
#
ajuste1=glm(cbind(Caso,Controle)~Sexo+Idade+Bebe+Fuma,family=binomial(link='logit'))
summary(ajuste1)
#
ajuste2=glm(cbind(Caso,Controle)~Sexo+Idade+Bebe+Fuma,family=binomial(link='probit'))
summary(ajuste2)
#
ajuste3=glm(cbind(Caso,Controle)~Sexo+Idade+Bebe+Fuma,family=binomial(link='cloglog'))
summary(ajuste3)
#
# Escolha de modelo
#
AIC(ajuste1,ajuste2,ajuste3)
#
step(ajuste3)
ajuste3.final=update(ajuste3,.~.-Sexo-Idade)
summary(ajuste3.final)
#
# Calculando o R² Nagelkerke
#
ajuste0=glm(cbind(Caso,Controle)~1,family=binomial(link='cloglog'))
22
#
n=length(Caso)
#
RN=1-exp(-2*(logLik(ajuste3.final)[1]-logLik(ajuste0)[1])/n)
RN
#
# Calculando o valor máximo de RN
#
Rmax=1-exp(2*logLik(ajuste0)[1]/n)
Rmax
#
# Calculando o R² Nagelkerke corrigido pelo valor máximo
#
RN/Rmax
#
# Calculando o R² Kullback-Liebler
#
media.y=mean(Caso/Controle)
#
numerador=sum(fitted(ajuste3.final)*log(fitted(ajuste3.final))+(Controlefitted(ajuste3.final)*log(Controle-fitted(ajuste3.final))))
denominador=sum(media.y*log(media.y)+(Controle-media.y)*log(Controle-media.y))
#
RKL=1-numerador/denominador
RKL
23
Exemplo Regressão Poisson
# Exemplo 6, pág. 21, livro de Clarice G,B. Demétrio et all.
#
diluicao=c(rep(0.3162,4),rep(0.1778,4),rep(0.1000,4),rep(0.0565,4),rep(0.0316,5))
Contagem=c(13,14,17,22,9,14,6,14,4,4,3,5,3,2,1,3,2,1,3,2,2)
#
ajuste1=glm(Contagem~diluicao,family=poisson(link='log'))
summary(ajuste1)
#
ajuste2=glm(Contagem~diluicao,family=poisson(link='identity'))
summary(ajuste2)
#
ajuste3=glm(Contagem~diluicao,family=poisson(link='sqrt'))
summary(ajuste3)
#
AIC(ajuste1,ajuste2,ajuste3)
#
par(mfrow=c(2,3))
plot(ajuste2,which=1:6)
#
# Calculando o R² Nagelkerke
#
ajuste0=glm(Contagem~1,family=poisson(link='log'))
#
n=length(Contagem)
#
RN=1-exp(-2*(logLik(ajuste2)[1]-logLik(ajuste0)[1])/n)
RN
#
# Calculando o valor máximo de RN
#
Rmax=1-exp(2*logLik(ajuste0)[1]/n)
Rmax
#
# Calculando o R² Nagelkerke corrigido pelo valor máximo
#
RN/Rmax
#
# Calculando o R² Kullback-Liebler
#
media.y=mean(Contagem)
#
RKL=1-sum(Contagem*log(Contagem/fitted(ajuste2))-(Contagemfitted(ajuste2)))/sum(Contagem*log(Contagem/media.y))
RKL
24
Exemplo Regressão Gama
# Exemplo do livro de Lawless, 1982, pág. 338)
#
dados=read.table("http://people.ufpr.br/~lucambio/CE225/1S2009/vidro.dat",h=T)
#
names(dados)
attach(dados)
#
Voltagem=factor(Voltagem)
Temperatura=factor(Temperatura)
#
# Modelo de regressão gama
#
ajuste1=glm(TMresist~Voltagem+Temperatura,family=Gamma(link='inverse'))
summary(ajuste1)
#
ajuste2=glm(TMresist~Voltagem+Temperatura,family=Gamma(link='identity'))
summary(ajuste2)
#
ajuste3=glm(TMresist~Voltagem+Temperatura,family=Gamma(link='log'))
summary(ajuste3)
#
AIC(ajuste1,ajuste2,ajuste3)
#
#
# Calculando o R² Nagelkerke
#
ajuste0=glm(TMresist~1,family=Gamma(link='identity'))
#
n=length(TMresist)
#
RN=1-exp(-2*(logLik(ajuste2)[1]-logLik(ajuste0)[1])/n)
RN
#
# Calculando o valor máximo de RN
#
Rmax=1-exp(2*logLik(ajuste0)[1]/n)
Rmax
#
# Calculando o R² Nagelkerke corrigido pelo valor máximo
#
RN/Rmax
#
# Calculando o R² Kullback-Liebler
#
media.y=mean(TMresist)
#
RKL=1-sum(log(TMresist/fitted(ajuste2))+(TMresistfitted(ajuste2))/fitted(ajuste2))/sum(log(TMresist/media.y))
RKL
25