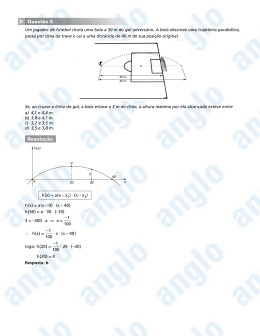
▼
Questão 3
Uma bola chutada horizontalmente de cima de uma laje, com velocidade V0 , tem sua trajetória parcialmente
registrada em uma foto, representada no desenho abaixo. A bola bate no chão, no ponto A, voltando a atingir
o chão em B, em choques parcialmente inelásticos.
Foto
V0
NOTE E ADOTE
Nos choques, a velocidade horizontal da bola não é alterada.
Desconsidere a resistência do ar, o atrito e os efeitos de rotação
da bola.
H1 = 3,2m
H2 = 1,8 m
1,6m
D=?
A
B
a) Estime o tempo T, em s, que a bola leva até atingir o chão, no ponto A.
b) Calcule a distância D, em metros, entre os pontos A e B.
c) Determine o módulo da velocidade vertical da bola VA, em m/s, logo após seu impacto com o chão no ponto A.
Resolução
a) Representando na figura abaixo o movimento da bola até o ponto A:
v0
1,6
x(m)
3,2
y(m)
A
Como na direção vertical do lançamento horizontal a bola executa movimento uniformemente variado,
com | ay | = g = 10 m/s2:
0
0
y = y0 + v0 y ⋅ t +
ay
2
⋅ t 2 ⇒ 3, 2 =
10 2
t ∴ t = 0, 8 s
2
b e c) Sendo, na direção horizontal, a velocidade da bola constante, podemos calcular a sua intensidade:
v0 = v x =
∆x 1, 6
=
= 2m / s
∆t 0, 8
1
Representando na figura abaixo o lançamento da bola entre os pontos A e B:
y(m)
1,8
D
x(m)
No lançamento oblíquo, nas direções x e y, os movimentos são uniforme e uniformemente variado, respectivamente, e há simetria no movimento, ou seja, o tempo de subida é o mesmo que o de descida.
• Analisando apenas a descida
0
y = y0 + v0 y ⋅ t +
0 = 1, 8 –
ay
2
⋅ t2
10 2
t d ⇒ t d = 0, 6 s
2
• Analisando todo o movimento
0
x = x0 + vx ⋅ t ⇒ D = v0 ⋅ tT
Como
tT = ts + td = 2td = 1,2 s
Logo
D = 2 ⋅ 1,2 ∴ D = 2,4 m
• Analisando apenas a subida
vy = voy + ay ⋅ t
0 = v0y – 10 ⋅ 0,6
∴ v0y = 6 m/s
2