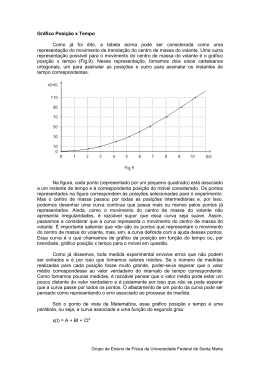
2.003 Primavera 2002
Prelab 2
Data de entrega: Terça feira, 19 de fevereiro de 2002
Neste lab examinamos a dinâmica de um eixo em rotação e os efeitos da adição de inércia e
amortecimento por um fluído viscoso. A figura 1 ilustra o instrumento. Modelamos o eixo e o
volante como uma inércia rotatória equivalente e o fluído viscoso como um amortecedor
rotatório equivalente conforme esquematizado na figura 2.
Figura 1: Desenho do sistema rotatório de primeira ordem.
(**Tradução dos termos existentes na fig. 1:
Flywheel = volante
Airberings = mancais de ar
Shaft = eixo
Cup with viscous fluid = copo com fluído viscoso)
Figura 2: Modelo de um sistema de parâmetro concentrado.
Primeiramente examinaremos a dinâmica de primeira ordem do eixo em rotação. A
aceleração de rotação da massa é proporcional ao torque aplicado:
T = I dω/dt
onde
T = torque aplicado à massa na direção de ω(t) (Nm)
I = momento de inércia do eixo (kg.m2 )
dω/dt = aceleração angular (rad/s2 )
Usando a tabela na página 14 do livro texto, o momento de inércia de um cilindro uniforme é
calculado por
onde
m = massa do eixo (kg)
d = diâmetro do eixo (m)
Adicionando um volante ao eixo, aumentamos a inércia total do sistema. Esta relação é linear
como segue
A base do conjunto eixo é esquematizada na figura 3. Para delimitar a posição vertical do
eixo, ligou-se uma esfera temperada ao eixo de modo que ela esteja em contato com uma
superfície temperada plana junto com o eixo de rotação. Pense a respeito de por que este
arranjo produz um bom pivô de baixa fricção. Uma camada fina de mel no espaço circular
entre o eixo e o copo produz amortecimento. A relação constitutiva mais simples para um
amortecedor deste tipo é
onde
Tviscous = torque aplicado ao amortecedor na direção de ω(t) (Nm)
c = coeficiente de amortecimento (Nms/rad)
dω/dt = velocidade angular (rad/s)
O coeficiente de amortecimento c pode ser razoavelmente modelado conforme consta na
tabela da página 263 do livro-texto.
Figura 3: Detalhe da configuração do amortecedor
(**Tradução das palavras, que aparecem na fig.3:
Honey = mel
Ball Bearing = esfera de apoio
Hardened Flat = superfície temperada plana)
Onde
µ = coeficiente de viscosidade do fluido (isto é, a espessura de (Ns/m2)
D = diâmetro do eixo (m)
L = altura do nível do fluido (m)
ε = o intervalo entre o eixo e o copo (m)
Não iremos explorar em detalhe esta fórmula neste lab. O ponto chave aqui é reconhecer que
o coeficiente de amortecimento é linearmente proporcional à altura L do fluído viscoso. Deste
modo podemos variar c linearmente, mudando L.
Na ausência de torques externos, o torque aplicado ao amortecedor (Tviscous) é igual e oposto
ao torque aplicado à massa (T):
T = -Tviscous
(6)
Substituindo de (1) e (4), teremos
Você pode observar que esta equação tem a mesma forma que o sistema de primeira ordem
que estudamos no lab 1.
Problemas
1. Suponha que ao eixo é aplicada uma velocidade angular inicial ω(0). Resolva (7) para
determinar uma expressão para a velocidade angular como função do tempo. Mostre
todos passos da sua solução. Como no primeiro lab, a solução da equação (7) terá a forma
Qual é a constante de tempo da resposta em termos dos parâmetros do sistema?
.
2. Em seguida obtenha uma expressão para a posição angular θ(t) a partir dessas condições
iniciais, assumindo que θ(0) = 0.Qual é a constante de tempo desta resposta? Faça um
esboço acurado de θ(t) e ω(t) com o mesmo eixo t.
3. O eixo de aço tem 0,01905 m de diâmetro e 0,3048 m de comprimento. O volante de
alumínio é mostrado na figura 5 e a braçadeira que liga o volante ao eixo é mostrada na
figura 7. Uma vista do corte transversal pode ser observada na figura 8. Determine a
inércia de rotação do sistema. Note: para todos os problemas suponha que ρal = 2700
kg/m3 e ρaço = 7850 kg/m3 .
4. No lab você medirá a resposta deste sistema. O diagrama dos dados (fig. 4) abaixo é
típico do que você verá. Deste diagrama:
(a) faça uma estimativa da constante de tempo do sistema
(b) determine o coeficiente de amortecimento c , dados: a inércia do eixo calculada acima
e a constante de tempo da parte (a)
(c) faça o gráfico das posições dos pólos do sistema no plano complexo
(d) use os dados das posições fornecidos para fazer um diagrama aproximado da
velocidade ω(t) como função do tempo.
i.
Explique como você criou este diagrama.
ii.
Qual é a condição da velocidade inicial? Explique. Observe que nos dados
experimentais a resposta não necessariamente “inicia” em t = 0.
Figura 4: Diagrama dos dados para o problema 4.
(**Tradução das expressões que aparecem na fig. 4:
θ(t) vs. Time = θ(t) vs. tempo
θ(t) (rads) = θ(t) (rad/s)
Time (s) = tempo (s) )
5. Suponha que o anel de latão, mostrado na fig. 6, é adicionado ao volante (uma vista do
corte diagonal pode ser observada na figura 9). Qual é o novo valor de I? (Relembre que a
inércia de um anel é 1/2M(r2 + R2 ), da página 14 do nosso livro texto). Use ρlatão = 7446
kg/m3 . Aplicando o coeficiente c determinado em (4), qual é a nova constante de tempo
do sistema, se o amortecimento é o mesmo que o determinado na seção anterior?
Figura 5: Dimensões do volante
Figura 6: Anel de latão
Figura 7: Colar (ou braçaderia) de retenção.
Figura 8: Eixo e volante, corte transversal.
Figura 9: Eixo, volante e anel de latão, corte transversal.
(**Tradução dos termos, que aparecem nas figuras 8 e 9:
Shaft =Eixo
Flywheel = volante
Collar = colar ou braçadeira de retenção
Ring = anel
Section = corte )