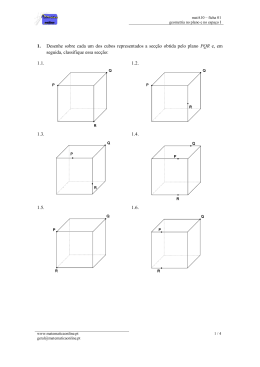
matA10 – ficha 01
geometria no plano e no espaço I, secções
1.
Desenhe sobre cada um dos cubos representados a secção obtida pelo plano PQR e, em
seguida, classifique essa secção:
1.1.
1.2.
1.3.
1.4.
1.5.
1.6.
www.matematicaonline.pt
[email protected]
1/4
matA10 – ficha 01
geometria no plano e no espaço I, secções
1.7.
1.8.
1.9.
1.10.
1.11.
1.12.
1.13.
1.14.
www.matematicaonline.pt
[email protected]
2/4
matA10 – ficha 01
geometria no plano e no espaço I, secções
2.
2.1.
3.
Determine a secção obtida no cubo pelo plano PQR e classifique-a quanto ao número de
lados.
P e Q pertencem à face [ABCD]
R pertence à face [DCGH]
2.2.
P, Q e R são os pontos médios dos
segmentos [BC], [AE] e [EF],
respetivamente.
Qual dos seguintes triângulos não pode ser obtido como secção produzida num cubo por
um plano?
(A)
Triângulo equilátero
(C)
Triângulo escaleno
(B)
Triângulo isósceles
(D)
Triângulo retângulo
4.
Identifique a secção ou as secções que se obtêm:
4.1.
intersetando um tetraedro regular com um plano paralelo a uma das faces.
4.2.
intersetando um cilindo com um plano perpendicular às bases.
4.3.
intersetando um cilindro com um plano paralelo às bases.
4.4.
intersetando uma pirâmide quadrangular com um plano paralelo à base.
4.5.
intersetando uma pirâmide quadrangular com um plano perpendicular à base.
5.
Considere um cubo e um plano perpendicular às bases e que contém uma das diagonais das
bases.
5.1.
Desenhe um cubo com a secção sugerida e classifique-a.
5.2.
Considrando que o cubo tem 20 cm de diagonal espacial, determine o valor exato da área
da secção obtida na alinea anterior.
No caso do resultado obtido ser uma fração, apresente-a com denominador inteiro.
Bom trabalho!!
www.matematicaonline.pt
[email protected]
3/4
matA10 – ficha 01
geometria no plano e no espaço I, secções
Principais Soluções
1.7.
1.14.
1.
1.1.
1.8.
2.
2.1.
1.2.
1.9.
2.2.
1.3.
1.10.
1.4.
1.11.
1.5.
1.12.
3.
3.1.
(D)
4.
4.1.
4.2.
4.3.
4.4.
4.5.
Triângulo equilátero
Retângulo
Circulo
Quadrado
Triângulo, trapézio
5.
5.1.
Retângulo
5.2.
A
400 2
3
1.6.
1.13.
www.matematicaonline.pt
[email protected]
4/4