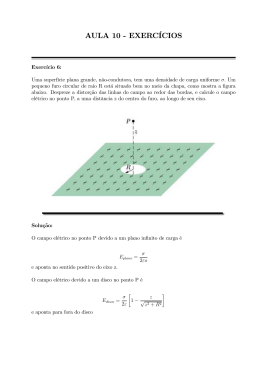
Exercı́cio 1. Considere uma placa infinita com espessura 2d de acordo com
a figura abaixo:
Figura 1: Placa infinita
d
Sua densidade de carga é dada por: ρ = k(y 2 − c2 ), |y| < d, sendo c = √
3
Calcule a densidade volumétrica de energia potencial eletrostática para
uma região desta placa de espesura 2d.
1
Resolução. Pretende-se usar a seguinte expressão para calcular a energia potencial eletrostática:
0 R ~ ~
U=
3 E · Edv
2 <
Logo necessita-se do campo elétrico em todo o <3 , comecemos calculando
o campo na região externa (|y| > d) tomando-se uma gaussiana paralela à
placa com área S.
H
~ · d~s = Qint ⇒ Ey = Qint
E
0 R
2S0
R
d
2
Qint = ρdv = −d k(y − c2 )Sdy
Rd
= 2kS 0 (y 2 − c2 )dy
Rd
= 2kS 0 (y 2 − c2 )dy
d
d
= 2kS (y 3 /3 − c2 y)0 = 0 (c = √ )
3
⇒ Ey = 0, (|y| > d)
Agora obter-se-á o campo interno (|y| < d)
H
~ · d~s = Qint ⇒ Ey = Qint
E
0 R
2S0
R
d
2
Qint = ρdv = −d k(y − c2 )Sdy
Rd
= 2kS 0 (y 2 − c2 )dy
Rd
= 2kS 0 (y 2 − c2 )dy
= 2kS(y 3 /3 − c2 y)d0
2kS 3
=
(d − 3c2 d) ⇒
3
k 3
Ey =
(d − 3c2 d)
30
Calculando então a energia:
0 R ~ ~
U=
3 E · Edv
2 <
R
0 d 2
=
E Sdy
2 −d y
2
k 3
0 R d
2
(d − 3c d) Sdy
=
2 −d 30
Sk 2 R d 6
=
y − 6c2 y 4 + 9c4 y 2 dy
90 0
Sk 2 R d 6
d
2 4
4 2
√
=
y
−
2d
y
+
d
y
dy
(c
=
)
90 0
3
2
Sk 2 d7
(1/7 − 2/5 + 1/3)
90
Logo a densidade no volume solicitado é:
U
k 2 d6
=
(1/14 − 1/5 + 1/6)
S2d
90
⇒U =
3