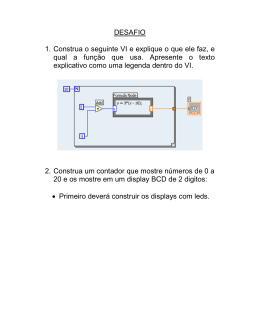
1. Generalidades
Exercı́cio 1. Seja X : Ω → R uma variável aleatória. A função
distribuição F de X fica definida por:
∀x ∈ R F (x) = P[X ≤ x] .
(1) Mostre que F tem as seguintes propriedades:
(a) 0 ≤ F ≤ 1, limx→−∞ F (x) = 0, limx→+∞ F (x) = 1 .
(b) F é não decrescente.
(c) F é contı́nua à direita. i.e. : limh→0, h≥0 F (x + h) = F (x)
(2) Seja g : R → R mensurável tal que E[|g(X)|] < +∞. Mostre
que:
+∞
g(x)dF (x) ,
E[g(X)] =
−∞
onde o integral à direita é um integral de Lebesgue-Stieltjes.
(3) Seja p(x) ≥ 0 uma função mensurável definida em R. Diz-se
que X tem como densidade (relativamente à medida de Lebesgue)
a função p se:
x
p(y)dy .
F (x) =
−∞
Sabendo que o movimento browniano a uma dimensão, Bt no
tempo t, tem densidade:
∀x ∈ R p(x) = √
x2
1
exp(− ) ,
2t
2πt
determine a densidade de Bt2 .
Exercı́cio 2.
(1) Seja X : Ω → Rn uma variável aleatória tal que:
∃p ∈]0, +∞[ E[|X|p ] < +∞ .
Mostre a desigualdade de Chebychev:
∀λ > 0 P[|X| ≥ λ] ≤
1
E[|X|p ] .
λp
(2) Suponha que existe k > 0 tal que:
M = E[exp(k|X|)] < +∞ .
Mostre que:
∀λ ≥ 0 P[|X| ≥ λ] ≤ M e−kλ .
Exercı́cio 3. Sejam X, Y : Ω → R variáveis aleatórias independentes e suponha também, para simplificar, que X e Y são limitadas.
Mostre que:
E[XY ] = E[X]E[Y ] .
1
2
Exercı́cio 4. Seja (Ω, F, P) um espaço de probabilidadee sejam A1 , A2 . . . ,
conjuntos em F tais que:
+∞
P[Ak ] < +∞ .
k=1
Mostre o lema de Borel-Cantelli:
P[
+∞
+∞
Ak ] = 0 ,
m=1 k=m
i.e., a probabilidade que ω pertença a uma infinidade dos conjuntos Ak
é zero.
Exercı́cio 5. Sendo W = (Wt )t≥0 o processo de Wiener, mostre que:
(1) E [Wt ] = 0, E [Wt2 ] = t, ∀t ≥ 0.
(2) E [W
s), ∀t, s ≥ 0.
t Ws ] = min(t,
(3) E (Wt − Ws )2 = t − s, t ≥ s.
Exercı́cio 6. Sejam W = (Wt )t≥0 o processo de Wiener e t0 ≥ 0 fixo.
t = Wt0 +t − Wt0 é um processo de Wiener.
Prove que W
Exercı́cio 7. Seja Bt um processo de Wiener em R tal que B0 = 0
(1) Mostre, usando propriedades conhecidas, que:
1
∀u ∈ R E[eiuBt ] = exp(− u2 t) .
2
(2) Usando o desenvolvimento de Taylor da função exponencial nos
dois membros da igualdade acima, compare os termos com a
mesma potência em u e deduza que:
E[Bt4 ] = 3t2
e, mais geralmente que:
∀k ∈ N E[Bt2k ] =
(2k)! k
t .
2k k!
(3) Uma outra justificação do resultado anterior é a seguinte. Mostre
que:
1
x2
f (x) exp(− )dx ,
E[f (Bt )] = √
2t
2πt R
para todas as funções f tais que o integral à direita converge.
Aplique então este resultado à função f (x) = x2k e use integração por partes e indução em k.
3
2. Integral de Ito, Tempos de Paragem e Martingalas
Exercı́cio 8. Mostre que com Bt o processo browniano e considerando
B0 = 0. Então
t
1
1
Bs dBs = Bt2 − t.
2
2
0
Exercı́cio 9. Mostre directamente usando a definição do integral de
Ito que:
t
t
sdBs = tBt −
Bs ds .
0
0
Indicação: Considere que B0 = 0 e que:
∆(sj Bj ) =
sj ∆(Bj ) +
Bj+1 ∆(sj ) .
j
j
j
Exercı́cio 10. Mostre directamente usando a definição do integral de
Ito que:
t
t
1 3
2
Bs dBs = Bt −
Bs ds .
3
0
0
Indicação: Considere que B0 = 0.
Exercı́cio 11. Seja X = (Xt )t∈[0,+∞[ um processo estocástico e seja
HtX = Ht para t ∈ [0, +∞[, a σ-álgebra gerada pela famı́lia de variáveis
aleatórias {Xt : 0 ≤ s ≤ t}. Isto é, HX = (Ht )t∈[0,+∞[ é a filtração
associada ao processo estocástico X.
(1) Mostre que se X é uma martingala relativamente a uma dada
filtração N = (Nt )t∈[0,+∞[ então X é também uma martingala
relativamente à filtração que lhe está associada HX .
(2) Mostre que se X é uma martingala relativamente a HX então:
∀t ∈ [0, +∞[ E[Xt ] = E[X0 ] .
Exercı́cio 12. Mostre que o processo de Wiener W = (Wt )t≥0 é uma
martingala com respeito à filtração
Ft = σ ({Ws ; s ≤ t}) .
Exercı́cio 13. Verifique quais os processos seguintes são ou não martingalas:
(1)
Xt = Bt + 4t ,
(2)
Xt = Bt2 ,
(3)
t
Xt = t2 Bt − 2
sBs ds ,
0
(4)
Xt = Bti × Btii ,
4
onde Bti e Btii são processos brownianos independentes.
Exercı́cio 14. Mostre directamente que:
Mt = Bt2 − t ,
é uma martingala relativamente à filtração do processo browniano.
Exercı́cio 15. Mostre que:
Mt = Bt3 − 3tBt ,
é uma martingala relativamente à filtração do processo browniano.
Exercı́cio 16. Seja ∆ = {s(1), s(2), . . . s(n)} uma subdivisão do intervalo [t, u] em R+ isto é, tal que: t = s(1) < s(2) < · · · < s(n) = u.
Seja δ(∆) o passo da subdivisão ∆ definido por:
δ(∆) =
sup |s(i + 1) − s(i)| .
1≤i≤n−1
Seja r2 (∆) a variação quadrática do processo browniano em ∆ dada
por:
n−1
(Bs(i+1) − Bs(i) )2 .
r2 (∆) =
i=1
Seja r1 (∆) a variação (simples) do processo browniano em ∆ dada por:
r1 (∆) =
n−1
|Bs(i+1) − Bs(i) | .
i=1
(1) Mostre que E[r2 (∆)] = u − t.
2
2
(2) Mostre que E[(r2 (∆))2 ] = 2 n−1
i=1 (s(i + 1) − s(i)) + (u − t) .
Indicações: Poderá usar que:
• E[(Bs(i+1) − Bs(i) )4 ] = 3(s(i + 1) − s(i))2 .
• Os incrementos do processo browniano são independentes.
(3) Mostre que E[(r2 (∆) − (u − t))2 ] = E[(r2 (∆))2 ] − (u − t)2 e
conclua que em L2 (P):
lim r2 (∆) = u − t .
δ(∆)→0
(4) Mostre que existe uma sucessão de partições (∆n )n∈N tal que,
salvo talvez num conjunnto de probabilidade nula:
lim r2 (∆n ) = u − t .
n→+∞
Indicação: A convergência em L2 (P) implica a existência de
uma sucessão convergente salvo talvez num conjunnto de probabilidade nula.
(5) Mostre que se ∆n = {s(1, n), s(2, n), . . . s(k(n), n)} com u =
s(1, n) < · · · < s(k(n), n) = t então:
k(n)
k(n)
2
i=1 |Bs(i+1,n) − Bs(i,n) |
|Bs(i+1,n) − Bs(i,n) | ≥
.
sup r1 (∆) ≥
sup
|B
−
B
|
∆
s(i+1,n)
s(i,n)
1≤i≤k(n)
i=1
5
(6) Conclua que salvo talvez num conjunto de probabilidade nula:
sup r1 (∆) = sup
∆
∆
n−1
|Bs(i+1) − Bs(i) | = +∞ .
i=1
Exercı́cio 17. Mostre que qualquer função constante não negativa é
um stopping time.
Exercı́cio 18. Mostre que se T é um stopping time de (Ft )t≥0 então
para
∀t ≥ 0{T < t} ∈ Ft .
Exercı́cio 19. Se T é um stopping time e a > 0 uma constante então
T + a é um stopping time.
Exercı́cio 20. Mostre que se T e S são stopping times então também
o são
T ∧ S e T ∨ S.
Exercı́cio 21. Prove que FT é uma σ−álgebra e que T é FT −mensurável.
Mostre que se ∀ω ∈ Ω T (ω) = a para a ≥ 0 constante, então FT = Fa
Exercı́cio 22. Mostre que para quaisquer dois stopping times T e S e
para qualquer A ∈ FS , temos A ∩ {S ≤ T } ∈ FT . Em particular, se
S ≤ T em Ω então FS ⊆ FT .
Exercı́cio 23. Dados S e T stopping times. Mostre que FT ∧S = FT ∩
FS .
Exercı́cio 24. Sejam Bt o processo browniano, ∆tk = tk+1 − tk e
∆Bk = Btk+1 − Btk com 0 = t0 < t1 < . . . < tn = t. Mostre que

2 
n
n
2


(∆Bk ) − t
(∆tk )2
=2
E
k=1
k=1
e conclua que
n
(∆Bk )2 → t quando ∆tk → 0 (n → ∞)
k=1
em L .
2
3. Fórmula de Ito
Exercı́cio 25. Use a fórmula de Ito para escrever os seguintes processos estocásticos na forma diferencial habitual:
dXt = u(t, ω)dt + v(t, ω)dBt .
(1) Xt = (Bt )2 .
(2) Xt = 2 + t + exp(Bt ).
6
Exercı́cio 26. Use a fórmula de Ito para demonstrar que:
t
t
1 3
2
Bs dBs = Bt −
Bt ds, B0 = 0.
3
0
0
Exercı́cio 27. Sejam Xt e Yt dois processos de Ito dados na forma
diferencial habitual por:
dXt = σ(t, ω)dt + µ(t, ω)dBt , dYt = ρ(t, ω)dt + ν(t, ω)dBt .
Mostre usando a fórmula de Ito e o facto
1
Xt Yt = ((Xt + Yt )2 − Xt2 − Yt2 ) ,
2
que:
d(Xt Yt ) = Xt dYt + Yt dXt + µ(t, ω)ν(t, ω)dt .
Exercı́cio 28. Sejam Xt e Yt dois processos de Ito. Mostre que
d(Xt Yt ) = Xt dYt + Yt dXt + dXt dYt
e conclua com a seguinte fórmula de integração por partes:
t
t
t
Xs dYs = Xt Yt − X0 Y0 −
Ys dXs −
dXs dYs .
0
0
0
Exercı́cio 29. Seja θ(t, ω) ∈ N ([0, T ]) onde N ([0, T ]) é o espaço das
funções integrandas para as quais o integral de Ito foi definido inicialmente. Seja para t ∈ [0, T ]:
t
1 t 2
θ (s, ω)ds) .
Zt = exp( θ(s, ω)dBs −
2 0
0
(1) Use a fórmula de Ito para mostrar que dZt = Zt θ(t, ω)dBt .
(2) Conclua que Zt é uma martingala para t ∈ [0, T ] se se verificar
que Zt θ(t, ω) ∈ N ([0, T ]).
Exercı́cio 30.
(1) Para c e α constantes seja Xt = exp(ct + αBt ).
Mostre que:
1
dXt = (c + α2 )Xt dt + αXt dBt .
2
(2) Para c e α1 , . . . , αn constantes e (Bti )i∈{1,...,n} famı́lia de n processos brownianos independentes seja:
n
αi Bti )
Xt = exp(ct +
i=1
Mostre que:
n
n
1 2
α )Xt dt + Xt (
αi dBti ) .
dXt = (c +
2 i=1 i
i=1
Exercı́cio 31. Seja Xt um integral de Ito dXt = v(t, ω)dBt .
7
(1) Dê um exemplo que mostre que Xt2 não é em geral uma martingala.
(2) Mostre que
t
2
|v(t, ω)|2 ds ,
Mt = Xt −
0
é uma martingala.
Exercı́cio 32. Sejam Bt1 e Bt2 dois processos brownianos independentes. Escreva na forma diferencial o processo bidimensional definido
por:
Zt = Zt1 , Zt2 = Bt1 Bt2 , exp(Bt1 )Bt2 .
Exercı́cio 33. Suponha-se que Xt satisfaz a equação
dXt = αXt dt + σXt dWt
e que Yt satisfaz a equação
dYt = γYt dt + δYt dVt ,
onde V é um processo de Wiener independente de W . Defina-se Z por
Z = XY e obtenha o desenvolvimento diferencial de Z.
Nota: Se X descreve o processo do preço de uma acção da IBM em
dólares e Y a taxa de conversão escudos/dólares então Z descreve a
dinamica do preço da acção da IBM em escudos.
Exercı́cio 34. Seja Xt o processo solução da equação:
dXt = (αXt + β) dt + (σXt + ρ) dWt
X0 = 0
Façamos St = exp((α − σ 2 /2) t + σWt ).
(1) Escreva a equação
diferencial
que St−1 satisfaz.
(2) Prove que d Xt St−1 = St−1 ((β − σρ)dt + ρdWt ).
(3) Obtenha a representação explicita de Xt .
Exercı́cio 35. O processo de Ornstein-Ulhenbeck é a solução da equação:
dXt = −cXt dt + σdBt
X0 = x0
t
(1) Mostre que Xt = x0 e−ct + σe−ct 0 ecs dBs .
(2) Calcule E [Xt ] e V [Xt ].
Indicação: Aplique a fórmula de Ito à função f (t, Xt ) = Xt exp(ct).
Exercı́cio 36. O movimento browniano geométrico é a solução da
equação:
dXt = αXt dt + σXt dWt
X0 = x0
σ2
(1) Mostre que Xt = x0 exp( α − 2 t + σWt ).
(2) Mostre que E [Xt ] = x0 exp(αt).
8
Indicação: Aplique a fórmula de Ito à função f (t, Xt ) = ln(Xt ).
4. O Modelo de Black-Scholes
Exercı́cio 37. Considere que no modelo de Black-Scholes a evolução
dos preços dos activos é dada pelas equações:
dSt = µSt dt + σSt dBt ,
dβt = rβt dt
onde (Bt )t∈R+ é um processo browniano usual.
1- Mostre que:
(2.1)
St+∆t = St exp(σ(Bt+∆t − Bt ) + (µ − 12 σ 2 )∆t)
e conclua que os retornos logarı́tmicos do activo em questão são normais
com média e variância definidas.
2- Usando a fórmula (2.1) mostre que:
E[ln(St+∆t /St )]
V[ln(St+∆t /St )]
1
, σ2 =
µ − σ2 =
2
∆t
∆t
onde E[X] e V[X] representam a média e a variância da variável
aleatória X.
3- Considere os seguintes dados para a evolução dos preços (St )t∈{0,...,11}
em que os preços são dados mensalmente.
t
0
1
2
3
4
5
St 6 900 6 710 6 535 6 281 6 232 6 098
t
6
7
8
9
10
11
St 6 021 5 536 5 419 5 641 5 380 5 216
Determine µ e σ.
4- Determine o preço de uma call option europeia, no instante t = 11
sobre o activo representado por St , com taxa nominal de 3,6% ao ano,
maturidade de 3 meses e preço de Execı́cio de 5 500.
Exercı́cio 38. Para c e α constantes, seja Xt = exp (ct + αBt ). Use
a fórmula de Ito para mostrar que
1 2
dXt = c + α Xt dt + αXt dBt
2
Exercı́cio 39. Considere que no modelo de Black-Scholes a evolução
dos preços dos activos é dada pelas equações:
dSt = µSt dt + σSt dBt ,
dβt = rβt dt
onde (Bt )t∈R+ é um processo browniano usual.
1- Mostre que:
(2.1)
St+∆t = St exp(σ(Bt+∆t − Bt ) + (µ − 12 σ 2 )∆t)
e conclua que os retornos logarı́tmicos do activo em questão são normais
com média e variância definidas.
9
2- Usando a fórmula (2.1) mostre que:
E[ln(St+∆t /St )]
V[ln(St+∆t /St )]
1
µ − σ2 =
, σ2 =
2
∆t
∆t
onde E[X] e V[X] representam a média e a variância da variável
aleatória X.
3- Considere os seguintes dados para a evolução dos preços (St )t∈{0,...,13}
em que os preços são dados mensalmente.
t
0
1
2
3
4
5
St 3 478 3 587 3 760 3 613 3 690 4 014
t
6
7
8
9
10
11
St 4 065 4 154 4 187 4 357 4 473 4 600
Determine µ e σ.
4- Determine o preço de uma put option europeia, no instante t = 11
sobre o activo representado por St , com taxa nominal de 3,6% ao ano,
maturidade de 4 meses e preço de Execı́cio de 4 500.
Exercı́cio 40. Considere que no modelo de Black-Scholes a evolução
dos preços dos activos é dada pelas equações:
dSt = µSt dt + σSt dBt ,
dβt = rβt dt
onde (Bt )t∈R+ é um processo browniano usual.
1- Mostre que:
(2.1)
St+∆t = St exp(σ(Bt+∆t − Bt ) + (µ − 12 σ 2 )∆t)
e conclua que os retornos logarı́tmicos do activo em questão são normais
com média e variância definidas.
2- Usando a fórmula (2.1) mostre que:
E[ln(St+∆t /St )]
V[ln(St+∆t /St )]
1
, σ2 =
µ − σ2 =
2
∆t
∆t
onde E[X] e V[X] representam a média e a variância da variável
aleatória X.
3- Considere os seguintes dados para a evolução dos preços (St )t∈{0,...,13}
em que os preços são dados mensalmente.
t
0
1
2
3
4
5
St 6 900 6 710 6 535 6 281 6 232 6 098
t
6
7
8
9
10
11
St 6 021 5 536 5 419 5 641 5 380 5 216
Determine µ e σ.
4- Usando a fórmula de Black-Scholes determine uma volatilidade implı́cita
para a qual a fórmula de apreçamento de uma Call Option europeia dá
um preço de 4, dado que o preço do activo subjacente é 45, o preço
10
de Execı́cio é 50, a taxa de juro sem risco mensal é 0.4% e que a
maturidade é 3 meses.
Sugestão: Poderá usar uma interpolação linear.