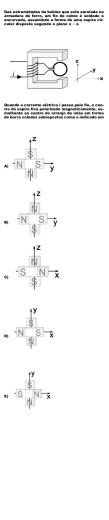
CES – Centro de Ensino Superior de C. Lafaiete
Faculdade de Engenharia Elétrica
Eletromagnetismo
Prof. Aloísio Elói
Lei de Faraday
Serway e Jewett – Capítulo 23
Michael Faraday
1. Fluxo magnético: Φ B = ∫ B i d A . Unidade SI 1 weber = 1 Wb = 1 Tm2. Ver figura 1.
2. Lei de Faraday da indução:
ε =−
dΦB
.
dt
3. Par N espiras idênticas concêntricas:
ε = −N
dΦB
dt
4. Para um campo uniforme através de uma espira:
ε =−
d
( BA cos θ ) . Ver figura 2.
dt
01 – Fluxo magnético
5. F.e.m. do movimento: ε = − Bℓv . Ver figura 3.
6. Gerador de C.A. : ε = NABω senωt . Ver figura 4.
7. Lei de Lenz: a polaridade da f.e.m. induzida em uma espira é tal que produz uma corrente cujo campo magnético se opõe à
variação do fluxo magnético através da espira. Isto é, corrente induzida está num sentido tal que o campo magnético induzido
tenta manter o fluxo original através da espira. Ver figura 5.
Figura 02 – Fluxo através de
espira com
B constante.
Figura 3
Figura 5 – Lei de Lenz
4 – Gerador de corrente alternada
8. Um campo elétrico é sempre gerado por um fluxo magnético variável. Ver figura 5.
9. Forma geral da lei de Faraday da indução:
ε = ∫ E ids = −
dΦB
.
dt
10. Auto-indutância: para uma bobina com N espiras com geometria fixa temos:
ε L = −N
dΦB
dI
Φ
= − L , onde L = N B ,
dt
dt
I
onde L é a indutância da bobina, característica que depende de fatores geométricos e físicos da objeto, e que é medida (no SI) em
henry = V.s/A. Ver figura 6.
11. Independentemente da forma, de uma bobina, de seu tamanho e de suas características físicas, a indutância de uma bobina pode
ser calculada através de L = −
εL
dI / dt
.
Figura 5
Figura 6
Figura 7
12. A figura 8 mostra o gráfico da corrente em função do tempo para um circuito da figura 7 quando a chave é fechada em t = 0. A
equação correspondente é
I (t ) =
ε
R
−
t
(1 − e τ ) onde τ =
L
.
R
13. A figura 9 mostra o gráfico de dI/dt em função do tempo para um circuito da figura 7 quando a chave é fechada em t = 0.
Figura 8
Figura 9
Figura 10
14. No circuito da figura 10, quando a chave S está virada para “a” a fonte está inserida no circuito. Quando viramos a chave para “b”,
a fonte é excluída do sistema. Tomando este instante como t = 0, teremos para a corrente a expressão a seguir e o gráfico
correspondente é o da figura 11.
I (t ) =
ε
R
−
t
τ
e =I i e
−
t
τ
onde τ =
15. Energia armazenada num campo magnético:
L
.
R
U B = 12 LI 2 .
16. Densidade de energia (energia armazenada por unidade de volume):
uB =
UB
B2
=
.
Aℓ 2 µ0
Figura 11
Exemplos e Exercícios
01 (23.1/pág.868) - Uma bobina está enrolada com 200 espiras de fio de cobre sobre o
perímetro de uma armação quadrada cujos lados têm 18 cm. Cada volta tem a mesma área,
igual à da armação, e a resistência total da bobina é 2,0 Ω. Um campo magnético é
perpendicular ao plano da bobina e tem a mesma magnitude em todos os pontos dentro da
área da bobina a qualquer instante. Se a magnitude do campo mudar a uma taxa constante
de 0 a 0,50 T em um período de 0,80 s, encontre a magnitude da fem induzida na bobina
quando o campo está variando. (|ε|
= 4,1 V).
Exercício S/Nº, pág. 868 – Qual é a magnitude da corrente induzida na bobina quando o
campo está variando? (i = 2,0 A).
Questão 02
02 (23.2/pág.868) – Uma espira plana, de área A, é colocada numa região onde o
campo magnético faz um ângulo θ com a normal ao plano e tem a mesma magnitude
em todos os pontos dentro da área da bobina a cada instante. A magnitude do campo
magnético varia com o tempo de acordo com a expressão
B = Bmáx e − at ,
isto é,
em t = 0 o campo é Bmáx e para t > 0, o campo decai exponencialmente com o tempo,
conforme a figura ao lado. Encontre a fem induzida na espira em função do tempo.
(ε
= aABmáx cosθ e − at ) .
Exercício S/Nº, pág. 868 – Uma espira plana consistindo de uma única volta com
área de secção transversal de 8,00 cm2 é perpendicular a um campo magnético que
aumenta de magnitude uniformemente de 0,50 T para 2,50 T em 1,00 s. Qual é a
corrente induzida resultante se a espira tem resistência de 2,00 Ω ? (i = 800µA).
03 (23.3/pág. 871) – Uma barra condutora de comprimento ℓ gira com uma
velocidade angular constante ω ao redor de um eixo que passa por uma de suas
extremidades. Um campo uniforme B é orientado perpendicularmente ao plano da
Questão 03
rotação, como indicado na figura ao lado. Encontre a fem induzida entre as
extremidades da barra.
(ε = Bω ℓ 2 ) .
04 (23.4/pág. 871) – Uma barra de massa m e comprimento ℓ desloca-se sobre dois
trilhos paralelos sem atrito na presença de um campo magnético uniforme orientado para
dentro do papel (ver figura abaixo). É fornecida uma velocidade
vi à barra apontando
para a direita e depois ela é liberada. Encontre a velocidade da barra em função do
tempo.
(v = vi e − t /τ ,τ = mR / B 2 ).
Exercício S/Nº, pág. 873 – As bobinas que giram em um campo magnético são usadas
frequentemente para medir campos magnéticos desconhecidos. Por exemplo, considere
uma bobina com raio de 1,0 cm, tendo 50 espiras, que gira em torno de um eixo
perpendicular ao campo com uma freqüência de 20 Hz. Se a fem induzida máxima na
bobina for 3,0 V, encontre o valor do campo magnético. (B = 1,5 T).
Questão 04
05 (23.5/pág. 876) – Uma bobina de fio é colocada perto de um
eletroímã como indicado na figura ao lado. Encontre a direção da
corrente induzida na bobina: (a) no instante em que a chave é fechada;
(b) depois que a chave foi fechada por vários segundos e (c) quando a
chave é aberta. (Respostas: a) ver “b”; b) i = 0; c) ver “c”).
06 (23.6/pág.878) – Um solenóide longo de raio R tem n espiras por
unidade de comprimento e conduz uma corrente que varia com o tempo
de maneira senoidal como I = I máx cos ωt , onde Imáx é a corrente
máxima e ω é a frequencia angular da fonte de corrente alternada (ver
figura correspondente).
(a) Determine a magnitude do campo elétrico induzido fora do
solenóide, a uma distância r > R de seu eixo longo central.
( E = ( µ nI
0
máx
)
ω R 2 senωt ) / 2r , para r > R .
(b) Qual é a magnitude do campo elétrico induzido dentro do solenóide,
a uma distância r do seu eixo?
( E = ( µ0 nI máxω.rsenωt ) / 2r , para r < R) .
Questão 05
07 (23.7/pág.882) - Encontre a indutância de um solenóide uniformemente enrolado que
tem N espiras e comprimento ℓ . Considere que ℓ seja longo comparado com o raio e
que o núcleo do solenóide seja cheio de ar. (
L = µ0 n 2V , onde V = Aℓ ).
08 (23.8/pág.882) –
a) Calcule a indutância de um solenóide que contém 300 espiras se o comprimento do
solenóide for 25,0 cm e sua área de secção transversal for 4,00 cm2 = 4,00 x 10-4 m2.
(L = 1,81 x 10-4 Tm2/A = 0,181 mH).
b) Calcule a fem auto-induzida no solenóide descrito em “a” se a corrente através dele
estiver diminuindo à taxa de 50,0 A/s. (εL = 9,05 mV).
Exercício S/Nº, pág. 882 – Um indutor de 0,388 mH na forma de um solenóide tem um
comprimento que é quatro vezes seu diâmetro. Se for enrolado com 22 espiras por
Questão 06
centímetro, qual será o seu comprimento? (0,109 m).
09 (23.9/pág.886) – Considere o circuito RL da figura ao lado.
a) Encontre a constante de tempo do circuito. ( τ = 5,00 ms).
b) A chave mostrada na figura é fechada em t = 0. Calcule a corrente no
circuito em t = 2,00 s. (I = 0,659 A).
Exercício S/Nº, pág. 886 – Calcule a corrente no circuito e a voltagem no
resistor após ter decorrido uma constante de tempo. ( I = 1,26 A e V = 7,56 V).
Exercício S/Nº, pág. 886 - Calcule a indutância em um circuito RL em série no
qual R = 0,50 Ω e a corrente aumenta para um quarto de seu valor final em
1,5 s. ( L = 2,6 H) .
10 (23.10/pág.888) - Considere o circuito RL mostrado na figura deste
exercício, em que a chave é mudada da posição “a” para a posição “b” em
t = 0. Recorde que a corrente na espira da direita decai exponencialmente com
o tempo de acordo com a expressão
I = I i e − t /τ , onde I i = ε / R é a corrente
inicial e τ = L / R é a constante de tempo. Mostrar que toda a energia
armazenada no campo magnético do indutor é transferida ao resistor.
(Demostração).
Exercício S/Nº, pág. 888 – Demonstre que a integral
∫
∞
0
Pdt tem o valor
L / 2 R . (Demonstração.
Questão 09
11(23.11/pág.889) – Um cabo coaxial longo consiste em dois condutores
cilíndricos concêntricos de raios a e b e comprimento ℓ , como mostra a figura
correspondente. Supõe-se que o condutor interno é uma casca cilíndrica fina. Os
condutores são percorridos por uma corrente I em sentidos opostos.
a) Calcule a auto-indutância L desse cabo. ( L =
µ0 ℓ  b 
ln   ).
2π  a 
b) Calcule a energia total armazenada no campo magnético do cabo.
(U B
=
µ0 ℓI 2  b 
ln   ).
4π
a
Exercício S/Nº, pág. 889 – Uma
bateria de 10,0 V, um resistor de
5,00 Ω e um indutor de 10,0 H
estão conectados em série.
Depois que a corrente alcançou
seu valor máximo calcule:
a) a potência fornecida pela
bateria. (P = 20,0 W).
b) a potência transferida para o
resistor. (P = 20,0 W).
Questão 10
c) a potência transferida para o
indutor. (P = 0).
d) a energia armazenada no campo magnético do indutor. ( UB = 20,0 J).
Questão 11