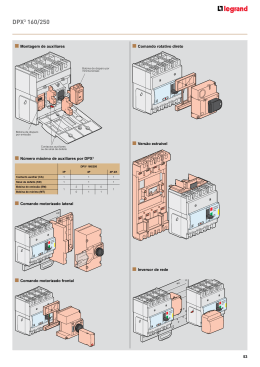
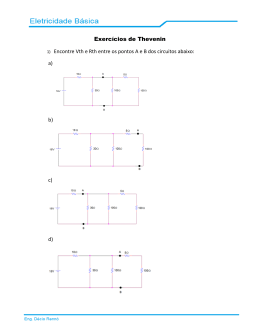
1º) Uma bobina condutora, ligada a um amperímetro, é colocada em uma região onde há um campo
magnético B, uniforme, vertical, paralelo ao eixo da bobina, como representado nesta figura:
Essa bobina pode ser deslocada horizontal
ou verticalmente ou, ainda, ser girada em
torno do eixo PQ da bobina ou da direção
RS,
perpendicular
a
esse
eixo,
permanecendo, sempre, na região do
campo.
Considerando-se
essas
informações,
em
qual
situação
o
amperímetro
indicará
uma
corrente
elétrica?
De acordo com a Lei de Faraday, é necessário que o fluxo magnético varie no interior da bobina
para que haja indução de corrente. Analise em qual situação isto ocorre.
2º) Dois resistores de resistência R1 = 50Ω e R2 = 110Ω são associados em série fazendo parte de
um circuito elétrico. A tensão V1 medida nos terminais de R1 é igual a 25V. Nessas condições,
determine a corrente que passa por R2 e a tensão em seus terminais.
Veja explicação na revisão da 1ª sub.
3º) A tensão do terminal Vc cai à medida que a corrente de carga Ic aumenta. Para uma bateria de
96 V com uma resistência interma de 2 ohm, variamos a resistência de carga de um valor bem alto
até zero, a fim de se observar a variação da tensão do terminal com a corrente de carga. Preencha
os valores que estão faltando na tabela (usar 2 casas decimais).
VB (V)
Ri (Ω)
Rc (Ω)
96
2
∞
96
2
24
96
2
12
96
2
9
96
2
5
96
2
3
96
2
1
96
2
0,5
96
2
0
VRc (V)
Ic (A)
1º Passo: Calcular Ic para cada caso lembrando que Ic = VB / (Rc + Ri).
2º Passo: Calcular Vrc para cada caso lembrando que Vrc = Rc * Ic.
4º) Na experiência abaixo, a bobina 1 é fixa e a bobina 2 se afasta da bobina 1 conforme indica o
vetor v. Indique na figura o sentido da corrente que passa pelo galvanômetro A.
Aplicação da Lei de Lenz e regra da mão direita.
5º) Calcular a potência em R2.
Como o enunciado não determina, pode-se usar Kirchhoff ou Thevenin para solução do
problema.
Por Thevenin:
Vth = V1 – VR1 – V2
VR1 = R1 * I
V1 – R1*I + V3 – R3*I = 0
I = (V1 + V3) / (R1 + R3)
Com I, obtêm-se VR1 e Vth.
Rth = R1 // R3
Desenhar o circuito equivalente de Thevenin.
IR2 = Vth / (Rth + R2)
PR2 = R2 * (IR2)²
Por Kirchhoff:
Definir I1 na malha da esquerda e I2 na malha da direita, ambas no sentido horário.
Definir I3 subindo pelo laço central.
I1 + I3 = I2 ∴ I3 = I2 – I1 (I)
Malha esquerda: V1 – R1*I1 – V2 + R2*I3 = 0
(II)
Malha direita: V2 + V3 – R3*I2 – R2*I3 = 0
(III)
Substituir I3 (I) em (II) e (III), obtendo (IV) e (V)
Isolar I1 em (IV) e (V) e igualar as equações, obtendo I2.
Substituir I2 em (IV) ou (V), obtendo I1.
Substituir I2 e I1 em (I), obtendo I3, que é igual a IR2.
PR2 = R2 * (IR2)²
Fórmulas e Unidades
Req = R1 + R2 + R3 + R4 + R5 + … (Associação Série)
1/Req = 1/R1 + 1/R2 + 1/R3 + … (Associação Paralela)
Tensão
Corrente
Resistência
Potência
Energia
[V]
[I]
[R]
[P]
[E]
(Volts - V)
(Amperes - A)
(Ohms - Ω)
(Watts – W)
(Kilowatt hora – KWh) = P*t (Potência * tempo)
“Em um circuito elétrico, a soma das potências consumidas é igual a soma das potências
fornecidas.”
Quadro RPVI
ρ
n
μ
m
K
M
G
T
10-12
10-9
10-6
10-3
103
106
109
1012
pico
nano
micro
mili
Kilo
Mega
Giga
Tera
“A soma das correntes que chegam e que saem de um nó é igual a zero.”
“A soma das tensões em um circuito fechado (malha) é igual a zero.”
Delta para Ípsilon = “Produto dos adjacentes dividido pela soma”
Ípsilon para Delta = “Soma dos produtos dois a dois dividido pelo oposto”