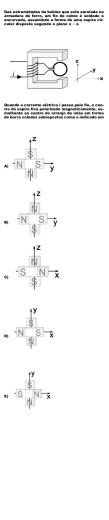
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
 Exemplos

– Lei de Faraday-Lenz
Seja B  B f  Bi
Linhas de Campo magnético
1.
Pólo norte de um ímã se aproximando do plano da espira.
y
ĵ
1
As linhas de força do campo magnético do ímã que entram no
plano da espira aumentam a medida que o ímã avança para baixo na

v  v  ˆj . Logo, há um maior número de linhas de força do

campo magnético externo B   B  ˆj do ímã sobre o plano da espira;
 
portanto o fluxo magnético  B  B  dA aumenta na direção vertical

para baixo( B   ˆj ); assim, o campo magnético induzido sobre a

espira estará na direção contrária: vertical para cima Bind  Bind  ˆj .
velocidade
Fluxo magnético:
 
   B  dS
s
Ou seja:

   B  nˆdS
s
Aqui
n̂ é o vetor unitário normal à superfície S.
Unidade: Weber: 1Wb = 1T. m2.
Observe que, na superfície fechada:
 
M  
 B  dS  0
S
Lei de Faraday
Qualquer mudança no fluxo magnético sobre uma espira causará
uma voltagem ¨induzida¨ na espira. Não importa como esta variação de
fluxo é feita, haverá voltagem gerada. Esta mudança pode ser produzida
movendo-se um magneto sobre a espira, onde haverá mudanças nas
linhas de força de campo magnético que atravessarão a área da espira.
A Lei de Faraday é uma relação fundamental cuja origem está nas
equações de Maxwell. Resumidamente ela diz que uma voltagem (fem)
pode ser gerada por mudança (variação) do fluxo magnético. A fem
induzida na espira é igual a menos a taxa de variação do fluxo
magnético em uma espira; multiplicando por N espiras, teremos a fem
em uma bobina.
 
Portanto, a corrente induzida, pela regra da mão direta, circulará
sobre a espira no sentido anti-horário.
2.
Pólo Sul de um ímã se afastando do plano da espira.
As linhas de força do campo magnético do ímã que entram no
plano da espira diminuem a medida que o ímã avança para cima na

v  v  ˆj . Logo, há um menor número de linhas de força do

campo magnético externo B  B  ˆj do ímã sobre o plano da espira;
 

portanto o fluxo magnético  B  B  dA diminui ( B   ˆj );
velocidade
assim, o campo magnético induzido sobre a espira estará na direção
contrária: vertical para cima

Bind  Bind  ˆj .
Portanto, a corrente induzida, pela regra da mão direta, circulará
sobre a espira no sentido anti-horário.
3.
Pólo norte de um ímã se afastando do plano da espira.
dB
dt
Lei de Lenz
Quando uma força eletromotriz é gerada pela mudança do fluxo
magnético de acordo com a Lei de Faraday, a polaridade da força
eletromotriz induzida é tal que produz uma corrente cujo campo
magnético se opõe às mudanças às quais. A indução magnética dentro de
qualquer fio em forma de espira sempre atua de forma a conservar o
fluxo magnético sobre a espira constante.
As linhas de força do campo magnético do ímã que entram no
plano da espira diminuem a medida que o ímã avança para cima na
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori

v  v  ˆj . Logo, haverá um menor número de linhas de força

do campo magnético externo B   B  ˆj do ímã sobre o plano da espira;
 

portanto o fluxo magnético  B  B  dA diminui ( B   ˆj );
velocidade
assim, o campo magnético induzido sobre a espira estará na direção

contrária: vertical para baixo: Bind
  Bind  ˆj .
 

 B  B  dA aumenta na direção vertical para baixo( B   ˆj );
assim, o campo magnético induzido sobre a bobina estará na direção
contrária: vertical para cima

Bind  Bind  ˆj .
Portanto, a corrente induzida, pela regra da mão direta, circulará
sobre a bobina no sentido anti-horário.
6. Chave sendo fechada num circuito com um indutor.
Portanto, a corrente induzida, pela regra da mão direta, circulará
sobre a espira no sentido horário.
4.
x̂
Pólo Sul de um ímã se aproximando do plano da espira.
iind
2
i
+
-
Ao fechar a chave, a corrente i no indutor irá aumentar. O campo
magnético no indutor, dado pela regra da mão direita, terá uma variação

B   xˆ
aumentando o fluxo magnético
 
 B  B  dA nessa
direção; logo, deve haver um campo magnético induzido na espira no sentido

As linhas de força do campo magnético do ímã que entram no
plano da espira aumentam a medida que o ímã avança para cima na

v  v  ˆj . Logo, haverá um maior número de linhas de força

do campo magnético externo B  B  ˆj do ímã sobre o plano da espira;
 

portanto o fluxo magnético  B  B  dA diminui ( B   ˆj );
oposto: Bind
 Bind  xˆ
que será causado, pela regra da mão direita por
uma corrente induzida (iind) na espira no sentido indicado .
velocidade
7. Chave sendo aberta num circuito com um indutor.
x̂
assim, o campo magnético induzido sobre a espira estará na direção
contrária: vertical para baixo

Bind   Bind  ˆj .
iind
Portanto, a corrente induzida, pela regra da mão direta, circulará
sobre a espira no sentido horário.
5. Bobina móvel com
aproximando de bobina fixa.
corrente
no
sentido
horário
se
i
+
-
Ao abrir a chave, a corrente i no indutor irá diminuir. O campo
magnético no indutor, dado pela regra da mão direita, terá uma variação

B  xˆ
aumentando o fluxo magnético
 
 B  B  dA nessa
direção; logo, deve haver um campo magnético induzido na espira no sentido

i
oposto: Bind
  Bind  xˆ
que será causado, pela regra da mão direita por
uma corrente induzida (iind) na espira no sentido indicado .
8. Chave já aberta num circuito com um indutor.
iind
Caso análogo ao de um ímã com o pólo Norte se aproximando a

v  v  ˆj há um maior

número de linhas de força do campo magnético externo B   B  ˆj do
uma espira. Conforme a bobina desce velocidade
ímã sobre o plano da bobina fixa; portanto o fluxo magnético
Nesse caso não haverá corrente induzida, pois não há corrente no
indutor.
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
9. Bobina imersa numa região de campo magnético uniforme.
12. Condutor com barra deslizante para a direita com velocidade
constante num campo magnético uniforme:
x
Nesse caso não haverá corrente induzida, pois não há variação de
fluxo magnético sobre o plano da bobina.
10. Espira imersa em um campo magnético variável.
3
Nesse caso:
 
Nesse caso:

dB
T 
 0.02    ˆj
dt
s
.Resistência da espira é R = 5.0 .
Como o fluxo aumenta na direção

estar na direção Bind
d l  x 
dB
dA
   B
   B
dt
dt
dt
v

dx
  B  l     B  l  v
dt
l
ĵ , o campo induzido deve
  Bind  ˆj ; pela regra da mão direita, a corrente
deverá circular no sentido horário.
dB
d
 
   ( B  A)
dt
dt
0.02

0.012
 dB
A 
dB
dt  i  0.048mA
  A
 R  iind  iind 
ind
dt
R

Nesse caso, a força será (sentido: regra da mão esquerda):

B l v
B2  l 2  v
F  i l  B  l  B 
lB  F 
R
R
R
2
2
B  l  v2
A potência da força: P  F  v  P 
R
13. Fechando a chave no primeiro circuito;
5
11. Bobina num campo magnético decrescente.
Uma bobina de 500 voltas e 4 cm de raio é colocada num campo
magnético decrescente a 0.2 T/s e forma 30° com o plano da bobina.
Encontre o módulo e o sentido da força induzida.
x̂
iB
iA
A corrente no primeiro circuito aumentará no sentido horário;
pela regra da mão direita, o campo magnético da bobina A:
N
 iA aumentará no sentido x̂ ; assim, o campo induzido na
l

ˆ
bobina B deverá estar no sentido Bind   Bind  x
B  0 
  N 
  N   r 2 
dB
dB
 N  A
 cos 30
dt
dt
dB
 cos 30    500    0.042  (0.2)  cos 30
dt
  0.435V
Pela regra da mão direita, a corrente deverá ter o sentido de b para a.
Se a chave for aberta depois do circuito estar funcionando por algum
tempo: O campo devido a bobina A diminuirá, causando uma variação

BA   xˆ ; assim, o campo induzido na bobina B deverá ter direção

BindB  xˆ ; pela regra da mão direita, a corrente induzida é de a para b.
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
14. Bobina em movimento em uma região de campo magnético
uniforme

B   B  kˆ

Potência:
2
P
R
Suponha bobina de 85 voltas; B = 1.5T; R = 6.2 e v = 18cm/s.
.
iind
 Espira entrando: 0 ≤ x ≤ b
Campo sobre sua área aumenta de forma que sua variação estará:


B  kˆ : Bind  kˆ
4
iind: anti-horária
Fluxo magnético:
B  N  B  A  B  N  B  L  x
 Espira totalmente na região de campo: b ≤ x ≤ d
Campo sobre sua área permanece constante:
 
B  0 não varia o fluxo magnético: iind =0
 Espira saindo: d ≤ x ≤ d+b
Campo sobre sua área diminui de forma que sua variação estará:


B  kˆ : Bind  kˆ
iind: horária.
Fluxo magnético:
B  N  B  A  B  N  B  L   d   x  b 

Força eletromotriz induzida:

3V
85
0.13


dB
d
 
   ( N  B  L  x)    N  
B  L  v
dt
dt
1.5
0.18

2.98

Corrente induzida:
i

R

 i  0.48 A
 15. Determinar o fluxo magnético através de um solenóide de 40
cm de comprimento, 2.5 cm de raio e 600 espiras, percorrido por uma
corrente de 7.5A.

 Força magnética:
85
0.13


F  N  i  l  
B  F  8.0 N
0.48

`1.5
Potência
8 0.18


P  F  v  P  1.4W
Suponha agora: N = 1; B = 2.0 T; R = 1.6  e v = 1.0 m/s e
L = 4cm; d = 15 cm; b = 10 cm. Faça os gráficos do fluxo magnético em
função de x, (x, B), força eletromotriz em função de x (x, ) e da Potência P
em função de x (x, P).

Fluxo magnético: mostre que:
0 se x  0


B  L  x se 0  x  b

B  
 B  L  b se b  x  d (8mWb)
 B  L   d   x  b   se d  x  b  d


Solução:
A    r 2  A    0.0252
N
 m  N  B  A   m  N  0   I    r 2
l
2
N
 m  0 
 I   r 2
l
6002
 m  4 107 
 7.5    0.0252
0.4
m  1.66 102Wb
6.2
 16. Um campo magnético uniforme faz um ângulo de 300 com o
eixo de uma bobina circular de 300 espiras com 4 cm de raio. O campo está
variando à razão de 85 T/s. Determine o módulo da tensão induzida na
bobina.

d m
dt
m  N  B  A  cos 
 
fem
v

dB
d  B dx
dB
 
 
   v 
dt
dx dt
dx
Solução: Pela Lei de Faraday:
 
d
dB
 N  B  A  cos     N  A  cos 
dt
dt
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
  300  0.042  cos30 85
(d) a potência dissipada no resistor.
  111V 
 17. Uma bobina de 80 espiras tem 5 cm e sua resistência é de 30
. Qual deve ser a taxa de variação de um campo perpendicular para que a
corrente induzida na espira seja 4.0 A ?

Solução:
m  N  B  A  m  N  B    r 2
m
B
N   r 2
d m
dB
1

2
dt N    r dt

(a)
Solução
Pela Lei de Faraday:
d m
dt
dB
1


dt N    r 2
dB
1

I R
dt N    r 2
dB
1

4  30
dt 80    0.052
dB
T
 191
dt
s
 
 18. Uma bobina retangular de 80 espiras, 20 cm de largura e 30
cm de comprimento, é submetida a um campo magnético B = 0.8 T dirigido
para dentro do papel, com apenas metade da bobina na região em que existe
campo magnético, que se extende indefinidamente para a esquerda e direita.
A resistência da bobina é de 30 . Determinar o módulo, a direção e o
sentido da corrente induzida se a bobina está se movendo com uma
velocidade de 2 m/s
(a) para a direita;
(b) para cima;
(c) para baixo.
 Solução:
(a) I = 0 pois o fluxo não varia!
(b)  m
 N  B  A  m  N  B  20  x
d m
dx
 N  B  20 
dt
dt
d m
dx
N  B  20 
d m
dt
 
 R  I  I  dt  I 
dt
R
R
I  0.853 A
A corrente está no sentido anti-horário.
(c) A corrente será a mesma que em (b) porém no sentido horário.
 19. No esquema da figura, faça B = 0.6 T ,v = 8m/s, l = 15 cm e
R = 25 ; suponha que a resistência da barra e dos trilhos possa ser
desprezada. Determine:
(a) a tensão induzida no circuito;
(b) a corrente no circuito;
(c) a força necessária para fazer com que a barra se desloque com
velocidade constante.
d m
dx
 N  B l 
dt
dt
  N  B l v
  1 0.6  0.15  8
  0.72V

0.72
I I
R
25
I  28.8mA
F  I  B  l  F  0.0288  0.6  0.15
F  2.59mN
2
P  R  I  20.7mW
Ou P  F  v  20.7mW

(b)
(c)
(d)
 20. Uma barra de massa m desliza sem atrito sobre trilhos
condutores em uma região onde existe um campo magnético uniforme
constante . No instante t = 0, a barra está se movendo com velocidade inicial
v0 e a força externa que agia sobre ela é removida. Determine a velocidade da
barra em função do tempo.
 Solução
F  ma  F  m
I

R
dv
 F  I  B l
dt
I

R
B l v
R
B l v
F  I  B l  F 
 B l
R
B2  l 2  v
dv
B2  l 2  v
F
 m  
R
dt
R
v
t
2
2
2
dv
B l
dv
B l2

dt  

dt
v
m R
v
m  R 0
v0
  Bl v  I 
ln v  ln v0  
B2  l 2
v
B2  l 2
t  ln  
t
m R
v0
m R
v  t   v0  e

B 2 l 2
t
m R
5
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
Figura 1 – Circuito RL.
Indutância L e indutor.
A indutância é a característica do comportamento de uma bobina
em resistir a qualquer mudança de corrente elétrica sobre a espira. Da Lei de
Faraday, teremos:
 
d
d
N
N  di
di


   0   i  A     0   A    L 
dt
dt 
l
l
dt


 dt
ou seja, a indutância L pode ser definida em termos da fem ()
gerada para se opor à mudança da corrente elétrica.
 
d
di
 L 
dt
dt
Verificamos que a indutância L depende das características
Geométricas do circuito. Se tivermos um solenóide, o fluxo será dado por:
N
l  Ai
l
  0  n2  l  A  i    L  i

A
L   L  0  n 2  A  l  0  N 2 
i
l
  B  N  A  0  n  i  N  A  0  n 
6
Figura 2 – Gráfico da corrente em função do tempo.
Unidade: Henry (H) 1H = 1 V.s/A
(1Henry=1 Volt.1Segundo/1 Ampére).
Circuito RL, Chave S1 aberta e S2 fechada, após a corrente no
indutor atingir o máximo valor.
Circuito RL, Chave S1 aberta e S2 fechada, após a corrente no
indutor atingir o máximo valor.
No circuito RL simples da figura anterior, as chaves S1 e S2 são
colocadas de modo que a bateria seja removida do circuito. Depois da
corrente no indutor ter atingido seu máximo valor, com a chave S1 fechada, a
chave S2 é fechada e a S1 aberta. A corrente diminuirá com o tempo
conforme mostra a figura a seguir.
Nesse caso a soma das tensões é igual a zero:
i
Circuito RL simples.
Podemos escrever a equação da leis de Kirchhoff como:
V  L
L
di
 R i  0
dt
R
 t
i
R
ln    t  i(t )  i0  e L
i0
L
( R / L ) dt
di R

  i   e
 e( R / L ) t
dt L
L
Multiplicando-se a equação pelo fator de integração:
R
t
d
 R t
(i  e L )   e L
dt
L
R
R
t
t
i eL  
0

L
R
t
R
t
eL  ieL 

L
eL

t
di
di
R
 R  i  0      dt
dt
i
L
i0
0
t
t
0
R
L
 RL t 
 e  1
R
 
  i (t )    1  e  L t 
i (t )  


R
t
R
R 

eL
Observe que quando t aumenta sem limite, I tende para /R, que é
a corrente prevista pela lei de Ohm quando não há indutância presente.
L
t c  , aqui é a chamada constante de tempo; i (t )  i0  e
R

t
tC
Energia Magnética
Quando instala-se uma corrente no circuito da figura acima, apenas parte da
energia fornecida pela bateria é dissipada no resistor, o restante da energia é
di
 R  i2  0 
dt
dU m
di
L  i2
 L  i   U m   dU m   L  idi 
dt
dt
2
armazenada no indutor: E  i
 L i 
Um 
B  0 
L  i2 B2  l  A

2
2  0
A
N
B l
e L  0  N 2 
i  i 
l
l
0  N
2
A  B l 

l  0  N 
B2  l  A
 Um 
2
2  0
0  N 2   
Um 
(Energia magnética armazenada num indutor)
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
Quando a corrente elétrica diminui, diminui a energia no indutor e
o campo magnético também diminui.
Analogamente, o mesmo acontece quando temos um capacitor
carregado, para o caso do campo Elétrico E. A energia eletrostática
armazenada num capacitor de placas paralelas.
Ue 
Densidade de energia magnética:
um 
Q V  0  E 2  A  d

2
2
u  ue  um  u  27.7  159
J
u  187 3
m
U 1
B2
2
   2 0  E 
V
2 0
Energia no interior da caixa:
A energia armazenada pela bobina de ignição produz a faísca
da vela no motor do automóvel.
 21. Calcular a taxa de variação na corrente para um solenóide de
10 cm de comprimento, 5 cm2 de área e 100 espiras quando a fem induzida
for de 20V.
dI
dI

20
A

 
 3,18.10 5
5
dt
dt
L
s
2 .10
22. Projetar uma bobina de raio R e número de voltas N para um
circuito RL de resistência 1K de forma que a constante de tempo seja de 10
s.

L
A
2
tc   L  R  t c  L   0  N 
R
l
2
R
R  tc  103 10  L  0  N 2 
l
  R2
104  4   107  N 2 
l
2
4
2
R
10
2 R
104  4   2 107 N 2 


N
l
4   2 107
l
 R2
N
J
1 0.022
 um  159 3
7
m
2 4 10
Densidade de energia:
(Energia eletrostática armazenada num capacitor)
Em geral, numa região do espaço onde há campo elétrico e
magnético, definimos densidade de energia à relação:
  L
1 B2
um  
2 0
U  u V  U  u  l 3  U  187  0.123
U  0.323J
 25. Uma bobina de auto-indutância 5.0 mH e resistência 15.0  é
ligada aos terminais de uma bateria de 12 V cuja resistência interna é
desprezível.
(a) Qual é a corrente final?
(b) Qual a corrente após 100s?
 Solução:
t
 

L

(a) I (t )  I f  1  e 
Com  
R



12
 I f  0.8 A
If  0  If 
R
15
L 5 103
(b)  

   333 s
R
15
100



I (t  100 s)  0.8  1  e 333 


I (t  100 s)  0.207 A
 26. Determine o calor total produzido pelo resistor R da figura
quando a corrente no indutor diminui do valor inicial I0 até 0.
2,533 109  l
R
Se montarmos uma bobina com um comprimento de l = 3 cm e
raio 2 cm teremos:
N
2.533 109 l
2.533 109  3 102

 3.4 105
2
R
2.5.10
 23.
Determine a auto-indutância de um solenóide de
comprimento l = 10 cm, área 5 cm2 e 100 espiras.
 Solução
L  0  n2  A  l
2
 100 
4
L  4 10  
  5 10  0.1
 0.1 
L  6.28 105 H

Solução:

dW
P
 dW  P  dt  W   R  i 2 (t )dt
dt
0
7
 24. Uma certa região do espaço contém um campo magnético de
200 G e um campo elétrico de 2.5.106 N/C. Determine:
(a) a densidade de energia na região.
(b) a energia contida em uma caixa cúbica de lado l = 12 cm.
 Solução:
Densidade de energia elétrica:
2
1
1
ue   0  E 2  ue  8.85 1012   2.5 106 
2
2
J
ue  27.7 3
m
i(t )  i0  e
R
 t
L
2

2R
R
 t
 t 

2
L
W   R   I 0  e  dt  W   R  I 0  e L dt


0
0

t 
W  R  I 02 
e


2R
t
L
2R
L
t 0
L  I 02
RL 2
W 
 I 0   0  1  W 
2
2R
7
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
 27. Um circuito RL alimentado por uma bateria de fem  = 12V
consiste em uma bobina de N = 7 voltas, raio R = 2.5 cm e comprimento 1
cm. A resistência possui valor R = 1.2 .
B1  0 
N1
 i1
l
(b) O fluxo magnético sobre a bobina externa.
(a) Determine o valor da indutância da bobina:
L  0  N 2 
L  4 107  7 2 
  R2
  0.0252
0.01
l
 L  1.2 105 H
(b) Encontre a constante de tempo do circuito e a corrente em
função do tempo quando a chave for ligada.

L 1.2 105

   1.0 105 s    0.01ms
R
1.2
(c) Qual a corrente elétrica após 0.02ms da chave ser ligada?
t
0.2
 


12 
 1  e    i(t ) 
 1  e 0.01 
R 
1.2 


0.865

0.02


12 
0.01
i (t  0.02ms) 
 1  e
  i  8.65 A
1.2 
0.135 
i(t ) 
 
(d) Determine o campo magnético sobre o eixo da bobina nesse
instante.
B  0 
N
7
 i  B  4 107 
 8.65
l
0.01
B  7.6mT
 28. Uma bobina de Tesla (um gerador de alta voltagem) consiste
de um longo solenóide de comprimento l, área de seção transversal A e N1
voltas de fio enrolado. Uma outra bobina externa (de N2 voltas) de raio maior
é colocada concêntrica à primeira.
Encontre:
(a) O Campo magnético B1 no eixo da bobina interna, se a
corrente ue a circula é i1.
N1
 i1    R12
l
2
 0  n1  n2  l    R1  i1
 mb2  N 2  B1  A1  b2  N 2  0 
mb2
(c) O valor da indutância mútua entre as bobinas:
M 2,1 
 mb2
i1
 M 2,1  0  n1  n2  l    R12
8
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
Tensão Alternada - geração
Mais de 99% da energia elétrica produzida no mundo é obtida por
geradores elétricos oeprando com corrente alternada (AC). A vantagem
sobre a corrente contínua é que pode ser transportada a longas distâncias, a
baixo valores de corrente e altos de tensão, para ser reduzida a perda de
energia por efeito Joule; podendo assim, ser transformada com o
transformador, o qual utiliza o princípio da indução magnética.
Um gerador simples de corrente alternada é uma bobina girando em um
campo magnético uniforme, como ilustramos na figura abaixo:
Figura 1 – Gerador AC.
IL  
m



cos t  I L  m  sen  t  
L
L
2

XL    L

Reatância Indutiva:



Fase:  = -900
UL adianta-se 900 em relação a IL ou IL atrasa-se 90°
Corrente alternada num Capacitor
Figura 4 – Circuito AC com capacitor. (a) Gráficos de tensão e corrente
versus tempo ediagrama de fasores (b).
9
m  N  B  A  cos 

Aqui, N é o número de espiras, e A a área da bobina. Seja  a
velocidade angular da bobina, que é mecanicamente acionada. Então:
 C   m sen t 
    t      2   f .
 m  N  B  A  cos t   
  N  B  A    sen   t   
Q
C
dQ
dt
 m


I C   m    C  cos   t  
 sen  t  
XC
2

Q  C   m sen t  I C 
A força eletromotriz induzida será dada pela Lei de Faraday-Lenz:
 m  N  B  A  cos   t       
Equações:
d m
dt

Reatância Capacitiva:
XC 
1
 C
Fase:  = + 900
UC atrasa-se 900 em relação a IC ou IC adianta-se.
Recordar por:ELI the ICE man…
 Valores médios, máximos e eficazes
Uma onda CA de tensão ou de corrente possui vários valores
instantâneos ao longo do ciclo. São eles:
 Vm, Im: Valor máximo ou de pico. Aplicado tanto ao pico negativo
como ao pico positivo.

Vpp ou Ipp: Vpp = 2 Vp = 2VM.


   m  sen   t   
 m  N  B  A   ( é a tensão máxima).
m
 Circuitos de tensão alternada.
Em eletrônica, representam-se fenômenos ondulatórios por
funções oscilantes como a seno e o cosseno. Exemplificando na teoria de
corrente alternada, temos uma tensão variando da forma senoidal, assim,
para cada caso, a corrente e a tensão serão estudadas quando submetemos
essa tensão à um:
 Corrente alternada com um Resistor:
Figura 2 – Circuito AC com resistor. (a) Gráficos de tensão e
corrente versus tempo ediagrama de fasores (b).

Valor Médio: V Média sobre todos os valores sobre uma onda
senoidal em meio período.
V
1
T 2
T 2
 V  t dt
0

Valor rms (root mean square): Vrms Quantidade de corrente ou
tensão contínua capaz de produzir a mesma potência de aquecimento. É
definido matematicamente por:
T
2
V
1
V  t   dt  Vrms  m  Vrms  0.707 Vm
T 0 
2
 Circuito RLC
Um importante circuito com muitas características da maior parte
dos circuitos ca é o circuito RLC em série com um gerador. A regra de
Kirchhoff :
dI
Q
L
 RI 
  m sen t
Vrms 

Equações:(Lei de Ohm)

   m sent  R  I
Reatância resistiva:
I 
m
R
sent
XR  R

Fase: Corrente alternada num Indutor:
Figura 3 – Circuito AC com indutor. (a) Gráficos de tensão e
corrente versus tempo ediagrama de fasores (b).
dt
C
Figura 5 -
I  I m  sen(t   )
Onde:
Im

U
 m 
Z
Um
R 2  ( X L  X C )2
tg 
Equações:
 L   m sen t  L
dI
dt

dI  m

sen t  I L  m  sen tdt
dt
L
L
X L  XC
R
Z  R 2  ( X L  X C )2
impedância do circuito RLC

Potência média:
Pmed 
Um  Im
 U ef  I ef
2
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
 29. Um circuito RCL em série, com L = 2H, C = 2F e R = 20 está
alimentado por um gerador de fem máxima de 100 V e frequência variável.
Determinar quando a frequência angular do gerador for de  = 400 rad/s:
(a) A Impedância . (b) A fase  (c) Acorrente máxima Im.
 Solução:
(a)
1
1

 1250
C 400  2 106
  L  400  2  800
XC 
XL
Para calcular a impedância, o valor de XL – XC é muito maior que R
nas condições afastadas da ressonância. Então teremos para a
Impedância Z:
Z 
( X L  X C ) 2  R 2  450
Z  (1250  800)2  202  (450)2  202  450
(b)
(c)
tg 
 30. Uma bobina de 250 voltas e 3 cm de área gira a 60 Hz sob um
campo magnético uniforme de 0.4T. Qual a fem máxima produzida?
2
 m  N  B  A     m  N  B  A  2  f
 m  250  0.4  3 104  2  60
 m  11.31V
 31. Um resistor de 12Ω está conectado a um gerador AC de pico 48
V. Encontre:
(a) A corrente rms.
(b) a potência média.
(c) a máxima potência.
 Solução:
(a)
Z  R2  ( X L  X C )2  02  (0  X C )2  X C
Im 
Vrms
R
Vp
48

 Vrms 
 Vrms  33.9411V
2
2
33.94
I rms 
12
I rms  2.83 A
XC 
1
1
1
 XC 
 XC 
 C
2 f  C
2  2000  20 106
X C  3.98
Im 
(b) Potência média: Pav
 RI
2
rms
Pav  12  2.832
Pav  96W
m
Z
Z  R2  ( X L  X C )2  02  (0  X C )2  X C
Im 
100
 I m  25 A
3.98
 33. Em um circuito RLC, R = 20 Ω, a capacitância eletrostática com
valor C = 2 µF e a indutância do indutor vale L = 2 H. O valor máximo da
fem do gerador é max = 100V e a freqüência do gerador é f = 60 Hz.
XC 
1
1
1
 XC 
 XC 
 C
2 f  C
2  60  2 106
X C  1326.3
X L    L  X L  2 f  L  X L  2 60  2
X L  753.98
I rms 
Vrms
100
 I m  0.75 A
132.63
(b) f 2= 2000Hz
X L  X c 450

 22,5    870
R
20
U
100
 m 
 0,222 A
Z
450
Im
1
1
1
 XC 
 XC 
 C
2 f  C
2  60  20 106
X C  132.63

Im  m
Z
XC 
Im 
m
Z
Z  R 2  ( X L  X C )2
Z  202  (753.98  1326.3)2  572.67
Im 
100
 I m  0.17 A
572.67
 34. Um resistor R e um capacitor C estão ligados em série com um
gerador . A tensão do gerador é dada por:
Vent  V0  cos   t
Determine o valor rms da tensão entre os terminais do capacitor,
Vsai,rms em função da freqüência angular .
2
 R  I max
V
 max
R
(c) Potência máxima: Pmax
I max
48
 I max  4 A
12
Pmax  192W
I max 
 32. Um capacitor de 20 µF é colocado com um gerador de CA com
tensão máxima de 100V. Encontre a reatância capacitiva e a máxima
corrente quando a freqüência for de:
(a) f 1 = 60 Hz
(b) f 2 = 2000 Hz.
(a) f 1= 60 Hz

Solução:
Vsai ,rms  X C  I rms
I rms 
Vent ,rms
Z
Z  R  X C2
2
10
Aulas - Física 3– Fluxo Magnético, Indutores Lei de Faraday-Lenz e Geração de corrente alternada e Circuitos CA – Prof. Dr. Cláudio S. Sartori
Vsai ,rms  X C 
Vsai ,rms  X C 
XC 
Vsai ,rms 
1

 C
Vent ,rms
Z
Vent ,rms
R 2  X C2
1
 C
Vent ,rms
1
 C2
V0
1
2
Vsai ,rms 

  C  2  C 2  R2  1
2 C2
V0
1
2
Vsai ,rms 

2
2
  C   C  R2  1
 C
V
1
Vsai ,rms  0 
2
2   C 2  R2  1
R2 
2
Observação: Esse circuito é denominado de filtro RC passa
baixas.
sen  a  b   sena  cos b  senb  cos a
 cos  a  b   cos a  cos b  sena  senb
11