FÍSICA 3 Indução Magnética Prof. Alexandre A. P. Pohl, DAELN, Câmpus Curitiba EMENTA • • • • • • • • • • • • Carga Elétrica Campo Elétrico Lei de Gauss Potencial Elétrico Capacitância Corrente e resistência Circuitos Elétricos em Corrente Contínua Campo Magnético Indução Magnética Indutância Magnetismo em Meios Materiais Atividades 1 Indução Magnética O fenômeno da indução eletromagnética se manifesta quando o fluxo magnético através de um circuito varia, provocando a indução de uma fem e de uma corrente no circuito. Segundo este fenômeno, um campo magnético que varia com o tempo pode atuar como uma fonte de campo elétrico. A Lei de Faraday descreve o princípio do fenômeno da indução eletromagnética. Tal fenômeno está por trás de inúmeras aplicações, tais como: • geração de energia elétrica em usinas (transformação de energia potencial gravitacional, energia química ou nuclear em energia elétrica) • diversas máquinas (liquidificadores, secadores de cabelo, etc) e dispositivos (técnica RFID, portões eletrônicos,…) Indução Magnética Durante a década de 1830 diversas experiências pioneiras (Faraday, Henry, Lenz) Procuraram entender o fenômeno da indução eletromagnética. Seja um imã e uma bobina conectada um medidor de corrente, como mostra a figura ao lado. Se os dois objetos permanecem estacionários (ou seja, não se movem um em relação ao outro), não haverá corrente circulando pelo circuito. 2 Indução Magnética O fenômeno da indução se manifesta quando: • se aproxima ou se afasta o imã do núcleo da bobina; • se move uma bobina (espira, circuito), onde já existe um campo magnético, para dentro ou para fora do núcleo de outra bobina. • se altera a corrente em uma bobina que se encontra inserida no núcleo de outra bobina. Indução Magnética A corrente provocada pela variação do fluxo magnético é chamada de corrente induzida e a fem gerada no circuito é conhecida como fem induzida. A figura ao lado mostra uma bobina inserida em um campo magnético. Os seguintes fenômenos podem ser observados: 1) Quando não existe corrente no eletroimã (B = 0), o medidor (galvanômetro) não indica nenhuma corrente; 2) Quando o eletroimã é ligado, surge momentaneamente uma corrente induzida indicada no medidor; 3) Ao se manter fixo o valor de B e se comprimir as espiras, o medidor indica uma variação momentânea de corrente; 4) Quando se gira a bobina em torno de um eixo horizontal, varia-se o fluxo de campo magnético através de sua área. Nesse caso, observa-se uma variação de corrente no medidor. 5) Quando se insere ou se retira a bobina de um campo magnético de valor constante observa-se uma corrente induzida no medidor. 3 Indução Magnética (continuação do slide anterior) 6) Quando se diminui ou se aumenta o número de espiras na bobina, surge uma corrente induzida no medidor. 7) Ao se ligar ou desligar o eletroimã verifica-se a ocorrência de corrente induzida no medidor; 8) Quanto maior for a variação do campo observada nos casos anteriores, maior será a corrente induzida; 9) Ao se repetir as experiências acima trocando-se a bobina ou seu material, porém com outra resistência, verifica-se que a corrente induzida será inversamente proporcional à resistência total do circuito (a fem induzida não depende do material da bobina, mas apenas de sua forma e da variação do fluxo magnético). Lei de Faraday Em todos os casos discutidos anteriormente é a variação do fluxo magnético através da bobina que provoca o surgimento da corrente, seja porque o fluxo magnético é variável ou porque a bobina se move através de um campo magnético não-uniforme. Lei de Faraday da indução: A fem induzida em uma espira fechada é dada pela taxa de variação do fluxo magnético, com sinal negativo, através da área delimitada pela espira. ε =− Em que: dΦ dt B r r Φ = B ⋅ A = B A cosϕ B 4 Exemplo Seja um campo magnético uniforme entre os polos de um eletroimã. Porém, seu módulo aumenta com uma taxa crescente de 0,020 T/s. Uma espira condutora se encontra posicionada de forma perpendicular ao campo. Se a área da espira condutora imersa no campo é igual a 120 cm2, e a resistência total do circuito é igual a 5,0 Ω. Calcule: a) o módulo da fem e da corrente induzidas no circuito; b) o que ocorreria com a fem e a corrente induzida no circuito se a espira condutora fosse substituída por uma espira isolante? dΦ d ( B Acosϕ ) dB =− =A = (0,012m )(0,020T s ) = 0,24mV dt dt dt ε 2,4 × 10 O módulo da corrente induzida é dada por: I = = = 0,048mA R 5,0 ε=− B 2 −4 Se o material da espira for trocado por um isolante perfeito, a corrente induzida será igual a zero, embora haja uma fem induzida no circuito! Sentido da fem Induzida O sentido da fem induzida pode ser compreendido a partir das figuras abaixo. 5 Sentido da fem Induzida 1) Define-se um sentido positivo para o vetor A (área) 2) A partir dos sentidos de A e B (campo magnético), determina-se o sinal do fluxo magnético ΦB 3) Quando o fluxo está aumentando (dΦB/dt > 0), então a fem ou a corrente induzida é negativa; Quando o fluxo está diminuindo (dΦB/dt < 0), então a fem ou a corrente induzida é positiva; 4) Utiliza-se a regra da mão direita para determinar o sentido da fem ou da Corrente: dobra-se os dedos da mão direita em torno do vetor A, mantendo o polegar apontando no sentido de A. Se a fem (ou corrente) no circuito é positiva, ela possui o mesmo sentido da rotação de seus dedos. Em caso contrário, a fem (ou corrente) negativa possuirá sentido contrário ao da rotação de seus dedos. Corrente Induzida A corrente induzida na espira também gera um campo magnético cujo sentido é oposto ao campo magnético (crescente ou decrescente) externo! Assim, todo efeito de indução possui sentido oposto á causa que o produziu. Este fenômeno é conhecido como Lei de Lenz (mas se trata apenas de uma outra interpretação da própria Lei de Faraday). No caso de uma bobina com N espiras idênticas, supondo que o fluxo magnético varie com a mesma taxa através de todas as espiras, a taxa de variação total é N vezes maior que a taxa através de uma única espira. Assim, a fem gerada será: ε = −N dΦ dt B 6 Exemplo 1 Uma bobina com 500 espiras circulares com raio igual a 4,0 cm é colocada entre os polos de um grande eletroimã, onde o campo magnético é uniforme forma um ângullo de 60° com o plano da bobina. O campo magnético diminui com uma taxa igual a 0,200 T/s. Qual é o módulo e so sentido da fem induzida? Exemplo 1 (solução) A taxa de variação do fluxo é: r r dΦ d (B ⋅ A) d ( B Acos30 ) dB = = = ( Acos30 ) dt dt dt dt 0 0 B = (− 0,200T s )(π 0,04 m )(cos30 ) = −8,71× 10 Wb / s 2 2 0 −4 Para uma bobina com N espiras obtém-se: ε = −N dΦ = −(500)(−8,71× 10 ) = +0,435V dt B −4 7 Exemplo 2 A figura abaixo mostra uma versão simples de um alternador, um dispositivo que gera uma fem. Faz-se a espira girar com velocidade angular ω no sentido indicado. O campo magnético B é uniforme e constante. No instante t=o, φ=0. determine a fem induzida. r r Φ = B ⋅ A = B Acosφ = B Acos(ωt ) B dΦ d ( cos(ωt )) ∴ = BA = −ω BAsen (ω t ) dt dt B Portanto, ε =− dΦ = +ω BAsen (ω t ) dt B Exemplo 2 (continuação) A fem possui seu módulo máximo quando quando a espira está paralela a B (φ = 90° ou 270°). 8 Exemplo 3 O alternador do exemplo anterior produz uma fem alternada que varia senoidalmente. Pode-se usar um esquema semelhante para construir um gerador de corrente contínua, que produz uma fem de mesmo sinal. Considere um motor com bobina quadrada com lado de 10,0 cm e 500 espiras. Se o Campo magnético possui módulo de 0,020 T, determine a velocidade angular para que a fem induzida média do motor seja igual a 112 V. Exemplo 3 (solução) Verifica-se que ε med = 2N ω B A π ⇒ω = π (112V ) = 176 rad / s 2(500)(0,20T )(0,10m ) 2 9 Exemplo 3 (solução) 10 11
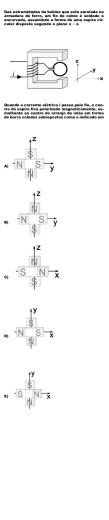
Baixar