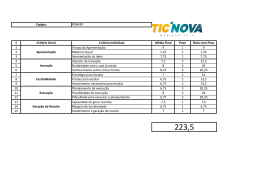
Campos vetoriais
. – p.1/??
Campo de vetores
a cada
, ou
um vetor 2D
ponto
numa região do plano
É uma função cujos valores são vetores e estabelece uma
regra que associa:
a
.
numa região do espaço
cada ponto
um vetor 3D
. – p.2/??
Campo de vetores
Exercício: Traçar o campo de vetores
.
. – p.2/??
Operador Nabla:
O operador Nabla é definido como :
coord. retangulares
. – p.3/??
é
O gradiente de uma função escalar
expresso como:
Gradiente:
coord. retangulares
O gradiente é interpretado como a direção em que a máxima variação da função ocorre.
. – p.4/??
atuando sobre campos vetoriais
1) um campo escalar
2) um campo vetorial
3) um campo tensorial
. – p.5/??
Divergente:
O divergente de um vetor é um escalar, expresso por:
coord. retangulares
Fisicamente, o divergente é interpretado como um fluxo
pontual.
. – p.6/??
Operador Laplaciano:
O operador Laplaciano é um escalar definido como
divergente de um campo gradiente
Fisicamente, o Laplaciano é interpretado como a concavidade no comportamento da função .
. – p.7/??
Função Harmônica
Uma função escalar é harmônica se essa função for de
classe
e se satisfizerem a Equação de Laplace
. – p.8/??
Rotacional
O rotacional de um vetor é um vetor, expresso por:
coord. retangulares
Fisicamente, o rotacional é interpretado como uma circulação no espaço.
. – p.9/??
é de classe
Se
Divergência do rotacional
. – p.10/??
Rotacional de um gradiente escalar
então
é uma função escalar de classe
Se
. – p.11/??
Rotacional de rotacional
. – p.12/??
Representação dos Campos de
Velocidade
Um campo de velocidade é associado aos seus campos
de:
divergência
Se o campo de
através de uma região, então
o fluxo é solenoidal ou incompressível.
vorticidade
Se o campo de
o fluxo é irrotacional.
. – p.13/??
Velocidade potencial
Para qq escalar
é irrotacional é natural achar uma função
tal que
Qdo
Essa função é obtida da equação diferencial,
. – p.14/??
Vetor potencial para
Para qq campo
tenta–se representar um fluxo incompressível como
Essa função é obtida da equação diferencial,
Linhas de
constantes são chamadas de linhas de cor-
rente
. – p.15/??
Fluxos Gerais
Idéia é representar como a soma de uma componente
incompressível e uma irrotacional formadas pelo potencial
e pelo vetor potencial
. – p.16/??
Integrais de linha
Integrais de linhas estão associadas a determinação de
um valor ao longo de um percurso.
Integrais de linhas são utilizadas para para calcular:
a taxa de escoamento de um fluido atravessando uma
ou o
curva orientada em um plano
trabalho realizado por um objeto, quando ele descreve
uma curva orientada no plano .
. – p.17/??
Integral de linha
No plano a integral de linha pode ser indicada por
Nesse caso pode–se interpretar a integral de linha como
uma diferença de áreas, como no caso usual de integral
curva
a função
definida, neste caso a área da superfície vertical entre a
para uma curva e funções
, em que
indica o deslocamento dessa curva.
.
. – p.18/??
Circulação de um vetor
A integral de linha de um gradiente é independente do caminho seguido, i.e., só depende dos limites de integração.
. – p.19/??