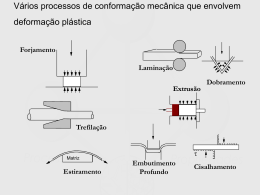
Capítulo 2
Tensão e deformação de
barra por carga axial
Noção de tensão
• Tensão normal ()
P
P
S
A
P
N
S
média
N

A
Noção de tensão
• Tensão de cisalhamento ()
P
P
P
Q
A
média
Q

A
Distribuição de  sob carga axial
• Tração (+)
N

A
P
S
• Compressão ()
N

A
P
S
• Unidades de tensão:
– N/m2 ou Pa (SI)
– kgf/mm2
– lb/in2 ou psi
– lb/ft2
• Conversões:
– 1kgf/mm2 = 9,8 MPa
– 1 psi = 6,8948.103 Pa
– lb/ft2 = 4,7880.101 Pa
Tensão admissível
Margem de segurança em relação a e,r
e e,r
• Justificativas
–
–
–
–
Valores imprecisos de esforços
Irregularidades do material
Pequenas deformações
Corrosão
• Tipos de aplicação
– Estática
– Dinâmica
• Fator de segurança (s)
 e ,r
s
adm
 e ,r
s
adm
Dimensionamento
• Impor tensão máxima igual à
admissível
N
A
adm
Q
A
adm
• Exemplo: No Problema 2,
dimensione o diâmetro do pino
que une a biela ao pistão. Adote
adm= 200 MPa.
Deformação por carga axial
• L: deformação
• L0: comprimento não
deformado
L
• Deformação linear ():  
– adimensional
L
Diagrama tensão-deformação
Dútil
Elástico
Frágil
Plástico
Lei de Hooke
• Proporcionalidade entre tensão e
deformação linear
E
1
Elástico

E

Plástico
  E
• E: módulo de elasticidade linear (ou
módulo de Young)
• Unidades: mesmas de tensão
Módulo de elasticidade para alguns materiais
Aço
200 GPa
Ferro fundido
cinzento
90 GPa
Poliolefinas e
estirenos
0.6 GPa - 2.5
GPa
Liga de alumínio
70 GPa
Deformação em barras axialmente carregadas
Nx
Ax
Nx
dx+du
x
Nx
du  x dx  dx 
dx

A x
B

 Nx
u   du  
dx
x A A x
A
xB
Deformação em barras axialmente carregadas
• Barra de seção e esforço axial
uniformes
PL
u
EA
Coeficiente de Poisson
encurta
alonga
Definição:
l

a
• Unidade: adimensional
• Faixa:
 1    0,5
Lei de Hooke generalizada
• Num ponto qualquer
dy
dz
dx
 x 
1
  1
 y   
  E 
 z


1

   x 
 
   y 

1   z 
• Invertendo:
   x 
 x 
  1 
E
 
    1    


 y
 y
2


  2    1  
   1  z 
 z

Cisalhamento em planos ortogonais entre si
z
zy
yz
’yz
’zy
x
yz   yz
zy  zy
 yz  zy
y
Lei de Hooke: x


 Distorção 
 Unidade: rad (adimensional)
 Lei de Hooke:
  G
 G: módulo de elasticidade transversal
 Unidade: mesma que E