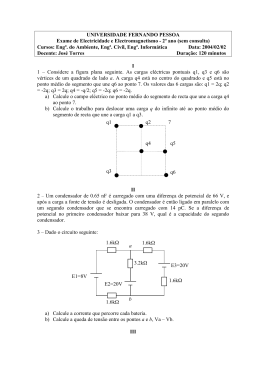
UNIVERSIDADE DA MADEIRA
TTC/LFC
PC5 - Condensador: Impedância e filtros.
1. Objectivos
Estudo dos filtros passa-baixo e passa-alto.
2. Material necessário
1 osciloscópio, 1 gerador de sinais, 1 resistência de 10 kΩ, 1 condensador de 10 nF.
3. Introdução Teórica
3.1. Condensadores
Podemos armazenar energia na forma de energia potencial puxando a corda de um arco de
flechas, esticando uma mola, comprimindo um gás, ou levantando um livro. Podemos também
armazenar energia na forma de energia potencial num campo eléctrico, um condensador é um
dispositivo que pode ser usado para isso mesmo.
Os condensadores são utilizados em variadíssimas aplicações, por exemplo, no flash de uma
máquina fotográfica (o condensador na máquina acumula carga relativamente devagar, durante
o tempo entre cada fotografia), são elementos vitais em rádios e televisões, como outro exemplo
temos condensadores microscópios que são usados nas memórias dos computadores.
Denomina-se condensador o conjunto formado por duas superfícies metálicas condutoras,
as armaduras (ou placas), que se encontram separadas por um meio isolante, o dieléctrico. No
caso mais simples temos apenas duas placas metálicas paralelas separadas por vácuo.
Uma maneira de carregar um condensador é colocá-lo num circuito eléctrico com uma bateria
(uma bateria é um dispositivo que mantém uma certa diferença de potencial entre os seus
terminais, por meio de reacções electroquímicas internas, nas quais forças eléctricas podem
mover carga interna). Na figura, uma fonte de tensão, um interruptor S, um condensador não
carregado, e cabos de ligação formam um circuito. O símbolo que usamos para representar um
condensador
é baseado na estrutura de um condensador de placas paralelas, mas é usado
para condensadores de todas as geometrias.
C
a
b
+
V
S
A fonte mantém uma diferença de potencial V entre os seus terminais. O terminal de
potencial mais elevado é designado + e é normalmente chamado o terminal positivo; o terminal
de potencial mais baixo é rotulado com − e é normalmente chamado o terminal negativo.
O circuito representado diz-se incompleto, porque o interruptor S está aberto; i.e., não estabelece ligação eléctrica entre os cabos ligados a si. Quando o interruptor é fechado, estabelecendose ligação eléctrica entre os cabos, o circuito fica completo e a carga (electrões) pode então fluir
através do interruptor e dos cabos, este movimento deve-se ao campo eléctrico produzido pela
fonte de tensão nos cabos de ligação. O campo faz mover os electrões da placa a do condensador
para o terminal positivo da fonte; assim, a placa a, perde electrões e fica carregada positivamente. O campo faz, também, mover a mesma quantidade de electrões do terminal negativo da
fonte para a placa b do condensador; assim, a placa b, ganha electrões e fica carregada, tanto
como a placa a, negativamente.
Inicialmente, quando as placas não estão carregadas, a diferença de potencial entre elas é
zero. À medida que as placas vão ficando carregadas simetricamente, a diferença de potencial
aumenta até igualar a diferença de potencial V entre os terminais da fonte. Então a placa a
e o terminal positivo da fonte ficam ao mesmo potencial, e deixa de existir o campo eléctrico
no fio entre eles. Análogamente, a placa b e o terminal negativo atingem o mesmo potencial, e
deixa de existir o campo eléctrico no fio entre eles. Assim, com o campo a zero, deixa de haver
transporte de electrões. O condensador diz-se completamente carregado.
3.1.1. Capacidade de um condensador
Da mesma maneira que um elemento resistivo se distingue pelo valor da sua resistência R
expressa em ohms, um condensador caracteriza-se pela sua capacidade C.
Denomina-se capacidade de um condensador a aptidão que este tem para acumular carga
eléctrica.
A capacidade é a relação entre a carga Q acumulada numa das suas armaduras1 e a diferença
de potencial Vab aplicada entre elas. Ou, dito de outra forma„ a carga eléctrica Q acumulada
no condensador é directamente proporcional à diferença de potencial Vab aos seus extremos,
sendo a constante de proporcionalidade denominada capacidade do condensador.
C=
Q
ou Q = CVab
Vab
Assim, para uma dada diferença de potencial um condensador terá acumulado tanto mais carga
quanto maior for a sua capacidade.
A unidade de capacidade é o farad (F), 1 farad = 1 coulomb / 1 volt.
O farad é uma unidade excessivamente grande, consequentemente, na prática, são utilizados
os seguintes submúltiplos: o milifarad (mF) = 10−3 F, o microfarad (µF) = 10−6 F, o nanofarad
(nF) ou kilopicofarad (kpF) = 10−9 F e o picofarad (pF) = 10−12 F.
3.1.2. Associação de condensadores
Montagem em série Quando os condensadores são ligados como na figura que se segue,
diz-se que estão em série:
C1
a
1
C2
b
C3
c
d
Quando um condensador é carregado, as suas placas têm cargas iguais e opostas +q e −q. No entanto,
referimo-nos à carga do condensador como sendo q, o valor absoluto das cargas nas placas. (Note que q não
é a carga total do condensador, que é zero.)
Vejamos qual o valor da capacidade equivalente. As armaduras ligadas pelo segmento b têm
carga total nula porque estão isoladas. Logo as cargas produzidas nestas placas por indução
electrostática serão simétricas.
Podemos dizer o mesmo em relação ao segmento c. O teorema das superfícies correspondentes garante que duas superfícies paralelas planas com igual área terão cargas simétricas e
de igual módulo. Em suma, a carga é igual em todos os condensadores. Portanto:
Vab =
Q
C1
;
Vbc =
Q
C2
;
Vcd =
Q
C3
Somando membro a membro as três expressões obtém-se:
Vab + Vbc + Vcd =
Q
Q
Q
+
+
C1 C2 C3
A soma das ddp em cada condensador é a ddp nos extremos da rede:
1
1
1
Vad = Q
+
+
C1 C2 C3
Dividindo os dois membros por Q resulta:
Vad
1
= :
Como, por definição,
Q
C
Vad
Q
=
1
C1
+
1
C2
+
1
C3
1
1
1
1
=
+
+
C
C1 C2 C3
(3.1)
C1 C2
.
C1 + C2
C1
No caso de todos os condensadores de uma rede serem iguais: C =
, onde n é o número
n
de condensadores.
Para o caso particular de dois condensadores ligados em série: C =
Montagem em paralelo A figura que se segue representa uma rede de condensadores montados em paralelo.
Q1
C1
a
Q2
C2
Q3
C3
b
A grandeza que neste caso é constante para todos eles é a ddp Vab .
A carga acumulada por cada condensador será:
Q1 = C1 Vab
;
Q2 = C2 Vab
;
Q3 = C3 Vab
A carga total acumulada pelo conjunto é igual à soma das cargas parciais:
Q = Q1 + Q2 + Q3
Substituindo Q1 , Q2 e Q3 pelo seu valor teremos: Q = C1 Vab + C2 Vab + C3 Vab .
Q
Dividindo os dois membros por Vab :
= C1 + C2 + C3 .
Vab
Como, por definição,
Q
=C:
Vab
C = C1 + C2 + C3
(3.2)
Nota O código dos condensadores é interpretado da seguinte maneira:
abc −→ ab × 10c pF
Exemplo:
224 corresponde a um condensador com a capacidade de 22 × 104 pF = 0, 22 µF.
3.2. Impedância
Para um sinal sinusoidal, qual é a relação entre a ddp aos extremos de um condensador e a
intensidade da corrente que flui? Será a Lei de Ohm válida para um condensador neste caso?
O circuito que traduz este problema é:
Num condensador sabemos que a relação geral entre a intensidade da corrente que flui e a
ddp aos seus terminais é:
dV
i=C
dt
Se a ddp (V) é sinusoidal:
V = A sin (ωt)
então a intensidade da corrente (i) é dada por:
i=C
dV
= CωA cos (ωt)
dt
Se representamos no mesmo gráfico a variação das duas grandezas com o tempo:
constatamos imediatamente que a razão V /i varia ao longo do tempo e por isso a Lei de
Ohm não é válida. Há aqui dois dados que não podem ser condensados num só número. Eles
são a razão entre as amplitudes e o desfasamento entre os dois sinais. Ou será que podem?
Vamos insistir nesta ideia e recorrer a um truque habitual em matemática quando pretendemos representar uma função que varia sinusoidalmente. Essa função pode ser descrita de
forma complexa. Ou seja o potencial varia de acordo com:
V = Aejωt
em que j é um número imaginário puro (utilizamos a letra j em vez de i para não confundir
com a intensidade da corrente). A intensidade da corrente eléctrica será então:
dV
i=C
= AjωCejωt
dt
A razão entre as duas grandezas é:
V
Aejωt
1
=
=
jωt
i
AjωCe
jωC
que é constante. Além disso vemos que conseguimos conjugar num só número os dois dados
que pretendíamos - razão entre amplitudes e desfasamento entre os sinais:
1 −j π
1
=
e 2
jωC
ωC
1
A razão entre as amplitudes é ωC
e o desfasamento é de − π2 rad (a intensidade está atrasada
em relação à ddp). Poderíamos intitular esta grandeza de resistência mas ela só é válida para
sinais sinusoidais e é representada por um número complexo. Sendo assim resolveu-se chamar
esta grandeza de impedância e representá-la pela letra Z. É uma generalização do conceito de
resistência.
Dizemos então que a impedância de um condensador é dada por:
1
ZC =
jωC
Para baixas frequências a impedância é alta e o condensador interrompe o circuito. Para
altas frequências a impedância é baixa e o condensador funciona como um curto circuito.
3.3. Filtros
Consideremos um circuito com dois conjuntos de terminais. Um dos terminais é considerado
como entrada do circuito e o outro como saída. Vamos estudar o caso em que a variável de
entrada é VE e a variável de saída é VS .
Chama-se ganho do circuito, G, à razão entre as amplitudes dos potenciais de saída e de
entrada:
VS
(3.3)
VE
Há circuitos em que o ganho depende da frequência. Esses circuitos têm a designação
genérica de filtros. Dois exemplos de filtros são os passa-baixo (deixam passar apenas as baixas
frequências) e os passa-alto (só deixam passar as altas frequências).
Neste tipo de circuitos, para além da amplitude do sinal de saída depender da frequência,
este também vem desfasado em relação ao original. Como o ganho do circuito tende para zero
mas nunca é zero não podemos identificar uma frequência de corte absoluto do sinal. No entanto
é necessário um critério de comparação. Para cada circuito convenciona-se uma frequência
√ de
corte. Neste caso, a frequência de corte é ω = 1/RC, o ganho tem módulo igual a 1/ 2 e a
fase é de 45o .
G=
4. Procedimento experimental
4.1. Parte 1
1. Construa o seguinte circuito, usando uma resistência de 10 kΩ e um condensador de 10 nF
e aplicando um sinal sinusoidal de 5 V à entrada (i.e., em VE ):
2. Determine o módulo da impedância do condensador.
3. Meça o desfasamento entre a tensão e a intensidade da corrente para o condensador.
4. Compare os resultados dos pontos anteriores com os valores teóricos.
4.2. Parte 2
Usando o mesmo circuito já montado na Parte 1 e com o mesmo sinal de entrada sinusoidal de
5 V, verifique experimentalmente como varia a amplitude do sinal de saída Vs para frequências
de 101 , 102 , 103 , 104 , 105 e 106 Hz. Que tipo de filtro é este circuito?
Trace o gráfico da dependência do ganho do circuito com a frequência. Com base nos
resultados qual é a sua frequência de corte? Compare com o valor teórico.
Verifique experimentalmente como varia a diferença de fase entre os sinais de entrada e de
saída para frequências de 101 , 102 , 103 , 104 , 105 e 106 Hz.
4.3. Parte 3
Construa o seguinte circuito:
Os valores do potencial de entrada da resistência e do condensador são iguais ao do circuito da
segunda parte.
Verifique experimentalmente como varia a amplitude do sinal de saída Vs para frequências
de 101 , 102 , 103 , 104 , 105 e 106 Hz. Que tipo de filtro é este circuito?
Trace o gráfico da dependência do ganho do circuito com a frequência. Com base nos
resultados qual é a sua frequência de corte? Compare com o valor teórico.
Verifique experimentalmente como varia a diferença de fase entre os sinais de entrada e de
saída para frequências de 101 , 102 , 103 , 104 , 105 e 106 Hz.
REFERÊNCIAS BIBLIOGRÁFICAS
[1] G. Gomes, Aulas teóricas da cadeira Electrónica, Universidade da Madeira, 2001
[2] G. Gomes, Protocolos das aulas práticas da cadeira Laboratórios I, Universidade da
Madeira, 2001