Centro Federal de Educação Tecnológica do Piauí - CEFET/PI
Vestibular 2007-1
CADERNO DE PROVA
CURSOS: LICENCIATURA EM MATEMÁTICA
Matemática
30 questões
Física
30 questões
DATA: 10/12/2006
TEMPO: 4 horas
NÚMERO DE QUESTÕES: 60 (sessenta)
LEIA COM ATENÇÃO AS INSTRUÇÕES ABAIXO:
1.
Este caderno é constituído da prova objetiva de Matemática e Física.
2.
Cada uma das questões da prova apresenta um enunciado seguido de 5 (cinco) alternativas,
designadas pelas letras a, b, c, d e e, das quais somente uma é correta.
3.
Caso o caderno esteja incompleto ou tenha qualquer defeito, solicite ao fiscal da sala que tome as
providências cabíveis.
4.
Decorrido o tempo determinado pela Comissão Encarregada para Realização do Concurso Vestibular,
será distribuído o cartão-resposta, o qual será o único documento válido para a correção da prova.
5.
Ao receber o cartão-resposta, verifique se seu nome e número de inscrição são os mesmos contidos
no seu Cartão de Informação. Reclame imediatamente se houver discordância.
6.
Para cada uma das questões, você deve marcar uma e somente uma das alternativas.
7.
Assine o cartão-resposta no espaço reservado no cabeçalho. Não haverá substituição do cartãoresposta.
8.
Não amasse nem dobre o cartão-resposta, para que não seja rejeitado pelo computador no momento
da leitura.
9.
Será anulada a resposta que contiver emenda, rasura ou que apresentar mais de uma alternativa
assinalada.
10. É vedado o uso de qualquer material, além de caneta, para marcação das respostas; qualquer forma de
comunicação entre os candidatos também implicará sua eliminação.
11. O candidato, ao sair da sala, deverá entregar, definitivamente, seu cartão-resposta e este caderno de
prova, devendo ainda assinar a folha de presença.
Nome do Candidato
Nº de Inscrição
MATEMÁTICA
1.
4.
Um quadrilátero ABCD, com AB = 2 ,
BC = 4 , ABˆ C = 120° e ACˆ D = 45° , está
inscrito num círculo. Nessas condições
AD vale:
a. ( )
42
3
b. ( )
2 42
3
a. (
b. (
c. (
d. (
e. (
5.
3 42
c. ( )
2
d. ( )
2 7
3
3 6
2
A probabilidade de um certo homem viver
3
4
mais 30 anos é e para sua mulher é . A
5
7
probabilidade de, daqui a 30 anos, somente o
homem estar vivo é:
e. ( )
2.
a. ( )
b. ( )
c. ( )
d. ( )
e. ( )
3.
9
35
10
35
12
35
7
12
21
35
Uma moeda viciada tem a probabilidade
de dar cara igual a 2 vezes a
probabilidade de dar coroa. Dois
jogadores Antônio e Beto lançam
alternadamente essa moeda até que algum
deles consiga obter coroa. Qual é a
probabilidade de Antônio ganhar, se é ele
quem começa o jogo?
a. ( )
3
5
b. ( )
4
5
c. ( )
2
3
d. ( )
3
4
e. ( )
1
2
Pretende-se distribuir 8 cadernos, 5
canetas e 6 lápis entre duas famílias. Cada
família deve receber pelo menos 2 de cada
um dos objetos. De quantos modos é
possível fazer essa distribuição?
20
30
40
50
60
Em certa loja, cada produto vendido tem
um acréscimo de 50% sobre o preço de
custo. No entanto, como a loja deve
recolher impostos correspondentes a 18%
do preço de venda, seu percentual de
lucro sobre o preço de custo é muito
inferior a 50%. Esse percentual é de:
a. (
b. (
c. (
d. (
e. (
6.
)
)
)
)
)
)
)
)
)
)
32%
30%
25%
23%
20%
A média aritmética das idades dos
candidatos a um concurso público federal
é de 36 anos. Quando separados por sexo,
essa média é de 37 anos para o grupo do
sexo masculino e 34 para o grupo do sexo
feminino. A razão entre o número de
mulheres e homens é:
a. ( )
61
73
b. ( )
17
37
c. ( ) 2
d. ( )
34
37
e. ( )
1
2
7.
Seja a função y = ax 2 + bx + c de
domínio real, a e c de sinais contrários e b
real. Nessas condições, pode-se afirmar:
a. ( ) O gráfico dessa função não corta o
eixo Ox.
b. ( ) O gráfico dessa função corta o
eixo Ox em apenas um ponto.
c. ( ) O gráfico dessa função corta o
eixo Ox em dois pontos distintos.
d. ( ) O gráfico dessa função é uma
parábola com a concavidade
voltada para cima.
e. ( ) O gráfico dessa função é uma
parábola com a concavidade
voltada para baixo.
8.
Uma função quadrática tem o eixo dos y
como eixo de simetria. A distância entre
os zeros da função é de 6 unidades, e a
função tem − 4 como valor mínimo. Essa
função quadrática é:
a. ( ) y = 4 x 2 − 6 x − 9
b. ( ) y = 4 x − 30
2
9.
c. ( ) y =
5 2
x − 5x
4
d. ( ) y =
4 2
x − 4x
9
e. ( ) y =
4 2
x −4
9
A função f , de domínio real mais amplo
ax + b − 3
possível, é tal que f ( x) =
. Se
ax + 2b
f (2) não existe e f (−1) = 4 , o valor de
a 2 + b 2 é:
a. ( )
3
100
3
b. ( )
10
3
c. ( )
5
9
d. ( )
50
e. ( )
18
50
f ( x) = 3 + 2 x ,
10. Se
[ f ( 2 ) − f (− 2 )]
2
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
então
é igual a:
2
4
6
8
10
11. Em um triângulo retângulo, a hipotenusa
mede 20cm e a altura relativa à
hipotenusa divide-a em dois segmentos
cujas medidas estão na razão de 1 para 3.
A área do triângulo é:
a. ( ) 20 3 cm 2
b. ( ) 30 3 cm 2
c. ( ) 50 3 cm 2
d. ( ) 50 2 cm 2
e. ( ) 20 2 cm 2
12. Uma panela cilíndrica de 40cm de
diâmetro está completamente cheia de
massa para doce, sem exceder a sua altura
de 16cm. Com toda a massa, são
fabricados pirulitos em forma de cone
circular reto de altura 6cm e raio da base
de medida 0,8 cm. O número de pirulitos
que podem ser fabricados com a panela
cheia dessa massa é:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
4000
4200
4500
4800
5000
13. Calculando
o
produto
1
2
3
4
50
P = i . i . i . i . ... . i , com i = − 1 ,
obtém-se:
a. ( ) i
b. ( ) − i
c. ( ) 0
d. ( ) 1
e. ( ) − 1
14.
Sejam h( x) = x 2 − 4 x − 5 e f ( x) = x 2 + 1 .
A soma dos zeros da função composta
h( f ( x )) é:
a. (
b. (
c. (
d. (
e. (
15.
)
)
)
)
)
19.
a. ( )
0
4
6
8
10
b. ( )
c. ( )
d. ( )
O domínio da função real dada por f(x) =
log 1 ( x − 1) é:
e. ( )
20.
3
a. (
b. (
c. (
d. (
e. (
16.
)
)
)
)
)
{x ∈ R / x > 1}
{x ∈ R / x ≤ 2}
{x ∈ R / x ≥ 2}
{x ∈ R / 1 < x ≤ 2}
{x ∈ R / x < 1 ou x ≥ 2}
Numa reunião de professores, em que cada
um cumprimentou todos os colegas,
registraram-se 210 apertos de mão. O número
de professores presentes à reunião foi de:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
20
15
10
21
24
18.
)
)
)
)
)
21.
4
3
2
1
5
B
Z
(
40º
60º
90º
50º
70º
Sejam A, B e C matrizes quadradas de
ordem 3, satisfazendo às seguintes
relações: AB = C −1 , B = 2 A . Se o
determinante de C é 32, qual é o valor do
módulo do determinante de A?
a. ( )
1
16
b. ( )
1
8
c. ( )
1
4
O
raio
da
circunferência
de
ky
equação x 2 + y 2 + kx − + k = 0 , e que
2
passa pelo ponto A(2 , − 4) é:
a. ( ) 2
b. ( ) 5
c. ( ) 3
1
d. ( )
2
e. ( ) 4
22.
Num C triângulo ABC , sabe-se que
AB = AC = 5 cm . A medida do lado BC
desse triângulo para que o mesmo tenha área
máxima é:
a. ( ) 5 2 cm
A
X
)
)
)
)
)
1
2
1
2
5
2
4
e. ( ) 4
Na figura, AB = AC, BX = BY e CZ =
CY. Se o ângulo  mede 40º, então o
ângulo XYˆZ mede: Y
a. (
b. (
c. (
d. (
e. (
expressão
d. ( ) 8
17. O número de soluções da equação
senx − cos x = 0 , com x ∈ [0 , 9] , é:
a. (
b. (
c. (
d. (
e. (
O
valor
da
(tg10° + cot g10°) . sen 20° , é:
b. ( ) 5 3 cm
c. ( ) 3 2 cm
d. ( )
2 cm
e. ( ) 2 3 cm
23.
De um recipiente cheio de água retiram-se
2
de seu conteúdo. Recolocando-se trinta
3
litros da água retirada, o conteúdo passa a
ocupar a metade do volume inicial. A
capacidade do recipiente é:
a. (
b. (
c. (
d. (
e. (
24
45 litros
75 litros
120 litros
150 litros
180 litros
)
)
)
)
)
29.
)
)
)
)
)
16π
24π
30π
64π
72π
27.
obtemos um resto que dividido
por x − 3 dá resto 5. Assim, o valor
de P (3) é:
)
)
)
)
)
66 litros
68 litros
70 litros
72 litros
74 litros
1
2
3
4
5
Sejam Ζ o conjunto dos números inteiros,
A = x ∈ Z / x 2 − 5x + 4 = 0
e
{
a. (
b. (
c. (
d. (
e. (
30.
 1 2 0
26. Sendo
A = − 1 0 2 , então o
 3 1 − 3 
elemento da primeira linha e terceira
coluna da sua inversa é:
a. (
b. (
c. (
d. (
e. (
Ao dividirmos um polinômio P (x) por
( x − 3) 2 ,
Colocando-se 27 litros de gasolina no
tanque de um carro, o ponteiro do
1
marcador que indicava
do tanque,
4
5
passa a indicar
. A capacidade total
8
desse tanque de gasolina é:
a. (
b. (
c. (
d. (
e. (
Os pontos ( x , y ) do plano cartesiano, que
satisfazem a equação x 2 − 6 y 2 + xy = 0
constituem:
a. ( ) uma hipérbole
b. ( ) uma parábola
c. ( ) duas retas paralelas
d. ( ) duas retas concorrentes
e. ( ) o conjunto vazio
Uma laranja pode ser considerada uma esfera
de raio 4 cm, composta de 8 gomos
“exatamente iguais”. A área da superfície total
de cada gomo, em centímetros quadrados, é:
a. (
b. (
c. (
d. (
e. (
25.
)
)
)
)
)
28.
}
B = {x ∈ Z / x − 1 ≤ 2}. O número
elementos do conjunto B − A , é:
a. ( ) 0
b. ( ) 1
c. ( ) 2
d. ( ) 3
e. ( ) 4
de
)
)
)
)
)
3
4
5
6
7
Considerando a existência dos logaritmos
da
equação
(log 3 x ). (log x 2 x ). (log 2 x y ) = log x x 2 , o
valor de y é:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
3
4
6
8
9
d. ( ) Três algarismos significativos,
sendo dois duvidosos e um certo;
FÍSICA
31. Relacione corretamente a 2° coluna, onde
se encontram listadas algumas unidades
SI de grandezas físicas, com a 1° coluna
formada pelas grandezas.
1° Coluna
2° Coluna
( 1 ) Pressão
( 2 ) Campo magnético
( 3 ) Intensidade luminosa
( 4 ) Carga elétrica
( 5 ) Fluxo magnético
(
(
(
(
(
)
)
)
)
)
13.452
43.125
34.152
25.314
41.325
32. Hoje em dia, a obtenção de medidas
acuradas é uma parte importante da
Física, chamada Metrologia. Mas
nenhuma medida obtida é absolutamente
precisa; sempre existe uma incerteza
associada a cada medida. A incerteza
advém de diferentes fontes. A mais
importante é a incapacidade, que temos,
de leituras de valores fracionários
menores que a menor divisão da escala do
instrumento de medida. Observe a figura
abaixo, em que uma régua graduada em
milímetros, é usada para medir o
comprimento de um segmento de reta.
De acordo com a figura, a medida exata
do comprimento situa-se entre 6,5cm e
6,6cm. Mas, podemos estimar, com uma
pequena margem de erro, que a medida
do comprimento é 6,54cm.
Sabendo que qualquer medida deve ser
expressa somente com algarismos
significativos, a medida acima possui:
a. ( ) Dois algarismos significativos,
sendo um duvidoso e um certo;
b. ( ) Três algarismos significativos,
sendo os três certos;
c. ( ) Dois algarismos significativos,
sendo os dois certos;
Três algarismos significativos,
sendo um duvidoso e dois
certos.
33. Uma grandeza física Q tem fórmula física
dada por
) candela
) coulomb
) pascal
) weber
) tesla
De cima para baixo forma-se o número:
a. (
b. (
c. (
d. (
e. (
e. ( )
Q = mv =
m0
v2
1- 2
c
.v
onde m0 tem dimensão de massa, v e c são
de diferentes velocidades. A fórmula
dimensional CORRETA dessa grandeza
física é:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
[Q] = M L T- 1
[Q] = M1/2 L3 T-2
[Q] = M L2 T
[Q] = M3 L –1 T
[Q] = M L T
34. Dois
conceitos
de
fundamental
importância no estudo da Mecânica são os
de referencial e trajetória. Considere que
o helicóptero na figura a seguir esteja
subindo verticalmente em relação ao solo,
com velocidade constante. A trajetória
descrita pelo ponto P da periferia da
hélice é:
a. ( ) Uma reta para o piloto e uma
circunferência para o observador
no solo;
b. ( ) Uma circunferência para o piloto
e uma reta para o observador no
solo;
c. ( ) Uma circunferência para o piloto
e uma hélice cilíndrica para o
observador no solo;
d. ( ) Uma hélice cilíndrica para o
piloto e uma reta para o
observador no solo;
e. ( ) Uma circunferência para o piloto
e uma circunferência para o
observador no solo.
35. Um veículo viaja de uma cidade A a uma
cidade B, com velocidade média de
36 km/h. O motorista pára 30 minutos
num posto na beira da estrada, para fazer
refeição e abastecer o veículo. Da cidade
A até o posto, gasta 1 hora e 30 minutos,
fazendo o percurso do posto a cidade B
em 30 minutos. A distância, em
quilômetros, entre as duas cidades é de:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
400
200
110
100
90
36. Um carrinho realiza movimento circular
uniforme de período 2s, diante de um
espelho plano vertical. A menor distância
entre o carrinho e sua imagem é 10cm, e a
maior distância vale 40cm. Os valores das
velocidades angular e linear do carrinho
valem, respectivamente:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
π rad/s
2π rad/s
2,5π rad/s
0,5π rad/s
π rad/s
e
e
e
e
e
7,0π cm/s
8,0π cm/s
7,5π cm/s
6,0π cm/s
7,5π cm/s
37. Em uma experiência, duas pequenas
esferas são postas em movimento com
velocidade constante sobre uma régua
graduada em centímetros, conforme
indica a figura a seguir.
3cm/s
5cm/s
10
14
As esferas irão colidir no instante:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
7s
5s
4s
3s
2s
38.
Num movimento uniformemente variado,
um objeto possui velocidade escalar v1 no
instante t1, e no instante posterior t2
possui velocidade v2. A velocidade
escalar média para esse intervalo de
tempo é dado por:
(Considere que não ocorreu mudança na
aceleração no intervalo de tempo).
a. ( ) A soma das velocidades dividida
pelo intervalo de tempo;
b. ( ) A soma das velocidades dividida
pelo tempo total;
c. ( ) O produto das velocidades
dividido por dois;
d. ( ) A
média
aritméticas
das
velocidades;
e. ( ) A
média
geométrica
das
velocidades.
39. Os “dragsters” são veículos que podem
atingir acelerações bastante altas. Eles
podem acelerar de 0 a 165 milhas/hora,
aproximadamente, em 73,7m/s, em
apenas 8,4 segundos, em um percurso de
pouco mais de 300m. Isso representa uma
aceleração média de aproximadamente
8,8m/s2. Para atingir uma aceleração
dessa magnitude, a força que impulsiona
o carro deve ser elevada, e isso é
conseguido com um motor bastante
potente, algo em torno de 800 hp. Para se
ter uma idéia dessa potência, basta dizer
que a de um carro popular varia de 70 a,
no máximo, 100hp. Mas, apenas um
motor potente não garante as altas
acelerações necessárias. O carro deve ter
também uma massa pequena, que, por
segurança, incluindo a do piloto, não deve
ser menor que 954 kg.
Com base na informação acima, a força
resultante média que age sobre o veículo
durante a arrancada é, em newtons,
aproximadamente de:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
13.436
10.860
8.395
5.579
3.457
40.
Todas as afirmações
verdadeiras, EXCETO:
a
seguir
a. ( ) No sistema de propulsão a jato de
aviões e foguetes, os gases
produzidos pela queima dos
combustíveis são lançados para
fora(força de ação), os jatos de
gases aplicam no foguete ou no
avião uma força de reação de
mesma
intensidade,
mesma
direção e sentido contrário.
b. ( ) Todo corpo continua em seu
estado de repouso ou de
movimento em linha reta com
velocidade escalar constante; a
menos que seja obrigado a alterar
esse estado pela ação de uma
força resultante externa - este
enunciado constitui o princípio
fundamental da Dinâmica.
c. ( ) Sempre que um corpo se
movimenta em trajetória nãoretilínea, age sobre ele uma força
cujo efeito é alterar a direção do
vetor velocidade, de modo a
permitir que o móvel percorra
essa trajetória curva.
d. ( ) Todo corpo mergulhado, total ou
parcialmente num líquido em
equilíbrio, sofre a ação de uma força
de baixo para cima, de intensidade
igual ao peso do volume de líquido
deslocado pelo corpo.
e. ( ) O quadrado do período de
translação de um planeta em torno
do Sol é diretamente proporcional
ao cubo do raio médio de sua órbita.
41.
Um cubo de certo material, com aresta de
20 cm, flutua em um líquido de densidade
1 g/cm3, com a face superior exatamente
coincidente com a superfície livre do
líquido. A pressão exercida pelo líquido na
face inferior do cubo vale:
a. (
b. (
c. (
d. (
e. (
42.
)
)
)
)
)
velocidade das duas bolinhas após a
colisão será:
são
1x103 Pa
2x102 Pa
3x103 Pa
4x103 Pa
5x103 Pa
Um garoto lança uma bolinha de argila
com velocidade 0,5m/s, que colide
frontalmente com outra, inicialmente
parada. Ambas possuem a mesma massa.
Após a colisão, as duas se grudam uma a
outra e passam a se mover juntas. A
a. (
b. (
c. (
d. (
e. (
43.
0,50 m/s
0,25 m/s
0,30 m/s
0,40 m/s
1,00 m/s
Um carrinho de massa 50g encontra-se em
repouso sobre uma mesa, subitamente ele
sofre a ação de uma força horizontal de
intensidade 2N. Após 2 segundos, o carrinho
terá adquirido uma velocidade igual a:
a. (
b. (
c. (
d. (
e. (
44.
)
)
)
)
)
)
)
)
)
)
20 m/s
12 m/s
10 m/s
8 m/s
4 m/s
Analise as proposições a seguir:
I. Dois corpos que estão à mesma
temperatura estão em equilíbrio
térmico.
II. A quantidade de calor que um corpo
possui depende de sua temperatura e
do número de partículas nele contido.
III. O calor é uma modalidade de energia
que flui espontaneamente de um
corpo de maior temperatura para um
de menor temperatura.
IV. A convecção térmica é o processo de
transmissão de calor no qual energia
térmica
muda
de
local,
acompanhando o deslocamento do
próprio material aquecido.
V. Entre as paredes duplas de vidro de
uma garrafa térmica é feito vácuo
para evitar trocas de calor por
radiação térmica.
São VERDADEIRAS:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
Apenas I e V
Apenas II, III e IV
Apenas I, III e IV
Apenas IV e V
Apenas III, IV e V
45.
De acordo com análise dos quadrinhos,
pode-se concluir que:
47.
a. (
b. (
c. (
d. (
e. (
a. ( ) Reduziu-se a força de coesão
entre as moléculas da garrafa e as
moléculas da tampa.
b. ( ) Reduziu-se a pressão do ar no
interior da garrafa.
redução
da
tensão
c. ( ) Houve
superficial existente entre a
garrafa e a tampa.
d. ( ) O coeficiente de dilatação do
material da garrafa é menor que o
coeficiente de dilatação do
material da tampa.
e. ( ) O coeficiente de dilatação do
material da garrafa é maior que o
coeficiente de dilatação do
material da tampa.
46.
Uma certa massa de água, ao cair de uma
altura igual a 836m, teve toda sua energia
mecânica transformada em térmica.
Admitindo que houve aquecimento
somente da água, a elevação de
temperatura da água foi de:
Dados:
calor específico da água 1,0 cal/g°C
aceleração da gravidade local 10 m/s2.
Considere 1 cal = 4,18 J
a. ( ) 10 °C
b. ( ) 8 °C
c. ( ) 4 °C
d. ( ) 3 °C
e. ( ) 2 °C
A temperatura de 5mols de gás
monoatômico varia de 27°C para 227°C,
numa expansão em que o gás realiza um
trabalho 8.310 joules. Sabendo que a
constante dos gases perfeito vale
R =8,310 joule/mol K, a variação de
energia interna sofrida pelo gás e a
quantidade de calor trocada pelo gás com
o ambiente valem, respectivamente:
48.
)
)
)
)
)
10.430 J e 20.775 J
12.465 J e 10.430 J
14.000J e 22.000J
8.546 J e 10.450J
12.465 J e 20.775 J
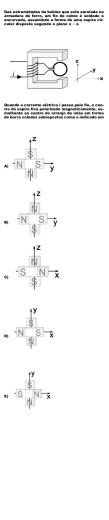
Um ímã em forma de barra é colocado
próximo a uma espira circular percorrida
por uma corrente elétrica. Com relação a
essa situação, é CORRETO afirmar que:
a. ( ) Haverá repulsão entre o ímã e a
espira, se o pólo norte do imã
estiver voltado para a espira, e a
corrente estiver no sentido antihorário.
b. ( ) Haverá repulsão entre o ímã e a
espira, se o pólo sul do ímã
estiver voltado para a espira e a
corrente estiver no sentido antihorário.
c. ( ) Haverá atração entre o ímã e a
espira, se o pólo sul do ímã
estiver voltado para a espira e a
corrente estiver no sentido
horário.
d. ( ) Haverá sempre atração entre o
ímã e a espira, qualquer que seja o
sentido da corrente.
e. ( ) Haverá sempre repulsão entre o
ímã e a espira, qualquer que seja o
sentido corrente.
49.
Considere a esfera metálica eletrizada em
equilíbrio eletrostático, conforme indica a
figura.
Responda de acordo com o código:
a. (
b. (
c. (
d. (
e. (
51.
)
)
)
)
)
Se todas estão corretas
Se existe apenas uma errada.
Se existem apenas duas erradas
Se existem apenas três erradas
Se todas estão erradas.
Observe o circuito representado na figura.
É CORRETO afirmar que:
a. ( ) A intensidade do campo elétrico
nos pontos 1, 2, 3 e 4 é nulo,
porém a intensidade do potencial
elétrico é constante diferente de
zero.
b. ( ) A intensidade do campo elétrico é
nula apenas no ponto 5, e a
intensidade do potencial elétrico é
nula em todos os pontos dentro da
esfera.
Não há perigo de “choque”:
a. (
b. (
c. (
d. (
e. (
52.
c. ( ) A intensidade do campo elétrico é
nula apenas no ponto 1, e a
intensidade do potencial elétrico
só não é nula no ponto 5.
e. ( ) Somente no ponto 5 a intensidade
do campo elétrico é diferente de
zero, e a intensidade do potencial
elétrico é nula em todos os
pontos.
50.
Considere as afirmativas a seguir:
I.
Na eletrização por atrito, os corpos
adquirem cargas com sinais opostos
II.
A capacitância de um capacitor
plano é tanto maior, quanto maior
fora a área de suas armaduras.
III.
Pólos magnéticos de mesmo nome
se atraem e pólos magnéticos de
nomes diferentes se repelem
IV.
Toda carga elétrica em movimento
gera em torno de si um campo
magnético.
53.
Entre os pontos A e B
Entre os pontos B e C
Entre os pontos C e E
Entre os pontos C e D
Entre os pontos D e E
O trabalho realizado pela força elétrica
que atua sobre uma partícula eletrizada
com carga elétrica 8,0 µC, quando esta é
desloca 100,0m ao longo de uma
equipotencial de 200 V, vale:
a. (
b. (
c. (
d. (
e. (
d. ( ) Em todos os pontos, a intensidade
do campo elétrico é nula e a
intensidade do potencial elétrico é
diferente de zero.
)
)
)
)
)
)
)
)
)
)
Zero
200 J
300 J
500 J
800 J
Segundo o modelo atômico de Bohr, o
átomo de hidrogênio é constituído por um
próton, em redor do qual um elétron
descreve uma órbita circular, de raio r,
com movimento uniforme. Neste caso, a
freqüência do movimento do elétron é:
Dados: Carga elementar = e
Massa do elétron = m
Constante eletrostática = K
e
k
a. ( )
2π m.r 3
e
π
e
c. ( )
3π
2e
d. ( )
π
k.m
r2
k
m.r 3
k
m.r 3
2e
3π
k.r 3
m
b. ( )
e. ( )
54.
Três espécies de partículas que se
propagam em linha reta, tem a mesma
velocidade e a mesma carga elétrica,
porém as massas são diferentes. Quando
essas partículas penetram num campo
magnético uniforme, saindo do plano da
página, com velocidade perpendicular ao
campo, observa-se a formação de três
trajetórias circulares de raios diferentes,
como mostra figura.
extremidade fixa da corda, o
pulso, então retorna invertido em
relação ao pulso incidente.
(
Filtro de
velocidade
Ondas estacionárias resultam da
superposição de duas ondas idênticas
que se propagam na mesma direção e
em sentidos contrários.
(
) O efeito fisiológico do som que nos
permite distinguir perfeitamente
uma mesma nota dó, emitida por
um violino e por um piano, é a
intensidade sonora.
(
) O efeito Doppler consiste em uma
mudança de velocidade da onda
percebida por um observador.
v
3
)
2 1
De cima para baixo a seqüência CORRETA é:
a. (
b. (
c. (
d. (
e. (
Marque a alternativa CORRETA.
55.
partículas
têm
cargas
a. ( ) As
negativas
b. ( ) A partícula de maior massa
descreve a trajetória de menor
raio, trajetória 3.
c. ( ) A partícula de maior massa
descreve a trajetória de raio
intermediário, trajetória 2.
d. ( ) A partícula de menor massa
descreve a trajetória de maior
raio, trajetória 3.
e. ( ) As partículas têm cargas positivas.
57.
O fluxo magnético através de uma
espira é reduzido de 5Wb para 2Wb, em
5x10 –2 s. A força eletromotriz induzida
vale:
58.
a. (
b. (
c. (
d. (
e. (
56.
)
)
)
)
)
As afirmativas a seguir podem ser
verdadeiras ou falsas. Indique com V, as
que forem verdadeiras e com F, as que
forem falsas.
(
(
) Uma onda mecânica é chamada
transversal quando as partículas do
meio vibram perpendicularmente à
direção de propagação da onda.
) Um pulso transversal propagandose em uma corda tensa, atinge a
)
)
)
)
)
20 cm
40 cm
60 cm
80 cm
100 cm
Dois pontos A e B estão distantes 20cm e
10cm, respectivamente, de um espelho
plano vertical. A distância horizontal
entre o ponto A e a imagem do ponto B é:
a. (
b. (
c. (
d. (
e. (
59.
VFVFV
FVFVF
VVVVF
FFVVV
VVVFF
Uma onda estacionária estabelece-se em
uma corda de comprimento 50cm fixa
pelas extremidades. Incluindo-se as
extremidades, observa-se, ao longo da
corda, a formação de seis regiões nodais.
O comprimento de onda das ondas que
originam as ondas estacionárias é:
a. (
b. (
c. (
d. (
e. (
100 V
110 V
80 V
60 V
90 V
)
)
)
)
)
)
)
)
)
)
55 cm
50 cm
45 cm
35 cm
30 cm
A luz se propaga no vácuo com
velocidade de 3,0x108 m/s, num meio de
índice de refração igual a 1,5. A
velocidade de propagação da luz será
igual a:
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
3,0x108 m/s
2,5x11108 m/s
1,5x108 ,/s
2,0x108 m/s
2,4x108 m/s
60.
Dois alunos trazem para a sala de aula as
receitas de óculos que lhes foram
prescritas por um oftalmologista. As
receitas estão expostas a seguir:
Aluno 1
Aluno 2
Os significados das abreviaturas OD, OE
e DP são, respectivamente, olho direito,
olho esquerdo e distância interpupilar,
isto é, distância entre os eixos dos olhos.
Analisando essas receitas, os alunos
chegaram as seguintes conclusões:
I.
O aluno 1 não enxerga bem de
perto, pois é hipermétrope e deve
usar lentes esféricas convergentes
de vergência +2,5 di (graus) para o
olho direito, e +2,0 di para o olho
esquerdo.
II.
O aluno 2 não enxerga bem de longe,
pois é míope e deve usar lentes
esféricas divergentes de vergência
– 1,25 di para os dois olhos.
III.
O aluno 1 não enxerga bem de longe,
pois é míope e deve usar lentes
esféricas convergentes de vergência
+2,5 di para o olho direito, e +2,0 di
para o olho esquerdo.
IV.
O aluno 2 não enxerga bem de perto,
pois é hipermétrope e deve usar lentes
esféricas convergentes de vergência
– 1,25 di para cada olho.
Está(ão) CORRETA(S):
a. (
b. (
c. (
d. (
e. (
)
)
)
)
)
Apenas I
Apenas II e III
Apenas III e IV
Apenas I e II
Apenas IV