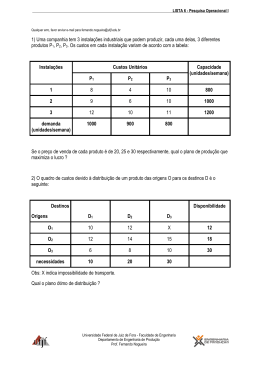
Utilizando o Pacote lpSolve
• Pacote utilizado para Resolução de
Problemas de Programação Linear e
Inteira.
Função:
lp(direction
=
"min",
objective.in,
const.mat,
const.dir,
const.rhs,
transpose.constraints = TRUE, int.vec,
presolve=0, compute.sens=0, binary.vec,
all.int=FALSE, all.bin=FALSE, scale = 196,
dense.const,
num.bin.solns=1,
use.rw=FALSE)
Descrição dos Parâmetros:
Max cx s.a Ax <= b, x≥0
direction = “min” ou “max” probl. Minimização ou
Maximização
objective= vetor com os coeficientes da função
objetivo ( c )
const.mat = matriz com os coeficientes associados às
restrições (A)
const.dir=vetor de caracteres associados com as
restrições (“=”,”<=”)
const.rhs= vetor com os termos de b (lado direito)
Exemplos:
(1) Problema da Dieta
Paula deseja saber quanto gastar para fazer uma dieta
alimentar que forneça diariamente toda a energia,
proteína
e
cálcio
que
ela
necessita.
Seu médico recomendou que ela se alimente de forma a
obter diariamente no mínimo 2000 kcal de energia, 65g
de proteína e 800 mg de cálcio.
Tabela 1 – Valor nutritivo e custo dos alimentos
alimento tamanho energia Proteína cálcio
da porção (kcal)
(g)
(mg)
arroz
ovos
leite
feijão
100g
2un
237ml
260g
205
160
160
260
32
13
8
14
12
54
285
80
1 porção de arroz ==> 205 kcal
1 porção de ovos ==> 160 kcal
1 porção de leite ==> 160 kcal
1 porção de feijão ==>260 kcal
x1=porções de arroz
x2=porções de ovos
x3=porções de leite
x4=porções de feijão
preço p/
porção
(centavos)
14
13
9
19
min z = 14 x1 + 13x2 + 9 x3 + 19 x4
205 x1 + 160 x2 + 160 x3 + 260 x4 ≥ 2000
32x1 + 13x 2 + 8x3 + 14x 4 ≥ 65
12x1 + 54x2 + 285x3 + 80x4 ≥ 800
Restrição de Energia
Restrição da Proteína
Restrição do Cálcio
Considerando que a dieta deve conter pelos uma unidade de
cada um dos alimentos:
Restringindo o número de unidades “leite” em 4
(2) Problema de Maximização de Produção
Uma firma faz três produtos e tem três máquinas
disponíveis para a produção. Para resolver sua escala de
produção, modela o seguinte PPL:
Max z = 4 x1 + 4 x2 + 7 x3
s.a
x1 + 7 x2 + 4 x3 ≤ 100
2 x1 + x2 + 7 x3 ≤ 100
8 x1 + 4 x2 + x3 ≤ 100
Horas maq. 1
Horas maq. 2
Horas maq. 3
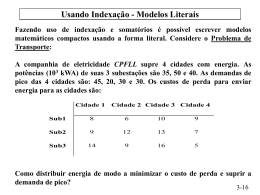
(3) Problema de Minimização de Custos com
Empregados
Uma companhia aérea está estudando a possibilidade de
aumentar o seu número de voos. Para esse efeito,
tornou-se necessário considerar a hipótese de contratar
mais funcionários para as mais diversas funções, como
por exemplo, para trabalharem no check-in, embora não
seja claro quantos são necessários.
Uma equipe de pesquisa operacional está estudando o
problema, no sentido de minimizar o custo com o
pessoal, garantindo uma qualidade de serviço imposta
pela administração da empresa. Com base nos voos
agendados, a equipe de IO obteve o número mínimo de
funcionários que são necessários para cada período de
tempo do dia, de acordo com a tabela abaixo. Por
imposição da legislação do trabalho, os turnos dos
funcionários não podem ultrapassar as oito horas de
trabalho diário. Após algum estudo, a equipe de IO
resolveu que existiriam cinco turnos, de oito horas cada
um. Os salários dos turnos variam por forma a cativar os
funcionários para os turnos menos agradáveis.
Minimizar 170x1+160x2+175x3+180x4+195x5
s.a
x1 ≥ 48
x1+x2 ≥ 79
x1+x2 ≥ 65
x1+x2+x3 ≥ 87
x2+x3≥ 64
x3+x4≥ 73
x3+x4≥ 82
x4≥ 43
x4+x5≥ 52
x5≥15
x1, x2, x3, x4, x5 = número de funcionários em cada
um dos turnos
(4) Problema de Padrões de Corte
O problema consiste a cortar bobinas de papel de largura
L em rolos de largura li (onde i = 1, . . . ,m) a fim de
satisfazer uma demande di .
Largura das bobinas: L = 100 cm.
Rolo
Rolo
Largura
1
25
2
30
3
42
4
55
Largura (li ) Demanda (di)
Total de
Rolos
150
175
80
75
Variáveis de decisão:
É preciso identificar primeiro os diferentes padrões de
corte realizados pela máquina de corte.
• Seja xj a variável que indica o número de bobinas
cortadas de segundo o padrão de corte j.
Minimizar
Z=20x2+8x3+15x4+3x5+20x6+10x7+15x8 +16x9 +3x10
4x1+ 2x2 +2x3 + 1x4 + 1x5 +1x6≥150 (Mínimo de
rolos tipo 1)
1x2+ 2x4 +1x5 +1x6+3x7 + 1x8 +≥175 (Mínimo de
rolos tipo 2)
1x3+ 1x5 +2x9 + 1x10 ≥80 (Mínimo de rolos tipo 3)
1x6+ 1x8 +1x10 ≥75 (Mínimo de rolos tipo 4)
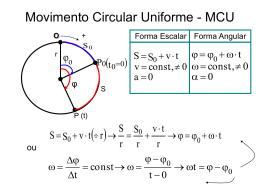
(5) Problema de Caminho Mínimo (Extraído de
Lachtermacher)
Uma fábrica de artigos de decoração, localizada em
Lambari (MG), deve entregar uma grande quantidade de
peças na cidade de Baependi (MG). A empresa quer
saber qual o caminho que seu caminhão de entregas
deve fazer para minimizar a distância total percorrida. A
figura a seguir, extraída de Lachtermacher (2004),
representa, na forma de rede, as ligações entre as
cidades da região. Deve-se determinar o caminho
mínimo de Lambari para Baependi.
Nesse problema xij é uma variável de decisão que assume
valor 1 se o arco [i,j] faz parte do caminho e zero caso
contrário.
Variáveis { x12, x13, x15, x24, x35, x46, x56} (Integralidade e
não-negatividade)
Função Objetivo:
Minimizar
41x12 + 44x13+ 50x15 +37x24 +27 x35 + 45x46 + 4x56
Nó origem = 1
Nó destino = 6
Restrições de Equilíbrio de Fluxo:
x12+x13+x15=1
x46+x56=1
x12-x24=0
x13-x35=0
x24-x46=0
x15+x35-x56=0
• Em relação à variável x1j, temos a soma dos fluxos
que saem do nó 1 deve igual a 1 => um arco
escolhido
• Em relação à variável xi6, temos a soma dos fluxos
que chegam ao nó 6 deve ser igual a 1 => um
escolhido.
• Para os outros vértices, temos que a soma dos
fluxos que chegam menos os fluxos que saem deve
ser igual à zero.
De forma a utilizar o lpSolve, vamos estabelecer a
seguinte correspondência:
x12, x13, x15, x24, x35, x46, x56
=> y1, y2, y3, y4, y5, y6, y7
Minimizar
41 y1 + 44 y2+ 50 y3 +37 y4 +27 y5 + 45 y6 + 4 y7
y1+ y2+ y3=1
y6+ y7=1
y1- y4=0
y2- y5=0
y4- y6=0
y3+ y5- y7=0
y3=1 e y7=1 => x15 =1 e x56=1
Caminho: Lambari -> Caxambu -> Baependi
(6) Problema da Cooperativa Agrícola
Uma cooperativa agrícola opera 3 fazendas que possuem
produtividades aproximadamente iguais entre si. A
produção total por fazenda basicamente da área
disponível para o plantio e da água de irrigação.
A cooperativa procura diversificar sua produção de
modo que vai plantar este ano três tipos de cultura em
cada fazenda a saber: milho, arroz e feijão.
Cada tipo de cultura demanda por certa quantidade de
água. Para reduzir o conflito no uso das colheitadeiras,
que são alugadas pela cooperativa estabeleceram-se
limites de área de produção dentro de cada tipo de
cultura.
Para evitar a concorrência entre os cooperados,
acordou-se que a proporção de área cultivada seja a
mesma para cada uma das fazendas.
As tabelas a seguir resumem os dados do problema.
Pede-se a elaboração de um programa de produção que
defina a área de cada cultura que será plantada em cada
fazenda, de modo a otimizar o lucro total da produção da
cooperativa.
Água Disponível e Área de Cultivo por Fazenda
Fazenda
1
2
3
Área Total p/ Cultivo
400
650
350
Água Disponível (Litros)
1800
2200
950
Consumo de Água, Área de Cultivo
e Lucro por Cultura
Cultura
Miho
Arroz
Feijão
Área Máxima
de Cultivo
(Acres)
660
880
400
Consumo
de Água
(L/Acre)
5,5
4,0
3,5
Lucro
(R$/Acre)
5000
4000
1800
• xij = Variáveis de decisão = quantidade de unidades
de acres que, na fazenda i será destinada à cultura j.
Função Objetivo:
Maximizar
z=5000(x11+x21+x31)+4000(x12+x22+x32)+1800(x13+x23+x33)
{Restrições de Cultivo}
x11+x12+x13≤400
x21+x22+x23≤650
x31+x32+x33≤350
{Restrições de Consumo}
5.5 x11+4.0 x12+ 3.5x13≤1800
5.5 x21+4.0 x22+ 3.5x23≤2200
5.5 x31+4.0 x32+ 3.5x33≤950
{Restrições de Plantio}
x11+ x21+ x31≤660
x12+ x22+ x32≤880
x13+ x23+ x33≤400
{Restrições associadas à proporção de área cultivada}
(x11+ x12+ x13)/400=( x21+ x22+ x23)/650
(x21+ x22+ x23)/650=( x31+ x32+ x33)/350