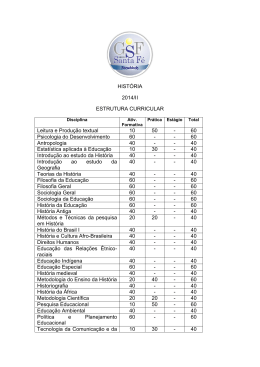
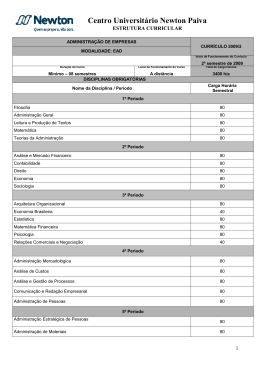
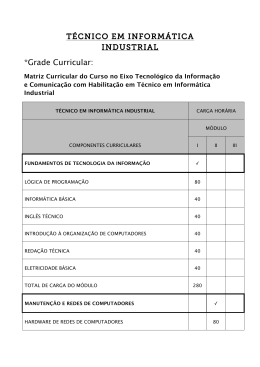
PROJETO PEDAGÓGICO DE CURSO SUPERIOR
(PPC) MATEMÁTICA - LICENCIATURA
RIO DO SUL
BLUMENAU/SC
OUTUBRO/2012
FRANCISCO JOSÉ MONTÓRIO SOBRAL
REITOR
JOSETE MARA STAHELIN PEREIRA
PRO-REITOR DE ENSINO
OSCAR EMILIO LUDTKE HARTHMANN
DIRETOR DO CÂMPUS
TIAGO BOECHEL
DIRETOR DE DESENVOLVIMENTO EDUCACIONAL DO CÂMPUS
MORGANA SCHELLER
COORDENADORA GERAL DE ENSINO DO CÂMPUS
LEONARDO DE OLIVEIRA NEVES
COORDENADOR DO CURSO
BLUMENAU/SC
NOVEMBRO/2012
COMISSÃO DE ELABORAÇÃO E SISTEMATIZAÇÃO
PAULA ANDREA GRAWIESKI CIVIERO
FATIMA PERES ZAGO DE OLIVEIRA
MARIZOLI REGUEIRA SCHNEIDER
LUIZ FERNANDO NAZARI
ANGELIZA BENETTI CLECSCH
OTÁVIO BOCHECO
LIANE VIZZOTTO
SANDRA LETICIA GRAF FERREIRA
SOLANGE APARECIDA DE OLIVEIRA HOELLER
ASSESSORIA PEDAGÓGICA
NÚCLEO PEDAGÓGICO - NuPe
BLUMENAU/SC
NOVEMBRO/2012
LISTA DE QUADROS
Quadro 1. Matriz curricular do Curso de Licenciatura em Matemática .......................... 18
Quadro 2. Quadro geral dos Componentes Curriculares .............................................. 20
Quadro 3. Componentes Curriculares do Estágio Curricular Supervisionado ............... 21
Quadro 4. Componentes Curriculares do Núcleo Básico (NBAS) ................................. 26
Quadro 5. Componentes Curriculares do Núcleo Pedagógico (NPED) ........................ 27
Quadro 6. Componentes Curriculares do Núcleo Específico (MAT) ............................. 28
Quadro 7. Relação de Docentes e Formação Profissional............................................ 33
Quadro 8. Integrantes do Núcleo Docente Estruturante................................................ 35
Quadro 9. Relação de cargo e regime de trabalho do corpo Técnico Administrativo do
Campus Rio do Sul do Instituto Federal Catarinense. .................................. 36
Quadro 10. Recursos didáticos pedagógicos existentes no Câmpus Rio do Sul –
Unidade Urbana ........................................................................................... 45
Quadro 11. Estrutura Física do Câmpus Rio do Sul – Unidade Urbana ....................... 45
Quadro 12. Relação de títulos e exemplares existentes no acervo bibliográfico .......... 47
SUMÁRIO
1. APRESENTAÇÃO ....................................................................................................... 1
2. ÁREA DE ORIGEM / IDENTIFICAÇÃO ...................................................................... 2
2.1. UNIDADE SEDE ................................................................................................... 2
2.2. UNIDADE URBANA .............................................................................................. 2
2.3. INFORMAÇÕES DO CURSO ............................................................................... 2
3. MISSÃO INSTITUCIONAL/IFC ................................................................................... 3
4. VISÃO INSTITUCIONAL/IFC ...................................................................................... 3
5. GÊNESE E IDENTIDADE DO INSTITUTO FEDERAL CATARINENSE ..................... 3
6. BREVE HISTÓRICO INSTITUCIONAL/IFC-CÂMPUS ................................................ 4
7. JUSTIFICATIVA DA CRIAÇÃO DO CURSO ............................................................... 4
8. MISSÃO DO CURSO .................................................................................................. 6
9. VISÃO DO CURSO ..................................................................................................... 6
10. PERFIL DO CURSO ................................................................................................. 6
10.1. FORMAS DE INGRESSO E ACESSO NO CURSO ........................................... 7
10.2. ACESSO E APOIO À PESSOAS COM DEFICIÊNCIAS OU MOBILIDADE
REDUZIDA (Decreto 5.296/2004) ................................................................................ 8
11. OBJETIVOS DO CURSO ........................................................................................ 10
11.1. GERAL .............................................................................................................. 10
11.2. ESPECÍFICOS .................................................................................................. 10
12. CONCEPÇÃO DO CURSO ..................................................................................... 12
12.1. PRINCÍPIOS FILOSÓFICOS E PEDAGÓGICOS DO CURSO ......................... 12
12.1.1. PRINCÍPIOS CURRICULARES .................................................................. 13
12.1.2. VALORES ................................................................................................... 13
12.3. DIRETRIZES CURRICULARES ....................................................................... 14
12.4. LEGISLAÇÃO E CAMPO DE ATUAÇÃO.......................................................... 15
12.4.1. LEGISLAÇÃO ............................................................................................. 15
12.4.2. CAMPO DE ATUAÇÃO .............................................................................. 17
13. PERFIL DO EGRESSO ........................................................................................... 17
14. ORGANIZAÇÃO CURRICULAR DO CURSO ......................................................... 18
14.1. MATRIZES CURRICULARES DO CURSO ...................................................... 18
14.2. CARGA HORÁRIA DE DISCIPLINAS ............................................................... 21
14.3. PRÁTICA COMO COMPONENTE CURRICULAR – PCC ................................ 21
14.4. ATIVIDADES ACADÊMICO-CIENTÍFICO-CULTURAIS ................................... 22
14.5. ESTÁGIO CURRICULAR SUPERVISIONADO ................................................ 23
14.6. RELAÇÃO TEORIA E PRÁTICA ....................................................................... 24
14.7. INTERDISCIPLINARIDADE .............................................................................. 26
15. RESUMO GERAL DA MATRIZ CURRICULAR ....................................................... 26
15.1. NÚCLEO COMUM ............................................................................................ 26
15.2. NÚCLEO ESPECÍFICO .................................................................................... 28
16. SISTEMA DE AVALIAÇÃO DO PROJETO DO CURSO ......................................... 28
17. SISTEMA DE AVALIAÇÃO INSTITUCIONAL ......................................................... 28
17.1. SISTEMA DE AVALIAÇÃO DO CURSO ........................................................... 28
17.1.1 AVALIAÇÃO EXTERNA............................................................................... 29
17.1.2 AVALIAÇÃO INTERNA ................................................................................ 30
18. SISTEMAS DE AVALIAÇÃO DE ENSINO E APRENDIZAGEM DO ALUNO .......... 30
19. CORPO DOCENTE................................................................................................. 33
19.1. QUADRO DE DOCENTES ............................................................................... 33
19.2. NÚCLEO DOCENTE ESTRUTURANTE........................................................... 34
20. CORPO TÉCNICO ADMINISTRATIVO ................................................................... 36
21. ATIVIDADES ACADÊMICAS .................................................................................. 36
21.1 ATIVIDADES ACADÊMICAS COMPLEMENTARES ......................................... 36
21.2. ATIVIDADES DE MONITORIA ......................................................................... 37
22. ESTÁGIO CURRICULAR ........................................................................................ 39
22.1. OPERACIONALIZAÇÃO DO ESTÁGIO CURRICULAR ................................... 39
22.2. ORIENTAÇÃO DE ESTÁGIO CURRICULAR ................................................... 40
22.3. SISTEMA DE AVALIAÇÃO DO ESTÁGIO CURRICULAR ............................... 41
23. ESTÁGIO NÃO OBRIGATÓRIO (Lei 11.788 de 25 de setembro de 2008) ............. 42
24. PESQUISA E EXTENSÃO ...................................................................................... 42
24.1. LINHAS DA PESQUISA .................................................................................... 42
24.2. AÇÕES DE EXTENSÃO ................................................................................... 43
25. CERTIFICAÇÃO E DIPLOMA ................................................................................. 43
26. INFRAESTRURA .................................................................................................... 45
26.1. ESTRUTURA FÍSICA E RECURSOS PEDAGÓGICOS NO CAMPUS............. 45
26.2. DESCRIÇÃO DA BIBLIOTECA E ACERVO BIBLIOGRÁFICO ........................ 46
27. CONSIDERAÇÕES FINAIS .................................................................................... 47
REFERÊNCIAS ............................................................................................................. 47
APÊNDICES ................................................................................................................. 50
A1 - Programa das Disciplinas Obrigatórias .............................................................. 50
A2 - Regulamento de Estágio Supervisionado Curricular Obrigatório ....................... 73
1
1. APRESENTAÇÃO
Os Institutos Federais de Educação, Ciência e Tecnologia, criados por meio da
Lei 11.892/2008, constituem um novo modelo de instituição de educação profissional e
tecnológica que visa responder de forma eficaz, às demandas crescentes por formação
profissional, por difusão de conhecimentos científicos e tecnológicos e de suporte aos
arranjos produtivos locais.
Presentes em todos os estados, os Institutos Federais contém a reorganização
da rede federal de educação profissional, oferecem formação inicial e continuada,
ensino médio integrado, cursos superiores de tecnologia, bacharelado em engenharias,
licenciaturas e pós-graduação.
O Instituto Federal Catarinense resultou da integração das antigas Escolas
Agrotécnicas Federais de Concórdia, Rio do Sul e Sombrio juntamente com os colégios
Agrícolas de Araquari e de Camboriú até então vinculados à Universidade Federal de
Santa Catarina.
O IFC oferecerá cursos em sintonia com a consolidação e o fortalecimento dos
arranjos produtivos locais, estimulando a pesquisa aplicada, a produção cultural, o
empreendedorismo e o cooperativismo, e apoiando processos educativos que levem à
geração de trabalho e renda, especialmente a partir de processos de autogestão.
Para que os objetivos estabelecidos pela lei 11.892/2008 sejam alcançados
faz-se necessário a elaboração de documentos que norteiem todas as funções e
atividades no exercício da docência, os quais devem ser construídos em sintonia e /ou
articulação com o PDI e o PPI, com as Políticas Públicas de Educação e com as
Diretrizes Curriculares Nacionais.
Nessa perspectiva, o presente documento apresenta o Projeto Pedagógico do
Curso (PPC) da Matemática – Licenciatura, com o intuito de expressar os principais
parâmetros para ação educativa, fundamentado, juntamente com o Projeto Pedagógico
Institucional (PPI), a gestão acadêmica, pedagógica e administrativa de cada curso.
Vale ressaltar que devido à importância do PPC, o mesmo deverá estar em
permanente construção, sendo elaborado, reelaborado, implementado e avaliado.
2
2. ÁREA DE ORIGEM / IDENTIFICAÇÃO
2.1. UNIDADE SEDE
CNPJ: 10.635.424.0002-67
Razão Social: Instituto Federal de Educação, Ciência e Tecnologia Catarinense
Câmpus: Rio do Sul
Esfera Administrativa: Federal
Endereço: Estrada do Redentor 5665 – Bairro Canta Galo - SC - 89160-000
Telefone/Fax: (47) 3531-3700 - Fax: (047) 3531-3700
2.2. UNIDADE URBANA
Endereço: Rua Abraham Lincoln, 210, – Bairro Jardim América – 89160 - 000
Telefone/Fax: (47) 3523 - 8600
E-mail de contato: [email protected]
Site da unidade: http://www.ifc-riodosul.edu.br
Área do Plano: Ciências Exatas e da Terra.
2.3. INFORMAÇÕES DO CURSO
Habilitação: Matemática – Licenciatura
Local: Unidade Urbana
Título: Licenciado em Matemática
Carga Horária Total: 2835 h
Prática como Componente Curricular: 405 h
Estágio Curricular Supervisionado: 420 h
Núcleo das Disciplinas Teóricas: 1800 h
Núcleo Comum: 1050h
Núcleo Específico: 750h
Atividades Acadêmico-Científico-Culturais: 210
Legislação e Atos Oficiais Relativos ao Curso: Parecer CNE/CP no 9/2007; Parecer
CNE/CP no 5/2006; Decreto no 5.626 de 22 de dezembro de 2005; Parecer CNE/CP n o
4/2005; Parecer CNE/CES no 15/2005; Parecer CNE/CES no 197/2004; Resolução
CNE/CES 3, de 18 de fevereiro de 2003; Resolução CNE/CP 2, de 19 de fevereiro de
2002; Resolução CNE/CP 1, de 18 de fevereiro de 2002.
3
3. MISSÃO INSTITUCIONAL/IFC
Ofertar uma educação de excelência, pública e gratuita, com ações de ensino,
pesquisa e extensão, a fim de contribuir para o desenvolvimento socioambiental,
econômico e cultural.
4. VISÃO INSTITUCIONAL/IFC
Ser referência em educação, ciência e tecnologia na formação de profissionaiscidadãos comprometidos com o desenvolvimento de uma sociedade democrática,
inclusiva, social e ambientalmente equilibrada.
5. GÊNESE E IDENTIDADE DO INSTITUTO FEDERAL CATARINENSE
O Instituto Federal Catarinense, com sede em Blumenau/SC, criado pela Lei
no. 11.892/08 (BRASIL, 2008b), possui atualmente sete Câmpus instalados no estado
de Santa Catarina, a saber: Araquari, Camboriú, Concórdia, Rio do Sul, Sombrio,
Luzerna e Videira.
De acordo com a lei é uma Autarquia Federal vinculada ao Ministério da
Educação gozando das seguintes prerrogativas: Autonomia administrativa, patrimonial,
financeira, didático-científica e disciplinar. Essa instituição abrange todo o território
catarinense, o que contribuirá para posicionar a nova estrutura do Instituto Federal
Catarinense, recém-implantado, numa instituição de desenvolvimento estadual e, seus
campi, em elos de desenvolvimento regional, garantindo-lhe a manutenção da
respeitabilidade, junto às comunidades onde se inserem suas antigas instituições, cuja
credibilidade foi construída ao longo de sua história.
No âmbito da gestão institucional, o Instituto Federal Catarinense busca
mecanismos participativos para a tomada de decisão, com representantes de todos os
setores institucionais e da sociedade. Com criação a criação dos Institutos Federais, a
rede de Educação Profissional e Tecnológica aumenta significativamente a inserção na
área de pesquisa e extensão, estimulando o desenvolvimento de soluções técnicas e
tecnológicas e estendendo seus benefícios à comunidade.
O Instituto Federal Catarinense oferece cursos em sintonia com a consolidação
e o fortalecimento dos arranjos produtivos locais, estimulando a pesquisa aplicada, a
4
produção cultural, o empreendedorismo e o cooperativismo, além de apoiar processos
educativos que levem à geração de trabalho e renda, especialmente a partir de
processos de autogestão.
6. BREVE HISTÓRICO INSTITUCIONAL/IFC-CÂMPUS RIO DO SUL
O câmpus de Rio do Sul integrante do Instituto Federal de Educação, Ciência e
Tecnologia Catarinense foi implantado inicialmente como Escola Agrotécnica Federal
de Rio do Sul, criada pela Lei 8.670 de 30 de junho de 1993.
A Escola Agrotécnica Federal de Rio do Sul iniciou suas atividades didáticas
com o curso de Técnico em Agropecuária, funcionando em regime de internato e semiinternato, com atividades em período integral, com aulas teóricas e práticas, nos
períodos matutino e vespertino.
Por meio da Lei no 11.892 de 29 de dezembro de 2008, que institui a Rede
Federal de Educação Profissional, Científica e Tecnológica, criou-se os Institutos
Federais de Educação, Ciência e Tecnologia, em que a Escola Agrotécnica Federal de
Rio do Sul passou a integrar o Instituto Federal Catarinense como um de seus câmpus.
Com a passagem de Escola Agrotécnica Federal de Rio do Sul para Instituto
Federal Catarinense, o câmpus de Rio do Sul instalou uma nova unidade denominada
de Unidade Urbana, onde funcionam três cursos superiores (Matemática - Licenciatura,
Bacharelado em Ciência da Computação, e Licenciatura em Física) e três cursos
técnicos (Técnico em Informática – concomitante externo e subsequente; Técnico em
Agrimensura – subsequente; e Técnico em Eletroeletrônica – subsequente).
Atualmente a instituição dispõe de um quadro docente efetivo com 92
professores do Ensino Básico, Técnico e Tecnológico, 15 docentes contratados, 72
servidores técnico-administrativos e 53 servidores terceirizados, todos voltados para o
desenvolvimento de uma educação profissionalizante de qualidade.
7. JUSTIFICATIVA DA CRIAÇÃO DO CURSO
Na Região do Alto Vale do Itajaí, existem “Demandas para Cursos Superiores”
para atender as necessidades de egressos do ensino médio, com base nos dados do
Censo escolar (IBGE, 2005). Ao considerar os alunos que estão frequentando a oitava
série do ensino fundamental em 2005, aptos para prestarem vestibular no ano de 2009,
5
os dados indicam a necessidade de aproximadamente 5500 vagas para os cursos
superiores no período de 2009 a 2016, sendo que para o ano de 2009 foram oferecidas
apenas 1780 vagas, pelas instituições de Ensino Superior da região.
Dessa forma a oferta atende aproximadamente 32% da demanda regional,
faltando ofertar em torno de 3700 vagas. Por outro lado soma-se ainda a esta
necessidade dos egressos do ensino médio, a deficiência de vagas de estudo
ocorridas no passado, como é o exemplo dos alunos da Educação de Jovens e
Adultos.
Quando é analisada especificamente a demanda para as licenciaturas, os
dados (IBGE, 2006) indicam que em Santa Catarina 8.857 professores atuantes
possuem apenas a formação no ensino de nível médio ou inferior. Isso representa
11,42% do total de professores do estado. Por outro lado os outros 68.676 professores
possuem graduação, no entanto a pesquisa não especifica quais as graduações,
destas, muitas devem não ser licenciaturas, apresentando assim ainda a falta de uma
formação pedagógica. Quando analisamos os dados (IBGE, 2005) sobre os
professores atuantes na região do Alto Vale do Itajaí, municípios pertencentes a
Associação dos Municípios do Alto Vale do Itajaí (AMAVI), percebemos que a
proporção de professores habilitados é ainda menor do que no estado, sendo que dos
3.583 professores atuantes, 793 possuem formação equivalente ao ensino médio, 11
apenas o fundamental, que contabilizam 23% do total de professores atuantes na
região que não estão habilitados, demonstrando desta forma, a necessidade de
oportunizar a formação superior na região de abrangência do Instituto Federal
Catarinense – câmpus de Rio do Sul.
Estudo realizado pela Comissão encarregada para realizar estudos sobre
cursos superiores, realizado em de 2008 apontou que na área de Ciências Exatas e da
Terra as preferências para a oferta de cursos superiores é área de Informática,
aparecendo em segundo a Matemática (fonte Prefeitura Municipal de Rio do Sul e na
GEECT de Rio do Sul).
A Lei 11.892, de 29 de dezembro de 2008 (Lei que criou os Institutos Federais)
prevê que 20% (vinte por cento) dos cursos superiores devam ser licenciaturas. Assim
concluiu-se que para a implantação de cursos superiores há a necessidade da
formação de uma equipe de docentes com formação em áreas específicas como
Física, Matemática, Química, Biologia, Zoologia, dentre outras, o que implica numa
certa “disponibilidade” de profissionais que poderão atuar em cursos de licenciatura,
6
necessitando apenas de um acréscimo de docentes da área pedagógica. Com a
presença dos profissionais da área pedagógica abre-se caminho para vários cursos de
Licenciatura, sendo que duas áreas – Matemática e Física – são realidades no câmpus
de Rio do Sul.
A demanda pela formação de professores nas áreas de Matemática,
juntamente com as Ciências Agrárias, aponta para uma oferta a curto espaço de tempo
de licenciatura ou de complementação nestas áreas.
Assim sendo, considerando a estrutura básica já presente no Câmpus para os
cursos técnicos e superiores implantados, em especial a agronomia e engenharias, o
próximo passo foi a complementação com cursos de graduação na área das
licenciaturas com fins de formação de docentes nas mais diversas áreas profissionais.
Dentro desta estrutura de formação básica e de licenciaturas ficaria constituído outro
núcleo denominado núcleo pedagógico da qual a Educação Matemática faz parte. O
núcleo pedagógico deverá ser constituído por professores nas áreas de didática,
metodologias de ensino, diretrizes educacionais, dentre outras para atender a
formação pedagógica nas diversas licenciaturas.
8. MISSÃO DO CURSO
Contribuir com a formação de professores de matemática capazes de realizar
uma leitura crítica da realidade, na busca de novas relações entre a sociedade e o
ambiente, a partir de uma sólida base comum científico-tecnológico-humanística-ética.
9. VISÃO DO CURSO
Ser referência nacional na formação dos docentes na área de matemática.
10. PERFIL DO CURSO
 Carga horária total do curso: 2835 horas
 Carga horária das atividades complementares: 210 horas
 Carga horária de estágio: 420 horas
 Duração do curso (semestre/ano): 8 semestres/4 anos
 Número de vagas: 45 vagas/ano
7
 Turno de funcionamento do curso: Aulas ministradas no período noturno,
podendo
contemplar atividades
acadêmicas
em
períodos matutino,
vespertino e/ou sábados.
 Câmpus: Rio do Sul
 Período de integralização (prazo de conclusão: mínimo e máximo):
Conforme art.2º da Resolução CNE/CP nº 2 de 19/02/2002 o curso de
Matemática- Licenciatura exige o mínimo de duração de 3 (três) anos
letivos. No IF Catarinense o curso está previsto do seguinte modo: tempo
mínimo de integralização curricular será de 4 (quatro) anos (8 semestres) e
o máximo 8 (oito) anos (16 semestres), contados a partir do ano de
matrícula de ingresso. O aluno que deixar ultrapassar o tempo de
integralização e tiver interesse em continuar e/ou concluir o curso deverá
submeter-se a novo processo de ingresso, conforme edital próprio,
obedecendo ao previsto nas leis e nos demais regulamentos que regem a
vida acadêmica do educando, inclusive no que diz respeito ao currículo.
Observa-se quanto a esse item que deverão ser cumpridas as exigências da
organização acadêmica do IF Catarinense e a organização didática do curso
de Matemática-Licenciatura.
10.1. FORMAS DE INGRESSO E ACESSO NO CURSO
O ingresso se fará mediante critérios adotados pelo Instituto, conforme edital. A
princípio o processo de Ingresso será realizado no segundo semestre de cada ano e a
matrícula dos aprovados será realizada em fevereiro do ano seguinte.
São formas de ingresso ao Curso será feita de duas formas:
1º) Admissão por processo seletivo: efetivação do ingresso, como aluno regular
do Instituto Federal Catarinense, de candidato aprovado em concurso vestibular
realizado pela Instituição;
2º) Admissão pelo ENEM – Exame Nacional do Ensino Médio: efetivação do
ingresso, como aluno regular do Instituto Federal Catarinense, de candidato aprovado
no Exame Nacional do Ensino Médio – ENEM com média estabelecida em Edital.
8
10.2. ACESSO E APOIO À PESSOAS COM DEFICIÊNCIAS OU MOBILIDADE
REDUZIDA (Decreto 5.296/2004)
Com a Lei Federal n° 10.098 de dezembro de 2000 e o decreto 5.296/2004,
estabelecem-se normas gerais e critérios básicos para a promoção da acessibilidade
das pessoas com deficiência ou com mobilidade reduzida. Desta forma, projetos de
natureza arquitetônica e urbanística, de comunicação e informação, de transporte
coletivo, bem como a execução de qualquer tipo de obra, tendo destinação pública ou
coletiva, devem considerar aspectos da acessibilidade e atendimento às necessidades
específicas de pessoas com deficiência no que concerne e regulamenta a Lei da
Acessibilidade.
Em consonância com tais aspectos a Portaria Ministerial N° 3.284 de 07 de
novembro de 2003, dispõe sobre os requisitos de acessibilidade de pessoas com
deficiências,
instruindo
também
sobre
os
processos
de
autorização
e
de
reconhecimento de cursos, bem como o credenciamento de instituições. Em virtude
disso, iniciou-se uma sensibilização em relação à inclusão.
Diante de tais considerações, convém ressaltar algumas informações
relevantes quanto ao acesso e apoio a pessoas com deficiências ou mobilidade
reduzida no âmbito do Instituto Federal Catarinense Câmpus Rio do Sul.
O Instituto Federal Catarinense Câmpus Rio do Sul é constituído atualmente
pela Sede e Unidade Urbana. A Sede está localizada a 5 km do centro da cidade, na
localidade de Serra Canoas. O acesso é por estrada sem pavimentação e o meio de
transporte utilizado pelos alunos e maioria dos servidores, é o transporte coletivo
urbano, o qual não possui nenhuma adaptação.
A partir da portaria do MEC/SETEC n° 151 de 11 de julho de 2005, que
disciplina a forma de operacionalização da ação TEC NEP – Educação Tecnológica e
Profissionalização para Pessoas com Necessidades Educacionais Especiais, que tem
por objetivo a inclusão, permanência e saída com sucesso destes alunos em cursos de
formação inicial e continuada, técnicos e tecnológicos, no âmbito da Rede Federal de
Educação Tecnológica, foi constituído através da portaria N° 200/05 de 28 de setembro
de 2005 o NAPNE (Núcleo de Apoio as Pessoas com Necessidades Específicas) da
então Escola Agrotécnica Federal de Rio do Sul, hoje Instituto Federal Catarinense.
O NAPNE do IF Catarinense – Rio do Sul possui como uma de suas principais
competências a articulação de ações conjuntas com a comunidade escolar, no intuito
9
de buscar promover a quebra de barreiras atitudinais, educacionais e arquitetônicas.
Dentre algumas das atividades ligadas ao acesso e apoio às pessoas com deficiência,
pode-se elencar:
- Sensibilização da comunidade escolar em relação ao processo de inclusão;
- Levantamento por meio de um CHECK LIST com 101 itens, de toda a
estrutura física e barreiras arquitetônicas no Instituto;
- Encaminhamento à direção geral de um relatório demonstrativo da
acessibilidade no Instituto, para que sejam tomadas as medidas necessárias a atender
às exigências da ABNT 9050;
- Participação de um servidor no curso de especialização a Distância em
Educação Profissional e Tecnológica Inclusiva;
- Encaminhamento de projeto para a implantação da infraestrutura de
acessibilidade das pessoas com deficiência;
- Solicitação de equipamentos e recursos materiais para adaptação de material
didático pedagógico e estruturação de sala multifuncional de modo a atender alunos
cegos, com visão subnormal e Surdos, nas suas especificidades;
- Aquisição de software leitor de tela a ser utilizado pelos alunos com
diagnóstico de baixa-visão;
- Valorização da cultura e singularidade Surda, buscando propiciar o serviço de
interprete/tradutor de LIBRAS, bem como a adoção de estratégias didáticometodológicas que considere o conteúdo semântico da escrita do surdo. Neste sentido
também são oferecidos cursos, palestras e oficinas acerca da LIBRAS e aspectos da
cultura Surda para a comunidade escolar;
- Solicitação e instalação de TDD, telefone com teclado para surdos.
Em relação a aspectos de infraestrutura das instalações é possível destacar:
 A sede da instituição, bem como a biblioteca onde estão as salas de
trabalho, laboratórios e salas de aula atendem as exigências da ABNT 9050, quanto
aos espaços livres de circulação e corredores, área de transferência e área de alcance;
 A biblioteca da sede possui opção de acesso através de rampas com
corrimãos, facilitando a circulação de cadeirantes e pessoas com mobilidade reduzida
e banheiro acessível;
10
 No prédio administrativo da sede, atualmente, existe um sanitário masculino
adaptado com barra de apoio;
 Sabe-se que as Unidades de Ensino e Produção também necessitam de
adequações e adaptações para atender os critérios de acessibilidade;
 A instituição possui reserva de vaga em estacionamento para pessoa com
deficiência;
 O prédio da Unidade Urbana possui sanitários acessíveis no segundo,
terceiro e quarto andar, bem como um elevador que possui internamente uma
sinalização tátil realizada através de Braille, facilitando a circulação de pessoas com
necessidades especiais.
Entende-se que a acessibilidade do Instituto Federal Catarinense câmpus Rio
do Sul possui uma estrutura física e espaços que possibilitam as modificações e
adequações necessárias.
A instituição entende que acessibilidade num espaço que visa à formação e
profissionalização de jovens e adultos é mais do que permitir que pessoas com
deficiências participem das suas atividades de ensino, pesquisa e extensão.
11. OBJETIVOS DO CURSO
11.1. GERAL
Preparar professores reflexivos com domínio do conhecimento matemático e
científico para atuarem na educação básica, com ênfase na formação para as séries
finais do ensino fundamental e ensino médio, com um currículo amplo e flexível, nas
mais diversas modalidades, desenvolvendo atitudes que integrem os conhecimentos
científicos, tecnológicos, sociais e humanísticos, capazes de produzir metodologias
pedagógicas e de acompanhar os avanços científicos e tecnológicos, visando
incorporar novas tecnologias à prática profissional, através das atividades de ensino,
pesquisa e extensão.
11.2. ESPECÍFICOS
 Construir competências profissionais referentes ao comprometimento com os
valores inspiradores da sociedade democrática, à compreensão do papel social
11
da escola, ao domínio do conhecimento pedagógico, ao conhecimento de
processos de investigação que possibilitem o aperfeiçoamento da prática
pedagógica, ao gerenciamento do próprio desenvolvimento profissional e
relativo ao domínio dos conteúdos a serem socializados de seus significados em
diferentes contextos e de sua articulação interdisciplinar;
 Propiciar aos alunos oportunidades de vivenciarem situações de aprendizagem
de maneira a construir um perfil profissional adequado à formação de
professores para a educação básica, e também compatível com a possibilidade
de atuação na educação profissional, principalmente no caso do ensino médio
integrado, oportunizando ao mesmo;
 Garantir uma sólida formação de conteúdos matemáticos com domínio nas
principais áreas da Matemática, formação pedagógica de qualidade necessária
ao exercício do magistério e uma formação que possibilite a vivência crítica da
realidade do ensino em sua região, dando-lhe condições de experimentar
propostas interdisciplinares com seus alunos;
 Preparar um profissional capaz de atuar como sujeito histórico na leitura e na
produção de significados aos conceitos matemáticos, na resolução de
problemas de seu cotidiano e na inserção da Matemática em outras áreas do
conhecimento a ela relacionada possibilitando uma leitura contextualizada de
sua realidade social;
 Fornecer uma nova linguagem para o entendimento do mundo físico, permitindo
o emprego do conhecimento matemático em setores da informática, geografia,
economia, engenharia, meteorologia, medicina ou mercado financeiro;
 Construir espaços de formação inicial e continuada de professores com linhas
de pesquisa na formação docente e interação com as escolas de educação
básica local;
 Compreender que os conteúdos de Matemática são inteirados às teorias
existentes e relacioná-los com o cotidiano;
 Evidenciar a educação científica em todas as atividades relacionando-a com o
avanço tecnológico e suas relações sociais;
 Propor atividades, do contexto curricular de Matemática, que proporcionem a
vivência do métodos científicos, desenvolvendo habilidades de investigação e
senso crítico do aluno;
12
 Vivenciar atividades com metodologia diversificada que expressem a melhoria
da qualidade de ensino;
 Estabelecer relações entre a matemática e outras áreas do conhecimento;
 Relacionar os conceitos e princípios matemáticos com as questões pertinentes
ao Professor;
 Desenvolver
habilidades
científicas
básicas
através
da
confecção
de
equipamentos para laboratório com materiais alternativos e a elaboração de
conceitos científicos básicos;
 Instrumentalizar o laboratório de Matemática para o desenvolvimento de
habilidades visando à melhoria do processo ensino-aprendizagem;
 Analisar, selecionar e produzir material didático.
12. CONCEPÇÃO DO CURSO
12.1. PRINCÍPIOS FILOSÓFICOS E PEDAGÓGICOS DO CURSO
As Diretrizes Curriculares Nacionais para a formação de professores apontam
para a necessidade do reconhecimento e fortalecimento da identidade dos cursos de
formação de professores/licenciaturas, indicando a docência como base comum na
formação de professores (qualquer área) e a unidade entre teoria e prática como
princípios indissociáveis da formação.
Diante destas orientações o Curso de Matemática - Licenciatura do IFC, adota
como princípio filosófico a Filosofia da Práxis (VÁZQUEZ, Adolfo Sánchez. Filosofia
da práxis. Rio de Janeiro: Paz e Terra, 1977).
Como princípio pedagógico a concepção da profissão como prática social
(produto e produtor) e plural, imbuída de processos teórico-práticos que levem o
estudante a compreensão das relações e implicações entre educação, escola e
sociedade/ambiente. Com vistas à superação da dicotomia entre formação e campo de
atuação profissional, enfatizando/valorizando a ideia de processo, de questionamento,
de provisoriedade do conhecimento, de compreensão e explicação de problemas
vividos no cotidiano escolar e outros espaços socioeducativos.
Para que este processo de formação se efetive, faz-se necessário uma sólida
fundamentação teórica em torno das questões da prática educativa e social
13
compromissado com os processos educativos global e local. Para tanto se tem como
necessário a compreensão de alguns princípios:

Sócio-histórico do conhecimento, compreensão do conhecimento como
produto da construção histórica;

Concepção de sociedade, justiça social e da diversidade cultural;

Compreensão da pesquisa como processo educativo, enquanto fio
condutor e elemento articulador dos demais componentes curriculares e da relação
teoria e prática;

Compreensão
da
práxis,
enquanto
unidade
teoria-prática.
12.1.1. PRINCÍPIOS CURRICULARES
 Articulação
e
integração
das
dimensões
epistemológica,
ética
e
profissionalizante;
 Articulação e integração dialética das dimensões histórica, pedagógica,
sociológica e filosófica (das ciências);
 Compreensão da matemática como ciência viva;
 Construção e reconstrução do conhecimento matemático;
 Flexibilização curricular e mobilidade;
 Articulação e integração da trajetória educativa do aluno como princípio
dinamizador da construção pessoal, coletiva e interdisciplinar do conhecimento do
profissional de Educação: “tornar o vivido pensado e o pensado vivido” (ANFOPE,
1998);
 Articulação e integração do Projeto Político Pedagógico da Instituição
Formadora/Escola com um projeto de sociedade como balizador da identidade
profissional;
 Articulação do ensino, pesquisa e extensão.
12.1.2. VALORES
Que se tem e que se quer construir:
1. Compromisso com a missão e visão do Curso e do IFC;
2. Conduta ética, cooperativa e responsável;
14
3. Respeito e compromisso com a profissão professor/educador;
4. Busca pela autonomia e autoria profissional;
5. Compromisso com o processo educativo inclusivo;
6. Reconhecimento e respeito aos diferentes saberes e as diferentes culturas;
7. A Ciência Pedagógica como base da superação do senso comum;
8. O processo pedagógico como ação-reflexão-ação.
12.3. DIRETRIZES CURRICULARES
As diretrizes curriculares propostas pelo Ministério da Educação para as
instituições de ensino de Matemática estão contidas na Resolução nº 3 de 18 de
fevereiro de 2003, que integra o Parecer CNE/CES 1.302/2001 de 06 de novembro de
2001.
Estas diretrizes orientam a elaboração do Projeto Pedagógico do curso,
estabelecendo a formulação do perfil dos formandos, competências e habilidades,
conteúdos curriculares, formato dos estágios, atividades complementares, avaliação e
estrutura do curso e determina, ainda, a observância da Resolução 01 e 02 do CNE/CP
de 19 de fevereiro de 2002, no que diz respeito à carga horária dos cursos de
licenciatura.
O formando de Matemática - Licenciatura, além de sólida formação de
conteúdos na área, deve estar preparado para enfrentar os desafios advindos das
rápidas mudanças na sociedade e mundo do trabalho, ter consciência do seu papel
social de educador e ter visão da importância da aprendizagem da Matemática, que
deve ser acessível a todos.
Os currículos devem ser elaborados de forma a desenvolver competências e
habilidades como a capacidade de expressão, aprendizagem continuada, capacidade
de trabalho em equipe, conhecimento de questões contemporâneas, relação entre a
Matemática e demais áreas do conhecimento, entre outras.
Os currículos também devem assegurar o desenvolvimento de conteúdos dos
diferentes âmbitos do conhecimento profissional de um matemático incluindo, além dos
conteúdos puramente matemáticos aqueles da Educação Básica, considerando-se as
Diretrizes Curriculares Nacionais para a formação de professores em nível superior.
15
12.4. LEGISLAÇÃO E CAMPO DE ATUAÇÃO
12.4.1. LEGISLAÇÃO
As licenciaturas dedicadas à Formação de Professores para a Educação Básica,
em nível superior, estão regulamentadas, basicamente, por duas leis maiores - a
Constituição Federal de 1998 e a Lei de Diretrizes e Bases 9394/96 – e por duas
resoluções emanadas do CNE – a Resolução CNE/CP nº 001/2002 e a Resolução
CNE/CP nº002/2002; Resolução CNE/CES nº03/ 2003 - Diretrizes Curriculares para os
cursos de Matemática; Parecer CNE/CES 1.302/2001 - Diretrizes Curriculares
Nacionais para os Cursos de Matemática, Bacharelado e Licenciatura. Quanto às
competências e habilidades o Parecer n. 1.302/2001 prevê que os currículos os cursos
de Bacharelado/Licenciatura em Matemática deverão ser elaborados de maneira a
desenvolver as seguintes competências e habilidades:
a) capacidade de expressar-se escrita e oralmente com clareza e
precisão;
b)
capacidade
de
trabalhar
em
equipes
multidisciplinares; c) capacidade de compreender, criticar e
utilizar novas ideias e tecnologias para a resolução de problemas;
d) capacidade de aprendizagem continuada, sendo sua prática
profissional também fonte de produção de conhecimento; e)
habilidade de identificar, formular e resolver problemas na sua
área de aplicação; utilizando rigor lógico-científico na análise da
situação-problema; f) estabelecer relações entre a Matemática e
outras áreas do conhecimento; g) conhecimento de questões
contemporâneas; h) educação abrangente necessária ao
entendimento do impacto das soluções encontradas num contexto
global e social; i) participar de programas de formação;
continuada; j) realizar estudos de pós-graduação; k) trabalhar na
interface da Matemática com outros campos de saber (BRASIL,
2001, p. 3).
Quanto à especificidade para a formação do licenciado, as competências e
habilidades próprias do educador matemático, o parecer citado acima observa os
seguintes aspectos:
a) elaborar propostas de ensino-aprendizagem de Matemática
para a educação básica; b) analisar, selecionar e produzir
materiais didáticos; c) analisar criticamente propostas curriculares
de Matemática para a educação básica; d) desenvolver
estratégias de ensino que favoreçam a criatividade, a autonomia
16
e a flexibilidade do pensamento matemático dos educandos,
buscando trabalhar com mais ênfase nos conceitos do que nas
técnicas, fórmulas e algoritmos; e) perceber a prática docente de
Matemática como um processo dinâmico, carregado de
incertezas e conflitos, um espaço de criação e reflexão, onde
novos conhecimentos são gerados e modificados continuamente;
f) contribuir para a realização de projetos coletivos dentro da
escola básica (BRASIL, 2001, p. 3).
A Resolução CNE/CP nº 001/2002 que estabelece as Diretrizes Curriculares
Nacionais para a Formação de Professores da Educação Básica, em nível superior é
vinculada ao Parecer CNE/CP nº 009/2001. Nesse Parecer, encontra-se uma extensa
fundamentação das mudanças de concepção sobre a formação de professores, mas
sendo de natureza conceitual não trata de questões de carga horária nem de duração
das licenciaturas. Essas matérias foram regulamentadas pela Resolução CNE/CP nº
002/2002. O Parecer CNE/CP nº 28/2001, vinculado a esta última Resolução, defende
a necessidade de prever para o componente curricular Estágio Supervisionado uma
carga horária mínima de 400 horas. Num contexto mais atual temos o Parecer CNE/CP
no 5/2006 e o Parecer CNE/CP no 9/2007 que preveem a reorganização da carga
horária mínima de 2800 para os cursos de formação de professores destacando a
necessidade de no mínimo 300 horas de estágio curricular e 2500 horas dedicadas as
demais atividades formativas;
Este curso de Matemática - Licenciatura do Instituto Federal Catarinense
apresenta uma organização curricular prevendo uma carga de 405 horas de prática
pedagógica; 420 horas de estágio curricular supervisionado; 1050 horas de núcleo
comum; 750 horas de núcleo específico; 210 horas de núcleo complementar,
perfazendo um total de 2835 horas, desta forma contempla as legislações em vigor
para os cursos de Licenciaturas para a Educação Básica, séries finais do Ensino
Fundamental, Ensino Médio e Ensino Técnico.
Atendendo, também, ao Decreto Federal nº 5626\5, que determina que Libras
deve ser inserida nos cursos de formação de professores para o exercício do
magistério, em nível médio e superior, foi introduzida Libras como disciplina curricular
obrigatória na matriz curricular do curso.
17
12.4.2. CAMPO DE ATUAÇÃO
O Licenciado em Matemática trabalha como professor em instituições de ensino
que oferecem cursos de nível fundamental e médio; em editoras e em órgãos públicos
e privados que produzem e avaliam programas e materiais didáticos para o ensino
presencial e a distância. Além disso, atua em espaços de educação não-formal, como
feiras de divulgação científica e museus; em empresas que demandem sua formação
específica e em instituições que desenvolvem pesquisas educacionais. Também pode
atuar de forma autônoma, em empresa própria ou prestando consultoria. (BRASIL,
2010).
13. PERFIL DO EGRESSO
O Licenciado em Matemática de acordo com as Diretrizes Curriculares
Nacionais dos Cursos de Bacharelado e Licenciatura (BRASIL, 2010) é o professor que
planeja, organiza e desenvolve atividades e materiais relativos à Educação
Matemática. Sua atribuição central é a docência na Educação Básica, que requer
sólidos
conhecimentos
sobre
os
fundamentos
da
Matemática,
sobre
seu
desenvolvimento histórico e suas relações com diversas áreas; assim como sobre
estratégias para transposição do conhecimento matemático em saber escolar. Além de
trabalhar diretamente na sala de aula, o licenciado elabora e analisa materiais
didáticos, como livros, textos, vídeos, programas computacionais, ambientes virtuais de
aprendizagem, entre outros. Realiza ainda pesquisas em Educação Matemática,
coordena e supervisiona equipes de trabalho. Em sua atuação, prima pelo
desenvolvimento do educando, incluindo sua formação ética, a construção de sua
autonomia intelectual e de seu pensamento crítico.
18
14. ORGANIZAÇÃO CURRICULAR DO CURSO
14.1. MATRIZES CURRICULARES DO CURSO
Código
Componentes Curriculares
MAT 03
Cálculo I
Fundamentos Teóricos e Metodológicos da
Formação e da Atuação Docente
Física I
Geometria Analítica
Psicologia do Desenvolvimento e da
Aprendizagem
SUBTOTAL
NPED 05
NBAS 05
MAT 04
NPED 06
Prática como
Componente
Curricular
Prática como
Componente
Curricular
Carga Horária
Teórica
30
30
60
30
60
60
60
30
300
4
2
4
4
4
2
20
60
30
60
60
60
30
300
-
--
Prática como
Componente
Curricular
Matemática Fundamental II
Lógica Básica
Informática Básica
Geometria Espacial
Teorias Educacionais e Curriculares
Educação e Mundo do Trabalho
SUBTOTAL
90
30
60
30
60
270
Carga Horária
Teórica
NBAS 03
MAT 02
NBAS 04
MAT 02
NPED 03
NPED 04
6
2
4
4
4
20
Carga Horária
Teórica
Componentes Curriculares
Créditos
Código
90
30
60
60
60
300
Créditos
Matemática Fundamental I
Metodologia Científica
História da Educação
Leitura e Produção de Texto
Geometria Plana
SUBTOTAL
Créditos
NBAS 01
NBAS 02
NPED 01
NPED 02
MAT 01
CH Total do
Semestre
Componentes Curriculares
CH Total do
Semestre
Código
CH Total do
Semestre
o
3 semestre
BCCT*
o
2 semestre
BCCT*
o
1 semestre
BCCT*
Quadro 1. Matriz curricular do Curso de Licenciatura em Matemática
60
4
60
-
60
4
30
30
60
60
4
4
60
60
-
60
4
30
30
300
20
240
60
o
6 semestre
BCCT*
ESTG 01
Código
NPED 11
MAT 09
NPED 12
MAT 10
ESTG 02
Componentes Curriculares
Pesquisa em Educação
Cálculo IV
Educação Inclusiva
Equações Diferenciais Ordinárias
Estágio Supervisionado II
TOTAL DISCIPLINA
TOTAL SEMESTRE
Créditos
Carga Horária
Teórica
Prática como
Componente
Curricular
4
30
30
45
30
315
3
2
21
30
30
270
15
45
Prática como
Componente
Curricular
NPED 10
60
60
4
30
30
60
60
4
4
60
60
-
60
4
-
60
60
240
300
4
20
150
90
Prática como
Componente
Curricular
MAT 07
MAT 08
Metodologia do Ensino de Matemática na
Educação Básica II
Cálculo III
Álgebra Linear II
Laboratório de prática de ensinoaprendizagem I
Estágio Supervisionado I
TOTAL DISCIPLINA
TOTAL SEMESTRE
-
Carga Horária
Teórica
NPED 09
Componentes Curriculares
60
60
60
Carga Horária
Teórica
o
5 semestre
BCCT*
Código
4
4
4
Créditos
NPED 08
NBAS 07
60
60
60
Créditos
NPED 07
Física II
Cálculo II
Álgebra Linear I
Metodologia do Ensino de Matemática na
Educação Básica I
Avaliação
Concepções em Educação Matemática
SUBTOTAL
CH Total do
Semestre
NBAS 06
MAT 06
MAT 05
Componentes Curriculares
4
4
4
4
10
26
30
60
30
60
180
30
30
60
CH Total do
Semestre
o
4 semestre
BCCT*
Código
CH Total do
Semestre
19
60
60
60
60
150
240
390
Componentes Curriculares
NPED 17
NBAS 08
MAT 12
NPED 18
ESTG 04
Laboratório de prática de ensino aprendizagem II
Estatística e probabilidade
Análise
Libras
Estágio Supervisionado IV
TOTAL DISCIPLINA
TOTAL SEMESTRE
Prática como
Componente
Curricular
2
4
4
4
30
30
60
60
30
-
60
4
60
-
60
270
330
4
22
240
30
Prática como
Componente
Curricular
o
8 semestre
BCCT*
Código
Carga Horária
Teórica
ESTG 03
30
60
60
60
Carga Horária
Teórica
NPED 16
Sociologia da Educação
Educação Matemática e Tecnologias
Cálculo Numérico
Filosofia da Educação
Políticas Educacionais – estruturas e
sistemas
Estágio Supervisionado III
TOTAL DISCIPLINA
TOTAL SEMESTRE
Créditos
NPED 13
NPED 14
MAT 11
NPED 15
Créditos
Componentes Curriculares
CH Total do
Semestre
o
7 semestre
BCCT*
Código
CH Total do
Semestre
20
60
4
-
60
60
60
60
150
240
390
4
4
4
10
26
60
60
30
150
30
90
Componentes Curriculares
Carga
horária
Créditos
Quadro 2. Quadro geral dos Componentes Curriculares
CH Disciplinas
1800
120
Prática como Componente Curricular
405
27
Atividades Acadêmico-Científico-Culturais
210
14
Estágio Curricular Supervisionado
Total
420
28
2835
189
21
Código
Componentes Curriculares
CH
Semestre
Créditos
Prática como
Componente
Curricular
Quadro 3. Componentes Curriculares do Estágio Curricular Supervisionado
ESTG 01
ESTG 02
ESTG 03
ESTG 04
Estágio Supervisionado I
Estágio Supervisionado II
Estágio Supervisionado III
Estágio Supervisionado IV
60
150
60
150
4
10
4
10
-
420
28
-
Total CH
14.2. CARGA HORÁRIA DE DISCIPLINAS
O Parecer do CNE/CP n. 21/2001 (BRASIL, 2001, p. 12) afirma que o ensino
que se desenvolve em aula é necessário, importante e a exigência de um segmento de
tal natureza no interior deste componente acadêmico-científico não poderá ter uma
duração abaixo de 1800 horas. Este Projeto Pedagógico do curso de Matemática –
licenciatura prevê a carga horária destinada às disciplinas do seguinte modo: 1050
horas de núcleo comum; 750 horas de núcleo específico; 210 horas de núcleo
complementar, perfazendo um total de 2835 horas.
14.3. PRÁTICA COMO COMPONENTE CURRICULAR – PCC
De acordo com Parecer CNE/CP 21/2001 a prática como componente curricular
é
pois, uma prática que produz algo no âmbito do ensino. Sendo a
prática um trabalho consciente cujas diretrizes se nutrem do
Parecer 9/2001 ela terá que ser uma atividade tão flexível quanto
outros pontos de apoio do processo formativo, a fim de dar conta
dos múltiplos modos de ser da atividade acadêmico-científica.
Assim, ela deve ser planejada quando da elaboração do projeto
pedagógico e seu acontecer deve se dar desde o início da
duração do processo formativo e se estender ao longo de todo o
seu processo. Em articulação intrínseca com o estágio
supervisionado e com as atividades de trabalho acadêmico, ela
concorre conjuntamente para a formação da identidade do
professor como educador.
O Parecer citado acima chama atenção para que haja distinção entre a prática
como componente curricular e a prática de ensino no estágio obrigatório, enfatizando
22
que a prática como componente curricular, terá necessariamente a marca dos projetos
pedagógicos das instituições formadoras ao transcender a sala de aula para o conjunto
do ambiente escolar e da própria educação escolar, pode envolver uma articulação
com os órgãos normativos dos executivos dos sistemas (BRASIL, Parecer CNE/CP nº
28/2001).
O curso de Matemática-Licenciatura estabelece que a PCC está diluída em
diversas disciplinas oferecidas ao longo do curso e poderá ocorrer parte presencialmente
nos horários aulas ou prever atividades que ocorram em outros momentos fora do espaço
da sala de aula e em outros períodos (matutino, vespertino ou sábados) podendo, em
alguns casos, contemplar atividades não-presenciais para os alunos: estudos dirigidos,
pesquisas em contextos escolares, em ambientes virtuais, entrevistas, etc.
Para que isto ocorra, é necessário que haja tempo e espaço para a prática, desde
o início do curso, com a devida supervisão da instituição formadora, tendo em vista o
apoio e a avaliação de sua qualidade e como contributo para formação docente dos
acadêmicos.
A efetivação do legal à prática é de responsabilidade de todas as instituições de
ensino superiores de acordo com as diretrizes curriculares e com a necessária mudança
dos projetos pedagógicos das instituições e isto também deve estar presente nas
intenções e na filosofia do IFCatarinense a serem implementadas pelas ações
desenvolvidas.
14.4. ATIVIDADES ACADÊMICO-CIENTÍFICO-CULTURAIS
Segundo as Diretrizes Curriculares Nacionais para os Cursos de Matemática,
Bacharelado e Licenciatura (BRASIL, 2001, p. 12) faz-se necessário contemplar a
diversificação dos espaços educacionais e ampliar do universo cultural em diferentes
áreas e disciplinas bem como a produção coletiva de projetos de estudos, elaboração
de pesquisas, as oficinas, os seminários, monitorias, tutorias, eventos, atividades de
extensão, o estudo das novas diretrizes do ensino fundamental, do ensino médio, da
educação infantil, da educação de jovens e adultos, dos portadores de necessidades
especiais, das comunidades indígenas, da educação rural e de outras propostas de
apoio curricular proporcionadas pelos governos dos entes federativos são exigências
de um curso que almeja formar os profissionais do ensino. Este enriquecimento exigido
está justificado pelas diretrizes do Parecer 9/2001 e não poderá contar com menos de
23
200 horas. Cabe às instituições, consideradas suas peculiaridades, enriquecer a carga
horária por meio da ampliação das dimensões dos componentes curriculares
constantes da formação docente.
14.5. ESTÁGIO CURRICULAR SUPERVISIONADO
As Diretrizes Curriculares
Nacionais para
os Cursos de Matemática,
Bacharelado e Licenciatura (BRASIL, 2001) observa que o educador matemático deve
ser capaz de tomar decisões, refletir sobre sua prática e ser criativo na ação
pedagógica, reconhecendo a realidade em que se insere. Mais do que isto, ele deve
avançar para uma visão de que a ação prática é geradora de conhecimentos. Nessa
perspectiva, o documento citado, afirma que o estágio é essencial nos cursos de
formação de professores, possibilitando desenvolver: “a) uma sequência de ações
onde o aprendiz vai se tornando responsável por tarefas em ordem crescente de
complexidade, tomando ciência dos processos formadores; b) uma aprendizagem
guiada por profissionais de competência reconhecida”. As atividades relativas ao
Estágio Curricular Supervisionado estão normatizadas em regulamento próprio
(Apêndice 2).
O Parecer CNE/CP 21/2001 (BRASIL, 2001, p. 10) defende que o estágio
curricular supervisionado pretende oferecer ao futuro licenciado um conhecimento do
real em situação de trabalho, isto é diretamente em unidades escolares dos sistemas
de ensino, sendo
também um momento para se verificar e provar (em si e no outro)
a realização das competências exigidas na prática profissional e
exigíveis dos formandos, especialmente quanto à regência. Mas é
também um momento para se acompanhar alguns aspectos da
vida escolar que não acontecem de forma igualmente distribuída
pelo semestre, concentrando-se mais em alguns aspectos que
importa vivenciar. É o caso, por exemplo, da elaboração do
projeto pedagógico, da matrícula, da organização das turmas e do
tempo e espaço escolares. O estágio curricular supervisionado é
pois um modo especial de atividade de capacitação em serviço e
que só pode ocorrer em unidades escolares onde o estagiário
assuma efetivamente o papel de professor, de outras exigências
do projeto pedagógico e das necessidades próprias do ambiente
institucional escolar testando suas competências por um
determinado período. Por outro lado, a preservação da
integridade do projeto pedagógico da unidade escolar que
recepciona o estagiário exige que este tempo supervisionado não
seja prolongado, mas seja denso e contínuo.
24
14.6. RELAÇÃO TEORIA E PRÁTICA
Segundo Ponte (2003) para se tornar um professor de Matemática, o licenciando
necessita de conhecimento matemático e conhecimento sobre o ensino de Matemática.
Mas, só isso não basta. Ele precisa também assumir papéis, normas e valores
fundamentais da profissão para qualificar-se à realização das atividades profissionais
inerentes de um professor e de identificar-se pessoalmente com a profissão. Este
aspecto, neste curso, procura ser reforçado pelo rol de disciplinas que integram as 405
horas de práticas como componente curricular.
É necessário, ao futuro professor, que ele compreenda o contexto escolar como
um processo contínuo e dinâmico, influenciado por múltiplas variáveis educacionais,
sociais, históricos e culturais, nos quais se aprende e se trabalha desenvolvendo a
identidade do professor em formação como agente ativo do processo educacional, ou
seja, com a reflexão e a investigação da prática.
A reflexão sobre a prática envolverá o planejamento e discussões sobre
questões curriculares e eventos em sala de aula, despertando a atenção do
licenciando para seu desenvolvimento contínuo enquanto professor de Matemática.
A investigação da prática diz respeito a envolver os licenciandos na resolução
de problemas de conteúdo pedagógico, em grupo, do tipo dos que são enfrentados por
professores ao planejar e desenvolver atividades diárias; na análise de vídeos da
própria prática do ensino; na análise e implementação de experiências de Educação
Matemática. Assim, nas disciplinas de prática, busca-se envolver os licenciandos na
análise de atividades realizadas no contexto profissional durante experiências de
campo, relacionadas à observação da prática de professores experientes ou a reflexão
sobre sua própria prática enquanto professor estudante. No entanto, a observação e
interação com o espaço escolar não é suficiente para que o futuro professor enxergue
para além das aparências aquilo que ele observa. O diálogo com referenciais teóricos
pode auxiliar o licenciando nas perspectivas de análise dos diversos contextos
(históricos, sociais, culturais, organizacionais, pedagógicos, dentre outros) nos quais se
dá a atividade docente e, também, a compreender a si mesmo enquanto profissional
em formação, de modo que possa neles intervir e transformá-los quando for preciso
(PIMENTA; LIMA, 2004).
Está perspectiva dialoga com o estabelecido na Resolução CNE/CES nº 1, de
18/02/2002, especialmente nos artigos:
25
Art. 12. Os cursos de formação de professores em nível superior terão a sua
duração definida pelo Conselho Pleno, em parecer e resolução específica sobre
sua carga horária.
§ 1º A prática, na matriz curricular, não poderá ficar reduzida a um
espaço isolado, que a restrinja ao estágio, desarticulado do restante
do curso.
§ 2º A prática deverá estar presente desde o início do curso e
permear toda a formação do professor.
§ 3º No interior das áreas ou das disciplinas que constituírem os
componentes curriculares de formação, e não apenas nas disciplinas
pedagógicas, todas terão a sua dimensão prática.
Art. 13. Em tempo e espaço curricular específico, a coordenação da dimensão
prática transcenderá o estágio e terá como finalidade promover a articulação das
diferentes práticas, numa perspectiva interdisciplinar.
§ 1º A prática será desenvolvida com ênfase nos procedimentos de
observação e reflexão, visando à atuação em situações
contextualizadas, com o registro dessas observações realizadas e a
resolução de situações-problema.
§ 2º A presença da prática profissional na formação do professor, que
não prescinde da observação e ação direta, poderá ser enriquecida
com tecnologias da informação, incluídos o computador e o vídeo,
narrativas orais e escritas de professores, produções de alunos,
situações simuladoras e estudo de casos.
§ 3º O estágio curricular supervisionado, definido por lei, a ser
realizado em escola de educação básica, e respeitado o regime de
colaboração entre os sistemas de ensino, deve ser desenvolvido a
partir do início da segunda metade do curso e ser avaliado
conjuntamente pela escola formadora e a escola campo de estágio.
Nesta ênfase, a teoria não mais comanda a prática, não mais a orienta no
sentido de torná-la dependente das ideias, como também não se dissolve na prática,
anulando-se a si mesma. A prática, por seu lado, não significa mais a aplicação da
teoria, ou uma atividade dada e imutável, mas pressupõe que a teoria e a prática
educativa devem ser trabalhadas simultaneamente, constituindo uma unidade
indissolúvel, e que isto deve acontecer em todos os componentes que tem como
proposta a aproximação do licenciando ao contexto real de sua futura profissão
(CANDAU; LELIS, 1995)
26
14.7. INTERDISCIPLINARIDADE
Embora a estrutura curricular do curso seja disciplinar, a metodologia e
abordagem dos conteúdos buscará estabelecer relações entre as disciplinas que
ocorrem concomitantemente, bem como as dos semestres anteriores. A articulação
entre o corpo docente do curso é que vai permitir maiores avanços nas relações
interdisciplinares a serem estabelecidas. Para garantir isso o planejamento semestral
será indispensável, a partir da internalização do projeto pedagógico pelo corpo
docente.
15. RESUMO GERAL DA MATRIZ CURRICULAR
15.1. NÚCLEO COMUM
Código
Componentes Curriculares
CH
Semestre
Créditos
Carga
Horária
Teórica
Prática
como
Component
e Curricular
Quadro 4. Componentes Curriculares do Núcleo Básico (NBAS)
NBAS 01
Matemática Fundamental I
90
6
90
-
NBAS 02
30
2
30
-
NBAS 03
Metodologia Científica
Matemática Fundamental II
60
4
60
-
NBAS 04
Informática Básica
60
4
60
-
NBAS 05
Física I
60
4
60
-
NBAS 06
Física II
60
4
60
-
NBAS 07
Concepções em Educação Matemática
30
2
30
-
NBAS 08
Estatística e probabilidade
60
4
60
-
450
30
450
-
Total
27
Código
Componentes Curriculares
CH
Semestre
Créditos
Carga
Horária
Teórica
Prática
como
Component
e Curricular
Quadro 5. Componentes Curriculares do Núcleo Pedagógico (NPED)
NPED 01
História da Educação
60
4
60
-
NPED 02
Leitura e Produção de Texto
Teorias Educacionais e Curriculares
60
4
30
30
60
4
60
-
30
2
15
15
60
4
30
30
60
4
30
30
60
4
30
30
45
3
45
-
60
4
30
30
60
4
-
60
NPED 11
Educação e Mundo do Trabalho
Fundamentos Teóricos e Metodológicos
da Formação e da Atuação Docente
Psicologia do Desenvolvimento e da
Aprendizagem
Metodologia do Ensino de Matemática na
Educação Básica I
Avaliação
Metodologia do Ensino de Matemática na
Educação Básica II
Laboratório de prática de ensinoaprendizagem I
Pesquisa em Educação
60
4
30
30
NPED 12
Educação Inclusiva
60
4
30
30
NPED 13
Sociologia da Educação
30
2
30
-
NPED 14
Educação Matemática e Tecnologias
60
4
30
30
NPED 15
Filosofia da Educação
Políticas Educacionais – estruturas e
sistemas
Laboratório de prática de ensino aprendizagem II
Libras
60
4
60
-
60
4
60
-
60
4
-
60
60
4
30
30
1005
67
585
405
NPED 03
NPED 04
NPED 05
NPED 06
NPED 07
NPED 08
NPED 09
NPED 10
NPED 16
NPED 17
NPED 18
Total
28
15.2. NÚCLEO ESPECÍFICO
Código
Componentes Curriculares
CH
Semestre
Créditos
Carga
Horária
Teórica
Quadro 6. Componentes Curriculares do Núcleo Específico (MAT)
MAT 01
60
4
60
MAT 02
Geometria Plana
Lógica Básica
30
2
30
MAT 03
Geometria Espacial
60
4
60
MAT 04
Cálculo I
60
4
60
MAT 05
Geometria Analítica
60
4
60
MAT 06
Álgebra Linear I
60
4
60
MAT 07
Cálculo II
60
4
60
MAT 08
Cálculo III
60
4
60
MAT 09
Álgebra Linear II
60
4
60
MAT 10
Cálculo IV
60
4
60
MAT 11
Equações Diferenciais Ordinárias
60
4
60
MAT 12
Cálculo Numérico
60
4
60
MAT 13
Análise
60
750
4
50
60
750
Total CH
16. SISTEMA DE AVALIAÇÃO DO PROJETO DO CURSO
A avaliação do Curso acontecerá por dois mecanismos, constituídos pelas
avaliações externa e interna, em consonância com o Sistema Nacional de Avaliação do
Ensino Superior - SINAES.
17. SISTEMA DE AVALIAÇÃO INSTITUCIONAL
17.1. SISTEMA DE AVALIAÇÃO DO CURSO
A avaliação do Curso Superior Matemática – Licenciatura será feita
regularmente, através do estudo do desempenho do Curso e dos aspectos relativos ao
atendimento das expectativas da comunidade. Esta avaliação, de acordo com as
determinações legais vigentes, será realizada em dois níveis: Externo e Interno,
através da CPA – Comissão Própria de Avaliação, observando as dimensões
propostas pelo SINAES.
29
De acordo com Instrumento de Avaliação de Cursos de Graduação presencial e
a distância BRASIL (2012) ocorrerá levando-se em consideração três dimensões e
seus respectivos indicadores
Dimensão 1: ORGANIZAÇÃO DIDÁTICO-PEDAGÓGICA
Fontes de Consulta: Plano de Desenvolvimento Institucional, Projeto Pedagógico do
Curso, Diretrizes Curriculares Nacionais, quando houver, e Formulário Eletrônico preenchido
pela IES no e-MEC.
Dimensão 2: CORPO DOCENTE E TUTORIAL
Fontes de Consulta: Projeto Pedagógico do Curso, Formulário Eletrônico
preenchido pela IES no e-MEC e Documentação Comprobatória.
Dimensão 3: INFRAESTRUTURA
Fontes de Consulta: Projeto Pedagógico do Curso, Diretrizes Curriculares
Nacionais, quando houver, Formulário Eletrônico preenchido pela IES no e-MEC e
Documentação Comprobatória.
Serão atribuídos conceitos a cada um dos indicadores. Os conceitos serão
contextualizados, com base nos indicadores, descritos de forma abrangente e
coerentes.
17.1.1 AVALIAÇÃO EXTERNA
A avaliação externa adotará mecanismos do MEC, através do Exame
Nacional de Desempenho dos Estudantes – ENADE previsto pelo Sistema Nacional de
Avaliação do Ensino Superior - SINAES, e indiretamente pela sociedade, incluindo exalunos.
30
17.1.2 AVALIAÇÃO INTERNA
Para a avaliação interna foi criada uma Comissão Própria de Avaliação CPA, que organizará e/ou definirá os procedimentos e mecanismos adotados para a
avaliação dos cursos.
Em conformidade com as diretrizes estabelecidas pela CPA e segundo as
atribuições previstas na Organização Acadêmica dos Cursos de Graduação do Instituto
Federal Catarinense, o NDE acompanhará a evolução dos seguintes pontos:
• Atividades de Ensino;
• Organização Didático-Pedagógica;
• Projeto Pedagógico do Curso;
• Atividades de Pesquisa e de Iniciação Científica;
• Atividades de Extensão;
• Biblioteca;
• Instalações;
• Auto-avaliação discente e docente.
18. SISTEMAS DE AVALIAÇÃO DE ENSINO E APRENDIZAGEM DO ALUNO
A avaliação deve ser contínua e cumulativa e fornecer subsídios para que a
Instituição possa retroalimentar o projeto pedagógico e o professor o processo de
ensino-aprendizagem, buscando compreender os processos de avanços e as
defasagens de aprendizagem. A avaliação deve também investigar os conhecimentos
prévios dos alunos e levantar seus anseios e suas necessidades.
O papel do professor na avaliação escolar deve ser o de agente crítico da
realidade, percebendo a avaliação escolar como um processo de construção do
conhecimento. Neste sentido, os acertos, os erros, as dificuldades, as dúvidas e o
contexto social e econômico que os alunos apresentam, são evidências significativas
de como eles interagem com a apropriação do conhecimento.
Os objetivos da avaliação são:
31
 Analisar a coerência do trabalho pedagógico com as finalidades
educativas previstas no Projeto Pedagógico do Curso e no Plano de Ensino de cada
disciplina;
 Avaliar a trajetória da vida escolar do aluno, visando obter indicativos que
sustentem tomadas de decisões sobre a progressão dos alunos e o encaminhamento
do processo ensino–aprendizagem;

Determinar, através de instrumentos de medidas, os aspectos qualitativos
e quantitativos do comportamento humano (motor, afetivo e cognitivo), coerente aos
objetivos planejados para acompanhar o processo de aprendizagem.
A avaliação possibilita a identificação das diferentes formas de apropriação
dos conceitos científicos elaborados pelos acadêmicos, seus avanços e dificuldades na
aprendizagem, além de possibilitar uma ação imediata e mais efetiva do professor,
como mediador, recuperando os conhecimentos necessários de maneira mais
significativa.
Cabe ao professor fazer todos os registros e anotações referentes às
avaliações, que servirão para orientá-lo em relação aos outros elementos necessários
para o avanço do processo ensino-aprendizagem.
Durante o período letivo, cada aluno receberá, no mínimo, 3 (três)
avaliações parciais, compondo a média semestral.
A avaliação do desempenho acadêmico, deverá ser feita pelo docente, com
atribuição de notas, expressas em grau numérico de 0 (zero) a 10 (dez), com um
decimal.
A avaliação será realizada com base nos seguintes instrumentos:
- Apresentação oral e escrita de trabalhos propostos, quando solicitado;
- Avaliação escrita (trabalhos e provas);
- Seminários;
- Projetos;
- Participação em eventos internos;
- Outros.
A avaliação estará embasada nos seguintes critérios:
- Domínio dos conteúdos básicos trabalhados;
32
- Assiduidade;
- Habilidade na utilização/aplicação dos conteúdos desenvolvidos em aula;
- Comprometimento com o curso;
- Outros.
A avaliação do rendimento acadêmico será feita através de testes, provas,
trabalhos e outros meios que permitam avaliar o progresso do aluno e o esforço
dispensado no processo de aprendizagem. O rendimento verificado nas atividades de
cada componente curricular, área de estudo ou atividade, dará origem à nota.
O professor tem autonomia para atribuir pesos diferentes às avaliações
parciais, conforme previsto no Plano de Ensino, devendo este, ser apresentado aos
alunos, no início das aulas.
O curso Matemática – Licenciatura não prevê exame final. Será considerado
aprovado o aluno que obtiver média semestral igual ou superior a 6,0 (seis) por
componente curricular e frequência igual ou superior a 75% (setenta e cinco por cento);
Será considerado reprovado o aluno que:
I – não obtiver frequência igual ou superior a 75%;
II – não alcançar a média semestral 6,0 (seis), pois o curso Matemática Licenciatura não prevê exame final.
É dever do professor apresentar ao aluno o resultado das avaliações parciais
no máximo, até 15 (quinze) dias após a sua realização.
Aos alunos que ingressaram entre 2010 e 2013, para as disciplinas que serão
cursadas na fase regular correspondente fica assegurado o sistema anterior em que
considerar-se-á aprovado em cada disciplina, o aluno que tiver frequência igual ou
superior a 75% (setenta e cinco por cento) e média semestral (MS) igual ou superior a
7,0 (sete inteiros).
Caso o aluno tiver frequência igual ou superior a 75% (setenta e cinco por cento)
mas não atinja o valor de média acima estabelecida o aluno será submetido a uma
nova prova (exame final). O aluno será aprovado caso atingir, no mínimo, média
aritmética (entre a média semestral e nota do exame final) igual ou superior a 5,0
(cinco inteiros).
33
Caso o aluno reprove e venha a cursar com outra turma deverá adequar-se a
nova sistemática de nota superior a 6,0 (seis inteiros) na disciplina sem direito ao
exame final.
A regulamentação completa da organização acadêmica, em geral, e da
avaliação, em particular, está materializada na “Organização Acadêmica dos Cursos de
Graduação do Instituto Federal Catarinense”.
19. CORPO DOCENTE
19.1. QUADRO DE DOCENTES
Quadro 7. Relação de Docentes e Formação Profissional.
Nome
Angelisa
Benetti
Clebsch
Emerson
Bianchini
Estivalete
Área de
conhecime
nto
40
Maior
Titulação
Concluída
Curriculum
Lattes
(link)
DE
X
Licenciatura
em Física
Mestrado
http://lattes.cnpq.br/70118
71290957566
História
X
Licenciatura
Plena
Especializaç
ão
http://lattes.cnpq.br/15043
13415692578
Bacharelado
em
Computação
Doutorado
http://lattes.cnpq.br/08278
93111042699
X
Licenciatura
em Ciências
com
habilitação em
Matemática
Mestrado
http://lattes.cnpq.br/29283
50526317146
X
Licenciatura
em
Matemática
Mestrado
http://lattes.cnpq.br/16672
57631243863
X
Bacharelado
em
Meteorologia
Doutorado
http://lattes.cnpq.br/64715
28381313886
Ciências
Exatas e da
Terra
Fatima Peres
Zago de
Oliveira
Ciências
Exatas e da
Terra
Leonardo de
Oliveira Neves
20
Formação
Acadêmica
Ciências
Exatas e da
Terra
Fabio
Alexandrini
Gilberto
Mazoco Jubini
Regime de
trabalho
(horas)
Ciências
Exatas e da
Terra
Ciências
Exatas e da
Terra
X
Liane Vizzotto
Educação
X
Pedagogia
Mestrado
http://lattes.cnpq.br/47350
83599333817
Luiz Fernando
Nazari
Ciências
Exatas e da
Terra
X
Licenciatura
em
Matemática
Mestrado
http://lattes.cnpq.br/83572
51043633484
Educação
X
Bacharelado
em Pedagogia
Especial
Especializaç
ão
http://lattes.cnpq.br/54098
02568530188
X
Licenciatura
em Ciências
Mestrado
http://lattes.cnpq.br/80128
42011752315
X
Licenciatura
em Ciências
Agrícolas
Mestrado
http://lattes.cnpq.br/46329
25979334196
X
Bacharelado
em
Matemática
Mestrado
http://lattes.cnpq.br/77769
82904929456
Marines Dias
Gonçalves
Marizoli
Regueira
Schneider
Moacir Gubert
Tavares
Morgana
Scheller
Ciências
Exatas e da
Terra
Ciências
Agrárias
Ciências
Exatas e da
Terra
34
Orlando
Cristofolini
Educação
X
Licenciaturae
m Letras
Especializaç
ão
http://lattes.cnpq.br/72448
54055447485
Otávio
Bocheco
Ciências
Exatas e da
Terra
X
Licenciatura
em Física
Mestrado
http://lattes.cnpq.br/14245
02743423069
Paula Andrea
Grawieski
Civiero
Ciências
Exatas e da
Terra
X
Mestrado
http://lattes.cnpq.br/66177
01172635064
Paulo César
Rodacki
Gomes
Ciências
Exatas e da
Terra
X
Doutorado
http://lattes.cnpq.br/91362
62673186413
Ricardo
Scopel Velho
Solange
Aparecida de
Oliveira
Hoeller
Ciências
Sociais
X
Mestrado
http://lattes.cnpq.br/72180
39580141052
Educação
X
Mestrado
http://lattes.cnpq.br/65079
66351170581
Licenciatura
em Ciências
com
habilitação em
Matemática
Bacharelado
em
Engenharia
Civil
Licenciatura
Ciências
Sociais
Pedagogia
19.2. NÚCLEO DOCENTE ESTRUTURANTE
O Núcleo Docente Estruturante (NDE) é o conjunto de professores, de elevada
formação e titulação, contratados em tempo integral e parcial, que respondem mais
diretamente pela criação, implantação e consolidação do Projeto Pedagógico do Curso.
Cada curso em cada câmpus possui seu NDE, composto pelos seguintes
membros:
I - Coordenador do Curso, que coordenará o NDE;
II - por um mínimo de 5 (cinco) professores pertencentes ao corpo docente do
curso;
III - ter pelo menos 60% de seus membros com titulação acadêmica obtida em
programas de pós-graduação stricto sensu;
IV - ter todos seus membros em regime de trabalho de tempo parcial ou integral,
sendo pelo menos 20% em tempo integral.
§1º. O NDE poderá ser assessorado por um técnico administrativo em educação
da área pedagógica ou NUPE, que deverá ser indicado pelos NDE.
As competências do NDE são:
a) Elaborar, implantar, supervisionar e consolidar o Projeto Pedagógico do
Curso em consonância com as Diretrizes Curriculares Nacionais (DCN), o Plano de
Desenvolvimento Institucional (PDI) e Projeto Político-Pedagógico Institucional (PPI) do
Instituto Federal Catarinense;
35
b) Acompanhar todo processo didático-pedagógico, analisando os resultados do
processo de ensino aprendizagem, observando o Projeto Pedagógico do Curso;
c) Manter atualizadas as ementas, os conteúdos e as referências das
disciplinas, em consonância com as Diretrizes Curriculares Nacionais (DCN);
d) Normatizar o desenvolvimento das atividades acadêmicas;
e) Acompanhar o processo do Exame Nacional de Desempenho de Estudantes
(ENADE) e propor ações que garantam um nível de avaliação adequado ao Ministério
da Educação (MEC) e IFC;
f)
Participar
e
motivar
grupos
de
pesquisa,
extensão
e
atividades
interdisciplinares;
g) Orientar e participar da produção de material científico ou didático para
publicação;
h) Contribuir para a definição das linhas de pesquisa do curso, respeitando-se o
PDI e PPI.
Quadro 8. Integrantes do Núcleo Docente Estruturante
Nome
Fátima Peres Zago de
Oliveira
Paula Andrea Grawieski
Civiero
Leonardo de Oliveira Neves
Luiz Fernando Nazari
Solange Aparecida de
Oliveira Hoeller
Otavio Bocheco
Gilberto Mazoco Jubini
Formação Acadêmica
Maior Titulação
Matemática
Mestrado
Matemática
Mestrado
Meteorologista
Matemática
Doutorado
Mestrado
Pedagogia
Mestrado
Física
Matemática
Mestrado
Mestrado
36
20. CORPO TÉCNICO ADMINISTRATIVO
Quadro 9. Relação de cargo e regime de trabalho do corpo Técnico Administrativo do
Campus Rio do Sul do Instituto Federal Catarinense.
Nome
Maior
Titulação
Adelar Benetti
Andressa Graziele Brandt
Caroline da Rosa F. Becker
Especialização
Especialização
Mestrado
Clóvis Cristiano Brignoli
Graduação
Eliane Ap. de Amorim
Dockhorn
Eurico da P. Pittaluga Neto
Especialização
Fabiano F. Maciel Guimarães
Graduação
Izolde Rejane do Carmo
Jorge Luis Araújo dos Santos
Graduação
Especialização
Katia Regina Koerich Fronza
Mestrado
Marisa Etel Maas
Maurício Machado
Nilton Segundo
Rogério Krause
Graduação
Ensino Médio
Graduação
Mestrado
Sandra Leticia Graf Ferreira
Especialização
Ensino Médio
Cargo/Função
Assistente em Administração
Supervisora Educacional
Bibliotecária
Técnico de Tecn. da
Informação
Operadora de Máquina
Copiadora
Tecnólogo em Cooperativismo
Analista de Tec. da
Informação
Auxiliar de Biblioteca
Psicólogo
Téc. em Assuntos
Educacionais
Técnico em Secretariado
Auxiliar em Eletricidade
Assistente em Administração
Assistente em Administração
Téc. em Assuntos
Educacionais
Carga
horária
40 h
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
21. ATIVIDADES ACADÊMICAS
21.1 ATIVIDADES ACADÊMICAS COMPLEMENTARES
As atividades acadêmicas complementares são de livre escolha do licenciando
e, portanto, atendem necessidades de interesses específicos durante o processo de
sua formação. O licenciado deverá estar apto a compreender e traduzir as
necessidades de indivíduos, grupos sociais e comunidades, com relação aos
problemas tecnológicos, sócio-econômico-ambientais e do processo de ensino
aprendizagem, sendo que as atividades acadêmicas terão fundamental importância
neste processo.
As atividades acadêmicas científicas e culturais serão desenvolvidas ao longo
do curso, envolvendo atividades de ensino, pesquisa e extensão, e são normatizadas
37
de acordo com a Resolução nº 48 de 17/12/2010 do IF Catarinense que dispõe sobre o
regulamento das Atividades Curriculares Complementares.
Para concretização desde conjunto de atividades no currículo, faz-se necessário
a apresentação das cópias dos certificados ou documentos comprobatórios. O
processo de validação ocorrerá após a análise do requerimento destinado ao
Coordenador de Curso, através do Protocolo Acadêmico.
As seguintes condições devem ser observadas:
a) As atividades são realizadas durante o período de vinculação do aluno ao curso;
b) As atividades afins ( humanísticas e profissional) à área de formação do Licenciado;
c) As solicitações devem ser encaminhadas até dois meses antes da conclusão do
curso;
d) Cada documento comprobatório que se enquadre em mais de um tipo de atividade
poderá ser validado uma única vez;
e) Outras atividades desenvolvidas pelos acadêmicos poderão ser consideradas de
formação complementar a critério do NDE;
f) Atividades complementares de Representação Estudantil de Extensão e de
Pesquisa.
21.2. ATIVIDADES DE MONITORIA
O Curso de Licenciatura em Matemática prevê a monitoria como uma atividade
de complementação e aprofundamento dos conteúdos e das ações de formação de
seu aluno e seguirá as normas já existentes no Regulamento da Instituição.
A atividade de monitoria visa atender os seguintes objetivos:
I - Propiciar ao acadêmico a oportunidade de desenvolver e compartilhar suas
habilidades e competências para a carreira docente nas funções de ensino;
38
II - Assegurar a cooperação didática entre o corpo docente e discente nas
funções universitárias;
III
-
Oferecer
aos
acadêmicos
oportunidades
de
complementação
e
aprofundamento de conteúdos e estratégias de ensino nas diversas disciplinas.
IV – Contribuir para a formação complementar do acadêmico.
A atividade de monitoria é exercida por acadêmico regularmente matriculado,
durante o período letivo e de acordo com as normas específicas de cada modalidade
citada em regulamento próprio.
Cabe ao professor da disciplina, solicitar o auxílio de monitor mediante projeto
de monitoria para a respectiva disciplina a ser encaminhado ao Coordenador do Curso.
Em todas as modalidades, após o cumprimento do programa de monitoria, o
monitor receberá um certificado emitido pela secretaria acadêmica do referido câmpus
do Instituto Federal Catarinense se aprovado na avaliação.
O Câmpus poderá oferecer aos seus acadêmicos a modalidade de monitoria
com bolsa auxílio em disciplinas já cursadas pelo acadêmico. Nesta modalidade, o
acadêmico monitor recebe ajuda de custo, fixada em proposta apresentada pela
Direção Geral, durante o período em que estiver realizando esta atividade.
Para candidatar-se a esta modalidade o acadêmico deve: comprovar a
aprovação na disciplina, com nota mínima de 6.0 (seis) através do histórico escolar; ser
indicado, após selecionado em teste classificatório específico, a ser proposto e
aplicado por comissão especialmente designada para este fim, segundo critérios e
procedimentos estabelecidos em Edital. Caberá ao Coordenador do Curso referendar e
homologar a classificação indicada pela comissão.
O programa de monitoria com bolsa auxílio, indicando o número de bolsas e
respectivos valores, poderá ser proposto anualmente pela Reitoria do Instituto.
São atribuições do monitor: auxiliar o docente nas atividades didático–
pedagógicas; atendimento e orientação de alunos, em períodos por ele já cursados;
atender pequenos grupos em horários que não coincidam com os seus horários de
aula. É importante salientar que fica evidente no regulamento que é vedado ao Monitor
elaborar, aplicar ou corrigir provas, ministrar aulas como substituto ou outras funções
exclusivamente docentes.
39
Em relação ao regime de trabalho o programa de monitoria não implica em
nenhum tipo de relação empregatícia entre o aluno e a Instituição. O monitor exerce
suas atividades sob orientação de professor responsável que zelará pelo fiel
cumprimento das atividades previstas. O horário das atividades do Monitor não pode,
em hipótese alguma, prejudicar as atividades discentes e será fixado no ato de
designação, a carga horária compatível com as funções e atividades a serem
desempenhadas. As atividades de monitoria terão no mínimo 4 horas semanais e no
máximo 20 horas semanais. As atividades do Monitor obedecem, em cada semestre,
ao projeto elaborado pelo professor, aprovado pelo Coordenador do Curso nas duas
modalidades.
Para divulgação e supervisão das monitorias, o edital para seleção de monitores
na modalidade de bolsa auxílio em disciplinas já cursadas deverá constar
obrigatoriamente: os critérios para seleção dos monitores; os planos de trabalho do
programa de monitoria; os mecanismos de acompanhamento e avaliação pelo
professor supervisor do trabalho do monitor; a forma de controle do encaminhamento
da frequência dos monitores.
As atividades de monitoria serão regulamentadas por meio de normatização a
ser elaborada pelo IFC.
22. ESTÁGIO CURRICULAR
22.1. OPERACIONALIZAÇÃO DO ESTÁGIO CURRICULAR
Como o curso de Matemática-Licenciatura objetiva a preparação do acadêmico
para a prática docente, o estágio supervisionado será desenvolvido dentro de uma
nova perspectiva, cujo enfoque principal é a pesquisa em ensino de Matemática,
integrado com a atuação docente do acadêmico.
O estágio supervisionado do curso de Matemática-Licenciatura terá carga
horária de 420 horas e será parte integrante do currículo do curso (obrigatório), sendo
realizado a partir do quinto semestre, visando assegurar o contato do aluno com
situações, contextos e instituições de ensino, permitindo que conhecimentos,
habilidades e atitudes se concretizem em ações profissionais reais, servindo de
experiência para um melhor exercício de sua profissão.
40
O estágio obedecerá ao disposto nas Diretrizes Curriculares Nacionais,
Resolução CNE/CP 2, de 19 de fevereiro de 2002, na Lei N o. 11.788, de 25 de
setembro de 2008, no Regimento Geral de Estágios do Instituto Federal Catarinense
(Anexo 1) e no Regulamento de Estágio do Curso de Matemática-Licenciatura.(A 2)
O estágio supervisionado é instância privilegiada que permite a articulação entre
o estudo teórico e os saberes práticos e tem como propósito a inserção do futuro
Licenciado em Matemática no mundo do trabalho das instituições de ensino. Neste
sentido, se apresentam como finalidades básicas, as seguintes proposições:
a) Complementar o ensino-aprendizagem a partir do contato com a realidade
das escolas;
b) Inserir o futuro educador à realidade educacional brasileira;
c) Avaliar a prática pedagógica como educador em construção;
d) Possibilitar uma prática que integre o saber popular e o científico.
22.2. ORIENTAÇÃO DE ESTÁGIO CURRICULAR
O estágio supervisionado da Matemática - Licenciatura será realizado em 04
(quatro) etapas:
1ª. Etapa: Estágio Supervisionado I - 60h – consiste na observação, em
escolas e turmas das séries finais do ensino fundamental, acompanhado de estudo,
análise e reflexão crítica do projeto pedagógico da escola e do plano de ensino de
matemática. Nos encontros realizados durante o semestre, entre outras atividades,
haverá a elaboração de um pré-projeto de prática da docência.
2ª. Etapa: Estágio Supervisionado II - 150h – Nesta etapa o acadêmico
solidifica os conhecimentos teóricos adquiridos ao longo do curso e concretiza
habilidades profissionais no decorrer da própria atuação docente. Acontecerá a
conclusão do pré-projeto e a organização do projeto com a preparação para a
respectiva aplicação, caracterizando-se em estágio de docência nas séries finais do
ensino fundamental. Ao final deste estágio será elaborado um relatório final que deverá
ser apresentado em Seminário.
41
3ª. Etapa: Estágio Supervisionado III - 60h – consiste na observação, em
escolas e turmas do ensino médio, acompanhado de estudo, análise e reflexão crítica
do projeto pedagógico da escola e do plano de ensino de matemática. Nos encontros
realizados durante o semestre, entre outras atividades, haverá a elaboração de um
pré-projeto de prática da docência.
4ª. Etapa: Estágio Supervisionado IV - 150h – Nesta etapa o acadêmico
solidifica os conhecimentos teóricos adquiridos ao longo do curso e concretiza
habilidades profissionais no decorrer da própria atuação docente. É a conclusão do
pré-projeto e organização do projeto com a respectiva aplicação, caracterizando em
estágio de docência no ensino médio. Ao final deste estágio será elaborado um
relatório final e artigo, que deverão ser apresentado em Socialização.
A primeira e terceira etapas do Estágio Supervisionado do curso de MatemáticaLicenciatura têm como objetivo a análise reflexiva da prática, por meio de observação
em salas de aula de matemática do Ensino Fundamental – séries finais e
posteriormente do ensino médio.
Na segunda e quarta etapas do Estágio Supervisionado serão dadas ênfase à
prática, por meio da aplicação de formas de organização didática no ensino
fundamental – séries finais e no ensino médio.
A Prática de Ensino do curso de Matemática- Licenciatura constituirá, portanto,
um espaço de aprofundamento teórico e prático de diferentes aspectos da educação
matemática que se completa com a realização do estágio.
O estudante deverá concluir o estágio no prazo máximo (8 anos) de conclusão
do curso.
A regulamentação dos estágios será organizada e aprovada pelo NDE de curso,
contendo as diferentes modalidades de operacionalização, formas de apresentação e
avaliação de relatórios finais e/ou artigo com acompanhamento individualizado,
inclusive durante a fase de realização e ao final do mesmo.
22.3. SISTEMA DE AVALIAÇÃO DO ESTÁGIO CURRICULAR
A avaliação dar-se-á em cada etapa conforme elaboração de critérios
especificados no Regulamento de Estágio da Matemática – Licenciatura (A2).
42
23. ESTÁGIO NÃO OBRIGATÓRIO (Lei 11.788 de 25 de setembro de 2008)
Além do estágio supervisionado obrigatório, o aluno poderá realizar estágio
extracurricular em qualquer período do curso, desde que seguidas as normas
institucionais e regulamentares do IF Catarinense e do câmpus onde o curso está
sendo oferecido.
24. PESQUISA E EXTENSÃO
A articulação dos processos de Ensino, Extensão e Pesquisa, é fundamental na
consolidação dos Institutos Federais. O curso de Matemática- Licenciatura pode
desempenhar um papel importante na consolidação dessa articulação. Além disso,
existe a necessidade dos professores participarem da produção dos currículos que
desenvolvem em suas salas de aula, como importante condição da sua formação
continuada.
Por isso, a criação de espaços interativos de articulação entre os Institutos
Federais de Educação, Ciência e Tecnologia e as escolas de educação básica,
constituindo grupos que envolvem professores das licenciaturas, licenciandos,
professores e estudantes da escola básica, podem possibilitar ganhos recíprocos: os
conhecimentos profissionais dos professores de escola enriquecem o currículo de
formação dos novos professores e os estudos acadêmicos e pesquisas sobre o
currículo enriquecem a formação dos professores em serviço.
As atividades de pesquisa e extensão estão regulamentadas pelas Resoluções
nº 005/2010 e Resolução 002/2011, contemplando programas para concessão de
bolsa de Iniciação Científica e de Extensão do IF Catarinense.
24.1. LINHAS DA PESQUISA
As linhas de pesquisa seguirão a política institucional em consonância aos
princípios e às peculiaridades do PDI e PPI do IFC e do Câmpus.
Estas, por sua vez, serão definidas ao longo do processo de acordo com as
necessidades dos projetos apresentados pelos docentes e discentes que farão os
grupos de pesquisas que atendem as grandes áreas do CNPq.
43
24.2. AÇÕES DE EXTENSÃO
A extensão nos cursos de Licenciatura do IFC deve estar articulada ao ensino e
à pesquisa e é compreendida como um processo eminentemente educativo, cultural,
técnico-científico e pedagógico. A mesma deverá ser desenvolvida por meio de
programas, projetos e ações em consonância com o PDI do IFC e dos câmpus.
O curso de Matemática-Licenciatura desenvolverá a extensão por meio de:

Programas – Ações continuadas/permanentes em estreita relação com o
ensino e a pesquisa, no intuito de estabelecer vínculos e compromissos com os
processos educativos regional;

Projetos – Ações desencadeadas dos programas (formação continuada,
assessoria pedagógica e técnica);

Ações – Ações eventuais de curta duração articuladas aos programas ou
projetos (palestras, seminários, congressos, semanas acadêmicas e demais eventos
desta natureza).
Os princípios orientadores:

A indissociabilidade entre ensino, pesquisa e extensão;

A inserção social/regional com vistas a educação de qualidade social;

O processo de diálogo e interação entre instituição formadora e
sociedade.
Os programas, projetos e ações do curso de Matemática-Licenciatura serão
propostos e normatizados pelo NDE de curso, tendo como preocupação a relevância
social, regional, cultural, pedagógica, metodológica e epistemológica.
25. CERTIFICAÇÃO E DIPLOMA
A emissão de certificados e diplomas ficará a cargo da Reitoria do Instituto
Federal Catarinense. Aos câmpus, caberá o controle da vida acadêmica do aluno, a
oferta de cursos extraclasse e de extensão, sua organização e controle.
44
Ao aluno concluinte do Curso Matemática - Licenciatura em todas as suas
etapas previstas na matriz curricular será concedido diploma com o título de
Matemática - Licenciatura.
Enquanto o diploma não for expedido definitivamente, o aluno concluinte poderá
requerer certificado de conclusão de curso.
A diplomação é o ato de emissão do documento oficial do Instituto Federal
Catarinense, que certifica a conclusão de curso de graduação e confere grau ao
formado. Sua aplicação é efetivada com aluno regular que tenha integralizado o
currículo do respectivo curso.
Pontos fundamentais:
• O diploma registrado confere ao seu titular todos os direitos e prerrogativas
reservados ao exercício profissional da carreira de nível superior;
• Para solicitar emissão/registro de diploma, o aluno deverá ter sido previamente
identificado pela Coordenação de Registros Escolares como provável formando do
período;
• A “Relação de Prováveis Formandos do Período” será afixada em mural da
Coordenação de Registros Escolares e no site da Instituição;
• A Coordenação de Registros Escolares fará a integralização curricular do aluno
considerando os registros que constam do “Histórico Escolar” e do “Histórico do
Período”, e confrontando-os com o currículo do curso e o período de acompanhamento
curricular;
• O aluno que se julgar na condição de provável formando e não tiver sido
identificado pela Coordenação de Registros Escolares deverá procurar o Departamento
de Desenvolvimento Educacional para verificação das pertinências de conclusão do
curso;
• A habilitação concluída será averbada no verso do Diploma;
• O aluno DCS (Portador de Diploma de Curso Superior) que estiver concluindo
nova habilitação do mesmo curso e grau anteriormente obtido deverá solicitar apenas
Registro/Averbação de Habilitação;
• A emissão de 2ª via do diploma dar-se-á com ônus para o solicitante;
• Para a entrega do diploma, o aluno concluinte estará sujeito às seguintes
condições: não ter débito junto à Biblioteca, Coordenação-Geral de Assistência ao
45
Educando, Laboratórios e órgãos que emprestem materiais/equipamentos; não ter
débito de documentação junto à Coordenação de Registros Escolares, como: Carteira
de Identidade, Título de Eleitor e comprovante de votação, Certificado de conclusão do
2º grau ou documento equivalente, Histórico Escolar do Ensino Médio ou documento
equivalente, Certificado de Alistamento Militar e Guia de Transferência (se for o caso);
bem como ter participado da solenidade de outorga de grau;
• Os dados de Diplomação constarão do “Livro de Registro de Diplomas”, de
periodicidade semestral.
• O aluno receberá o diploma junto à Coordenação de Registros Escolares, no
período estabelecido no calendário da Instituição, após verificação da “Ata de Outorga
de Grau”.
26. INFRAESTRURA
26.1. ESTRUTURA FÍSICA E RECURSOS PEDAGÓGICOS NO CÂMPUS
A infraestrutura física do curso está em acordo com os Referenciais Curriculares
Nacionais dos Cursos de Bacharelado e Licenciatura (BRASIL, 2010)
Os equipamentos, laboratórios e recursos disponíveis nos Câmpus estão
descritos nas tabelas abaixo, e poderão ser utilizados por todos os alunos dos cursos
oferecidos pela Instituição.
Quadro 10. Recursos didáticos pedagógicos existentes no Câmpus Rio do Sul –
Unidade Urbana
Equipamentos
Quant.
Microcomputadores
60
Projetor Multimídia
20
Impressoras
4
Pontos de Acesso a Rede
2
Quadro 11. Estrutura Física do Câmpus Rio do Sul – Unidade Urbana
AMBIENTE
Salas de Aula
Laboratórios
Biblioteca
Auditórios
Administrativos
Nº
13
05
01
01
01
46
Atendimento ao Aluno*
Serviços Gerais
01
01
A Instituição conta atualmente com 7 (seis) laboratórios: cinco de informática e
um de matemática e um de física, todos equipados e em condições de funcionamento
para fins didáticos e de pesquisa.
O Laboratório de Educação Matemática será ao mesmo tempo lugar de criação
e ensino, dando suporte às aulas dos cursos e a extensões para grupos de professores
e escolas da rede escolar. Este laboratório é um espaço com diversos recursos
pedagógicos, equipado com materiais didáticos e materiais confeccionados pelos
professores e pelos alunos do curso de Matemática-Licenciatura, utilizado nos
componentes curriculares de práticas para o ensino e em componentes curriculares
específicos do curso.
26.2. DESCRIÇÃO DA BIBLIOTECA E ACERVO BIBLIOGRÁFICO
A Biblioteca do Instituto Federal Catarinense - Câmpus Rio do Sul, unidade
Urbana, dispõe de uma área de aproximadamente 40 m2, com capacidade de
atendimento de 50 usuários por turno (matutino, vespertino e noturno). Conta com uma
equipe de 4 (quatro) servidores, sendo 3 (três) efetivos e 1 (um) temporário,
responsáveis pela atuação junto a organização e administração da biblioteca, seleção
e aquisição de obras em geral, conservação de acervo, estatísticas e relatórios. A
Biblioteca mantém-se em funcionamento de segunda a sexta, nos três turnos, das 08
horas às 22 horas sem fechar ao meio-dia.
O ambiente climatizado proporciona aos usuários conforto e bem estar além
de garantir de forma segura a conservação do acervo, evitando assim a depredação
das obras por agentes físicos.
A biblioteca possui espaço para uso de notebook facilitando o acesso do
usuário a informação, uma vez que o prédio da Biblioteca encontra-se equipado com
um moderno sistema de internet sem fio (rede integrada wireless).
A Biblioteca da unidade urbana conta com um acervo de mais de 1069 (Hum
mil e sessenta e nove) títulos e 2951 (dois mil novecentos e cinquenta e um)
exemplares, além de possuir 2 computadores destinados à pesquisa.
47
Quadro 12. Relação de títulos e exemplares existentes no acervo bibliográfico
Área de conhecimento
Título
Exemplar
Ciências exatas e da terra
386
1592
Ciências Biológicas
2
3
Engenharia
37
193
Ciências sociais Aplicadas
37
91
Ciências Humanas
339
647
Linguística – Letras
268
425
TOTAL
1069
2951
27. CONSIDERAÇÕES FINAIS
Este Projeto é o resultado da construção coletiva de professores, técnicos
administrativos e alunos, no que se refere às dimensões que fundamentam a
educação, o político e o pedagógico, de um determinado período histórico. Neste
sentido, se pensou o político e o pedagógico sempre interligados dialeticamente, com
vistas a uma educação que reflita as condições em que vivem os atores do processo
educativo, do curso de Licenciatura em Matemática, e a partir disto promover a
melhoria das condições sociais da comunidade onde se insere o curso.
Por fim,
salienta-se que este projeto não está pronto e acabado, já que o mesmo reflete o
começo do curso de Matemática-Licenciatura no Instituto Federal Catarinense. Assim,
novas mudanças poderão acontecer ao longo do processo, pois o saber é um fazer
cotidiano que é sempre dinâmico, provisório e inconcluso.
REFERÊNCIAS
ALARCÃO, I. Professor-investigador: Que sentido? Que formação? In: B. P. Campos
(Ed). Formação profissional de professores no ensino superior (Vol.1, pp. 2131). Porto: Porto Editora. 2001.
BRASIL. Ministério da Educação - Secretaria da Educação Fundamental. Parâmetros
curriculares nacionais: matemática. Brasília: MEC/SEF, 1997.
BRASIL. Educação Profissional: referenciais curriculares nacionais da educação
profissional de nível técnico. Ministério da Educação. Brasília: MEC, 2000.
48
BRASIL. Diretrizes curriculares nacionais para formação de professores da educação
básica, em nível superior, curso de licenciatura, de graduação plena. Brasília:
Ministério da Educação, 2001.
BRASIL. Ministério da Educação. Secretaria de Educação Profissional e Tecnológica.
Educação profissional e tecnológica: legislação básica. 6.ed. Brasília: Secretaria
de Educação Profissional e Tecnológica, 2005.
BRASIL. Decreto-lei no 73/99/M. Publicada no BO no 44/1999 em 1 de novembro de
1999, p. 4684. < http://bo.io.gov.mo/bo/i/99/44/declei73.asp> acesso em
02/07/2008.
BRASIL. Referenciais Curriculares Nacionais dos Cursos de Bacharelado e
Licenciatura Ministério da Educação. Brasília: MEC, 2010.
BRASIL. Educação Superior: referenciais curriculares nacionais dos Cursos de
Bacharelado e Licenciatura. Ministério da Educação. Brasília: MEC, 2010.
BRASIL. Ministério da Educação. Contribuições para o processo de construção
dos cursos de Licenciatura dos Institutos Federais de Educação, Ciência e
Tecnologia. Brasília, 2008. Disponível em http://portal.mec.gov.br/dmdocuments/
licenciatura_05.pdf, acessado em 13-06-2009.
CANDAU, Vera Maria & LELIS, Isabel Alice. A relação teoria-prática na formação do
educador. In: CANDAU. Vera Maria. Rumo a uma nova didática. 7. ed. Petrópolis
(RJ): Vozes, 1995. p. 49-63.
FIORENTINI, Dario. Alguns modos de ver e conceber o ensino da matemática no
Brasil. In: Ver. Zetetiké. 3(4): 1-37. Campinas, CEMPEM/FE – UNICAMP, 1995.
INSTITUTO DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA CATARINENSE. Plano de
desenvolvimento institucional-PDI. Blumenau: Instituto Federal Catarinense,
maio 2009.
INSTITUTO DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA CATARINENSE. Projeto
Político-Pedagógico Institucional-PPI. Blumenau: Instituto Federal Catarinense,
maio 2009.
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA CATARINENSE
CAMPUS RIO DO SUL - SC. Organização didática da EAFRS. Rio do Sul, SC:
2009.
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA CATARINENSE
CAMPUS RIO DO SUL - SC. Regulamentação de estágio do Instituo Federal
Catarinense, campus Rio do Sul. Rio do Sul, SC: 2009.
LOPES, Alice C. Políticas de Currículo: Mediação por Grupos Disciplinares de Ensino
de Ciências e Matemática. In LOPES & MACEDO (orgs) Currículo de Ciências em
Debate. Campinas-SP: Papirus, 2004.
PIMENTA, S. G.; LIMA, M. S. L. Estágio e docência. 2. ed. São Paulo: Cortez, 2004.
49
PIRES, C.M.C. Reflexões sobre os cursos de Matemática, tomando como
referência as orientações propostas nas Diretrizes Curriculares Nacionais
para a formação de professores da Educação Básica. Educação Matemática em
Revista, São Paulo, SBEM, v. 11A, p. 44-56, abril, 2002.
PONTE, João P. da. Investigações matemáticas na sala de aula. Autêntica, Belo
Horizonte,2003.
UNIVERSIDADE FEDERAL DE MINAS GERAIS. Revista da Universidade Federal
de Minas Gerais. Ano 3 - nº. 7 - Julho de 2005 - Edição Vestibular.
<http://www.ufmg.br/diversa/7/mundouniversitario.htm> acesso em 02/06/2008.
50
APÊNDICES
A1 - Programa das Disciplinas Obrigatórias
O desenvolvimento das aulas, disciplinas e avaliação deverá contar com
metodologias diversificadas (projetos, modelagem, modelação, resolução de
problemas, jogos, oficinas, seminários); além da utilização do laboratório de Educação
Matemática e de softwares.
1° Semestre
Matemática Fundamental I - 90h
Ementa: Conceitos matemáticos do Ensino Fundamental e Médio: Sistema de
numeração. Regra de Três. Conjuntos numéricos. Relações. Equação e Função de 1º
grau. Equação e Função do 2º grau. Equação e Função modular. Equação e Função
Exponencial. Equação e Função Logarítmica. Relações trigonométricas, Equação e
Função Trigonométricas. História da Matemática relacionada ao conteúdo.
Bibliografia Básica
DEMANA, F. D. et al. Pré-Cálculo.Tradução técnica Eliana Crepaldi Yazawa e Aldy
Fernandes da Silva. São Paulo: Addison Wesley, 2009.
IEZZI, G.; DOLCE, O.; MURAKAMI, C. Fundamentos da Matemática Elementar:
logaritmos. São Paulo: Atual, 1996.
IEZZI, G. Fundamentos da Matemática Elementar: Trigonometria . Vol.4. São Paulo:
Atual, 2004.
Bibliografia Complementar
BOULOS, Paulo. Pré-cálculo. São Paulo: Pearson Makron Books, 2001.
DANTE, Luiz Roberto. Matemática: contexto e aplicações. Volume Único. 3.ed. São
Paulo: Ática, 2010.
FLORIANI, Valdir. Função Logarítmica. Blumenau: Ed. da Furb, 1999.
IEZZI, G. Trigonometria. São Paulo: Atual, 2000. v. 3.
LDSTEIN, Larry J. LAY, David C.; SCHNEIDER, David I. Matemática Aplicada:
Economia, Administração e Contabilidade. 10. ed. Porto Alegre: Bookmann, 2006.
Metodologia científica - 30h
Ementa: Ciência e conhecimento. Ciência e método científico. A pesquisa científica:
método, organização e orientação. Redação e Difusão do conhecimento científico.
Bibliografia Básica
LAKATOS, E. M.; MARCONI, M. de A. Fundamentos de metodologia científica. 6.
ed. São Paulo: Atlas, 2005.
PIMENTA, S. G. Metodologia do trabalho científico. São Paulo: Atlas, 2007.
SEVERINO, Antonio Joaquim. Metodologia do trabalho científico. 23. ed. São Paulo:
51
Cortez, 2007.
Bibliografia Complementar
BOOTH, W. C. (et all). A arte da pesquisa. 2. ed. São Paulo: Martins Fontes, 2005.
(número de chamada: 001.42 B725a)
PIMENTA, S. G. Metodologia científica. São Paulo: Atlas, 1991.
PESCUMA, D.; CASTILHO, A. P. F. de. Trabalho acadêmico - o que é? como fazer?:
um guia para suas apresentações. São Paulo: Olho d´Água, 2005.
PESCUMA, D.; CASTILHO, A. P. F. Projeto de pesquisa - o que é? como fazer?: um
guia para sua elaboração. São Paulo: Olho d´Água, 2005.
RAMPAZZO, Lino. Metodologia Científica. 3.ed. São Paulo: Loyola, 2005.
História da Educação - 60h
Ementa: A educação nas diversas épocas. O contexto histórico-social, político e
econômico da educação brasileira. História da educação de Santa Catarina. A história
da escola no contexto histórico brasileiro.
Bibliografia Básica
ARANHA, Maria Lúcia de Arruda. História da educação e da pedagogia: geral e
Brasil. 3.ed.rev. e ampl. São Paulo: Moderna, 2006.
CAMBI, F. História da pedagogia. Tradução de Álvaro Lorencini. São Paulo:
Fundação Editora da UNESP (FEU), 1999.
GADOTTI, M. História das Idéias Pedagógicas. São Paulo: Ática, 2010.
Bibliografia Complementar
D’AMBRÓSIO, U. Da realidade à ação. São Paulo: Papirus, 1986.
FREIRE, P. Pedagogia da esperança: um reencontro com a pedagogia do oprimido.
8. ed. Rio de Janeiro: Paz e Terra, 2009.
FREIRE, P. Pedagogia da Autonomia. São Paulo: Paz e Terra, 2010.
HILSDORF, M. L. S. História da educação brasileira: leituras. 2. Reimp. São Paulo:
Thomson-Learning, 2006.
LOPES, Eliane T. e outros, (orgs.) 500 anos de educação no Brasil. Belo Horizonte:
Autêntica, 2000.
Leitura e Produção de Textos - 60h
Ementa: Padrão culto da língua portuguesa. Textos acadêmicos na perspectiva da
metodologia científica. Gêneros textuais acadêmicos: Resenha crítica; artigo científico;
ensaio; resumo. (PPC – prática como componente curricular).
Bibliografia Básica
FIORIN, J. L. As astúcias da enunciação: as categorias de pessoa, espaço e tempo.
2. ed. São Paulo:Ática, 2002.
HOFFNAGEL, J. C.; DIONÍSIO, Â. P.. Gênero, agência e escrita. São Paulo: Cortez,
2006. pp. 59-77.
MACHADO, A. R.; LOUSADA, E.; ABREU-TARDELLI, L. S. (orgs.). Planejar gêneros
52
acadêmicos. São Paulo: Parábola, 2005.
Bibliografia Complementar
ANTUNES, I. Aula de Português: Encontro & interação. São Paulo: Parábola,
Editorial, 2003.
CUNHA, C. F. da. Nova gramática do português contemporâneo. 3. ed. Rio de
Janeiro: Nova Fronteira, 2001.
FIORIN, J. L. As astúcias da enunciação: as categorias de pessoa, espaço e tempo.
2. ed. São Paulo:Ática, 2002.
INFANTE, Ulisses. Do texto ao texto: curso prático de leitura e redação . 5. ed. São
Paulo: Scipione, 1996.
MACHADO, A. R; LOUSADA, E.; ABREU-TARDELLI, L S (orgs.). Resumo. São
Paulo: Parábola, 2004.
Geometria Plana - 60h
Ementa: História da Matemática – Geometria Plana. Noções e Proposições Primitivas.
Segmento de Reta. Ângulos. Paralelismo. Perpendicularidade. Triângulos: conceito elementos – classificação, Congruência de Triângulos; Pontos Notáveis de um
Triângulo; Semelhança de triângulos, Triângulos Retângulos; Triângulos quaisquer.
Quadriláteros Notáveis. Polígonos e seus elementos. Circunferência: ângulos;
comprimento. Círculos. Áreas de figuras Planas. Teorema de Tales. Lugares
geométricos.
Bibliografia Básica
DOLCE, O.; POMPEO, J. N. Fundamentos de matemática elementar: geometria
plana. 7. ed. São Paulo: Atual, 1999.
DANTE, L. R. Matemática. Volume único. São Paulo: Ática, 2005.
EUCLIDES. Os Elementos. Tradução e Introdução de Irineu Bicudo. São Paulo:
Editora UNESP, 2009.
Bibliografia Complementar
BARBOSA, J. L. M. Geometria euclidiana plana. Fortaleza: SBM, 1997.
BEZERRA, M. J. Matemática para o ensino médio. 5.ed. São Paulo: Scipione, 2001.
MARANHÃO, M. C. S. de A . Matemática. São Paulo: Cortez, 1990.
OLIVEIRA, E. C. de. Introdução aos métodos da matemática aplicada. Campinas,
São Paulo: UNICAMP, 1997.
REZENDE, E. Q. F. Geometria Euclidiana plana e construções geométricas, 2. ed.
Unicamp. 2008.
53
2° Semestre
Matemática Fundamental II - 60h
Ementa: Progressões Aritméticas e Geométricas. Números Complexos. Polinômios e
Equações Algébricas. Inequações. Análise Combinatória. História da Matemática
relacionada ao conteúdo.
Bibliografia Básica
ÁVILA, G. Variáveis complexas e aplicações. Rio de Janeiro: LTC,1990.
DEMANA, F.D. et al. Pré-Cálculo.Trad. téc. Eliana Crepaldi Yazawa e Aldy Fernandes
da Silva. São Paulo: Addison Wesley, 2009.
HAZZAN, S. Combinatória e Probabilidade. Fundamentos de Matemática Elementar.
5. ed. São Paulo: Atual, 1993.
Bibliografia Complementar
BOULOS, Paulo. Pré-Cálculo. São Paulo: Pearson Makron Books, 2001.
DANTE, Luiz Roberto. Matemática: contexto e aplicações. Volume Único. 3.ed. São
Paulo: Ática, 2010.
DANTE, Luiz Roberto. Matemática: contexto e aplicações. V. 1. 4. ed. São Paulo:
Ática, 2010.
DANTE, Luiz Roberto. Matemática: contexto e aplicações. V. 2. 4. ed. São Paulo:
Ática, 2010.
IEZZI, G. Fundamentos da Matemática Elementar: complexos, polinômios e
equações. 7.ed. São Paulo: Atual, 2005. V. 6.
Lógica Básica - 30h
Ementa: Cálculo proposicional. Cálculo de predicados. Sistemas Dedutivos. Tabelasverdades e árvores de refutação. Prova de Teoremas.
Bibliografia Básica
ALENCAR, E. Iniciação à Lógica Matemática. São Paulo:Nobel, 2000.
BASTOS, C. L.; KELLER, V. Aprendendo lógica. 5.ed. Petrópolis: Vozes, 1997.
DAGHLIAN, J. Lógica e Álgebra de Boole. 4. ed. São Paulo: Atlas, 1995.
Bibliografia Complementar
ANTON, H.; BIVENS, I.; DAVIS, S. Cálculo. Porto Alegre: Bookman, 2000. v. 1.
ANTON, H.; BIVENS, I.; DAVIS, S. Cálculo. Porto Alegre: Bookman, 2000. v. 2.
COPI, I. Introdução lógica. 2.ed. São Paulo: Mestre Jou, 1978.
FLEMMING, D. M.; GONÇALVES, M. B. Cálculo A e B. Editora Prentice Hall Brasil,
2006.
GUIDORIZZI, H. L. Um curso de cálculo .Rio de Janeiro: LTC, 2001. v. 1.
54
Informática Básica - 60h
Ementa: Conceitos de Matemática Computacional. Máquinas de Estado (Modelo de
Turing). Algoritmos: conceito e especificação. Técnicas de Programação. Estruturas de
Dados. Indução, Iteração e Recursão. Desenvolvimento de aplicações matemáticas.
Bibliografia Básica
MANZANO, André Luiz N. G; MANZANO, Maria Izabel Navarro Garcia. Estudo
dirigido de informática básica. 7. ed. rev. e ampl. São Paulo: Érica, 2010.
RUGGIERO, M. A. G. Cálculo Numérico: aspectos teóricos e computacionais. São
Paulo: MARKRON Books, 1996.
TAJRA, S. F. Informática na educação: novas ferramentas pedagógicas para o
professor na atualidade. 8. ed. rev. e ampl. São Paulo: Editora Érica, 2008.
Bibliografia Complementar
ALBERTIN, A. L. Administração de informática: funções e fatores críticos de
sucesso. 4. ed., atual. e ampl. São Paulo, SP: Atlas, 2002.
ALCALDE, L. E.; GARCIA LOPEZ, Miguel; PEÑUELAS FERNANDEZ, Salvador.
Informática básica. São Paulo: Makron Bocks, 1991.
CORMEN, T. H. Algoritmos e prática. Rio de Janeiro: Elsevier, 2002.
TAJRA, S. Informática na Educação. 7.ed. São Paulo: Érica, 2007.
VELLOSO, F, de C. Informática - conceitos básicos. Rio de Janeiro: Campus, 2002.
Geometria Espacial - 60h
Ementa: História da Matemática - Geometria Espacial. Determinação de Plano.
Posições relativas de planos e retas. Paralelismo e Perpendicularidade. Diedros e
Triedros. Poliedros Convexos. Cilindro, Cone e Esfera. Sólidos Semelhantes: Troncos.
Áreas e Volumes. Representação plana de objetos tridimensionais.
Bibliografia Básica
CARVALHO, P. C. P. Introdução à geometria espacial. Coleção do Professor de
Matemática. SBM, 2005.
DOLCE, O.; POMPEO, J. N. Fundamentos de matemática elementar: geometria
espacial. São Paulo: Atual, 1997.
MONTGOMERY, M.; SHULTE, A. P. (orgs.). Aprendendo e ensinando geometria.
São Paulo: Atual, 1994.
Bibliografia Complementar
FLORES, C. R. Olhar, saber, representar: sobre a representação em perspectiva.
São Paulo: Musa, 2007.
GUIDORIZZI, H. L. Um curso de cálculo .Rio de Janeiro: LTC, 2001. v. 1.
LIMA, E. L. Medida e forma em geometria. Coleção do Professor de Matemática.
SBM, 1991.
POLYA, G. A arte de resolver problemas. trad. de Heitor Lisboa de Araújo. Rio de
Janeiro: Interciência, 1978.
55
WAGNER, E. Construções geométricas. São Paulo: SBM, 1998.
Teorias Educacionais e Curriculares - 60h
Ementa: Teorias educacionais e curriculares e suas relações com as práticas
pedagógicas. Correntes pedagógicas e curriculares. Currículo à luz das diferentes
concepções curriculares. Novos paradigmas teóricos e curriculares.
Bibliografia Básica
COSTA, M. V. (org.). O currículo nos limiares do contemporâneo. Rio de Janeiro:
DP&A, 2001.
FREIRE, P. Política e educação. São Paulo: Cortez, 2000.
SILVA, T, T. Documentos de Identidade: uma introdução às teorias do currículo. Belo
Horizonte: Autêntica, 2003.
Bibliografia Complementar
FREIRE, P. Pedagogia da autonomia. São Paulo: Paz e Terra, 1997.
GADOTTI, M. História das idéias pedagógicas. São Paulo: Ática, 2003.
LOPES, A, C. e MACEDO, E. Currículo: debates contemporâneos. São Paulo: Cortez,
2002. (Série cultura, memória e currículo). v. 2.
VEIGA-NETO, Alfredo. Crítica pós-estruturalista e educação. Porto Alegre: Sulina,
1995.
VIGOTSKY, L. S. A formação social da mente: o desenvolvimento dos processos
psicológicos superiores. 7. ed. São Paulo: Martins Fontes, 2007.
Educação e Mundo do Trabalho - 30h
Ementa: As inter-relações entre Educação e Trabalho. Trabalho e produção capitalista.
Educação e crise. Os movimentos sociais, rural e urbano, a cultura afro-brasileira e a
questão indígena no campo educacional.
Bibliografia Básica
FERRETTI, C. J. (org.). Trabalho, formação e currículo. São Paulo: Xamã, 1999.
FRIGOTTO, G.; CIAVATTA, M. (org). A experiência do trabalho e a educação básica.
Rio de Janeiro: DP&A, 2002.
MELLO, G. N. de. Cidadania e competitividade: desafios educacionais do terceiro
milênio. Colaboração Madza Julita Nogueira. 7.ed. São Paulo: Cortez, 1998.
Bibliografia Complementar
KOBER, C. M. Qualificação profissional: uma tarefa de Sísifo. Campinas: Autores
Associados, 2004.
LOMBARDI, J. C.; SAVIANI, D.; SANFELICE, J. L. (orgs.). Capitalismo, trabalho e
educação. 3.ed. Campinas: Autores Associados, 2005.
MARKET, W. Trabalho, comunicação e competência: contribuições para a
construção crítica de um conceito e para a formação do profissional transformativo.
56
Campinas: Autores Associados, 2004.
MÉSZÁROS, I. A educação para além do capital. São Paulo: Boitempo, 2005.
MORIN, E. A cabeça bem-feita: repensar a reforma, reformar o pensamento . 18. ed.
Rio de Janeiro: Bertrand Brasil, 2010.
3° Semestre
Cálculo I - 60h
Ementa: Sequências numéricas, Sequências monótonas e limitadas. Limite de uma
sequência. Limite e Continuidade de Funções. Derivada. Aplicações da Derivada:
Comportamento de Funções e Regra de L’hôpital.
Bibliografia Básica
ANTON, H.; BIVENS, I.; DAVIS, S. Cálculo. Porto Alegre: Bookman, 2000. v. 1.
FLEMMING, D. M.; GONÇALVES, M. B. Cálculo A: funções, limite, derivação,
integração. 6.d. São Paulo: Pearson Prentice Hall, 2006.
LEITHOLD, L. O cálculo com geometria analítica. São Paulo: Harbra, do 1994. v. 1.
Bibliografia Complementar
NUNEM, M.A.; FOULIS, D.J. Cálculo. Rio de Janeiro: LTC, 2011.
BOULOS, P. Cálculo diferencial e Integral. São Paulo: Pearsom Makron Books,
1999.
GUIDORIZZI, H. L. Um curso de cálculo .Rio de Janeiro: LTC, 2001. v.1.
GUIDORIZZI, H. L. Um curso de cálculo .Rio de Janeiro: LTC, 2001. v.2.
LAURENCE, D. H.; BRADLEY, G. L. Cálculo: um curso moderno e suas aplicações.
Rio de Janeiro: LTC, 2010.
Fundamentos Teóricos e Metodológicos da Formação e da Atuação Docente - 60h
Ementa: Educação formal e não formal. Bases epistemológicas da formação docente.
Didática na formação do professor. Construção didático-pedagógica do conhecimento.
O docente como profissional e sujeito da educação. (PCC – prática como componente
curricular).
Bibliografia Básica
MACHADO, N. J. Epistemologia e didática. 4. ed. São Paulo: Cortez, 2000.
PIMENTA, S. G. (org.). Saberes pedagógicos e atividade docente. São Paulo:
Cortez, 1999. (Coleção Docência em formação. Série Saberes Pedagógicos).
VEIGA, I. P. Didática: o ensino e suas relações. São Paulo: Papirus, 1996.
Bibliografia Complementar
BICUDO, M. A. V. et al. Formação do educador e avaliação educacional – avaliação
institucional, ensino e aprendizagem. São Paulo: UNESP, 1999. (Seminários &
Debates) v. 4.
D’AMBRÓSIO, U. Da realidade à ação. São Paulo: Papirus, 1986.
CANDAU, Vera Maria (org.) Rumo a uma nova didática. 3. ed. Petrópolis: Vozes,
1990.
57
LIBÂNEO, J. C. Didática. São Paulo: Cortez, 2000.
ZABALA, A. A prática educativa: como ensinar. Porto Alegre: Artes Médicas, 1998.
Física I - 60h
Ementa: Mecânica. Hidrostática. Hidrodinâmica. Termodinâmica. Abordagem histórica.
Instrumentos pedagógicos para a contextualização do conhecimento.
Bibliografia Básica
HEWITT, P. G. Física conceitual. Porto Alegre: Bookman, 2002.
SEARS, F. W.& ZEMANSKI, M. W., YOUNG, H. D. & FREEDMAN. Física I: mecânica.
São Paulo: Addison Wesley, 2008.
SEARS, Francis Weston & ZEMANSKI, Mark W., YOUNG, Hugh D. & FREEDMAN.
Física II: termodinâmica e ondas. São Paulo: Addison Wesley, 2008.
Bibliografia Complementar
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: mecânica v. 1.
Rio do Janeiro: LTC, 2009.
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: Termodinâmica e
óptica v. 2. Rio do Janeiro: LTC, 2009.
MÁXIMO, A. & ALVARENGA, B. Curso de física. V. 02. 4. ed. São Paulo: Scipione,
1997.
MÁXIMO, Antônio & ALVARENGA, Beatriz. Curso de física. v. 01. 4. ed. São Paulo:
Scipione, 1997.
NUSSENZVEIG, H. M. Curso de física básica - V. 1. Edgard Blucher, 1997.
Geometria Analítica - 60h
Ementa: Noções de vetores no R2 e R3. Plano Cartesiano e Coordenadas cartesianas
no plano. Estudo da reta no plano e no espaço. Estudo do plano. Posição relativa de
retas e planos. Cônicas. Quadráticas.
Bibliografia Básica
ANTON, H. Álgebra linear com aplicações. 8. ed. Porto Alegre: Bookman, 2001.
BOULOS, P. Geometria analítica: um tratamento vetorial. São Paulo: Editora McGrawHill Ltda, 1987.
STEINBRUCH, A. Geometria analítica plana. São Paulo: Editora McGraw-Hill Ltda,
1991.
Bibliografia Complementar
DANTE, L. R. Matemática. São Paulo: Ática, 2005.
EZZI, G. Fundamentos da matemática elementar – geometria analítica. São Paulo:
Atual, 1993.
GIOVANI, JR.; BONJORNO, J. R.; GIOVANI JR, J. R. Matemática fundamental, uma
nova abordagem. Editora FTD, 2002.
LEITHOLD, L. O cálculo com geometria analítica. São Paulo: Harbra&Row do Brasil,
1977.v. 1.
58
LEITHOLD, L. O cálculo com geometria analítica. São Paulo: Harbra&Row do Brasil,
1977.v. 2.
Psicologia do desenvolvimento e da aprendizagem - 60h
Ementa: Escolas clássicas em psicologia e a relação com ensino e aprendizagem.
Inter-relação entre a Psicologia e a Educação. Processo psicológico de aprendizagem
e inter-relação com as dimensões biológicas, socioculturais, afetivas e cognitivas. O
desenvolvimento humano e as características individuais no processo de
aprendizagem. Teorias da aprendizagem e relações com as concepções de
desenvolvimento. (PCC – prática como componente curricular).
Bibliografia Básica
KELLER, F. S. Aprendizagem: teoria do reforço. São Paulo: EPU, 1973.
VIGOTSKY, L. S.; LÚRIA, A. R.; LEONTIEV, A. N. Linguagem, desenvolvimento e
aprendizagem. São Paulo: Ícone, 1988.
WALLON, Henry. A evolução psicológica da criança. São Paulo: Martins Fontes,
2007.
Bibliografia Complementar
DAVIS, C.; OLIVEIRA, Z. M. R. Psicologia na educação. 2. ed. São Paulo: Cortez,
1994.
GROSSI, E. P.; BORDIN, J.(Org). Construtivismo pós-piagetiano: um novo
paradigma sobre aprendizagem . 12. ed. Petrópolis: Vozes, 2009.
NOGUEIRA, A. L. H. A linguagem e o outro no espaço escolar: Vygotsky e a
construção do conhecimento. 9. ed. São Paulo: Papirus, 2003.
OLIVEIRA, M. K. Vygotsky: aprendizado e desenvolvimento: um processo sóciohistórico. São Paulo: Scipione, 1997.
VIGOTSKY, L. S. A formação social da mente: o desenvolvimento dos processos
psicológicos superiores. 7. ed. São Paulo: Martins Fontes, 2007.
4° Semestre
Física II - 60h
Ementa: Eletricidade. Magnetismo. Ótica. Abordagem
pedagógicos para a contextualização do conhecimento.
histórica.
Instrumentos
Bibliografia Básica
HEWITT, P. G. Física conceitual. Porto Alegre: Bookman, 2002.
SEARS, F. W. & ZEMANSKI, M. W., YOUNG, H. D. & FREEDMAN. Física IV: ótica e
física moderna. São Paulo: Addison Wesley, 2008.
SEARS, F. W. & ZEMANSKI, M. W., YOUNG, Hugh D. & FREEDMAN. Física III:
eletromagnetismo. São Paulo: Addison Wesley, 2008.
Bibliografia Complementar
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: eletromagnetismo.
v. 3. Rio do Janeiro: LTC, 2009.
59
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de física: óptica, física
moderna. v. 4. Rio do Janeiro: LTC, 2009.
MÁXIMO, Antônio & ALVARENGA, Beatriz. Curso de física. v. 02. 4. ed. São Paulo:
Scipione, 1997.
MÁXIMO, Antônio & ALVARENGA, Beatriz. Curso de física. v. 03. 4. ed. São Paulo:
Scipione, 1997.
NUSSENZVEIG, H. M. Curso de física básica – Eletromagnetismo. v. 3. Edgard
Blucher, 1997.
Cálculo II - 60h
Ementa: Funções Contínuas por Partes. Somas de Riemann. Integral indefinida e
definida. Técnicas de Integração. Aplicações da Integral. Coordenadas Polares.
Cálculo de Área por Coordenadas Polares.
Bibliografia Básica
ANTON, H.; BIVENS, I.; DAVIS, S. Cálculo. Porto Alegre: Bookman, 2000. v. 1 e 2.
FLEMMING, D. M.; GONÇALVES, M. B. Cálculo A e B. Editora Prentice Hall Brasil,
2006.
LEITHOLD, L. O cálculo com geometria analítica. São Paulo: Harbra&Row do Brasil,
1977.v. 1 e 2.
Bibliografia Complementar
BATSCHELE, E. Introdução à matemática para biocientistas. Rio de Janeiro:
Interciência, 1978.
BOULOS, P. Cálculo diferencial e Integral. São Paulo: Pearsom Makron Books,
1999.
GUIDORIZZI, H. L. Um curso de cálculo .Rio de Janeiro: LTC, 2001. v. 1.
GUIDORIZZI, H. L. Um curso de cálculo .Rio de Janeiro: LTC, 2001. v. 2.
LAURENCE, D. H.; BRADLEY, G. L. Cálculo: um curso moderno e suas aplicações
Rio de Janeiro: LTC, 2010.
Álgebra linear I - 60h
Ementa: Matrizes, determinantes e sistemas lineares. Vetores. Espaços Vetoriais.
Espaços Vetoriais Euclidianos.
Bibliografia Básica
ANTON, H.; RORRES, C. Álgebra linear com aplicações. 8. ed. Porto Alegre:
Bookman, 2001.
BOLDRINI, J. L. Álgebra linear. 2. ed. ampl. e rev. São Paulo: Harper & Row do Brasil,
1980.
CAMARGO, I.; BOULOS, P. Geometria analítica: um tratamento vetorial. 3. ed. São
Paulo: Pearson, 2005.
Bibliografia Complementar
CAROLI, A.; CALLIOLI, C. A.; FEITOSA, M. O. Matrizes, vetores, geometria
analítica: teoria e exercícios. São Paulo: Nobel, 1984.
60
LANG, S. Álgebra linear. São Paulo: Edgard Blucher LTDA, 1971.
LEITHOLD, Louis. O cálculo com geometria analítica. 3. ed. São Paulo: Harbra,
1994.
LIPSCHUTZ, S. Álgebra linear: teoria e problemas. 3. ed. rev. e ampl. São Paulo:
Pearson Makron Books, 2004.
STEINBRUCH, A.; WINTERLE, P. Álgebra linear. 2. ed. São Paulo: McGraw-Hill,
Pearson Makron Books, 1987.
Metodologia do Ensino de Matemática na Educação Básica I - 60h
Ementa: Aspectos de conteúdos e metodologias para o ensino de matemática nas
séries finais do ensino fundamental. Tendências em Educação Matemática.
Parâmetros Curriculares Nacionais, Proposta Curricular do Estado de Santa Catarina.
Livros didáticos (PCC – prática como componente curricular).
Bibliografia Básica
BECKER, F. Epistemologia do professor de matemática. Petrópolis, RJ: Ed. Vozes,
2012.
BICUDO, M. A. V.; BORBA, M. C. (org.). Educação matemática: pesquisa em
movimento. São Paulo: Cortez, 2004.
MACHADO, N. J.; CUNHA, M. O. (orgs). Linguagem e conhecimento matemático:
ensaios de epistemologia e didática. São Paulo: Escrituras Editora, 2003.
Bibliografia complementar
BRASIL. Ministério da Educação e do Desporto. Parâmetros Curriculares Nacionais:
Matemática. Secretaria de Educação Fundamental. Brasília: MEC/SEF, 1997.
D'AMBROSIO, U. Da realidade à ação: reflexos sobre Educação Matemática.
Campinas: UNICAMP, 1986.
DEMO, P. Desafios modernos da educação. Petrópolis: Vozes, 1996.
MARQUES, M. O. Aprendizagem na mediação social do aprendido e da docência.
2.ed. Ijuí: UNIJUÍ, 2000.
SANTA CATARINA. Secretaria de Estado da Educação e do Desporto. Proposta
Curricular de Santa Catarina: Educação Infantil, Ensino Fundamental e Médio:
Disciplinas curriculares. Florianópolis: COGEN, 1998.
Avaliação – 45h
Ementa: Avaliação e suas formas. Avaliação como parte integrante do processo
pedagógico (PCC – prática como componente curricular).
Bibliografia Básica
HOFFMANN, J. M. L. Avaliação: mito & desafio: uma perspectiva construtivista. 40.
ed. Porto Alegre: Mediação, 2010.
LUCKESI, C. C. Avaliação da aprendizagem escolar: Estudos e proposições. São
Paulo: Cortez, 1999.
RAPHAEL, S.; KESTER, C. (orgs.). Avaliação sob exame. 9.ed. Campinas: Autores
Associados, 2008.
Bibliografia Complementar
61
GANDIN, D. Planejamento como prática educativa. São Paulo: Edições Loyola,
2010.
HOFFMANN, J. M. L. Avaliar: respeitar primeiro, educar depois. 2. ed. Porto Alegre:
Mediação, 2010.
HOFFMANN, J. M. L. Avaliar para promover: as setas do caminho. 14. ed. Porto
Alegre: Mediação, 2011.
SAUL, A. M. Avaliação emancipatória: desafio à teoria e à prática de avaliação e
reformulação de currículo. 5.ed. São Paulo: Cortez, 2000.
VASCONCELLOS, C. S. Planejamento: projeto de ensino-aprendizagem e projeto
político-pedagógico – elementos metodológicos para elaboração e realização. 10. ed.
São Paulo: Libertad, 2002.
Concepções em Educação Matemática - 30h
Ementa: A matemática e a educação matemática enquanto áreas de conhecimento. A
Educação Matemática no Brasil. Pesquisas brasileiras em Educação Matemática.
Bibliografia Básica
BICUDO, M. A. V.; BORBA, M. C. Educação matemática: pesquisa em movimento. 2.
ed. revisada. São Paulo: Cortez, 2005.
FIORENTINI, D. & LORENZATO, S. Investigação em educação matemática:
percursos teóricos e metodológicos. 3 ed. rev. Campinas- SP: Autores associados,
2009. (Coleção Formação de Professores).
SKOVSMOSE, O. Educação crítica: incerteza, matemática, responsabilidade. São
Paulo: Cortez, 2007.
Bibliografia Complementar
_________. Desafios da reflexão em educação matemática crítica. Campinas:
Papirus, 2008.
BICUDO A. M. V. (org). Pesquisa em Educação Matemática: concepções &
perspectivas. São Paulo: UNESP, 1999.a
D’AMBROSIO. U. Da realidade à ação: reflexões sobre Educação Matemática. São
Paulo: Summus, 1986.
MACHADO, S. D. A. Educação Matemática: uma (nova) introdução. 3. ed. São Paulo:
EDUC, 2010.
SKOVSMOSE, O. Educação matemática crítica: a questão da democracia.
Campinas: Papirus, 2001.
5° Semestre
Metodologia do Ensino de Matemática na Educação Básica II - 60h
Ementa: Aspectos de conteúdos e metodologias para o ensino de matemática no
Ensino Médio. Tendências em Educação Matemática. Parâmetros Curriculares
Nacionais, Proposta Curricular do Estado de Santa Catarina. Livros didáticos.
Bibliografia Básica
BARALDI, Ivete Maria. Matemática na escola: que ciência é esta? Bauru: EDUSC,
1999.
62
MACHADO, S. A. (org.). Educação matemática: uma introdução. São Paulo: EDUC,
1999.
PAIS, L. C. Didática da matemática: uma análise da influência francesa. Belo
Horizonte: Autêntica, 2001.
Bibliografia Complementar
BICUDO, M A. V. (org.). Pesquisa em educação matemática: concepções e
perspectivas. São Paulo: UNESP, 1999.
CHARLOT, B. Relação com o saber, formação dos professores e globalização:
questões para a educação hoje. Porto Alegre: Artmed, 2005.
D´AMBROSIO, Ubiratan. Educação matemática: da teoria à prática. 4. ed. São
Paulo: Papirus, 1996. (Coleção perspectivas em educação Matemática).
PARA, C.; SAIZ, I.(orgs.) Didática da matemática: reflexões psicopedagógicas. Porto
Alegre : Artes Médicas, 1996.
TARDIF, M. Saberes docentes e formação profissional. Petrópolis, RJ: Vozes, 2002.
Cálculo III - 60h
Ementa: Séries numéricas. Convergência de Séries e Critérios de Convergência.
Expansão de uma Função em séries de Potências. Funções de várias variáveis.
Limites; Continuidade. Derivadas parciais. Funções Vetoriais. Gradiente. Máximos e
mínimos. Multiplicadores de Lagrange.
Bibliografia Básica
ANTON, H.; BIVENS, I.; DAVIS, S. Cálculo. Porto Alegre: Bookman, 2000. v. 1 e 2.
FLEMMING, D. M.; GONÇALVES, M. B. Cálculo A e B. Editora Prentice Hall Brasil,
2006.
LEITHOLD, L. O cálculo com geometria analítica. São Paulo: Harbra&Row do Brasil,
1977.v. 1 e 2.
Bibliografia Complementar
BOULOS, P. Cálculo diferencial e integral. São Paulo: Pearsom Makron Books,
1999.
GUIDORIZZI, H. L. Um curso de cálculo .Rio de Janeiro: LTC, 2001. v. 1 e 2.
LAURENCE, D. H.; BRADLEY, G. L. Cálculo: um curso moderno e suas aplicações
Rio de Janeiro: LTC, 2010.
STEWART, J. Cálculo. São Paulo: Pioneira Thomson, 2003. v. 1.
STEWART, J. Cálculo. São Paulo: Pioneira Thomson, 2003. v. 2
Álgebra Linear II - 60h
Ementa: Transformações lineares. Mudança de base. Produto interno. Transformações
ortogonais. Autovalores e autovetores de um operador. Diagonalização de operadores.
Mínimos quadrados. Introdução à programação linear.
Bibliografia Básica
ANTON, H.; RORRES, C. Álgebra linear com aplicações. 8. ed. Porto Alegre:
Bookman, 2001.
63
BOLDRINI, J. L. Álgebra linear. 2. ed. ampl. e rev. São Paulo: Harper & Row do Brasil,
1980.
CAMARGO, I.; BOULOS, P. Geometria analítica: um tratamento vetorial . 3. ed. São
Paulo: Pearson, 2005.
Bibliografia Complementar
CAROLI, A.; CALLIOLI, C. A.; FEITOSA, M. O. Matrizes, vetores, geometria
analítica: teoria e exercícios. São Paulo: Nobel, 1984.
LEITHOLD, L. O cálculo com geometria analítica. 3. ed. São Paulo: Harbra, 1994.
LANG, S. Álgebra Linear. São Paulo: Edgard Blucher LTDA, 1971.
LIPSCHUTZ, S. Álgebra linear: teoria e problemas. 3. ed. rev. e ampl. São Paulo:
Pearson Makron Books, 2004.
STEINBRUCH, A.; WINTERLE, P. Álgebra linear. 2. ed. São Paulo: McGraw-Hill,
Pearson Makron Books, 1987.
Laboratório de prática de ensino-aprendizagem I - 60h
Ementa: Fundamentação teórica. Recursos didáticos: criação, aplicação e Produção
textual. Procedimentos Metodológicos para o ensino de matemática nas séries finais do
ensino fundamental. (PCC – prática como componente curricular).
Bibliografia Básica
FIORENTINI, D.; LORENZATO, S. Investigação em educação matemática: percursos
teóricos e metodológicos. Campinas: Autores Associados, 2006.
LORENZATO, S. (Org.) O laboratório de ensino de matemática na formação de
professores. Campinas: Autores Associados, 2006.
POLYA, G. A arte de resolver problemas: um novo aspecto matemático. Rio de
Janeiro: Interciência, 1995.
Bibliografia Complementar
D’AMBROSIO. U. Da realidade à ação: reflexões sobre educação matemática. São
Paulo: Summus, 1986.
MOREIRA, P. C. DAVID, M. M. M. S. Formação matemática do professor –
Licenciatura e prática docente escolar. Belo Horizonte: Autêntica, 2011.
MIGUEL A. MIORIM M. A. História na educação matemática: propostas e desafios. 2.
ed. Belo Horizonte: Autêntica, 2011.
MURARI, C. & BARBOSA, R. M. Conexões e educação matemática: belas formas em
caleidoscópios, caleidosciclos e caleidostrótons. Vol. 3. Belo Horizonte: Autêntica, 2011.
SILVA. M. S. Clube de matemática: jogos educativos. 6. Ed. São Paulo: Papirus,
2011.
Estágio Supervisionado I - 60h
Ementa: Escolas e turmas das séries finais do ensino fundamental (observação).
Projeto pedagógico da escola de ensino fundamental. Plano de ensino de matemática
das séries finais do ensino fundamental. Pré-projeto de docência para as séries finais
do ensino fundamental. Socialização do Estágio I.
Bibliografia Básica
64
ANDRÉ, M. (Org.). O papel da pesquisa na formação e na prática dos professores.
Campinas: Papirus, 2000.
PIMENTA, S. G. (org.). Saberes pedagógicos e atividade docente. São Paulo:
Cortez, 1999. (Coleção Docência em formação. Série Saberes Pedagógicos).
PIMENTA, S. O estágio na formação de professores: unidade teoria e prática? São
Paulo: Cortez, 2006.
Bibliografia complementar
DEMO, P. Pesquisa: princípio científico e educativo. São Paulo: Cortez: Autores
Associados, 1990.
FREIRE, P. Pedagogia da esperança: um reencontro com a pedagogia do oprimido.
8. ed. Rio de Janeiro: Paz e Terra, 2009.
NOGUEIRA, A. L. H. A linguagem e o outro no espaço escolar: Vygotsky e a
construção do conhecimento. 9. ed. São Paulo: Papirus, 2003.
VEIGA, I. P. A.; FONSECA, M. (Org.). Dimensões do projeto político-pedagógico:
novos desafios para a escola. Campinas: Papirus, 2001. (Papirus).
VIGOTSKY, L. S.; LÚRIA, A. R.; LEONTIEV, A. N. Linguagem, desenvolvimento e
aprendizagem. São Paulo: Ícone, 1988.
6° Semestre
Pesquisa em Educação - 60h
Ementa: Ciência e conhecimento. Atitude e pesquisa em educação. (PCC – prática
como componente curricular).
Bibliografia Básica
DEMO, P. Pesquisa: princípio científico e educativo. São Paulo: Cortez: Autores
Associados, 1990.
PIMENTA, S. G. Educar pela pesquisa. 8.ed. Campinas: Autores Associados, 2007.
ZAMBONI, S. A pesquisa em arte: um paralelo entre arte e ciência. 3. ed. rev.
Campinas:Autores Associados, 2006. (Coleção polêmicas de nosso tempo, 59).
Bibliografia Complementar
BOOTH, W. C. (et all). A arte da pesquisa. 2. ed. São Paulo: Martins Fontes, 2005.
COSTA, M. V. Caminhos investigativos II: outros modos de pensar e fazer pesquisa
em educação. Rio de Janeiro: Lamparina, 2007.
PESCUMA, D.; CASTILHO, A. P. F. Referências bibliográficas: um guia para
documentar suas pesquisas. 4. ed. São Paulo: Olho d´Água, 2003.
PESCUMA, D.; CASTILHO, A. P. F. Projeto de pesquisa - o que é? como fazer?: um
guia para sua elaboração. São Paulo: Olho d´Água, 2005.
SANTOS, B. de S. Um discurso sobre as ciências. 12. ed. Porto: Afrontamento,
2002.
Cálculo IV - 60h
Ementa: Coordenada polares, cilíndricas e esféricas. Transformações. Matrizes
65
Jacobianas. Integração de funções de várias variáveis. Mudanças de coordenadas em
integrais. Integral de linha.
Bibliografia Básica
ANTON, H.; BIVENS, I.; DAVIS, S. Cálculo. Porto Alegre: Bookman, 2000. v. 1 e 2.
FLEMMING, D. M.; GONÇALVES, M. B. Cálculo A e B. Editora Prentice Hall Brasil,
2006.
LEITHOLD, L. O cálculo com geometria analítica. São Paulo: Harbra&Row do Brasil,
1977.v. 1 e 2.
Bibliografia Complementar
BOULOS, P. Cálculo diferencial e integral. São Paulo: Pearsom Makron Books,
1999.
GUIDORIZZI, H. L. Um curso de cálculo .Rio de Janeiro: LTC, 2001. v. 1 e 2.
MUNEM, M. A.; FOULIS, D. J. Cálculo. Rio de Janeiro: LTC, 1982.
STEWART, J. Cálculo. São Paulo: Pioneira Thomson, 2003. v. 1.
STEWART, J. Cálculo. São Paulo: Pioneira Thomson, 2003. v. 2.
Educação Inclusiva - 60h
Ementa: Aspectos históricos da educação “inclusiva”. Processos de inclusão e
exclusão escolar. Políticas e práticas para o atendimento educacional do educando
com necessidades especiais. Formas organizativas do trabalho pedagógico e sua
relação com os processos de inclusão e exclusão escolar relacionado aos educandos
com necessidades especiais.
Bibliografia Básica
JESUS, D. M.; BAPTISTA, C. R.; BARRETO, M. A. S. C.; VICTOR, S. L. (Orgs.)
Inclusão, práticas pedagógicas e trajetórias de pesquisa. Porto Alegre: Mediação,
2007.
SKLIAR, C. (Org.). Educação e exclusão – Abordagens sócio-antropológicas em
educação especial. 5. Ed. Porto Alegre: Editora Mediação, 1997.
VIGOTSKY, L.S.; LÚRIA, A. R.; LEONTIEV, A. N. Linguagem, desenvolvimento e
aprendizagem. São Paulo: Ícone, 1988.
Bibliografia Complementar
ARAÚJO, U. F. et al. Programa ética e cidadania: construindo valores na escola e na
sociedade: relações étnico-raciais e de gênero. Brasília, DF: Secretaria de Educação
Básica, 2007. 4v.
BRASIL. Ministério da Educação. Diretrizes Nacionais para a Educação Especial na
Educação Básica. Brasília. Secretaria de Educação Especial – MEC – SEESP, 2001.
CARVALHO, R. Educação inclusiva com os pingos nos is. Porto Alegre: Mediação,
2004.
BUENO, J. G. S.; MENDES, G.M.L; SANTOS, R.A. dos (Orgs.) Deficiência e
escolarização: novas perspectivas de análise. Junqueira e Marín, Araraquara, SP;
Brasília, D. F., 2008.
66
MANTOAN, M. T. E.; PRIETO, R. G. Inclusão escolar: pontos e contrapontos. São
Paulo: Summus, 2006.
Equações Diferenciais Ordinárias - 60h
Ementa: Equações diferenciais de 1ª ordem; Campo Vetorial; Equações Diferenciais
Separáveis; Equações Diferencias Lineares de 1ª ordem e o fator integrante. Equações
Diferencias Lineares de 2ª ordem; EDL homogêneas; Princípio da superposição;
Transformada de Laplace; Resolução de EDO´s utilizando transformada de Laplace.
Bibliografia Básica
SIMMONS, G. Equações diferenciais: teoria, técnica e prática. Mcgraw Hill Brasil,
2007.
BOYCE, W. E.; DIPRIMA, R. C. Equações diferenciais elementares e problemas.
Editora LTC, 2006.
ZILL, D. G. Equações diferenciais. Editora Thomson Pioneira, 2003.
Bibliografia Complementar
DOERING, C. I.; LOPES, A. O. Equações diferenciais ordinárias. Rio de Janeiro:
IMPA, 2012.
BASSANEZI, R. C. Ensino-aprendizagem com modelagem matemática: uma nova
estratégia. São Paulo: Contexto, 2002.
LAURENCE, D. H.; BRADLEY, G. L. Cálculo: um curso moderno e suas aplicações
– Tópicos Avançados. Rio de Janeiro: LTC, 2010.
OLIVEIRA, E. C.; MAIORINO, J. E. Introdução aos métodos da matemática
aplicada. São Paulo: UNICAMP, 2003.
ANTON, H.; BIVENS, I.; DAVIS, S. Cálculo. Porto Alegre: Bookman, 2000. v. 2.
Estágio Supervisionado II - 150h
Ementa: Projeto de docência para as séries finais do ensino fundamental. Plano de
aulas/intervenções para as séries finais do ensino fundamental. Docência nas séries
finais do ensino fundamental. Relatório de Estágio II. Socialização do Estágio II.
Bibliografia Básica
D’AMBRÓSIO, U. Da realidade à ação. São Paulo: Papirus, 1986.
PIMENTA, S. G. (org.). Saberes pedagógicos e atividade docente. São Paulo:
Cortez, 1999. (Coleção Docência em formação. Série Saberes Pedagógicos).
PIMENTA, S. O estágio na formação de professores: unidade teoria e prática? São
Paulo: Cortez, 2006.
Bibliografia Complementar
BRASIL. Parâmetros Curriculares Nacionais para o Ensino Fundamental
(Matemática). Brasília: MEC/SEF, 1997.
BENIGNA, M. F. V. B. Projeto de intervenção na escola: mantendo as aprendizagens
em dia. Campinas: Papirus, 2012. (Papirus).
GROSSI, Esther Pillar; B., Jussara (Org). Construtivismo pós-piagetiano: um novo
67
paradigma sobre aprendizagem . 12. ed. Petrópolis: Vozes, 2009.
OLIVEIRA, Martha Kohl De. Vygotsky: aprendizado e desenvolvimento: um processo
sócio-histórico . São Paulo: Scipione, 1997.
VEIGA, I. P. A.; FONSECA, M. (Org.). Dimensões do projeto político-pedagógico:
novos desafios para a escola. Campinas: Papirus, 2001. (Papirus).
7° Semestre
Sociologia da Educação - 30h
Ementa: A construção do pensamento sociológico. Olhar sociológico sobre a escola. O
lugar da escola na modernidade e na contemporaneidade. A Escola: dinâmicas, atores,
processos e contextos. (prática como componente curricular)
Bibliografia Básica
MARX, K. E ENGELS, F. Textos sobre educação e ensino. Centauro, 2004.
MÉSZÁROS, I. A educação para além do capital. 2. ed. São Paulo: Boitempo, 2010.
RODRIGUES, A. T. Sociologia da educação. 7. ed. Rio de Janeiro: DP&A, 2007.
Bibliografia Complementar
BOURDIEU, P. Escritos de educação. 2. ed. Petrópolis: Vozes, 1999.
BOURDIEU, P. A reprodução: elementos para uma teoria do sistema de ensino. 2. ed.
Rio de Janeiro: F. Alves, 1982.
FRIEDRICH E. A origem da família, da propriedade privada e do Estado. 15. ed.
São Paulo: Escala Educacional, 2009.
FREIRE, P. Pedagogia da esperança: um reencontro com a pedagogia do oprimido.
8. ed. Rio de Janeiro: Paz e Terra, 2009.
SAVIANI, D. Escola e democracia. 41. ed. Campinas: Autores Associados, 2009.
Educação matemática e tecnologias - 60h
Ementa: Análise e proposta de utilização de diferentes softwares para o ensino e
aprendizagem da Matemática. Análise de sites web na área de Educação Matemática e
suas possíveis aplicações. Construção de referencial teórico na área de tecnologia
informática aplicada à Educação Matemática (prática como componente curricular)
Bibliografia Básica
BICUDO M. A. V. & BORBA, M. de C. (Orgs). Educação matemática: pesquisa em
movimento. São Paulo: Cortez, 2004.
BORBA, M. & PENTEADO, M. G. Informática e educação matemática. Coleção
Tendências em Educação Matemática. 2.ed. Belo Horizonte: Autêntica, 2001.
Disponível em editora autêntica.
KENSKI, V. M. Educação e tecnologias: o novo ritmo da informação. Campinas:
Papirus, 2008.
Bibliografia Complementar
BAZZO, Walter Antonio. Ciência, tecnologia e sociedade e o contexto da educação
tecnológica. 3.ed. ver. Florianópolis: Ed. da UFSC, 2011.
68
BICUDO, M. A. V. & ROSA, M. Realidade e cibermundo: horizontes filosóficos e
educacionais antevistos. Canoas, RS: Editora da Ulbra, 2010.
DEMO, P. Formação permanente e tecnologias educacionais. Petrópolis, RJ:
Vozes, 2006.
KALINKE, M. A. Internet na educação. Curitiba: Chain, 2003.
MACHADO, S. D. A (Org). Educação matemática: uma (nova) introdução. 3. ed. São
Paulo: EDUC, 2010.
Cálculo Numérico - 60h
Ementa: Erros. Solução de equações algébricas e transcendentes. Solução de
equações polinomiais. Solução de sistemas e equações lineares. Interpolação e
diferenciação. Ajuste de curvas. Integração numérica. Solução numérica de equações
diferenciais. Estudo de construção de algoritmos e implementação em linguagem de
Programação.
Bibliografia Básica
BARROSO, C. L.; BARROSO M. M. A; CAMPOS F. F.; C M. L. B.; MAIA M. L. Cálculo
numérico. 2. ed. São Paulo: Harbra, 1987.
BURDEN, R, L.; FAIRES, J. D. Análise numérica. São Paulo: Thompson, 2003.
SPERANDIO, D; MENDES, J T; SILVA, L. H. M. Cálculo numérico: características
matemáticas e computacionais dos métodos numéricos. São Paulo: Prentice Hall,
2003.
Bibliografia Complementar
ANTON, H.; BIVENS, I.; DAVIS, S. Cálculo. Porto Alegre: Bookman, 2000. v. 2.
ARENALES, S. H. V.; DAREZZO, A. Cálculo numérico. São Paulo: Thomson Pioneira,
2007.
BURIAN, R.; LIMA, A. C. Cálculo numérico. São Paulo: LTC, 2007.
CUNHA, M. C. C., Métodos numéricos. 2.ed. Campinas: UNICAMP, 2003.
SCHERER, C. Métodos computacionais da física. São Paulo: Livraria da Física da
USP, 2005.
Filosofia da Educação - 60h
Ementa: Educação e filosofia. Processo educativo e suas relações com a ciência ao
longo da história da humanidade ocidental. Razão, ética e epistemologia.
Bibliografia Básica
CHAUI, Marilena. Introdução à história da filosofia. Volume I. Dos Pré-Socráticos a
Aristóteles. Editora Companhia da Letras, 2007.
CHAUI, Marilena. Introdução à história da filosofia. Volume II. Editora Companhia
das Letras, 2010.
MORIN, E. A cabeça bem-feita: repensar a reforma, reformar o pensamento . 18. ed.
Rio de Janeiro: Bertrand Brasil, 2010.
Bibliografia Complementar
ARANHA, M. L. A. Filosofia da educação. Editora Moderna, 2002.
69
CHAUÍ, M. Cultura e democracia – o discurso componente e outras falas. São Paulo:
Cortez, 1993.
PINHEIRO, C. M. Kant e a educação: Reflexões filosóficas. Caxias do Sul: EDUCS,
2007.
ROUSSEAU, J. J. Emílio ou da educação. São Paulo: Martins Fontes, 2004.
STREZITKOSKI, J. Paulo Freire e a educação. Belo Horizonte: Autêntica, 2010.
Políticas Educacionais - Estruturas e Sistemas - 60h
Ementa: A organização do ensino brasileiro. Legislação educacional e as politicas
públicas. A implantação das políticas públicas em educação. Sistemas Educacionais.
Bibliografia Básica
MÉSZÁROS, I. A educação para além do capital. São Paulo: Boitempo, 2005.
SAVIANI. D. Da nova LDB ao FUNDEB. 4. ed. Campinas: Autores Associados, 2011.
SHIROMA, E. O; MORAES, M. C. M. de; EVANGELISTA, O. Política educacional. Rio
de Janeiro, DP&A, 2002.
Bibliografia Complementar
FERREIRA.Eliza Bartolozzi; OLIVEIRA, Dalila Andrade. (orgs). Crise da escola e
políticas educativas. Belo Horizonte: Autêntica, 2009.
GARÓFALO, G. L. PINHO, T. F. (Orgs.). Políticas públicas: limites e possibilidades.
São Paulo: Atlas, 2011.
MORIN, E. A cabeça bem-feita: repensar a reforma, reformar o pensamento. 18. ed.
Rio de Janeiro: Bertrand Brasil, 2010.
OLIVEIRA. D.; ROSAR. M. F. F. Política e gestão da educação. Belo Horizonte:
Autêntica, 2002.
SAVIANI, Dermeval. Educação brasileira: estrutura e sistema. 8. ed. Campinas/São
Paulo: Editores Associados, 2000.
Estágio Supervisionado III - 60h
Ementa: Escola e turmas do ensino médio (observação). Projeto pedagógico da escola
de ensino médio. Plano de ensino de matemática do ensino médio. Pré-projeto de
docência para o ensino médio. Socialização do Estágio III.
Bibliografia Básica
ANDRÉ, M. (Org.). O papel da pesquisa na formação e na prática dos professores.
Campinas: Papirus, 2000.
PIMENTA, S. G. (org.). Saberes pedagógicos e atividade docente. São Paulo:
Cortez, 1999. (Coleção Docência em formação. Série Saberes Pedagógicos).
PIMENTA, S. O estágio na formação de professores: unidade teoria e prática? São
Paulo: Cortez, 2006.
Bibliografia Complementar
DEMO, P. Pesquisa: princípio científico e educativo. São Paulo: Cortez: Autores
Associados, 1990.
70
FREIRE, P. Pedagogia da esperança: um reencontro com a pedagogia do oprimido.
8. ed. Rio de Janeiro: Paz e Terra, 2009.
NOGUEIRA, A. L. H. A linguagem e o outro no espaço escolar: Vygotsky e a
construção do conhecimento. 9. ed. São Paulo: Papirus, 2003.
VEIGA, I. P. A.; FONSECA, M. (Org.). Dimensões do projeto político-pedagógico:
novos desafios para a escola. Campinas: Papirus, 2001.
VIGOTSKY, L. S.; LÚRIA, A. R.; LEONTIEV, A. N. Linguagem, desenvolvimento e
aprendizagem. São Paulo: Ícone, 1988.
8° Semestre
Laboratório de prática de ensino-aprendizagem II – 60h
Ementa: Produção de recursos didáticos: criação, experimentação e testagem.
Produção de ensaios teóricos sobre o ensino da matemática. Metodologias alternativas
para o ensino de matemática no ensino médio. (prática como componente curricular)
Bibliografia Básica
MACHADO, N. J. Epistemologia e didática. 4.ed. São Paulo: Cortez, 2000.
FIORENTINI, D.; LORENZATO, S. Investigação em educação matemática:
percursos teóricos e metodológicos. Campinas: Autores Associados, 2006.
LORENZATO, S. (Org.) O laboratório de ensino de matemática na formação de
professores. Campinas: Autores Associados, 2006.
Bibliografia Complementar
SKOVSMOSE, Ole. Educação crítica: incerteza, matemática, responsabilidade.
São Paulo: Cortez, 2007.
PONTE, J. P. da; BROCARDO, J.; OLIVEIRA, H. Investigações matemáticas na sala
de aula. Belo Horizonte: Autêntica, 2003.
BARBOSA, R. M. Conexões e Educação Matemática: Brincadeiras, explorações e
ações. Vol. 2. Belo Horizonte: Autêntica, 2011.
BARBOSA, R. M. Descobrindo a Geometria Fractal: para a sala de aula. 3. ed. Belo
Horizonte: Autêntica, 2011. Coleção Tendências em Educação Matemática.
MIGUEL A. MIORIM M.A. História na Educação Matemática: Propostas e Desafios.
2. ed. Belo Horizonte: Autêntica, 2011.
Estatística e probabilidade - 60h
Ementa: Análise descritiva e probabilidade. Amostragem e análise inferencial de dados
quantitativos obtidos através de experimentos.
Bibliografia Básica
LARSON, R.; FARBER, B. Estatística aplicada. 4. ed. São Paulo: Pearson Prentice
Hall, 2010. (519.5 L318e)
MAGALHÃES, M. N.; LIMA, A. C.P. Noções de probabilidade e estatística. 7. ed. São
Paulo: EDUSP, 2010 (519.5 M188n)
MORETTIN, P. A.; BUSSAB, W. O. Estatística básica. 6. ed., rev. e atual. São Paulo:
Saraiva, 2010. ( 519.5 M845e)
71
Bibliografia Complementar
BARBETTA, P. A. Estatística aplicada às ciências sociais. 5. ed. Florianópolis:
UFSC, 2003.
HEATH, O. V. S. A estatística na pesquisa científica. São Paulo: E.P.U/EDUSP,
1981.
MORETTIN, L. G. Estatística básica: probabilidade e inferência: vol. único. São
Paulo: Pearson Addison Wesley, 2010. (519.5 M845e)
TRIOLA, Mario F. Introdução à estatística. 10. ed. Rio de Janeiro: LTC, 2008. (519.5
T834i)
WALPOLE, Ronald E. Probabilidade & estatística: para engenharia e ciências. 8. ed.
São Paulo: Pearson Prentice Hall, 2009. (519.2 P964)
Introdução à Análise - 60h
Ementa: Conjuntos Enumeráveis e Não-Enumeráveis.
Convergência. Continuidade. Noções Topológicas na Reta.
Supremo
e
Ínfimo.
Bibliografia Básica
ÁVILA, G. Introdução à análise matemática, 2.ed. São Paulo: Edgard Blucher, 1999.
ELON L L. Curso de Análise. 2. ed. Rio de Janeiro: Projeto, 1985.
FIGUEIREDO, D. G. Análise I.2 ed. Rio de Janeiro: Livros Técnicos e Científicos,
1996.
Bibliografia Complementar
ELON L L. Analise no espaço Rn. Brasília: Unb, 1970.
ELON L L. Análise real. 4 ed. Rio de Janeiro: IMPA, 1999.
GUIDORIZZI, H. L. Um curso de cálculo .Rio de Janeiro: LTC, 2001. v. 2.
HOFFMANN, L. D. Cálculo: Um curso Moderno e suas Aplicações. 10. ed. Rio de
Janeiro: LTC, 2010.
LAURENCE, D. H.; BRADLEY, G. L. Cálculo: um curso moderno e suas aplicações
Rio de Janeiro: LTC, 2010.
Libras - 60h
Ementa: Língua Brasileira de Sinais: aspectos históricos, legais, linguísticos e
pragmáticos; cultura e comunidades surdas; aspectos gramaticais e vocabulário
linguístico da libras; vivências práticas da utilização da libras.
Bibliografia Básica:
MACHADO, P. A política educacional de integração/inclusão: um olhar do egresso
surdo. Florianópolis: UFSC, 2008.
QUADROS, R. M.. Educação de surdos: a aquisição da linguagem. Porto Alegre:
Artes Médicas. 1997.
SKILIAR, C. Atualidade da educação bilíngüe para surdos. Mediação, 1999. v. 1.
Bibliografia Complementar
FERDANDES, E. Linguagem e surdez. Artmed, 2003.
72
QUADROS, R. M. de & KARNOPP L. B. Língua de sinais brasileira: estudos
linguísticos. Porto Alegre: Artes Médicas, 2004
SANTANA, Ana Paula. Surdez e linguagem: aspectos e implicações neurolingüísticas.
São Paulo: Plexus, 2007.
SKILIAR, C. Atualidade da educação bilíngüe para surdos. Mediação, 1999. v. 2.
STROBEL, Karin. As imagens do outro sobre a cultura surda. Florianópolis: Editora
da UFSC, 2008.
Estágio Supervisionado IV - 150h
Ementa: Projeto de docência para o ensino médio. Plano de aulas/intervenções para o
ensino médio. Docência no ensino médio. Relatório de Estágio IV. Artigo de Conclusão
dos Estágios. Socialização do Estágio IV.
Bibliografia Básica
D’AMBRÓSIO, U. Da realidade à ação. São Paulo: Papirus, 1986.
PIMENTA, S. G. (org.). Saberes pedagógicos e atividade docente. São Paulo:
Cortez, 1999. (Coleção Docência em formação. Série Saberes Pedagógicos).
PIMENTA, S. O estágio na formação de professores: unidade teoria e prática? São
Paulo: Cortez, 2006.
Bibliografia Complementar
BENIGNA, M. F. V. B. Projeto de intervenção na escola: mantendo as
aprendizagens em dia. Campinas: Papirus, 2012.
BRASIL. Parâmetros Curriculares Nacionais para o Ensino Médio (Matemática).
Brasília: MEC/SEF, 1997.
GROSSI, Esther Pillar; B., Jussara (Org). Construtivismo pós-piagetiano: um novo
paradigma sobre aprendizagem . 12. ed. Petrópolis: Vozes, 2009.
OLIVEIRA, Martha Kohl De. Vygotsky: aprendizado e desenvolvimento: um processo
sócio-histórico . São Paulo: Scipione, 1997.
VEIGA, I. P. A.; FONSECA, M. (Org.). Dimensões do projeto político-pedagógico:
novos desafios para a escola. Campinas: Papirus, 2001.
73
A2 - Regulamento de Estágio Supervisionado Curricular Obrigatório
REGULAMENTO DE ESTÁGIO SUPERVISIONADO CURRICULAR OBRIGATÓRIO
CURSO DE MATEMÁTICA - LICENCIATURA
Dezembro / 2011
74
TÍTULO I – DA IDENTIFICAÇÃO
Art. 1o O presente documento regulamenta as atividades de Estágio Supervisionado
Curricular Obrigatório e de Prática como Componente Curricular (Prática de Ensino) do
Curso de Matemática – Licenciatura do Campus Rio do Sul do Instituto Federal
Catarinense - IFC
Art. 2o A regulamentação constante neste documento está de acordo com Plano de
Desenvolvimento Institucional (PDI), Projeto Pedagógico Institucional (PPI), Regimento
Geral de Estágio do IFC, Regulamento de Estágio do IFC, Orientação Didática dos
Cursos Superiores do IFC, Projeto Pedagógico do Curso de Matemática - Licenciatura
(PPC), as Diretrizes para a realização de prática de ensino e estágio supervisionado de
cursos de licenciatura nas escolas de educação básica da rede pública estadual
(SED/DES/DEBP).
CAPÍTULO I – BASES LEGAIS
Art. 3o O Estágio Supervisionado Curricular Obrigatório e a Prática como Componente
Curricular (Prática de Ensino) na formação de professores estão pautados na
legislação vigente: Lei nº 11.788, de 25 de setembro de 2008. Lei no 6.494, de 7 de
dezembro de 1977, regulamentada pelo Decreto Lei n o 87.497 de 18 de agosto de
1982 e alterada pela Lei no 8.859, de 23 de março de 1994; Lei no 9.394 de 20 de
dezembro de 1996 (LDB); Parecer CNE/CES no 503/98, aprovado em 3 de agosto de
1998; Parecer CNE/CP no 09/2001; Parecer CNE/CP no 27/2001, que dá nova redação
ao Parecer CNE/CP no 09/2001; Resolução CNE/CP no 1, de 18 de fevereiro de 2002;
Parecer CNE/CES no 197, de 7 de julho de 2004; Parecer CNE/CES no 15, de 2 de
fevereiro de 2005; Resolução CNE/CEB no 2, de 4 de abril de 2005, que modifica a
redação do § 3o do artigo 5o da Resolução CNE/CEB no 1/2004, até nova manifestação
sobre estágio supervisionado pelo Conselho Nacional de Educação.
Art. 4º A Lei 11.788, no Artigo 3º § 1o aponta que o “[...] estágio é ato educativo
escolar supervisionado, desenvolvido no ambiente de trabalho, que visa à preparação
para o trabalho produtivo de educandos que estejam frequentando o ensino regular em
instituições de educação superior, de educação profissional, de ensino médio, da
educação especial e dos anos finais do ensino fundamental, na modalidade
profissional da educação de jovens e adultos”.
§ 1o O estágio visa ao aprendizado de competências próprias da atividade profissional
e à contextualização curricular, objetivando o desenvolvimento do educando para a
vida cidadã e para o trabalho (Lei 11.788).
§ 2o Os cursos de graduação e de ensino técnico devem definir em seu PPC a
modalidade de estágio, coerente com as Diretrizes Curriculares Nacionais e com a
filosofia do curso (Regulamento Geral de Estágios do IFC).
§ 3º As atividades de extensão, de monitorias e de iniciação científica nos cursos
superiores, somente poderão ser equiparadas ao estágio em caso de previsão no
Projeto Pedagógico do Curso (Lei 11.788).
75
TÍTULO II – DO ESTÁGIO CURRICULAR OBRIGATÓRIO
Art. 5º O Estágio Supervisionado Curricular Obrigatório, é aquele definido como tal no
projeto do curso, cuja carga horária é requisito para aprovação e obtenção de diploma.
Art. 6º De acordo com a Lei 11.788, o estágio, como ato educativo escolar
supervisionado, deverá ter acompanhamento efetivo pelo Professor Orientador da
instituição de ensino superior e por supervisor da parte concedente. O estágio não cria
vínculo empregatício de qualquer natureza, observados os seguintes requisitos:
I - matrícula e frequência regular do educando em curso de educação superior, de
educação profissional, de ensino médio, da educação especial e nos anos finais do
ensino fundamental, na modalidade profissional da educação de jovens e adultos e
atestados pela instituição de ensino;
II - celebração de termo de compromisso entre o educando, a parte concedente do
estágio e a instituição de ensino;
III - compatibilidade entre as atividades desenvolvidas no estágio e aquelas previstas
no termo de compromisso.
CAPÍTULO I - DOS OBJETIVOS
Art. 7º São objetivos do Estágio Supervisionado Curricular Obrigatório:
I - proporcionar ao acadêmico a participação em situações de trabalho e experiências
de ensino e de aprendizagem visando a complementação da educação profissional
fundamentada pelo desenvolvimento de competências e habilidades (Artigo 5º
Regulamento Geral de Estágio do IFC);
II - promover a integração entre a realidade acadêmica e sócio-econômico-política
como forma de ampliar a qualificação do futuro profissional (Artigo 5º Regulamento
Geral de Estágio do IFC);
III - integrar o ensino com a realidade, possibilitando a vivência de conhecimentos
teóricos e práticos relacionada à sua formação acadêmica;
IV - oportunizar ao acadêmico estagiário, situações que possibilitem apresentar sua
visão de análise crítica e domínio do conhecimento específico, através da definição de
uma proposta de ação;
V - incentivar a criação e o desenvolvimento de métodos e processos inovadores,
tecnologias e metodologias alternativas, visando atingir as metas do ensino de
matemática.
VI - integrar atividades de ensino, pesquisa e extensão a partir do desenvolvimento das
temáticas observadas nos campos de estágio.
CAPÍTULO II – DA ESTRUTURA ORGANIZACIONAL
Art. 8º A estrutura organizacional para o Estágio Supervisionado Curricular Obrigatório
envolverá, além da IES, Direção de Educação Superior – DIES, Órgão Regional de
Educação e Escolas de Educação Básica da Rede Estadual de Ensino:
I - Coordenador de Estágios (CIEC);
II - Coordenadores de Curso;
III - Professor Supervisor dos Estágios (Instituição Concedente ou Unidade de Ensino –
UE);
76
IV - Professor da Disciplina de Estágios;
V - Professor Orientador de Estágio;
VI - Professor Co-orientador de Estágio;
VII - Instituição Concedente do estágio – UE;
VIII - Professor Regente de Classe da Instituição Concedente – UE;
IX - Acadêmicos.
Seção I - Do Coordenador de Estágios
Art. 9º Ao Coordenador de Estágios competirá:
I - estabelecer parcerias com as instituições públicas, privadas e do terceiro setor para
a realização do Estágio Supervisionado Curricular Obrigatório;
II - apresentar-se ao órgão regional de educação e às Instituições Concedentes ou
Unidades de Ensino;
II - providenciar o Termo de Convênio (Anexo I) e os respectivos Termos de
Compromisso (Anexo II ou III), junto às instituições públicas, privadas e do terceiro
setor para a realização do Estágio Supervisionado Curricular Obrigatório;
III - encaminhar oficialmente os Professores Orientadores de Estágio e acadêmicos
aos respectivos campos do estágio;
IV - prestar assistência técnico-administrativa aos Professores Orientadores de Estágio
Supervisionado Curricular Obrigatório e acadêmicos, quando houver necessidade;
V - apresentar à Supervisão de Educação Superior do Órgão Regional de Educação,
no início de cada semestre letivo, a relação dos acadêmicos da Licenciatura em
Matemática que estarão em fase de Estágio Supervisionado Curricular Obrigatório;
VI - organizar os acadêmicos, inserindo-os no Campo de Estágio, de forma que
possam conhecer a realidade escolar;
VII - efetuar seguro de acidentes pessoais para o acadêmico e firmar Termo de
Compromisso de Estágio como convenente;
VIII - emitir certificado de formação em serviço para o Professor das Unidades de
Ensino que participar como Supervisor de Estágio;
IX - propor, a qualquer tempo, rescisão do convênio se ocorrer inadimplemento de
qualquer uma das condições.
Seção II – Do Coordenador de Curso
Art. 10. Ao Coordenador de Curso competirá:
I - auxiliar no desenvolvimento das atividades de Estágio Supervisionado Curricular
Obrigatório;
II - auxiliar na solução de problemas oriundos do Estágio Supervisionado Curricular
Obrigatório com a equipe de professores pertencentes à estrutura organizacional;
III - prestar orientação pedagógica aos Professores Orientadores de Estágio
Supervisionado Curricular Obrigatório e acadêmicos, quando houver necessidade;
IV - organizar, a cada início de semestre que envolve o estágio, um calendário para
realização do Estágio Supervisionado Curricular Obrigatório e da Prática como
Componente Curricular (Prática de Ensino), em comum acordo com o Órgão Regional
de Educação;
V - apresentar ao Coordenador de Estágios, no início de cada semestre letivo, a
relação dos acadêmicos da Licenciatura em Matemática que estarão em fase de
estágio;
77
VI - organizar o Estágio Supervisionado Curricular Obrigatório e a Prática como
Componente Curricular (Prática de Ensino) em parceria com o Órgão Regional de
Educação e a Unidade de Ensino;
VII - promover, junto com os Professores responsáveis pelas disciplinas de Estágio
Supervisionado Curricular Obrigatório, a socialização das atividades do estágio;
VIII - elaborar, ao final do semestre, relatório síntese dos estágios realizados e
apresentar em reunião regional de avaliação, juntamente com os Supervisores de
Educação Superior e de Educação Básica e Profissional;
IX - cumprir e fazer cumprir as disposições deste Regulamento e demais atos
normativos internos.
Seção III – Dos Professores das Disciplinas de Estágio Supervisionado Curricular
Obrigatório
Art. 11. Compete aos Professores das Disciplinas de Estágio Supervisionado
Curricular Obrigatório as seguintes atribuições:
I - organizar encontros e reuniões, para a definição de ações gerais de planejamento,
acompanhamento e avaliação das atividades relacionadas ao Estágio Supervisionado;
II - orientar os acadêmicos quanto às vagas disponíveis para o Estágio Supervisionado
Curricular Obrigatório nas Instituições Concedentes ou Unidades de Ensino;
III - definir o número de orientandos conforme os Professores Orientadores disponíveis,
observando o limite máximo de 04 (quatro) orientações, ou 06 (seis) co-orientações, ou
o máximo de 03 (três) orientações mais 03 (três) co-orientações simultâneas;
IV - organizar a socialização das etapas II e IV das atividades desenvolvidas nas
Instituições Concedentes ou Unidades de Ensino, durante o período de estágio;
V - receber as avaliações emitidas pelas Instituições Concedentes ou Unidades de
Ensino e Professor Orientador;
VI - encaminhar para as Instituições Concedentes e Unidades de Ensino, com
antecedência, os programas ou planos de ensino das disciplinas ou projetos de
trabalho que serão desenvolvidos no Estágio Supervisionado Curricular Obrigatório,
para ciência e concordância, considerando os Parâmetros Curriculares Nacionais, a
Proposta Curricular de Santa Catarina e o Projeto Pedagógico da Instituição
Concedente ou Unidade de Ensino;
VII - disponibilizar os relatórios finais do Estágio Supervisionado Curricular Obrigatório
e da Prática como Componente Curricular (Prática de Ensino) às Instituições
Concedentes ou Unidades de Ensino, campo de estágio;
VIII - cumprir e fazer cumprir as disposições deste Regulamento e demais atos
normativos internos.
Seção IV – Do Professor Orientador do Estágio
Art. 12. A Orientação de Estágio Supervisionado Curricular Obrigatório é obrigatória
em todas as etapas dos Estágios Supervisionados e será realizada por Professores do
IFC – Câmpus Rio do Sul com o compromisso de visita ao local de estágio, podendo a
mesma acontecer de forma ocasional, aleatória ou quando se fizer necessária.
Parágrafo único: Nas etapas I e III do Estágio Supervisionado, a orientação
preferencialmente será realizada pelo Professor da Disciplina de Estágio.
78
Art. 12. Compete ao Professor Orientador:
I - orientar e dar suporte técnico-pedagógico ao acadêmico estagiário nas distintas
fases do estágio, acompanhando o desenvolvimento do Estágio Supervisionado
Curricular Obrigatório em intervalos regulares, mediante visitas ou outras formas de
comunicação, registrando os dados na ficha de acompanhamento de orientação de
estágio. (Anexo IV);
II - orientar o planejamento e relatório, indicando os materiais que auxiliem no
embasamento teórico-prático, necessário ao desenvolvimento do estágio;
III - decidir pela necessidade ou não de escolha de um coorientador em conjunto com o
acadêmico;
IV - avaliar o plano e relatório antes de encaminhar o estagiário para a próxima etapa
do estágio, mediante aprovação;
V - participar da socialização do Estágio Supervisionado Curricular Obrigatório para
avaliação de seu orientando;
VI - emitir notas referentes às atividades inerentes à orientação e encaminhá-las ao
professor da Disciplina de Estágio, conforme formulário (Anexo V);
VII - cumprir e fazer cumprir as normas do presente regulamento.
Seção V – Do Professor Coorientador do Estágio
Art. 14. A coorientação é facultativa e será realizada pelos professores do IFC –
Câmpus Rio do Sul sendo de sua competência auxiliar e ou substituir o professor
orientador, quando houver necessidade.
Seção VI - Da Instituição Concedente do Estágio / Unidade de Ensino
Art. 15. Compete à Instituição Concedente do Estágio / Unidade de Ensino, campo de
estágio:
I - receber o acadêmico e facilitar o acesso às informações e documentos necessários
à realização e atualização do diagnóstico da realidade escolar e do estágio;
II - inserir os acadêmicos nos projetos, trabalhos específicos, considerando as metas
previamente estabelecidas nas Instituições Concedentes / Unidades de Ensino,
supervisionadas pelo Órgão Regional de Educação;
III - encaminhar o acadêmico para ao professor responsável pelo estágio;
IV - informar à IES e ao Órgão Regional de Educação o desempenho do acadêmico;
V - orientar e acompanhar os acadêmicos na área de formação pretendida, garantindo
professores devidamente habilitados na área de formação do acadêmico;
VI - solicitar à IES a suspensão do acadêmico que por motivo de natureza técnica,
administrativa ou disciplinar, não for considerado apto a continuar suas atividades de
estágio;
VII - apresentar o acadêmico aos segmentos da Instituição Concedente de Estágio /
Unidade de Ensino;
VIII - responsabilizar-se pelo acompanhamento do acadêmico pelo professor regente;
IX - acompanhar e avaliar o desempenho do acadêmico;
X - garantir o cumprimento da carga horária proposta e assinar a documentação
pertinente.
79
Seção VIII – Do professor supervisor do estágio da Instituição Concedente /
Unidade de Ensino
Art. 16. Compete ao professor supervisor de estágio da Instituição Concedente /
Unidade de Ensino:
I - acompanhar as atividades que o acadêmico estagiário desenvolve;
II - analisar o planejamento elaborado pelo acadêmico e aprovado pelo professor
orientador sugerindo alterações, se necessário;
III - avaliar o estagiário e preencher os formulários solicitados pelo IFC, logo após a
conclusão do estágio.
Seção IX – Do Acadêmico
Art. 17. Ao acadêmico compete:
I - participar de todas as atividades previstas para o Estágio Supervisionado Curricular
Obrigatório;
II - apresentar plano de estágio, seguindo o cronograma do mesmo;
III - desenvolver as atividades do estágio com responsabilidade, criatividade e senso
crítico, respeitando as normas da unidade de ensino, campo de estágio;
IV - observar atentamente a aplicação dos princípios de comunicação, relações
humanas e ética profissional;
V - tomar conhecimento da documentação necessária para a realização do estágio e
cumprir o cronograma para entrega dos mesmos e de todas as etapas do Estágio;
VI - receber e preencher a documentação necessária levando à Instituição Concedente
/ Unidade de Ensino e devolvendo ao IFC com as devidas informações e assinaturas;
VII - tomar conhecimento da data, local, horário e tempo, das atividades relacionadas
ao estágio;
VIII - providenciar os recursos materiais necessários para o desenvolvimento do
Estágio Supervisionado Curricular Obrigatório;
IX - decidir, em conjunto com o Professor Orientador, pela necessidade ou não de
escolha de um coorientador;
X - estar presente em todas as orientações agendadas pelo Professor Orientador;
XI - elaborar e entregar ao Professor Orientador as produções escritas via impressa
e/ou em formato digital, conforme data estipulada no Plano Pedagógico de Ensino da
disciplina de estágio;
XII - comparecer ao local de estágio, pontualmente, nos dias e horários estipulados;
XIII - apresentar à Instituição Concedente / Unidade de Ensino o relatório final de
estágio;
XIV - informar à Instituição Concedente / Unidade de Ensino sobre possíveis alterações
na proposta de estágio;
XV - cumprir as normas do presente regulamento e demais normatizações relativas ao
Estágio Supervisionado Curricular Obrigatório do Curso de Matemática – Licenciatura
do IFC.
Art. 18. No Estágio Supervisionado Curricular Obrigatório I e III o acadêmico não
poderá assumir a docência no campo de estágio.
80
CAPÍTULO III – DA OPERACIONALIZAÇÃO DO ESTÁGIO SUPERVISIONADO
CURRICULAR OBRIGATÓRIO
Art. 19. Para operacionalização do Estágio Supervisionado Curricular Obrigatório é
necessário que se satisfaçam as seguintes condições:
Seção I – Da Matrícula
Art. 20. O acadêmico deverá estar regularmente matriculado nas disciplinas Estágio
Supervisionado I, II, III ou IV.
Seção II – Da Frequência
Art. 21. A frequência nas disciplinas Estágio Supervisionado I, II, III, IV, obedecerá aos
seguintes critérios:
I - a frequência exigida para os Estágios Supervisionados I, II, III, e IV, no campo de
estágio, será de 100% da carga horária, conforme disposto no cronograma das
respectivas disciplinas, para as atividades presenciais do Curso e Pré-projeto de
Estágio organizado pelo acadêmico sob a orientação e aprovação do Professor
Orientador de Estágio;
II - no estágio não há abono de faltas, excetuando-se os casos previstos no Regimento
Geral do IFC e na Resolução no51 de 17/12/2010 do Conselho Superior, que dispõe
sobre o Regime Especial de Exercício Domiciliar;
III - no caso de abono de faltas prevista no inciso anterior, o acadêmico deverá repor a
carga horária correspondente ao período de sua ausência, desde que esta reposição
seja estabelecida em acordo com o Professor Orientador de Estágio e a Instituição
Concedente / Unidade de Ensino, campo de estágio;
IV - a frequência do acadêmico em atividades na Instituição Concedente / Unidade de
Ensino, campo de estágio, será registrada em formulário próprio (Anexo VI), controlada
pelo Professor Supervisor de Estágio e registrada no diário de classe pelo(s)
professor(es) da disciplina de Estágio.
Seção III – Da Definição do Campo de Estágio
Art. 22. Os Estágios poderão ser realizados em estabelecimentos de ensino públicos
ou privados e do terceiro setor, em instituições de ensino regular e em diferentes
modalidades de ensino que possibilitem a execução da proposta pedagógica
programada pelo acadêmico.
Art. 23. Será permitida a realização de estágio nas instituições com as quais o IFC
mantém convênio ou, na medida do possível, no próprio local de trabalho do
acadêmico quando este já leciona.
Seção IV - Da Programação e da Duração
Art. 24. A programação de Estágio Supervisionado Curricular Obrigatório do Curso
Matemática - Licenciatura compreende um conjunto de atividades previstas no PPC,
81
planejadas pelo Professor Orientador, avalizadas pelo NDE e equipe integrante da
estrutura organizacional do estágio.
§ 1º. Os Estágios Supervisionados I e III poderão ser realizados em duplas, de acordo
com as normas deste regulamento.
§ 2º. Os Estágios Supervisionados II e IV poderão ser realizados em duplas, desde que
as atividades sejam elaboradas, acompanhadas e realizadas em tempo integral pela
dupla, de maneira ininterrupta, na qual cada estagiário cumpra a carga horária mínima
de intervenção na série/ano escolhido.
Art. 25. O Estágio Supervisionado Curricular Obrigatório do Curso Matemática –
Licenciatura é um espaço de aprofundamento teórico e prático de diferentes aspectos
da educação em matemática, devendo ser orientado por um professor do IFC e
corresponde às seguintes etapas, conforme o PPC:
I - 1ª Etapa: Estágio Supervisionado I - 60h – subdivididas em:
a) Orientações gerais e trocas de experiências entre os acadêmicos conforme plano
pedagógico de ensino.
b) Observação, em escolas, de turmas das séries finais do ensino fundamental,
acompanhado de estudo, análise e reflexão crítica do projeto pedagógico da escola, do
plano de ensino de matemática e análise do livro/material didático adotado pela
instituição concedente do estágio.
c) Organização do esboço do Pré-Projeto de docência. (Anexo VII).
II - 2ª Etapa: Estágio Supervisionado II - 150h – Nesta etapa o acadêmico realiza a
intervenção, preferencialmente em uma das turmas observadas na etapa I solidificando
conhecimentos teóricos adquiridos ao longo do curso e concretizando habilidades
profissionais no decorrer da própria atuação docente com orientações gerais e trocas
de experiências entre os acadêmicos. Planejamento, intervenção, produção escrita e
socialização.
III - 3ª Etapa: Estágio Supervisionado III - 60h – subdivididas em:
a) Orientações gerais e trocas de experiências entre os acadêmicos conforme plano
pedagógico de ensino.
b) Observação, em escolas, de turmas das séries do ensino médio, acompanhado de
estudo, análise e reflexão crítica do projeto pedagógico da escola, do plano de ensino
de matemática e análise do livro/material didático adotado pela instituição concedente
do estágio.
c) Organização do esboço do Pré-Projeto de docência. (Anexo VII).
IV - 4ª Etapa: Estágio Supervisionado IV - 150h – Nesta etapa o acadêmico realiza a
intervenção, preferencialmente em uma das turmas observadas na etapa III
solidificando conhecimentos teóricos adquiridos ao longo do curso e concretiza
habilidades profissionais no decorrer da própria atuação docente com orientações
gerais e trocas de experiências entre os acadêmicos. Planejamento, intervenção,
produção escrita e socialização.
Subseção I – Da Observação
82
Art. 26. A observação compreenderá conhecimento e levantamento da realidade
escolar, contando com coleta de dados/informações para intervenção pedagógica,
análise reflexiva da prática e produção escrita.
Subseção II – Do Planejamento
Art. 27. O acadêmico, sob acompanhamento e orientação do Professor Orientador de
Estágio, realizará período de observação na Instituição Concedente de Estágio/
Unidade de Ensino, com a finalidade de coletar dados para diagnóstico e elaboração
do Plano de Estágio.
Art. 28. O acadêmico elaborará seu Plano de Estágio considerando os Parâmetros
Curriculares Nacionais, a Proposta Curricular de Santa Catarina, o Projeto Político
Pedagógico da Instituição Concedente / Unidade de Ensino e/ou demais orientadores
curriculares e o apresentará na data especificada no cronograma do semestre letivo
submetendo-o à aprovação do Professor Orientador de Estágio.
Art. 29. Após aprovação do Professor Orientador de Estágio, o Plano de Estágio
deverá ser apresentado à Unidade de Ensino, que submete ao professor regente de
classe da instituição concedente de estágio, que emitirá o aceite para sua execução,
com antecedência de, no mínimo, uma semana.
Art. 30. O Planejamento do Estágio Supervisionado Curricular Obrigatório contemplará
as seguintes ações:
I - observação na instituição concedente de campo de estágio e elaboração da
produção escrita sob orientações do Professor Orientador de Estágio.
II - elaboração de Planos de aula obedecendo ao roteiro definido pelo professor da
disciplina de (Anexo VIII) e avalizado pelo NDE.
III - produção de material didático-pedagógico e de subsídios teórico-metodológicos
necessários à execução do Planejamento.
Subseção III – Da Intervenção
Art. 30. Entende-se por intervenção as atividades de planejamento, organização
didático-metodológica e efetivo exercício de docência.
Art. 31. O desenvolvimento da intervenção compreenderá a realização da prática
pedagógica em sala de aula (docência) a partir da coleta de dados e avaliação, como
processo, para a retroalimentação da docência.
Subseção IV – Da Produção Escrita
Art. 32. A produção escrita compreende o relatório e/ou artigo produzidos
individualmente ou em dupla, com registro e análise fundamentada das atividades de
estágio desenvolvidas em cada uma das etapas, com base nos resultados da
docência, discussão, análises e sínteses.
Art. 33. Os relatórios serão elaborados conforme roteiro estabelecido pelo professor da
disciplina de estágio (Anexo IX ou Anexo X) e avalizado pelo NDE do campus;
83
Art. 34. Ao término de cada etapa o acadêmico deverá entregar a produção escrita, de
acordo com cronograma, observando os procedimentos avaliativos constantes do PPE.
Art. 35. As produções escritas deverão atender as normas da (ABNT) e às orientações
metodológicas do IFC.
Parágrafo único. A entrega da produção escrita aprovada pelo professor orientador é
requisito para conclusão e aprovação nas respectivas etapas.
Subseção V – Da Socialização
Art. 36. A socialização do estágio acontecerá após a finalização dos estágios II e IV:
CAPÍTULO IV – DA REDUÇÃO DA CARGA HORÁRIA DO ESTÁGIO CURRICULAR
SUPERVISIONADO
Art. 37. A Resolução CNE/CP 02 de 19 de fevereiro de 2002, publicada em 4/3/2002,
assegura o direito da redução da carga horária do estágio curricular supervisionado até
o máximo de 200 horas para os que exerçam atividade docente regular na Educação
Básica.
Art. 38. Neste regulamento estabelece-se que o acadêmico do Curso de Matemática –
Licenciatura do IFC, poderá solicitar dispensa, via requerimento, das disciplinas:
I - 40% da intervenção no Estágio Supervisionado II, desde que exerça ou tenha
exercido, nos últimos 2 anos, a atividade de docência, na disciplina de Matemática, em
turmas de sexto, sétimo, oitavo ou nono anos do Ensino Fundamental, por um período
não inferior a dois anos letivos;
II - 40% da intervenção no Estágio Supervisionado IV, desde que exerça ou tenha
exercido, nos últimos 2 anos, a atividade de docência, na disciplina de Matemática, em
turmas do Ensino Médio, por um período não inferior a dois anos letivos.
III - A solicitação de dispensa deverá ser entregue, na forma de requerimento, junto à
secretaria acadêmica, que encaminha ao coordenador de curso, devidamente
documentada, conforme calendário acadêmico.
Art. 39. O acadêmico deverá anexar:
I - cópias autenticadas de documentos que comprovem o exercício da docência,
constando a nomenclatura da unidade curricular, série e período trabalhado;
II - cópia dos planos de aula, assinado pela coordenação pedagógica ou direção da
UE.
Art. 40. A coordenação do curso e orientador do estágio avaliarão a documentação e
emitirão parecer sobre o requerimento.
CAPÍTULO V – DA AVALIAÇÃO
Art. 41. A avaliação do Estágio Supervisionado Curricular Obrigatório configura-se
como elemento integrador da teoria e da prática e será realizado pelo professor da
disciplina de estágio nas etapas I e III e pelos professores orientadores de estágio e
84
professor regente de classe ou professor supervisor da instituição concedente do
estágio nas etapas II e IV.
Art. 42. A avaliação de cada etapa dar-se-á conforme indicado no PPC do curso de
Matemática – Licenciatura e conforme critérios definidos no PPE da disciplina de
Estágio Supervisionado.
CAPÍTULO VI - DAS DISPOSIÇÕES GERAIS
Art. 43. O roteiro do relatório dos estágios será definido pelo NDE e professores
envolvidos na equipe da estrutura organizacional do estágio.
Art. 44. As instituições concedentes do Estágio Supervisionado Curricular Obrigatório
serão definidas pela SDR a partir do convênio firmado, devendo ser aprovados os
campos de estágio a cada semestre pelo coordenador de estágio, com aprovação do
Colegiado de Curso e acompanhamento do NDE e professores envolvidos na equipe
da estrutura organizacional do estágio.
Art. 45. Os casos omissos nesse regulamento serão resolvidos, pelo Colegiado de
Curso, pela Coordenação do Curso, NDE do Curso Matemática - Licenciatura e
professores envolvidos na equipe da estrutura organizacional do estágio de cada
campus.
Rio do Sul, 2012.
85
ANEXO I
TERMO DE CONVÊNIO (SDR)
(CIEC)
TERMO DE CONVÊNIO (SDR)
(CIEC)
CONVÊNIO Nº _____
Termo de Convênio de Cooperação que entre si celebram o
Estado de Santa Catarina, através da SECRETARIA DE
ESTADO DA EDUCAÇÃO, e a _____________(nome da
IES)___________________________ com sede no Município de
____________________.
O Estado de Santa Catarina, através da Secretaria de Estado da Educação,
doravante denominada SECRETARIA, CGC nº 82.951328/0001-58, neste ato
representado pelo seu Secretário, Paulo Roberto Bauer, residente a Av. Trompowsky,
00300, ap. 601, centro, município de Florianópolis-SC, portador da C.I. Nº 2/R-488416,
expedida em 20/11/1974, e do CPF N° 293.970.579-88, e a UNIVERSIDADE
____________________, doravante denominada simplesmente ______________,
inscrita no CGC/MF sob o nº ________________, com sede no Campus
___________________, em _____________________, neste ato representada pelo
Pró-Reitor de Ensino de Graduação, Professor _____________________, RG nº
__________________, com a interveniência da Secretaria de Desenvolvimento
Regional de ___________, doravante denominada simplesmente SDR, CGC nº
______________,
neste
ato
representada
pelo
seu
secretário,
____________________, RG nº ______________, resolvem celebrar o presente
Termo de Convênio de Cooperação, de acordo com as seguintes cláusulas e
condições:
CLÁUSULA PRIMEIRA: DO OBJETO
O presente Termo de Convênio de Cooperação tem como objeto a regulamentação
das condições de realização de estágio supervisionado e prática de ensino dos cursos
da ___________ com base na Lei nº 6.494 de 07/12/77, alterada pela Lei n° 8.859 de
23/03/94 e artigo 82 da Lei nº 9.394 (LDB) de 20/12/96 e regulamentadas pelo Decreto
87.497 de 18/08/82, modificado pelos Decretos 89.467 de 21/03/84 e 2.080 de
26/11/96, bem como as Resoluções 01 e 02/02 do CNE que estabelecem as diretrizes
e regulamenta os Cursos de Formação dos Professores e a Portaria N/5, de
17.04.2008, que fundamenta a regulamentação da Prática de Ensino e Estágio
Supervisionado dos alunos do Ensino Superior.
86
I - Para fins deste Convênio, entende-se como Estágio Supervisionado e Prática de
Ensino as atividades assistidas, proporcionadas ao estudante para a sua formação
profissional docente em situações reais de vida e de trabalho ligadas à sua área de
formação.
II - Os estágios e as práticas de ensino, objeto deste convênio, tem caráter curricular e
obrigatório e se constituem em elemento essencial à diplomação do aluno, de acordo
com
a
legislação
vigente
aprovada
na
_____________
(nome
da
IES)___________________________ .
III - O Estágio Supervisionado e a Prática de Ensino terão a duração e carga horária
fixada de acordo com o previsto nos regulamentos internos dos cursos/áreas,
obedecida à legislação em vigor;
IV - O prazo de realização do Estágio Supervisionado e da Prática de Ensino poderá
ser ajustado de acordo com o calendário acadêmico em andamento mediante ciência e
anuência da instituição concernente do estágio.
CLÁUSULA SEGUNDA: DAS OBRIGAÇÕES DA SECRETARIA
A Secretaria, através da GERED, deverá:
I - Conceder campos de Estágio Supervisionado e de Prática de Ensino aos
acadêmicos da _____________(nome da IES)___________________________ em
suas Unidades de Ensino, a saber: Escolas, Colégios, Projetos ou Programas
Educacionais Regulares na Educação Infantil, Ensino Fundamental, Programas
Especiais como Educação de Jovens e Adultos, Educação Indígena, Educação
Especial e Ensino Médio de sua jurisdição, de acordo com as disposições deste
Convênio;
II - Informar semestralmente as vagas de estágio supervisionado e prática de ensino à
_____________(nome da IES)___________________________ disponíveis;
III - Incluir os acadêmicos nos projetos, trabalhos específicos e com metas previamente
estabelecidas com as Unidades de Ensino, supervisionadas pelo Órgão Regional de
Educação;
IV - Articular, orientar e acompanhar os acadêmicos na área de formação pretendida
que serão de responsabilidade: no Órgão Central, pela Diretoria de Educação Superior
e pela Diretoria de Educação Básica e Profissional; no Órgão Regional de Educação,
pela Supervisão de Educação Superior e pela Supervisão de Educação Básica e
Profissional e na Unidade de Ensino, pelo Responsável Pedagógico e pelos
Professores Regentes de Classes;
V - Informar à _____________(nome da IES)___________________________ através
da Unidade Concedente de Estágios o desempenho dos acadêmicos;
VI - Informar a _____________(nome da IES)___________________________ , para
ser substituído, o acadêmico que, por motivo de natureza técnica, administrativa ou
disciplinar, não for considerado apto a continuar suas atividades de estágio;
CLÁUSULA TERCEIRA:
IES)______________
DAS
OBRIGAÇÕES
DA _____________(nome
da
I - Encaminhar os acadêmicos às Unidades concedentes dentro das normas
estabelecidas pelas partes convenientes;
II - Firmar os Termos de Compromisso de Estágio (TCE), como interveniente, através
das respectivas Coordenadorias de Estágios dos Cursos;
87
III - Designar um professor supervisor responsável pela disciplina ou modalidade de
estágio;
IV - Encaminhar com antecedência, os programas, planos de ensino das disciplinas e
projetos de trabalho onde o Estágio Supervisionado ou a Prática de Ensino serão
desenvolvidos, às Unidades Concedentes de Estágio para ciência e concordância,
considerando a Proposta Curricular do Estado de Santa Catarina e o Projeto Político
Pedagógico da Unidade de Ensino;
V - Disponibilizar os relatórios finais do Estágio Supervisionado e da Prática de Ensino
às Unidades Concedentes e ao Órgão Regional de Educação, para ciência, consulta e
pesquisa;
VI - Efetuar Seguro de Acidentes pessoais para o acadêmico em estágio e ou prática
de ensino;
VII - Emitir certificado de formação em serviço para o Responsável Pedagógico e para
os Professores Regentes de Classe das Unidades Concedentes que participarem
como supervisores de estágios;
VIII - Promover a integração e o aperfeiçoamento dos professores das Unidades
Concedentes de estágio e de prática de ensino através de: cursos, seminários,
mostras, eventos e outras atividades;
IX - Promover Seminários de apresentação do trabalho desenvolvido durante o período
do estágio e de prática de ensino para disponibilizar em capacitações, proporcionando
a integração da ____________(nome da IES)_________________ com a Escola
Pública Estadual, objetivando a melhoria da qualidade do ensino da Educação Básica.
CLÁUSULA QUARTA: DAS OBRIGAÇÕES DA SDR
A SDR, através do Órgão Regional de Educação, obriga-se a:
I - Encaminhar e acompanhar os estagiários nos projetos e programas específicos
desenvolvidos nas Unidades de Ensino, com metas previamente estabelecidas e
acordadas com as Unidades de Ensino e com as IES;
II - Viabilizar a articulação entre a IES e a Unidade de Ensino para a realização do
estágio supervisionado e da prática de ensino;
III - Articular, com as IES, reuniões de trabalho para organizar o processo de
socialização do Estágio Supervisionado e da Prática de Ensino.
CLÁUSULA QUINTA: DO PRAZO E DA VIGÊNCIA
O presente convênio vigorará pelo período de 04 (quatro) anos, a contar da data de
sua assinatura, podendo ser prorrogado através de termo aditivo, com ciência das
partes.
CLÁUSULA SEXTA: RESCISÃO
A Secretaria de Estado da Educação e
_____________(nome da
IES)_______________________ poderão propor, a qualquer tempo, a rescisão do
presente Convênio se ocorrer inadimplemento de qualquer uma de suas cláusulas e
condições, pelas superveniências legais que tornem material, financeira e normalmente
inexequível, ou por mútuo consenso.
CLÁUSULA SÉTIMA: DAS DISPOSIÇÕES GERAIS
88
I- O Estágio Supervisionado e a Prática de Ensino não geram qualquer vínculo
empregatício dos acadêmicos com a Secretaria de Estado da Educação, conforme
artigo 4º da Lei nº 6.494, de 07 de dezembro de 1977.
CLÁUSULA SÉTIMA: DO FORO
Fica eleito o Foro da Comarca de Florianópolis, capital do Estado de Santa Catarina,
para dirimir questões oriundas do presente Convênio.
E, por assim estarem em pleno acordo, lavrou-se o presente instrumento em 03 (três)
vias de igual teor e forma, assinam as partes o presente Convênio na presença das
testemunhas identificadas.
Florianópolis_______________, de _______________ de 20 __.
________________________________
________________________________
(nome do secretário por extenso)
(nome representante da IES por extenso)
________________________________
________________________________
Secretário de Estado da Educação
Pró-Reitor de Ensino de Graduação de Santa
Catarina
___________________________________________________________
(nome do secretário por extenso)
Secretário de Estado de Desenvolvimento Regional
TESTEMUNHAS:
1 - ________________________________
CPF_________________________________
2 - _________________________________
CPF_________________________________
89
ANEXO II
TERMO DE COMPROMISSO
TERMO DE COMPROMISSO PARA REALIZAÇÃO DE ESTÁGIO CURRICULAR
OBRIGATÓRIO – ETAPAS I E III
Curso: Licenciatura em Matemática
Pelo presente instrumento é celebrado
o Termo de Compromisso de Estágio
Curricular Obrigatório, de acordo com
a Lei n.11.788 de 25 de setembro de
2008, com a Lei n.9394 de 20 de
dezembro de 1996 – Lei de Diretrizes e
Bases da Educação Nacional.
O INSTITUTO FEDERAL CATARINENSE – Campus Rio do Sul, situado na Estrada
do Redentor, n. 5665, Bairro Cantagalo – Rio do Sul/SC, inscrito no CNPJ/MF sob
n.10.635.424/0002-67, doravante denominada simplesmente INSTITUTO, neste ato
representado por sua Coordenadoria de Integração Escola Comunidade, e de outro
lado (nome da parte concedente) inscrita no CNPJ sob o n. _________________,
Inscrição Estadual n° __________________, localizada à _____________ na cidade
de _____________ doravante designada como CONCEDENTE e representada pelo
Sr. _________________, e o estudante _________________ CPF n. _____________,
R.G. n. ______________, matrícula n° _________, residente à Rua ______________,
____, Bairro __________, CEP ________-___, na cidade de ________-SC, doravante
simplesmente ESTAGIÁRIO, resolvem, de comum acordo, firmar o presente Termo de
Compromisso, na forma da Lei 11.788 de 25 de setembro de 2008, Lei n. 9.394 de 20
de dezembro de 1996 (LDB) Documentos Institucionais - Plano de Desenvolvimento
Institucional (PDI), Projeto Pedagógico Institucional (PPI), Regimento Geral de Estágio
do IFC, Regulamento de Estágio do IFC, Orientação Didática dos Cursos Superiores
do IFC, Projeto Pedagógico do Curso de Matemática - Licenciatura (PPC), as Diretrizes
para a realização de prática de ensino e estágio supervisionado de cursos de
licenciatura nas escolas de educação básica da rede pública estadual
(SED/DES/DEBP), conforme as cláusulas a seguir estabelecidas:
CLÁUSULA PRIMEIRA – OBJETIVOS
1 - O Estágio Curricular Obrigatório tem por objetivos:
I - proporcionar ao acadêmico a participação em situações de trabalho e experiências
de ensino e de aprendizagem visando a complementação da educação profissional
90
fundamentada pelo desenvolvimento de competências e habilidades (Artigo 5º
Regulamento Geral de Estágio do IFC);
II - promover a integração entre a realidade acadêmica e sócio-econômico-política
como forma de ampliar a qualificação do futuro profissional (Artigo 5º Regulamento
Geral de Estágio do IFC);
III - integrar o ensino com a realidade, possibilitando a vivência de conhecimentos
teóricos e práticos relacionada à sua formação acadêmica;
IV - oportunizar ao acadêmico estagiário, situações que possibilitem apresentar sua
visão de análise crítica e domínio do conhecimento específico, através da definição de
uma proposta de ação;
V - incentivar a criação e o desenvolvimento de métodos e processos inovadores,
tecnologias e metodologias alternativas, visando atingir as metas do ensino de
matemática.
VI - integrar atividades de ensino, pesquisa e extensão a partir do desenvolvimento das
temáticas observadas nos campos de estágio.
CLÁUSULA SEGUNDA – JORNADA DE ATIVIDADES
2 – A jornada de atividades do(a) ESTAGIÁRIO(A), será compatível com o seu horário
escolar e com o horário do(a) CONCEDENTE, desenvolvendo atividades em
consonância com sua linha de formação educativa profissional.
3 – O Estágio Curricular Obrigatório (etapa I e/ou III) será realizado na (nome da
instituição de ensino), no município de _________-SC e terá uma carga de duração
de 21 horas – de acordo com a disponibilidade da Unidade de Ensino concedente e
com organização do estagiário – ocorrendo entre as seguintes datas: __/__/20__ e
__/__/20__, podendo ser interrompido a qualquer momento, unilateralmente, mediante
comunicação escrita, feita com 5 dias de antecedência, e comunicada ao INSTITUTO
FEDERAL CATARINENSE – Campus Rio do Sul/SC, desde que observado o
Regulamento de Estágio Curricular Obrigatório do Curso de Matemática - Licenciatura
do INSTITUTO FEDERAL CATARINENSE – Campus Rio do Sul/SC.
4 – Constituem motivos para a interrupção automática do estágio, a constatação, por
parte da Instituição de Ensino, de irregularidades, ou o não cumprimento do
convencionado neste Termo.
5 – A duração mínima do Estágio Curricular Obrigatório é aquela definida pelo Projeto
Pedagógico do Curso.
CLÁUSULA TERCEIRA – REMUNERAÇÃO DO ESTAGIÁRIO E VÍNCULO
EMPREGATÍCIO
6 – De acordo com a Lei n. 11.788/08 o presente Termo visa ao Estágio Curricular
Obrigatório, não remunerado, sendo que nenhum valor, a qualquer título, será devido
pela CONCEDENTE.
7 – Nos termos do art. 3o da Lei n.11.788/08 o Estágio Curricular Obrigatório e o
Estágio não Obrigatório não geram vínculo empregatício de qualquer natureza,
ressalvado o disposto sobre a matéria na legislação previdenciária.
91
8 – O ESTAGIÁRIO(A), na vigência deste compromisso, compromete-se a observar as
normas de segurança bem como as instruções aplicáveis a terceiros e declara
concordar com as normas internas da Instituição concedente, conduzir-se dentro da
ética profissional e submeter-se ao acompanhamento e avaliação de seu desempenho.
CLÁUSULA QUARTA – PROGRAMA DE ATIVIDADES
9 – O Pré-projeto de Estágio de Docência do ESTAGIÁRIO(A) deve ser elaborado de
acordo com as partes envolvidas no processo, respeitando os horários e obrigações do
ESTAGIÁRIO(A) para com as partes envolvidas, que deverá cumprir a programação,
comunicando, em tempo hábil, qualquer impossibilidade de cumprimento.
10 - O Pré-projeto de Estágio de Docência do ESTAGIÁRIO(A), poderá sofrer
alterações, desde que com a anuência de todos os partícipes, desde que esteja
contemplado no Projeto Pedagógico do Curso e deverá conter, objetiva e
detalhadamente as competências a serem desenvolvidas pelo ESTAGIÁRIO(A),
visando a sua formação para a vida e o trabalho.
11 – O ESTAGIÁRIO(A) compromete-se a elaborar as produções escritas (relatório
e/ou artigo), apresentando-o à CONCEDENTE, após a conclusão do estágio.
CLÁUSULA QUINTA – OBRIGAÇÕES DA CONCEDENTE
12 – Cabe à CONCEDENTE:
a) Proporcionar ao ESTAGIÁRIO(A) o aprendizado de competências próprias da
atividade profissional e à contextualização curricular, objetivando o
desenvolvimento para a vida cidadã e para o trabalho, oferecendo instalações
adequadas que propiciem a realização de atividades de aprendizagem social,
profissional e cultural.
b) Oportunizar aos ORIENTADORES acesso ao local do estágio durante todo o
período de desenvolvimento das atividades desenvolvidas a partir do Pré-projeto
de Estágio de Docência.
c) Ter como Supervisor Responsável o Sr. (a) _______________, para
acompanhá-lo e supervisioná-lo.
d) Entregar, quando da finalização da realização do estágio, Ficha de frequência e
Ficha de Avaliação entregue pelo IFC – Campus Rio do Sul.
e) Zelar pelo cumprimento das cláusulas pactuadas no Termo de Compromisso e
Pré-projeto de Estágio de Docência.
f) Permitir que o(a) ESTAGIÁRIO(A) inicie seu estágio somente quando o Termo
de Convênio, Termo de Compromisso e o Pré-projeto de Estágio de Docência
estiverem devidamente assinadas por todas as partes envolvidas.
CLÁUSULA SEXTA– OBRIGAÇÕES DA INSTITUIÇÃO DE ENSINO
13 – Cabe à INSTITUIÇÃO, além das atribuições constantes nas Diretrizes para a
Realização de Prática como Componente Curricular (Prática de Ensino) e de Estágio
Supervisionado de Curso de Licenciatura nas Escolas de Educação Básica da Rede
Pública Estadual:
92
a) Celebrar o Termo de Compromisso com o(a) ESTAGIÁRIO(A) ou representante
legal e com a parte CONCEDENTE, indicando as condições de adequação do
estágio ao Projeto Pedagógico do Curso, à etapa e modalidade de formação do
ESTAGIÁRIO(A) e ao horário e calendário escolar.
b) Avaliar as instalações da parte CONCEDENTE do estágio e sua adequação à
formação cultural e profissional, bem como a segurança do(a) ESTAGIÁRIO(A).
c) Orientar o(a) ESTAGIÁRIO(A) sobre seguro de cobertura contra acidentes que
possam ocorrer no local de estágio, na forma da Lei.
d) Acompanhar a atuação do(a) professor(a) orientador, por ser este o responsável
pelo desempenho e avaliação das atividades do(a) ESTAGIÁRIO(A), na área do
Estágio Curricular Obrigatório.
e) Zelar pelo cumprimento do termo de compromisso, reorientando o(a)
ESTAGIÁRIO(A) para outro local, em caso de descumprimento de suas normas.
CLÁUSULA SÉTIMA – OBRIGAÇÕES DO(A) ESTAGIÁRIO(A)
16 – Cabe a(o) ESTAGIÁRIO(A), além das atribuições constantes nas Diretrizes para
a Realização de Prática como Componente Curricular (Prática de Ensino) e de Estágio
Supervisionado de Curso de Licenciatura nas Escolas de Educação Básica da Rede
Pública Estadual:
a) Envidar esforços para aplicar na prática os conhecimentos teóricos aprendidos
na atividade discente, bem como desenvolver as competências necessárias ao
seu futuro exercício profissional.
b) Preservar o patrimônio da CONCEDENTE, utilizando os meios e bens
disponibilizados por esta, de maneira responsável e ética e se responsabilizar
por quaisquer danos causados ao patrimônio da CONCEDENTE, seja por dolo
ou culpa, cabendo a(o) ESTAGIÁRIO(A) a imediata reparação do dano, sob
pena de rescisão do Termo de Comprometimento.
c) Informar imediatamente e por escrito à CONCEDENTE, qualquer fato que
interrompa, suspenda ou cancele sua matrícula, ficando o(a) ESTAGIÁRIO(A)
responsável por quaisquer despesas causadas pela ausência dessa informação.
d) Cumprir regularmente o horário do estágio estipulado, assim como a entrega
dos relatórios de atividades.
e) Ficar ciente de que, caso pratique ações contra o patrimônio ou funcionários da
CONCEDENTE, tais como furto, roubo ou vandalismo, será responsabilizado
pela imediata reparação, sob pena de rescisão unilateral do seu Estágio
Curricular Obrigatório, sem que isto o isente das responsabilidades civis e
criminais de seus atos.
CLÁUSULA OITAVA – DISPOSIÇÕES FINAIS
17 – O controle de frequência será realizado por meio de ficha de freqüência, conforme
modelo constante no regulamento de Estágio Supervisionado Curricular Obrigatório e
Prática como Componente Curricular (Prática de Ensino).
18 – Quando em razão da programação do estágio, fica o(a) ESTAGIÁRIO(A) sujeito à
despesa que normalmente não teria.
19 – E por estarem justos e de comum acordo, o presente Termo de Compromisso é
firmado em 3(três) vias de igual teor e forma, que vai assinado pelas partes, na
presença de testemunhas abaixo indicadas.
93
Rio do Sul, __ de ______ de 20__.
_______________________________________________
INSTITUIÇÃO DE ENSINO
_________________________________ _________________________________
CONCEDENTE
SUPERVISOR DO ESTAGIÁRIO
__________________________________
ESTAGIÁRIO
TESTEMUNHAS:
1 - ________________________________
CPF_________________________________
2 - _________________________________
CPF_________________________________
94
ANEXO III
TERMO DE COMPROMISSO PARA REALIZAÇÃO DE ESTÁGIO CURRICULAR
OBRIGATÓRIO – ETAPAS II E IV
TERMO DE COMPROMISSO PARA REALIZAÇÃO DE ESTÁGIO CURRICULAR
OBRIGATÓRIO – ETAPAS II E IV
Curso: Licenciatura em Matemática
Pelo presente instrumento é celebrado
o Termo de Compromisso de Estágio
Curricular Obrigatório, de acordo com
a Lei n.11.788 de 25 de setembro de
2008, com a Lei n.9394 de 20 de
dezembro de 1996 – Lei de Diretrizes e
Bases da Educação Nacional.
O INSTITUTO FEDERAL CATARINENSE – Campus Rio do Sul, situado na Estrada
do Redentor, n. 5665, Bairro Cantagalo – Rio do Sul/SC, inscrito no CNPJ/MF sob
n.10.635.424/0002-67, doravante denominada simplesmente INSTITUTO, neste ato
representado por sua Coordenadoria de Integração Escola Comunidade, e de outro
lado (nome da parte concedente) inscrita no CNPJ sob o n. _________________,
Inscrição Estadual n° __________________, localizada à _____________ na cidade
de _____________ doravante designada como CONCEDENTE e representada pelo
Sr. _________________, e o estudante _________________ CPF n. _____________,
R.G. n. ______________, matrícula n° _________, residente à Rua ______________,
____, Bairro __________, CEP ________-___, na cidade de ________-SC, doravante
simplesmente ESTAGIÁRIO, resolvem, de comum acordo, firmar o presente Termo de
Compromisso, na forma da Lei 11.788 de 25 de setembro de 2008, Lei n. 9.394 de 20
de dezembro de 1996 (LDB) Documentos Institucionais - Plano de Desenvolvimento
Institucional (PDI), Projeto Pedagógico Institucional (PPI), Regimento Geral de Estágio
do IFC, Regulamento de Estágio do IFC, Orientação Didática dos Cursos Superiores
do IFC, Projeto Pedagógico do Curso de Matemática - Licenciatura (PPC), as Diretrizes
para a realização de prática de ensino e estágio supervisionado de cursos de
95
licenciatura nas escolas de educação básica da rede
(SED/DES/DEBP), conforme as cláusulas a seguir estabelecidas:
pública
estadual
CLÁUSULA PRIMEIRA – OBJETIVOS
1 - O Estágio Curricular Obrigatório tem por objetivos:
I - proporcionar ao acadêmico a participação em situações de trabalho e experiências
de ensino e de aprendizagem visando a complementação da educação profissional
fundamentada pelo desenvolvimento de competências e habilidades (Artigo 5º
Regulamento Geral de Estágio do IFC);
II - promover a integração entre a realidade acadêmica e sócio-econômico-política
como forma de ampliar a qualificação do futuro profissional (Artigo 5º Regulamento
Geral de Estágio do IFC);
III - integrar o ensino com a realidade, possibilitando a vivência de conhecimentos
teóricos e práticos relacionada à sua formação acadêmica;
IV - oportunizar ao acadêmico estagiário, situações que possibilitem apresentar sua
visão de análise crítica e domínio do conhecimento específico, através da definição de
uma proposta de ação;
V - incentivar a criação e o desenvolvimento de métodos e processos inovadores,
tecnologias e metodologias alternativas, visando atingir as metas do ensino de
matemática.
VI - integrar atividades de ensino, pesquisa e extensão a partir do desenvolvimento das
temáticas observadas nos campos de estágio.
CLÁUSULA SEGUNDA – JORNADA DE ATIVIDADES
2 – A jornada de atividades do(a) ESTAGIÁRIO(A), será compatível com o seu horário
escolar e com o horário do(a) CONCEDENTE, desenvolvendo atividades em
consonância com sua linha de formação educativa profissional.
3 – O Estágio Curricular Obrigatório (etapas II e/ou IV) será realizado na (nome da
instituição de ensino), no município de _________-SC e terá uma carga de duração
de ___ horas diárias, no período (matutino, vespertino, integral) das __:__ até as __:__
totalizando __ horas semanais, com início em __/__/20__ e término em __/__/20__,
podendo ser interrompido a qualquer momento, unilateralmente, mediante
comunicação escrita, feita com 5 dias de antecedência, e comunicada ao INSTITUTO
FEDERAL CATARINENSE – Campus Rio do Sul/SC, desde que observado o
Regulamento de Estágio Curricular Obrigatório do Curso de Matemática - Licenciatura
do INSTITUTO FEDERAL CATARINENSE – Campus Rio do Sul/SC.
96
4 – Constituem motivos para a interrupção automática do estágio, a constatação, por
parte da Instituição de Ensino, de irregularidades, ou o não cumprimento do
convencionado neste Termo.
5 – A duração mínima do Estágio Curricular Obrigatório é aquela definida pelo Projeto
Pedagógico do Curso.
CLÁUSULA TERCEIRA – REMUNERAÇÃO DO ESTAGIÁRIO E VÍNCULO
EMPREGATÍCIO
6 – De acordo com a Lei n. 11.788/08 o presente Termo visa ao Estágio Curricular
Obrigatório, não remunerado, sendo que nenhum valor, a qualquer título, será devido
pela CONCEDENTE.
7 – Nos termos do art. 3o da Lei n.11.788/08 o Estágio Curricular Obrigatório e o
Estágio não Obrigatório não geram vínculo empregatício de qualquer natureza,
ressalvado o disposto sobre a matéria na legislação previdenciária.
8 – O ESTAGIÁRIO(A), na vigência deste compromisso, compromete-se a observar as
normas de segurança bem como as instruções aplicáveis a terceiros e declara
concordar com as normas internas da Instituição concedente, conduzir-se dentro da
ética profissional e submeter-se ao acompanhamento e avaliação de seu desempenho.
CLÁUSULA QUARTA – PROGRAMA DE ATIVIDADES
9 – O Pré-projeto de Estágio de Docência do ESTAGIÁRIO(A) deve ser elaborado de
acordo com as partes envolvidas no processo, respeitando os horários e obrigações do
ESTAGIÁRIO(A) para com as partes envolvidas, que deverá cumprir a programação,
comunicando, em tempo hábil, qualquer impossibilidade de cumprimento.
10 - O Pré-projeto de Estágio de Docência do ESTAGIÁRIO(A), poderá sofrer
alterações, desde que com a anuência de todos os partícipes, desde que esteja
contemplado no Projeto Pedagógico do Curso e deverá conter, objetiva e
97
detalhadamente as competências a serem desenvolvidas pelo ESTAGIÁRIO(A),
visando a sua formação para a vida e o trabalho.
11 – O ESTAGIÁRIO(A) compromete-se a elaborar as produções escritas (relatório
e/ou artigo), apresentando-o à CONCEDENTE, após a conclusão do estágio.
CLÁUSULA QUINTA – OBRIGAÇÕES DA CONCEDENTE
12 – Cabe à CONCEDENTE:
g) Proporcionar ao ESTAGIÁRIO(A) o aprendizado de competências próprias da
atividade profissional e à contextualização curricular, objetivando o
desenvolvimento para a vida cidadã e para o trabalho, oferecendo instalações
adequadas que propiciem a realização de atividades de aprendizagem social,
profissional e cultural.
h) Oportunizar aos ORIENTADORES acesso ao local do estágio durante todo o
período de desenvolvimento das atividades desenvolvidas a partir do Pré-projeto
de Estágio de Docência.
i) Ter como Supervisor Responsável o Sr. (a) _______________, para
acompanhá-lo e supervisioná-lo.
j) Entregar, quando da finalização da realização do estágio, Ficha de frequência e
Ficha de Avaliação entregue pelo IFC – Campus Rio do Sul.
k) Zelar pelo cumprimento das cláusulas pactuadas no Termo de Compromisso e
Pré-projeto de Estágio de Docência.
l) Permitir que o(a) ESTAGIÁRIO(A) inicie seu estágio somente quando o Termo
de Convênio, Termo de Compromisso e o Pré-projeto de Estágio de Docência
estiverem devidamente assinadas por todas as partes envolvidas.
CLÁUSULA SEXTA– OBRIGAÇÕES DA INSTITUIÇÃO DE ENSINO
13 – Cabe à INSTITUIÇÃO, além das atribuições constantes nas Diretrizes para a
Realização de Prática como Componente Curricular (Prática de Ensino) e de Estágio
Supervisionado de Curso de Licenciatura nas Escolas de Educação Básica da Rede
Pública Estadual:
f) Celebrar o Termo de Compromisso com o(a) ESTAGIÁRIO(A) ou representante
legal e com a parte CONCEDENTE, indicando as condições de adequação do
estágio ao Projeto Pedagógico do Curso, à etapa e modalidade de formação do
ESTAGIÁRIO(A) e ao horário e calendário escolar.
g) Avaliar as instalações da parte CONCEDENTE do estágio e sua adequação à
formação cultural e profissional, bem como a segurança do(a) ESTAGIÁRIO(A).
h) Orientar o(a) ESTAGIÁRIO(A) sobre seguro de cobertura contra acidentes que
possam ocorrer no local de estágio, na forma da Lei.
98
i) Acompanhar a atuação do(a) professor(a) orientador, por ser este o responsável
pelo desempenho e avaliação das atividades do(a) ESTAGIÁRIO(A), na área do
Estágio Curricular Obrigatório.
j) Zelar pelo cumprimento do termo de compromisso, reorientando o(a)
ESTAGIÁRIO(A) para outro local, em caso de descumprimento de suas normas.
CLÁUSULA SÉTIMA – OBRIGAÇÕES DO(A) ESTAGIÁRIO(A)
16 – Cabe a(o) ESTAGIÁRIO(A), além das atribuições constantes nas Diretrizes para
a Realização de Prática como Componente Curricular (Prática de Ensino) e de Estágio
Supervisionado de Curso de Licenciatura nas Escolas de Educação Básica da Rede
Pública Estadual:
f) Envidar esforços para aplicar na prática os conhecimentos teóricos aprendidos
na atividade discente, bem como desenvolver as competências necessárias ao
seu futuro exercício profissional.
g) Preservar o patrimônio da CONCEDENTE, utilizando os meios e bens
disponibilizados por esta, de maneira responsável e ética e se responsabilizar
por quaisquer danos causados ao patrimônio da CONCEDENTE, seja por dolo
ou culpa, cabendo a(o) ESTAGIÁRIO(A) a imediata reparação do dano, sob
pena de rescisão do Termo de Comprometimento.
h) Informar imediatamente e por escrito à CONCEDENTE, qualquer fato que
interrompa, suspenda ou cancele sua matrícula, ficando o(a) ESTAGIÁRIO(A)
responsável por quaisquer despesas causadas pela ausência dessa informação.
i) Cumprir regularmente o horário do estágio estipulado, assim como a entrega
dos relatórios de atividades.
j) Ficar ciente de que, caso pratique ações contra o patrimônio ou funcionários da
CONCEDENTE, tais como furto, roubo ou vandalismo, será responsabilizado
pela imediata reparação, sob pena de rescisão unilateral do seu Estágio
Curricular Obrigatório, sem que isto o isente das responsabilidades civis e
criminais de seus atos.
CLÁUSULA OITAVA – DISPOSIÇÕES FINAIS
17 – O controle de frequência será realizado por meio de ficha de freqüência, conforme
modelo constante no regulamento de Estágio Supervisionado Curricular Obrigatório e
Prática como Componente Curricular (Prática de Ensino).
18 – Quando em razão da programação do estágio, fica o(a) ESTAGIÁRIO(A) sujeito à
despesa que normalmente não teria.
99
19 – E por estarem justos e de comum acordo, o presente Termo de Compromisso é
firmado em 3(três) vias de igual teor e forma, que vai assinado pelas partes, na
presença de testemunhas abaixo indicadas.
Rio do Sul, __ de ______ de 20__.
_______________________________________________
INSTITUIÇÃO DE ENSINO
_________________________________ _________________________________
CONCEDENTE
SUPERVISOR DO ESTAGIÁRIO
__________________________________
ESTAGIÁRIO
TESTEMUNHAS:
1 - ________________________________
CPF_________________________________
2 - _________________________________
CPF_________________________________
100
ANEXO IV
FICHA DE AVALIAÇÃO FINAL
ESTÁGIO I, II, III e IV
FICHA DE ACOMPANHAMENTO DE ORIENTAÇÃO ESTÁGIO I, II, III e IV
Curso: Matemática - Licenciatura
Estagiário(a):
Área de Atuação: Séries finais do
Ensino Fundamental e Ensino Médio
(
) Nome do Professor(a)
Orientador(a):
_______________________________
(
) Nome do Professor(a) da
Disciplina
de
Estágio:_________________________
Local do Estágio:
Telefone para Contato:
( ) Estágio Supervisionado I
( ) Estágio Supervisionado II
( ) Estágio Supervisionado III
( ) Estágio Supervisionado IV
Carga horária total das atividades de orientação:
Rubrica
Data
Orientações Realizadas
do
professor
Rubrica
do
estagiário
Declaro para fins de comprovação de frequência que o(a) estudante supra citado
esteve presente às atividades de orientação, conforme especificado acima.
______________________
Assinatura do Professor
Data: __/__/____
__________________
Estagiário
_________________________
Professor Orientador
___________________
Coordenador do Curso
101
ANEXO V
FICHA DE AVALIAÇÃO REFERENTE À ORIENTAÇÃO ESTÁGIO I, II, III e IV
FICHA DE AVALIAÇÃO REFERENTE À ORIENTAÇÃO ESTÁGIO I, II, III e IV
Curso: Matemática - Licenciatura
Área de Atuação: ( ) Séries finais do
Ensino Fundamental / ( ) Ensino
Médio
Nome
do (
) Nome do Professor(a)
Estagiário(a):___________________
Orientador(a):
__________________________________ _______________________________
___
____
( ) Estágio Supervisionado I
( ) Nome do Professor(a) da
( ) Estágio Supervisionado II
Disciplina de
( ) Estágio Supervisionado III
Estágio:_________________________
( ) Estágio Supervisionado IV
___
Local do Estágio:
Telefone para Contato:
N.
Aspectos Avaliados
Nota (0 a
10)
1.
2.
Nota da Ficha de avaliação do professor supervisor da UE
Organização do esboço do Pré-Projeto ou do projeto de
docência (orientador atribui)
3. Relatório (orientador atribui)
4. Nota da observação da prática da docência na UE (orientador
atribui)
5. Socialização das atividades de estágio (professor da Disciplina
de Estágio atribui)
6. Artigo (Somente na Disciplina de Estágio IV) (orientador
atribui)
MÉDIA FINAL DO ESTÁGIO SUPERVISIONADO
Observações Gerais:
__________________
Estagiário
_________________________
Professores(as) da Disciplina de
Estágio
___________________
Coordenador do Curso
102
ANEXO VI
FICHA DE FREQUÊNCIA EM ATIVIDADES DE ESTÁGIO NA INSTITUIÇÃO
CONCEDENTE / UNIDADE DE ENSINO
FICHA DE FREQUÊNCIA EM ATIVIDADES DE ESTÁGIO NA INSTITUIÇÃO
CONCEDENTE / UNIDADE DE ENSINO
Curso: Matemática - Licenciatura
Área de Atuação:
( ) Séries finais
do Ensino Fundamental / ( ) Ensino
Médio
Nome
do(a) Nome
do(a)
Professor(a)
Estagiário(a):___________________
Supervisor(a):
_________________________________
______________________________
(
(
(
(
) Estágio Supervisionado I
) Estágio Supervisionado II
) Estágio Supervisionado III
) Estágio Supervisionado IV
Local do Estágio:
Nome do(a) Professor(a) da Disciplina
de Estágio:
Telefone para Contato:
Carga horária total das atividades de estágio:
Data
Síntese das Atividades Desenvolvidas
Horário
de
Entrada
Assinatura
Horário
do Professor
de
Supervisor
Saída
de Estágio
TOTAL DE HORAS
Carimbo e Assinatura do Responsável pela Instituição Concedente / Unidade de
Ensino:
Carimbo
_______________________________
Assinatura do Responsável pela Instituição Concedente / Unidade de Ensino
__________________
Estagiário(a)
_________________________
Professor(a) Supervisor
___________________
Coordenador(a) do
Curso
103
ANEXO VII
ESBOÇO DO PRÉ-PROJETO DE DOCÊNCIA
ESBOÇO DO PRÉ-PROJETO DE DOCÊNCIA
Curso: Matemática - Licenciatura
Nome do(a) Estagiário(a):
__________________________________
( ) Estágio Supervisionado I
( ) Estágio Supervisionado II
( ) Estágio Supervisionado III
( ) Estágio Supervisionado IV
Local do Estágio:
Área de Atuação:
( ) Séries finais do Ens. Fundamental
( ) Ensino Médio
Nome do(a) Professor(a) da Disciplina
de Estágio:_______________________
Nome
do(a)
Professor(a)
Orientador(a)____________________
Telefone para Contato:
Horário de Estágio:
Total Carga Horária Diária:
Área de Estágio:
Início do Estágio:
Total Carga Horária
Semanal:
Final do Estágio:
ESBOÇO DOS PRINCIPAIS CONHECIMENTOS/CONTEÚDOS* A SEREM
DESENVOLVIDOS NA INTERVENÇÃO
Proposta de Instrumentos de Avaliação**
a serem utilizados
Proposta de
Cronograma*
**
Levantamento dos
Recursos Didáticos a
serem utilizados****
104
Data: __/__/____
_________________________________
Estagiário(a)
_________________________________
Orientador do Estágio
_________________________________
Professor da Disciplina de Estágio
(*) Temáticas gerais de ensino e aprendizagem e sua possível distribuição nas aulas
previstas. Devem integrar ao que já vem sendo trabalhado na turma e devem
considerar os projetos da escola e os Documentos Curriculares oficiais (Parâmetros
Curriculares Nacionais, Proposta Curricular de Santa Catarina).
(**) Modalidades, instrumentos e critérios de avaliação possíveis de serem
empregadas durante a intervenção.
(***) Possibilidades de datas para a intervenção prática.
(****) Formas, métodos e técnicas possíveis de serem empregadas durante a
intervenção.
105
ANEXO VIII
ROTEIRO DO PLANO DE AULA
INDICADORES DE ORGANIZAÇÃO DO PLANO DE AULA
IDENTIFICAÇÃO
Escola:
Série/ano:
Disciplina:
Professor da Disciplina:
Professor Supervisor:
Estagiário(a):
Data: __/__/____
Turno:
Bimestre:
quantidade de aulas:
OBJETIVOS
No caso do plano de aula, devem indicar aquilo que os alunos deverão ser capazes de
fazer após as ações implementadas pelo professor naquela aula específica: o que eu
quero que meus alunos aprendam hoje? Que atitudes? Que habilidades ou
competências meus alunos devem desenvolver e/ou aprimorar?
Análise
Analisar
Calcular
Comparar
Contrastar
Criticar
Debater
Diferenciar
Distinguir
Examinar
Experimentar
Investigar
Aplicação
Avaliação Compreensão Conhecimento
Aplicar
Apreciar
Descrever
Demonstrar Aquilatar
Discutir
Empregar
Avaliar
Explicar
Esboçar
Calcular
Expressar
Ilustrar
Escolher
Identificar
Interpretar
Estimar
Localizar
Inventariar
Julgar
Narrar
Operar
Medir
Reafirmar
Praticar Selecionar
Revisar
Traçar
Validar
Traduzir
Usar
Valorar
Transcrever
Apontar
Assinalar
Citar
Definir
Escrever
Inscrever
Marcar
Relacionar
Registrar
Relatar
Sublinhar
Síntese
Coordenar
Conjugar
Construir
Criar
Enumerar
Esquematizar
Formular
Listar
Organizar
Planejar
Reunir
106
CONTEÚDOS
Indicar os assuntos selecionados e organizados em função da definição dos objetivos.
Os conteúdos não se restringem só aos conhecimentos de cada matéria. São na
verdade o conjunto de conhecimentos, habilidades, comportamentos organizados
didaticamente, tendo em vista a apreensão e aplicação pelos alunos em sua vida
prática.
METODOLOGIA
Indicar a ação docente e discente para alcançar os objetivos pretendidos. São
atividades, métodos e procedimentos selecionados com o intuito de facilitar a
aprendizagem.
MATERIAL DIDÁTICO
Indicar os recursos materiais utilizados para facilitar e motivar a aprendizagem. São
materiais didáticos, por exemplo: textos, cartazes, mapas, filmes, gravuras, fitas
gravadas, etc, dos quais o professor se serva para a aula.
AVALIAÇÃO
Explicar o modo como o aluno será avaliado, ou seja, quais as formas e instrumentos
utilizados para verificar o rendimento dos alunos, sempre em função dos objetivos a
serem atingidos. Expressar claramente os instrumentos de avaliação: testes,
exercícios, trabalhos de pesquisa, etc.
OBSERVAÇÕES
Relatar os principais acontecimentos, reflexões e avaliações sobre a aula.
BIBLIOGRAFIA
São os textos a partir dos quais os estudos serão realizados. Podem ser livros,
revistas, jornais, etc.
107
ANEXO IX
ROTEIRO DO RELATÓRIO DE ESTÁGIO I e III
INSTITUTO FEDERAL CATARINENSE
CAMPUS RIO DO SUL
Digite o número do estágio que
você está cursando.
RELATÓRIO DE ESTÁGIO SUPERVISIONADO ___
CURSO DE MATEMÁTICA - LICENCIATURA
NOME DO ACADÊMICO
(se realizado em dupla entregar
somente um relatório)
RIO DO SUL
2011
108
Instituto Federal Catarinense – Campus Rio do Suç
Sul
Educacional Leonardo Da Vinci
NOME DO(A) ACADÊMICO(A)
(se o estágio foi realizado em dupla, entregar somente um relatório)
RELATÓRIO DE ESTÁGIO SUPERVISIONADO __
CURSO DE MATEMÁTICA - LICENCIATURA
Digite o número do estágio que
você está cursando.
Relatório de Estágio ___ do curso de
Matemática - Licenciatura do Instituto
Federal Catarinense (IFC) Câmpus Rio
do Sul realizado na Unidade de Ensino
__________, requisito parcial para
conclusão da disciplina de Estágio
Supervisionado ____.
PROFESSOR ORIENTADOR:
RIO DO SUL
mm/aa
109
SUMÁRIO
1 espaço entre linhas - 1,5
1 INTRODUÇÃO ..................................................................................................
2 RELATO DA OBSERVAÇÃO ...........................................................................
3. CONTEXTUALIZAÇÃO HISTÓRICO-PEDAGÓGICA DA uE ..........................
3.1 CONDIÇÕES FÍSICAS E MATERIAIS DA UNIDADE DE ENSINO ................
3.2 CARACTERÍSTICAS BÁSICAS CORPO TÉCNICO, ADM E DOCENTE .......
3.3 A DINÂMICA DO COTIDIANO ESCOLAR ......................................................
3.4 PROJETO PEDAGÓGICO ..............................................................................
3.5 CARACTERÍSTICAS DO PROFESSOR DA TURMA .....................................
3.6 CARACTERÍSTICAS DA TURMA ...................................................................
3.7 ORGANIZAÇAO DO ESPAÇO FÍSICO...........................................................
3.8 ALTERNATIVAS .............................................................................................
4 CONSIDERAÇÕES FINAIS ..............................................................................
5 REFERÊNCIAS..................................................................................................
ANEXOS ...............................................................................................................
Para configuração do índice,
utilize fonte tamanho 12.
110
1 INTRODUÇÃO
Na introdução apresenta-se com clareza o que, onde e como foi realizado o
estágio. Ou seja, deve caracterizar resumidamente, o local, as pessoas envolvidas e as
circunstâncias gerais que cercam o desenvolvimento do estágio. Deve, também, conter
a importância do trabalho, sua finalidade (objetivos), os procedimentos adotados, suas
limitações (o que deixou de ser abordado), problemas surgidos (se for o caso).
Espaçamento entre linhas 1,5; texto
justificado.
Para os elementos textuais, a posição do
número da página será no canto
superior direito. Na primeira página, o
número não deve ser exibido.
111
2. RELATO DA OBSERVAÇÃO
Neste item, o acadêmico deverá relatar os dados da observação,
fundamentando teoricamente (conforme o roteiro de observação – Apêndice IX).
3. CONTEXTUALIZAÇÃO HISTÓRICO-PEDAGÓGICA DA UE
3.1 CONDIÇÕES FÍSICAS E MATERIAIS DA UNIDADE DE ENSINO
3.2 CARACTERÍSTICAS BÁSICAS CORPO TÉCNICO, ADM E DOCENTE
3.3 A DINÂMICA DO COTIDIANO ESCOLAR
3.4 PROJETO PEDAGÓGICO
3.5 CARACTERÍSTICAS DO PROFESSOR DA TURMA
3.6 CARACTERÍSTICAS DA TURMA
3.7 ORGANIZAÇAO DO ESPAÇO FÍSICO
3.8 ALTERNATIVAS
4. CONSIDERAÇÕES FINAIS
5. REFERÊNCIAS
ANEXOS
112
ANEXO X
ROTEIRO DO RELATÓRIO DE ESTÁGIO II e IV
INSTITUTO FEDERAL CATARINENSE
CAMPUS RIO DO SUL
Digite o número do estágio que
você está cursando.
RELATÓRIO DE ESTÁGIO SUPERVISIONADO ___
CURSO DE MATEMÁTICA - LICENCIATURA
NOME DO ACADÊMICO
(se realizado em dupla entregar
somente um relatório)
RIO DO SUL
2011
113
Instituto Federal Catarinense – Campus Rio do Suç
Sul
Educacional Leonardo Da Vinci
NOME DO(A) ACADÊMICO(A)
(se o estágio foi realizado em dupla, entregar somente um relatório)
RELATÓRIO DE ESTÁGIO SUPERVISIONADO __
CURSO DE MATEMÁTICA - LICENCIATURA
Digite o número do estágio que
você está cursando.
Relatório de Estágio ___ do curso de
Matemática - Licenciatura do Instituto
Federal Catarinense (IFC) Câmpus Rio
do Sul realizado na Unidade de Ensino
__________, requisito parcial para
conclusão da disciplina de Estágio
Supervisionado ____.
PROFESSOR ORIENTADOR:
RIO DO SUL
mm/aa
114
SUMÁRIO
1 espaço entre linhas - 1,5
1 INTRODUÇÃO ..................................................................................................
2 ASPECTOS REFLEXIVOS DA OBSERVAÇÃO ..............................................
3. RELATÓRIO DA INTERVENÇÃO ....................................................................
3.1 FUNDAMENTAÇÃO TEÓRICA
3.2 Apresentação do Plano de Aula - Aula 1.........................................................
3.2.1 ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA .........
3.2.2 AMOSTRA DE UM TRABALHO ...................................................................
3.3 Apresentação do Plano de Aula - Aula 2.........................................................
3.3.1 ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA ........
3.3.2 AMOSTRA DE UM TRABALHO ...................................................................
3.4 Apresentação do Plano de Aula - Aula 3.........................................................
3.4.1 ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA ........
3.4.2 AMOSTRA DE UM TRABALHO ...................................................................
3.5 Apresentação do Plano de Aula - Aula 4.........................................................
3.5.1 ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA ........
3.5.2 AMOSTRA DE UM TRABALHO ...................................................................
3.6 Apresentação do Plano de Aula - Aula 5.........................................................
3.6.1 ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA ........
3.6.2 AMOSTRA DE UM TRABALHO ...................................................................
4 ARTIGO (SOMENTE PARA O ESTÁGIO IV) ....................................................
5 CONSIDERAÇÕES FINAIS ..............................................................................
6 REFERÊNCIAS..................................................................................................
ANEXOS (PROJETO DE DOCÊNCIA) ................................................................
Para configuração do índice,
utilize fonte tamanho 12.
115
1. INTRODUÇÃO
Na introdução apresenta-se com clareza o que, onde e como foi realizado o
estágio. Ou seja, deve caracterizar resumidamente, o local, as pessoas envolvidas e as
circunstâncias gerais que cercam o desenvolvimento do estágio. Deve, também, conter
a importância do trabalho, sua finalidade (objetivos), os procedimentos adotados, suas
limitações (o que deixou de ser abordado), problemas surgidos (se for o caso).
Espaçamento entre linhas 1,5; texto
justificado.
Para os elementos textuais, a posição do
número da página será no canto
superior direito. Na primeira página, o
número não deve ser exibido.
2. ASPECTOS REFLEXIVOS DA OBSERVAÇÃO
Neste
item, o acadêmico
deverá
resgatar os principais aspectos
relacionados aos dados da observação (conforme o roteiro de observação entregue
pelo professor da disciplina de estágio supervisionado I e III).
É importante esse resgate para que o leitor tenha claro o que o levou a
organizar o planejamento da intervenção, considerando a realidade da turma, professor
e escola.
3 RELATÓRIO DA INTERVENÇÃO
Neste item o acadêmico deverá apresentar fundamentação teórica que
norteie sua intervenção/docência. O texto abaixo fornece informações sobre
fundamentação teórica.
116
De acordo com Martins (2006, p. 84) a fundamentação teórica,
É a ocasião de se relacionar a literatura mais relevante
sobre o assunto, estabelecendo um diálogo crítico com
diversos autores que escreveram sobre o tema em estudo. A
revisão bibliográfica [ou fundamentação teórica] procura
estabelecer o estado atual da questão e examinar as
diversas correntes teóricas sobre o assunto. Daí resulta a
escolha do marco teórico que será utilizado para orientar e
embasar o trabalho. Trata-se também de conceituar os
termos que são essenciais para a melhor compreensão do
trabalho. O objetivo da definição de termos é torná-los
claros, compreensivos, objetivos e adequados ao contexto
do trabalho.
Desse modo, na fundamentação teórica constarão idéias e discussões sobre
os temas tratados ao longo do relatório. Lembrando que se faz necessário o uso de
autores e/ou documentos que fundamentem as reflexões ao longo dessa seção.
Os autores e/ou documentos podem ser utilizados de forma direta (utilizando
palavras tiradas literalmente da obra do autor e/ou documento), ou de forma indireta
(quando a ideia é retirada do autor, porém a escrita é feita com a interpretação de
quem escreve no caso o acadêmico).
No caso de citações diretas de até três linhas, a citação permanece no
parágrafo. Exemplo:
De acordo com Martins (2006, p. 84) a fundamentação teórica, “É a ocasião
de se relacionar a literatura mais relevante sobre o assunto, estabelecendo um diálogo
crítico com diversos autores que escreveram sobre o tema em estudo”.
No caso de citações diretas com mais de três linhas, a citação se desprende
do parágrafo, na próxima linha a 4,0 cm da margem esquerda, como exemplo acima
escrito, no primeiro parágrafo dessa seção.
Quando os autores e/ou documentos são utilizados de forma indireta, faz-se
necessário o nome do autor entre parênteses, com letras maiúsculas, vírgula e ano.
Exemplo:
O conhecimento é social, histórico e culturalmente construído. Desde o
nascimento, os sujeitos constroem e adquirem significados, por meio do convívio
familiar, da relação com outras pessoas e pelo uso de objetos necessários a sua
sobrevivência (VYGOTSKY, 1991).
117
3.1. APRESENTAÇÃO DO PLANO DE AULA
AULA 1
Inserir plano de aula (modelo de plano de aula – ANEXO VIII)
3.1.1 ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA
Refere-se a reflexões sobre a aplicação de cada aula; se os objetivos foram
atingidos, os alunos participaram, como foi o seu desempenho, as atividades foram
adequadas. neste item também relacionar teoria e prática.
3.1.2 AMOSTRA DE UMA ATIVIDADE
Anexar neste item amostra de, pelo menos, uma atividade desenvolvida em sala
de aula, com a descrição e uma análise dos resultados da atividade.
3.2. APRESENTAÇÃO DO PLANO DE AULA
AULA 2
Inserir plano de aula (modelo de plano de aula – ANEXO VIII)
3.2.1. ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA
Refere-se a reflexões sobre a aplicação de cada aula; se os objetivos foram
atingidos, os alunos participaram, como foi o seu desempenho, as atividades foram
adequadas. neste item também relacionar teoria e prática.
3.2.2. AMOSTRA DE UMA ATIVIDADE
Anexar neste item amostra de, pelo menos, uma atividade desenvolvida em sala
de aula, com a descrição e uma análise dos resultados da atividade.
118
3.3. APRESENTAÇÃO DO PLANO DE AULA
AULA 3
Inserir plano de aula (modelo de plano de aula – ANEXO VIII)
3.3.1. ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA
Refere-se a reflexões sobre a aplicação de cada aula; se os objetivos foram
atingidos, os alunos participaram, como foi o seu desempenho, as atividades foram
adequadas. neste item também relacionar teoria e prática.
3.3.2. AMOSTRA DE UMA ATIVIDADE
Anexar neste item amostra de, pelo menos, uma atividade desenvolvida em sala
de aula, com a descrição e uma análise dos resultados da atividade.
3.4. APRESENTAÇÃO DO PLANO DE AULA
AULA 4
Inserir plano de aula (modelo de plano de aula – ANEXO VIII)
3.4.1. ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA
Refere-se a reflexões sobre a aplicação de cada aula; se os objetivos foram
atingidos, os alunos participaram, como foi o seu desempenho, as atividades foram
adequadas. neste item também relacionar teoria e prática.
3.4.2. AMOSTRA DE UMA ATIVIDADE
119
Anexar neste item amostra de, pelo menos, uma atividade desenvolvida em sala
de aula, com a descrição e uma análise dos resultados da atividade.
3.5. APRESENTAÇÃO DO PLANO DE AULA
AULA 5
Inserir plano de aula (modelo de plano de aula – ANEXO VIII)
3.5.1 ANÁLISE DA INTERVENÇÃO COM FUNDAMENTAÇÃO TEÓRICA
Refere-se a reflexões sobre a aplicação de cada aula; se os objetivos foram
atingidos, os alunos participaram, como foi o seu desempenho, as atividades foram
adequadas. neste item também relacionar teoria e prática.
3.5.2 AMOSTRA DE UMA ATIVIDADE
Anexar neste item amostra de, pelo menos, uma atividade desenvolvida em sala
de aula, com a descrição e uma análise dos resultados da atividade.
4. ARTIGO
TÍTULO DO ARTIGO
Nome do autor(a)
RESUMO: xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx.
Palavras-chave: xxxxxx, xxxxx, xxxxx.
1 INTRODUÇÃO (DO ARTIGO)
xxxxxxxxxxxxxxxxxxxxxxxxx
120
2 DESENVOLVIMENTO
xxxxxxxxxxxxxxxxxxxxxxxxxx.
Não esquecer do referencial teórico, com citações curtas e longas,
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
(AUTOR,
ano,
página).
xxxxxxxxxxxxxxxxxxx.
3 CONSIDERAÇÕES FINAIS (DO ARTIGO)
xxxxxxxxxxxxxxxxxx.
REFERÊNCIAS (DO ARTIGO)
SOBRE NOME DO AUTOR, Nome do Autor. Título: sub título. 2. ed. Local de
Publicação: Editora, Ano de publicação.
4. CONSIDERAÇÕES FINAIS (DA INTERVENÇÃO)
Apresenta-se uma análise sobre o estágio desenvolvido: informar resultados
e reflexões sobre o estágio. Também poderá ser relatada uma opinião pessoal sobre o
valor da experiência que acaba de realizar, apresentando recomendações e sugestões
referentes ao aperfeiçoamento de futuros trabalhos.
5. REFERÊNCIAS DO RELATÓRIO
121
ANEXOS
122
ANEXO XI
PAUTA DE INDAGAÇÕES
ROTEIRO DA PAUTA DE INDAGAÇÕES
Para os professores
1) onde e quando realizou sua formação inicial?
2) fez pós-graduação? Qual? Em que instituição de ensino?
3) quanto tempo de atuação na educação, como professor de matemática?
4) em sua opinião qual a importância da matemática no currículo escolar?
5) quantos professores de matemática tem essa escola?
6) qual sua opinião sobre as condições materiais (didático-pedagógicas) e físicas
(salas de aula, laboratórios) da escola?
7) quais são os fatores que mais interferem nas suas aulas?
8) como a gestão interage com o professores de matemática?
9) os alunos participam do processo de definição dos conteúdos a serem trabalhados?
Como esses conteúdos são organizados? Considera importante a construção coletiva
do planejamento dos conteúdos das disciplinas?
10) como ocorre a integração com os demais professores e conteúdos na escola?
11) como é desenvolvida sua formação continuada e permanente?
12) investe em livros pra atualizar o seu trabalho?
13) como realiza a avaliação dos alunos?
14) em sua opinião, como os alunos enfrentam as diferenças de competências durante
as aulas?
Para supervisores, orientadores e diretores
1) qual a importância da matemática na organização curricular e no contexto escolar?
2) qual o papel do seu setor na organização das atividades das aulas de matemática?
3) a escola tem PPP? (consultar e destacar informações importantes)
123
4) como são escolhidos os livros para as aulas de matemática?
124
ANEXO XII
PAUTA DE OBSERVAÇÕES
ROTEIRO DA PAUTA DE OBSERVAÇÕES
1. Contextualização histórico-pedagógica da Unidade de Ensino
Trata-se de uma contextualização dos diversos momentos históricos da unidade de
ensino com as teorias/concepções de aprendizagem, ensino, educação, escola,
avaliação estudadas no decorrer do curso. Através de entrevistas com alunos, pais,
professores, membros da comunidade, pesquisa em documentos escolares, será
possível perceber somo se deu e como se dá a materialização dessas concepções no
“chão” da unidade de ensino. A análise e sistematização das falas dos entrevistados e
dos documentos se darão com base nos autores que caracterizam as diversas
concepções acima referidas. Será possível perceber como os agentes educacionais
produziram e produzem suas práticas pedagógicas a partir de determinados
referenciais explícitos ou não; como os sistemas de ensino, através da implementação
de suas políticas educacionais – nunca epistemologicamente neutras – influenciaram e
influenciam o fazer pedagógico; como muitos professores, através de sua práxis,
conseguiram e conseguem subverter os paradigmas hegemônicos; como os alunos se
percebiam e se percebem participando desses momentos históricos.
2. Condições físicas e materiais da Unidade de Ensino
Deve-se estar atento para a localização geográfica da unidade de ensino e a
relevância
social
disso;
conservação
das
dependências/construção
(quantidade/qualidade das salas de aula, banheiros, cozinha, refeitório, área de lazer,
quadras esportivas etc., em relação à demanda); mobiliário (mesas, cadeiras, carteiras,
125
etc., e sua relação com as necessidades dos alunos, professores e funcionários);
biblioteca.
3. Características básicas do corpo técnico, administrativo e docente
Relação entre a quantidade e necessidade de funcionários, professores e bolsistas;
características dos serviços prestados; nível de formação escolar de cada um dos
segmentos de trabalhadores e a repercussão disso na sua pratica diária.
4. A dinâmica do cotidiano escolar
Esse item é de extrema relevância. As informações poderão ser obtidas através de
entrevistas com pessoas ligadas ao cotidiano da unidade de ensino. Mas a melhor
maneira de perceber a dinâmica do cotidiano escolar é a observação e o contato com
as pessoas envolvidas. Deve-se estar atento ao funcionamento da escola como um
todo. Na secretaria e direção, observar e descrever os trâmites administrativos e
burocráticos básicos como a admissão de alunos, transferências, confecção de
boletins,
arquivamento
de
dados,
emissão
de
certificados/diplomas,
admissão/substituição de professores, fichas funcionais, relação da direção com a
comunidade, professores, funcionários e alunos, confecção do horário das aulas,
dentre outros. No intervalo das aulas, perceber as relações dos alunos entre si e com
os professores, funcionários e direção. Conversar com os especialistas e professores
sobre o seu trabalho e comparar com as impressões dos alunos. Assistir a, pelo
menos, uma reunião pedagógica, um conselho de classe, uma reunião de pais para
analisá-los. Prestar atenção às relações de poder no interior da escola (poder
público/direção,
escola/comunidade,
direção/professores,
direção/alunos,
professores/alunos, alunos/alunos, APP com a direção/professores/alunos).
5. Projeto Pedagógico
Perceber como foi ou está sendo o processo de elaboração do projeto pedagógico,
como foi/é a participação da comunidade escolar no processo; como é implementado o
projeto no dia-a-dia; qual a concepção norteadora implícita ou explícita; que tipos de
avanços e/ou retrocessos são possíveis identificar no projeto; qual a relação entre o
126
que está escrito e o que efetivamente é vivenciado no cotidiano escolar. Qual a relação
do planejamento das aulas de matemática com o projeto pedagógico.
6. Caracterização do professor da turma
Formação. Maneira como atua em sala de aula. Relacionamento com os estudantes.
7. Planejamento
Existe? Como ele é realizado, diariamente, semanalmente, anualmente? Pelo
professor com planos de aula? Qual é o referencial? Observa o Projeto PolíticoPedagógico? Qual a importância real do planejamento para as aulas?
8 Caracterização da turma
Número de estudantes, faixa etária, religião, saúde, lazer, condições de moradia,
constituição familiar, nível socioeconômico, número de irmãos, quantos componentes
da família trabalham, nível de escolaridade da família. Obs.: fazer uma média desses
dados.
9. Como está organizado e estruturado o espaço físico na unidade de ensino
Qual o material didático-pedagógico em matemática existente para os estudantes, há
laboratório de matemática ou outros utilizados nas aulas de matemática? TV,
retroprojetor, tamanho da sala.
8. Alternativas
Quais são as alternativas que os(as) professoras buscam para resolver as questões
dos limites em relação a espaço físico, falta de material pedagógico, número excessivo
de estudantes? Como se Sá a inclusão de estudantes?
Observações
127
Este roteiro tem por finalidade apenas apontar alguns dos elementos que podem
contribuir na constituição do relatório de observação do cotidiano escolar. Muitas
outras questões poderão surgir no momento do contato com a realidade, as quais
deverão ser cuidadosamente anotadas. O texto que resultará desse processo de
investigação será de extrema importância para todos os momentos da prática. A partir
dele surgirão questões que poderão servir de base para elaboração do planejamento
da intervenção/prática de ensino e um projeto de pesquisa. Além disso, este texto
comporá um dos itens obrigatórios do relatório final de estágio. Por isso, quanto mais
bem elaborado ele for, menor será o trabalho posterior.
e-mail do(a) professor(a) – [email protected]
128
CARTA DE APRESENTAÇÃO
Rio do Sul, __ de ______ de 201_.
Da Coordenação de Estágios do IFC – Campus Rio do Sul
À Direção da Escola (nome da escola)
Senhor(a) Diretor(a):
Temos a satisfação de apresentar o(a) acadêmico(a) (nome do acadêmico)
do Curso de (nome do curso) e solicitar a colaboração de Vossa Senhoria no sentido
de recebê-lo a fim de realizar a atividade referente à (Prática de Ensino) da Disciplina
de (nome da disciplina) ou (Estágio Supervisionado I).
O(a) Acadêmico(a) frequentará o estabelecimento dirigido por Vossa
Senhoria durante o primeiro semestre de 2011.
Agradecemos vossa valiosa colaboração e expressamos nosso apreço e
consideração.
Atenciosamente,
___________________________
(assinatura)
Coordenação de Estágios